加严试验方法的实质是将成败型产品置于相对实际条件更严酷的环境/载荷下进行试验,通过“降低”其可靠性指标要求来实现样本量的减小,进而利用加严条件下的试验结果推断正常条件下的可靠性指标[6]。该方法的关键是实现原可靠性指标与加严条件下可靠性指标的转换,对于结构类产品来说,转换的基础即是应力-强度干涉模型[7-9]。但已有的研究是应力与强度独立条件下的加严转化方法,未考虑应力与强度相关的情况。
对于特定航天器结构的可靠性设计与验证问题,应力与强度独立假设条件下的分析结果往往具有一定的近似性。部分场合下的结构可靠性分析应当考虑变量间的相关关系及其相关程度。因此,研究应力与强度间可能存在的相关性对加严试验中试验样本量大小的影响具有重要实际意义。
本文基于传统加严试验的思想,结合相关性应力-强度干涉模型,研究加严条件下的结构可靠性验证问题。
1 基于Copula的相关性分析 对于一些特殊的结构产品(如飞行器舵面等),自身结构强度与所受载荷应力间有时并不满足独立性条件,即二者存在典型的共载荷相关性,如零件的许用载荷(强度Δ)通常会随着零件尺寸参数的增大、表面状况良好等因素而增大,而零件所受的应力S则会随之减小[10]。由于Copula函数在刻画变量间相关关系时有很多优越性质,如其边缘分布灵活、形式多样等,故引入Copula函数研究应力与强度间的相关性对加严试验验证方案的影响。
1.1 Copula相关应力-强度干涉模型 若应力与强度之间的相关结构为Copula函数Cθ(u, v),θ为模型参数,应力S和强度Δ的累积分布函数分别为F(s)和G(δ),则使得对于任意的应力S和强度Δ有
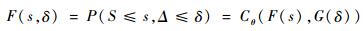 | (1) |
式中:F(s, δ)为应力S和强度Δ的联合分布函数;u=F(s),v=G(δ)。
根据二维概率密度函数可得相关性干涉下的可靠度模型为[11]
 | (2) |
式中:f(s, δ)为应力S和强度Δ的联合概率密度函数;f(s)为应力S的概率密度函数; g(δ)为强度Δ的概率密度函数。该模型是考虑应力、强度相关情况下加严试验验证的基础。
1.2 数据相关性分析和Copula模型选择 在利用成败型加严试验方法进行新的结构产品可靠性验证时,为了得出较为正确的可靠性验证结果,首先应根据研究者的理论知识和实践经验对结构产品的应力和强度做出定性的相关性分析,在相关性不可忽略的情况下,有必要对历史类似的结构产品测试得到的应力、强度数据做定量的相关性分析,在确定相关性的定量指标后再进行原可靠性指标与加严条件下可靠性指标的转化。
应力、强度数据的经验分布函数散点图可用于相关性的初步分析,并指导Copula函数的选择。如通过散点图发现数据之间存在明显的尾部相关性,那么Gumbel Copula、Clayton Copula及Frank Copula可以作为待选Copula函数[12-14]。
Copula函数的进一步选择可先通过参数估计得到Copula函数的具体表达式,再通过计算Copula函数和经验分布函数的的平方欧氏距离选择合适的Copula函数,距离越小,Copula函数的拟合程度越好。
2 考虑相关性的加严试验评定模型 由于本文目的在于验证应力和强度的相关性对加严试验样本量的影响,故以Clayton Copula函数为例描述应力和强度之间的相关结构,并在应力和强度均服从正态分布时,即S~N(μs, σs),Δ~N(μδ, σδ),建立考虑相关性的加严试验评定模型。
2.1 模型系数定义 为实现原可靠性指标与加严条件下可靠性指标的转化并建立加严试验评定模型,需先定义相关的模型系数。
1) 加严系数
加严系数为应力在加严试验条件下均值μs′与实际使用条件下均值μs的比值。
 | (3) |
2) 变差系数
变差系数为标准差相对于均值大小的相对量,具体有强度(应力)变差系数,其为强度(应力)标准差与强度(应力)均值的比值。
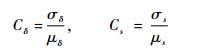 | (4) |
3) 生存系数
生存系数为强度均值μδ与应力均值μs的比值。比值越大,产品生存裕度越大,即
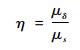 | (5) |
2.2 恒加严条件下的评定模型 Clayton Copula函数的形式为
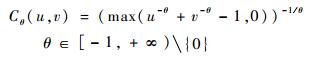 | (6) |
参数θ与Kendall秩相关系数τ(变量间的相关性度量指标)的关系为
 | (7) |
可知当θ→-1时,变量关系趋于完全负相关;当θ→0时,变量关系趋于独立;当θ→+∞时,变量趋于完全正相关,因此下文称θ为相关程度参数。相关程度参数可基于材料基础数据通过有限元仿真产生的应力、强度数据进行极大似然估计得到。
由式(2)~式(6) 可得加严条件下的可靠度为
 | (8) |
式中:?()为标准正态概率密度函数;Φ()为标准正态分布函数。
式(8) 可记为η和k的函数,即R=f(η, k),当k一定时,可推导R为η的严格单调递增函数。特别地,当k=1时,即为结构产品在实际应力下的可靠度R=f(η, 1)。若在置信水平1-α下,可靠度的下限值要求达到RL,则有
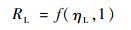 | (9) |
于是有
 | (10) |
若加严条件确定(k>1),则可求解得到加严条件下要求的可靠度下限RLH为
 | (11) |
在置信水平1-α时,验证考虑相关性的结构可靠性所需的加严条件无失效试验样本量n为
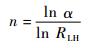 | (12) |
2.3 变加严条件下的评定模型 由于设计、制造等环节的影响,产品间必然存在一定的个体差异,因此可以考虑为每个受试产品选取不同的加严应力条件,从而提高结果的准确度[15]。变加严系数定义为
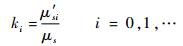 | (13) |
即有
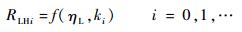 | (14) |
类似有
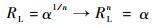 | (15) |
满足无失效结构验证试验样本量为n,可得
 | (16) |
采用循环计算法,当其首次接近α时,即得到了当前的无失效试验样本量n。
3 案例分析 承受大机动过载的某型飞行器关键部位结构采取了可靠性设计,现需试验验证在应力均值为μs=30 MPa,置信度1-α=0.9下,可靠度置信下限是否满足设计要求RL=0.999。
3.1 相关条件下加严试验样本量的确定方法 若根据相关实践经验定性分析得到该结构产品所受应力和自身强度之间可能存在某类相关性,并通过类似产品历史数据定量分析得到应力变差系数Cs=0.15,强度变差系数Cδ=0.1,相关程度参数的极大似然估计为:θ=-0.36。
1) 恒加严条件
根据式(8),通过数值计算可得到不同相关程度参数θ下可靠度R与生存系数η间的关系,如图 1所示。
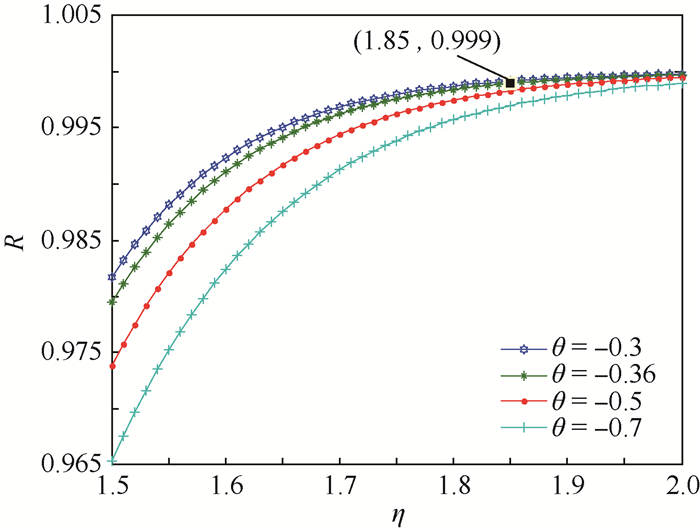 |
| 图 1 不同θ下可靠度-生存系数变化 Fig. 1 Variation of reliability-survival coefficient with different θ |
| 图选项 |
由图 1可得,θ=-0.36时生存系数的下限值为
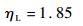 |
若取加严系数k=1.2,由式(11) 可得恒加严条件下的可靠度置信下限为
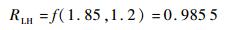 |
由式(12) 可得所需的试验样本量为
 |
2) 变加严条件
为了简化计算又不失一般性,令加严系数为递增等差序列:
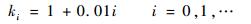 |
由式(14) 与式(16),经迭代计算,可得变加严条件下的试验样本量为
 |
式中:inf表示下确界。
这里试验样本量相对于恒加严条件减少了,这是因为变加严的平均加严程度kmean大于恒加严的加严程度,即
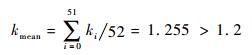 |
3.2 应力强度的相关性对加严试验样本量的影响 应力与强度独立时的加严试验方法类似于相关时的情形,这里不再赘述。由相关计算得到了应力与强度独立时的不同加严条件及不同可靠度下限指标下的试验样本量,并将其与相关的情形作进行对比(部分),如表 1所示,其中置信度1-α=0.9,θ=-0.36。
表 1 独立与相关情况下试验样本量的比较 Table 1 Comparison of test sample size between independent and correlative conditions
| k | RL=0.998 | RL=0.996 | RL=0.994 | |||||
| 相关 | 独立 | 相关 | 独立 | 相关 | 独立 | |||
| 1.2 | 97 | 64 | 57 | 39 | 41 | 29 | ||
| 1.3 | 39 | 24 | 24 | 16 | 18 | 13 | ||
| 1.4 | 19 | 11 | 13 | 8 | 10 | 7 | ||
| 1.5 | 10 | 6 | 7 | 5 | 6 | 4 | ||
表选项
此外,为进一步考察应力与强度的相关性对样本量的影响,在置信度1-α=0.9,可靠度下限RL=0.999,加严程度k=1.2的条件下,给出了试验样本量随相关程度参数θ变化的曲线,不失一般性,取θ∈[-1, 1]\{0}作为研究范围,θ=0即为独立情形时的试验样本量,如图 2所示。
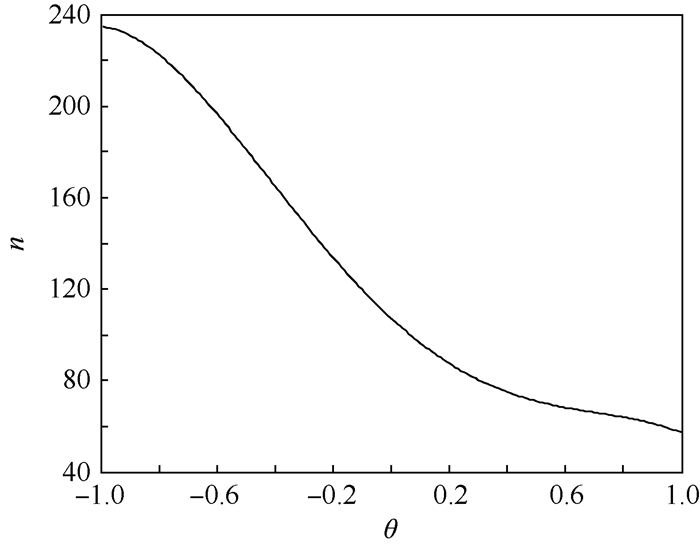 |
| 图 2 试验样本量与相关程度参数的关系 Fig. 2 Relationship between test sample size and correlation coefficient |
| 图选项 |
从表 1和图 2可以看出,当应力与强度呈负相关时,一方面试验样本量要多于同样加严条件下应力与强度独立时的试验样本量,另一方面,随着负相关程度的减弱,试验样本量逐渐减少;当应力与强度呈正相关时,一方面试验样本量要少于同样加严条件下应力与强度独立时的试验样本量,另一方面,随着正相关程度的增强,试验样本量逐渐减少。
4 结论 1) 本文建立了可描述应力与强度相关性的加严可靠性验证试验条件与试验样本量确定方法,可通过Copula函数的选择及参数的求解来判定和度量应力与强度间的相关特性及大小。
2) 当应力与强度呈负相关时,试验样本量多于相同加严条件下独立时的试验样本量,且随着负相关程度的减弱,试验样本量逐渐减少。
3) 当应力与强度呈正相关时,试验样本量少于相同加严条件下独立时的试验样本量,且随着正相关程度的增强,试验样本量逐渐减少。
参考文献
| [1] | 温玉全, 洪东跑, 王玮. 基于试验熵的火工品可靠性评估理论与方法研究[J].爆炸与冲击, 2007, 27(6): 553–556. WEN Y Q, HONG D P, WANG W. Study on theory and method of reliability assessment of explosive initiator based on testing entropy[J].Explosion and Shock Waves, 2007, 27(6): 553–556.DOI:10.11883/1001-1455(2007)06-0553-04(in Chinese) |
| [2] | 荣吉利, 白美, 刘志权. 加严条件下火工机构可靠性评估方法[J].北京理工大学学报, 2004, 24(2): 117–120. RONG J L, BAI M, LIU Z Q. Reliability assessment of pyrotechnical devices under rigorous conditions[J].Transactions of Beijing Institute of Technology, 2004, 24(2): 117–120.(in Chinese) |
| [3] | 刘智洋, 刘鲁, 黄敏. 可靠性增长的单调约束模型[J].北京航空航天大学学报, 2009, 35(9): 1104–1107. LIU Z Y, LIU L, HUANG M. Monotone restriction model of reliability growth evaluation[J].Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(9): 1104–1107.(in Chinese) |
| [4] | SCHICK G J, DRNAS T M.Bayesian reliability dmonstration[M]//HENKE M, JAEGER A, WARTMANN R, et al.Proceedings in operations research.Heidelberg:Physica-Verlag HD, 1972:92-102. |
| [5] | 卓洛托夫А А, 季托夫М И. 空间运载器的可靠性保证[M]. 王廼斌, 译. 北京: 宇航出版社, 1996: 17-24. 3ОЛОТОВ А А, ТИТОВ М И.Reliability ensures for the space vehicles[M].WANG N B, translated.Beijing:China Astronautic Publishing House, 1996:17-24(in Chinese). |
| [6] | 荣吉利, 张涛. 航天火工机构可靠性的强化试验验证方法[J].宇航学报, 2013, 30(6): 2426–2430. RONG J L, ZHANG T. Reliability validation on spacecraft pyrotechnical devices using the hardened test method[J].Journal of Astronautics, 2013, 30(6): 2426–2430.(in Chinese) |
| [7] | 马斌捷, 张俊华. 已知强度和载荷变差系数的结构可靠性分析[J].机械强度, 1994, 16(1): 1–6. MA B J, ZHANG J H. The structural reliability analysis for known variation coefficients of strength and load[J].Journal of Mechanical Strength, 1994, 16(1): 1–6.(in Chinese) |
| [8] | 荣吉利, 宋乾强. 正态应力-正态强度下可靠度精确置信下限[J].兵工学报, 2015, 36(2): 332–336. RONG J L, SONG Q Q. The exact lower confidence limit of reliability for normal stress and normal strength[J].Acta Armamentarii, 2015, 36(2): 332–336.(in Chinese) |
| [9] | SUN Y, MA L, MORRIS J. A practical approach for reliability prediction of pipeline systems[J].European Journal of Operational Research, 2009, 198(1): 210–214.DOI:10.1016/j.ejor.2008.07.040 |
| [10] | 唐家银, 何平, 陈崇双. 相关性失效机械系统的可靠性分析方法[M].北京: 国防工业出版社, 2014: 15-48. TANG J Y, HE P, CHEN C S. The reliability analysis method for mechanical system with relational failure[M].Beijing: National Defence Industry Press, 2014: 15-48.(in Chinese) |
| [11] | 唐小松, 李典庆, 周创兵, 等. 联合分布函数构造的Copula函数方法及结构可靠度分析[J].工程力学, 2013, 30(12): 8–17. TANG X S, LI D Q, ZHOU C B, et al. Modeling bivariate distribution using Copulas and its application to component reliability analysis[J].Engineering Mechanics, 2013, 30(12): 8–17.(in Chinese) |
| [12] | WU X Z. Modelling dependence structures of soil shear strength data with bivariate copulas and applications to geotechnical reliability analysis[J].Soils and Foundations, 2015, 55(5): 1243–1258.DOI:10.1016/j.sandf.2015.09.023 |
| [13] | MICHIELS F, DE SCHEPPER A. A new graphical tool for copula selection[J].Journal of Computational and Graphical Statistics, 2013, 22(2): 471–493.DOI:10.1080/10618600.2012.672080 |
| [14] | NELSEN R B. An introduction to copulas[M].Berlin: Springer, 2010: 157-222. |
| [15] | 王鹏, 杜志明. 变加严系数的加严试验方法[J].质量与可靠性, 2007, 130(4): 24–28. WANG P, DU Z M. The hardened test method considering the changing hardened cofficient[J].Quality and Reliability, 2007, 130(4): 24–28.(in Chinese) |
