航天器电池阵供电能力受太阳光入射角、表面污染、阴影遮挡、温度等影响[6-8]。Rausehenbach[1]提出了一种遮挡率法对大规模太阳电池阵供电能力进行计算;马世俊[2]提出了一种光电转换率法对太阳电池阵最大输出功率进行估算;NASA格伦研究中心Delleur等[9-10]针对国际空间站电源系统研制了SPACE(Station Power Analysis for Capability Evaluation)系统,以太阳电池片中心点代表整片,忽略电池片部分遮挡,计算太阳电池阵供电能力,并对航天员出舱更换电池阵分流调节器过程中太阳电池阵的供电进行了预计,为航天员出舱维修安全性分析提供了支持,该方法忽略了电池片部分遮挡,累积误差较大;张臻等[11]通过Saber软件仿真和实验对固定遮挡情况下的太阳电池片和电池组件供电特性进行了分析,并对旁路二极管的影响进行了分析;翟载腾等[12]、张忠政[13]基于太阳电池一般电流模型,利用开路点、短路点、最大功率点数据,通过微分求导计算了电池片伏安模型参数,并利用Maple软件的LambertW函数对伏安模型方程进行了显示表达;Mahmoud[14]、Ramaprabha[15]等对太阳电池理论模型进行简化,并利用MATLAB搭建了仿真模型进行验证。以上方法均无法根据航天器在轨实际光照、温度、遮挡对大规模太阳电池阵供电性能进行动态分析。
本文以太阳电池片理论模型为基础,提出了一种航天器太阳电池阵供电能力的计算方法。该方法根据一组标准测试条件(STC)下的电池片测试数据以及在轨实际光强和温度得到其在轨伏安特性,并利用基尔霍夫定律推导带旁路二极管和隔离二极管的电池阵的伏安模型。仿真试验表明,本文方法可以计算航天器入轨后任意光强、温度和遮挡阴影下的旁路二极管和隔离二极管的通断、压降情况,可精确计算太阳电池阵伏安特性。
1 太阳电池阵供电模型 太阳电池阵供电能力计算原理如图 1所示。首先,利用一组标准测试条件下的太阳电池片测试数据建立电池片伏安模型,并利用在轨光强、温度、遮挡修正模型参数得到电池片在轨伏安模型;然后,结合隔离二极管模型、旁路二极管模型以及电池阵电路建立电池阵伏安模型,即可根据母线电压计算电池阵输出电流。
 |
| 图 1 太阳电池阵供电能力计算流程 Fig. 1 Calculating process of solar array's power supply capability |
| 图选项 |
1.1 太阳电池片在轨伏安模型 太阳电池片伏安模型是推导电池阵伏安模型的基础,由太阳电池理论可得太阳电池片等效电路模型如图 2所示[1]。
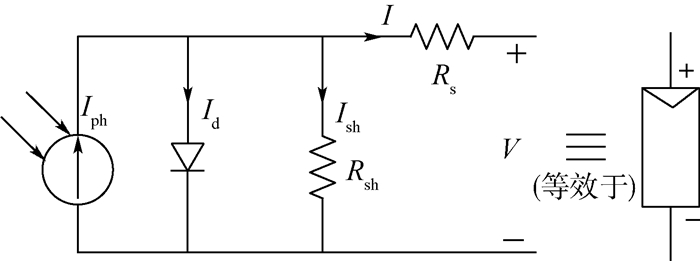 |
| 图 2 太阳电池片等效模型[1] Fig. 2 Solar cell equivalent model[1] |
| 图选项 |
根据基尔霍夫定律,电池片输出电流I和电压V的关系如式(1) 所示:
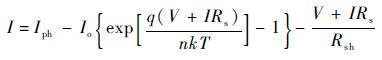 | (1) |
式中:Iph为光生电流,A;Io为二极管饱和电流,A;q为电子电荷,q=1.6×10-19 C;n为二极管理想因子,其值在1~5之间;k为玻尔兹曼常数,k=1.38×10-23 J/K;T为工作绝对温度,K;Rs为串联电阻,Ω;Rsh为并联电阻,Ω。
利用电池片厂家在标准测试条件下的I-V曲线数据[12](见图 3),图中:Isc为短路点电流;Voc为开路点电压;Imp为最大功率点电流;Vmp为最大功率点电压,确定式(1) 中的5个未知参数Iph、Io、n、Rs、Rsh,方法如下。
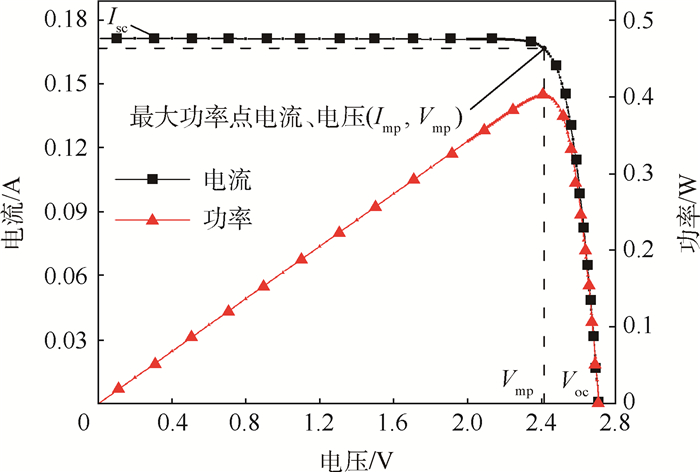 |
| 图 3 标准测试条件下太阳电池片伏安测试数据 Fig. 3 I-V test data of solar cell under standard test condition |
| 图选项 |
短路点:I=Isc,V=0,代入式(1) 得
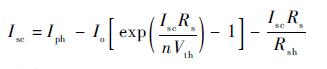 | (2) |
式中:Vth=kT/q。
开路点:I=0,V=Voc,代入式(1) 得
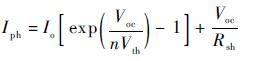 | (3) |
最大功率点:I=Im,V=Vm,代入式(1) 得
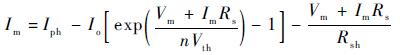 | (4) |
对式(1) 求导得
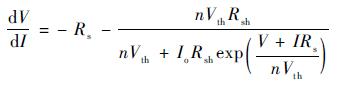 | (5) |
从电池片I-V曲线中提取短路点一阶导数值dsc,代入式(5) 得
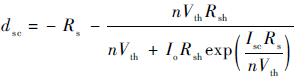 | (6) |
从电池片I-V曲线中提取开路点一阶导数值doc,代入式(5) 得
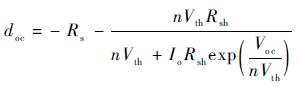 | (7) |
利用式(2)~式(4)、式(6)、式(7) 联合求解,可以得到5个未知参数的计算公式,如式(8)~式(12) 所示[12]:
 | (8) |
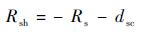 | (9) |
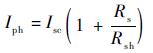 | (10) |
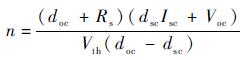 | (11) |
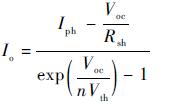 | (12) |
式中:e1=(doc-dsc)[dsc(Isc-Im)+Vm];e2=(dscIm+Vm)(dscIsc+Voc)。
太阳电池片在轨工作的光强和温度与地面标准测试条件不同,因此需根据在轨实际光强和温度对电池片伏安模型参数进行修正。
光生电流与光强成线性关系,其修正函数如式(13) 所示:
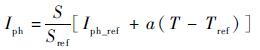 | (13) |
式中:Tref为标准测试条件下的绝对温度,K;Sref为标准测试条件下光强,W/m2;a为电流温度系数,A/℃;S为在轨工作等效光强,W/m2,S可通过式(14) 进行计算:
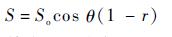 | (14) |
其中:So为航天器所在轨道位置的环境光强,对于地球轨道航天器取1353W/m2;θ为太阳电池片法线与太阳光的夹角,rad;r为太阳电池片的遮挡率。
二极管反向饱和电流修正函数如式(15) 所示:
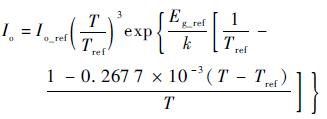 | (15) |
式中:Eg_ref为标准测试条件下太阳电池片材料能带宽度,对于三砷化镓电池取1.42 eV;Io_ref为标准测试条件下的二极管反向饱和电流。
串联电阻修正函数如式(16) 所示:
 | (16) |
式中:b为串联电阻修正系数,取值0.217[13];Rs_ref为标准测试条件下太阳电池片串联电阻。
并联电阻修正函数如式(17) 所示:
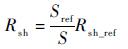 | (17) |
式中:Rsh_ref为标准测试条件下的并联电阻。
二极管理想因子n不随温度和光强变化。
通过以上方法,确定了太阳电池片I-V方程,该方程是超越方程,无法将I和V分离到等号两边,利用该方程的单调性和一阶可导性,通过牛顿迭代法进行求解。
太阳电池片输出电流I是自变量,输出电压V计算公式如式(18) 所示:
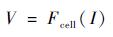 | (18) |
式中:I∈[0, Isc];Fcell(I)的算法如下:
步骤1??Vi=Voc。
步骤2??
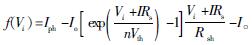
步骤3??

步骤4??

步骤5??如果|Vi+1-Vi| < 10-6,则跳转到步骤6;否则,Vi=Vi+1,跳转到步骤2。
步骤6??V=Vi+1,结束迭代。
综上,利用厂家提供的一组标准测试条件下I-V数据,结合太阳电池片在轨实际光强、温度、遮挡,即可求解太阳电池片在轨伏安模型,并可以计算任意工作点的电压和电流。
1.2 太阳电池串伏安模型 航天器太阳电池串由多个电池片串联而成,为避免热斑和母线电流回流问题,太阳电池片两端并联旁路二极管,电池串与母线之间串联隔离二极管,假设电池串由N块电池片组成,其等效电路模型如图 4所示。
 |
| 图 4 太阳电池串等效模型 Fig. 4 Solar cell string equivalent model |
| 图选项 |
利用太阳电池片在轨伏安模型,计算各太阳电池片在不同光强、遮挡下的I-V曲线,如图 5所示,根据基尔霍夫电流定律,电池串电流I如式(19) 所示:
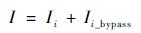 | (19) |
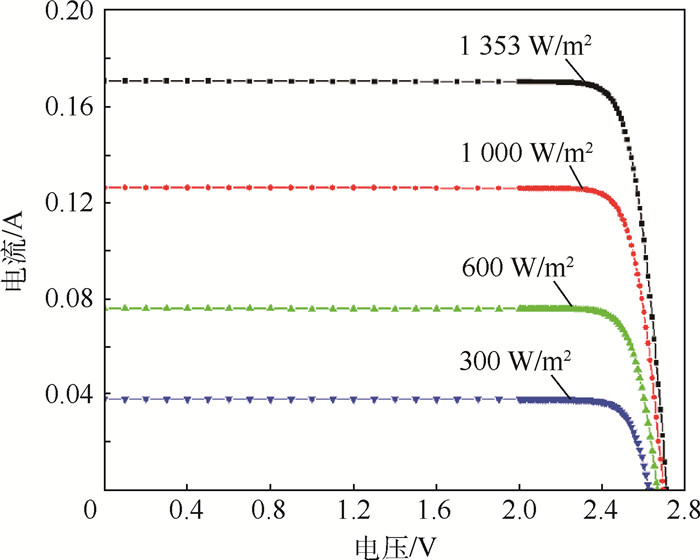 |
| 图 5 不同光强下的太阳电池片I-V曲线 Fig. 5 Solar cell I-V curves under different irradiation intensity |
| 图选项 |
式中:Ii为第i个太阳电池片输出电流,A;Ii_bypass为电池片两端并联的旁路二极管流过电流,A。对于电池串中任意一个电池单片,当I大于电池片最大输出电流Isc_i时,旁路二极管导通,通过旁路二极管的电流Ii_bypass=I-Isc_i。
根据基尔霍夫电压定律,电池串输出电压等于各电池片两端电压之和。当电池片两端旁路二极管阻断时,电池片两端电压由电池片输出电压决定;当旁路二极管导通时,电池片短路,两端电压由旁路二极管压降决定。假设太阳电池串工作电流为I,则电压V计算公式如式(20) 所示:
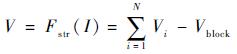 | (20) |
式中:Vi为第i个电池片两端电压,其计算公式如式(21) 所示;Vblock为隔离二极管导通压降,其计算公式如式(22) 所示。
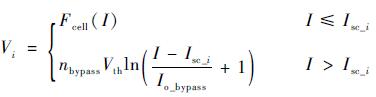 | (21) |
式中:Fcell(I)计算公式如式(18) 所示;nbypass为旁路二极管理想因子;Io_bypass为旁路二极管饱和电流。
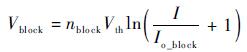 | (22) |
式中:nblock为隔离二极管理想因子;Io_block为隔离二极管饱和电流。
为计算任意工作点电压和电流,还需给出根据电池串工作电压计算电流的方法。假设太阳电池串工作电压为V,则电流I计算公式如式(23) 所示:
 | (23) |
式中:Fstr-1(V)可利用电池串I-V曲线式(20) 的单调性递减特性进行迭代计算,算法如下:
步骤1??Imin=0,Imax=Isc_str。
步骤2??
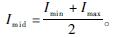
步骤3??Vmid=Fstr(Imid)。
步骤4??如果Vmid-V| < 10-6,则跳转到步骤6;否则,跳转到步骤5。
步骤5??如果Vmid < V,则Imax=Imid;如果Vmid > V,则Imin=Imid,跳转到步骤2。
步骤6??I=Imid,结束迭代。
通过以上方法,即得到太阳电池串的伏安模型,通过该模型可计算太阳电池串任意工作点的电流和电压。
1.3 太阳电池阵伏安模型 航天器太阳电池阵由多个电池串并联而成,假设电池阵由M条支路组成,每条支路含有N块电池片,其等效电路模型如图 6所示。
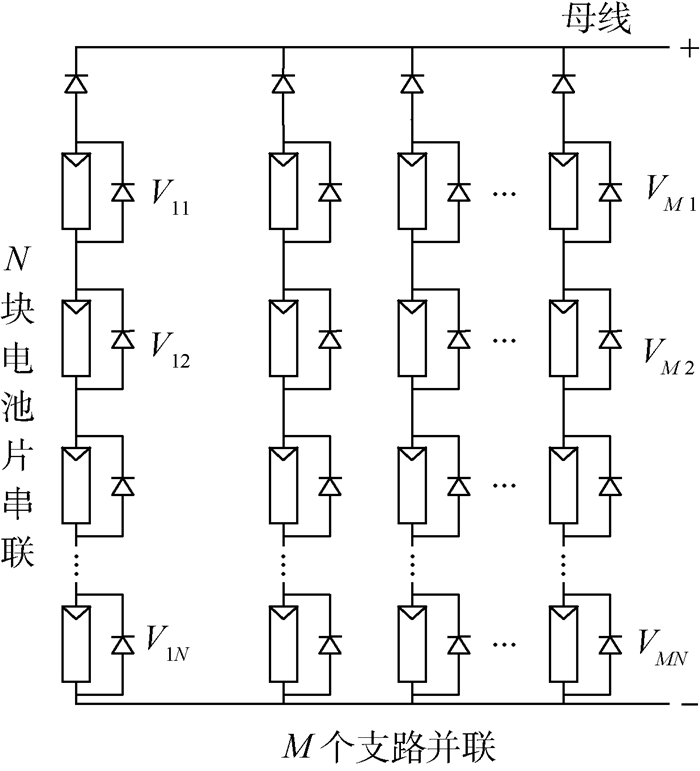 |
| 图 6 太阳电池阵等效模型 Fig. 6 Solar cell array equivalent model |
| 图选项 |
利用电池串伏安模型,可以计算电池串I-V曲线,如图 7所示,根据基尔霍夫电流定律,电池阵输出的总电流Ibus是各电池串支路电流之和,其计算公式如式(24) 所示:
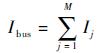 | (24) |
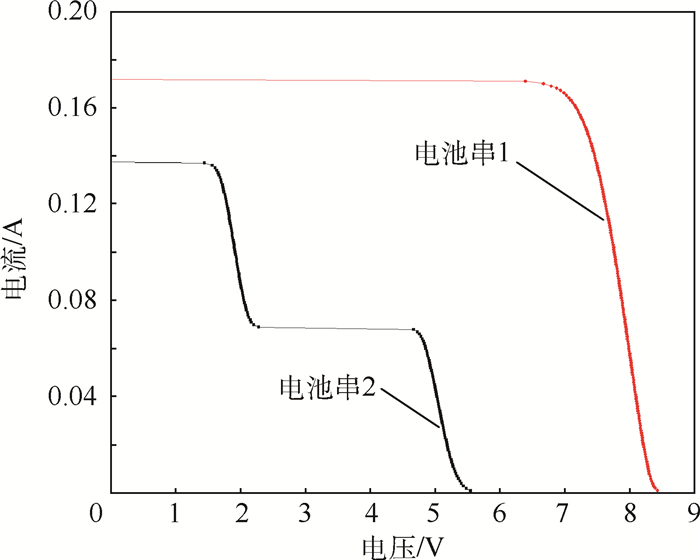 |
| 图 7 太阳电池串I-V曲线 Fig. 7 Solar cell string's I-V curves |
| 图选项 |
式中:Ij为第j条支路输出电流,Ij计算公式如式(25) 所示:
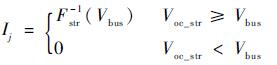 | (25) |
其中:Fstr-1(Vbus)由式(23) 计算得出;Vbus为太阳电池阵母线设定的输出电压;Voc_str为支路开路电压。当支路开路电压低于母线电压时,隔离二极管反向阻断,该电池串无输出。
2 仿真分析 2.1 计算方法正确性验证 Saber软件可以对太阳电池片伏安模型进行仿真,但其无法根据大规模太阳电池阵在轨光强、温度和遮挡情况进行动态分析,因此使用Saber对2并4串的简单太阳电池阵进行静态计算,以验证本文方法的正确性。太阳电池片参数如表 1所示[16],旁路二极管和隔离二极管参数如表 2所示,太阳电池电路以及遮挡阴影如图 8所示,其中电池片PV12遮挡60%,PV13遮挡20%,其他电池片无遮挡,电池阵工作温度75 ℃,温度均匀。
表 1 标准测试条件(25 ℃,1353W/m2)下太阳电池片参数[16] Table 1 Solar cell parameters under STC (25 ℃, 1353W/m2)[16]
| 参数 | 数值 |
| 短路点电流Isc/A | 0.17123 |
| 短路点导数dsc | -0.87479 |
| 开路点电压Voc/V | 2.71 |
| 开路点导数doc | -5000.5 |
| 最大功率点电流Im/A | 0.16725 |
| 最大功率点电压Vm/V | 2.41 |
| 电池片尺寸/(mm×mm) | 50×38 |
| 电流温度系数a/(A·℃-1) | 0.011×10-3 |
表选项
表 2 旁路二极管和隔离二极管参数 Table 2 Parameters of bypass diode and block diode
| 参数 | 数值 |
| 理想因子n | 1.95 |
| 二极管饱和电流Io/A | 0.9×10-8 |
表选项
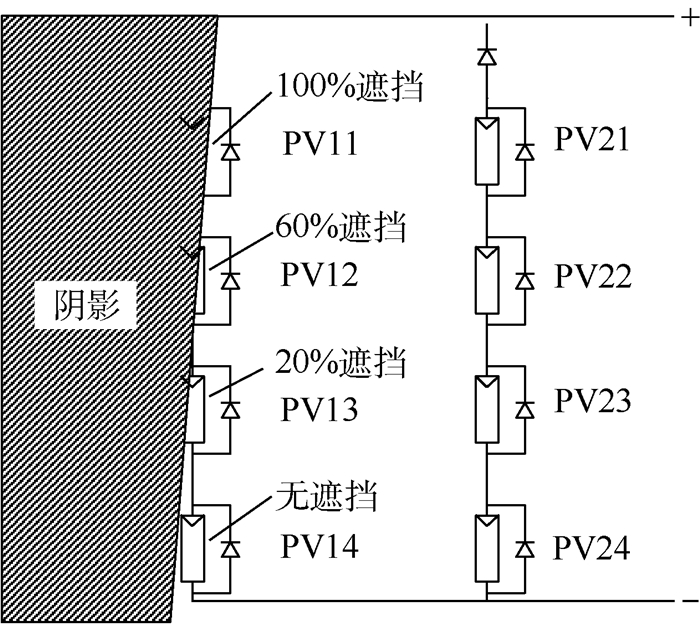 |
| 图 8 简单太阳电池阵电路模型 Fig. 8 Simple solar array's circuit model |
| 图选项 |
利用太阳电池片伏安模型计算各电池片I-V曲线,如图 9所示,结果表明航天器入轨后电池阵温度升高,电池片开路电压降低,短路电流基本不变,太阳电池片被部分遮挡,导致接收的有效太阳光减少,电池片短路电流随遮挡面积增大而线性减少,开路电压基本不变。
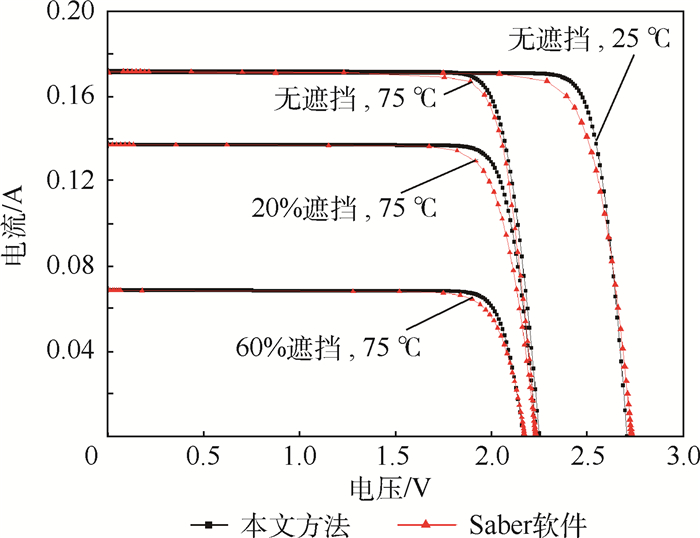 |
| 图 9 太阳电池片I-V曲线 Fig. 9 I-V curves of solar cell |
| 图选项 |
利用电池串和电池阵伏安模型计算各电池串以及电池阵的I-V曲线,如图 10所示。结果表明,电池串1中2片电池片被部分遮挡,导致旁路二极管导通,使太阳电池串I-V曲线出现多个波峰,波峰数量等于被部分遮挡的电池片个数,电池串2没有遮挡,其输出电压是各个电池片之和;从电池阵I-V曲线可以看出,当电池阵工作点电压大于电池串1的最大输出电压时,隔离二极管反向,导致电池串1无输出,电池阵的输出特性由电池串2决定。图 9和图 10中,本文方法计算结果与Saber软件计算结果基本一致,表明了本文方法的正确性。
 |
| 图 10 太阳电池串和电池阵I-V曲线 Fig. 10 I-V curves of solar cell strings and array |
| 图选项 |
2.2 航天器太阳电池阵供电能力仿真分析 为验证本文方法的适应性和计算精度,以近地轨道大型航天器为例,进行太阳电池阵供电能力分析。航天器轨道参数如表 3所示,几何模型和电池片模型如图 11所示。航天器在轨三轴对地稳定,帆板单自由度对日定向,温度均匀。每块帆板有528串电池串,每串有60块太阳电池片,太阳电池片和二极管参数如表 1和表 2所示,航天器负载需求电压为100V,传输线路压降为10V,太阳电池阵母线电压控制为110V。
表 3 航天器轨道参数 Table 3 Orbit parameters of spacecraft
| 参数 | 数值 |
| 轨道高度/km | 393 |
| 轨道倾角/(°) | 42 |
| 太阳入射角(太阳矢量与轨道面夹角)/(°) | 0~60 |
| 轨道环境光强/(W·m-2) | 1353 |
| 太阳电池阵温度/℃ | 75 |
表选项
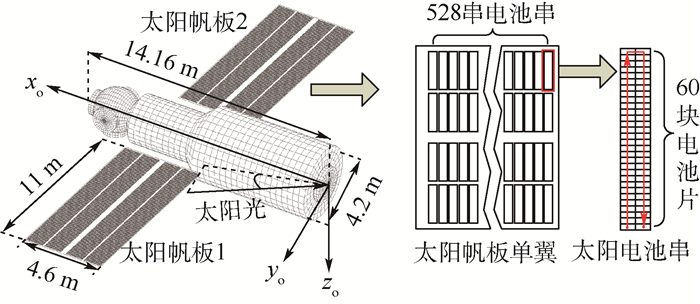 |
| 图 11 航天器几何模型与太阳电池片电路模型 Fig. 11 Spacecraft geometric model and solar cell circuit model |
| 图选项 |
航天器在轨飞行期间,太阳电池阵温度在一定范围内变化,为验证本文方法对温度变化的适应性,以太阳入射角0°为例,对电池阵不同温度下I-V曲线进行计算,如图 12所示。结果表明,最大功率点电压Vmp随温度升高而下降,当在轨温度升至75 ℃时,Vmp降至117.2V。工作电压Von设置为110V时,输出电流随温度变化不大,但如果Von设置大于117.2V,则电流随温度降低而迅速降低,由此可见Von需小于最高温度下的Vmp,并留有一定余量,可确保在轨温度波动时,电池阵输出稳定。
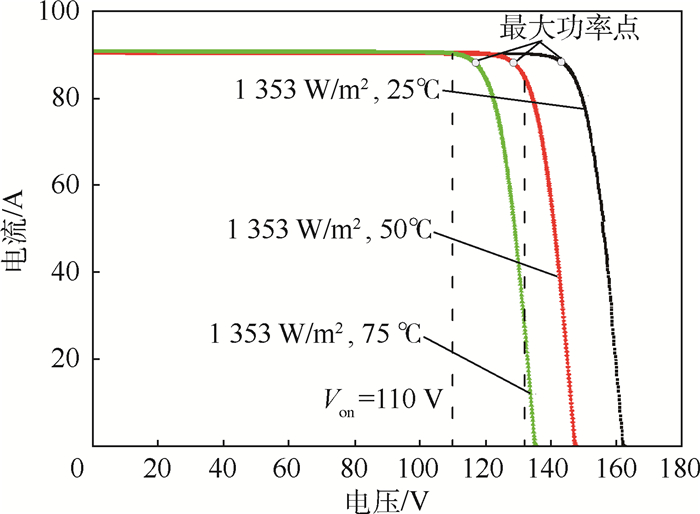 |
| 图 12 不同温度下的太阳电池阵I-V曲线 Fig. 12 I-V curves of solar array at different temperatures |
| 图选项 |
为验证计算精度,利用传统的遮挡率法和本文方法对航天器一个轨道周期内的供电能力进行计算。一个轨道周期内,太阳方位角0°~360°,每5°计算一次。传统遮挡率法计算公式如式(26) 所示:
 | (26) |
式中:Ion为太阳光垂直照射电池阵时的输出电流,本文为90.0A。
太阳帆板1输出电流如图 13所示,电流与太阳入射角余弦关系如图 14所示,图中:0°~60°为太阳入射角。太阳方位角变化过程中,太阳帆板1均无遮挡,计算结果表明,帆板无遮挡时本文方法与遮挡率法分析结果一致,太阳电池阵输出电流与太阳入射角的余弦成正比。
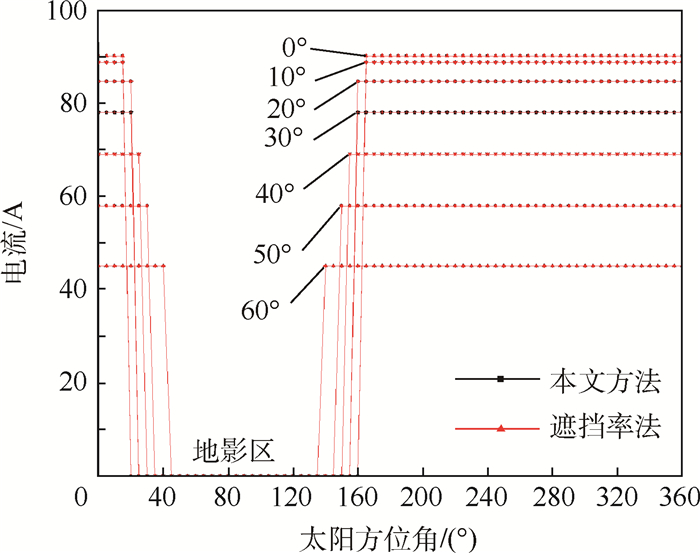 |
| 图 13 太阳帆板1输出电流 Fig. 13 Output current of solar array 1 |
| 图选项 |
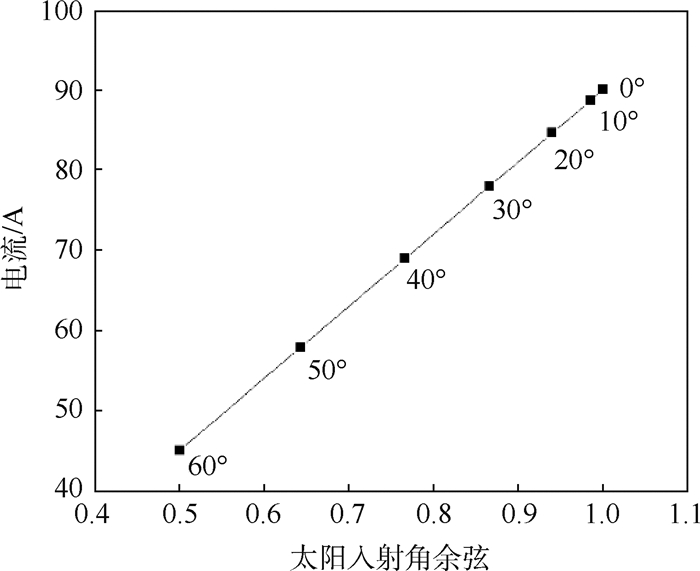 |
| 图 14 太阳帆板1电流与太阳入射角余弦关系 Fig. 14 Relationship between current of solar array 1 and cosine of sun incident angle |
| 图选项 |
太阳帆板2输出电流如图 15所示,本文方法与遮挡率法电流计算误差如图 16所示,图中:0°~60°为太阳入射角。结果表明,随着太阳入射角增大,遮挡越来越严重,电池阵输出电流逐渐变小,利用遮挡率和夹角计算的电池阵输出电流误差较大,最高可达6.5A,占航天器总输出的20%。
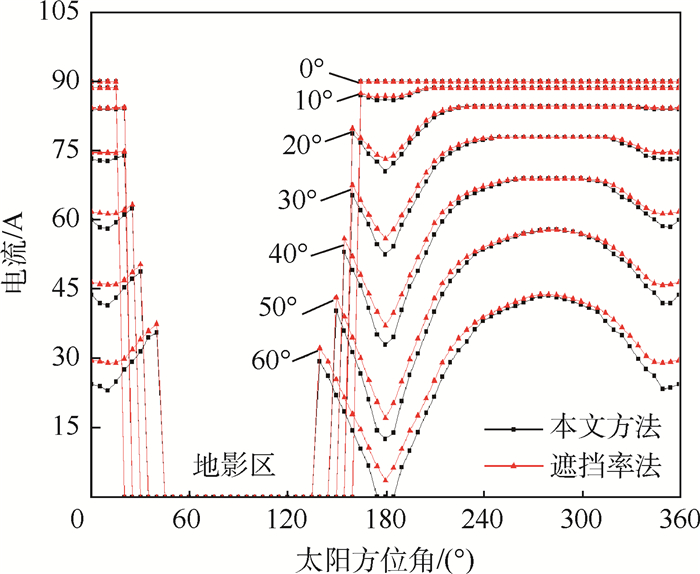 |
| 图 15 太阳帆板2输出电流 Fig. 15 Output current of solar array 2 |
| 图选项 |
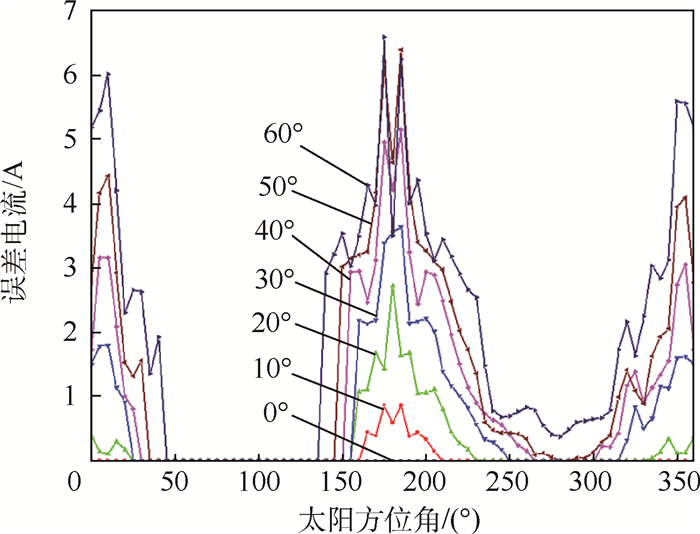 |
| 图 16 太阳帆板2输出电流误差 Fig. 16 Output current error of solar array 2 |
| 图选项 |
以太阳入射角60°,方位角175°为例,对遮挡率法和本文方法的计算误差进行分析。太阳帆板2遮挡率为85.36%,阴影形状如图 17所示,遮挡率法计算结果为6.5A,本文方法计算结果为0A。由阴影图 17可知,帆板中各电池串至少有14块电池片被遮挡,导致电池串开路电压低于母线电压110V,隔离二极管断开,整个电池阵损失全部输出,由此可见,遮挡率法的误差在于没有考虑隔离二极管断开的情况。
 |
| 图 17 太阳帆板2遮挡阴影 Fig. 17 Shadow pattern of solar array 2 |
| 图选项 |
使用面积相同、形状不同的阴影对太阳电池阵进行遮挡,电池阵工作电压为110V,遮挡率为27.97%,计算结果如图 18所示。结果表明,遮挡电池串数量越多,电池阵输出电流越小,遮挡面积相同的电池阵输出电流差距超过6A,可见太阳电池阵被遮挡时,其伏安特性与阴影形状有关,利用遮挡率进行供电能力计算,误差较大。
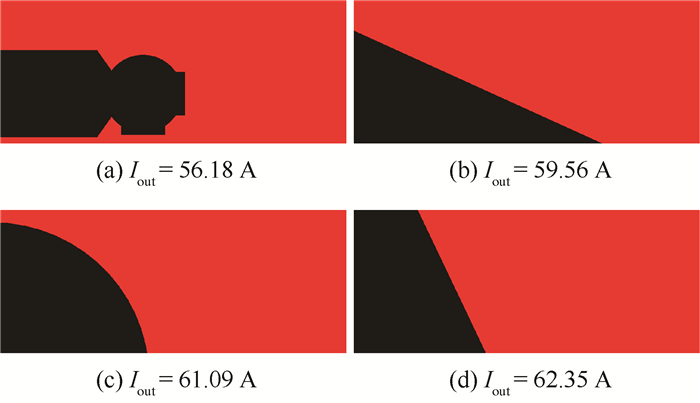 |
| 图 18 不同阴影形状下的太阳电池阵输出电流 Fig. 18 Output currents of solar array with different shadow patterns |
| 图选项 |
3 结论 本文以太阳电池片理论模型为基础,提出了一种航天器太阳电池阵供电能力的计算方法,该方法以一组标准测试条件下太阳电池片的I-V数据为输入,推导出带旁路二极管和隔离二极管的电池阵的在轨伏安模型。
1) 本文方法可以根据一组标准测试条件下太阳电池片I-V数据,结合在轨实际光强、温度和遮挡情况,推导出电池片在轨伏安模型,并根据基尔霍夫定律推导电池阵中旁路二极管、隔离二极管开关情况,进而精确计算太阳电池阵伏安模型。
2) 太阳电池阵工作温度上升,会导致最大功率点电压下降,工作点电压小于最大功率点电压,并有一定余量,可确保温度变化期间,工作点电压始终小于最大功率点电压,从而保持电池阵输出电流稳定。
3) 太阳电池阵被部分遮挡,可能导致电池阵整体无输出;利用遮挡率和太阳光夹角计算电池输出电流的方法误差较大,最大可至6.5A,其原因是电池串被部分遮挡后,无法提供母线电压,隔离二极管反向断开,导致整串无输出,遮挡率方法无法分析这种情况。
4) 太阳电池阵输出电流与阴影形状有关,遮挡面积相同而形状不同的阴影,造成电池阵伏安模型不同,本文方法可以分析任意阴影形状下的电池阵伏安模型,避免遮挡率分析方法的误差,计算精度可提高20%。
参考文献
| [1] | RAUSEHENBACH H S. 太阳电池阵设计手册[M]. 张金熹, 廖春发, 傅德棣, 等译. 北京: 中国宇航出版社, 1987: 20-77. RAUSEHENBACH H S.Solar array design handbook[M]. ZHANG J X, LIAO C F, FU D L, et al, translated.Beijing:China Astronautic Publishing House, 1987:20-77(in Chinese). |
| [2] | 马世俊. 卫星电源技术[M].北京: 中国宇航出版社, 2005: 23-89. MA S J. Satellite power system technology[M].Beijing: China Astronautic Publishing House, 2005: 23-89.(in Chinese) |
| [3] | 刘志全, 杨淑利, 濮海玲. 空间太阳电池阵的发展现状及趋势[J].航天器工程, 2012, 21(6): 112–118. LIU Z Q, YANG S L, PU H L. Development and trend of space solar array technology[J].Spacecraft Engineering, 2012, 21(6): 112–118.(in Chinese) |
| [4] | SEYEDMAHMOUDIAN M, MEKHILEF S, RAHMANI R, et al. Maximum power point tracking of partial shaded photovoltaic array using an evolutionary algorithm:A particle swarm optimization technique[J].Journal of Renewable and Sustainable Energy, 2014, 6(23102): 1–13. |
| [5] | 任筱强, 王鹏鹏. 航天器组合体能量平衡分析系统设计及应用[J].航天器工程, 2013, 22(2): 60–64. REN X Q, WANG P P. Design and implementation of energy balance analysis system for spacecraft combination[J].Spacecraft Engineering, 2013, 22(2): 60–64.(in Chinese) |
| [6] | 孙永卫, 曹鹤飞, 原青云. 月尘对太阳电池阵开路电压影响研究[J].太阳能学报, 2015, 36(36): 551–555. SUN Y W, CAO H F, YUAN Q Y. Effect of lunar dust to open circuit voltage of solar cell array[J].Acta Energiae Solaris Sinica, 2015, 36(36): 551–555.(in Chinese) |
| [7] | 李安寿, 张东来, 杨炀, 等. 一种精确计算航天器本体对太阳电池阵遮挡的方法[J].宇航学报, 2013, 34(10): 1403–1409. LI A S, ZHANG D L, YANG Y, et al. A method for accurately calculating the shadow of solar array shaded by spacecraft itself[J].Journal of Astronautics, 2013, 34(10): 1403–1409.DOI:10.3873/j.issn.1000-1328.2013.10.015(in Chinese) |
| [8] | 韩新月, 屈健, 郭永杰. 温度和光强对聚光硅太阳电池特性的影响研究[J].太阳能学报, 2015, 36(7): 1585–1590. HAN X Y, QU J, GUO Y J. Dependence of silicon concentrator solar cells parameters on temperature and light intensity[J].Acta Energiae Solaris Sinica, 2015, 36(7): 1585–1590.(in Chinese) |
| [9] | DELLEUR A M, KERSLAKE T W. Electrical performance from bifacial illumination international space station photovoltaic array[J].Journal of Spacecraft and Rockets, 2005, 42(1): 171–176.DOI:10.2514/1.5660 |
| [10] | DELLEUR A M, KERSLAKE T W, LEVY R K. Managing space station solar array electrical hazards for sequential shunt unit replacement[J].Journal of Propulsion and Power, 2006, 22(1): 16–23.DOI:10.2514/1.13731 |
| [11] | 张臻, 沈辉, 李达. 局部阴影遮挡的太阳电池组件输出特性实验研究[J].太阳能学报, 2012, 33(1): 5–12. ZHANG Z, SHEN H, LI D. Experimental study on characteristics of partial shaded solar module[J].Acta Energiae Solaris Sinica, 2012, 33(1): 5–12.(in Chinese) |
| [12] | 翟载腾, 程晓舫, 杨臧健, 等. 太阳电池一般电流模型参数的解析解[J].太阳能学报, 2009, 30(8): 1078–1082. ZHAI Z T, CHENG X F, YANG Z J, et al. Analytic solutions of solar cell model parameters[J].Acta Energiae Solaris Sinica, 2009, 30(8): 1078–1082.(in Chinese) |
| [13] | 张忠政. 太阳电池应用理论研究[D]. 合肥: 中国科学技术大学, 2014. ZHANG Z Z.Theoretical study of solar cells utilization[D]. Hefei:University of Science and Technology of China, 2014(in Chinese). |
| [14] | MAHMOUD Y, EI-SAADANY E. Accuracy improvement of the ideal PV model[J].IEEE Transactions on Sustainable Energy, 2015, 6(3): 909–911.DOI:10.1109/TSTE.2015.2412694 |
| [15] | RAMAPRABHA R, MATHUR B L. A comprehensive review and analysis of solar photovoltaic array configurations under partial shaded conditions[J].International Journal of Photoenergy, 2012, 12(6): 1–16. |
| [16] | 程保义. 空间三结砷化镓太阳电池辐照衰减模型研究[D]. 天津: 南开大学, 2010. CHENG B Y.Research on the radiation model of space triple-junction solar cell[D]. Tianjin: Nankai University, 2010(in Chinese). |
