美国海军研制了自动着舰系统(ACLS)并投入使用[3],其中的飞控系统的着舰控制策略(称为常规控制策略)为升降舵通过调节俯仰间接改变升力来控制高度,同时通过调节油门改变推力来控制空速或迎角进行动力补偿。事实上,该控制策略存在着抗扰能力不足的问题。目前研究人员主要基于该控制策略,围绕补偿甲板运动扰动[4-6]和抵抗舰尾流扰动[7-9]这两方面进行研究,力图提高着舰精度。
文献[4-6]针对甲板运动扰动提出对其进行预估与补偿相结合的方式来减小甲板跟踪偏差,但是在设计中未考虑舰尾流扰动的影响。文献[7-9]仅针对抑制舰尾流扰动进行控制系统设计,未考虑甲板运动扰动,并且在控制系统的抗扰验证与参数设计方面也存在着不足。其中,文献[7]在验证系统抗风能力时,仅选用单位阶跃信号代表的垂直突风作为扰动输入,不足以证明系统抑制舰尾流扰动的能力。文献[8]从系统对阶跃信号的响应方面进行控制律参数的设计,并采用人工调校的方法整定控制律参数,调参过程耗时复杂。文献[9]先针对舰尾流扰动中的自由大气紊流分量、周期性分量以及随机分量利用遗传算法对控制律参数进行寻优,后对舰尾流扰动中的雄鸡尾流分量按着舰时间历程向控制系统中叠加控制补偿量进行抑制,其中的补偿时刻和补偿量是在先期参数寻优结果的基础上仿真优化得到。无人机的着舰时间历程受海面风、船速影响较大,因此,该方法所确定的固定的补偿时刻和补偿量所产生的补偿效果是不确定的,甚至会起反作用。
针对常规控制结构抗扰能力不足的问题,本文首先提出无人机着舰纵向多操纵面平衡态直接力控制(DFC)控制策略及控制结构,从飞行力学机理上使无人机着舰的抗扰潜力更大。然后,提出面向着舰点散布的控制律参数优化设计方法,该方法在保证系统满足稳定裕度指标的基础上,综合考虑舰尾流扰动和甲板运动扰动对着舰点散布的影响,使2种扰动造成的着舰点散布最小,最大限度地挖掘出飞行控制的抗扰潜力。最后,通过算例设计与仿真,验证了本文提出的多操纵面平衡态DFC控制策略和控制结构在抵抗舰尾流扰动和甲板运动扰动方面的优异性能,以及所提控制律参数设计方法的有效性。
1 无人机着舰纵向多操纵面平衡态DFC控制策略及控制结构 常规控制策略及控制结构如图 1所示。图中:Hg为理想下滑轨迹的高度指令;H为无人机高度;Kph、Kih和Kdh分别为高度控制外回路PID控制系数;?为无人机俯仰角; K?和Kωz为姿态控制内回路的系数;ωz为无人机俯仰角速率; δz为无人机升降舵。甲板运动信号通过补偿网络GDMC(s)叠加到高度指令中,GDMC(s)的形式[4]为
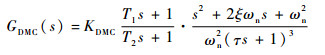 | (1) |
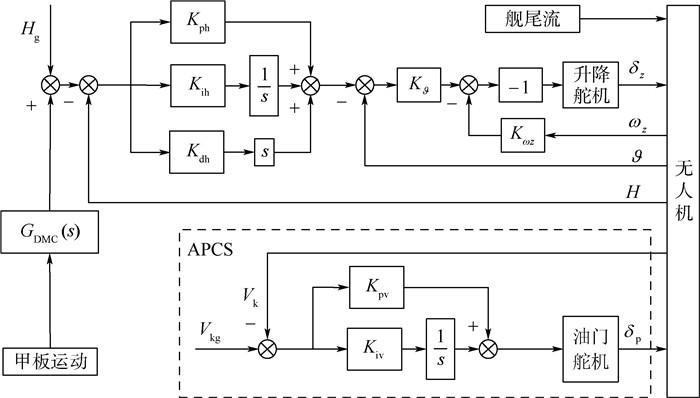 |
| 图 1 ACLS常规纵向控制结构 Fig. 1 Regular longitudinal control structure of ACLS |
| 图选项 |
式中:KDMC为补偿网络增益;T1和T2为一阶校正环节时间参数;τ为二阶校正环节时间参数;ωn为二阶校正环节自然频率;ξ为二阶校正环节阻尼比。
图 1中采用速度恒定的进场动力补偿系统(APCS),Vkg为平衡态空速,Kpv和Kiv分别为PI控制系数,Vk为无人机空速,δp为无人机油门。
常规控制策略存在抗扰能力不足的问题:由于无人机俯仰转动惯量较大,通过升降舵调节俯仰间接改变升力的过程较慢,因此升降舵控制高度的过程具有较大的滞后;无人机质量较大,通过改变推力进行动力补偿具有延迟性,而从发动机改变油门到推力变化也需要一定时间。因此该控制策略限制了无人机抑制舰尾流扰动和甲板运动扰动的能力。
为了充分发挥无人机抑制扰动的潜力,本文提出无人机着舰纵向多操纵面平衡态DFC控制策略:升降舵控制无人机迎角处于平衡态迎角,襟翼控制无人机高度,消除高度偏差;油门处于平衡态油门,阻力板控制无人机空速跟踪平衡态空速。
上述策略中,升降舵可以快速产生俯仰力矩抑制扰动,使迎角处于平衡态迎角,保证基准升力,襟翼偏转可以直接产生升力,对总升力进行快速调节,两者共同保持无人机升力方向上的力平衡;阻力板偏转可以直接改变阻力,实现空速的快速调节,油门和阻力板共同保持阻力方向上的力平衡。平衡态油门处于较大油门状态,无人机在不能安全着舰时,可将阻力板快速收回并增大油门,实现快速复飞,保证舰机安全。
本文所提控制策略充分利用了无人机多操纵面的操纵资源(升降舵、襟翼、油门和阻力板),增加了抗扰潜力。可通过对下滑平衡态的优化设计,使下滑平衡态下的升降舵、襟翼和阻力板具有充分的双向操纵余量和最大的操纵效率。基于以上控制策略的控制结构如图 2所示。图中:αg和δpg分别为无人机无扰动下滑平衡态下的平衡态迎角和平衡态油门;Kpα和Kiα为升降舵迎角控制器PI控制系数;α为迎角;δj和δb分别为无人机襟翼和阻力板。
 |
| 图 2 多操纵面平衡态DFC控制结构 Fig. 2 Control structure based on multi-surface equilibrium-state DFC |
| 图选项 |
2 复杂着舰环境 舰尾流扰动和甲板运动扰动构成了舰载机基本的着舰环境。在此,需要明确这些扰动的形式和组成,并对其进行功率谱分析,确定扰动的频率范围,使控制律设计更具有针对性,减少设计的保守性,从而最大限度地提高着舰精度。
2.1 舰尾流扰动 文献[10]给出了舰尾流的工程化模型。舰尾流由自由大气紊流分量(u1、v1、w1)、雄鸡尾流分量(u2、w2)、周期性分量(u3、w3)以及随机分量(u4、v4、w4)等4种成分组成,其中u*、v*、w*分别为各组成成分的水平分量、横向分量和垂直分量。舰尾流的水平分量u、横向分量v和垂直分量w可表示为
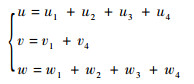 | (2) |
关于各个分量的表达式可参见文献[10-11],本文不再赘述。现给出某无人机空速Vk=55.4 m/s、甲板风Vw/d=15 m/s、下滑角θ=-3.17°的状态下舰尾流水平分量u和垂直分量w的时间历程如图 3所示。
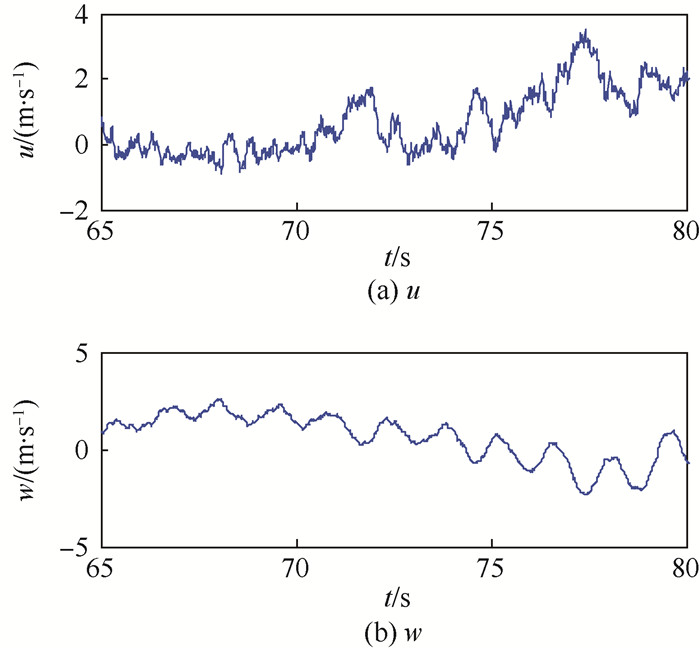 |
| 图 3 舰尾流水平分量和垂直分量 Fig. 3 Horizontal component and vertical component of air-wake |
| 图选项 |
对图 3所示的舰尾流水平分量和垂直分量基于周期图法采用快速傅里叶变换(FFT)进行功率谱分析,得到u和w的功率谱密度(Su和Sw)曲线如图 4所示。从图中可以看出,舰尾流水平分量和垂直分量的主要成分的频率fm处于区间[0~5]rad/s之内,在设计控制律时应重点考虑上述频率范围内的舰尾流扰动。
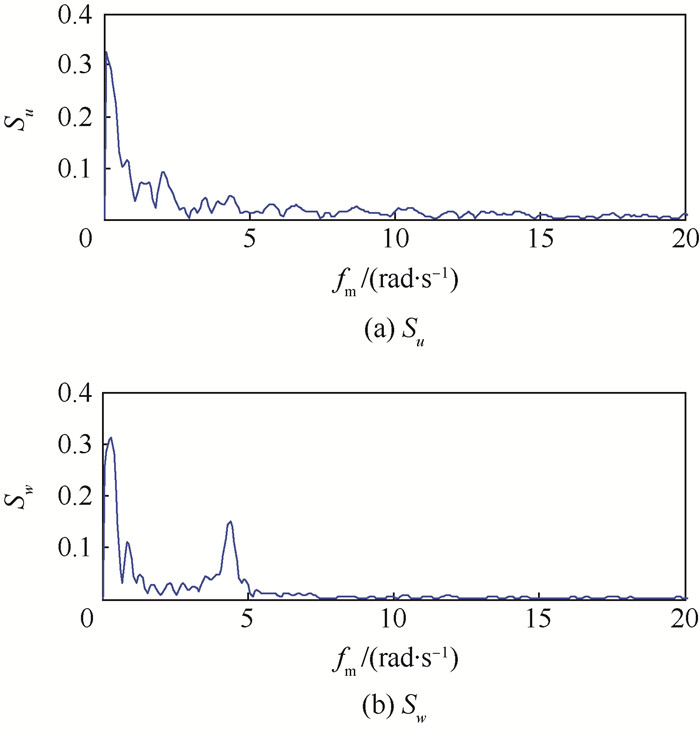 |
| 图 4 舰尾流水平和垂直分量功率谱密度 Fig. 4 Power spectrum density of air-wake horizontal and vertical component |
| 图选项 |
2.2 甲板运动扰动 本文以文献[11]给出的甲板运动模型为例,进行功率谱分析。文献[11]给出了美国ESSEX航空母舰以8 kn速度航行,在中心高度为17英尺(约5.2 m)的浪涌作用下,产生的沉浮运动、俯仰角的功率谱密度曲线以及相应的成形滤波器,如式(3) 所示。
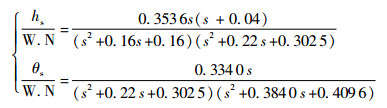 | (3) |
式中:hs为甲板沉浮运动,m;θs为甲板俯仰角,(°);W.N代表单位高斯白噪声。
为了获得理想着舰点的高度变化信号和功率谱密度曲线,需对图 5所示的甲板运动仿真模型进行仿真,得到时域内的甲板沉浮运动信号和俯仰角信号,进而得到理想着舰点的高度变化信号HDM。HDM与hs、θs的关系如式(4) 所示。
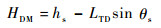 | (4) |
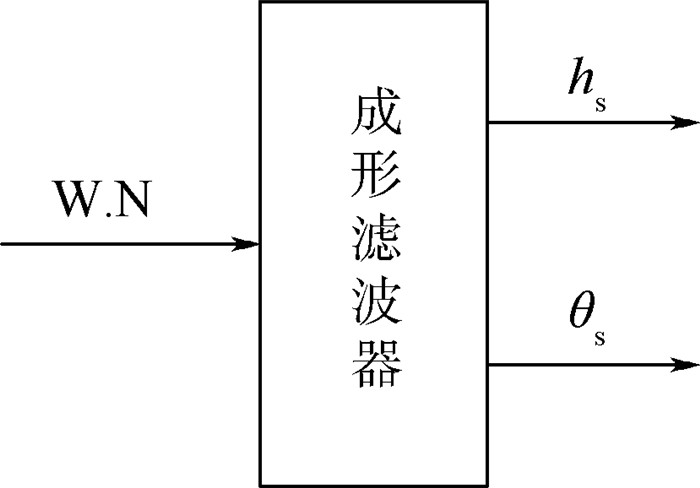 |
| 图 5 甲板运动仿真模型 Fig. 5 Simulation model of deck motion |
| 图选项 |
式中:LTD为舰船俯仰中心到理想着舰点的水平距离(本例中取87 m)。
理想着舰点高度变化的时间历程如图 6(a)所示。采用FFT对HDM进行功率谱分析,得到HDM的功率谱密度SH曲线如图 6(b)所示。从图 6(b)可以看出,理想着舰点高度变化信号主要成分的频率分布在[0~1.0] rad/s之间,因此重点针对该频率范围进行控制律设计。
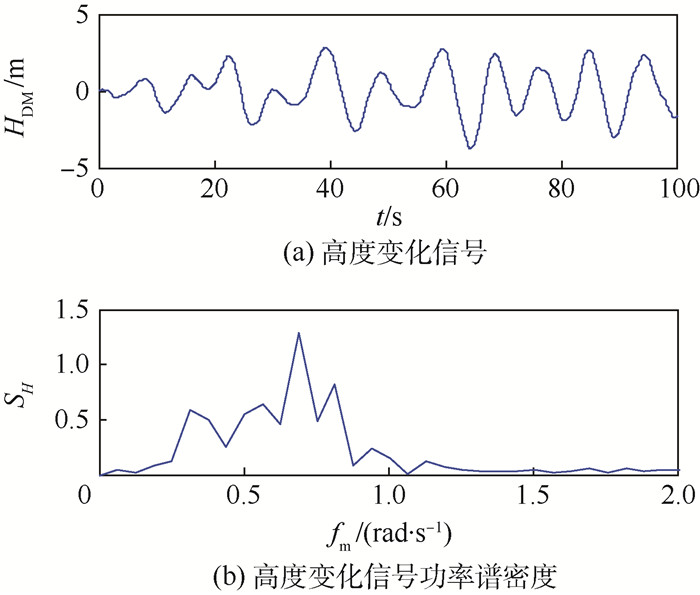 |
| 图 6 理想着舰点高度信号及其功率谱密度 Fig. 6 Altitude signal of ideal touchdown point and its power spectrum density |
| 图选项 |
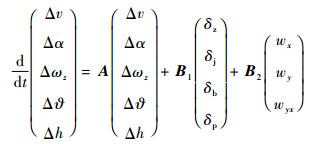
3 非平静大气下无人机模型 文献[12]给出了苏联坐标系下非平静大气中以δz和δp为输入的偏量形式的运动方程。本文以无人机着舰下滑飞行状态为基准点进行配平和线性化,对输入量进行拓展,给出了非平静大气中以δz、δj、δb和δp为输入的偏量形式的无人机纵向运动方程,如式(5) 所示。
 | (5) |
式中:wx、wy和wyx分别为x方向紊流速度、y方向紊流速度和紊流梯度;Δv和Δh分别为无人机速度增量和高度增量;A、B1和B2分别为[12]
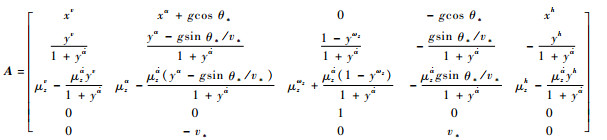 |
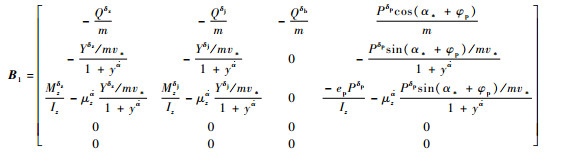 |
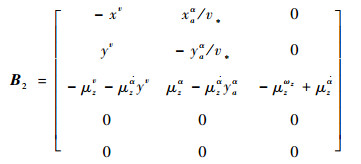 |
式中:各变量与无人机的气动参数、结构参数、飞行状态相关,具体可参见文献[12]。由于紊流梯度wyx对无人机的作用并不显著[13],因此可以忽略其影响。
4 面向着舰点散布的控制律参数优化设计 在无人机着舰的最后阶段,无人机既受到舰尾流的干扰,又受到甲板运动的干扰,导致无人机与理想下滑轨迹存在偏差herr,最终造成着舰点纵向散布lerr,偏差与散布之间的关系如式(6) 所示。
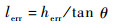 | (6) |
本文提出面向着舰点散布的控制律参数优化设计方法。该方法在保证系统满足稳定裕度指标的基础上,综合考虑舰尾流扰动以及甲板运动扰动对着舰点散布的影响,使2种扰动造成的着舰点散布最小。
在图 1和图 2所示的控制结构的基础上,给出控制律优化设计结构示意图,如图 7所示,HDM通过甲板运动补偿网络叠加到Hg中。
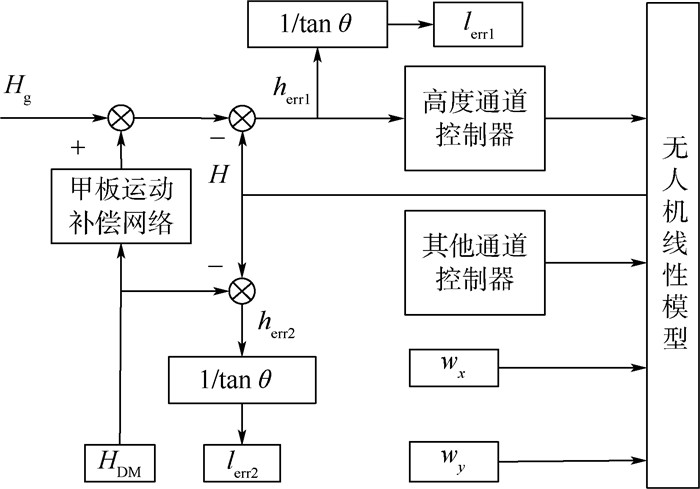 |
| 图 7 控制律优化设计结构示意图 Fig. 7 Schematic diagram of control law optimization design structure |
| 图选项 |
当HDM=0,以wx和wy为输入时,herr1为舰尾流扰动影响下的无人机偏离理想下滑轨迹的高度偏差,lerr1为herr1造成的着舰点纵向散布。此时,可以求出以大气扰动wx和wy为输入,着舰点散布lerr1为输出的闭环传递函数,进而得到幅值放大倍数Awx(ω)和Awy(ω),两者均是频率ω的函数。
当wx=0和wy=0,以HDM为输入时,herr2为无人机的甲板跟踪偏差,lerr2为herr2造成的着舰点纵向散布。此时,可以求出以HDM为输入,着舰点散布lerr2为输出的闭环传递函数,进而得到幅值放大倍数As(ω)。
根据经典控制理论,闭环放大倍数在某频率区间上越小,则其对该频率区间的信号的抑制能力越强。因此,为使舰尾流扰动和甲板运动扰动造成的着舰点散布最小,应使Awx(ω)和Awy(ω)在舰尾流扰动的主要成分所处的频率区间[ω1min, ω1max]上最小;同时,使As(ω)在HDM的主要成分所处的频率区间[ω2min, ω2max]最小。
根据以上思想,构建控制律优化设计的目标函数如下:
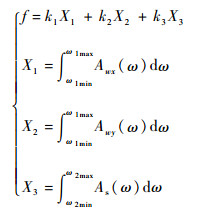 | (7) |
式中:X1和X2分别为Awx(ω)和Awy(ω)在频率区间[ω1min, ω1max]上的积分值;X3为As(ω)在频率区间[ω2min, ω2max]上的积分值;k1、k2和k3为加权系数。使目标函数的值f最小,就是使舰尾流扰动和甲板运动扰动所造成的着舰点散布最小。
采用粒子群优化(PSO)算法进行控制律参数优化设计。PSO是由Eberhart和Kennedy提出的优化算法,属于进化算法的一种,具有容易实现、可全局优化、收敛快等优点,在解决实际问题中展现出了优越性[14-16]。
以式(7) 中的目标函数作为PSO的适应度函数,采用PSO求解满足适应度值最小的控制器参数流程图如图 8所示。图中:c1、c2、w和r为PSO基本参数,分别为认知因子、社会因子、惯性因子和约束因子;N、D、M和R分别表示种群规模、待优化参数个数、最大迭代次数和待优化参数范围;第k代中的第i个粒子是一个D维向量,表示为[p1, p2, …, pD]ik,p*表示每个待优化参数的取值。
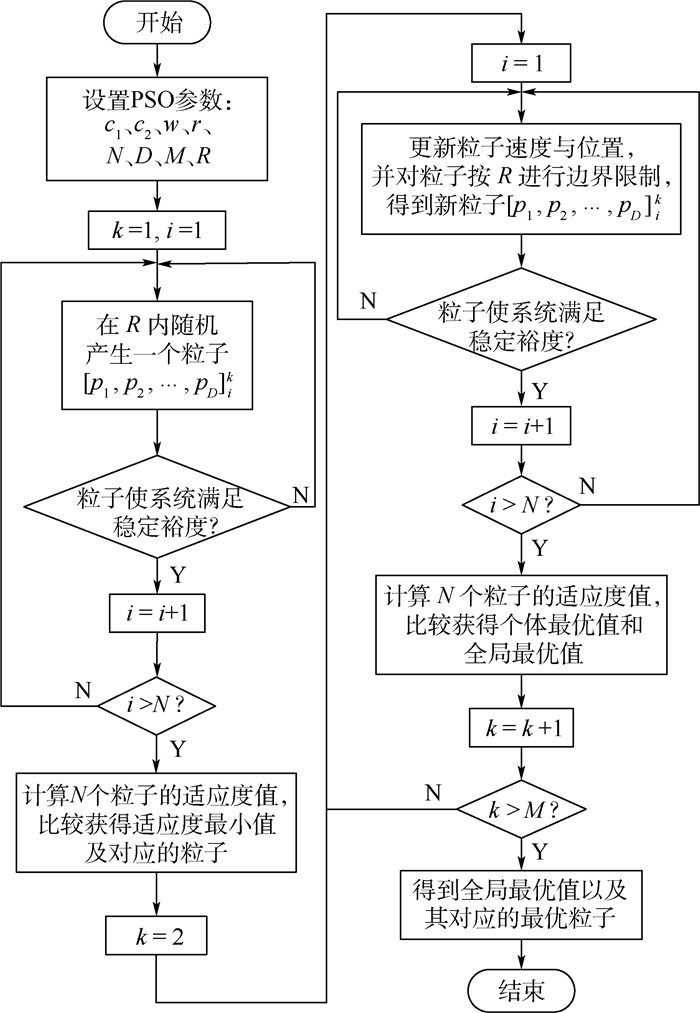 |
| 图 8 PSO参数寻优流程图 Fig. 8 Flowchart of parameter optimization with PSO |
| 图选项 |
5 算例 5.1 控制律优化设计 以某无人机为研究对象,根据其气动参数及相关结构参数,在下滑状态下配平并建立无人机线性模型。采用上述面向着舰点散布的控制律优化设计方法分别对常规控制结构(如图 1所示)和多操纵面平衡态DFC控制结构(如图 2所示)进行控制律参数设计。常规控制结构中有13个待优化参数,分别为Kph、Kih、Kdh、K?、Kωz、Kpv、Kiv、KDMC、T1、T2、ξ、ωn和τ;多操纵面平衡态DFC控制结构(简称DFC控制结构)中有14个待优化参数,分别为Kph、Kih、Kdh、Kpα、Kiα、Kωz、Kpv、Kiv、KDMC、T1、T2、ξ、ωn和τ。
设置PSO认知因子c1=2,社会因子c2=2,惯性因子w=0.9,约束因子r=1,种群规模N=50,最大迭代次数M=50。稳定裕度指标为幅值裕度GM≥9 dB,相角裕度PM≥55 °。式(7) 中,目标函数的加权系数k1=k2=k3=1。结合第2节分析,舰尾流的主要成分的频率区间为[0~5]rad/s,甲板运动的主要成分的频率区间为[0~1.0] rad/s。
按图 8寻优流程分别对2种控制结构中的控制律参数进行优化设计,适应度值变化曲线如图 9所示。由图 9可见,2种控制结构的控制律寻优适应度值变化曲线均收敛到最优值。寻优得到的常规结构控制律参数为Kph=1.315,Kih=0.12,Kdh=2.18,K?=4.0,Kωz=2.13,Kpv=12.95,Kiv=0.13,KDMC=0.97,T1=10.0,T2=20.0,ξ=2.1,ωn=0.81,τ=0.1;寻优得到的多操纵面平衡态DFC控制结构控制律为Kph=15,Kih=2.12,Kdh=25.0,Kpα=1.10,Kiα=0.42,Kωz=1.65,Kpv=40.0,Kiv=5.0,KDMC=0.5,T1=19.3,T2=10.65,ξ=0.69,ωn=0.788,τ=0.1。
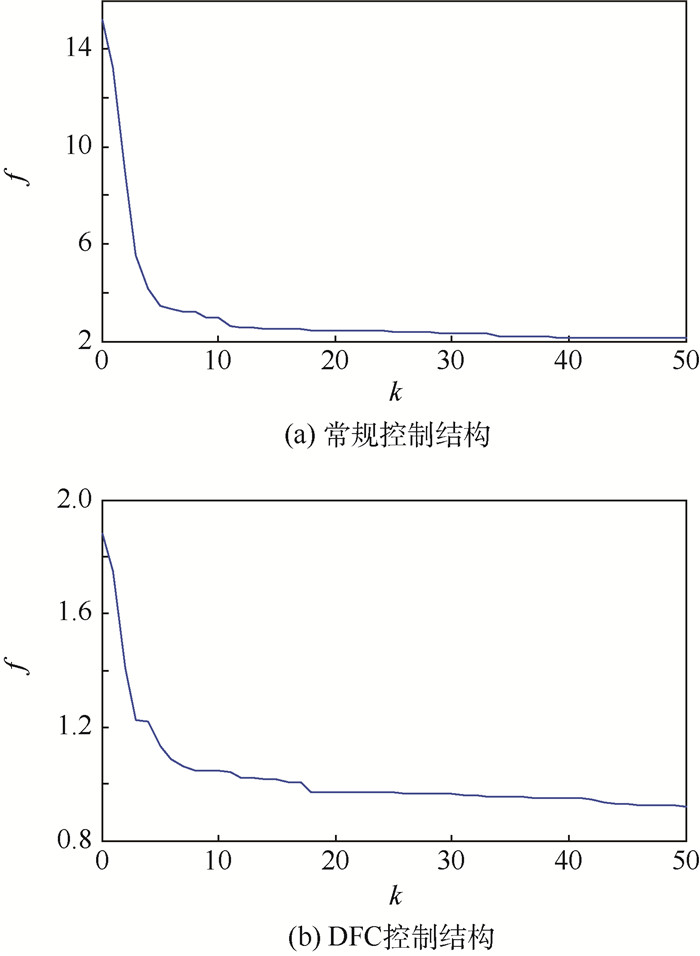 |
| 图 9 适应度变化曲线 Fig. 9 Changing curves of fitness |
| 图选项 |
5.2 仿真分析
5.2.1 舰尾流扰动下跟踪下滑线效果仿真分析 2种控制结构以舰尾流扰动水平分量u为输入量,无人机高度H为输出的闭环放大倍数A(ω)见图 10(a)。在相同下滑状态下,对2种控制结构分别仅引入相同的舰尾流水平分量u进行干扰,跟踪下滑线效果对比见图 10(b)。
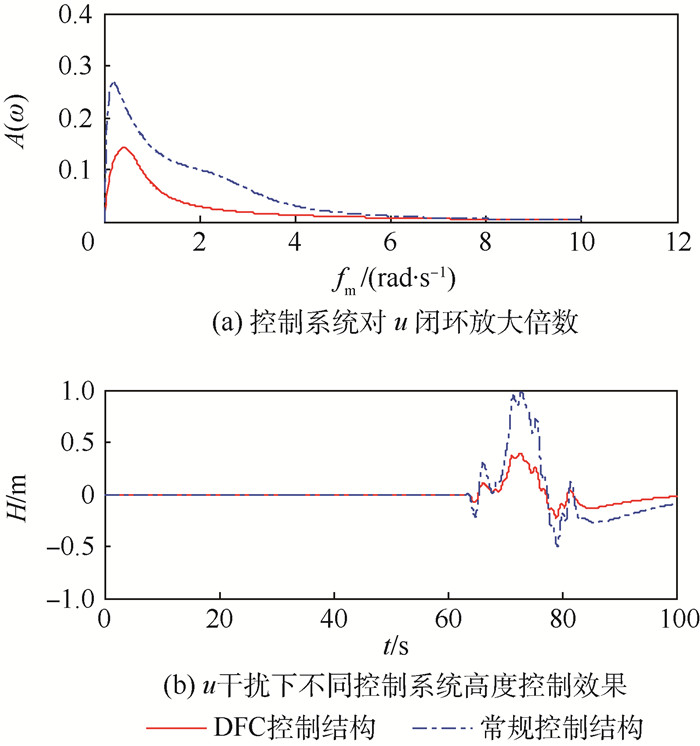 |
| 图 10 不同控制结构对u的抑制能力对比 Fig. 10 Comparison of u inhibition ability between different control structures |
| 图选项 |
2种控制结构以舰尾流垂直分量w为输入量、无人机高度H为输出的闭环放大倍数A(ω)如图 11(a)所示。在相同下滑状态下,对2种控制结构分别仅引入相同的舰尾流垂直分量w进行干扰,跟踪下滑线效果对比如图 11(b)所示。
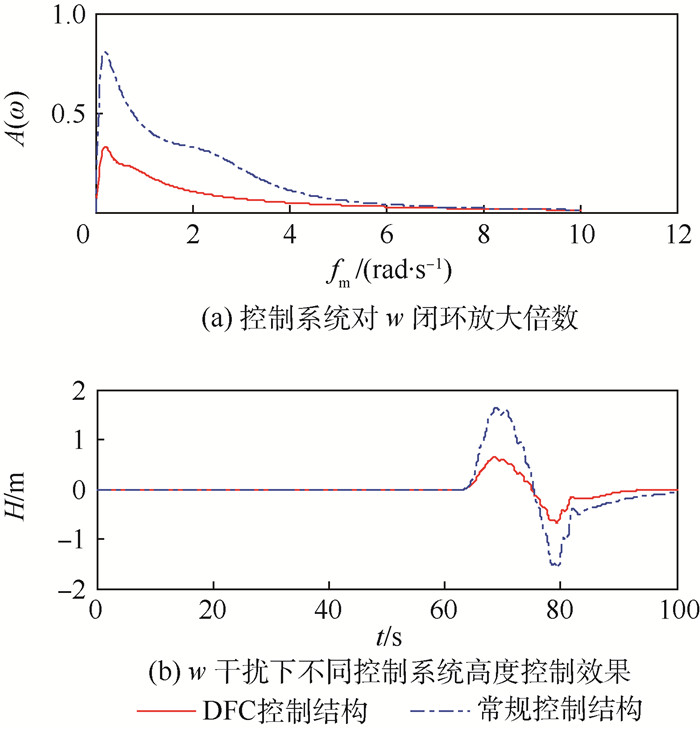 |
| 图 11 不同控制结构对w的抑制能力对比 Fig. 11 Comparison of w inhibition ability between different control structures |
| 图选项 |
将相同的舰尾流水平分量u与垂直分量w同时引入到2种控制结构中进行对比,跟踪下滑线效果如图 12所示。
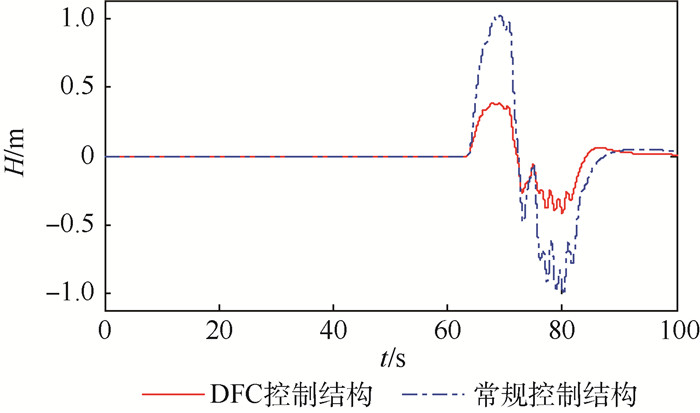 |
| 图 12 不同控制结构的舰尾流扰动抑制能力对比 Fig. 12 Comparison of inhibition ability of air-wake disturbance between different control structures |
| 图选项 |
从图 10~图 12可看出,多操纵面平衡态DFC控制结构比常规控制结构具有更强的舰尾流扰动抑制能力,高度控制精度提升至少1倍,从而大大减小着舰点散布。
5.2.2 甲板运动扰动下补偿效果仿真分析 在无舰尾流扰动的情况下,在第50 s时向控制系统中引入相同的甲板运动,观察2种控制结构的高度跟踪情况,如图 13(a)所示,2种控制结构的高度跟踪误差对比如图 13(b)所示。
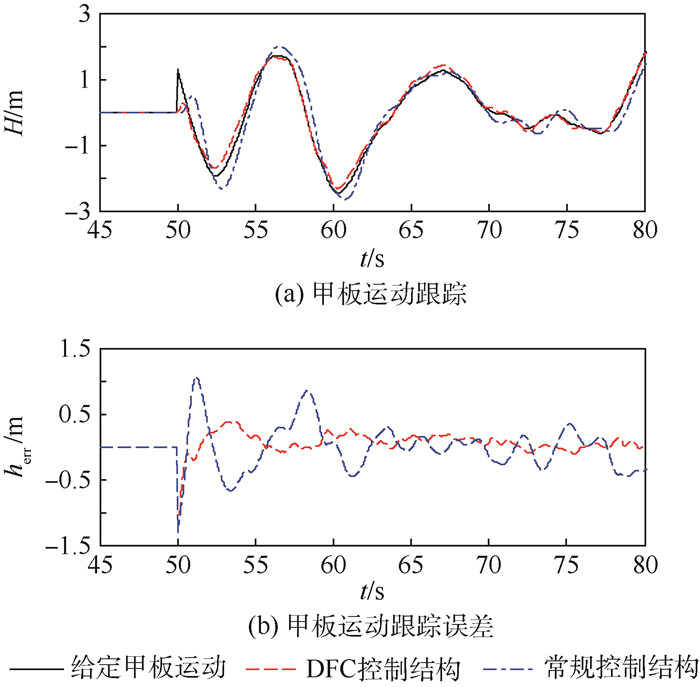 |
| 图 13 不同控制结构跟踪甲板运动能力对比 Fig. 13 Comparison of ability to track deck motion between different control structures |
| 图选项 |
由图 13可以看出,多操纵面平衡态DFC控制结构在多操纵面的共同参与下,减小了无人机跟踪甲板运动的误差,无论是从幅值上还是相位上跟踪效果均明显优于常规控制结构,从而可大大减小着舰点散布。
5.2.3 综合扰动下着舰仿真分析 舰尾流扰动和甲板运动扰动称为综合扰动,由于它具有较大随机性[6],因此有必要进行多次着舰仿真来获取着舰点纵向位置及散布情况。在仿真时,可通过为白噪声发生器设定不同的随机种子来分别构建舰尾流扰动和甲板运动扰动[11]。通过上述方式随机产生100个不同的综合扰动样本。对具有多操纵面平衡态DFC控制结构的飞控系统和具有常规控制结构的飞控系统引入上述100个不同的综合扰动分别进行着舰仿真,记录各自的着舰点纵向位置P及散布情况,如图 14所示,仿真次数为ks。图中,纵轴为着舰点纵向位置。纵向位置为正,表示无人机相对理想着舰点提前着舰;纵向位置为负,表示无人机越过理想着舰点着舰。文献[17-18]给出了着舰偏差等级分类原则,其理想偏差区为[-6.1, 6.1] m,允许偏差区为[-12.2, 12.2] m。依据该等级分类原则,对图 14中100次着舰点纵向位置进行统计分类,结果见表 1所示。从图 14和表 1可得,在抵抗着舰各种扰动实现精确着舰控制方面,多操纵面平衡态DFC控制结构相对常规控制结构具有明显优势,可有效提高着舰成功率。
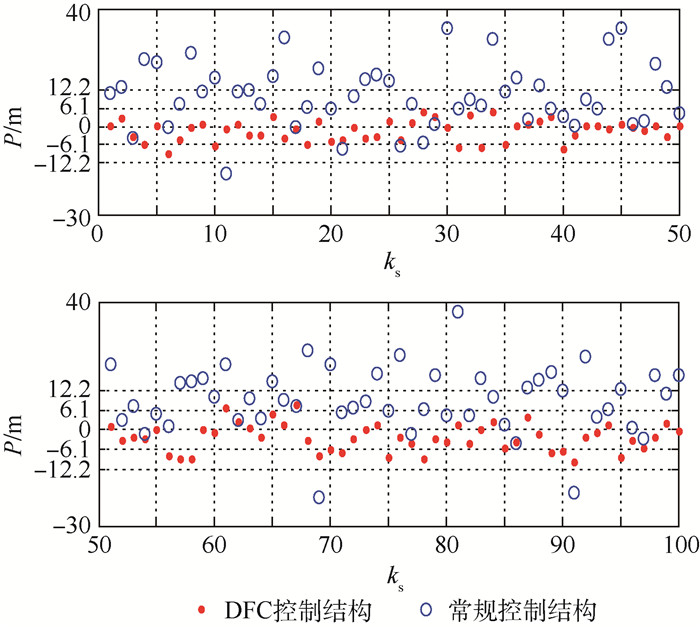 |
| 图 14 不同控制结构着舰点纵向散布对比 Fig. 14 Comparison of longitudinal distribution of touchdown points between different control structures |
| 图选项 |
表 1 100次着舰仿真纵向散布统计结果 Table 1 Longitudinal deviation statistic results of 100 carrier landing simulations
| 控制结构类型 | 着舰偏差均值 | 着舰偏差均方根 | 理想着舰次数 | 允许着舰次数 | 着舰成功率/ % |
| DFC | -1.84 | 3.97 | 80 | 100 | 100 |
| 常规 | 10.04 | 10.53 | 30 | 57 | 57 |
表选项
6 结论 针对无人机着舰过程中舰尾流扰动和甲板运动扰动对着舰点散布的影响,对无人机着舰纵向控制策略、控制结构和控制律设计方法进行较为深入的研究,可得:
1) 提出的多操纵面平衡态DFC控制策略以及控制结构在抵抗舰尾流扰动和甲板运动扰动方面具有优异性能,能大大减小着舰点的散布,明显提高复杂着舰环境下的着舰成功率。
2) 提出的面向着舰点散布的控制律参数优化设计方法,直接面向着舰点散布,综合考虑了复杂着舰环境下各种扰动的特性,使控制律参数设计更具有针对性,减小了设计的保守性,进一步挖掘出控制结构的抗扰潜力。
3) 本文控制策略和控制结构具有较强的工程可实现性。在控制律设计中使用的舰尾流扰动和甲板运动扰动的频率范围仅是通过对特定状态下各扰动进行功率谱分析得到的。实际应用中可通过对各种可能的舰船运动状态下舰尾流扰动和甲板运动扰动进行功率谱分析,得到涵盖所有运动状态的扰动频率范围,然后以此频率范围采用本文的控制方案和控制律设计方法进行设计。
参考文献
| [1] | 王永庆, 罗云宝, 王奇涛, 等. 面向机舰适配的舰载飞机起降特性分析[J].航空学报, 2016, 37(1): 269–277. WANG Y Q, LUO Y B, WANG Q T, et al. Carrier suitability-oriented launch and recovery characteristics of piloted carrier-based aircraft[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(1): 269–277.(in Chinese) |
| [2] | 李晓磊, 赵廷弟. 基于模糊推理的舰载机进舰过程安全性仿真分析[J].航空学报, 2013, 34(2): 325–333. LI X L, ZHAO T D. Carrier-based aircraft landing process safety simulation analysis based on fuzzy inference[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(2): 325–333.(in Chinese) |
| [3] | STEINBERG M.Development and simulation of an F/A-18 fuzzy logic automatic carrier landing system[C]//Second IEEE International Conference on Fuzzy Systems, 1993.Piscataway, NJ:IEEE Press, 1993:797-802. |
| [4] | 张永花, 周鑫. 纵向甲板运动补偿技术研究[J].电光与控制, 2012, 19(4): 18–22. ZHANG Y H, ZHOU X. Study on the longitudinal deck motion compensation technique[J].Electronics Optics & Control, 2012, 19(4): 18–22.(in Chinese) |
| [5] | 张永花, 周鑫. 舰载机着舰点垂直运动补偿技术仿真研究[J].系统仿真学报, 2013, 25(4): 826–830. ZHANG Y H, ZHOU X. Simulation study on landing point vertical motion in carrier landing[J].Journal of System Simulation, 2013, 25(4): 826–830.(in Chinese) |
| [6] | 周鑫, 彭荣鲲, 袁锁中. 舰载机理想着舰点垂直运动的预估与补偿[J].航空学报, 2013, 34(7): 1663–1669. ZHOU X, PENG R K, YUAN S Z. Prediction and compensation for vertical motion of ideal touchdown point in carrier landing[J].Acta Aeronautica et Astronautica Sinica, 2013, 34(7): 1663–1669.(in Chinese) |
| [7] | 满翠芳, 江驹, 王新华, 等. 舰载机动力补偿系统模糊逻辑设计技术[J].南京航空航天大学学报, 2010, 42(5): 656–660. MAN C F, JIANG J, WANG X H, et al. Carrier-based aircraft approach power compensator system design based on fuzzy logic techniques[J].Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(5): 656–660.(in Chinese) |
| [8] | 董然. ACLS纵向内回路控制系统研究[D]. 哈尔滨: 哈尔滨工程大学, 2013: 56-61. DONG R.Research on the longitudinal inner loop configuration in ACLS[D].Harbin:Harbin Engineering University, 2013:56-61(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10217-1014132721.htm |
| [9] | 张智, 李佳桐, 董然, 等. 针对舰艉流抑制的ACLS纵向控制律优化设计[J].哈尔滨工程大学学报, 2016, 37(6): 802–811. ZHANG Z, LI J T, DONG R, et al. Optimal design on longitudinal automatic carrier landing system for carrier air wake rejection[J].Journal of Harbin Engineering University, 2016, 37(6): 802–811.(in Chinese) |
| [10] | DAVID J M, ROBERT J W. 军用规范——有人驾驶飞机的飞行品质(MIL-F-8785C)的背景资料和使用指南[M]. 李成忠, 肖亚伦, 方振平, 等译. 西安: 飞行力学, 1985: 149-153. DAVID J M, ROBERT J W.Backgroud information and user guide for MIL-F-8785C, military specification-flying qualities of poloted airplanes[M].LI C Z, XIAO Y L, FANG Z P, et al translated. Xi'an:Flight Dynamics, 1985:149-153(in Chinese).http://kns.cnki.net/KCMS/detail/detail.aspx?filename=fhlx198301004&dbname=CJFD&dbcode=CJFQ |
| [11] | 杨一栋. 舰载飞机着舰导引与控制[M].北京: 国防工业出版社, 2007: 30-42. YANG Y D. Guidance and control of carrier aircraft landing[M].Beijing: National Defend Industry Press, 2007: 30-42.(in Chinese) |
| [12] | 肖亚伦. 飞行器运动方程[M].北京: 航空工业出版社, 1987: 99-103. XIAO Y L. Motion equations of aerial vehicles[M].Beijing: Aeronautics Industry Press, 1987: 99-103.(in Chinese) |
| [13] | 肖亚伦, 金长江. 大气扰动中的飞行原理[M].北京: 国防工业出版社, 1993: 99-101. XIAO Y L, JIN C J. Flight principle in atmospheric turbulence[M].Beijing: National Defend Industry Press, 1993: 99-101.(in Chinese) |
| [14] | KENNEDY J.Particle swarm optimization[M]//SAMMUT C, WEBB G I.Encyclopedia of machine learning.New York:Springer, 2011:760-766. |
| [15] | SCHUTTE J F, GROENWOLD A A. A study of global optimization using particle swarms[J].Journal of Global Optimization, 2005, 31(1): 93–108.DOI:10.1007/s10898-003-6454-x |
| [16] | LIAO W, WANG J, WANG J.Nonlinear inertia weight variation for dynamic adaptation in particle swarm optimization[C]//International Conference in Swarm Intelligence. Berlin:Springer, 2011:80-85. |
| [17] | ANDERSON M R.Inner and outer loop manual control of carrier aircraft landing[C]//AIAA Guidance, Navigation and Control Conference.Reston:AIAA, 1996:1-10. |
| [18] | 许东松, 刘星宇, 王立新. 航母运动对舰载飞机着舰安全性的影响[J].北京航空航天大学学报, 2011, 37(3): 289–294. XU D S, LIU X Y, WANG L X. Influence of carrier motion on landing safety for carrier-based airplanes[J].Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(3): 289–294.(in Chinese) |
