由于受大气层内稠密空气影响与自身尺寸、燃料制约，防空导弹在保证射程的同时，还需尽量提高拦截末端速度，使导弹能以最低能量损耗实现对空袭目标的有效拦截^[1]。因此，对弹目交会角与机动性能约束条件下的导引律进行研究具有重要意义。
国内外对考虑交会角约束的制导策略的研究从未间断。2006年，Ryoo等^[2]以剩余时间的函数作为权函数，通过最小值原理推导了一种满足一定攻击角度对固定目标攻击的导引律。2008年，Shaferman和Shima^[3]应用线性二次型理论推导了一种指定终端交会角的导引律，能对高速机动目标进行有效拦截。2008年，张友安和马培蓓^[4]基于Lyapunov稳定性理论设计了一种带攻击角度约束的制导律, 将导弹有效导引到期望的攻击角度，并对攻击时间进行估算。这些制导律都是基于可用过载无穷大的理想情况下进行推导的。
2005年，Cloutier^[5]对考虑常值过载边界饱和的导引律进行了研究。2007年，Hexner和Shima^[6]对考虑常值过载约束的随机最优导引律进行了研究。2014年，董晨等^[7]提出了一种带落角约束与控制约束的纵向制导律，并给出了制导律参数的在线整定方法。这些方法都是基于控制饱和的前提，即过载约束在导弹拦截阶段为时不变的常值，这与稠密大气中的拦截情况有较大出入。
2003年，Cho及其团队研究了二维平面内的一种最优制导律，该制导律的关键在于考虑到导弹速度时变对制导带来的影响，推导出适用于反舰导弹的带落角约束的导引律^[8-9]。2014年，王辉和林德福等^[10]以导弹剩余飞行时间的幂函数为基础构建扩展的目标罚函数，并探讨了不同指数取值对弹道成型的影响。以上方法均可认为是对时变可用过载边界的近似估计，与实际情况差别较大，工程上难以实现。
本文针对考虑机动性能的带交会角约束的导引律展开研究，在以可用过载为时变权系数的基础上，引入当地阻力系数，提出一种不仅满足时变过载约束又能保证导弹机动损耗能量最小(即机动效率)的导引律，并通过迭代确定约束边界，保证了时变过载约束的精度，为防空导弹拦截高速机动目标提供了方法参考。
1 弹目相对运动数学模型 交会角即目标速度与导弹速度反方向之间的夹角^[11]。建立导弹与目标相对运动关系，如图 1所示^[3]。图中：M为导弹所在位置；T为目标所在位置；V_M为导弹速度方向；V_T为目标速度方向；q为弹目视线角；a_M为导弹加速度；a_T为目标加速度; γ_M为导弹与水平面夹角；γ_T为目标与水平面夹角；γ_MT为导弹与目标夹角；q₀为初始弹目视线角；LOS为弹目视线; LOS₀为初始弹目视线。

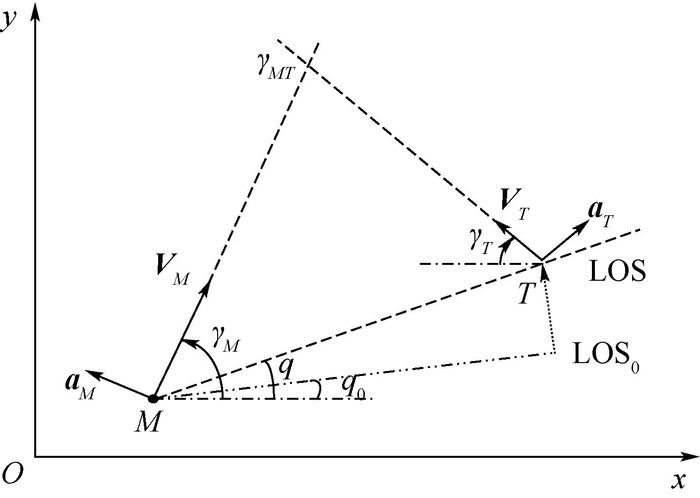图 1 弹目相对运动关系示意图[3] Fig. 1 Schematic diagram of missile-target relative movement geometry[3]

图选项

R为弹目相对距离，有

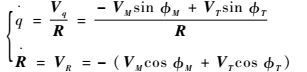(1)

式中：V_q为垂直视线的速度分量；φ_M=γ_M-q；φ_T=γ_T+q。
γ为弹目交会角，则弹目相对速度和相对交会角速度分别为

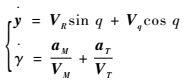(2)

当q为小量时，对式(2) 线性化：

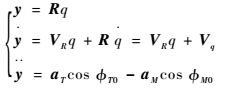(3)

状态空间可表示为

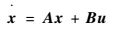(4)

式中：u为控制量；。
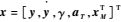
对x求导，得

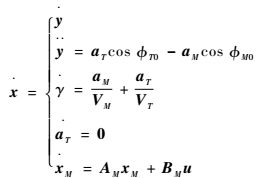(5)

则

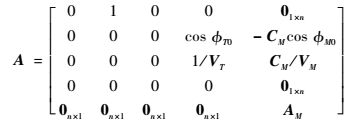(6)

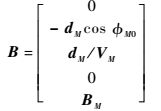(7)

式中：C_M和d_M为常数矩阵。该问题中，目标函数可表示^[12]为

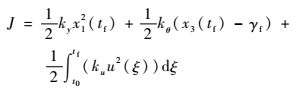(8)

式中：t_f为终端时刻；γ_f为期望交会角; k_y、k_θ和k_u分别为位置加权系数、交会角加权系数和控制量加权系数^[13]；期望的终端位置x₁(t_f)=0，终端交会角x₃(t_f)=γ_f。
2 多约束导引律 应用Bryson降阶理论，定义新的状态变量为

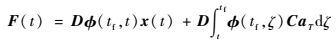(9)

式中：D为恒定的常数矩阵；C为控制量矩阵；φ(t_f, t)为状态转移矩阵。在不考虑动态特性交会角约束问题的研究中，取

(10)

对F(t)求微分，得

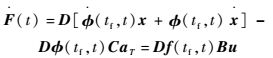(11)

式中：f(t_f, t)为转换矩阵。
又有

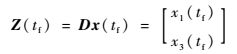(12)

此时，目标函数可以表示成

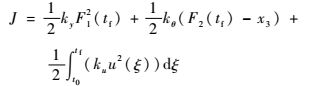(13)

引入拉格朗日乘子矢量λ，得到Hamilton函数为

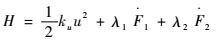(14)

求解协态方程，可得

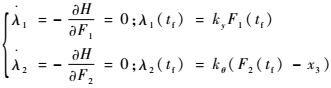(15)

求得

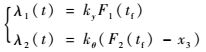(16)

不考虑弹体的动态特性，则弹体加速度响应延迟为0，此时a_M=u，则

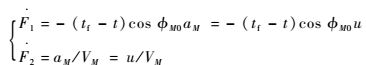(17)

求解控制方程

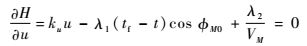(18)

得到

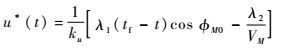(19)

将式(16) 中λ₁(t)、λ₂(t)代入式(19)，求得

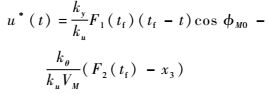(20)

将式(20) 代入式(17)，并对式(17) 求t到t_f积分，根据式(12) 终端条件，可得方程组为

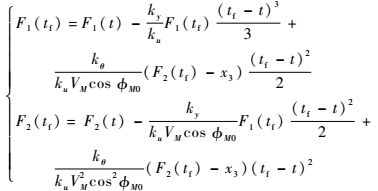(21)

定义剩余时间t_g=t_f-t，求解式(21) 二元一次方程组，得F₁(t_f)、F₂(t_f)，代入式(20)，得

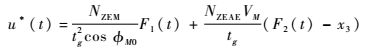(22)

式中：

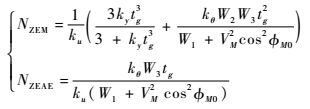(23)

其中：

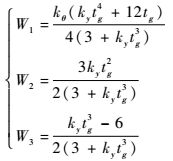(24)

根据零效脱靶量ZEM与零效角误差ZEAE的定义^[14]，有

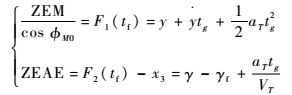(25)

得优化导引律为

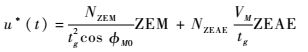(26)

视线转率可以由零效脱靶量垂直于视线的分量表示^[14]，故有

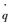
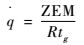(27)

代入ZEM、ZEAE，得到工程上更易接受的形式，即

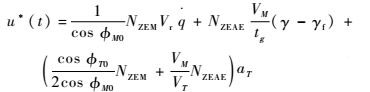(28)

式中：V_r为导弹目标相对速度；cosφ_M0≈cosφ_T0≈1。
式(23) 中，N_ZEM、N_ZEAE取k_y、k_θ趋于无穷, k_u取为与时变约束相关的函数形式。
此时导引律可表示为

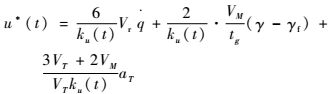(29)

当目标不做机动时，式(29) 中a_T=0。
3 机动性能权系数的确定 对时变可用过载权系数k_u与时变机动效率权系数k_u^′的计算方法分别在3.1节与3.2节加以说明，2种系数的确定都需要对弹道进行迭代仿真，而k_u^′的计算无须对迎角、舵偏角进行配平计算，极大提升了计算速度。
3.1 时变可用过载权系数 防空导弹基本保持在大气层内飞行，空气密度直接取决于导弹飞行高度，导弹速度受阻力、重力共同作用，而阻力又是空气密度与飞行速度的函数，几个因素共同影响弹道形式，从而影响导弹飞行高度。这决定了弹道过载边界无法得到解析解，若希望得到闭环制导形式，必须通过迭代计算。
首先考虑可用过载约束情况。导弹法向过载可按式(30) 计算^[15]：

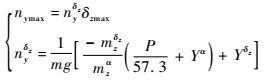(30)

式中：n_ymax为导弹可用过载；n_y^δ_z为法向过载对舵偏角的导数；m为导弹总质量；g为重力加速度；导弹飞行被动段推力P=0；Y^α和Y^δ_z分别为单独迎角产生升力和单独舵偏角产生升力；m_z^α和m_z^δ_z分别为迎角引起的俯仰力矩系数和舵偏角引起的俯仰力矩系数；δ_zmax为俯仰通道舵偏角限幅，其由舵面失速迎角、铰链力矩与舵机能力共同制约。
当舵偏角达到限幅，需验证此时迎角是否达到临界迎角，如达到则需要用临界迎角反算舵偏角，求得平衡状态下可用过载，如式(31) 所示：

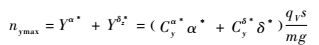(31)

式中：C_y^α*和C_y^δ*分别为法向力对迎角和舵偏角的导数；α^*和δ^*分别为平衡迎角和平衡舵偏角；q_V为动压；s为参考面积。
式(29) 中，取k_u(t)≡1，相当于未考虑过载约束的导引律。将导引律代入末制导弹道进行仿真，由式(30)、式(31) 可得末制导全程可用过载，将终端可用过载取为1，并表示为剩余时间t_g的函数，通过最小二乘法进行多项式拟合，得单位化过载边界，如图 2所示。

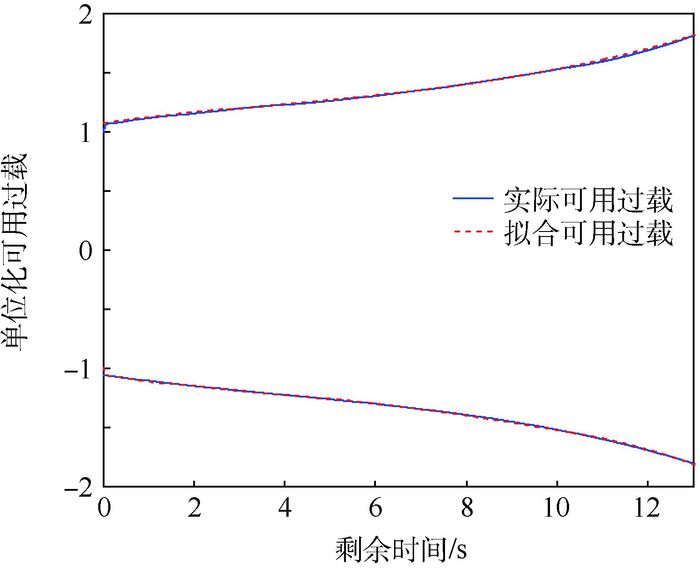图 2 可用过载拟合曲线与实际可用过载曲线对比 Fig. 2 Contrast between available overload fitted curve and practical available overload curve

图选项

设过载拟合曲线为n_u，取

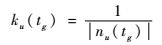(32)

一般情况下，由式(32) 可见，随剩余时间t_g的减少，可用过载n_u绝对值越小，则k_u越大，表明此时对控制指令的“惩罚”越厉害。
将式(32) 代入式(29)，将新的制导指令代入弹道方程进行迭代。最后2次迭代得到k_u(t)误差小于0.1%，认为迭代收敛，得到机动性能约束下的闭环导引律。
然而，防空导弹可用过载的计算需要对每一时刻的迎角、舵偏角进行配平迭代求解，计算量较大，极大降低了时变可用过载权系数的迭代速度。
3.2 时变机动效率权系数 以3.1节中方法，当防空导弹可用过载较大，即机动能力较强，此时有利于导弹完成需要大过载的动作，如较大的转弯。然而，在导弹具有较大可用过载的同时，一般具有较大的动压，此时导弹的阻力也较为显著，当导弹在大可用过载下完成大的机动，同时会带来大的能量损耗，这在试图保证末端速度和射程的防空导弹中是不希望的。
基于以上分析，提出一种新的控制项加权系数，满足时变过载约束同时保证导弹机动损耗能量最小，即机动效率最优。
将式(31) 除以导弹当地阻力系数，有

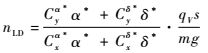(33)

由式(33) 可见，导弹机动效率n_LD可以看成由两部分变量(导弹升阻比C_y/C_x与动压q_V再乘以常量s/mg)组成，即

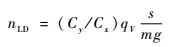(34)

常规防空导弹升阻特性如图 3所示。升阻比C_y/C_x是马赫数Ma和迎角α的函数，达到使C_y/C_x最大的迎角前，C_y/C_x随迎角变化近似满足线性关系，而在给定迎角下，C_y/C_x随Ma变化也可近似作线性变化，故可将马赫数、迎角的函数C_y/C_x降维为仅关于马赫数Ma的函数，即

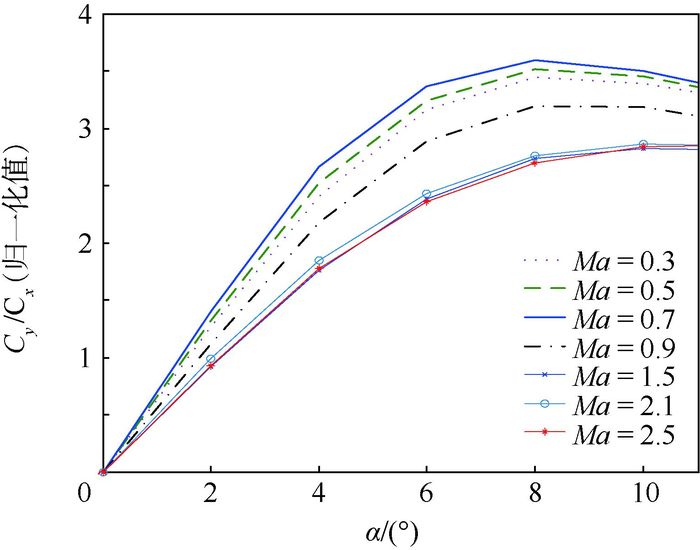图 3 常规防空导弹升阻比曲线 Fig. 3 Common air-defense missile's lift-drag ratio curves

图选项

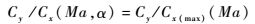(35)

因此，可用C_y/C_x(max)表征导弹满足需用过载时的能量消耗程度，即机动效率。
常规防空导弹C_y/C_x(max)随Ma的变化如图 4所示。

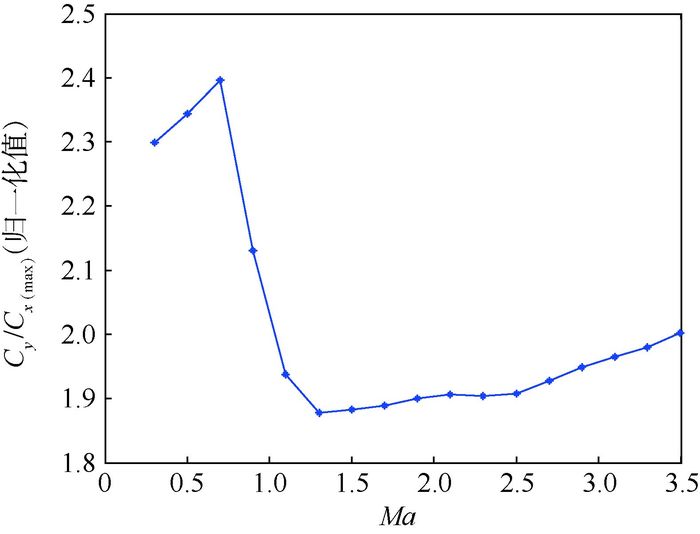图 4 常规防空导弹Cy/Cx(max)随Ma变化 Fig. 4 Variation of common air-defense missile Cy/Cx(max) with Ma

图选项

令

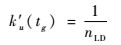(36)

式(36) 中，n_LD越小，表示导弹做同等机动需要消耗的能量越大，k_u^′越大，则此时对控制指令的“惩罚”越厉害。通过权系数k_u^′的选取，使导弹在机动效率较高的情况下尽量做大机动，在机动效率较低的情况下做小机动或不做机动，使防空导弹在满足一定交会角的前提下对空袭目标进行有效拦截。
同3.1节所述，n_LD要经过多次迭代确定，当最后2次迭代仿真结果误差在0.1%以内，认为迭代收敛。
时变机动效率权系数的确定无需经过配平迭代，仅需知道弹道的速度与动压信息，在保证导弹机动效率的同时，极大提高了时变权系数的迭代速度。
4 弹道仿真分析 基于以上分析，取典型防空导弹进行弹道仿真。取低空常速飞行目标V_Tx=-60 m/s, V_Ty=5 m/s, 导弹初始速度V₀=1 000 m/s，以末端交会角81°拦截。
分别对比不考虑机动约束(文献[3]导引律)、考虑可用过载约束、考虑机动效率约束3种不同导引律下末制导弹道仿真结果，如图 5~图 9所示。

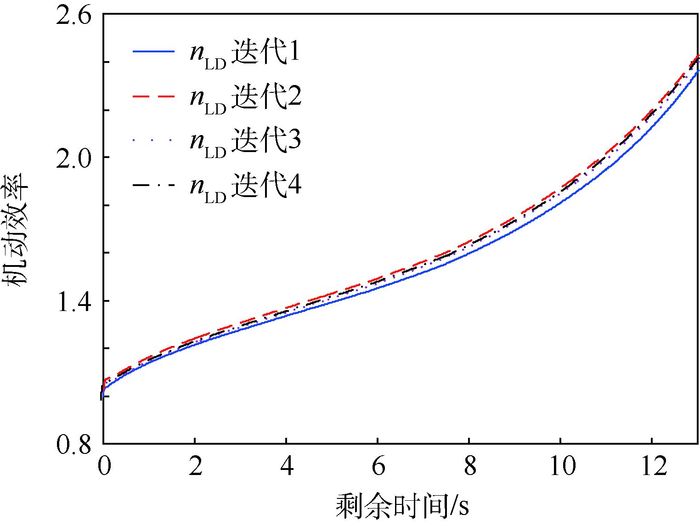图 5 导弹机动效率随迭代次数变化 Fig. 5 Variation of missile maneuvering efficiency with iteration times

图选项

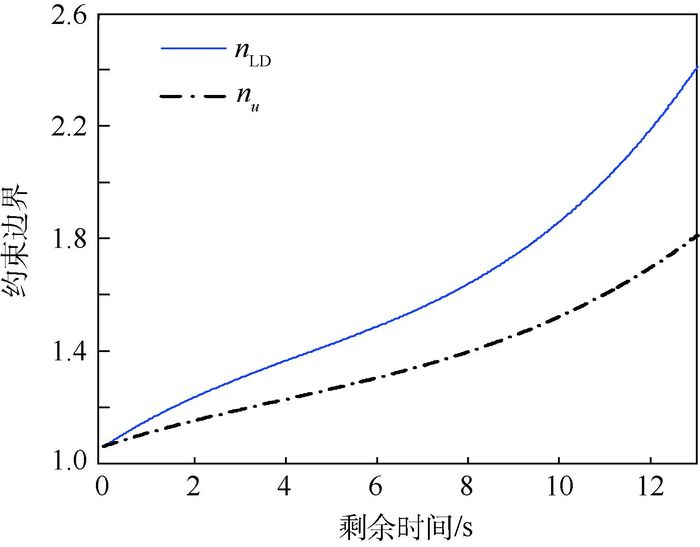图 6 性能约束边界与剩余时间关系 Fig. 6 Relationship between performance constrained boundary and time-to-go

图选项

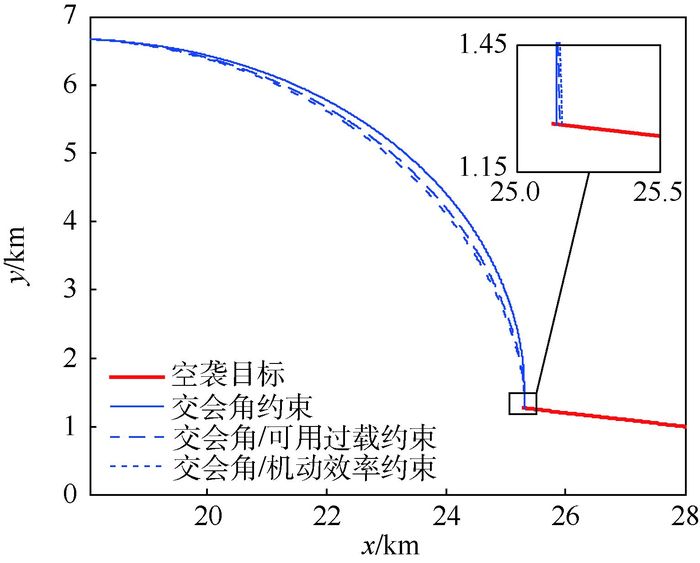图 7 3种导引律末制导弹道对比(匀速目标) Fig. 7 Three guidance laws' terminal trajectory contrast(constant target)

图选项

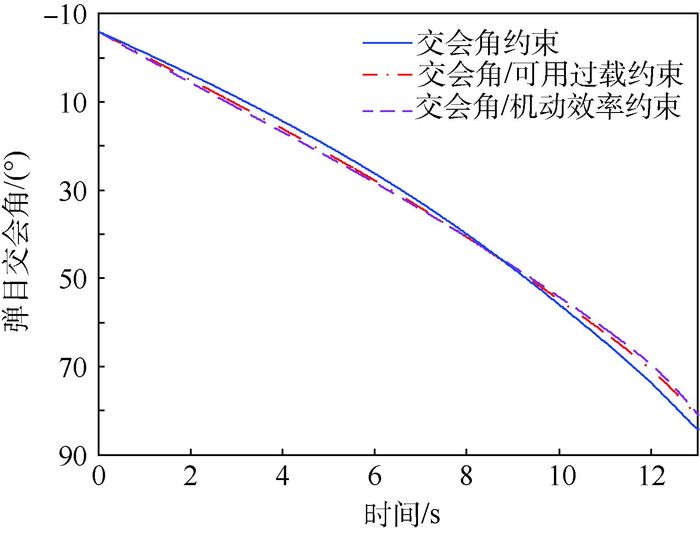图 8 3种导引律弹目交会角对比(匀速目标) Fig. 8 Three guidance laws' missile-target intercept angle contrast(constant target)

图选项

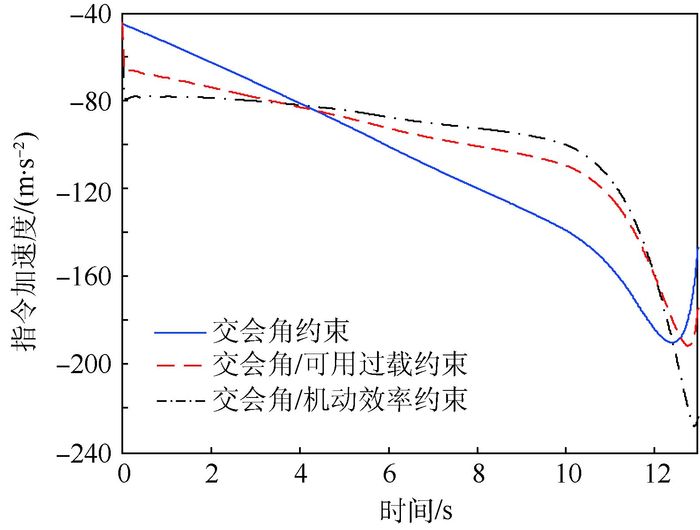图 9 3种导引律指令加速度对比(匀速目标) Fig. 9 Three guidance laws' command acceleration contrast (constant target)

图选项

图 5为导弹机动效率随迭代次数的变化曲线，因为导弹约束边界会因弹道变化而改变，所以必须通过迭代确定，一般约束边界须经过4~7次迭代趋于收敛。当后2次迭代误差在0.1%以内，认为约束边界确定。
经过对制导弹道进行仿真迭代，图 6为2种约束边界随剩余时间的变化曲线，机动效率约束边界曲线n_LD要明显高于可用过载约束边界曲线n_u，这是由于仿真算例中，导弹飞行速度正处于机动效率随速度变化的单调区间。
对比不考虑机动约束、考虑可用过载约束、考虑机动效率约束的末制导弹道仿真结果，如图 7所示，由于所要求交会角较大，3种导引律使导弹在末制导阶段机动策略各不相同。
对比3种导引律下的弹目交会角变化情况，如图 8所示，考虑机动性能的导引律在导弹机动性能较好的情况下实现较大转弯，而未考虑机动性能的导引律在导引末端期望实现较大转弯，因可用过载难以满足指令需求，导致较大的交会角误差。
图 9分别对比3种导引律下的指令加速度，对比结果显示，考虑机动性能的导引律过载指令在末制导阶段充分考虑了导弹的机动过载能力，保证导弹在大可用过载下做较大机动，分配更为合理。而考虑可用过载与考虑机动效率的导引方式因权系数的侧重因素不同，导致过载指令有明显差异。
对比3种导引律下，拦截末端时刻的仿真结果如表 1所示。结果对比表明，未考虑机动性能的导引律因对机动性能分配不合理导致脱靶。考虑机动性能的2种导引律均能实现对空袭目标的有效拦截，而考虑机动效率约束的导引律相比考虑可用过载约束的导引律能有效降低导弹的拦截时间，提高导弹末端速度，有效提高了防空导弹的拦截能力与毁伤效果。
表 1 不同导引律仿真结果对比(匀速目标) Table 1 Different guidance laws' simulation results contrast (constant target)

导引律	脱靶量/m	末端速度/(m·s-1)	末端交会角/(°)	拦截时间/s	交会角误差/(°)
交会角约束	5.75	455.2	84.29	13.63	3.29
交会角/可用过载约束	0.43	514.5	80.31	13.38	-0.69
交会角/机动效率约束	0.51	519.4	81.05	13.29	0.05

表选项






为分析本文中导引律式(29)，拦截机动目标的有效性，取速度V_Tx=-180m/s, V_Ty=0m/s, 并以过载a_T=1g单侧机动飞行的目标进行仿真分析。导弹初始速度V₀=1 000 m/s，以末端交会角0°逆轨拦截。3种制导形式的末制导段弹道如图 10所示，3种导引律指令加速度对比如图 11所示。

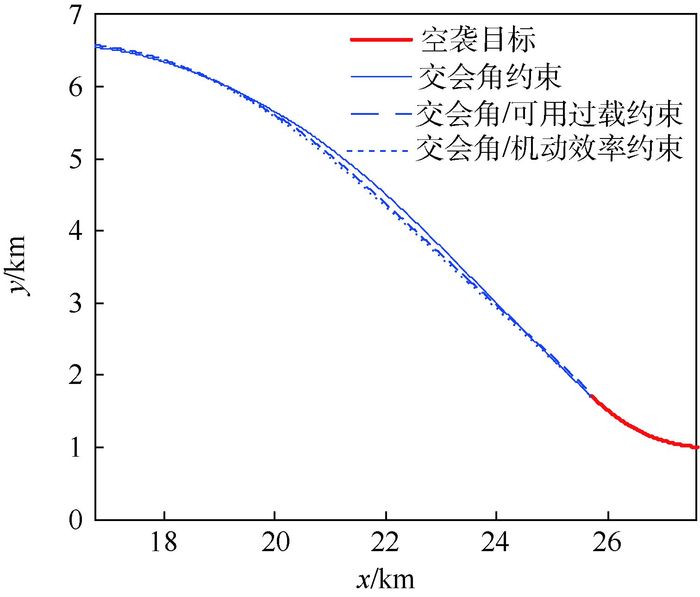图 10 3种导引律末制导弹道对比(机动目标) Fig. 10 Three guidance laws' terminal trajectory contrast (manevering target)

图选项

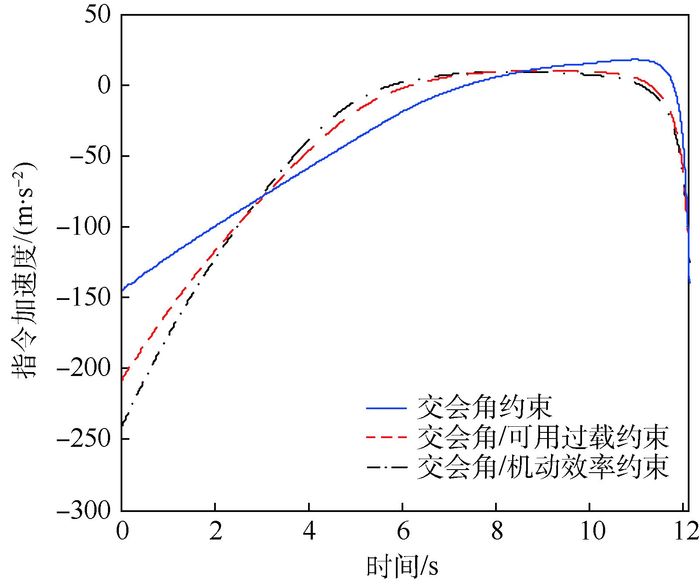图 11 3种导引律指令加速度对比(机动目标) Fig. 11 Three guidance laws' command acceleration contrast (manevering target)

图选项

对比3种导引规律下拦截末端时刻的仿真结果，如表 2所示。
表 2 不同导引律仿真结果对比(机动目标) Table 2 Different guidance laws' simulation results contrast (manevering target)

导引律	脱靶量/m	末端速度/(m·s-1)	末端交会角/(°)	拦截时间/s	交会角误差/(°)
交会角约束	1.58	570.2	-1.00	12.30	-1.00
交会角/可用过载约束	0.14	569.5	-0.66	12.29	-0.66
交会角/机动效率约束	0.22	571.1	-0.60	12.29	-0.60

表选项






对单侧机动目标拦截仿真结果表明，3种导引律均能对机动目标进行有效拦截，考虑机动性能的2种导引律较未考虑机动性能的导引律脱靶量和交会角误差明显降低。但是对末端速度的提升效果并不明显，这是由于逆轨拦截对导弹过载能力的要求较要求大交会角情况下要小很多，考虑机动性能的导引律优势未能充分体现。
本文中导引律推导是以小角度线性化假设为前提展开的，在以上的仿真中，初始的φ_M0=q₀=21.5°，已不符合小角度线性化假设条件。因此，该导引律的推导中，在φ_M0、q₀较大的情况下，仍具有适用性。
5 结论 本文针对考虑机动性能的带交会角约束导引律展开研究:
1) 推导了一种通过迭代确定时变控制项权系数的闭环制导规律。
2) 考虑以可用过载约束的导引律在机动同时会带来较大的附加阻力，在以可用过载为时变权系数的基础上，引入当地阻力系数，提出一种不仅满足时变过载约束又能保证导弹机动损耗能量较小的导引形式。
3) 将3种导引律进行仿真验证，证明所设计导引律的有效可行，特别对过载要求较高的情况下效果明显。同时极大提高了迭代速度，为防空导弹拦截高速机动目标提供了方法参考。

参考文献

[1]	斯维特洛夫Β Γ, 戈卢别夫И C. 防空导弹设计[M]. 《防空导弹设计》编译委员会, 译. 北京: 中国宇航出版社, 2004: 111-116. SVATROV Β Γ, GRUBIEF И C.Air-defense missile design[M].Air-defense Missile Design Compliation Committee, translated.Beijing:Chinese Space Press, 2004:111-116(in Chinese).
[2]	RYOO C K, CHO H, TAHK M J. Time-to-go weighted optimal guidance with impact angle constraints[J].IEEE Transactions on Control System Technology, 2006, 14(3): 483–492.DOI:10.1109/TCST.2006.872525
[3]	SHAFERMAN V, SHIMA T. Linear quadratic guidance laws for imposing a terminal intercept angle[J].Journal of Guidance, Control, and Dynamics, 2008, 31(5): 39–48.
[4]	张友安, 马培蓓. 带有攻击角度和攻击时间控制的三维制导[J].航空学报, 2008, 29(4): 1020–1026. ZHANG Y A, MA P B. Three-dimensional guidance law with impact angle and impact time constraints[J].Acta Aeronautica et Astronautica Sinica, 2008, 29(4): 1020–1026.(in Chinese)
[5]	CLOUTIER J R.All-aspect acceleration limited homing guidance[C]//AIAA Guidance, Navigation, and Control Conference and Exhibit.Reston:AIAA, 2005, 8:9-11.
[6]	HEXNER G, SHIMA T. Stochastic optimal control guidancelaw with bounded acceleration[J].IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(1): 71–78.DOI:10.1109/TAES.2007.357155
[7]	董晨, 晁涛, 王松艳, 等. 带落角约束与控制约束的纵向制导律[J].固体火箭技术, 2014, 37(3): 285–290. DONG C, CHAO T, WANG S Y, et al. Longitudinal guidance law with constraints on impact angle and control[J].Journal of Solid Rocket Technology, 2014, 37(3): 285–290.(in Chinese)
[8]	SONG T L, SHIN S J, CHO H. Impact angle control for planer engagements[J].IEEE Transactions on Aerospace and Electronic Systems, 1999, 35(4): 1439–1444.DOI:10.1109/7.805460
[9]	RYOO C K, CHO H, TAHK M J.Closed-form solutions of optimal guidance with terminal impact angle constraint[C]//Proceedings of 2003 IEEE Conference on Control Application.Piscataway, NJ:IEEE Press, 2003:504-509.
[10]	王辉, 林德福, 崔晓曦. 一类扩展的弹道成型制导律[J].北京理工大学学报, 2014, 34(6): 597–603. WANG H, LIN D F, CUI X X. Extended trajectory shaping guidance laws[J].Transactions of Beijing Institute of Technology, 2014, 34(6): 597–603.(in Chinese)
[11]	王丽英, 张友安, 黄诘. 带约束的末制导率与伪谱法轨迹优化[M].北京: 国防工业出版社, 2015: 92-96. WANG L Y, ZHANG Y A, HUANG J. Guidance law under multiple constrained and GPOPS trajectory optimization[M].Beijing: Nationnal Defense Industry Press, 2015: 92-96.(in Chinese)
[12]	王青, 陈宇, 张颖昕, 等. 最优控制——理论、方法与应用[M].北京: 高等教育出版社, 2010: 65-71. WANG Q, CHEN Y, ZHANG Y X, et al. Optimal control theory, mehod and application[M].Beijing: Higher Education Press, 2010: 65-71.(in Chinese)
[13]	ZARCHAN P. Tactical and strategic missile guidance, progress in astronautics and aeronautics[M].Reston: AIAA, 2003.
[14]	钱杏芳, 林瑞雄. 导弹飞行力学[M].3版北京: 北京理工大学出版社, 2008: 62-63. QIAN X F, LIN R X. Missile flight dynamics[M].3rd edBeijing: Beijing Institute of Technology Press, 2008: 62-63.(in Chinese)
[15]	孙未蒙. 空地制导武器多约束条件下的制导率设计[D]. 长沙: 国防科学技术大学, 2008: 8-13. SUN W M.Research on guidance law design with terminal impact angle constraints in air-to-surface guided weapon[D].Changsha:National University of Defense Technology, 2008:8-13(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-90002-2010164860.htm