乔志德[7]首次提出了层流超临界翼型设计思想,杨青真和张仲寅[8]研究了雷诺数对边界层特性和对气动力的影响。在设计层流翼型过程中,有2个主要的关键点:① 能比较精确地预测层流转捩;② 有效的优化设计策略。
目前层流转捩预测方法主要有:大涡模拟(LES)、直接数值模拟(DNS)、N-因子(eN)方法[9-10]以及转捩经验方法。前3种方法的计算量过大,很难应用于工程设计;而经验方法的精度有限。Menter等[11]提出了将γ-Reθt转捩模型[12]耦合剪切应力输运(SST)[13]两方程湍流的方法,通过求解雷诺平均的Navier-Stokes方程组,模拟翼型的转捩流动,可针对不同的转捩问题进行计算。这种方法由于计算量相对较小,且计算结果与实验数据吻合较好,可用于工程设计。
在优化策略方面,邓磊等[14]采用了基于响应面方法的优化策略对自然层流翼型进行了多目标优化设计; Han等[15-16]基于eN方法,采用Kriging代理模型的优化策略对翼型和机翼进行了研究;赵轲等[17]基于γ-Reθt转捩模型,取样1 000个样本点,采用Kriging代理模型的优化策略对NASA SC(2)0412进行了层流超临界翼型稳健设计研究;张宇飞等[18]采用直接CFD计算,使用基于遗传优化算法的策略对RAE2822翼型进行了层流优化设计,共进行了3 200次CFD计算,并研究了压力分布对层流的影响;马晓永等[19]利用TRANAIR程序与eN方法相结合,采用基于梯度的优化策略对某自然层流机翼进行了多点优化设计,耗时25~30 h。在设计层流翼型过程中,大部分国内外作者选择应用全局优化方法,这是因为应用基于梯度的优化算法,容易陷入局部最优解,并且当初始翼型不是层流翼型时,可能无法寻找到具有层流翼型特征的翼型。但使用全局优化方法时,如果采用直接CFD计算,往往需要几千次的计算才能达到满意的结果,计算量过大。如果在计算中采用代理模型,虽然计算量较小,但存在一定的误差,特别是由于转捩点问题具有高度非线性,构建高精度的代理模型难度很大。
针对上述这些问题,考虑到层流超临界翼型压力分布的特点(转捩点后会存在弱激波),本文提出一种两轮优化策略。在第1轮优化中,利用基于代理模型的遗传算法寻求较好的超临界层流翼型,这轮优化的目的是获得较好的初始解,对代理模型的精度要求并不高。第2轮采用基于梯度的优化算法,在第1轮优化结果的基础上,进一步削弱转捩点后的激波。
1 数值模拟方法 本文采用自行开发的CFD气动程序,该程序中采用基于格点格式的有限体积法对Navier-Stokes方程进行空间离散,采用广义最小残差算法(GMRES)隐式推进格式进行时间离散,并采用γ-Reθt转捩模型耦合剪切应力输运模式的湍流模型对翼型边界层转捩进行预测。
1.1 转捩模型 为了准确地预测外形变化对边界层转捩和分离的影响,在CFD程序中引入了基于流场当地变量的转捩模式,即γ-Reθt转捩模型。这个模型是2个分别关于间歇因子γ和临界动量厚度雷诺数Reθt的输运方程。无量纲守恒形式γ的运输方程为
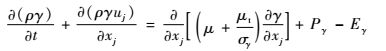 | (1) |
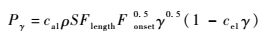 | (2) |
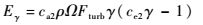 | (3) |
式中:ρ为密度;t为时间;uj为速度;σγ=1为关于间歇因子输运方程中粘性项的经验常数;Pγ为间歇因子γ的生成项;Eγ为间歇因子γ的耗散项;S为应变率的模;Ω为涡量的模;μ为层流黏性系数;μt为湍流黏性系数;Flength为控制转捩区长度的经验参数;Fonset为控制转捩开始的位置;xj为翼型坐标;Fturb为在边界层外防止再次层流化的源;常数ce1=0.1,ce2=50,ca1=2,ca2=0.06。
临界动量厚度雷诺数Reθt的运输方程为
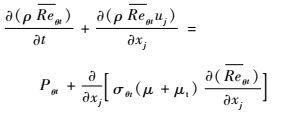 | (4) |
 | (5) |
式中:Reθt为转捩动量厚度雷诺数,在边界层外,Reθt等于Reθt,在边界层内,Reθt由式(4) 计算;cθt=0.03为常数;Pθt为临界动量厚度雷诺数Reθt的生成项;σθt=2.0为常数;Fθt为混合函数,在边界层以外Fθt=0,而在边界层内Fθt=1.0。
1.2 CFD程序验证 为了验证自编CFD程序对边界层转捩的有效性,对典型层流翼型NLR-7301的转捩流动进行了数值模拟。计算条件为:马赫数Ma范围0.299~0.774,迎角在0.3°附近,雷诺数范围1.0×106~2.4×106。当湍流度设为1.5%时,计算结果与实验结果[20]基本吻合,如图 1和图 2所示。图 1为上下翼面转捩点位置(x/c为翼型弦向相对坐标)计算值与实验值的对比,图 2为阻力系数(CD)计算值与实验值的对比。从图 1可看出,在Ma<0.7时,翼型上表面转捩位置基本不变,而在跨声速范围内,随着激波的出现,在激波前的顺压梯度范围增大,使转捩点显著后移。
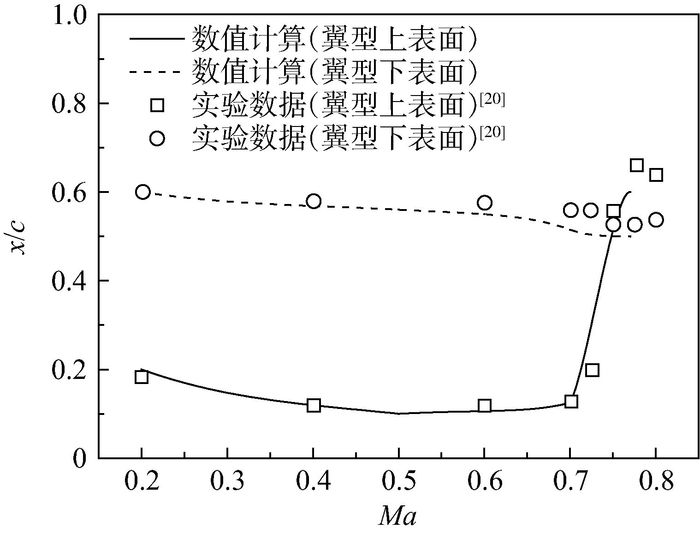 |
| 图 1 转捩点位置计算与实验[20]对比 Fig. 1 Comparison of transition position between computation and experiment[20] |
| 图选项 |
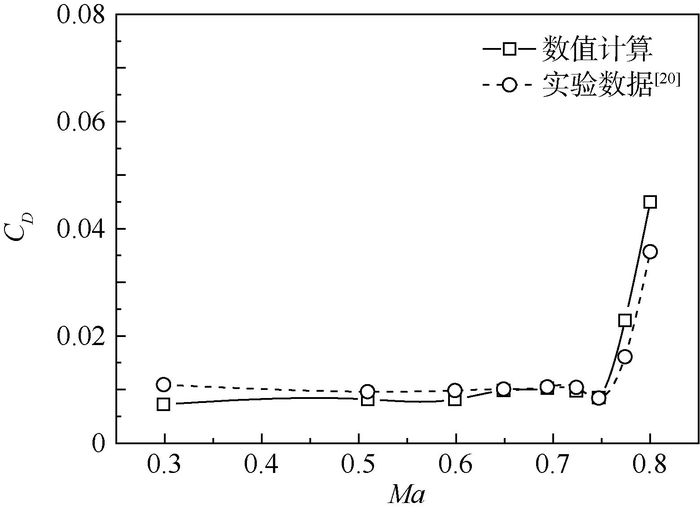 |
| 图 2 阻力系数计算与实验[20]对比 Fig. 2 Comparison of drag coefficient between computation and experiment[20] |
| 图选项 |
2 优化策略 现有的超临界翼型往往并不是层流翼型,上下表面的层流区过小,特别是上表面,层流区很小。因此,在设计时应首先设法增加翼型的层流区的比例。但另一方面,层流区较多的翼型可能有较强的激波,会增加波阻。为此,本文提出了一种两轮优化策略来获得超临界层流翼型。
2.1 第1轮优化 第1轮优化的目的是:在满足几何特性、设计升力系数和升阻比约束要求的前提下,设法提高层流区域比例。为了获得层流翼型,需要在整个设计空间进行搜索,应采用具有全局寻优功能的优化算法,因此在第1轮优化中,采用遗传算法。但遗传算法收敛速度慢,调用气动分析模型次数过多,计算量太大。为减少计算量,采用基于代理模型的优化方法。通过样本点分析建立代理模型,可有效减少优化迭代过程中的计算量。代理模型建立后,采用遗传算法在设计空间内寻优,使用罚函数的方法剔除不满足约束的解,最终获得最优解。第1轮优化的问题表述如下。
目标:上下表面层流区域最大。
约束:① 设计升力系数;② 升阻比;③ 翼型厚度;④ 翼型前缘半径。
设计变量:① 描述翼型的参数;② 迎角。
在这轮优化中,对代理模型的精度要求并不高,因为这一轮优化的目的是为下一轮优化提供一个好的初始解。
2.2 第2轮优化 第2轮优化的目的是:对第1轮优化获得的翼型进行“微调”,在保证层流区比例前提下,减弱或消除激波,进一步提高翼型的升阻比,第2轮优化中的初始解为第1轮优化的最优解。由于第2轮优化是对第1轮的最优解进行“微调”,可采用基于梯度的优化算法,梯度计算采用有限差分的方法。考虑到基于梯度的优化算法收敛速度快,为了避开代理模型的精度问题,气动分析模型采用直接调用CFD程序,以保证气动分析的计算精度。
第2轮优化中,目标函数为升阻比,层流区域为约束,几何约束不变。其优化问题表述如下。
目标:升阻比最大。
约束:① 设计升力系数;② 上下表面层流区域比例;③ 翼型厚度和前缘半径与第1轮优化中的约束要求相同。
设计变量:① 描述翼型的参数;② 迎角。
3 优化设计平台 根据第2节优化策略,建立计算流程和计算平台,计算流程如图 3所示。首先选择一种初始翼型(超临界翼型);然后对翼型进行参数化建模,并建立气动分析的代理模型;之后基于代理模型进行第1轮优化;最后通过基于梯度优化算法完成第2轮优化。以下各小节对流程中主要环节进行说明。
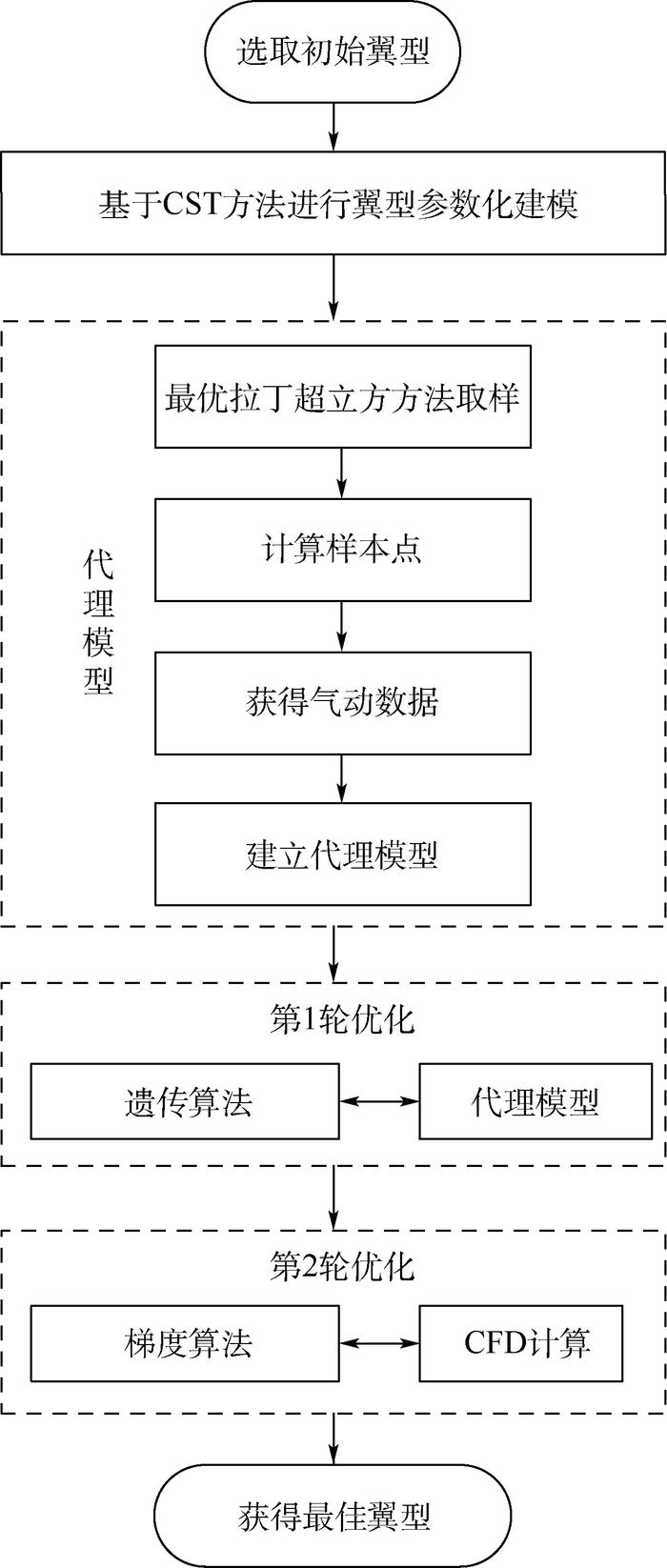 |
| 图 3 超临界层流翼型优化设计流程 Fig. 3 Optimization process of supercritical laminar flow airfoil design |
| 图选项 |
3.1 翼型参数化建模 在进行翼型参数化建模时,希望参数化方法具有较少的参数并能包含较大的设计空间。近年来,形状分类函数转换(CST)方法[21]广泛应用于翼型设计优化中,CST包含有类函数和型函数,其数学表达式为
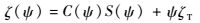 | (6) |
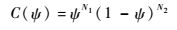 | (7) |
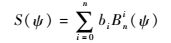 | (8) |
式中:ζ(ψ)为CST表达式,ψ为变量;Bni(ψ)为伯恩斯坦多项式;C(ψ)为类函数;N1、N2决定类函数的外形;S(ψ)为型函数,用来描述给定类函数的特性;ζT为翼型后缘厚度;bi为型函数中的各项系数,用于决定型函数的外形。
对于C(ψ),本文中,N1=0.5,N2=1,分别表示翼型的圆前缘和尖后缘。在S(ψ)中:
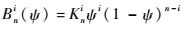 | (9) |
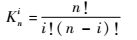 | (10) |
式中:Kni为系数因子,n为伯恩斯坦多项式的阶数。
根据式(6)~式(10),编写了一个翼型参数化几何模型程序,可描述或拟合各种翼型。式(10) 中伯恩斯坦多项式的阶数作可为输入值,实现对翼型任意阶数的拟合。根据Bogue和Crist[22]对伯恩斯坦多项式阶数的研究表明,当伯恩斯坦多项式阶数n=6时,能够以足够的精度描述翼型的几何形状,因此本文研究中取n=6,共有16个翼型设计参数,包括描述翼型上表面的参数bi(i=1~7) 和翼型上表面后缘厚度ζT1,描述翼型下表面的参数bi(i=8~14) 和翼型下表面后缘厚度ζT2,这些参数可作为设计变量。考虑到将层流翼型配置到机翼上时要考虑最佳安装角问题[23],所以将翼型来流迎角α也作为设计变量,优化后的迎角可作为安装角。设计变量总计有17个,如表 1所示,变量初始值通过拟合得到。例如,若初始翼型为NASA SC(2) 0412,应用6阶CST方法拟合的翼型的相对误差如图 4所示,拟合最大误差位于下表面。表 1中初始值为CST方法拟合后获得的各参数值,设计变量取值范围为初始值上下浮动50%。
表 1 设计变量 Table 1 Design variables
| 变量名 | 下限 | 初始值 | 上限 |
| b1 | 0.091 7 | 0.183 4 | 0.275 1 |
| b2 | 0.054 35 | 0.108 7 | 0.163 05 |
| b3 | 0.098 1 | 0.196 2 | 0.294 3 |
| b4 | 0.041 85 | 0.083 7 | 0.125 55 |
| b5 | 0.135 1 | 0.270 2 | 0.405 3 |
| b6 | 0.050 8 | 0.101 6 | 0.152 4 |
| b7 | 0.116 25 | 0.232 5 | 0.348 75 |
| ζT1 | 0.001 65 | 0.003 3 | 0.004 95 |
| b8 | -0.259 65 | -0.173 1 | -0.086 55 |
| b9 | -0.214 8 | -0.143 2 | -0.071 6 |
| b10 | -0.197 1 | -0.131 4 | -0.065 7 |
| b11 | -0.279 45 | -0.186 3 | -0.093 15 |
| b12 | -0.282 3 | -0.188 2 | -0.094 1 |
| b13 | -0.117 6 | -0.078 4 | -0.039 2 |
| b14 | 0.105 | 0.21 | 0.315 |
| ζT2 | -0.003 3 | -0.002 2 | -0.001 1 |
| α/(°) | 0 | 0.3 | 0.6 |
表选项
 |
| 图 4 翼型NASA SC(2) 0412拟合的相对误差 Fig. 4 Relative error for airfoil NASA SC(2) 0412 fitting |
| 图选项 |
3.2 气动分析 整个气动分析过程由5个部分组成,如图 5所示:① 应用3.1节中参数化建模方法生成翼型几何模型;② 应用网格生成软件Pointwise生成二维结构网格;③ 生成CFD程序中输入文件,设置飞行参数,包括迎角、马赫数等;④ 调用CFD程序,进行流场数值计算;⑤ 计算结束后,提取升阻特性数据、转捩点位置等。
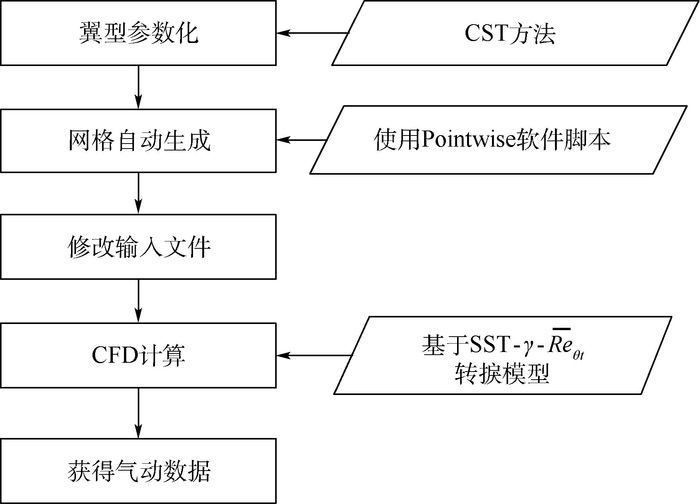 |
| 图 5 气动分析流程 Fig. 5 Process of aerodynamic analysis |
| 图选项 |
3.3 建立代理模型 应用最优拉丁超立方的方法对表 1中的设计变量进行取样,生成样本点。最优拉丁超立方的方法具有良好的空间填充能力,样本点分布均匀,适合拟合非线性响应。采用Kriging模型进行建立近似模型(即代理模型)。相较于其他拟合方式,Kriging模型可以较好地拟合非线性问题,可用于模拟气动特性和转捩特性。
3.4 第1轮优化 在第1轮优化计算中,气动分析模型采用上述建立的代理模型,优化算法采用iSIGHT-FD软件中的多岛遗传算法。这种优化算法具有良好的全局搜索能力,但收敛较慢,所需迭代次数多。由于这一轮优化计算中气动分析是代理模型,因此分析模型的计算量很小,适于采用遗传算法。
3.5 第2轮优化 因在第1轮优化中采用代理模型进行优化,虽然可以在短时间内收敛到最优解,但因为代理模型的精度有限,会带来一定的误差,因此需要进一步修正。另外,在第1轮优化中采用多岛遗传算法,此算法虽然具有全局寻优能力,但局部搜索到精确最优解的能力较弱。基于以上原因,在第2轮优化中,为保证气动分析的精度需实施进一步寻优,气动分析模型直接为CFD计算程序,优化算法采用iSIGHT-FD软件中基于梯度的修正可行方向(MMFD)算法。第1轮优化计算中,由于代理模型存在误差,第2轮的初始解有可能会稍不满足某些约束,MMFD算法不仅收敛快,而且当初始解不满足约束时,具有快速找到可行解和最优解的能力。
3.6 计算平台 应用多学科集成与优化软件iSIGHT-FD,集成上述计算流程,开发了超临界层流翼型优化设计计算平台。该计算平台的应用过程为:① 选取初始的超临界翼型;② 根据翼型参数化建模方法,确定翼型设计变量的上下界;③ 分别设置第1轮优化和第2轮优化的目标函数、约束条件、设计变量。完成上述设置后,整个优化计算过程即可自动进行。
4 算例 以NASA SC(2) 0412超临界翼型为初始翼型,应用所建立的优化计算平台,设计一种超临界层流翼型,以验证本文优化策略的有效性。
参考桁架支撑机翼布局方案[5-6]和巡航速度,给定的设计条件为:Ma=0.75;大气来流下平均雷诺数Re=1.0×107;湍流度为1.5%[11];设计升力系数CL=0.5。
翼型NASA SC(2) 0412在设计升力系数为0.5时,升阻比为59.312。在此算例中,第1轮优化的目的是在保证翼型升阻比不小于59.312的条件下,大幅增加翼型上下表面层流区域,并要求翼型设计升力系数和相对厚度不变,且前缘半径不能小于规定的数值。因此,第1轮优化问题定义如下。
目标:Xup+Xlow最大。
设计变量:① bi(i=1~7), ζT1;② bi(i=8~14), ζT2;③ α。
约束:① t/c=12%;② CL=0.5;③ Γ>Γ0;4RLE>1%。
其中:Xup为翼型上表面转捩位置;Xlow为翼型下表面转捩位置;t/c为翼型相对厚度;CL为翼型设计升力系数;Γ为翼型升阻比;Γ0为翼型初始升阻比;RLE为翼型前缘相对半径。
在第1轮优化中,在建立代理模型时,用最优拉丁超立方的方法取样1 000个样本点,每个样本点需计算5 min,采用分布式计算,共花费500 min,采用代理模型与CFD直接计算对比的方式检查精度,误差最大为转捩点的预测,为7.37%,其他参数相对误差均在2%左右。代理模型建立完成之后,应用多岛遗传算法进行优化计算,进化代数取10 000,耗时3 min后获得最优解,优化历程如图 6所示。
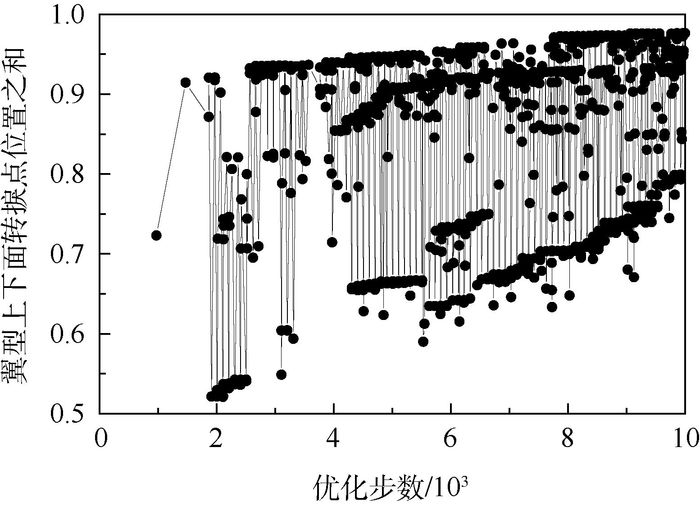 |
| 图 6 第1轮优化计算历程 Fig. 6 Computational history of the first step of optimization |
| 图选项 |
最优解能满足所有的约束条件,且升阻比从59.3提高到76.05。优化前后的外形特征如图 7所示,y/c为翼型各处纵向相对坐标,图中展示了初始翼型的轮廓和第1轮优化后翼型轮廓的对比,迎角由初始的0.3°降低到0.148°。压力系数Cp分布如图 8所示,优化后激波减弱,并且激波位置向后推移,前部区域具有顺压梯度。摩擦阻力系数Cf分布如图 9所示,初始翼型的上表面层流区域比例为25.1%、下表面层流区域比例为38.5%,优化设计后,翼型的上表面层流区域比例为50.3%,下表面层流区域比例为47.0%,翼型上下表面的层流比例分别提高了100.4%和22.1%。
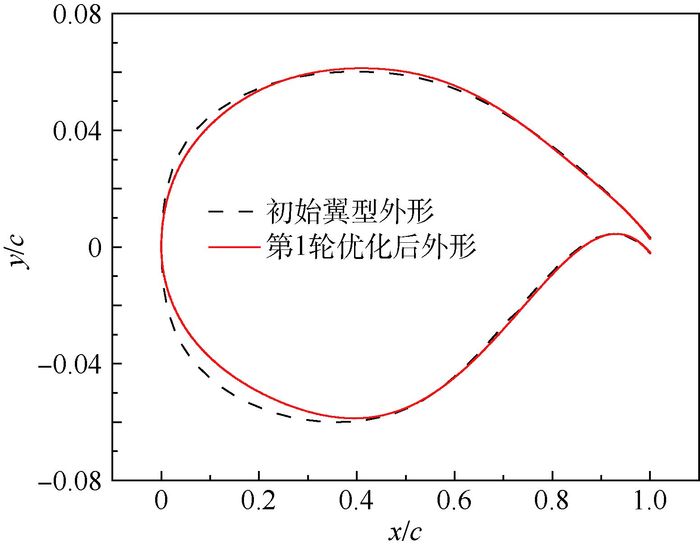 |
| 图 7 初始翼型和第1轮优化后外形对比 Fig. 7 Comparison of geometry between initial airfoil and the first step of optimization |
| 图选项 |
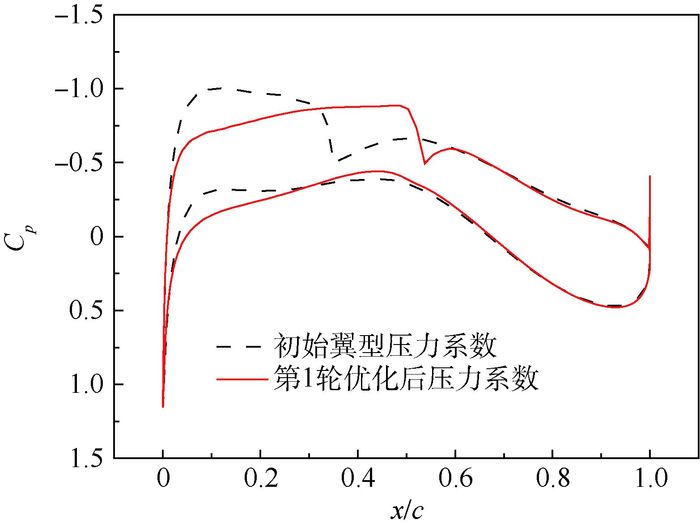 |
| 图 8 初始翼型和第1轮优化后压力系数分布对比 Fig. 8 Comparison of pressure coefficient distribution between initial airfoil and the first step of optimization |
| 图选项 |
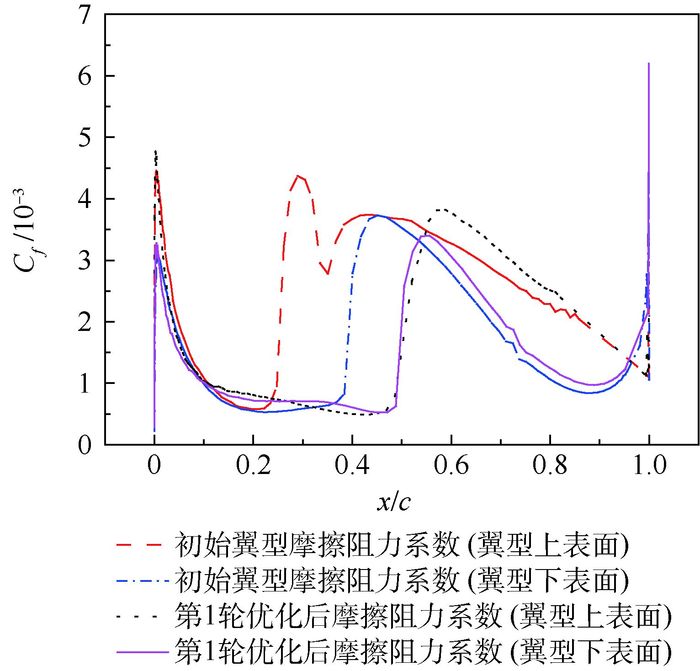 |
| 图 9 初始翼型和第1轮优化后摩擦阻力系数分布对比 Fig. 9 Comparison of friction drag coefficient distribution between initial airfoil and the first step of optimization |
| 图选项 |
第2轮优化目的是在保持上下表面层流区域不减小的前提下,进行减阻优化。因此,第2轮优化问题定义如下。
目标:Γ最大。
设计变量:① bi(i=1~7), ζT1;② bi(i=8~14), ζT2;③ α。
约束:① t/c=12%;② CL=0.5;③ Xup>Xup_opt1;④ Xlow>Xlow_opt1;⑤ RLE>1%。
其中:Xup_opt1为第1轮优化后翼型上表面转捩位置; Xlow_opt1为第1轮优化后翼型下表面转捩位置。
在第2轮优化中,经过93次迭代,耗时465 min,计算收敛,获得最优解,优化历程如图 10所示。优化前后的外形特征如图 11所示,可以看出第2轮优化只是对第1轮优化的结果进行了“微调”,迎角也未发生变化,仍然保持在0.148°。翼型的压力系数分布如图 12所示,优化后激波位置进一步向后推移,升阻比从76.05增加到81.87。摩擦阻力系数分布如图 13所示,上表面层流区域比例提高到55.5%,增加了10.34%,下表面的层流区域几乎保持不变。
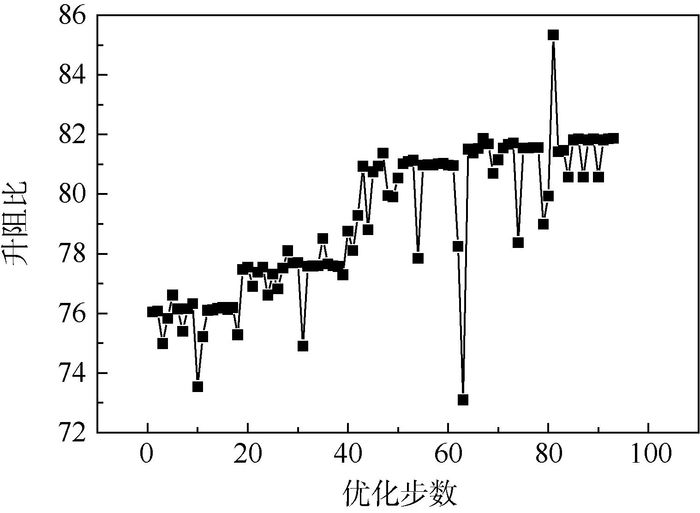 |
| 图 10 第2轮优化收敛历程 Fig. 10 Convergence history of the second step of optimization |
| 图选项 |
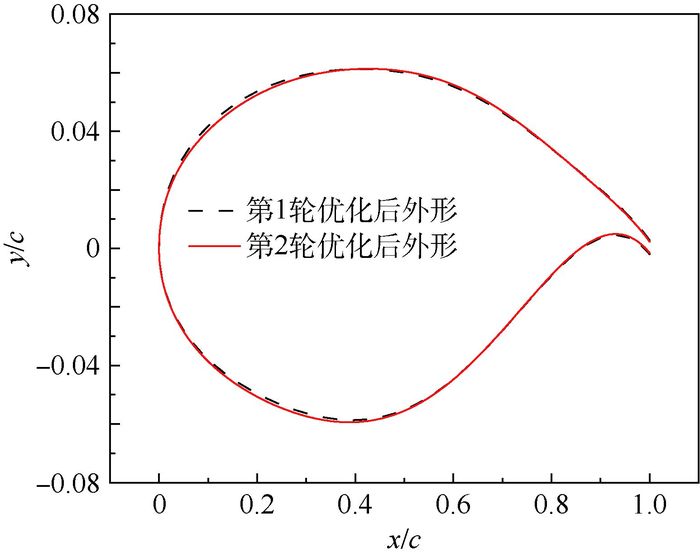 |
| 图 11 第1轮和第2轮优化后翼型外形对比 Fig. 11 Comparison of airfoil geometry between the first and second step of optimization |
| 图选项 |
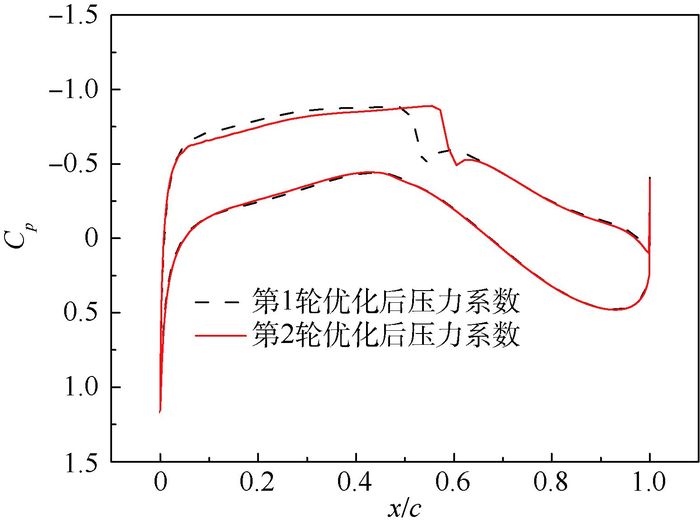 |
| 图 12 第1轮和第2轮优化后压力系数分布对比 Fig. 12 Comparison of pressure coefficient distribution between the first and second step of optimization |
| 图选项 |
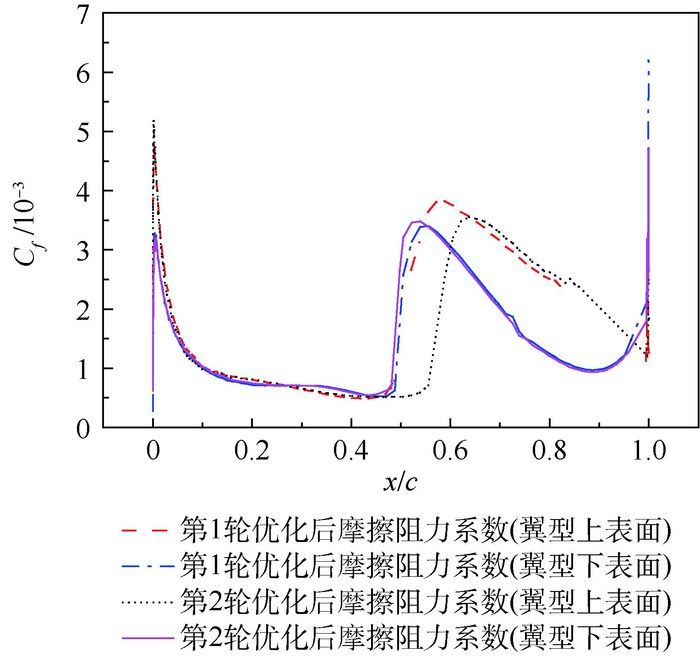 |
| 图 13 第1轮和第2轮优化后摩擦阻力系数分布对比 Fig. 13 Comparison of friction drag coefficient distribution between the first and second step of optimization |
| 图选项 |
该算例优化计算共耗时968 min。从算例可以看出,要想在高雷诺数、高马赫数下获得阻力较小的自然层流翼型,翼型上下表面在转捩点前部应具有顺压梯度,转捩点后以逆压梯度保持平滑向后缘恢复,转捩点的位置是翼型上下表面压力系数最小值的位置,这可为翼型反设计提供借鉴。
5 结论 针对超临界层流翼型设计问题,提出了一种两轮优化策略。第1轮优化中,采用了基于代理模型的遗传算法,第2轮优化中,采用基于梯度的修正可行方向法,既避开了代理模型的精度问题,又可较快地收敛到最优解,并建立了超临界层流翼型优化流程和计算平台。算例结果表明:
1) 通过第1轮优化,翼型上下表面层流区域比例显著增加,且翼型的升阻比得到明显提高。
2) 第2轮优化可进一步增加上表面的层流区域的比例,激波强度减弱,进一步提高翼型升阻比。
3) 这种两轮优化策略充分利用了代理模型、遗传算法和基于梯度优化算法的特点,能稳健地获得超临界层流翼型。
参考文献
| [1] | SCHRAUF G. Status and perspectives of laminar flow[J].Aeronautical Journal, 2005, 109(1102): 639–644.DOI:10.1017/S000192400000097X |
| [2] | THIBERT J J, RENEAUX J, SCHMITT V.Onera activities on drag reduction[C]//Proceedings of the 14th Congress of ICAS.Bonn:ICAS, 1990:1053-1064. |
| [3] | FUJINO M, YOSHIZAKI Y, KAWAMURA Y. Natural-laminar-flow airfoil development for a lightweight business jet[J].Journal of Aircraft, 2003, 40(4): 609–615.DOI:10.2514/2.3145 |
| [4] | FUJINO M. Design and development of the HondaJet[J].Journal of Aircraft, 2005, 42(3): 755–764.DOI:10.2514/1.12268 |
| [5] | BRADLEY M K, DRONEY C K.Subsonic ultra green aircraft research:Phase Ⅰ:Final report:NASA/CR-2011-216847[R].Washington, D.C.:NASA, 2011. |
| [6] | BRADLEY M K, DRONEY C K.Subsonic ultra green aircraft research phase Ⅱ:N+4 advanced concept development:NASA/CR-2012-217556[R].Washington, D.C.:NASA, 2012. |
| [7] | 乔志德. 自然层流超临界翼型的设计研究[J].实验流体力学, 1998(4): 23–30. QIAO Z D. Design of supercritical airfoils with natural laminar flow[J].Journal of Experiments in Fluid Mechanics, 1998(4): 23–30.(in Chinese) |
| [8] | 杨青真, 张仲寅. 超临界层流机翼边界层及气动特性分析[J].航空学报, 2004, 25(5): 438–442. YANG Q Z, ZHANG Z Y. Analysis of the boundary layer and aerodynamic characteristics of a supercritical laminar wing[J].Acta Aeronautica et Astronautica Sinica, 2004, 25(5): 438–442.(in Chinese) |
| [9] | 孙朋朋, 黄章峰. 后掠角对后掠机翼边界层稳定性及转捩的影响[J].北京航空航天大学学报, 2015, 41(7): 1313–1321. SUN P P, HUANG Z F. Effect of sweep angle on stability and transition in swept-wing boundary layer[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(7): 1313–1321.(in Chinese) |
| [10] | 靖振荣, 孙朋朋, 黄章峰. 小攻角对后掠机翼边界层稳定性及转捩的影响[J].北京航空航天大学学报, 2015, 41(11): 2177–2183. JING Z R, SUN P P, HUANG Z F. Effect of attack angle on stability and transition in swept-wing boundary layer[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(11): 2177–2183.(in Chinese) |
| [11] | MENTER F R, LANGTRY R B, LIKKI S R, et al. A correlation-based transition model using local variables-Part Ⅰ:Model formulation[J].Journal of Turbomachinery, 2006, 128(3): 413–422.DOI:10.1115/1.2184352 |
| [12] | MENTER F R. Two-equation eddy-viscosity turbulence models for engineering applications[J].AIAA Journal, 1994, 32(8): 1598–1605.DOI:10.2514/3.12149 |
| [13] | LANGTRY R B.A correlation based transition model using local variables for unstructured parallelized CFD codes[R].Stuttgart:Stuttgart of University, 2006. |
| [14] | 邓磊, 乔志德, 杨旭东, 等. 高升阻比自然层流翼型多点/多目标优化设计[J].空气动力学学报, 2011, 29(3): 330–335. DENG L, QIAO Z D, YANG X D, et al. Multi-point/objective optimization design of high lift-to-drag ratio for NLF airfoils[J].Acta Aerodynamica Sinica, 2011, 29(3): 330–335.(in Chinese) |
| [15] | HAN Z H, CHEN J, ZHU Z, et al.Aerodynamic design of transonic natural-laminar-flow (NLF) wing via surrogate-based optimization:AIAA-2016-2041[R]. Reston:AIAA, 2016. |
| [16] | HAN Z H, DENG J, LIU J, et al.Design of laminar supercritical airfoils based on navier-stokes equations[C]//Proceedings of 28th International Congress of the Aeronautical Sciences. Bonn:ICAS, 2012:1-9. |
| [17] | ZHAO K, GAO Z H, HUANG J T. Robust design of natural laminar flow supercritical airfoil by multi-objective evolution method[J].Applied Mathematics and Mechanics, 2014, 35(2): 191–202.DOI:10.1007/s10483-014-1783-6 |
| [18] | ZHANG Y F, FANG X M, CHEN H X, et al. Supercritical natural laminar flow airfoil optimization for regional aircraft wing design[J].Aerospace Science and Technology, 2015, 43: 152–164.DOI:10.1016/j.ast.2015.02.024 |
| [19] | 马晓永, 张彦军, 段卓毅, 等. 自然层流机翼气动外形优化研究[J].空气动力学学报, 2015, 33(6): 812–817. MA X Y, ZHANG Y J, DUAN Z Y, et al. Study of aerodynamic shape optimization for natural laminar wing[J].Acta Aerodynamica Sinica, 2015, 33(6): 812–817.(in Chinese) |
| [20] | BARCHE J, BINJON T W, WINTER K G, et al. Experimental data base for computer program assessment:AGARDAR-138[R].London:Technical Editing and Reproduction Ltd., 1979:1-22. |
| [21] | 郑宇宁, 邱志平, 黄仁, 等. 二元可变后缘翼型的鲁棒优化设计[J].北京航空航天大学学报, 2015, 41(5): 897–903. ZHENG Y N, QIU Z P, HUANG R, et al. Robust design optimization of a two-dimensional airfoil with deformable trailing edge[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(5): 897–903.(in Chinese) |
| [22] | BOGUE D, CRIST N.CST transonic optimization using tran-air++:AIAA-2008-321[R].Reston:AIAA, 2008. |
| [23] | 赵童, 张宇飞, 陈海昕, 等. 面向三维机翼性能的超临界翼型优化设计方法[J].中国科学:物理学力学天文学, 2015, 45(10): 104708. ZHAO T, ZHANG Y F, CHEN H X, et al. Aerodynamic optimization method of supercritical airfoil geared to the performance of swept and tapered wing[J].Scientia Sinica Physica, Mechanica & Astronomica, 2015, 45(10): 104708.(in Chinese) |
