飞管系统安全性设计过程中,预算和后续维修保障成本是2个主要制约因素[2]。航空装备研制、装备使用、维护过程中,在保证多种约束条件同时满足的情况下,如何尽可能提高飞管系统安全性是航空装备研制必须要考虑的问题。
航空装备全生命周期成本可以分为设计制造阶段成本与使用过程中维修保障的成本。设计制造阶段成本在不考虑研制费用的情况下,主要体现为设备采购预算(下文称经济性);而使用过程中维修保障的成本通常利用基本可靠性作为约束[3],因为基本可靠性直接反映了各设备故障对维修保障资源的消耗。
对于飞管系统而言,提升系统安全性的主要手段之一是进行余度设计。然而,在余度设计过程中,安全性与经济性、基本可靠性存在着相互制约的关系,因而如何对三者进行综合权衡,实现合理的余度配置,是航空装备设计过程中的重要问题。通过国内外文献梳理和飞机设计企业调研,目前工程上尚缺乏针对三者制约权衡关系,且同时适用于高复杂度系统的最优余度设计方法。
从安全性、经济性、基本可靠性三者制约权衡关系的角度,选择最为适合的余度配置方案,从本质上看实质是非线性整数规划问题。以可靠性为目标,经济成本为约束的余度最优配置问题,即为非线性整数规划问题。由于整数规划问题的可行解区域为离散点,通常不能直接使用基于连续区域的求解算法,传统的整数规划算法包括分支定界法、割平面法、分解算法、图论法、交集及交集余集解法、罚函数法、群论法等[4-6]。上述传统整数规划算法主要属于一种确定性算法,即从一个搜索点到另一个搜索点的转移有确定的转移方法和转移关系。然而,传统整数规划算法适用于小规模决策空间的问题,当求解问题为非线性、大规模决策空间时,计算时间将极大增加,甚至无法求解。例如本文所阐述的余度配置优化问题,需要在6×107种可能性中选择最优余度配置策略,传统算法求解需要耗时几周;另一方面,本问题的非凸特性使得大部分传统规划算法不能使用。与传统整数规划算法相对应的智能优化算法广泛采用并行搜索技术,克服了传统规划算法的单点搜索效率低问题。遗传算法是典型的智能启发式优化算法,它是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化算法。
为了提高遗传算法在求解整数规划问题时的寻优收敛速度和求解效率,在决策变量和约束条件很多时,大部分文献对遗传算法的编码和算子进行了改进[7]。例如,文献[8]通过改变遗传算法编码形式,使之更适用于整数规划。本文针对飞管系统的余度配置优化问题,在保证种群多样性的前提下,通过引入不同交叉、选择、变异算子,实现算法在整数约束下快速收敛。
本文以航空装备飞管系统为研究背景,基于飞管系统的安全性、基本可靠性及经济性数学模型,利用改进后适用于整数优化的遗传算法,提出一种以安全性为目标、基本可靠性与经济性为约束的余度配置优化方法,并进行敏感性分析得到了三者在余度配置方面综合权衡的若干规律。
1 飞管系统组成 飞管系统是以计算机为核心的高级区域导航、制导系统和性能管理系统。
飞管系统通常由控制系统、传感器系统、伺服作动系统构成,每个子系统又通常采用余度设计的方法,把失效率相对较高或重要度较高的设备进行多余度备份[9-10]。采用较多的余度数量通常会提高飞行器安全性,但是同样会导致飞机成本上升。因此,良好的余度配置应该是两者综合权衡的结果。对于结构简单的系统或设备,可采用枚举法尝试多种余度设置策略对不同设计因素的影响,例如多次尝试某一总线不同的余度设置方案,寻找安全性较高,同时全生命周期成本的余度设置方案。然而,一旦系统复杂度提升到一定程度,余度设置方案的数量呈指数增长,随着越来越多的设计因素纳入考虑范围,余度设置可行域无可避免地组合爆炸[11-13]。面对这种非线性混合整数优化问题,本文提出一种适用于整数优化的遗传算法,解决最优余度配置选取问题。本文考虑的飞管系统构成如图 1所示。
 |
| 图 1 飞管系统组成 Fig. 1 Composition of flight management system |
| 图选项 |
2 飞管系统建模 2.1 飞管系统基本可靠性模型 基本可靠性反映的是产品对维修资源的需求,定义为产品在规定条件下无故障工作的能力,因此基本可靠性模型是全串联模型。
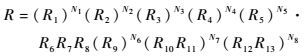 | (1) |
式中:R1~R13为图 1第3层所示设备在时刻t的可靠度;N1~N8为需要进行优化的余度数量。由于控制系统3个设备从功能要求上来说不需要进行额外的余度配置,因此模型中并没有设定这3个设备的余度数量。
2.2 飞管系统安全性模型 安全性实际上反映了飞机的安全,也就是说关注的是飞管系统发生哪些故障会导致飞机自身的安全受到损害。安全性的表征方法较多,目前航空武器装备研制普遍采用概率形式指标,其定义与可靠度类似。为了把安全性定量化,本文参考国军标GJB 451A—2005安全性的内涵[14],将飞管系统安全性指标定义为:飞管系统在规定的时间、规定的条件不发生致命性故障的概率,其中致命性故障指的是由于自身设计原因导致飞机自身非战斗损失的故障,其平均间隔时间用MTBCF表示。安全性指标用符号S表示[15]。
由定义可知,安全性指标的计算公式与可靠性类似。区别在于可靠性关注无故障概率,计算时使用MTBF作为参数,而安全性指标重点关注无致命性(非战斗损伤)故障的概率,计算时使用MTBCF作为参数。
经过故障树分析,安全性指标表达式如下:
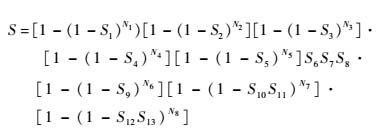 | (2) |
式中:S1~S13为图 1第3层所示设备在时刻t的发生影响飞机安全的故障的概率。
2.3 飞管系统经济性模型 经济性主要考量增加余度配置而带来的成本增加,在不考虑设计要素等其他因素情况,经济性模型如下:
 | (3) |
式中:C1~C13为图 1第3层所示设备的单价。
3 余度配置优化方法 从本质上讲,以可靠性为目标、经济成本为约束的余度最优配置问题是非线性整数规划问题。遗传算法适用于求解非线性优化问题,具有良好的全局最优特性。遗传算法运行流程如图 2所示。
 |
| 图 2 遗传算法流程图 Fig. 2 Flowchart of genetic algorithm |
| 图选项 |
传统遗传算法最大的问题在于决策变量适用于连续变量,若决策变量为余度等整数,需要对交叉、变异及适应度函数进行相应的调整。在决策变量为整数的情况下,使优化结果稳定,且不易陷入局部最优。
为了使遗传算法具备整数优化的能力,需要分别设计交叉算子、变异算子及整数约束选择方法。
3.1 交叉算子 若2个父代个体x1=(x11, x21, …, xn1),x2=(x12, x22, …, xn2),生成了2个子代个体y1=(y11, y21, …, yn1),y2=(y12, y22, …, yn2),交叉算子采用Laplace算子,为了运用Laplace算子,引入随机变量βi,βi的定义如下:
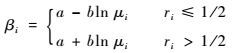 | (4) |
式中:μi和ri服从0~1的均匀分布,因此βi服从Laplace分布;a为位置参数;b为尺度参数。
为了适应整数优化,尺度参数b设定成整数,较小的尺度参数会产生比较接近父代的子代个体,较大的尺度参数更容易产生与父代差异较大的子代个体,即
 | (5) |
3.2 变异算子 为了确保经过交叉和变异之后,决策变量仍然满足整数限制,强制按照如下规则把决策变量xi转化为整数变量x:
如果xi为整数,则x=[xi]; 否则,有0.5概率x=[xi]与0.5概率x=[xi]+1,其中[xi]为xi的整数部分[16-19]。
变异算子采用幂函数算子,利用幂函数生成一个随机变量g=(g1)p,g1服从0~1的均匀分布,p为变异强度,为了使算子适用于整数优化,令p为整数。变异方法如下:
 | (6) |
式中:
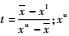
4 以安全性为目标的飞管系统余度优化配置 飞管系统是飞机安全性的重要保障,从提高飞机安全性的角度而言,固然是可以选配的余度备份越高越好,然而越多的余度配置会带来额外的故障发生概率,同时增加飞机成本[20-21],因此本节通过基于遗传算法的整数优化方法,寻找满足基本可靠性和成本要求的使飞机安全性最好的余度配置策略。
转化为如下优化问题:
 | (7) |
式中:N为式(1) ~式(3) 中余度配置向量(N1, N2, …, N8);R0为基本可靠性最低可接受值;C0为成本最高可接受值。
飞管系统有关参数如表 1所示。
表 1 飞管系统相关参数 Table 1 Related parameters of flight management system
| 设备名称 | MTBF/(106h) | MTBCF/(106h) | 单价/万元 | 余度范围 |
| 大气数据传感器 | 3.0 | 3.8 | 3 | 1~4 |
| 速率陀螺组 | 1.2 | 2.9 | 5 | 1~4 |
| 加速度计组 | 2.7 | 7.6 | 2 | 1~4 |
| 激光惯导 | 3.3 | 8.7 | 8 | 1~4 |
| 无线电高度表 | 0.6 | 4.6 | 1 | 1~4 |
| 飞管计算机 | 0.9 | 5.7 | 98 | 1 |
| 模拟接口设备 | 12.9 | 72.7 | 0.8 | 1 |
| 数字接口设备 | 8.9 | 56.6 | 0.9 | 1 |
| 作动器远程控制终端 | 1.2 | 22.8 | 3.2 | 1~4 |
| 舵机1 | 2.3 | 12.4 | 1.2 | 1~4 |
| 作动筒1 | 0.8 | 6.3 | 0.5 | 1~4 |
| 舵机2 | 2.3 | 12.4 | 1.2 | 1~4 |
| 作动筒2 | 0.8 | 6.3 | 0.5 | 1~4 |
表选项
令R0=0.99,C0=150万元,若不满足约束条件,适应度函数取值为1,若满足约束条件,适应度函数取值为-S (N)。图 3显示了通过本文所述遗传算法进行余度配置优化的过程。如图 3(a)所示,随着优化的进展,目标函数最优值与种群目标函数均值逐渐收敛,种群在进化70代左右时,目标函数均值趋于稳定,目标函数均值在-0.5~-1.0之间波动,整个过程不同代种群的目标函数最优值较为稳定,且收敛较快。种群分散性的变化也呈现出类似规律,如图 3(c)所示,种群间目标函数平均距离逐渐缩小,在70代左右时种群分散性趋于稳定。最终决策变量结果在图 3(b)中显示。
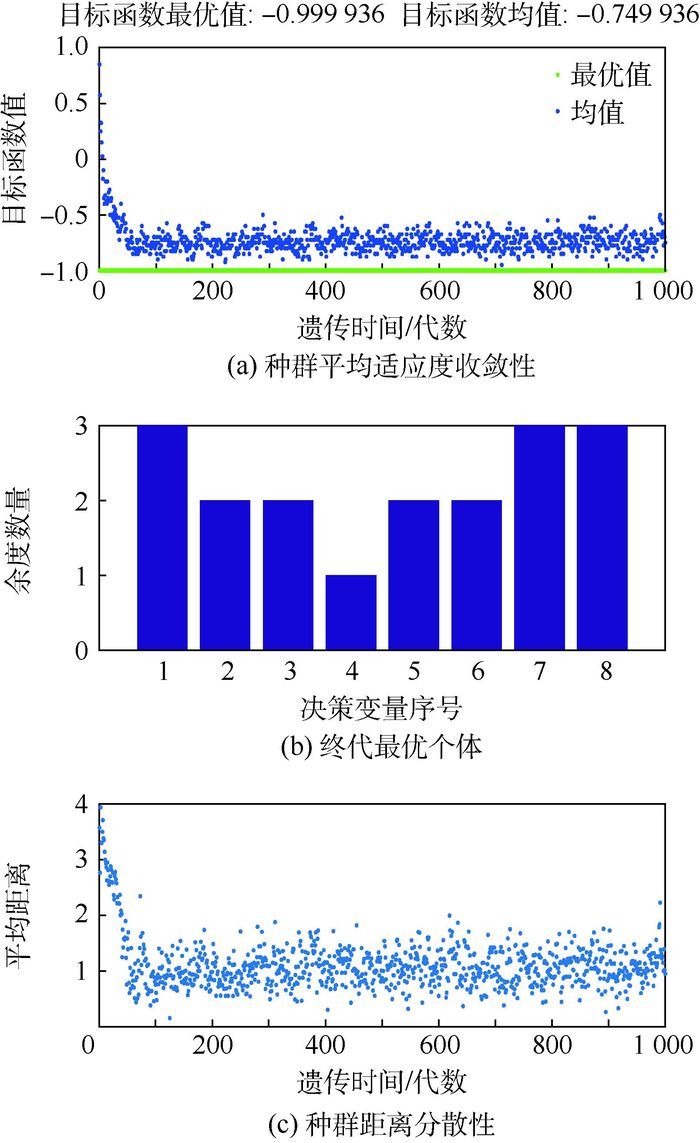 |
| 图 3 余度优化结果 Fig. 3 Redundancy optimization results |
| 图选项 |
表 2给出了本文遗传算法进行余度优化配置的结果,同时类比了文献[8]提出的经过编码改进的整数遗传算法的优化结果以及传统的贪婪搜索规划算法[22]。从优化结果可以看出,本文算法具有较高的精度以及较低的计算资源消耗。
表 2 最优余度配置 Table 2 Optimal redundancy allocation
| 设备名称 | 余度 | ||
| 本文遗传算法 | 编码改进遗传算法[8] | 贪婪搜索规划算法[22] | |
| 大气数据传感器 | 3 | 3 | 3 |
| 速率陀螺组 | 2 | 2 | 2 |
| 加速度计组 | 2 | 2 | 2 |
| 激光惯导 | 1 | 1 | 1 |
| 无线电高度表 | 2 | 2 | 2 |
| 作动器远程控制终端 | 2 | 1 | 1 |
| 舵机1 | 3 | 3 | 3 |
| 作动筒1 | 3 | 3 | 3 |
| 舵机2 | 3 | 3 | 3 |
| 作动筒2 | 3 | 3 | 3 |
| 安全性最优值 | 0.999 936 | 0.999 927 | 0.999 936 |
| 时间消耗 | 6 min | 3 min | 53 h |
表选项
5 余度敏感性分析 为了分析最优安全性指标以及各设备余度配置与约束条件的关系,把最低可靠性要求变化范围放宽到0.8~0.99,经济性约束上限变化范围放宽到140~180万元,分别进行遗传算法优化,结果如图 4所示。
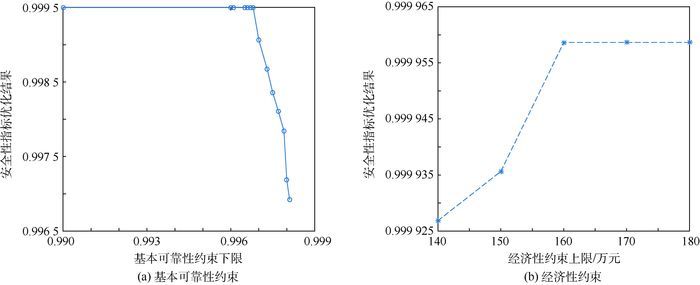 |
| 图 4 基本可靠性和经济性约束下敏感性分析 Fig. 4 Sensitivity analysis of basic reliability and economy constraints |
| 图选项 |
由图 4(a)可知,在经济性约束上限为150万元的情况下,随着基本可靠性约束下限的增加,安全性指标一开始变化不显著,在基本可靠性约束下限增加到接近0.997时,安全性指标最优值迅速减小,当基本可靠性约束下限升高到0.998 2时,找不到满足要求的优化结果。
安全性指标之所以会随着基本可靠性约束收窄而降低,是因为基本可靠性反映了系统故障所消耗的维修资源,基本可靠性要求越高意味着维修资源消耗的越少,在单个设备可靠性水平不变的情况下必然要减少余度数量,而余度数量的减小又必然会导致安全性指标的降低。
不同基本可靠性约束条件下,各设备余度配置情况如表 3所示。
表 3 不同基本可靠性约束下限对应余度优化结果 Table 3 Equipment redundancy optimization results with different basic reliabilities lower bounds
| 基本可靠性约束下限 | 余度 | |||||||||
| 大气数据传感器 | 速率陀螺组 | 加速度计组 | 激光惯导 | 无线电高度表 | 作动器远程控制终端 | 舵机1 | 作动筒1 | 舵机2 | 作动筒2 | |
| 0.990 0 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 3 | 2 | 2 |
| 0.996 0 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 3 | 2 | 2 |
| 0.996 1 | 2 | 2 | 2 | 2 | 2 | 1 | 3 | 2 | 2 | 2 |
| 0.996 5 | 2 | 2 | 3 | 2 | 2 | 1 | 2 | 2 | 2 | 2 |
| 0.996 6 | 2 | 2 | 3 | 2 | 2 | 1 | 2 | 2 | 2 | 2 |
| 0.996 7 | 2 | 2 | 3 | 2 | 2 | 1 | 2 | 2 | 2 | 2 |
| 0.996 8 | 2 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 2 | 2 |
| 0.997 0 | 3 | 2 | 2 | 2 | 1 | 1 | 2 | 2 | 3 | 2 |
| 0.997 3 | 2 | 2 | 2 | 2 | 1 | 2 | 2 | 1 | 2 | 2 |
| 0.997 5 | 2 | 2 | 2 | 1 | 1 | 1 | 2 | 1 | 2 | 2 |
| 0.997 7 | 3 | 2 | 2 | 2 | 1 | 1 | 1 | 1 | 3 | 2 |
| 0.997 9 | 2 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 2 | 2 |
| 0.998 0 | 2 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 2 | 1 |
| 0.998 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
表选项
由图 4(b)可知,在基本可靠性约束下限为0.83的情况下,随着经济性约束上限的增加,安全性指标单调递增,增幅先增大后减小,最后趋于平稳,拐点在150万元附近。这说明预算的增加能显著提高系统安全性水平,然而安全性水平增加到一定程度后,预算的增加给安全性带来的边际效用递减,在本例中150万元附近是边际效用最高的预算限制。在160万元之后,预算的增加对安全性水平影响基本消失,此时基本可靠性已经成为安全性水平的主要约束。
不同经济性约束上限所对应的余度优化结果如表 4所示。
表 4 不同经济性约束上限对应余度优化结果 Table 4 Equipment redundancy optimization results with different economy upper bounds
| 经济性约束上限/万元 | 余度 | |||||||||
| 大气数据传感器 | 速率陀螺组 | 加速度计组 | 激光惯导 | 无线电高度表 | 作动器远程控制终端 | 舵机1 | 作动筒1 | 舵机2 | 作动筒2 | |
| 140 | 2 | 2 | 2 | 1 | 2 | 1 | 2 | 2 | 2 | 2 |
| 150 | 3 | 2 | 2 | 1 | 2 | 2 | 3 | 3 | 3 | 3 |
| 160 | 3 | 3 | 2 | 2 | 3 | 2 | 2 | 2 | 2 | 2 |
| 170 | 3 | 3 | 3 | 2 | 4 | 3 | 3 | 3 | 3 | 3 |
| 180 | 3 | 3 | 3 | 3 | 3 | 3 | 4 | 4 | 4 | 4 |
表选项
从上述敏感性分析可知,安全性指标随着基本可靠性约束收窄而降低,随着经济性约束上限的增加而递增,且降低或增加幅度存在拐点。这是由于2种约束存在竞争关系,同一时间仅有1种约束条件起主要约束作用。
6 结论 1) 本文提出了一种基于遗传算法的余度配置优化方法,并利用改进后适用于整数优化的遗传算法对飞管系统展开了以安全性为目标、基本可靠性与经济性为约束的余度配置优化研究。
2) 进行了多约束条件对优化目标的敏感性分析。结果表明了该遗传算法可以有效求出满足基本可靠性和经济性约束下的安全性指标最优解及相对应的余度配置策略,且该方法具有良好的精度与收敛速度。
3) 通过敏感性分析发现,安全性指标的最优值随着基本可靠性约束下限的提高而降低,随着经济性约束上限的增加而增加。且这2种约束条件对优化目标竞争约束,在同一时刻只有一种约束条件起主要约束作用,说明了提高产品安全性的手段,除了需要增加前期预算投入外,还需要增加后期维修资源的投入。
参考文献
| [1] | 陈志勇. 飞行管理系统与基于性能的导航的历史与发展[J].中国民航飞行学院学报, 2010, 21(3): 14–18. CHEN Z Y. The history and development of flight management system and performance based navigation[J].Journal of Civil Aviation Flight University of China, 2010, 21(3): 14–18.(in Chinese) |
| [2] | RZEVSKI G, KNEZEVIC J, SKOBELEV P, et al. Managing aircraft lifecycle complexity[J].International Journal of Design & Nature & Ecodynamics, 2016, 11(2): 77–87. |
| [3] | VERMA A K, AJIT S, KARANKI D R.Basic reliability mathematics[M]//VERMA A K, AJIT S, KARANKI D R.Reliability and safety engineering.London:Springer, 2016:15-70. |
| [4] | SHERALI H D, DRISCOLL P J. Evolution and state-of-the-art in integer programming[J].Journal of Computational & Applied Mathematics, 2000, 124(1-2): 319–340. |
| [5] | GOMORY R E. Outline of an algorithm for integer solutions to linear programs[J].Bulletin of the American Mathematical Society, 1958, 64(5): 275–278.DOI:10.1090/S0002-9904-1958-10224-4 |
| [6] | BELL D E, SHAPIRO J F. A convergent duality theory for integer programming[J].Operations Research, 1977, 25(3): 419–434.DOI:10.1287/opre.25.3.419 |
| [7] | 杜祜康, 赵英凯. 整数规划问题智能求解算法综述[J].计算机应用研究, 2010, 27(2): 408–412. DU H K, ZHAO Y K. Survey on intelligent optimization algorithms for solving integer programming problems[J].Application Research of Computers, 2010, 27(2): 408–412.(in Chinese) |
| [8] | DAMOUSIS I G, BAKIRTZIS A G, DOKOPOULOS P S. A solution to the unit-commitment problem using integer-coded genetic algorithm[J].IEEE Transactions on Power Systems, 2004, 19(2): 1165–1172.DOI:10.1109/TPWRS.2003.821625 |
| [9] | RAMASAMY S, SABATINI R, GARDI A, et al.Novel flight management system for real-time 4-dimensional trajectory based operations:AIAA-2013-4763[R].Reston:AIAA, 2013. |
| [10] | HESSE K, DIESSEL G.Check device for a redundant flight control apparatus:US4601169[P].1986-07-22. |
| [11] | 臧红伟. 非相似余度计算机系统及其可靠性分析[J].哈尔滨工业大学学报, 2008, 40(3): 492–494. ZANG H W. Dissimilar redundancy computer system and reliability analysis[J].Journal of Harbin Institute of Technology, 2008, 40(3): 492–494.(in Chinese) |
| [12] | 王琦, 崔巍. 基于遗传算法的多余度电传系统可靠性设计研究[J].南昌航空大学学报(自然科学版), 2015, 29(2): 16–20. WANG Q, CUI W. Study of redundancy reliability design based on the genetic algorithm[J].Journal of Nanchang University of Aeronautics and Astronautics (Natural Science Edition), 2015, 29(2): 16–20.(in Chinese) |
| [13] | 张民悦, 李丹丹. 基于遗传算法的桥式网络可靠度和冗余度分配优化[J].湖北大学学报(自然科学版), 2014, 36(6): 505–510. ZHANG M Y, LI D D. Reliability and redundancy distribution optimization of bridge network based on genetic algorithm(GA)[J].Journal of Hubei University(Natural Science Edition), 2014, 36(6): 505–510.(in Chinese) |
| [14] | 中国人民解放军总装备部. 可靠性维修性保障性术语: GJB 451A—2005[S]. 北京: 中国人民解放军总装备部, 2005. People's Liberation Army General Armaments Department.Reliability, maintainability and supportability terms:GJB 451A—2005[S].Beijing:People's Liberation Army General Armaments Department, 2005(in Chinese). |
| [15] | WALTER M, SCHNEEWEISS W G. Review of "the modeling world of reliability/safety engineering"[J].IEEE Transactions on Reliability, 2006, 55(2): 391. |
| [16] | NOROUZI A, ZOLFAGHARI A, MINUCHEHR A H, et al. An enhanced integer coded genetic algorithm to optimize PWRs[J].Progress in Nuclear Energy, 2011, 53(5): 449–456.DOI:10.1016/j.pnucene.2011.03.005 |
| [17] | FOSTER J D, BERRY A M, BOLAND N, et al. Comparison of mixed-integer programming and genetic algorithm methods for distributed generation planning[J].IEEE Transactions on Power Systems, 2014, 29(2): 833–843.DOI:10.1109/TPWRS.2013.2287880 |
| [18] | DEB K. An efficient constraint handling method for genetic algorithms[J].Computer Methods in Applied Mechanics and Engineering, 2000, 186(2-4): 311–338.DOI:10.1016/S0045-7825(99)00389-8 |
| [19] | DEEP K, SINGH K P, KANSAL M L, et al. A real coded genetic algorithm for solving integer and mixed integer optimization problems[J].Applied Mathematics & Computation, 2009, 212(2): 505–518. |
| [20] | 周元钧, 赵运坤, 葛云海. 复合式余度机电作动系统容错控制与性能分析[J].北京航空航天大学学报, 2008, 34(3): 285–289. ZHOU Y J, ZHAO Y K, GE Y H. Fault-tolerant control method and characteristic analysis of hydraulic redundant EMA system[J].Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(3): 285–289.(in Chinese) |
| [21] | 陈喆. 混合三余度无人机飞控计算机硬件结构设计及可靠性分析[J].计算机测量与控制, 2015, 23(8): 2753–2755. CHEN Z. Mixed three redundant FCC of UAV hardware structure design and reliability analysis[J].Computer Measurement & Control, 2015, 23(8): 2753–2755.(in Chinese) |
| [22] | CHICKERING D M. Optimal structure identification with gree-dy search[J].Journal of Machine Learning Research, 2003, 3(3): 507–554. |
