1 大气环控系统工作原理 大气环控系统主要包括温湿度控制系统(THCS)、二氧化碳去除装置(CDRA)、电解制氧系统(SPES)、供气调压系统(ACSS)和LiOH净化装置[2]。这5个子系统之间通过舱室大气相互耦合,并由中央控制系统实现联合工作。
1) 舱室参数控制方程
舱室气体成分服从质量守恒方程:
 | (1) |
式中:下标i为子系统编号,i=1,2,…,5;下标j为空气组分;m为气体质量,kg;win和wout分别为舱室入口和出口处气体质量流量,kg/s;xin和xout分别为舱室入口和出口气体质量分数;wcrew为成员质量流量,kg/s。
舱室内部空气的内能计算公式为
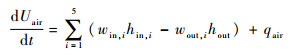 | (2) |
式中:Uair为舱内空气的内能,J;hin和hout分别为各系统对舱室入口和出口的比焓,J/kg; qair为舱空气的总热负载,W。
qair包括了人员散热量、舱壁散热量、设备散热量。人员散热量是由航天员活动量的实验数据确定,舱壁散热量是由舱壁内外温差决定,设备散热量较难准确确定,因此在本文研究中将每个设备散热与额定工况散热量进行了线性折合处理。
2) 温湿度控制模型
舱室温度控制主要由温湿度控制系统中的冷凝换热器实现,冷凝换热器能量守恒方程为[4]
 | (3) |
 | (4) |
式中:Tair, put和Tcold, out分别为出口气体和冷媒体出口温度,K; Qex为离开温湿度控制系统的能量,W; WTHCS为温湿度控制系统通风流量,kg/s, wair, out为出口气体流量,kg/s;hair, in和hair, out分别为系统的入口和出口气体比焓,J/kg;hdrain为冷凝水比焓,J/kg;Mdry, air为冷凝换热器质量, kg;Cpdry为冷凝换热器比热, J/(kg·℃);wcold, in为温湿度控制系统冷媒体入口流量,kg/s;wcold, out为THC的冷媒体出口流量,kg/s;hcold, in为温湿度控制系统的冷媒体入口比焓,J/kg;hcold, out为冷媒体出口比焓,J/kg;ρcold, in为冷媒体密度,kg/m3;wdrain为冷凝水流量。
3) 供氧模型
供氧主要包括电解制氧和非再生氧气罐。电解制氧的制氧流量与电解电流之间关系[11]为
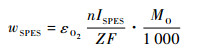 | (5) |
式中:wSPES为制氧流量,kg/s;εO2为氧电流效率;n为电解芯体个数;F为法拉第常数,C/mol;Z为电化学反应式中电荷的摩尔数;ISPES为电解电流,A;MO为氧原子的摩尔质量,g/mol。
当舱室氧分压低于控制下限PO2, min时,需ACSS氧气罐辅助供氧,直至氧分压达控制上限PO2, max。因此,氧气瓶氧气使用时长可表示为
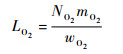 | (6) |
式中:LO2为氧气使用时长,d;mO2为初始可使用氧气质量,kg;NO2为氧气瓶的个数;wO2为氧气瓶平均供氧流量,kg/d。
4) 二氧化碳去除模型
舱室二氧化碳浓度由再生二氧化碳去除装置和非再生LiOH净化装置联合控制。
再生二氧化碳去除装置为四床分子筛吸附床,其中CO2吸附床的控制微分方程为[12]
 | (7) |
式中:q为单位吸附质吸附二氧化碳质量,kg/kg;β为吸收速率,1/s;kc为亨利系数,m3/kg;C为气体中的CO2浓度,kg/m3;Dz为轴向扩散系数, m2/s; u为风速,m/s;z为吸附床层轴向长度,m;εb为床层空隙率;ρb为吸附床密度,kg/m3。
当CO2浓度高于规定浓度时,启动非再生LiOH净化系统辅助控制CO2浓度。单个LiOH净化罐可净化CO2总质量控制方程:
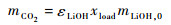 | (8) |
式中:mCO2为单个LiOH净化罐可去除CO2总质量,kg;xload为单位质量LiOH最大可吸收CO2的质量,kg/kg;εLiOH为LiOH装载效率;mLiOH, 0为单个LiOH净化罐内装填的LiOH质量。
LiOH净化罐可使用时长(单位为d)为
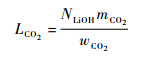 | (9) |
式中:NLiOH为LiOH净化罐的个数;wCO2为LiOH净化罐吸收CO2平均流量,kg/d。
5) 子系统耗能模型
大气环控系统中可调节参数多为功率可调设备,如风机、加热器、电解池等。其他耗电设备由于工作模式固定,认为是功率固定设备,如水汽分离器、循环泵、节气泵及各种传感器、控制器等。因此,THCS、SPES和CDRA的电能需求可分别表示为
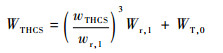 | (10) |
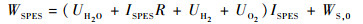 | (11) |
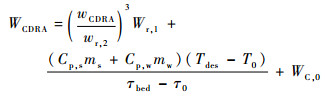 | (12) |
式中:WTHCS、WSPES和WCDRA分别为THCS、SPES和CDRA的电能需求,W;WT, 0、WS, 0和WC, 0分别对应为3个系统的固定电能消耗部分, W;wr, 1和wr, 2分别为THCS和CDRA的额定流量,kg/s;Wr, 1和Wr, 2分别为THCS和CDRA中风机额定功率,W; UH2O为水的电解电压,V;R为电解槽总电阻,Ω;UO2和UH2分别为氧气和氢气的超电位,V;Cp, s和Cp, w分别为吸附材料和吸附床内CO2气体的比热容,J/(kg·℃);ms和mw分别为吸附材料和吸附床内气体的质量,kg;Tdes和T0分别为吸附床解析温度和吸附床初始温度,℃;τbed为吸附床吸附周期,s; τ0为吸附床初始周期,s。
ACSS和LiOH净化装置作为应急控制系统,需保持待机状态,两系统电能消耗为常数。因此,大气环控系统总电能需求可表示为
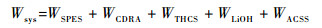 | (13) |
式中:Wsys为ECS总电能需求,W;WLiOH和WACSS分别为非再生LiOH净化系统和供气调压系统的固定电能需求,W。
2 应急运行策略优化 针对长期运行的空间站突然面临能源不足,各个耗能子系统需要重构其运行策略,这是一个优化问题。
2.1 优化变量和约束条件 系统优化变量确定为各子系统的可调关键参数,分别为THCS的通风流量wTHCS,SPES的电解电流ISPES,以及CDRA的通风流量wCDRA,可表示为
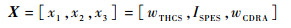 | (14) |
根据空间站设计指标要求[2]、实际设备可调节范围和工作情况,设置系统优化变量的变化范围,可以借鉴表 1。其中,THCS最低风量是为了保证舱室内基本的空气循环;考虑到再生加热器性能,wCDRA应设有下限。
表 1 优化变量及可调范围 Table 1 Optimization variables and adjustable range
| 变量 | 最小值 | 最大值 |
| wTHCS/(kg·min-1) | 5 | 14 |
| ISPES/A | 0 | 16 |
| wCDRA/(kg·h-1) | 5 | 22 |
表选项
应急运行下舱室5个重要环境参数应在应急容许范围内。参考国际空间站美国段标准,正常和应急状态下五大参数控制范围。
2.2 目标函数 非再生物资使用时长和总电能需求被确定为该优化问题的多目标优化函数。非再生物资使用时长即为氧气存储量可用时长和LiOH可用时长,且系统非再生物资使用时长为两者最小值。
第1个优化目标f1(X)为系统非再生物资使用时长Lsys最大化:
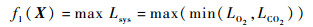 | (15) |
稳定控制舱室环境五大参数的最低总电能需求,可以作为第2个优化目标函数f2(X),即最小化大气环控系统总电能Wsys需求:
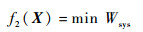 | (16) |
2.3 优化方法 本文基于非支配排序遗传算法-Ⅱ(NSGA-Ⅱ)算法[13-14],建立空间站大气环控系统应急运行策略优化方法。在稳定控制舱室环境五大参数为约束下,以wTHCS、ISPES、wCDRA为优化变量,非再生物资使用时长最大、电能需求最小为目标函数,获得不同供给电能情况下系统Pareto最优解集[15]。该方法如图 1所示。
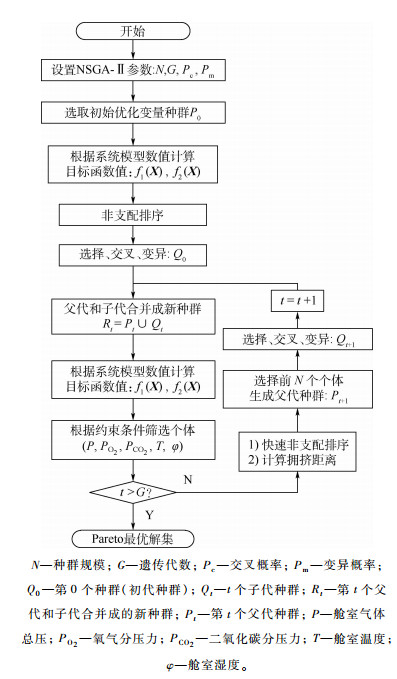 |
| 图 1 应急运行策略优化流程 Fig. 1 Flow of emergency operation strategy optimization |
| 图选项 |
3 仿真算例 3.1 优化条件 本文讨论三人值守空间站环控生保系统供电突然出现故障情况下,实现大气环控系统应急运行方法。应急情况下,航天员作息采用应急状态下的作息规律。同时,舱室主要环境参数采用应急控制标准,如表 2所示。算例中NSGA-Ⅱ的参数设置如下:种群规模为200、迭代次数为100、交叉概率为0.9、变异概率为0.1。成员热湿数据如表 3所示,其他相关参数如表 2所示。
表 2 相关参数 Table 2 Related parameters
| 参数 | 数值 |
| 舱室体积/m3 | 100 |
| 氧气存储质量/kg | 9.762 |
| 氧气罐个数 | 2 |
| LiOH质量/kg | 12 |
| LiOH罐个数 | 2 |
| 供氧速率/(L·min-1) | 40 |
| 供氮速率/(L·min-1) | 40 |
表选项
表 3 人体热湿实验数据 Table 3 Experimental data of human body heat and humidity
| 热湿参数 | 睡眠 | 静息 | 轻度 | 中度 |
| 耗氧消耗量/(kg·d-1) | 0.468 | 0.571 2 | 0.823 2 | 1.545 6 |
| CO2消耗量/(kg·d-1) | 0.528 | 0.648 | 0.936 | 1.752 |
| 产热/W | 83 | 93 | 150 | 280 |
| 排湿/(kg·d-1) | 1.2 | 1.44 | 1.92 | 3.72 |
表选项
3.2 优化结果分析 由优化变量变化范围及子系统电能模型可知,大气环控系统总电能需求范围约为750~2 000 W[2]。在本文研究中,仅考虑应急供给总电能大于系统最低功率750 W的情况。
3.2.1 Pareto最优解集 当供电系统出现故障,总电能突然发生衰减,采用本文提出的多目标优化方法可以得到系统总电能与非再生物资使用时长的Pareto最优解集及Pareto最优前沿(POF),如图 2所示。最优POF为图 2中星号点。分析图 2可以得到如下结论:
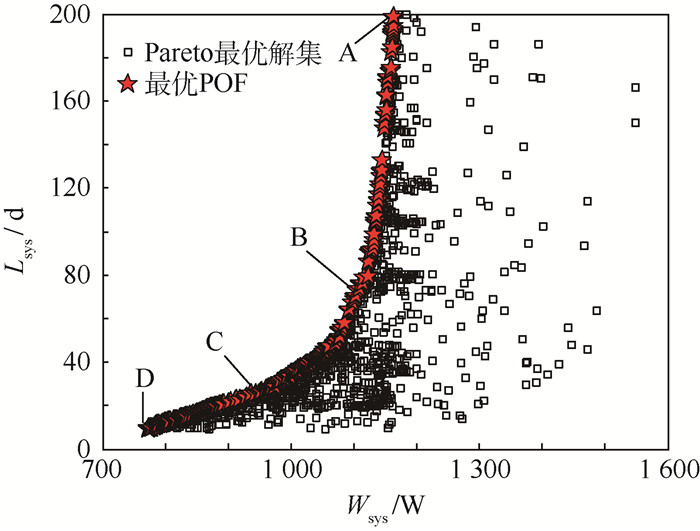 |
| 图 2 Pareto最优解 Fig. 2 Pareto optimal solution |
| 图选项 |
1) 非再生物资使用时长Lsys与总电能需求Wsys之间存在正相关关系。任何降低系统耗电量的系统参数调整,都会导致最大Lsys的相应减少,反之亦然。因此,采用多目标优化技术优化运行参数,使系统在任意给定系统电能情况下使Lsys最大化,具有重要意义。
2) 随着应急系统启动,航天员采用应急作息,非再生物质消耗速率降低,系统电能需求一定程度上可以降低,由正常情况下的2 000 W下降到应急可持续运行200 d的1 170 W,降低为原来的58%。
3) D点代表了系统电能需求的下限,即当系统电能低于该点时,3个子系统将不能同时启动,此时非再生物资使用时长也达到下限值约为9 d。
4) A点对应的系统电能是维持系统持续运行200 d的最低电能需求,当总电能超过该值时,多余的电能应用于改善系统环境,如优化舱室温度、降低舱室二氧化碳浓度等,不再是约束系统使用时长的主要因素。
3.2.2 优化变量与系统电能关系 分析POF上不同系统总电能情况下的优化结果,得到系统总电能与各优化变量之间的变化曲线,如图 3所示。分析图 3可知,随着系统总电能的降低,系统优化变量均呈现下降趋势。
 |
| 图 3 POF上的优化变量随系统总电能变化曲线 Fig. 3 Curves of optimization variables changing with system total electric energy on POF |
| 图选项 |
1) wTHCS受系统总电能影响较小,系统总电能的降低导致部分电子热设备停止工作或间歇式工作,引起舱室热负荷降低,从而在保证系统温湿度约束条件下,wTHC有所降低,由8 kg/min下降到约6.6 kg/min,此时舱室温度控制在约束上限,26.7℃。
2) ISPES逐渐由13.14 A下降到下限值,同时随着wCDRA下降到最小值,ISPES下降速率明显增大。
3) wCDRA逐渐由8.6 kg/h下降到下限值5 kg/h。
3.3 大气环控系统应急运行实例 本文给出供电系统故障情况下,4种非正常电能情况下的系统最优运行实例,如图 2中A~D点所示,对应大气环控系统运行策略最优重构方案如表 4所示。由此优化结果得出的相应舱室主要气成分浓度控制结果如图 4所示,Tair为舱室温度, RH为相对湿度。图 4为4种电能情况下舱室主要气体成分控制结果。分析舱室主要气体成分控制结果可知:
表 4 4种给定电能情况下系统运行策略最优重构方案 Table 4 Optimal reconfiguration scheme of system operation strategy under given electric energy
| 应急工况 | Lsys/ d | Wsys/ W | wCDRA/ (kg·h-1) | ISPES/ A | wTHCS/ (kg·min-1) |
| A | 199 | 1 164 | 8.60 | 12.95 | 7.80 |
| B | 79 | 1 123 | 8.34 | 12.05 | 7.92 |
| C | 26 | 950 | 6.07 | 8.89 | 7.41 |
| D | 9 | 774 | 5.16 | 0.32 | 6.68 |
表选项
 |
| 图 4 4种给定电能情况下舱室主要气体成分控制结果 Fig. 4 Results of principal gas composition control under four given electric energy conditions |
| 图选项 |
1) 采用本文提出的空间站大气环控系统应急运行策略优化方法,可以在给定应急功率下确定出各子系统的应急运行测策,并保证舱室各主要气体参数稳定控制在参数要求范围内。图 4内水平虚线即为舱室内参数规定的上下限。
2) 由于乘员组的作息变化,其氧气消耗量、二氧化碳排放量及热量排放量呈周期性变化,导致舱室主要气体参数均呈周期性波动。
3) A~D 4种应急情况的变化可以看出,随着系统总电能的降低,电解制氧系统供氧量逐渐降低,氧气瓶的使用频率相应增加,同时,由于再生二氧化碳去除系统风量降低,非再生LiOH净化装置使用频率也逐渐升高,从而共同导致环控系统使用时长相应降低。
采用本文提出的空间站大气环控系统应急运行策略优化方法,可以获得不同应急电能下的大气环控系统的最优运行策略。并能保证舱室五大环境参数稳定在参数要求范围,从而为应急运行提供理论依据。
4 结论 本文采用NSGA-Ⅱ算法,开展了空间站能量系统供能突变情况下,大气环控系统应急运行策略优化方法研究。该方法以大气环控系统3个主要子系统关键参数(wCDRA、ISPES、wTHCS)为优化变量,系统非再生物资使用时长最大、总电能需求最小为2个目标函数,在环境参数约束条件,研究了系统非再生物资使用时长与系统总电能及子系统可调参数之间的关系。
本文给出了三人值守空间站能量系统供能突变情况下的大气环控系统应急运行策略优化仿真实例,得到了相应的Pareto最优前沿,讨论了4种不同供给电能情况下的系统最优运行策略。可以得出以下结论:
1) 系统非再生物资使用时长随着总电能的增加而增加,存在正相关关系。
2) 随着系统总电能的降低,关键子系统优化变量(wCDRA、ISPES、wTHCS)均为降低趋势。
3) 为了最大化非再生物资使用时长,应在保证舱室环境约束条件前提下,控制温湿度控制系统风量为最小。
本文提出的多目标优化方法可以获得大气环控系统能量系统供能突变情况的最优运行控制策略,为空间站大气环控系统实际柔性运行提供理论参考。
参考文献
| [1] | LARSON W J, PRANKE L K. Human spaceflight:Mission analysis and design[M].Columbus: McGraw-Hill, 2007: 539-574. |
| [2] | WIELAND P O. Living together in space:The design and operation of the life support systems on the international space station[M].Huntsville, AL: National Aeronautics and Space Administration, Marshall Space Flight Center, 1998: 120-156. |
| [3] | ROMANI R, GOES L C S.Cabin temperature control model for commercial aircraft[C]//Proceedings of AIAA Modeling and Simulation Technologies Conference.Reston:AIAA, 2012:1-15. |
| [4] | 靳健, 侯永青. 载人航天器空气环境参数控制非定常仿真分析[J].航空学报, 2014, 35(11): 2970–2978. JIN J, HOU Y Q. Unsteady simulation analysis on air environment parameters control of manned spacecraft[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(11): 2970–2978.(in Chinese) |
| [5] | ANDERSON G, MARTIN C E.Evaluation and application of Apollo ECLS/ATCS systems to future manned missions[C]//43rd AIAA Aerospace Sciences Meeting and Exhibit.Reston:AIAA, 2005:1-13. |
| [6] | HAJELA G, COHEN F, DALTON P. International space station power reinitialization[J].IEEE Aerospace and Electronic Systems Magazine, 2003, 18(4): 19–24.DOI:10.1109/MAES.2003.1194085 |
| [7] | MAK T. A study of on-orbit spacecraft failures[J].Acta Astronautica, 2009, 64(2): 195–205. |
| [8] | KIM S Y, CASTET J F, SALAH J H. Spacecraft electrical power subsystem:Failure behavior, reliability, and multi-state failure analyses[J].Reliability Engineering and System Safety, 2012, 98: 55–65.DOI:10.1016/j.ress.2011.10.005 |
| [9] | 孙晨, 徐向华, 梁新刚. 空间站主动热控回路的热负荷分配优化[J].工程热物理学报, 2014, 35(10): 2049–2052. SUN C, XU X H, LIANG X G. Heat load distribution optimization of active thermal control system for space station[J].Journal of Engineering Thermophysics, 2014, 35(10): 2049–2052.(in Chinese) |
| [10] | LIN K P, LUO Y Z, TANG G J. Optimization of logistics strategies for long-duration space-station operation[J].Journal of Spacecraft And Rockets, 2014, 51(5): 1709–1720.DOI:10.2514/1.A32773 |
| [11] | 任建勋, 张信荣, 尚传勋, 等. 载人航天器SPE制氧系统性能分析[J].清华大学学报(自然科学版), 2002, 42(8): 1102–1105. REN J X, ZHANG X R, SHANG C X, et al. Performance analysis of SPE oxygen generation system in manned spacecraft[J].Journal of Tsinghua University(Natural Science Edition), 2002, 42(8): 1102–1105.(in Chinese) |
| [12] | LIU M, YANG D, PANG L, et al. Experimental and computational investigation of adsorption performance of TC-5A and PSA-5A for manned spacecraft[J].Chinese Journal of Aeronautics, 2015, 28(6): 1583–1592.DOI:10.1016/j.cja.2015.08.003 |
| [13] | DEB K, PRATAP A, AGARWAL S, et al. A fast and elitist multiobjective genetic algorithm:NSGA-Ⅱ[J].IEEE Transactions on Evolutionary Computation, 2002, 6(2): 182–197.DOI:10.1109/4235.996017 |
| [14] | ARIAS-MONTA A, COELLO C A C, MEZURA-MONTES E. Multiobjective evolutionary algorithms in aeronautical and aerospace engineering[J].IEEE Transactions on Evolutionary Computation, 2012, 16(5): 662–694.DOI:10.1109/TEVC.2011.2169968 |
| [15] | DEB K. An efficient constraint-handling method for genetic algorithms[J].Computer Methods in Applied Mechanics & Engineering, 2000, 186(2-4): 311–338. |
