在此背景下,因难以实现原位监测及在线监测的传统无损检测技术(NDT)无法满足监测需求,而基于超声导波理论的结构健康监测技术则可以弥补其不足[2-5]。但无论是传统的超声波监测技术及目前较为流行的基于超声的结构健康监测技术,其理论基础均是依靠声波在缺陷处的反射、散射及衰减等线性特征,且可监测的裂纹尺寸理论上不可小于波长的一半。由于真实结构中的疲劳裂纹存在闭合状态,裂纹界面存在接触作用,在裂纹张开及增长到一定尺寸前,声波在裂纹界面的反射及散射不太明显,因此限制了该方法的使用范围[6-8]。
为了解决线性技术在小裂纹及闭合裂纹监测领域的不足,国内外****们针对超声在小裂纹及疲劳裂纹界面的非线性相应展开了大量研究,发现了部分非线性特征,如高次谐波及1/2分次谐波的产生、直流(DC)效应、慢动效应及振动声调制效应等[9-10]。试验证明,声波在裂纹界面的非线性效应对裂纹更为敏感,因此基于振动声调制效应的损伤监测是一种前景广阔的监测方法[11-14]。目前基于振动声调制进行裂纹监测的研究,主要集中在判断裂纹有无,而在裂纹定位成像方面,开展的研究相对较少[15]。Sohn等通过线性响应减法(LRS)及同步解调的方法,实现了低频基频谐波成分的提取,并以此与基准信号进行比较,确定了裂纹的有无[16];胡海峰通过高通滤波器直接获得了传感信号中的高频基频谐波成分,并以此采用延时叠加算法对板类裂纹进行了成像[17]。焦敬品等采用振动声调制的方法,基于小波变换,分别提取并比较了基准信号与监测信号在低频振动频率的信号成分,并以此进行了接触类缺陷的成像处理[18]。Kim等采用风力发电叶片在工作时的振动作为低频振动,结合振动声调制的方法,实现了风力发电机叶片裂纹的监测[19]。上述研究中,普遍需要结构在原始健康状态的健康信号作为基准,而因结构的长时间服役,传感器或者其他与采集信号相关的部件状态会发生改变,故导致采集信号发生畸变,在结构不发生损伤的情况下,采集信号也可能与基准信号有较大差异。因此,基于基准信号的健康监测方法将不再适用。
本文基于振动声调制理论,分析了仅有高频(HF)激励及高低频(HF和LF)同时激励时,声波的传播路径及信号成分组成,提出了一种含损伤信息信号的提取技术;结合延时叠加算法,实现了板类结构中裂纹损伤的定位成像,并通过试验证明了该方法的可行性。
1 振动声调制原理 振动声调制方法就是向结构中输入两频率不同的激励信号,一个信号为低频激励,其幅值较大,应用于推动裂纹面的相对运动。而另一信号为高频激励,频率较高,幅值较小,对裂纹的敏感性较高。假设两信号的频率分别为ωa和ωb,分别对应LF和HF,当结构中不存在裂纹时,可将结构看作一个线性系统,两列波输入系统后的输出,可看作两列波分别单独输入系统后的对应输出的线性叠加,其接收信号u1可表示为
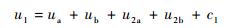 | (1) |
式中:ua和ub为入射波所对应频率的基频谐波;u2a和u2b为二次谐波;c1为其他谐波成分,包括三次谐波及更高次谐波等。
当结构中存在裂纹时,因裂纹的作用,两列波会在裂纹处发生幅值和相位调制,进而在频域产生了新的频率成分,包括两列基频谐波、调制边频谐波及高次谐波[8]。则接收信号可表示为
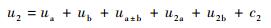 | (2) |
式中:ua±b为调制边频谐波;c2为其他谐波成分,包括三次谐波及更高次谐波、二倍调制边频谐波及高次谐波附近的边频谐波等。
振动声调制的过程如图 1所示。
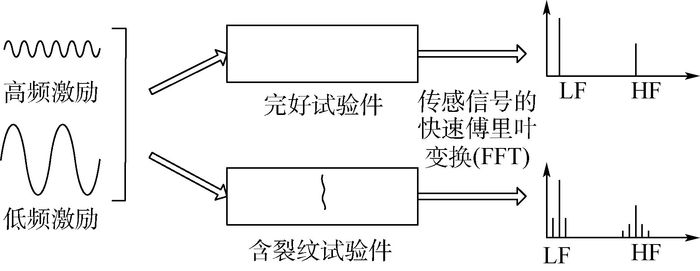 |
| 图 1 振动声调制示意图 Fig. 1 Schematic of vibro-acoustic modulation |
| 图选项 |
最初,普遍认为引发振动声调制的原因是低频振动引发裂纹的张开与闭合。但后续研究表明,裂纹面的位错、摩擦、应力集中及温度等均会对调制作用有一定的影响。目前,对于裂纹引起振动声调制效应的机理仍不确定[8],试验研究表明:① 该方法可以实现裂纹在成长为张开裂纹前被监测到;② 低频振动的幅值在无法引起裂纹面张开闭合的情况下,依然能够引起振动声调制现象。这为采用振动声调制进行裂纹监测提供了便利[11]。
2 基于振动声调制的板类裂纹损伤成像方法 2.1 含损伤信息信号的提取技术 因裂纹的存在,接收信号中其成分较为复杂,而能够携带损伤信息的信号,主要是调制边频谐波和高次谐波。因信号的调制仅发生在裂纹界面处,故可认为激励信号在传播到裂纹界面前及界面后,均为线性传播,满足信号的线性叠加[8]。同时,因为损伤位置往往不能再准确地落到传感路径上,故如图 2所示,传感信号一般由两部分组成,第1部分为直达波信号S(m);第2部分为激励信号经由损伤位置到达的信号S(n)。本文采取以下方法进行含损伤信号的提取,即提取S(n)。
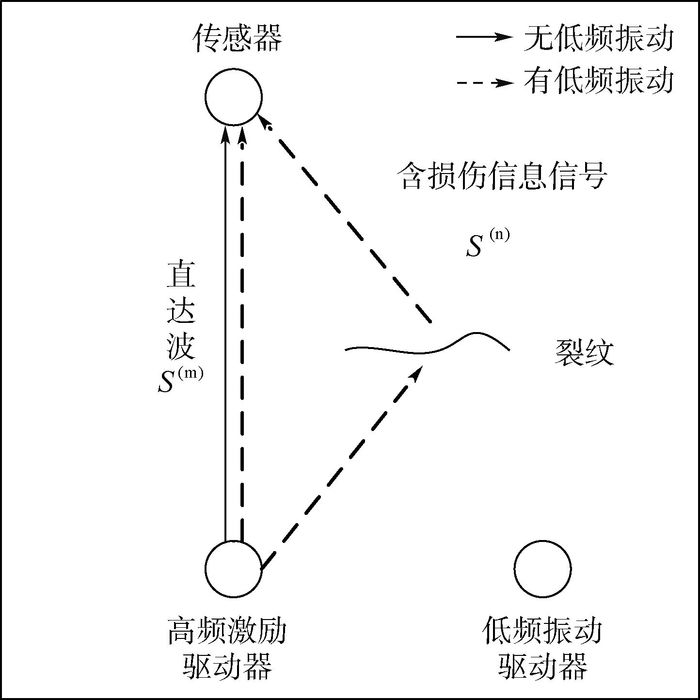 |
| 图 2 有低频振动及无低频振动高频信号的传播路径示意图 Fig. 2 Schematic of HF signal propagation path when there is LF vibration and no LF vibration |
| 图选项 |
1) 仅向结构中输入高频信号,获得传感信号为
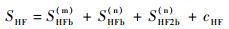 | (3) |
式中:SHFb(m)为高频输入直达波信号;SHFb(n)为高频输入下含损伤信号的基频谐波成分;SHF2b(n)为高频输入下含损伤信号的二倍频成分;cHF为高频输入下含损伤信号的其他谐波成分。当裂纹处于闭合状态时,信号的散射及反射不明显,故有Sb(n)和S2b(n)的幅值较低。
2) 向结构中同时输入高频和低频信号,且高频信号同上,得到传感信号为
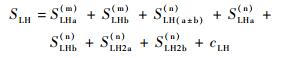 | (4) |
式中:SLHa(m)和SLHb(m)分别为双频输入下的直达波低高频成分;SLH(a±b)(n)为含损伤信号中的调制边频成分;SLHa(n)和SLHb(n)分别为双频输入下含损伤信号的低高频成分;SLH2a(n) 和SLH2b(n)为双频输入下含损伤信号的二倍频成分;cLH为高频输入下含损伤信号的其他谐波成分。
3) 因除裂纹界面外的非线性调制作用外,其他均为线性系统,故可将两信号进行做差处理,即
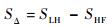 | (5) |
又因为线性叠加原理,有SHFb(m)=SLHb(m),则有
 | (6) |
由式(6) 可以看出,直达波信号的成分仅存在低频部分,而含损伤信号在高频部分信号的成分依旧很复杂。
4) 采用带通滤波器,过滤掉在高频基频谐波之外的信号成分,保留笔者最关注的含损伤信号中高频部分的基频谐波成分及调制边频成分,即
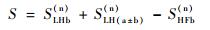 | (7) |
则信号S包含了损伤的相关信息,其频域成分主要有基频谐波及调制边频谐波组成,可以此进行裂纹损伤的定位。
2.2 延时叠加算法 目前,基于Lamb波的损伤成像算法主要有椭圆定位法、延时叠加算法及时间反转法等,为减少时间延迟确定带来的误差影响,采用延时叠加算法进行损伤成像处理[20]。
首先,获取由驱动器Pi激发,传感器Pj接收的含损伤信息的信号Sij(t)可采用复数表示形式
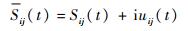 | (8) |
式中:uij(t)为信号Sij(t)的希尔伯特变换。
其次,通过希尔伯特变换确定含损伤信息信号的包络:
 | (9) |
然后,计算激励信号从驱动器Pi经由板中某点O(x, y),到达传感器Pj的时间延时为
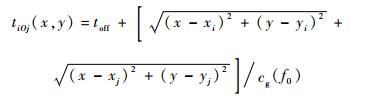 | (10) |
式中:cg(f0)为中心频率为f0时的群速度;toff为信号传播中的固有时延。
最后,通过多条传感路径进行监测后,板中O点的像素值为
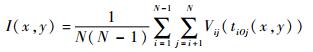 | (11) |
式中:N为传感器数量。
图 3为基于延时叠加算法成像原理,根据其原理可知,延时叠加成像是通过叠加损伤到各传感器的距离来定位损伤。对于一对传感器而言,其成像结果应该是绘制了以两传感器为焦点的多个椭圆,而损伤所在的椭圆幅值相对较大,随着传感器数目的增加,各幅值较大的椭圆将在损伤位置聚焦。
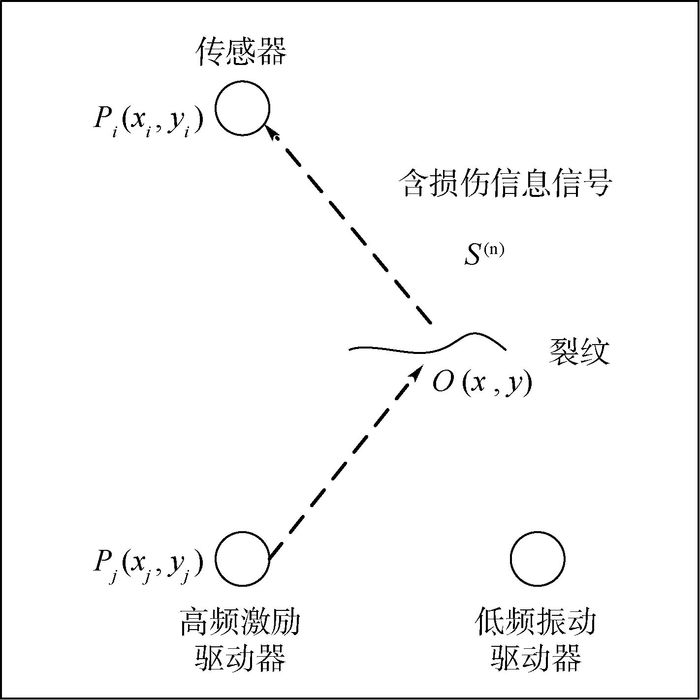 |
| 图 3 延时叠加成像原理 Fig. 3 Principle of delay and sum imaging |
| 图选项 |
因正弦激励信号无法确定损伤位置,故借鉴基于线性Lamb波进行损伤定位的经验,采用汉宁窗调制的正弦信号作为高频激励。
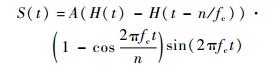 | (12) |
式中:A为信号的幅值;fc为中心频率;H(t)为Heaviside函数;n为正弦波峰的个数。本文试验中,取中心频率fc=50 kHz,n=5。
根据2.1节获得的含损伤信息信号主要是由基频谐波信号及调制边频信号组成,因其频率值相差不大,故可假定含损伤信号的波包群速度均为基频谐波频率所对应的群速度,并根据延时叠加成像算法进行损伤成像处理。
3 试验研究 为验证上述方法的可行性,选取尺寸为300 mm×700 mm×1.5 mm的矩形板作为试验件,板中间位置有8 mm通孔,并采用MTS810疲劳试验机进行疲劳加载直至出现疲劳裂纹,裂纹位于圆孔两侧,其尺寸约为15 mm。为避免边界条件带来的调制效应的影响,试验件进行悬挂处理。在裂纹周围布置8个直径为5 mm的压电陶瓷(PZT)片,且每相邻两传感器的距离约为100 mm,具体位置如图 4所示,在图中标识序号为1~8。
 |
| 图 4 试验件及传感器布置 Fig. 4 Test specimen and sensor arrangement |
| 图选项 |
高频信号采用NI数字采集设备进行激发和采集,由控制器PIXe-8 133、任意波形发生卡PIX-5 412和采集卡PIX5 105组成,同时采用HAS-4052功率放大器对输出信号及采集信号进行放大。低频振动采用LA-200功率放大器、Agilent 33220 A波形发生器和JZQ电磁激振器进行激发。为避免边界反射对本文试验结果的影响,试验采用悬挂的方式。为在较低低频激励电压下,能更好地推动裂纹面的运动,可采用该板的固有模态作为激励频率。通过扫频,采用第8阶固有模态对应的频率287.2 Hz,作为低频振动激励频率。
3.1 损伤信息提取技术的验证 为能够在频域更直观地反映损伤信息提取技术的可行性,低频及高频振动均采用正弦激励的方法。首先,输入低频振动,频率为287.2 Hz,激励电压为50 V,在形成稳态振动后,单个压电片激发高频振动信号,频率为50 kHz(高频信号在相对低频段,A0模态的幅值较大,而S0模态幅值较小[21]),其余7个压电片同时进行信号采集。以路径3—2为例,获得频谱如图 5所示。
 |
| 图 5 传感信号的频谱图 Fig. 5 Spectrogram of sensing signal |
| 图选项 |
从图 5中可以看出,信号主要由基频谐波、二次谐波、三次谐波及更高次谐波信号组成。为考察调制边频谐波的情况,将图 5进行局部放大,其结果如图 6所示。
 |
| 图 6 信号频谱图在各谐波频率附近的局部放大图 Fig. 6 Locally amplified spectrogram of sensing signal near different harmonic frequency |
| 图选项 |
当不施加低频振动,仅通过压电片激发高频振动时,测得信号其频谱图 7所示。
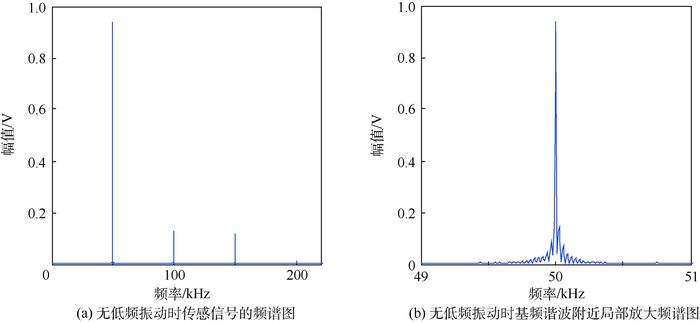 |
| 图 7 无低频振动时传感信号的频谱图及其在基频谐波频率附近的局部放大图 Fig. 7 Spectrogram of sensing signal without low frequency vibration and its locally amplified spectrogram near by fundamental waves frequency |
| 图选项 |
从图 6中可以看出,不仅基频谐波附近出现了调制边频谐波,在二次及三次谐波附近同样出现了调制边频,这是二次及三次谐波形成驻波后,与低频入射波在裂纹处再次相互作用所导致的。从图 7(a)中,可知当低频振动不存在时,传感信号中仍会产生二次及更高次谐波,这与文献[17]中所推导的单列纵波在界面出传播的结论相吻合。图 7(b)为基频谐波附近的频域放大图,从图中可以看出,当低频振动不存在时,调制边频谐波亦不存在。对比图 6(a)及图 7(a)中二次及三次谐波成分的幅值可以发现,当低频振动存在时,二次及三次谐波的幅值大于当低频振动不存在的情况,这是因为低频振动引起了裂纹面的相对运动,且改变了裂纹非线性弹簧模型的两阶刚度,进而导致了此现象的发生。
运用2.1节提出的含损伤信息信号的提取技术,对两次采集信号进行相减运算,并采用带通滤波器滤波后,得到的信号频域如图 8所示。
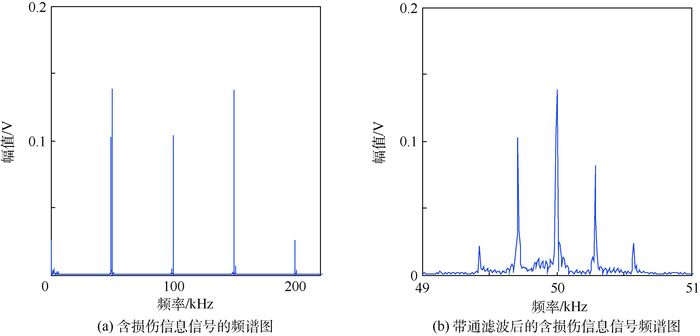 |
| 图 8 含损伤信息信号及带通滤波后含损伤信息信号的频谱图 Fig. 8 Spectrogram of signal with damage information and of band-pass filtered signal with damage information |
| 图选项 |
从图 8(a)中可以看出,差信号中依然存在基频谐波、二次及三次谐波和调制边频谐波,图 8(b)为带通滤波后的结果,从图中可以看出,作为最能反映裂纹位置信息的调制边频谐波在差信号中较为明显,说明该损伤信息提取技术可较好的获取裂纹损伤位置信息,为下文采用脉冲串激励的方法进行裂纹成像提供了基础。
3.2 板类结构中裂纹损伤成像 为了实现基于振动声调制进行板类结构裂纹损伤成像,采用中心频率为50 kHz的汉宁窗调制5波峰正弦信号作为高频激励信号,低频激励信号不变,试验件、试验设备及传感器布局同上。测得中心频率为50 kHz的Lamb波群速度cg≈1 537 m/s。为模拟结构所处的真实环境,将试验件上下段采用螺栓连接进行固定,如图 9所示。由超声波在界面的传播理论可知,边界位置同样会发生振动声调制效应。
 |
| 图 9 试验现场 Fig. 9 Test site |
| 图选项 |
取1、3、6、7共4个传感器进行裂纹损伤的定位,采用一发多收的方式循环激励接收,共获得12组信号,根据第2节所提方法分别对采集的信号进行处理,得到了滤波后的12组差信号及其包络,取6激励,1、3、7接收到的信号为例进行分析,其结果如图 10所示。
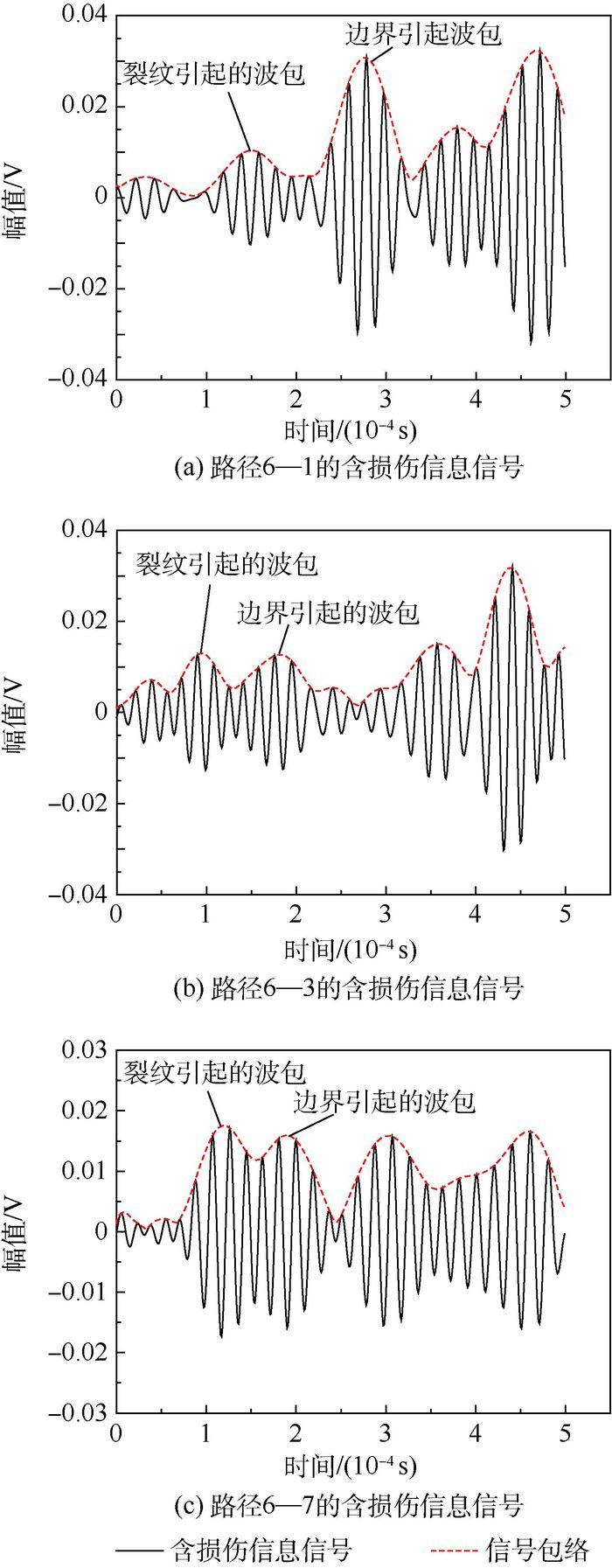 |
| 图 10 各传感路径的含损伤信息信号 Fig. 10 Signal of damage information for each sensing path |
| 图选项 |
从图 10中可以看出,由裂纹引起散射波包较为明显,但边界发射引起的波包也较为强烈,采用延时叠加算法,直接进行成像,结果如图 11所示,x和y分别为对应试验件的长、宽坐标。
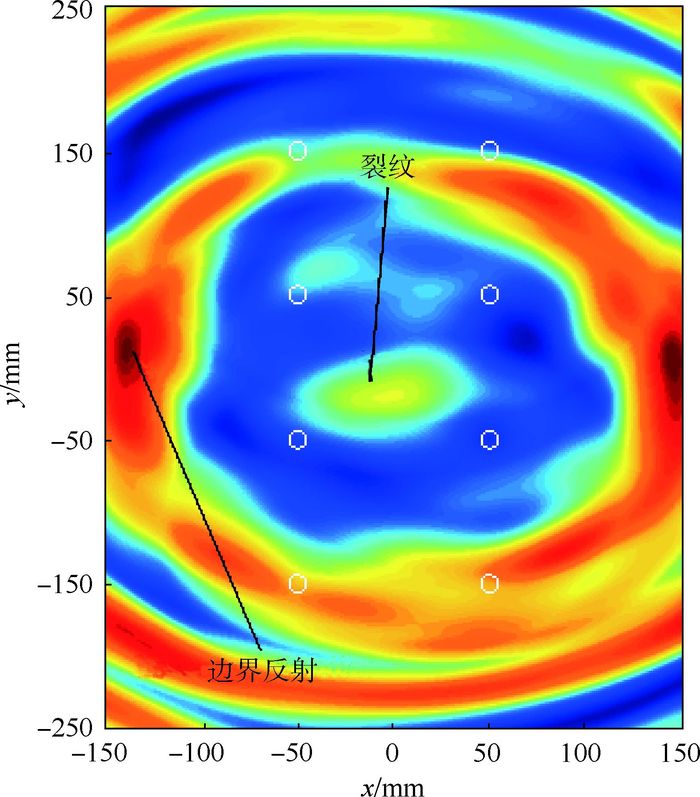 |
| 图 11 有边界反射时的定位成像结果 Fig. 11 Localization and imaging results with boundary reflection |
| 图选项 |
从图 11中可以看出,本文所提方法可以较好地定位损伤的位置,同时,因板的左右两侧边界距离传感器距离较近,该区域的像素值较大。而板的上下两侧边界,因为螺栓连接存在接触界面,也会发生振动声调制效应,结合该区域的边界反射,故该区域的像素值也比较大。为避免边界反射给定位带来的困扰,将边界反射信号予以截断处理。为提高成像对比度,采用全乘算法,基于截断后的信号进行了成像处理,可成功确定损伤的位置信息,且成像分辨率较高,成像结果如图 12所示。
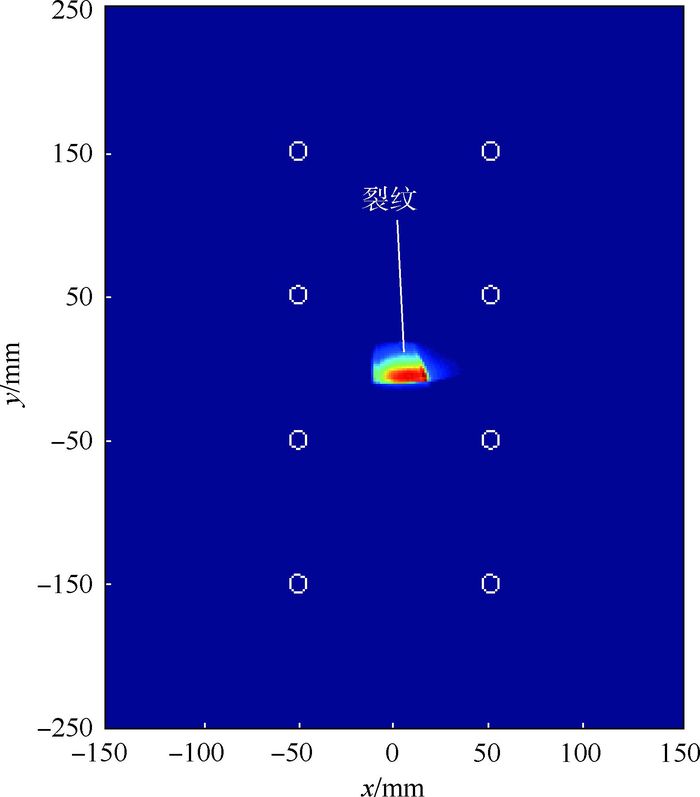 |
| 图 12 信号截断后的定位成像结果 Fig. 12 Localization and imaging results after signal truncation |
| 图选项 |
4 结论 1) 采用本文所提出的含损伤信息信号提取技术,可有效消除直达波信号,保留因裂纹的调制作用引起的调制边频信号及高次谐波信号。
2) 基于振动声调制效应的板类结构裂纹定位成像结果真实地反映了裂纹所在位置,同时,边界反射及接触边界引起的调制信号会干扰裂纹的定位结果,故本文所提方法需要远离边界或者需要对信号进行边界波包截断处理。
3) 本文方法无需结构在健康状态时测得的信号作为基准信号,仅需要无低频振动和有低频振动时,激发高频信号所测得的信号即可。一定条件下,可采用结构工作时的振动作为低频激励,为无基准下的裂纹监测提供了方法。
参考文献
| [1] | 张行. 断裂与损伤力学[M].北京: 北京航空航天大学出版社, 2006: 1-38. ZHANG X. Fracture and damage mechanics[M].Beijing: Beihang University Press, 2006: 1-38.(in Chinese) |
| [2] | 袁慎芳. 结构健康监控[M].北京: 国防工业出版社, 2007: 206-212. YUAN S F. Structural health monitoring and damage control[M].Beijing: National Defence Industry Press, 2007: 206-212.(in Chinese) |
| [3] | STASZEWSKI W J, BOLLER C, TOMLINSON G R. Health monitoring of aerospace structures:Smart sensor technologies and signal processing[M].Chichester: Wiley & Sons Ltd, 2004: 102-137. |
| [4] | GRABOWSKI K, GAWRONSKI M, BARAN I, et al. Time-distance domain transformation for acoustic emission source localization in thin metallic plates[J].Ultrasonics, 2016, 68: 142–149.DOI:10.1016/j.ultras.2016.02.015 |
| [5] | ZHAO X, ROYER R L, OWENS S E, et al. Ultrasonic Lamb wave tomography in structural health monitoring[J].Smart Materials & Structures, 2011, 20(10): 105002–105011. |
| [6] | NOVAK A, BENTAHAR M, TOURNAT V, et al. Nonlinear acoustic characterization of micro-damaged materials through higher harmonic resonance analysis[J].NDT & E International, 2011, 45(1): 1–8. |
| [7] | PIECZONKA L, KLEPKA A, STASZEWSKI W J. Nonlinear vibroacoustic wave modulation for structural damage detection:An overview[J].Optical Engineering, 2016, 55(1): 011005. |
| [8] | ROSE J L. Ultrasonic guided waves in solid media[M].Cambridge: Cambridge University Press, 2014: 61-89. |
| [9] | BRODA D, STASZEWSKI W J, MARTOWICZ A, et al. Modelling of nonlinear crack-wave interactions for damage detection based on ultrasound-A review[J].Journal of Sound & Vibration, 2014, 333(4): 1097–1118. |
| [10] | 吴斌, 颜丙生, 何存富, 等. AZ31镁合金早期力学性能退化非线性超声检测[J].航空材料学报, 2011, 31(1): 87–92. WU B, YAN B S, HE C F, et al. AZ31 magnesium early mechanical performance degradation nondestructive testing using nonlinear ultrasonic[J].Journal of Aeronautical Materials, 2011, 31(1): 87–92.(in Chinese) |
| [11] | 焦敬品, 孙俊俊, 吴斌, 等. 结构微裂纹混频非线性超声检测方法研究[J].声学学报, 2013, 38(6): 648–656. JIAO J P, SUN J J, WU B, et al. A frequency-mixing nonlinear ultrasonic technique for micro-crack detection[J].Acta Acusitca, 2013, 38(6): 648–656.(in Chinese) |
| [12] | DUTTA D, SOHN H, HARRIES K, et al.A nonlinear acoustic technique for crack detection in metallic structures[C]//Proceedings of Health Monitoring of Structural and Biological Systems.Orlando:SPIE, 2009:251-262. |
| [13] | SOLODOV I, PFLEIDERER K, BUSSE G. Nonlinear acoustic NDE:Inherent potential of complete nonclassical spectra[M].New York: Springer, 2006: 467-486. |
| [14] | DZIEDZIECH K, PIECZONKA L, KIJANKA P, et al. Enhanced nonlinear crack-wave interactions for structural damage detection based on guided ultrasonic waves[J].Structural Control & Health Monitoring, 2016, 23(8): 1108–1120. |
| [15] | PIECZONKA L, KLEPKA A, UHL T, et al.Damage imaging in nonlinear vibro-acoustic modulation tests[C]//Proceedings of Health Monitoring of Structural and Biological Systems.Orlando:SPIE, 2015:9438E. |
| [16] | SOHN H, LIM H J, DESIMIO M P, et al. Nonlinear ultrasonic wave modulation for online fatigue crack detection[J].Journal of Sound & Vibration, 2014, 333(5): 1473–1484. |
| [17] | 胡海峰. 板状金属结构健康监测的非线性超声理论与关键技术研究[D]. 长沙: 国防科学技术大学, 2011: 45-50. HU H F.Research on theory and key technologies of nonlinear ultrasonics for health monitoring of plate-like metallic structures[D].Changsha:National University of Defense Technology, 2011:45-50(in Chinese). |
| [18] | 焦敬品, 何存富, 吴斌. 接触缺陷的振动调制超声导波检测技术研究[J].声学学报, 2009, 34(3): 242–248. JIAO J P, HE C F, WU B. Vibro-modulation and guided wave techniques for contact defect detection in plate[J].Acta Acustica, 2009, 34(3): 242–248.(in Chinese) |
| [19] | KIM S, ADAMS D E, SOHN H, et al. Crack detection tech-nique for operating wind turbine blades using vibro-acoustic modulation[J].Structural Health Monitoring, 2014, 13(6): 660–670.DOI:10.1177/1475921714553732 |
| [20] | ZHANG C, QIU J, JI H, et al. Damage localization using warped frequency transform in active structural health monitoring[J].International Journal of Applied Electromagnetics & Mechanics, 2015, 47(4): 897–909. |
| [21] | GIURGIUTIU V. Tuned Lamb wave excitation and detection with piezoelectric wafer active sensors for structural health monitoring[J].Journal of Intelligent Material System and Structures, 2005, 16(4): 291–305.DOI:10.1177/1045389X05050106 |
