当MIMO-SAR应用于目标散射特征近场诊断成像时,天线阵列的非均匀性采样、合成孔径角以及带宽效应的存在共同造成了阵列输出的有效孔径数据呈扇环形,而并非常规的矩形孔径,这种非矩形的有效孔径数据导致了MIMO-SAR图像的旁瓣呈非正交性。目前,对于非正交旁瓣的研究大多是基于超宽带合成孔径雷达(UWB-SAR)的分析[4-6]。在旁瓣抑制方法中,传统的加窗处理虽然能够有效地抑制旁瓣,但会造成主瓣的展宽[6-7],这将导致图像分辨率显著下降。基于现代谱估计的方法虽然可以得到较高的分辨率,但是巨大的运算量是诊断成像难以承受的,而且需要满足理想点目标假设[7-9]。变迹滤波技术具有算法简洁、运算量小等优点[9-14]。因此,采用变迹滤波技术进行MIMO-SAR图像的非正交旁瓣抑制具有实际的应用价值。Vu等[5-6]综合矩形窗、Hanning窗以及Hamming窗的三变迹滤波方法进行了UWB-SAR非正交旁瓣的抑制,由于后2种窗函数的主瓣展宽比较严重,导致输出图像的主瓣展宽残余较强,因此处理效果不够理想。空间变迹滤波(SVA)可看作多变迹滤波的极限形式,其通过在图像域对每个像素点寻求最优的窗函数权值,使得输出的图像具有最窄的主瓣(sinc函数主瓣)和最低的旁瓣,然而SVA要求图像的点扩散函数(PSF)必须满足sinc核函数假设。
本文针对MIMO-SAR图像非正交旁瓣难以通过常规方法进行有效抑制的问题,对基于变迹滤波技术的旁瓣抑制方法进行了研究。首先分析了MIMO-SAR图像非正交旁瓣的产生机理,然后对SVA和多变迹滤波技术的适用条件进行了研究,在此基础上给出了2种有效的基于变迹滤波的旁瓣抑制方法。
1 MIMO-SAR图像旁瓣分析 1.1 MIMO-SAR成像原理 典型的用于成像的MIMO-SAR天线阵列的布阵方式如图 1所示,其中包括M个位于阵列两端的发射阵元,N个接收阵元位于2组发射阵元之间且非均匀分布。在阵元个数和阵列长度相同的条件下,这种布阵方式构成的M×N个虚拟阵元(或者数据采集通道)具有最高的孔径利用率。发射阵元之间的间距为d,接收阵元之间的间距为Md/2,发射阵列与接收阵列之间的间距为d/2,那么总的阵列长度为L=(MN/2+M/2-1) d,虚拟孔径长度为Lvir=(MN-1) d/2,虚拟孔径间隔dvir=d/2。θ为收发通道的双站角, R0表示天线阵列中心到目标坐标系中心的参考距离,RTm表示第m个发射天线到目标上任意一点σ(x, y)处的距离,RRn表示第n个接收天线到目标上任意一点σ(x, y)处的距离。那么,接收到的回波可以表示为
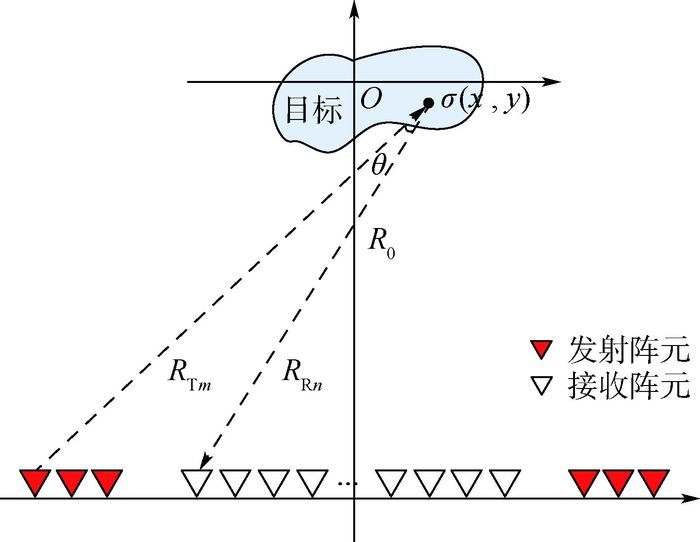 |
| 图 1 天线阵列结构及成像几何关系 Fig. 1 Antenna array configuration and imaging geometry |
| 图选项 |
 | (1) |
式中:xTm为第m个发射阵元的位置;xRn为第n个接收阵元的位置;fk为步进频信号的第k个频率采样点;D为包含目标的成像区域;c为光速;σ为目标的散射强度;x、y为散射点在目标本体坐标系中的位置坐标;

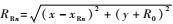
从式(1) 可以得到重建目标图像的离散表达式为
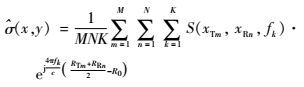 | (2) |
式中:

1.2 旁瓣特性分析 常规点目标的有效孔径数据呈矩形状,因此二维点扩散函数是正交的,且距离向和方位向切片满足sinc核函数。由于受到近场效应、带宽效应以及合成孔径角的影响,MIMO-SAR点目标的有效孔径数据呈扇环形,其二维点扩散函数非正交,距离向满足sinc核函数,而方位向则非sinc核函数。图 2分别给出了MIMO-SAR的近场二维点扩散函数、二维切片的幅度及相位分布。
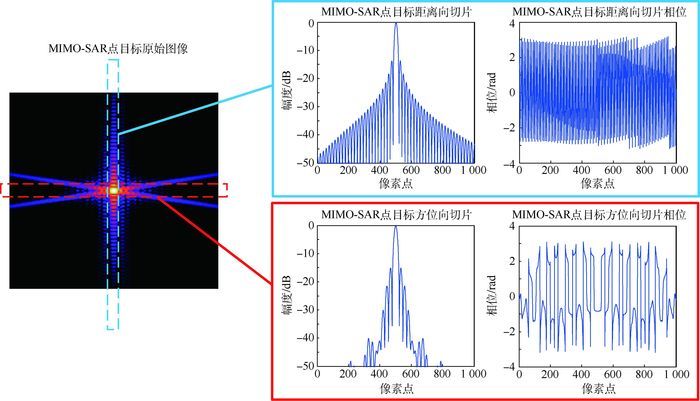 |
| 图 2 MIMO-SAR近场点目标二维点扩散函数及二维切片 Fig. 2 MIMO-SAR near-field point target 2D PSF and 2D cut |
| 图选项 |
MIMO-SAR雷达系统的数据采集通道是由不同的收发天线对组合而成。各通道之间硬件属性的差异导致阵列输出幅度和相位的不一致性,从而造成图像散焦以及旁瓣形变。因此,在进行旁瓣抑制前首先要对回波数据进行幅相不一致性校准。根据单双站等效原理,每对收发分置天线阵元可等效为单个收发同置天线阵元。因此,等效虚拟阵列的孔径数据为扇环形(夹角为合成孔径角,宽度为带宽)。这种方位向采样随频率的变化呈现非均匀性的扇环形数据,使得成像结果在方位向上的旁瓣呈现非正交特性以及非sinc核函数特性。
可以预见,当阵列的合成孔径角不变时,随着参考距离的增大,方位向采样的非均匀性会逐渐减弱,当距离足够远时,实际的有效孔径数据可近似为矩形,此时的方位向和距离向旁瓣基本满足正交特征。这与Goodman[4]以及Vu[5-6]等对UWB-SAR图像非正交旁瓣的分析具有一致性。不同之处在于MIMO-SAR图像的旁瓣除了合成孔径角和带宽效应之外,还受到虚拟孔径等效方位向采样的不均匀性影响。
2 基于变迹滤波的旁瓣抑制方法 在成像处理中,最传统的旁瓣抑制方法是数据域加窗处理。加窗处理能够较好地抑制旁瓣,然而会导致主瓣的展宽,从而降低图像的分辨率。
数据域的加窗处理可以看作是线性变迹滤波过程,非线性变迹处理则是在2个或者多个窗函数处理图像的基础上通过选取最优值来获得最佳旁瓣衰减和最小的主瓣展宽性能[11]。这种非线性的变迹过程,根据其使用窗函数的个数(矩形窗必须作为参考窗)分为双变迹(dual-apodization)滤波、三变迹(tri-apodization)滤波以及多变迹(multi-apodization)滤波[12]。易见,在每个像素点处选取响应的三点加权窗函数以使得输出图像具有较低的旁瓣和最小的主瓣展宽,这就是所谓的SVA处理[14-15]。需要注意的是,当采用SVA处理时,输入图像必须要满足点目标假设,即旁瓣的幅度和相位要满足sinc核函数假设。
如图 2所示,MIMO-SAR图像距离向旁瓣的幅度和相位均满足sinc核函数,方位向幅度满足部分sinc核函数(主值附近),而相位则完全不满足。因此,可以采用双变迹、三变迹以及多变迹等非线性变迹处理,而不能直接采用SVA进行处理。类似的问题,Vu等[5-6]针对UWB-SAR图像中的非正交旁瓣,采用双变迹(矩形窗和Hamming窗)以及三变迹(矩形窗、Hanning窗和Hamming窗)进行处理,从结果来看效果不够理想,主要是主瓣展宽的残余比较强,这是因为Hanning窗和Hamming窗的主瓣展宽比较显著。根据上述分析,本文提出了对方位向和距离向旁瓣独立进行变迹滤波处理的2种方法:① 距离向SVA与方位向三变迹滤波处理相结合(方法1);② 二维可分离SVA处理(方法2)。
2.1 距离向SVA与方位向三变迹滤波处理相结合 MIMO-SAR图像的距离向旁瓣满足sinc核函数假设,因此可采用SVA来消除距离向的旁瓣,并在此基础上选取合适的窗函数实现方位向的三变迹滤波。本文通过综合考虑主瓣的展宽以及旁瓣的衰减性能,分别选取了矩形窗(参考窗)、Hamming窗以及Kaiser窗(形状参数为2) 来进行三变迹滤波。选取的依据是Hamming窗第一旁瓣较低,而Kaiser窗的主瓣展宽小。图 3给出了具体的处理流程。
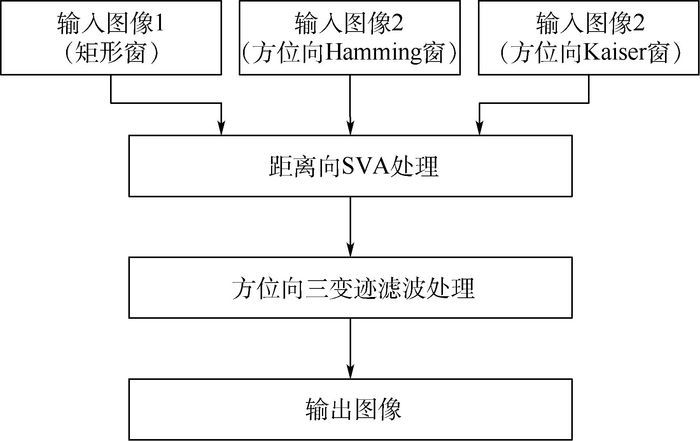 |
| 图 3 距离向SVA与方位向三变迹滤波处理流程 Fig. 3 Processing flow of down range SVA and cross range tri-apodization filtering |
| 图选项 |
图 4给出了方法1和Vu方法[5-6]的窗函数响应曲线的对比。可以看出,方法1相对于Vu方法脉冲响应的主瓣展宽残余降低了约5 dB,而且高阶旁瓣的衰减大大加快。
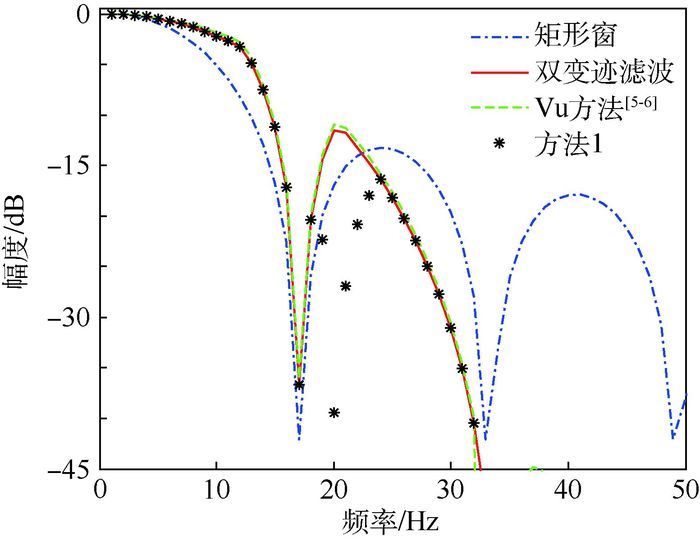 |
| 图 4 方法1与Vu方法[5-6]窗函数响应对比 Fig. 4 Comparison of window function response betweenproposed method and Vu's method[5-6] |
| 图选项 |
2.2 二维可分离SVA处理 根据2.1节的分析,方位向旁瓣的幅度近似具有sinc特征,而相位则完全不满足。SVA处理需要利用图像的相位信息,只有在满足主瓣和各阶副瓣的相位正负交替变化时,才能有效地抑制旁瓣。图 5(a)为没有经过相位校正的MIMO-SAR单点目标方位向切片相位,其具有连续变化的相位包络特征,主瓣和各阶副瓣的相位变化信息丢失,因此,在采用SVA进行方位向旁瓣抑制时需要进行相位校正。本文通过对距离向SVA处理后的图像进行二维IFFT-FFT处理(线性运算,不改变幅度),使得偶数点处的相位值在±π/2附近,这样便可以对方位向进行SVA处理[11]。图 5(b)给出了校正后的相位,图 6给出了具体的处理流程。
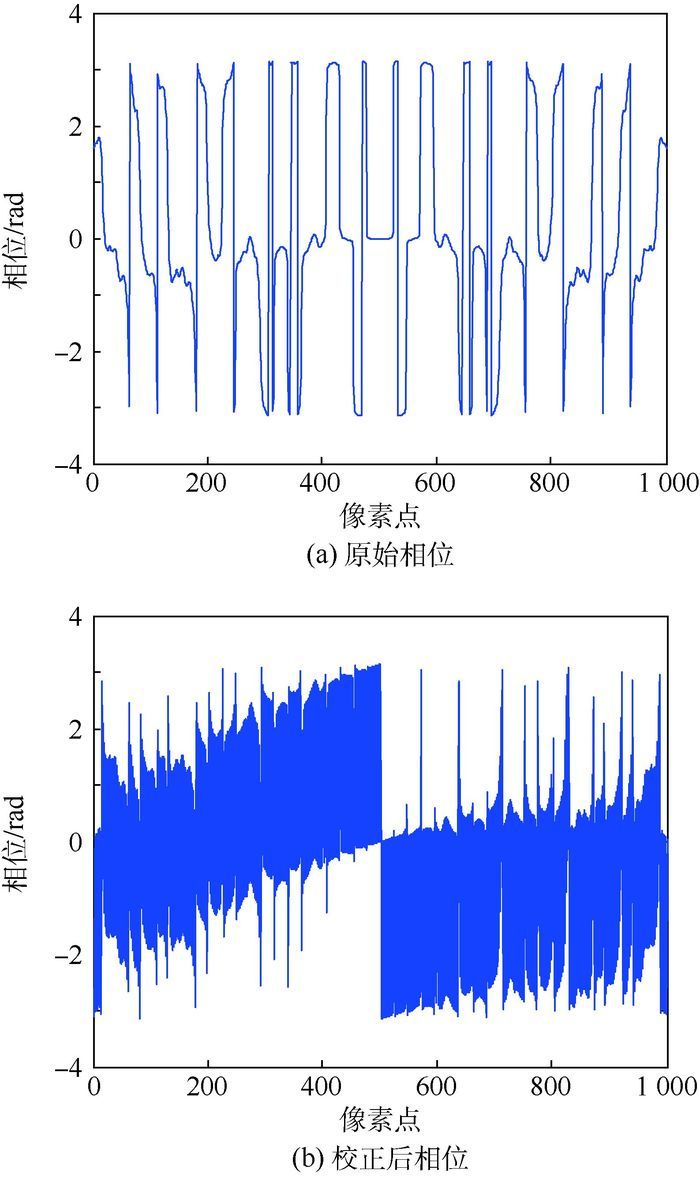 |
| 图 5 方位向切片相位校正前后结果对比 Fig. 5 Comparison of cross range cut before and after phase correction |
| 图选项 |
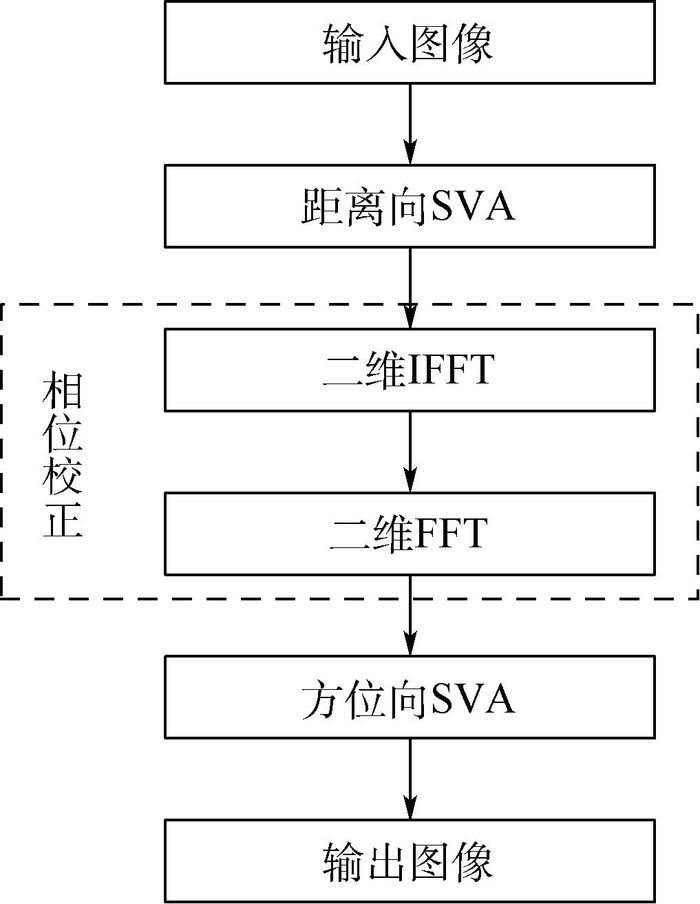 |
| 图 6 二维可分离SVA处理流程 Fig. 6 Processing flow of 2D separable SVA |
| 图选项 |
3 仿真及实验结果分析 为了说明本文方法的有效性,首先仿真近场条件下3个间隔较远的点目标,具体的参数设置为:参考距离R0=5 m,目标1位置(0,0) m,目标2位置(0.5,0.5) m,目标3位置(-0.5,-0.5) m,频率f=8~12 GHz, 步进频率为5 MHz,801个频点,FFT点数为3 208,像素点数为1 001×1 001,成像视场2 m×2 m。
图 7(a)为原始的扇环形数据直接采用滤波逆投影算法的成像结果,非正交副瓣比较明显;图 7(b)为传统的加窗处理结果,可以看出图像的旁瓣得到了有效抑制,但主瓣方位向和距离向的展宽比较明显;图 7(c)为Vu方法[5-6]处理结果,在方位向和距离向均有主瓣展宽残余;图 7(d)为方法1的结果,距离向的旁瓣得到了很好的抑制,而且距离向主瓣没有展宽,方位向有少量的主瓣展宽残余;图 7(e)为方法2的结果,距离向和方位向主瓣均没有展宽,而且2个方向上的旁瓣都得了很好的抑制。图 8对比了3种方法对中间目标处理得到的距离向和方位向切片。
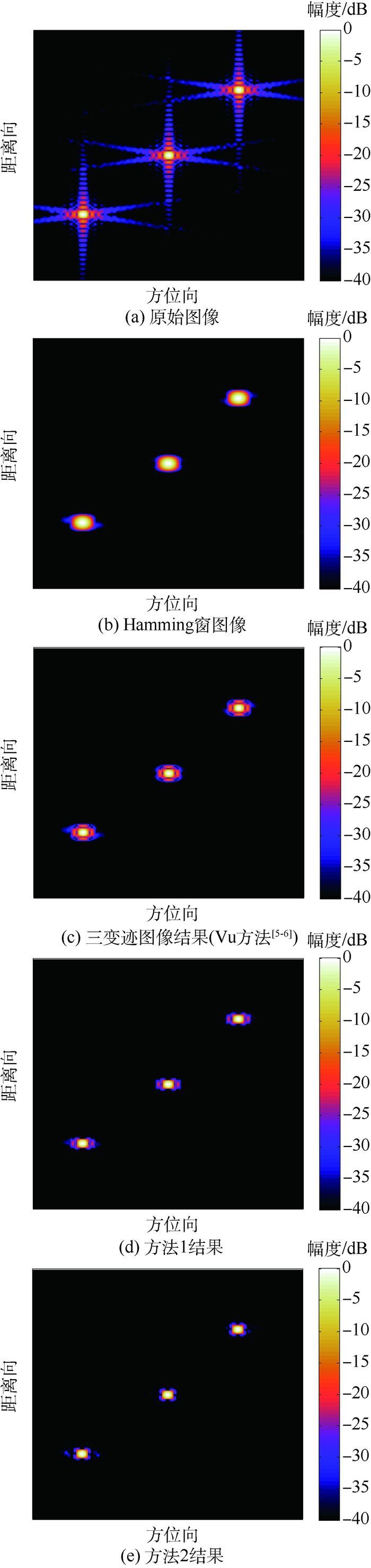 |
| 图 7 大间隔三点目标不同变迹滤波处理的结果 Fig. 7 Processing results of different apodization filtering of a large-space three points target |
| 图选项 |
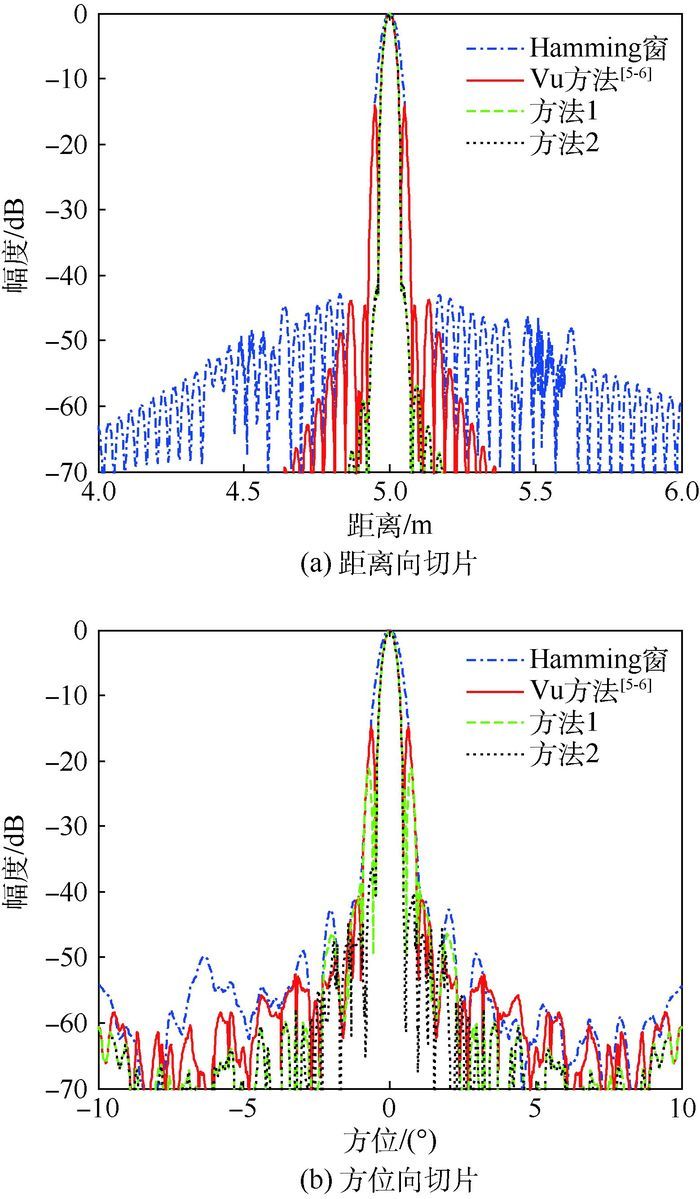 |
| 图 8 大间隔三点目标视场中心处的二维切片 Fig. 8 2D cuts at center of filed of view at a large-space of three points target |
| 图选项 |
从图 8(a)可以看出,Vu方法[5-6]在距离向上的主瓣剩余较严重,而本文2种方法均能很好地消除距离向旁瓣。从图 8(b)可以看出,本文2种方法的方位向主瓣展宽剩余比Vu方法[5-6]低约5 dB左右,方法2对于距离向和方位向旁瓣的抑制效果更佳。
为了进一步验证本文方法对MIMO-SAR图像二维分辨率的增强性能,仿真了在距离和方位上间隔很小的3个点目标,目标1位置(0,0) m,目标2位置(0,0.08) m,目标3位置(0.08,0) m,其余参数同上。
图 9(a)为原始的扇环形数据直接采用滤波逆投影算法的成像结果,较强的非正交副瓣降低了图像的动态范围;图 9(b)为传统窗函数得到的图像,虽然旁瓣得到了抑制,但是3个目标已经无法区分;图 9(c)中采用Vu方法[5-6]的结果,虽然可以区分3个目标的主瓣,但是对于旁瓣的抑制不理想;图 9(d)、图 9(e)中结果明显优于前2种方法,尤其是方法2对于方位向的非正交旁瓣抑制效果更好。图 10对视场中心处的距离向和方位向切片进行了对比。
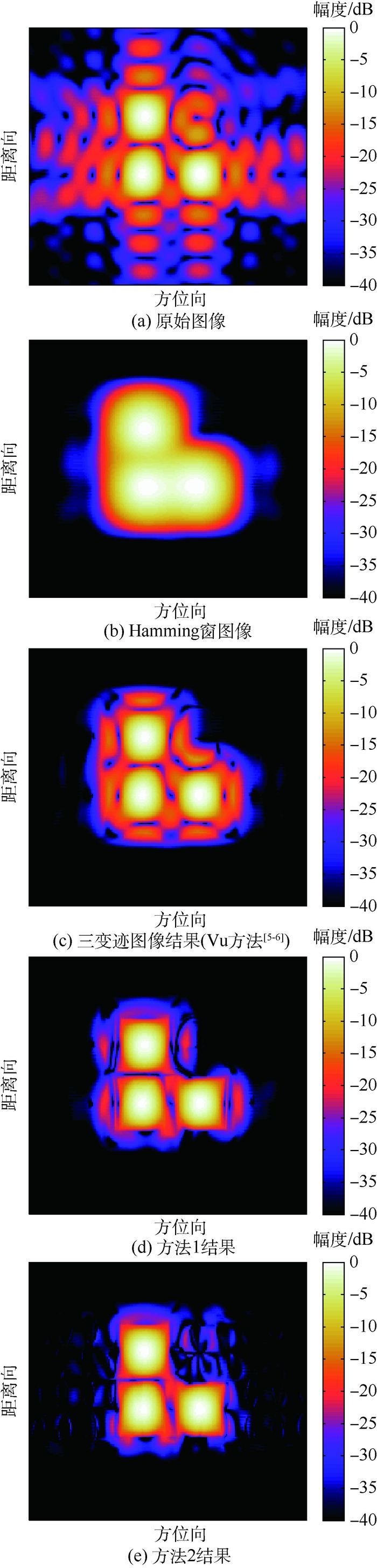 |
| 图 9 小间隔三点目标不同变迹滤波处理的结果 Fig. 9 Processing results of different apodizationfiltering of a small-space three points target |
| 图选项 |
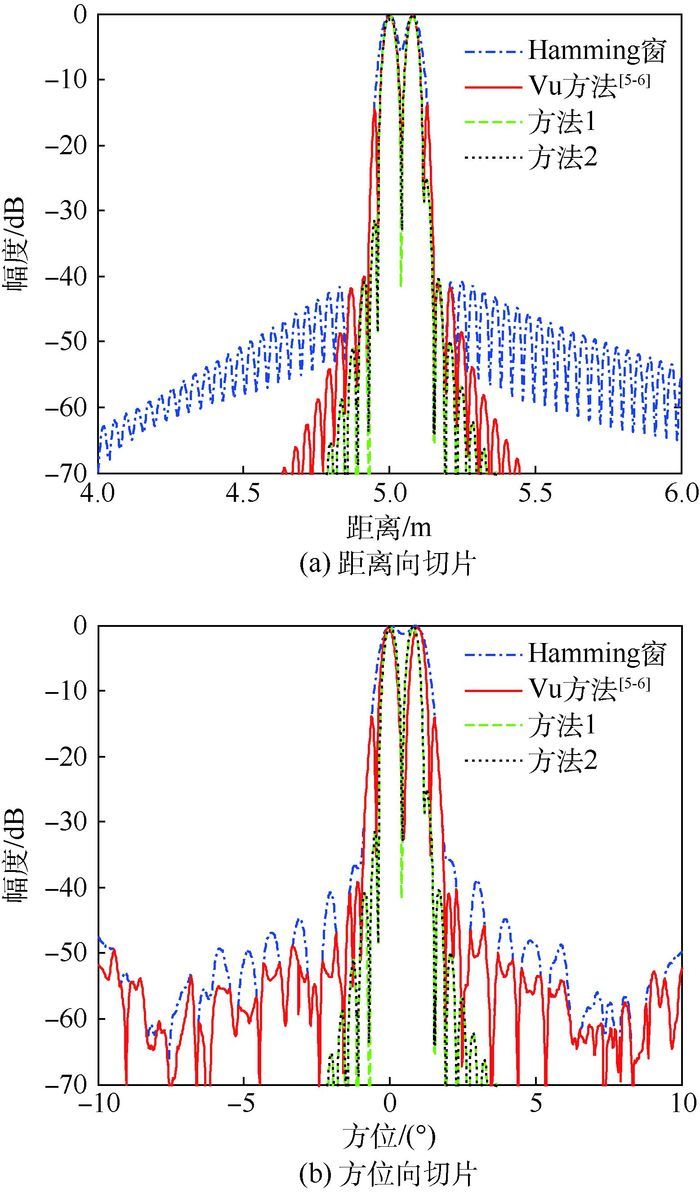 |
| 图 10 小间隔三点目标视场中心处的二维切片 Fig. 10 2D cuts at center of filed of view at asmall-space of three points target |
| 图选项 |
由图 10(a)可以看出,传统的加窗处理导致主瓣展宽, 使得2个目标在距离向难以分辨,其余3种方法可以分辨2个目标的主瓣,而本文的2种方法具有较低的旁瓣,有利于分辨率增强;图 10(b)中方位向切片的对比进一步验证了上述结论,不赘述。
对某型飞机模型的实测数据进行了处理。测试环境是在局部地方简单铺设了吸波材料的普通实验室,采用的雷达是本实验室研制的第一代MIMO-SAR成像测量系统,参数设置与本节中的雷达仿真参数一致。在成像处理前对原始数据进行了零距离相位校准以及背景抵消,尚未进行天线阵元的空间位置误差校准。图 11给出了不同变迹处理的成像结果。
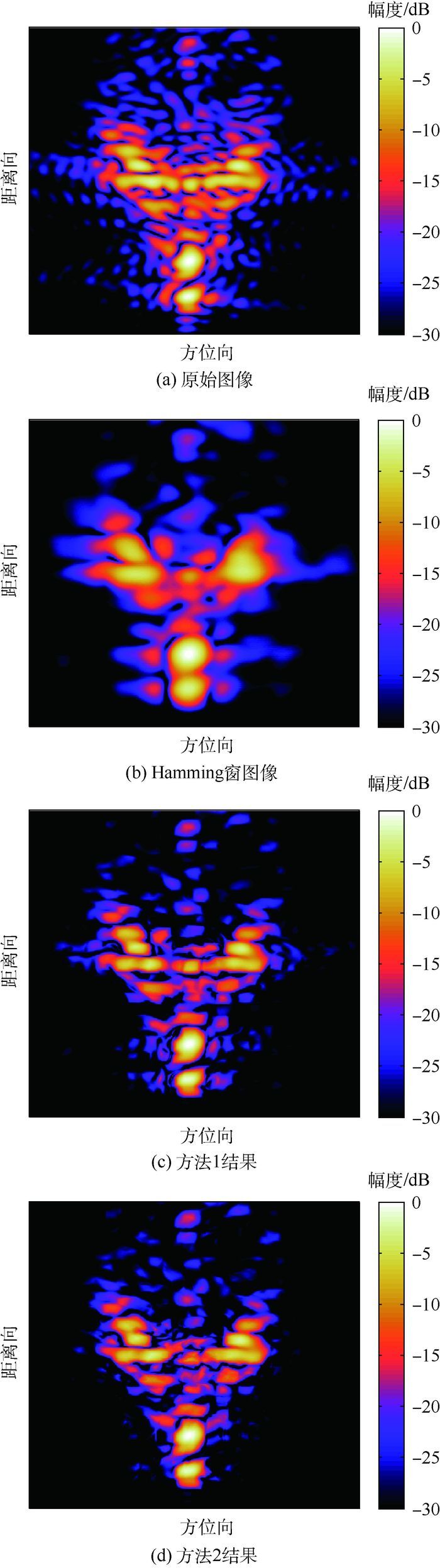 |
| 图 11 某飞机模型实测数据处理的结果 Fig. 11 Measured data processing results of an airplane model |
| 图选项 |
从图 11可见,本文的2种方法均能有效抑制旁瓣,提高图像的分辨率,特别是方法2的效果更佳。但总体上Vu方法[5-6]和本文方法对于实测数据的处理效果均要劣于仿真数据,这主要是由于现有的MIMO-SAR成像数据尚未实现对天线阵元的空间位置误差所导致的相位误差进行精确校准(只进行了粗略的幅度和相位补偿)。
4 结论 本文概括了MIMO-SAR图像非正交旁瓣的产生机理,提出了基于变迹滤波的旁瓣抑制方法。仿真结果表明:
1) 本文方法在保证主瓣分辨率的情况下,可以有效抑制距离向和方位向旁瓣,提高了图像的二维分辨率和动态范围。
2) 对于实测数据而言,在对MIMO-SAR天线阵元空间位置误差进行精确校准的基础上可进一步提高方法的实用性。
参考文献
| [1] | 黄培康, 殷红成, 许小剑. 雷达目标特性[M].北京: 电子工业出版社, 2005. HUANG P K, YIN H C, XU X J. Radar target characteristics[M].Beijing: Publishing House of Electronics Industry, 2005.(in Chinese) |
| [2] | 许小剑, 黄培康. 雷达系统及其信息处理[M].北京: 电子工业出版社, 2010: 10-46. XU X J, HUANG P K. Radar systems and principles[M].Beijing: Publishing House of Electronics Industry, 2010: 10-46.(in Chinese) |
| [3] | LIU Y Z, XU X J.Azimuth sidelobe suppression technique for near field MIMO radar imaging[C]//Proceedings of SPIE on Remote Sensing XXI:Image and Signal Processing.Bellingham, WA:SPIE, 2015:1-8. |
| [4] | GOODMAN R, TUMMALA S, CARRARA W.Issues in ultra-wideband, widebeam SAR image formation[C]//Proceedings of IEEE International Radar Conference.Piscataway, NJ:IEEE Press, 1995:479-485. |
| [5] | VU V T, SJ?GREN T K, PETTERSSON M I.On apodization techniques for ultra-wideband SAR imaging[C]//Proceedings of EURAD 2009.Piscataway, NJ:IEEE Press, 2009:529-532. |
| [6] | VU V T. An impulse function for evaluation of UWB SAR imaging[J].IEEE Transactions on Signal Processing, 2010, 58(7): 3927–3931.DOI:10.1109/TSP.2010.2047503 |
| [7] | HARRIS F J. On the use of windows for harmonic analysis with the discrete Fourier transform[J].Proceedings of the IEEE, 1978, 66(1): 51–83.DOI:10.1109/PROC.1978.10837 |
| [8] | LI J, STOICA P. An adaptive filtering approach to spectral estimation and SAR imaging[J].IEEE Transactions on Signal Processing, 1996, 44(6): 1469–1484.DOI:10.1109/78.506612 |
| [9] | STOICA P, MOSES R. Introduction to spectral analysis[M].Upper Saddle River, NJ: Prentice Hall, 1997: 23-65. |
| [10] | WANG Y W, LI J, STOICA P. Rank-deficient robust capon filter-bank approach to complex spectral estimation[J].IEEE Transactions on Signal Processing, 2005, 53(8): 2713–2726.DOI:10.1109/TSP.2005.850365 |
| [11] | XU X J, NARAYANAN R M. Enhanced resolution in SAR/ISAR imaging using iterative sidelobe apodization[J].IEEE Transactions on Image Processing, 2005, 14(4): 537–546.DOI:10.1109/TIP.2004.841198 |
| [12] | XU X J, NARAYANAN R M.SAR image enhancement using noninteger Nyquist SVA technique[C]//IEEE Antennas and Propagation Society International Symposium, 2002.Piscataway, NJ:IEEE Press, 2002:298-301. |
| [13] | STANKWITZ H C, KOSEK M R.Super-resolution for SAR/ISAR RCS measurement using spatially variant apodization (super-SVA)[C]//Proceedings of 17th Antenna Measurement Techniques Association, 1995:251-256. |
| [14] | STANKWITZ H C, DALLAIRE R J, FIENUP J R. Nonlinear apodization for sidelobe control in SAR imagery[J].IEEE Transactions on Aerospace and Electronic System, 1995, 31(1): 267–278.DOI:10.1109/7.366309 |
| [15] | SMITH B H. Generalization of spatially variant apodization to noninteger Nyquist sampling rates[J].IEEE Transactions on Image Processing, 2000, 19(6): 1088–1093. |
