1 共聚焦干涉式SPs显微成像方法 共聚焦干涉式SPs显微成像技术的系统原理示意图如图 1所示。样品由宽角度范围的入射光进行照明,探测器探测到的信号主要来自光路P1和P2。光路P1包含与入射光非常接近的入射光和反射光,光路P2包含激发表面等离子体角度的入射光,这发生在表面等离子体的“a”点;这2种光在所有位置返回,然而,在共焦系统中只有来自焦点的光(相当于从“b”点发射)穿过了针孔。表面等离子体激发于“b”,在纳米金的表面进行传播,其中部分表面等离子体在“a”点再辐射回显微物镜,通过光路P2被探测器探测并与P1光路进行干涉。
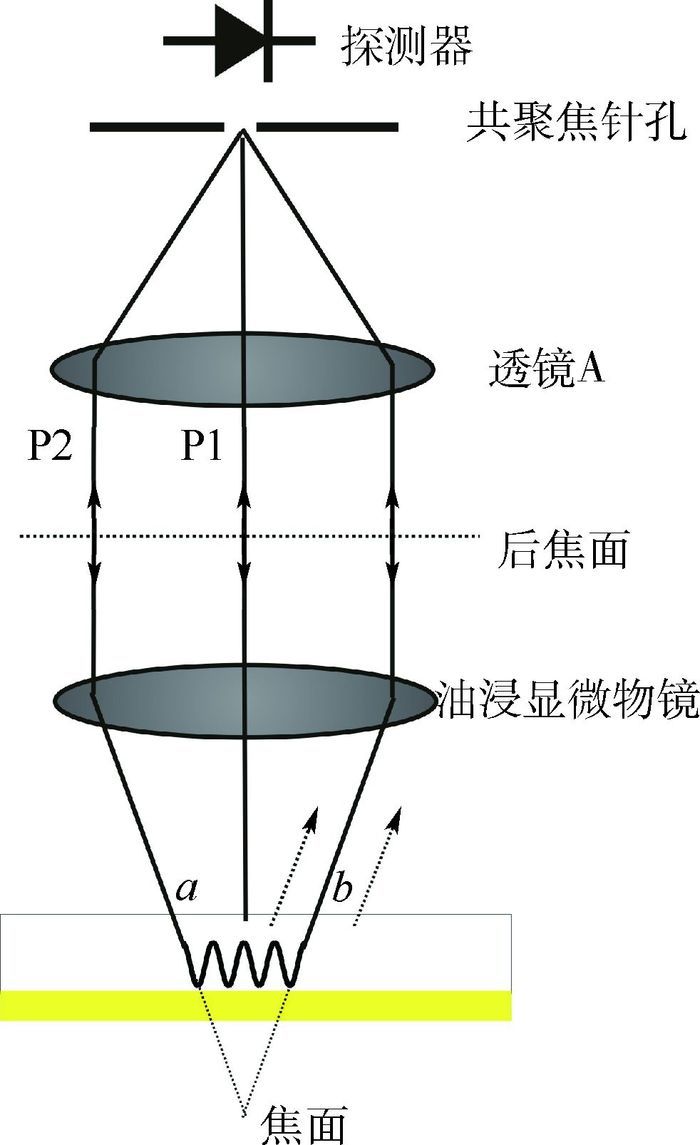 |
| 图 1 SPs共聚焦系统的原理示意图 Fig. 1 Schematic diagram of principle concept of confocal SPs system |
| 图选项 |
共聚焦干涉式SPs显微成像技术的光学系统结构简化示意图如图 2所示。该光学系统主要包括两部分,分别为入射光路和成像光路。其中照射光路采用632.8 nm氦-氖激光(Coherent, 10 mW)作为照明光源。光束扩束器用来扩充光束以充满物镜的通光孔径(满足SPs的激发),本系统采用10倍扩束光路。薄膜分光器用来分开入射光路和成像光路。该系统采用数值孔径(NA)为1.25的油浸显微物镜(Olympus,100倍,∞)来激发SPs并将样品反射回来的信号通过薄膜分光器传到探测器上。该系统共使用了2台电荷耦合器件(CCD)图像传感器,一台用于对样品进行成像(CCD1,Sony,像素大小为7.4 μm),一台用于对物镜的后焦面进行成像(CCD2,型号同CCD1)。样品上面被扫描到的点(1.22 λ/NA, λ为光在真空中的波长),经过两级放大系统(100×20) 共放大2 000倍,这样点扩散函数即焦点的相在CCD1上占据大约100像素。系统中本文采用“虚拟针孔”的技术,即仅使用CCD上一部分像素上的信号,其余像素设为0。① 可以方便地定位焦点和针孔的相对位置;② 方便对“针孔”的大小快速地定义;③ 方便取平均效应避免了由于个别像素过饱和的问题。样品安装在一个由压电陶瓷驱动平台组成的三维微纳米操控平台上。三维微纳米操控平台和2台CCD相机由基于LabVIEW编写的软件控制,图像处理算法基于MATLAB平台。
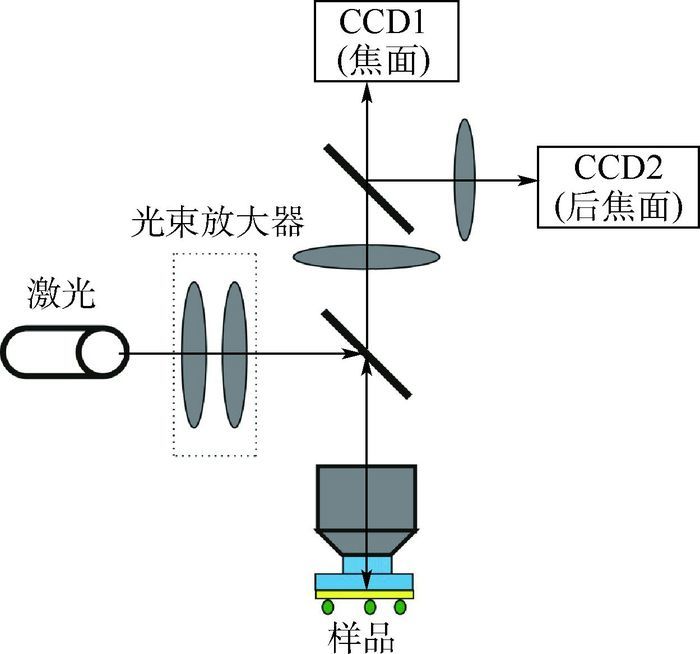 |
| 图 2 简化的光学系统结构示意图 Fig. 2 Simplified schematic diagram of optical system strcture |
| 图选项 |
该系统的样品采用SPs系统中典型的“三明治”结构,即折射率为1.52、厚度为0.17~0.19 mm的玻片(材料为BK7,厚度型号为1.5) 上镀一层50 nm的金薄膜,样品放在金的上面(如图 3所示)。实验中为了避免金纳米层脱落,通常在会在玻片和金之间镀1~2 nm的铬或钛,起黏附作用。仿真及实验结果都说明铬或钛的黏附层的厚度在1~2 nm时,SPs效应不会有明显的减弱[14]。
 |
| 图 3 样品结构示意图 Fig. 3 Schematic diagram of sample structure |
| 图选项 |
2 V(z)理论及仿真 带有针孔的共轴共焦干涉仪的输出信号为
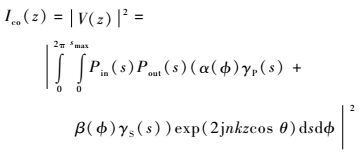 | (1) |
式中:Ico(z)为关于离焦距离z的输出信号;V(z)为测量的场强,在系统中通过对“虚拟孔径”中的强度叠加后取平方根得到;Pin和Pout分别是瞳孔函数的输入和输出复振幅;γP(s)和γS(s)分别对应P和S偏振方向上的复振幅反射系数,s为后焦面上及坐标的半径;θ为透镜入射角度;α(φ)和β(φ)分别为方位角φ的函数对应P和S偏振方向的光线的变化比例,对于入射光为线偏振的情况,α(φ)=cos2 φ,β(φ)=sin2 φ,其中α(φ)=1,β(φ)=0;n为油浸显微物镜上使用的油的折射率,k=2π/λ为光矢量。
共聚焦干涉系统在不同虚拟孔径大小下的仿真结果如图 4所示,图中对应的样品为50 nm裸金即金上面无镀层,环境为空气。为了更清楚地展示仿真结果,每一条曲线归一化后分别上移0.1以示区分。虚拟孔径大小通过艾里斑的半径(0.61/NA)成比例地进行定义。从图中可以看出在离焦距离为负(样品离物镜更近的这一侧),且虚拟孔径较小时(如图 4中标注为孔径为0.1的曲线),图 1所示的P1和P2之间发生了干涉并产生周期性的变化曲线。对于图 1的P2光路,SPs在位置“a”激发并在位置“b”反射回显微物镜(反之亦然)。很明显SPs在样品表面进行了传播,然而由于针孔的存在意味着只有那些来自焦点附近的光才能通过针孔并被像面上的CCD1检测到,由此产生一个独特的带有周期特性的干涉曲线即V(z),其周期Δz为
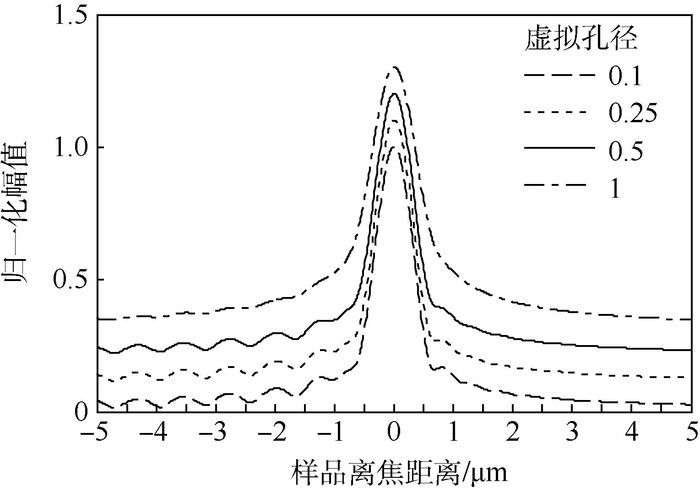 |
| 图 4 不同虚拟孔径下的V(z)归一化仿真曲线 Fig. 4 Simulated V(z) normalized curves for different virtual pinhole radii |
| 图选项 |
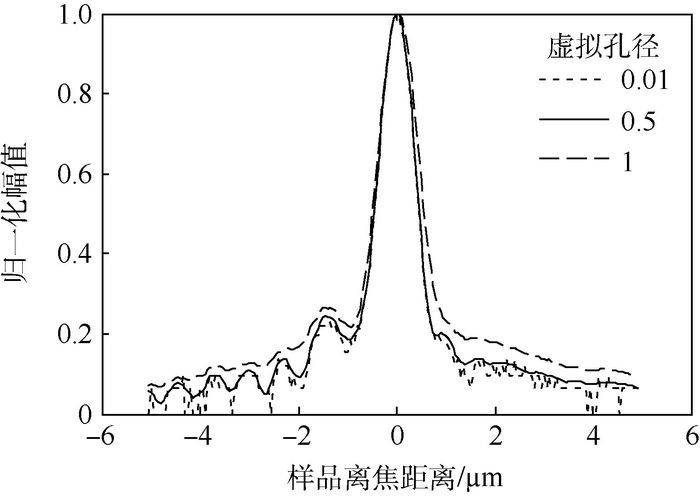
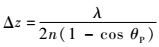 | (2) |
式中: θP为表面等离子体的最佳激发角。式(2) 可以通过计算垂直入射的光路和用于激发SPs的光线(图 1中的P1和P2) 之间的相位差进行推算。采用光线追踪的方法对P1和P2分别进行追踪同样可以得到式(2)。需要注意的是在使用光线追踪的方法时,必须将SPs作为一个具有传播特性的向量进行考虑。
图 4表明当虚拟孔径变大时,由于其他非SPs激发角的反射光也能被探测到,受此影响使得V(z)上的波纹变小。当虚拟孔径继续变大超出共聚焦的孔径范围(大于艾里斑)时,波纹消失。
3 实验结果 3.1 虚拟孔径大小对V(z)效应的影响 样品为玻片上镀有2 nm的铬和50 nm金薄膜时所对应的实验V(z)曲线如图 5所示。当虚拟孔径大于等于艾里斑时(图 5中标注为孔径为1对应的曲线),该系统等同于非共焦的扫描显微系统,V(z)曲线上不出现信号干涉波纹,与图 4中的仿真结果一致。当虚拟孔径非常小(图 5为艾里斑直径的1%,标注为孔径为0.01对应的曲线)时,干涉波纹虽然存在,但是由于CCD探测的光非常微弱因此信噪比极低。因此在实验中,选择虚拟孔径在0.1~0.5之间较为合适,这一结论与传统的非SPs共聚焦成像系统取值一致。
 |
| 图 5 空气环境下,玻片上镀有50 nm金薄样品在不同虚拟孔径下的V(z)仿真曲线 Fig. 5 Simulated V(z) curves of samples with substrates coated with 50 nm gold film for different virtual pinhole radii in air environment |
| 图选项 |
3.2 V(z)显微成像技术 V(z)技术可以用于传感,也可以用于成像。本文主要探讨该技术在厚度在纳米尺度下的薄膜结构上的应用。为了证明共轴共聚焦SPs系统可以用于纳米结构的成像,这里使用一种由牛血清蛋白(BSA)组成的蛋白质光栅结构验证。BSA是一种典型的生物蛋白,在金表面的有效折射率约为1.4。BSA置于镀有50 nm金的盖玻片上(折射率1.52),光栅阵列间隔25 μm,其中BSA占据10 μm。原子力显微镜(AFM)测量结果显示光栅的厚度约为10 nm。图 6(a)、图 6(b)和图 6(c)分别给出了当离焦距离分别为-1.25、-1.80 μm和在焦平面时,BSA光栅的一维轨迹。可以看到离焦距离为-1.25和-1.80 μm时图像的对比度是相反的。这一现象在图 6(d)实验扫描中得到的V(z)曲线很容易理解,当离焦距离不同时(位置A与位置B),有BSA和没BSA样品(裸金)的V(z)的值相反,因此对比度翻转。而在焦平面上光栅对比非常微弱。应注意的是在焦平面,强度比样品离焦时大得多。为了在离焦时得到更好的值的比较,通过增加入射光的能量来使聚焦时的信号趋于CCD饱和状态,而离焦距离为0的图像是在聚焦分布未饱和的低亮度下得到。
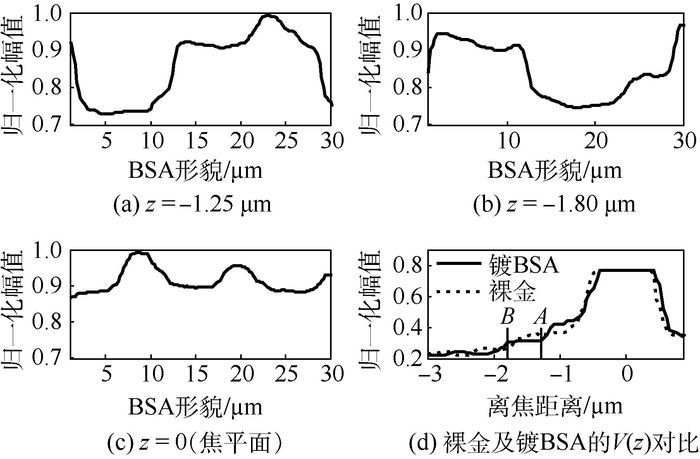 |
| 图 6 不同离焦距离下的光栅样品的一维实验扫描表面形貌 Fig. 6 1D experimental scanning grating sample surface profiles for different defocus distances |
| 图选项 |
在不同针孔半径下BSA蛋白质光栅的一维图像如图 7所示,可以看到虚拟孔径的大小对成像对比度的影响。当针孔半径为艾里斑半径的2倍时,也就是与普通的扫描显微镜相当时,探测到的光栅形状近乎消失;当虚拟针孔的半径缩小至艾里斑的0.8时,光栅形状基本可以显现出来但是对比度仍然较低;当该半径继续减小至艾里斑半径的10%或者1%时,图像可以得到更好的对比度。对于非常小的针孔直径如0.01,虽然成像的对比度仍然在可接受范围,但是与图 5的结论一致,即由于能通过小孔并被探测到的总光强太弱从而信噪比较差。可以看到共轴共聚焦干涉式SPs显微成像技术能够对厚度在10 nm左右的薄膜结构进行成像,且能提供很好的对比度和成像质量。在本系统中,照射光的偏振方向与BSA蛋白质光栅结构的边缘平行。
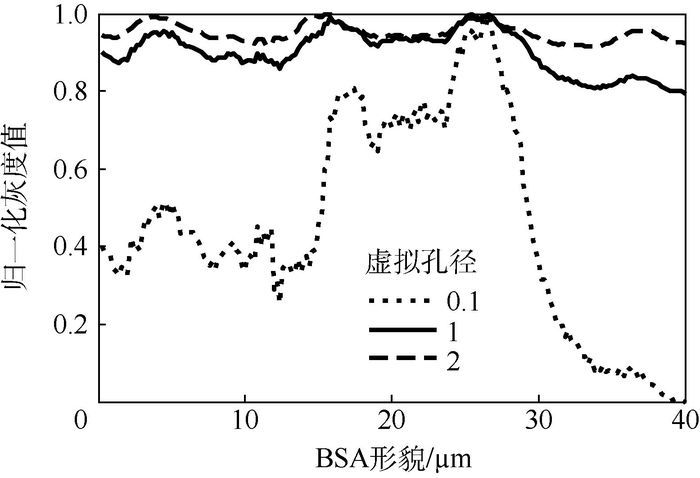 |
| 图 7 离焦距离为-1.25 μm时,不同虚拟孔径大小下的BSA蛋白质光栅结构一维图像 Fig. 7 1D BSA protein grating images for different virtual pinhole radii with defocus distance of -1.25 μm |
| 图选项 |
综上本文介绍了共轴共聚焦干涉式SPs显微成像技术及实验结果,表 1给出了灰度式成像、双臂干涉式成像以及本文提出的成像技术参数的比较。通过技术参数的对比,可以看出3种技术的轴向分辨率都维持在亚纳米量级;而灰度式成像技术的横向分辨率可优化至1 μm左右[3],双臂干涉式和共聚焦干涉式成像的横向分辨率则可以达到衍射极限即半波长以下。在系统架构上,共聚焦干涉技术采用单轴系统,而且不需要双轴干涉技术中的频率调制等相关器件,系统更为简洁,且成本更低。
表 1 3种成像技术的参数比较 Table 1 Comparison of parameters among three imaging techniques
| 成像技术 | 轴向分辨率 | 横向分辨率 | 频率调制器件 | 系统架构 | 振动隔离平台 |
| 灰度式 | Sub-nm | >1 μm | × | 单轴 | × |
| 双臂干涉式 | Sub-nm | λ/2 | √ | 双轴 | √ |
| 本文 | Sub-nm | λ/2 | × | 单轴 | × |
表选项
4 结论 本文提出了一种新型的共轴共聚焦干涉式表面等离子体显微成像技术:
1) 分别从理论和实验上验证了使用本文提出的共轴共聚焦结构实现SPs干涉显微技术的可能性,提供了一种更加简便和稳定的SPs干涉成像方法。
2) 使用该技术可以得到与双轴差分干涉系统类似的V(z)曲线效应,并用其来检测局部表面等离子体的传播。
3) 应用该技术实现了10 nm的薄膜结构的成像,而且对比度可控。
4) 相比较于文献[8]中提到的双轴差分共模干涉技术,本系统具有系统简单、成本低、与传统的光学显微系统例如共聚焦显微技术等完全兼容、对环境和实验要求低等优点。
笔者将继续研究入射光的偏振状态[15]对于成像对比度和分辨率的影响。同时使用超材料人工纳米金结构来替代本系统的纳米金薄膜以进一步提高对比度和分辨率也是本课题的延续。
参考文献
| [1] | BERGER C E H, KOOYMAN R P H, GREVE J. Resolution in surface-plasmon microscopy[J].Review of Scientific Instruments, 1994, 65(9): 2829–2836.DOI:10.1063/1.1144623 |
| [2] | KANO H, MIZUGUCHI S, KAWATA S. Excitation of surface-plasmon polantons by a focused laser beam[J].Journal of the Optical Society of America B, 1998, 15(4): 1381–1386.DOI:10.1364/JOSAB.15.001381 |
| [3] | EATMAN E, ASH E A. Surface-plasmon microscopy[J].Electronics Letters, 1987, 23(20): 1091–1092.DOI:10.1049/el:19870762 |
| [4] | MOH K J, YUAN X C, BU J, et al. Surface plasmon resonance imaging of cell-substrate contacts with radially polarized beams[J].Optical Society of America, 2008, 16(25): 20734–20741. |
| [5] | SOMEKH M G, LIU S G, VELINOV T S, et al. Optical V(z) for high-resolution 2 pi surface plasmon microscopy[J].Optics Letters, 2000, 25(11): 823–825.DOI:10.1364/OL.25.000823 |
| [6] | BERGUIGA L, BOYER-PROVERA E, ELEZGARAY J, et al. Sensing nanometer depth of focused optical fields with scanning surface plasmon microscopy[J].Plasmonics, 2013, 8(2): 715–722.DOI:10.1007/s11468-012-9462-1 |
| [7] | BOYER-PROVERA E, ROSSI A, ORIOL L, et al. Wavelet-based decomposition of high resolution surface plasmon microscopy V(z) curves at visible and near infrared wavelengths[J].Optics Express, 2013, 21(6): 7456–7477.DOI:10.1364/OE.21.007456 |
| [8] | SOMEKH M G, LIU S G, VELINOV T S, et al. High-resolution scanning surface-plasmon microscopy[J].Applied Optics, 2000, 39(34): 6279–6287.DOI:10.1364/AO.39.006279 |
| [9] | ZHOU H, SHEPPARD R. Aberration measurement in confocal microscopy:Phase retrieval from a single intensity measurement[J].Journal of Modern Optics, 1997, 44(8): 1553–1561.DOI:10.1080/09500349708230757 |
| [10] | MATTHEWS H J, HAMILTON D K, SHEPPARD C J R. Aberration measurement by confocal interferometry[J].Journal of Modern Optics, 1989, 36(2): 233–250.DOI:10.1080/09500348914550281 |
| [11] | SOMEKH M G, STABLER G, LIU S, et al. Wide-field high-resolution surface-plasmon interference microscopy[J].Optics Letters, 2009, 34(20): 3110–3112.DOI:10.1364/OL.34.003110 |
| [12] | BERGUIGA L, ZHANG S J, ARGOUL F, et al. High-resolution surface-plasmon imaging in air and in water:V(z) curve and operating conditions[J].Optics Letters, 2007, 32(5): 509–511.DOI:10.1364/OL.32.000509 |
| [13] | BAO Y J, PENG R W, SHU D J, et al. Role of interference between localized and propagating surface waves on the extraordinary optical transmission through a subwavelength-aperture array[J].Physical Review Letters, 2008, 101(8): 087401.DOI:10.1103/PhysRevLett.101.087401 |
| [14] | WONG C L, OLIVO M. Surface plasmon resonance imaging sensors:A review[J].Plasmonics, 2014, 9(4): 809–824.DOI:10.1007/s11468-013-9662-3 |
| [15] | LIU X, QIU B, CHEN Q, et al. Characterization of graphene layers using super resolution polarization parameter indirect microscopic imaging[J].Optics Express, 2014, 22(17): 20446–20456.DOI:10.1364/OE.22.020446 |
