目前,国内外****投入了很多精力进行研究,开展了各种地基、空基和天基试验,并研制了多种反射信号接收机,来用于反射信号的接收处理和反演研究[5-8]。由于GNSS-R的许多试验不仅需要耗费大量的人力物力,而且对测试场景的要求也很苛刻。同时,由于受到气候的影响,海况条件复杂多变,使得试验可重复性非常差。因此,非常需要研制可在实验室测试的GNSS-R信号产生器,以便于GNSS反射信号接收机的测试。
对于GNSS-R信号产生源的研制还处于起步阶段,可用于反射信号产生源的信号模型还在探索中。本文在分析海面反射信号特点的基础上,根据双基雷达方程建立反射信号的模型,并对计算的信号参数进行了相关验证。
1 海面反射信号特征分析 GNSS反射信号应用中,GNSS卫星、海洋表面、反射信号接收机可组成一个双基雷达系统。接收机一般需要采用两副天线,一副向上的右旋圆极化天线,用于接收直射信号;另一副向下的左旋圆极化天线,用于接收海面反射信号(海反信号)。GNSS海面反射信号传播的几何结构如图 1所示,h为载机飞行的高度。
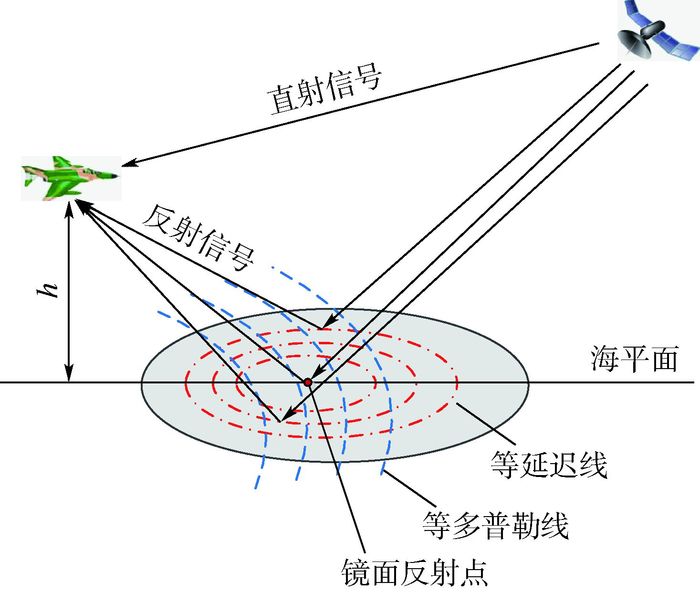 |
| 图 1 GNSS海面反射信号传播示意图 Fig. 1 Schematic diagram of GNSS sea surface reflection signal propagation |
| 图选项 |
为了方便研究,引入镜面反射点概念,即从发射机经反射点到达接收机的路径最小的点。接收机接收的海反信号主要来自镜面反射点周围的区域,即所谓的闪烁区。GNSS卫星的信号经海面反射后将在闪烁区上形成一系列的等延迟线和等多普勒线。
1.1 等延迟线和等多普勒线 以镜面反射点为坐标原点的坐标系统相对应,则沿这一路径的传播时间[9]为
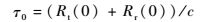 | (1) |
式中:Rt(0) 为卫星到镜面反射点的距离;Rr(0) 为镜面反射点到接收机的距离;c为光在空气中传播的速度。
信号沿任意一条反射路径的传播时间可以表示为
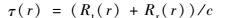 | (2) |
式中:r为海面上除镜面反射点外的某个反射点。
以τ0为参考,定义其他路径上信号传播的时间与τ0的差值为时间延迟,即
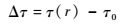 | (3) |
反射面上由Δτ等于常数的点组成的线称为等延迟线,其形状为椭圆。
以镜面反射点为参考点,由该点反射信号得到的多普勒频率f0=fD(0) 为参考频率。可得各散射点与参考点的多普勒频差为
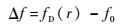 | (4) |
式中:
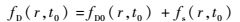 | (5) |
 | (6) |
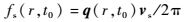 | (7) |
其中:m和n分别表示卫星到散射点和散射点到接收机的单位矢量;q为散射向量;fD(r, t0)为总的多普勒频移; fD0(r, t0)和fs(r, t0)分别为由卫星和接收机相对运动以及由散射点相对运动引起的多普勒频移;vt和vr分别为卫星和接收机的速度矢量;vs为散射点速度矢量; λ为载波的波长。
由Δf相等的点组成的曲线称为等多普勒线,其形状为类双曲线的弧线。
以GPS卫星C/A码信号为例,设卫星高度为20 200 km,接收机高度为5 km,卫星高度角为60°,接收机的速度为(0, 120, 0) m/s,卫星的速度为(-570, -219, 236) m/s,等延迟线和等多普勒线如图 2所示,其中:(0, 0) 点为镜面反射点。椭圆线为等延迟线,每个椭圆延迟0.25 chip。3条弧线为等多普勒线,相邻两条弧线间隔是100 Hz。过镜点的等多普勒线为-183.05 Hz。
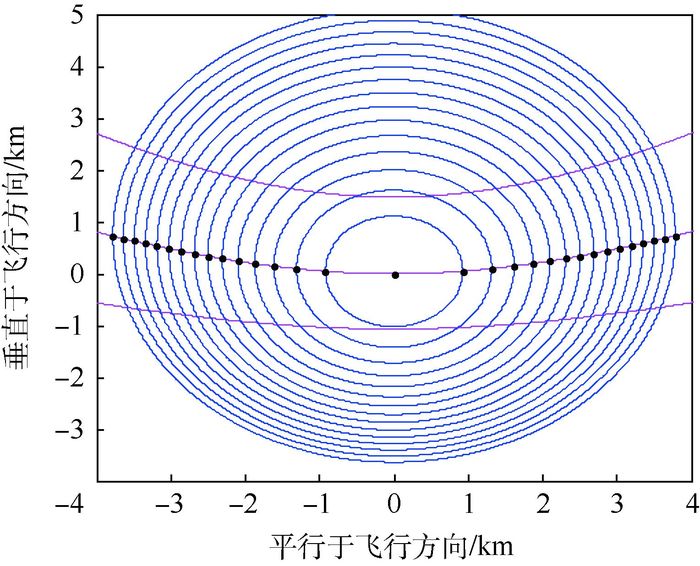 |
| 图 2 等延迟/等多普勒线 Fig. 2 Iso-delay/iso-Doppler lines |
| 图选项 |
在机载高度下一般不需要考虑多普勒频移对散射信号功率的影响。因此,只需要将镜面反射点和过镜点的等多普勒线与各等延迟线的交点作为观测点即可。在反射信号的应用中,一般以镜面反射点的时延值和多普勒值作为参考值。由GNSS-R几何关系可知,镜点反射信号相对于发射信号的时延约为68 911 chip。
1.2 反射信号相位在海面上的映射 由于GNSS信号的波长较长,可将海反信号认为是海洋表面一系列散射点反射信号的集合,只是由于多径效应分别对应不同的时间延迟、相位和幅值,设每个个体反射信号的时间延迟为τk,相位为φk,幅值为ak,则海反信号的电磁场[10]为
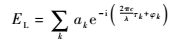 | (8) |
设GNSS发射的伪码为x(t),y(t)为海反信号,则由式(8) 可得
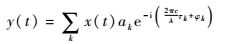 | (9) |
为了方便分析,式(9) 中的时延τk可对应于伪码相位,载波相位φk可认为主要由多普勒频移引起,幅值ak是反射功率的平方根。这样,每个反射信号基本上可用幅值、伪码时延和多普勒频移3个参量来完整描述。
由于海面的粗糙性,海反信号特性较为复杂,具体表现就是信号幅值的衰减以及不同的时延和不同多普勒信号的叠加[11]。特定的时延与多普勒又与反射面的特定反射单元是相对应的,如图 3所示。
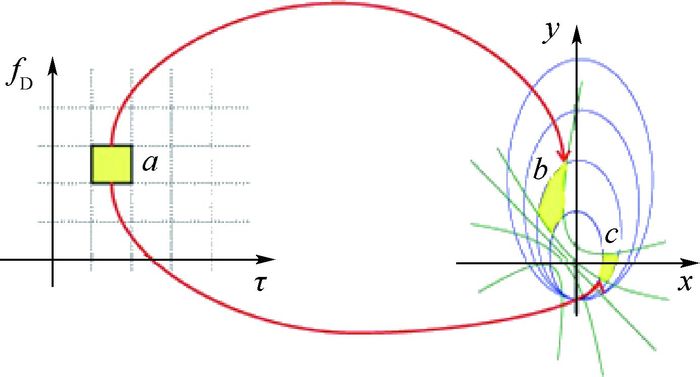 |
| 图 3 反射单元与时延-多普勒单元的对应关系 Fig. 3 Correspondence between reflection unit and delay-Doppler unit |
| 图选项 |
从图 3可以看出,具有相同的时延和多普勒的反射信号可能会来自2个不同的区域。时延-多普勒点a对应于海面的2个点b和c。也就是说,a点反射信号的能量是海面b和c 2个点信号能量的叠加。设a点信号的功率为Pa,b点信号的功率为Pb,c点信号的功率为Pc,则满足
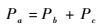 | (10) |
因此,从图 2可知,共有15个等延时环,再加上镜面反射点,那么反射信号的数目为16(即k=1, 2, …, 16),相应地海面上的反射点有31个。
2 海面反射信号的功率计算 2.1 双基雷达方程 在GNSS-R双基雷达中,设卫星发射功率为Pt,发射天线的功率增益为Gt,接收天线的功率增益为Gr,卫星距海面反射点的距离为R1,接收机距海面反射点的距离为R2,则海面上j反射点信号的接收功率[12]为
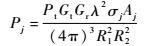 | (11) |
式中:σj为双基散射系数;Aj为σj所对应的海面散射截面积。从式(11) 可以看出,散射系数和散射面积是求得反射信号接收功率的关键。
2.2 散射系数计算 标准化的双基散射截面形式如下:
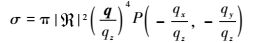 | (12) |
式中:q=(qx,qy,qz)为散射向量;
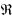
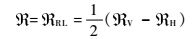 | (13) |
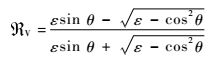 | (14) |
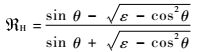 | (15) |
其中:ε为海面的复介电常数;θ为卫星的高度角。
P为各向异性的二维高斯分布的概率密度函数[14],其表达式为
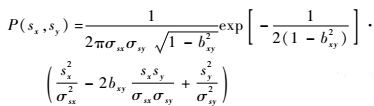 | (16) |
式中:sx=-qx/q和sy=-qy/q分别为平行于载机飞行方向和垂直于载机飞行方向的海面倾斜度;σsx2和σsy2分别为海面平行于载机飞行方向和垂直于载机飞行方向的均方倾斜度;bxy为sx、sy的相关系数。然后,可以通过海浪谱建立起海面倾斜方差和相关系数与海面风场的如下关系:
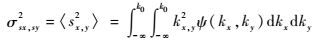 | (17) |
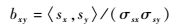 | (18) |
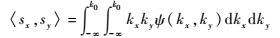 | (19) |
式中:σsx, sy2为海面倾斜方差;sx, y2为sx和sy的二维联合密度函数;kx和ky为海浪的波数;k0为截止波数;ψ(kx, ky)为海浪谱函数。如果风向沿x方向或者y方向,则bxy=0,否则bxy≠0。假设海浪谱主要是由海风产生的,那么ψ(kx, ky)可由Elfouhaily模型[15]来计算。
设风速为5 m/s,风向为0°,波龄为0.84,海温为25 ℃,盐度为20%,可计算得到整个闪烁区的散射系数,如图 4所示。
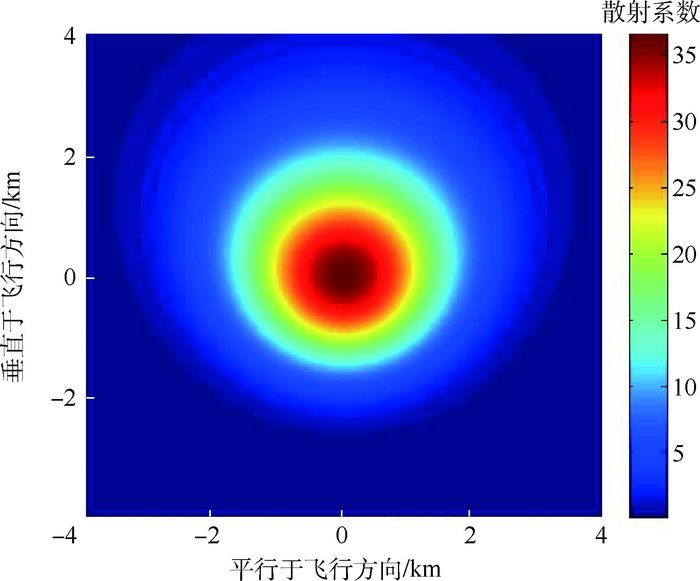 |
| 图 4 整个闪烁区的散射系数 Fig. 4 Scattering coefficient of whole glistening zone |
| 图选项 |
2.3 散射面积计算 为了求出选取海面反射点的反射信号功率,还需要得到适当的每个反射点周围的区域面积。考虑到信号辐射的特点,每个反射点所对应的周围区域设为圆形。假设过(0, 0) 点的等多普勒线为l1,等延迟线从内到外依次为c1,c2,…。
由镜面反射点定义可知,镜点反射信号在海面的反射单元是唯一的。设椭圆c1的长轴为a0,短轴为b0,那么镜面反射点反射单元的圆形半径为
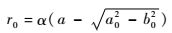 | (20) |
式中:α为选择系数,α≤0.5。
设弧线l1与椭圆c1相交的右侧点为A,坐标为(x1, y1);弧线l1与c2椭圆相交的右侧点为B,坐标为(x2, y2);那么反射点A反射单元的圆形半径为
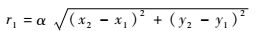 | (21) |
为了每个反射单元的散射面积在海面上不重复,设α=0.4。以此类推,就可以求得其余反射点反射单元的圆形半径。每个反射单元的散射面积如图 5所示。
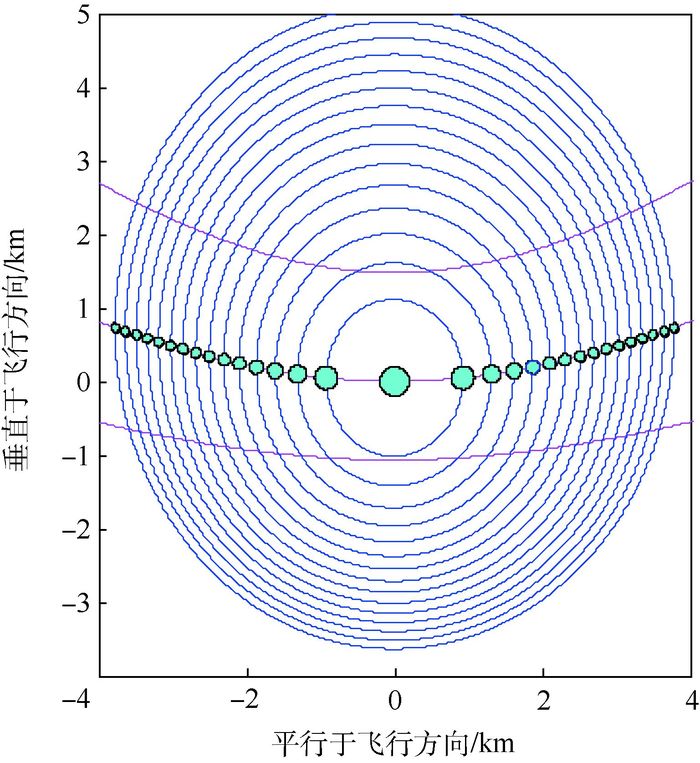 |
| 图 5 反射单元的散射面积 Fig. 5 Scattering area of reflection units |
| 图选项 |
求出散射系数和散射面积后,就可以由式(11) 和式(10) 求得每个反射信号的功率。设卫星发射功率为26.8 dBW,发射增益为1 dB,接收增益为3 dB,可求得镜点反射信号(τ0,f0)的功率为-170.65 dBW。延迟镜点信号0.25 chip的反射信号(τ0+0.25,f0)的功率为(-174.88 dBW)+(-174.88 dBW)=-171.87 dBW。以此类推,可以求出其余反射信号的功率值。
3 海面反射信号的相关处理 为了验证该方法所取的海面反射点是否恰当以及计算的反射信号功率是否正确,需对由16个反射信号组成的海反信号进行相关处理。根据文献[16]中的处理结构图,对接收机接收到的海反信号进行相关处理仿真。在模拟过程中,设本地伪码共有64个相关器,相互间隔1/4个码片。处理得到的海反信号相关功率如图 6中的星形线所示。
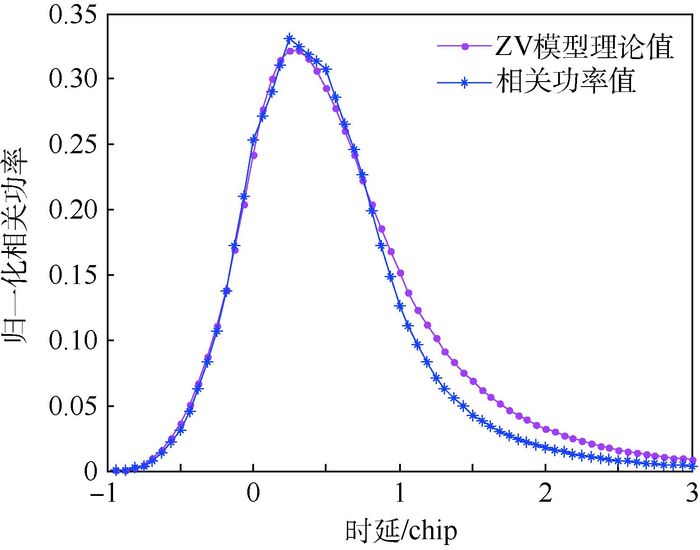 |
| 图 6 反射信号处理结果 Fig. 6 Reflection signal processing result |
| 图选项 |
在利用GNSS海面散射信号进行海面风场遥感的研究中,Zavorotny和Voronovich[17]建立了较为成熟的GNSS海面散射信号相关功率模型,即ZV模型。ZV模型的时延一维相关功率是指在某个特定的多普勒频移f0下的相关功率,其表达式为
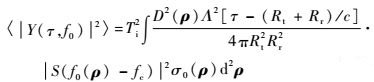 | (22) |
式中:Ti为相干积分时间;D为接收天线的增益;Λ为GNSS伪码的自相关函数;S为多普勒滤波函数;fc为载波中心频率;σ0为海面的标准化散射截面;ρ为镜面反射点到平均海面上某一点的向量;Rt和Rr分别为卫星和接收机到ρ端点的距离。
在相同的条件下,即可得到ZV模型的时延一维相关功率波形,如图 6中的点形线。从图 6可以看出两者的近似度很高,经计算得到相关系数为0.982 2。
然后,对分别由12、14和15个反射信号组成的海反信号进行了相关处理,其相关系数分别为0.981 6、0.982 1和0.982 2。由15与16个反射信号组成的海反信号相关处理的结果相同。说明随着时延的增加,相应的信号越来越弱,对于相关功率的影响也就越来越小。因此,在模拟的时候,选择前15个反射信号即可。
4 结论 1) 海面反射点的选取方法既符合海面反射信号的特点,又使复杂的信号模型得到了简化,降低了信号建模的实现难度。
2) 计算反射单元散射面积的方法是方便可行的,为应用双基雷达方程计算GNSS海面反射信号的功率奠定了基础。
3) 通过所得海面反射信号的相关处理与ZV理论模型的比较,验证了该建模方法的合理性和科学性。
为使本文提出的方法能够适用于不同的条件,后续将进一步研究不同多普勒频率与时延的海面反射点选取和相应散射面积计算等问题。
参考文献
| [1] | CAMPS A, MARCHAN-HERNANDEZ J F, BOSCH-LLUIS X, et al. Review of GNSS-R instruments and tools developed at the Universitat Politecnica de Catalunya-Barcelona tech[C]//2014 IEEE Geoscience and Remote Sensing Symposium (IGARSS).Piscataway, NJ:IEEE Press, 2014:3826-3829. |
| [2] | SCHIAVULLI D, GHAVIDEL A, CAMPS A, et al. GNSS-R wind-dependent polarimetric signature over the ocean[J].IEEE Geoscience and Remote Sensing Letters, 2015, 12(12): 2374–2378.DOI:10.1109/LGRS.2015.2477685 |
| [3] | YAN Q Y, HUANG W M. Spaceborne GNSS-R sea ice detection using delay-Doppler maps:First results from the U.K.TechDemo-Sat-1 mission[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2016, 9(10): 1–7.DOI:10.1109/JSTARS.2016.2610658 |
| [4] | KAINULAINEN J, RAUTIAINEN K, LEMMETYINEN J, et al. Detection of a sea surface salinity gradient using data sets of airborne synthetic aperture radiometer HUT-2-D and a GNSS-R instrument[J].IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(11): 4561–4571.DOI:10.1109/TGRS.2011.2151864 |
| [5] | LOWE S T, KROGER P, FRANKLIN G, et al. A delay/Doppler-mapping receiver system for GPS-reflection remote sensing[J].IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(5): 1150–1164.DOI:10.1109/TGRS.2002.1010901 |
| [6] | YOU H, GARRISON J L, HECKLER G, et al. The autocorrelation of waveforms generated from ocean-scattered GPS signals[J].IEEE Geoscience and Remote Sensing Letters, 2006, 3(1): 78–82.DOI:10.1109/LGRS.2005.856704 |
| [7] | CARDELLACH E, RUFFINI G, PINO D, et al. Mediterranean balloon experiment:Ocean wind speed sensing from the stratosphere, using GPS reflections[J].Remote Sensing of Environment, 2003, 88(3): 351–362.DOI:10.1016/S0034-4257(03)00176-7 |
| [8] | LI W Q, YANG D K, ZHANG B. Real-time processing of reflected GNSS signal for remote sensing:System and experiments[J].The Journal of Navigation, 2011, 64(S1): 127–140.DOI:10.1017/S0373463311000403 |
| [9] | 杨东凯, 王烨. 全球导航卫星系统反射信号几何关系数值分析[J].电波科学学报, 2012, 27(4): 637–643. YANG D K, WANG Y. Numerical analysis on geometric relationship of the global navigation satellite system reflectometry[J].Chinese Journal of Radio Science, 2012, 27(4): 637–643.(in Chinese) |
| [10] | GEORGE A H, ZUFFADA C. Theoretical description of a bistatic system for ocean altimetry using the GPS signal[J].Radio Science, 2003, 38(5): 10–19. |
| [11] | 杨东凯, 张其善. GNSS反射信号处理基础与实践[M].北京: 电子工业出版社, 2012: 164-174. YANG D K, ZHANG Q S. GNSS reflected signal processing:Fundamentals and applications[M].Beijing: Publishing House of Electronics Industry, 2012: 164-174.(in Chinese) |
| [12] | 丁鹭飞, 耿富录. 雷达原理[M].3版.西安: 西安电子科技大学出版社, 2002: 128-130. DING L F, GENG F L. Principle of radar[M].3rd ed.Xi'an: Xidian University Press, 2002: 128-130.(in Chinese) |
| [13] | MAURICE W L. Radar reflectivity of land and sea[M].Boston: Artech House, 2001: 156-159. |
| [14] | ELFOUHAILY T, THOMPSON D R, LINDSTROM L. Delay-Doppler analysis of bistatical reflected signals from the ocean surface:Theory and application[J].IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(3): 560–573.DOI:10.1109/TGRS.2002.1000316 |
| [15] | ELFOUHAILY T, CHAPRON B, KATSAROS K, et al. A unified directional spectrum for and short wind-driven waves[J].Journal of Geophysical Research, 1997, 104(C7): 15781–15796. |
| [16] | 杨东凯, 丁文锐, 张其善. 软件定义的GNSS反射信号接收机设计[J].北京航空航天大学学报, 2009, 35(9): 1048–1051. YANG D K, DING W R, ZHANG Q S. Software defined GNSS reflections receiver design[J].Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(9): 1048–1051.(in Chinese) |
| [17] | ZAVOROTNY V, VORONOVICH A. Scattering of GPS signals from the ocean with wind remote sensing application[J].IEEE Transactions on Geoscience and Remote Sensing, 2000, 38(2): 951–964.DOI:10.1109/36.841977 |
