随着微小卫星和一箭多星等航天技术的发展，卫星编队以其独特的优势成为航天领域的研究热点。卫星编队的功能多样、性能优异，可以通过星间协同实现数据的获取、处理、分析^[1]，从而完成许多传统单一大型卫星难以完成的空间任务，这使得微小卫星编队在空间科学、对地观测等领域具有广阔的应用前景^[1-3]，尤其是空间物理场的探测, 典型的有加拿大的CANX-4, 5^[4], 冯卡门研究所负责的QB50^[5]和NASA的EDSN项目^[6]等。
由于空间摄动力的存在，尤其在J2摄动力的作用下，编队构型常常会发散，因而J2摄动下的构型保持和重构控制成为国内外****的研究重点^[7-11]。对于编队的法向控制，一般根据高斯变分方程(也称为高斯摄动方程)解析计算。由于常常认为编队的轨道面内运动和法向运动是解耦的，因此很少有文献专门研究编队的法向控制，多数文献主要研究三维和轨道面内的控制，而相对动力学方程对于编队控制至关重要。编队构型的相对动力学方程有2种描述方式：一种是以相对位置和速度为变量的直角坐标系描述法，比如HCW方程(也称为Hill方程或者C-W方程)^[12]和Lawden方程^[13]等，由于相对位置速度便于测量，因而被最早应用^{[7, 9]}，此时构型控制所需的速度增量通过动力学方程直接求解。但J2摄动下使用该方法描述的相对动力学表达式较为复杂；另一种是以相对轨道根数为变量的轨道要素法，在J2摄动模型下采用该方法可以得到解析的构型无漂移条件，目前应用较为广泛，此时构型控制所需的速度增量常常采用高斯摄动方程求解^[8-11]。
为了实现对空间物理场的三维立体协同测量，空间物理场探测任务常常采用空间四面体卫星编队实现三维数据采集，4颗卫星分别位于空间四面体的4个顶点，四面体的几何特性对探测性能有较大的影响，其中几何特性最好的是正四面体^[3]。此时，为了实现空间四面体的编队飞行，卫星需要进行2种类型的法向机动：首先，构型的初始化部署需要进行法向机动，以形成法向基线；其次，在构型保持中，由于J2摄动力作用，轨道升交点赤经存在长期漂移，导致空间四面体的法向距离发生漂移，使得空间四面体性能退化。为了修正法向漂移从而实现良好的空间四面体几何特性，卫星需要定期实施法向机动控制。然而，在法向机动过程中，通过将脉冲推力等效为作用时间趋于0的有限推力通过高斯摄动方程来求解速度增量，常常忽略了法向机动引起的切向耦合效应，从而导致构型会沿切向发散，进而影响空间四面体的几何特性。此外，由于大气阻力等摄动本身会造成构型的漂移，因此，为了研究编队卫星法向机动的切向耦合效应引起的漂移，本文主要考虑的摄动力是J2摄动。
为了实现更加精确的构型控制和良好的四面体几何特性，本文提出了一种解析的切向补偿方法消除法向机动引起的切向漂移。首先，介绍了J2摄动下保持构型无漂移需要满足的条件，阐释了法向机动引起切向漂移的机理。其次，研究了通过解析补偿方法消除法向机动引起的切向耦合效应。最后，以某磁层探测任务为例通过仿真验证了方法的有效性。
1 理论基础 1.1 坐标系定义 在编队飞行控制中，常采用当地水平垂直(Local-Vertical Local-Horizontal，LVLH)坐标系描述星间的相对运动。如图 1所示，Ref为主星或者虚拟中心，Sat为从星。

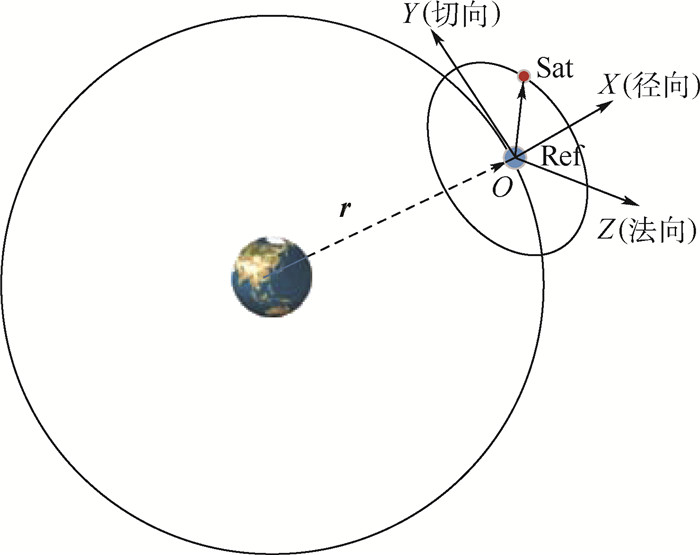图 1 LVLH坐标系示意图 Fig. 1 Schematic diagram of LVLH coordinate system

图选项

建立以主星质心为原点O的LVLH坐标系，OX轴为径向，沿地心与主星质心连线方向远离地心，OZ轴指向轨道面法向，OY轴由右手定则确定，称为切向，特殊地，当主星为圆轨道时，OY在轨道面内与主星速度方向一致，r为卫星在地球惯性系下的位置矢量。
1.2 相对动力学方程 在质点中心引力体模型下，主星是圆轨道的编队相对动力学方程可用HCW方程描述^[12]。
在地球非球形项摄动的影响下，轨道的半长轴只存在短周期项，偏心率和倾角不存在长期漂移，但存在长周期项和短周期项，轨道的升交点经度、近心点幅角、平近点角既存在长期项也存在长周期项和短周期项。
对于近地轨道卫星，非球形引力摄动中影响最主要的是J2摄动，常常忽略长短周期项，仅包含长期项，采用平均轨道根数来描述轨道长期演化趋势。其中，长期漂移项可由线性微分方程式(1) 求得^[1]。

(1)

式中：t为时间；为平均半正焦弦，a为轨道平均半长轴，e为平均偏心率；为轨道平均角速度, μ=398 600.441 8 km³/s²为地球中心引力常数；R_e为地球平均半径；J₂=1.082 63×10^－3为地球二阶带状谐系数；为平均轨道根数，i为平均轨道倾角，Ω为平均升交点赤经，ω为平均近地点幅角，M为平均平近点角。
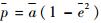
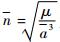
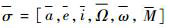
根据相对运动一阶近似方程^{[7, 9]}，当从星和虚拟中心的轨道半长轴相等时有

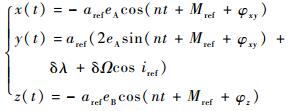(2)

式中：

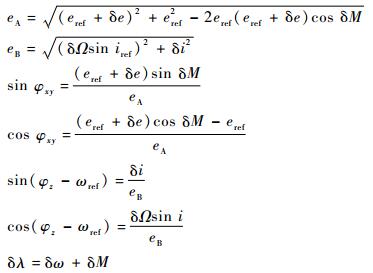x(t)、y(t)和z(t)分别为卫星在LVLH坐标系中径向、切向和法向的位置；n为主星轨道角速度；λ为瞬时平纬度幅角；φ_xy为在LVLH坐标系中XY平面运动的相位；φ_z为在LVLH坐标系中Z向运动的相位；为虚拟参考中心的轨道根数，a_ref、e_ref、i_ref、Ω_ref、ω_ref和M_ref分别为虚拟中心瞬时半长轴、瞬时偏心率、瞬时轨道倾角、瞬时升交点赤经、瞬时近地点幅角和瞬时平近点角；为从星和虚拟中心之间的相对轨道根数，a、e、i、Ω、ω和M分别为轨道瞬时半长轴、瞬时偏心率、瞬时轨道倾角、瞬时升交点赤经、瞬时近地点幅角和瞬时平近点角。
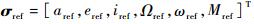
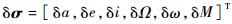
由式(2) 可知，法向运动的幅值ae_B即法向基线可由轨道倾角差、升交点赤经差组合而成，前者有利于极区覆盖, 后者有利于赤道覆盖。
为了得到良好的探测性能，需要保证构型的稳定即无漂移，因此在考虑J2摄动时，需要在平根数空间下合理设计J2项无漂移条件^[7-8]:

(3)

式中：; 。
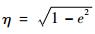
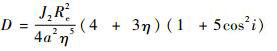
显然，由式(3) 可知，为了确保编队卫星构型的稳定，δa、δe和δi中只要确定了其中一个变量，其他2个变量即可求出。例如，对于环绕运动，当δe确定后，通过式(3) 修正δa和δi, 即可实现对漂移的修正。
在编队任务中，常常将有限推力看作是作用在卫星上的摄动力，采用经典高斯摄动方程^{[1, 10-11]}求解有限推力作用下的轨道根数变化。

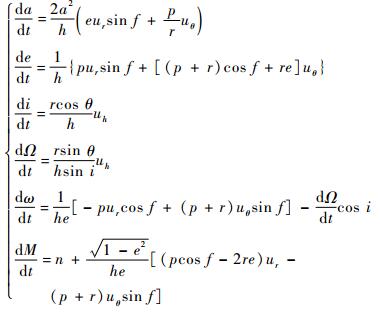(4)

式中：p=a(1－e²)为半正焦弦；为轨道角动量矢量的大小；r为卫星地心距大小；σ=[a, e, i, Ω, ω, M]^T为施加机动时卫星的瞬时轨道根数；θ=ω+f为施加机动时卫星的纬度幅角，f为施加机动时卫星的真近点角；u=[u_r, u_θ, u_h]^T为摄动加速度，u_r、u_θ和u_h分别为摄动加速度沿径向、切向和法向的分量。
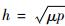
由高斯摄动方程式(4) 可知，当有限推力沿轨道面法向作用时，轨道半长轴不变。这是由于任意时刻法向推力与速度方向垂直，因此推力所做的功，F为发动机推力矢量，v为卫星在地球惯性系下的速度矢量，故而轨道能量守恒，从而轨道半长轴不变。如图 2所示，地球质点引力模型下，卫星质量为50 kg, 推力大小为10 N，方向实时更新始终沿轨道面法向(此时纬度幅角为0°)，作用时间为50 s时，法向推力改变轨道倾角时，不会引起轨道半长轴的变化。

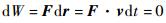
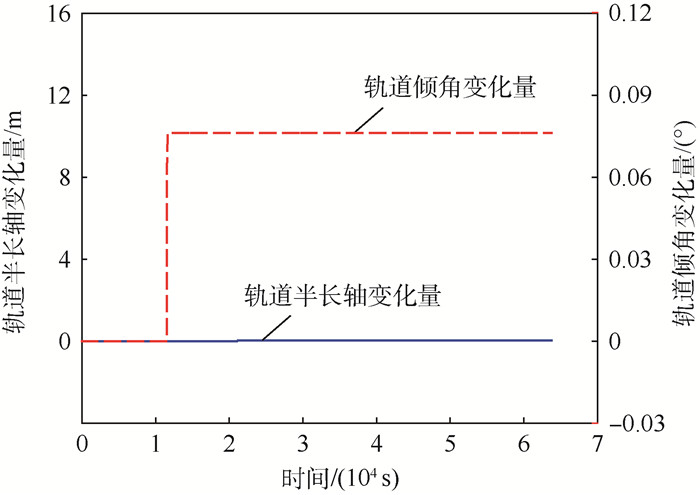图 2 法向有限推力作用时卫星轨道半长轴和倾角变化量随时间的变化 Fig. 2 Variation of orbital semi-major axis and inclination with time for satellite with cross-track finite thrust

图选项

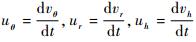
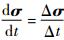
根据加速度定义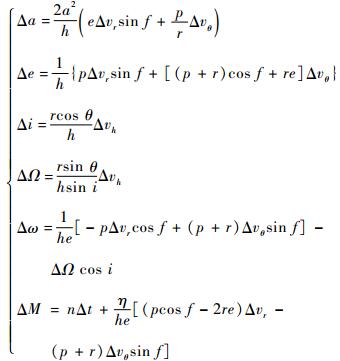，v_θ、v_r和v_h分别为脉冲机动速度沿切向、径向和法向分量的大小，同时由导数定义，。因此，脉冲推力可以认为是作用时间Δt→0时的有限推力^[5-8]，即此时。代入式(4)，左右两端乘以Δt，可得脉冲推力下的高斯摄动方程式(5)：

(5)

式中：为施加机动前后卫星的瞬时轨道根数改变量；Δv =[Δv_r, Δv_θ, Δv_h]^T为施加脉冲机动的速度增量。
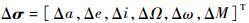
由脉冲推力下的高斯摄动方程式(5) 可知，法向机动不会引起改变半长轴a，也不会引起偏心率e的改变，由星轨道的总能量E=－μ/2a, p= a(1－e²)和可知，法向摄动不会引起轨道的总能量E和角动量矩大小h的改变。然而，实际上施加法向机动的瞬时，必然伴随着燃料的化学能转化为动能，位置不变，速度瞬时发生改变，因此总能量必然改变，此外，由于法向速度方向不经过地心，因此存在着动量矩的改变。所以脉冲推力下的高斯摄动方程式(5) 不满足能量守恒和动量矩守恒定律。因此，有必要对式(5) 进行修正。如图 3所示，地球质点引力模型下，卫星质量为50 kg, 速度增量大小为10 m/s，方向沿轨道面法向(此时纬度幅角为0°)，法向机动在改变轨道倾角时会引起轨道半长轴的变化。

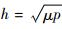
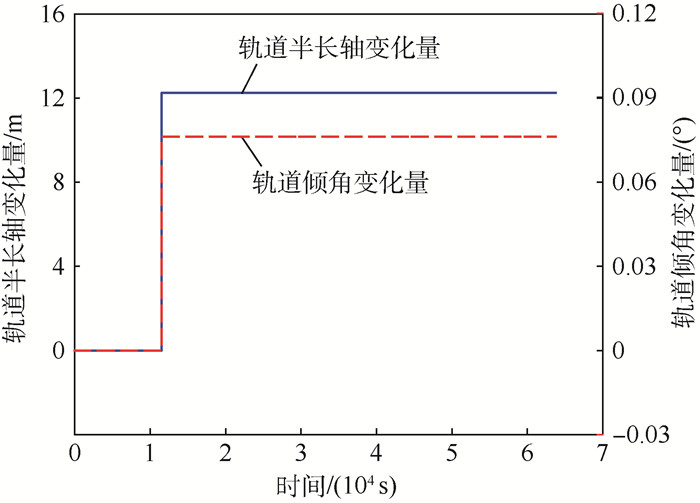图 3 法向脉冲推力作用时卫星轨道半长轴和倾角变化量随时间的变化 Fig. 3 Variation of orbital semi-major axis and inclination with time for satellite with cross-track impulsive thrust

图选项

实际工程中，脉冲推力是通过短时间内的有限推力实现的，因此脉冲推力的高斯摄动方程式(5) 和有限推力的高斯摄动方程式(4) 出现矛盾。这主要是由于式(4) 要求有限推力作用时始终沿着瞬时轨道面法向，对卫星姿态要求较高，在工程上难以实现。因此，工程上常常采用姿态惯性定向，法向机动的推力法向始终与发动开机时的轨道面法向一致。显然，此时会引起轨道半长轴的变化。如图 4所示，地球质点引力模型下，卫星质量为50 kg, 推力大小为10 N，方向沿发动机开机时的轨道面法向(此时纬度幅角为0°)，作用时间为50 s时，法向推力改变轨道倾角时，会引起轨道半长轴的变化。显然，这种方向固定的有限推力更接近脉冲推力，在工程上也更容易实现。

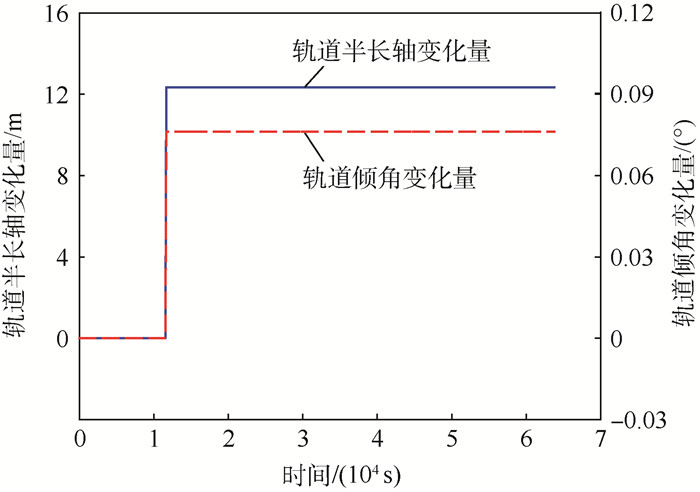图 4 固定方向推力作用时轨道半长轴和倾角变化量随时间的变化 Fig. 4 Variation of orbital semi-major axis and inclination with time for satellite with fixed direction thrust

图选项

2 切向补偿方法设计 施加法向机动(机动速度大小为v_h)瞬时，卫星在地惯系下的位置矢量不变，因此地心距大小不变，即，r₀、p₀、e₀和f₀分别为施加机动前卫星的瞬时地心距大小、瞬时半正交弦、瞬时偏心率和瞬时真近点角，速度瞬时发生改变，等于原速度v₀和机动速度v_h的矢量和。因而，由式(6) 可求得施加法向机动v_h后轨道的能量和动量矩。

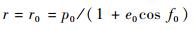
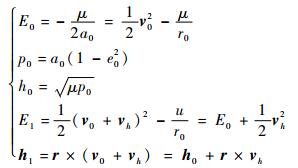(6)

式中：E₀和h₀分别为机动前轨道的总能量和角动量；E₁和h₁分别为机动后轨道的总能量和角动量。
由于卫星速度的改变是瞬时完成的，因而可以在这瞬时忽略摄动力的作用，认为机动前后是2个开普勒轨道之间的变化，为了简化计算，只考虑通过能量守恒和角动量守恒对瞬时轨道半长轴和偏心率的修正，其他轨道根数仍按照高斯摄动方程式(5) 求解。因此，法向机动后的瞬时轨道根数由式(7) 求得：

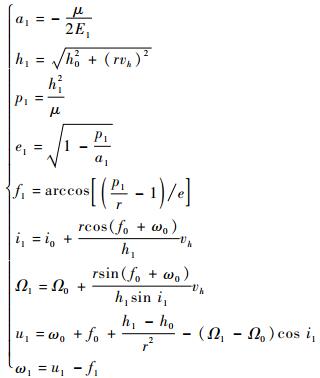(7)

式中：为机动前的瞬时轨道根数，i₀、Ω₀和ω₀分别为卫星机动前的瞬时轨道倾角、瞬时升交点赤经和瞬时近地点幅角；为机动后的瞬时轨道根数，a₁、e₁、i₁、Ω₁、ω₁和f₁分别为卫星机动后的瞬时轨道半长轴、瞬时偏心率、瞬时轨道倾角、瞬时升交点赤经、瞬时近地点幅角和瞬时真近点角；p₁和h₁分别为机动后轨道的半正焦弦和角动量矢量的大小。
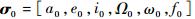
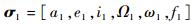
根据平均轨道根数的定义，由于半长轴没有长期项和长周期项，当忽略高阶短周期项只考虑一阶短周期项时，平均轨道根数的表达式如式(8) 所示：

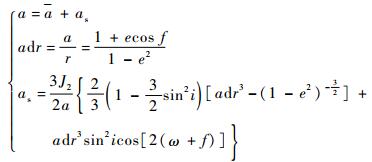(8)

式中：a_s为轨道半长轴的一阶短周期项。
由式(7) 可知，法向机动将造成瞬时轨道根数的变化，而由式(8) 可知瞬时轨道根数的改变会引起轨道平均半长轴的变化，从而造成构型发生切向漂移。此外，由式(3) 可知，当轨道根数尤其是轨道倾角变化时，J2无漂移条件遭到破坏，因此需要补偿半长轴从而使得满足J2无漂移条件，从而实现J2项无漂移周期相对运动轨道。
因此，消除法向机动的切向耦合效应需要的切向的补偿速度包括以下2个方面：首先，由于法向机动对切向漂移影响最大的是平均半长轴的改变，因此需要将平均半长轴恢复至机动前的平均半长轴，补偿法向机动引起的平均半长轴变化；其次，星间的倾角差发生改变，J2无漂移条件遭到破坏，因此需要补偿di改变引起的da修正项，使得满足J2无漂移条件。
1) 补偿法向机动引起的平均半长轴变化
将机动前后的瞬时轨道根数分别代入式(8) 求得机动前后的平均轨道半长轴a₀和a₁，然后代入式(9), 得到补偿法向机动引起的平均半长轴变化需要的速度增量为

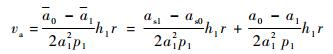(9)

式中：a_s1和a_s0分别为机动前和机动后轨道半长轴的一阶短周期项。
2) 补偿di改变引起的da修正项，使得满足J2无漂移条件
为了保持从星相对虚拟中心的构型稳定，da、de和di需要满足J2项无漂移条件式(3)，当偏心率e很小(近圆轨道)时，式(3) 可简化为式(10)，实现修正编队沿切向的漂移^[14]：

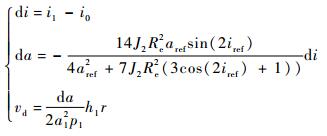(10)

式中：v_d为满足J2无漂移条件需要补偿的速度增量。
将式(9) 和式(10) 相加，可得消除耦合效应引起的切向漂移需要的总速度增量即v_T=v_a+v_d。
3 仿真验证 以某磁层探测任务为例进行仿真校验，图 5是一个空间四面体构型的编队，4颗卫星分别位于空间四面体的4个顶点，Ref为编队的虚拟中心。其中Sat2、Sat3、Sat4通过三切向脉冲实现分离部署^[15]，与虚拟中心Ref形成平面绕飞椭圆构型，Sat1通过法向机动与构型虚拟中心Ref形成法向的周期振荡运动。为了使得编队卫星在两极地区获得最佳的探测效果，应满足δΩ=0，即Sat1和Ref只能通过轨道倾角差δi实现法向相对运动，获得法向基线。整个任务中存在2类切向补偿：一是构型初始化分离时施加法向机动需要切向补偿; 二是构型维持阶段施加法向机动需要切向补偿。

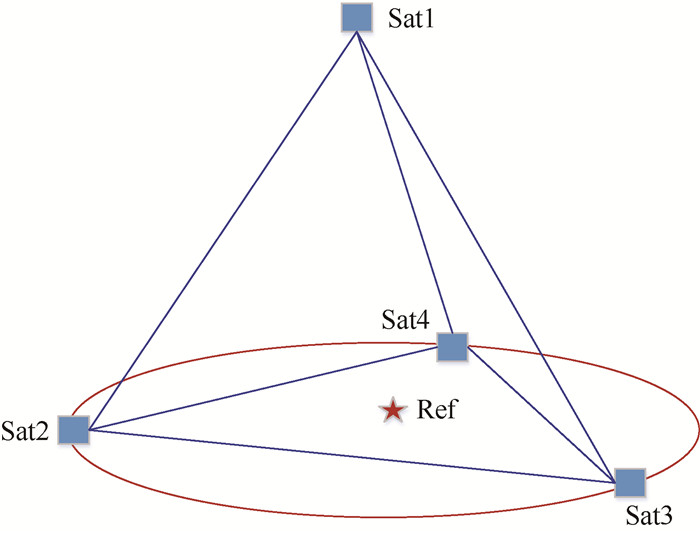图 5 卫星编队四面体构型示意图 Fig. 5 Schematic diagram of tetrahedron formation of satellites

图选项

初始化分离阶段：初始Sat1位于虚拟中心Ref处。在初始化分离阶段，Sat1通过法向机动改变轨道倾角，形成法向基线，与其他3颗星实现空间四面体构型。根据高斯摄动方程式(5) 可知，当纬度幅角ω+f=kπ(k=0, 1, …)时，施加法向机动改变轨道倾角需要的速度增量最小。此时，为了实现良好的空间四面体几何特性需要施加切向补偿，该切向补偿既要补偿法向机动引起的平均半长轴变化，也需要补偿di改变引起的da修正项，使得满足J2无漂移条件。
构型维持阶段：根据式(1), 由于虚拟中心Ref和Sat1存在轨道倾角差，两者之间的升交点赤经差将会随着时间积累逐渐增大，同时轨道倾角不存在长期漂移，故而由式(2), 两者之间的法向运动的振幅将会随着时间逐渐增加，从而造成空间四面体几何特性越来越差。因此，当法向振幅超过给定阈值时，必须施加法向机动，消除升交点赤经差，使得δΩ=0。根据脉冲推力的高斯摄动方程式(5) 可知，在纬度幅角(k=0, 1, …)时，施加法向机动改变升交点赤经需要的速度增量最小。此时，为了防止由于施加法向机动时发生切向漂移，导致空间四面体几何特性遭到破坏，需要对Sat1进行切向补偿。由于平均轨道倾角随时间不发生变化，因此只需要补偿法向机动引起的平均半长轴变化。
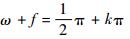
1) 仿真初始条件
根据探测任务要求，编队的虚拟中心Ref的初始瞬时轨道根数为[a₀, e₀, i₀, Ω₀, ω₀, f₀]=[6 978.159 5 km, 0.001 18，97.792 3°, 100.702°, 0°, 0°]。初始时刻Sat1位于虚拟中心Ref处。Sat1和Ref之间的法向振幅为10 km，给定阈值是20 km，仿真中卫星受地球中心引力和J2摄动力。
2) 仿真结果
Sat1在0.134 2 d时(此时纬度幅角为0°)，施加速度增量为10.843 6 m/s的法向机动，实现构型初始化分离，使得法向距离振幅达到10 km，根据式(9) 和式(10) 同时需要施加速度增量为-5.126 54 mm/s的切向补偿速度消除切向漂移。然后，法向运动的振幅不断增大，最终在14.039 5 d时(此时纬度幅角为90°)超过了给定阈值20 km，此时施加速度增量为-19.014 4 m/s的法向机动，使得法向运动的振幅恢复至10 km。为了防止构型发生切向漂移，根据式(9)，需要同时施加速度增量为-24.040 8 mm/s的切向补偿速度。整个过程，Sat1和Ref之间的法向距离变化如图 6所示，由图可知，法向运动的振幅可以实现保持在10~20 km范围内，满足任务要求。

图 6 法向距离随时间的变化 Fig. 6 Variation of cross-track range with time

图选项

图 7分别给出了无切向补偿时和有切向补偿时切向距离随时间的变化。通过比较可知，如果不施加切向补偿，15 d Sat1将沿切向漂移超过25 km，空间四面体的几何特性将会严重遭到破坏。而根据本文提出的切向补偿方法进行切向补偿，切向漂移将得到显著抑制，从而保证了较好的空间四面体几何特性，证明了方法的有效性。

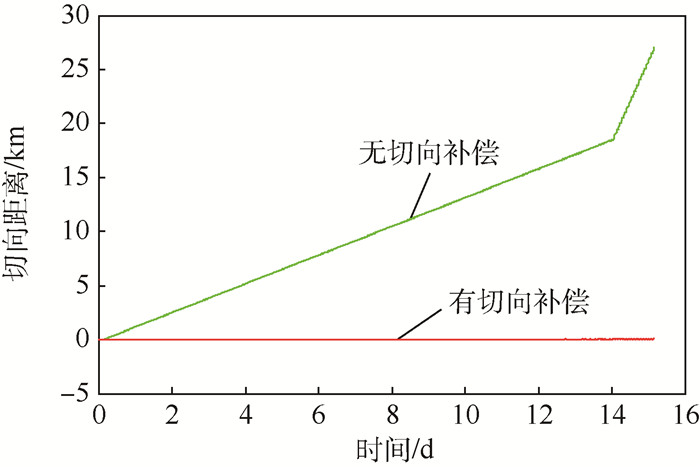图 7 切向补偿对切向距离变化的影响 Fig. 7 Influence of in-track compensation on in-track range

图选项

图 8表示在构型维持阶段，法向机动的速度增量大小和切向补偿的速度增量速度大小的关系，由图可知，当卫星位于当前位置时，两者在2.5×10^-4量级。其中，当法向机动速度增量大小为4 m/s时，切向补偿的速度增量可达到-1.063 6 mm/s，相当于一个周期漂移18.5 m。所以，脉冲机动的高斯摄动方程式(5) 常常会忽略法向切向耦合效应。但是，对于法向速度增量较大的构型初始化部署、构型重构和构型保持，必须考虑法向机动的切向耦合效应。

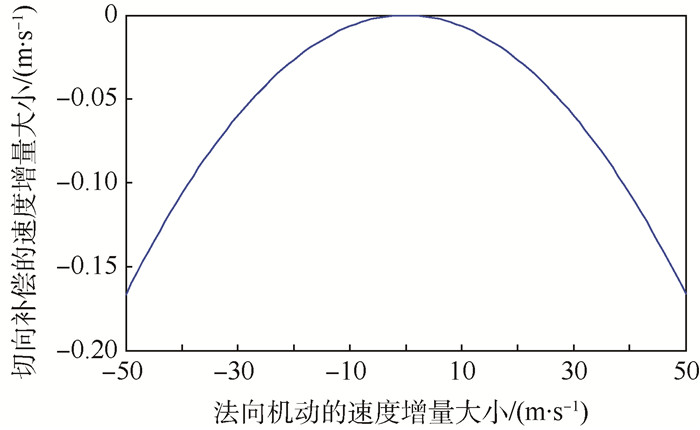图 8 切向补偿的速度增量大小和法向机动的速度增量大小的关系 Fig. 8 Relationship between velocity increments of in-track compensation over and cross-track maneuver

图选项

4 结论 1) J2摄动下编队卫星的法向机动会引起编队构型发生切向漂移，主要有两方面原因：① 法向机动引起平均半长轴发生变化；② 法向机动改变轨道倾角时会导致J2无漂移条件遭到破坏。
2) 通过对高斯摄动方程的修正，可以解析地计算出消除由于法向机动的切向耦合效应造成的切向漂移需要的切向补偿速度增量，从而实现更精确的构型控制。该切向补偿方法可应用于法向速度增量较大的构型初始化部署、构型重构和构型保持。

参考文献

[1]	ALFRIEND K T, VADALI S R, GURFIL P. Spacecraft formation flying:Dynamics, control and navigation[M].New York: Oxford University Press, 2010: 6-7.
[2]	曹喜滨, 张锦绣, 王峰. 航天器编队动力学与控制[M].北京: 国防工业出版社, 2013: 1-4. CAO X B, ZHANG J X, WANG F. The dynamics and control of spacecraft formation flying[M].Beijing: National Defense Industry Press, 2013: 1-4.(in Chinese)
[3]	杨震, 孟新, 牛文龙, 等. 多航天器协同探测星簇构型探测效能的评价方法[J].宇航学报, 2015, 36(9): 981–987. YANG Z, MENG X, NIU W L, et al. An evaluation method for multi-spacecraft formation detection efficiency[J].Journal of Astronautics, 2015, 36(9): 981–987.(in Chinese)
[4]	CAILLIBOT E P, GRANT C C, KEKEZ D D, et al.Formation flying demonstration missions enabled by CanX nanosatellite[C]//Proceeding of 19th Annual AIAA/USU Conference on Small Satellite.Reston:AIAA, 2005:1-9.
[5]	GILL E, SUNDARAMOORTHY P, BOUWMEESTER J, et al. Formation flying within a constellation of nano-satellite:The QB50 mission[J].Acta Astronautica, 2013, 82(1): 110–117.DOI:10.1016/j.actaastro.2012.04.029
[6]	HALL L. Edison demonstration of smallsat networks (EDSN)[EB/OL].Moffett Field, CA:NASA Ames Research Center, 2013(2015-11-25)[2016-05-21].http://www.nasa.gov/directorates/spacetech/small_spacecraft/edsn.html.
[7]	杨乐平, 朱彦伟, 黄涣. 航天器相对运动轨迹规划与控制[M].北京: 北京国防工业出版社, 2010: 104-107. YANG L P, ZHU Y W, HUANG H. Spacecraft relative trajectory planning and control[M].Beijing: National Defense Industry Press, 2010: 104-107.(in Chinese)
[8]	SCHAUB H, ALFRIEND K T. J2 invariant relative orbits for spacecraft formations[J].Celestial Mechanics and Dynamical Astronomy, 2001, 79(2): 77–95.DOI:10.1023/A:1011161811472
[9]	刘鲁华, 孟云鹤, 安雪滢. 航天器相对运动轨道动力学与控制[M].北京: 中国宇航出版社, 2013: 93-94. LIU L H, MENG Y H, AN X Y. The dynamics and control of spacecraft relative motion[M].Beijing: China Astronautic Publishing House, 2013: 93-94.(in Chinese)
[10]	BREGER L, HOW J P.J2-modified GVE-based MPC for formation flying spacecraft[C]//AIAA Guidance, Navigation and Control Conference and Exhibit.Reston:AIAA, 2005:1-12.
[11]	VADALI S R, ALFRIEND K T, VADALI S R, et al. Formation establishment and reconfiguration using impulsive control[J].Journal of Guidance, Control, and Dynamics, 2005, 28(2): 262–268.DOI:10.2514/1.6687
[12]	CLOHESSY W H, WILTSHIRE R S. Terminal guidance system for satellite rendezvous[J].Journal of the Aerospace Sciences, 1960, 27(5): 653–674.
[13]	LAWDON D F. Optimal trajectories for space navigation[M].London: Butterworths, 1963: 79-84.
[14]	张玉锟, 戴金海. 考虑J2项摄动的卫星编队飞行[J].国防科技大学学报, 2002, 24(2): 6–10. ZHANG Y K, DAI J H. Satellite formation flying with J2 perturbation[J].Journal of National University of Defense Technology, 2002, 24(2): 6–10.(in Chinese)
[15]	雷博持, 郑建华, 李明涛. 椭圆轨道编队构型的初始化控制研究[J].空间科学学报, 2015, 35(1): 86–93. LEI B C, ZHENG J H, LI M T. Research on formation initialization control for elliptic reference orbit[J].Chinese Journal of Space Science, 2015, 35(1): 86–93.(in Chinese)