现有的检测算法主要从时域、频域和能量域来对瞬态信号进行处理[3-4],包括短时相关法、Power-Law法、短时傅里叶变换(Short Time Fourier Transform,STFT)和小波变换。短时相关法采用分段的统计估计对信号进行相关处理,这种方法能够达到较高的正确检测率,但是破坏了频率分辨率;Power-Law法将瞬态信号检测问题转化为N点离散傅里叶变换(Discrete Fourier Transform,DFT)数据中M点信号的检测问题,适用于未知系统产生的瞬态信号检测,但是在有色噪声环境中算法的性能会迅速下降;STFT对信号进行加窗处理,认为在短时间间隔内瞬态信号是平稳的,但是由于固定的窗函数STFT只有单一的分辨力,不能做到时频分辨力的平衡;小波变换能针对信号高频和低频部分各自的特点实现多分辨检测,但是不同的小波基会得到差异很大的检测效果,使得算法的鲁棒性不强。希尔伯特-黄变换(HHT)不需要任何先验知识,以固有模态函数(Intrinsic Mode Function,IMF)作为瞬态信号的基函数,能够克服传统傅里叶变换只适用于线性平稳信号的缺陷。研究证明HHT是一种适用于含有非线性成分、奇异点及突变信号的自适应信号处理方法[5-8]。
本文在分析了经典HHT理论的基础上,针对其存在的模态混叠、虚假IMF分量等问题,结合集合经验模式分解(Ensemble Empirical Mode Decomposition, EEMD)与虚假IMF滤除两部分提出了改进HHT算法。通过对复杂电磁环境中通信信号的分析, 建立了瞬态信号模型和非高斯噪声模型,并提出基于改进HHT的非高斯噪声中瞬态通信信号的检测算法。通过仿真对比分析了本文算法与其他算法在不同条件下的检测效果,验证了本文算法对于非高斯噪声中瞬态通信信号检测的准确性与鲁棒性。
1 HHT时频分析法 1.1 HHT变换基本原理 HHT主要由经验模态分解(Empirical Mode Decomposition,EMD)和Hilbert谱变换组成,其主要流程如图 1所示。
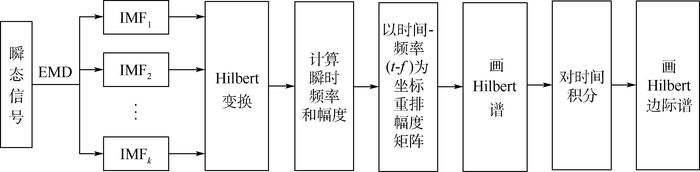 |
| 图 1 HHT算法流程图 Fig. 1 Flowchart of HHT algorithm |
| 图选项 |
其中,EMD的分解结果由若干个IMF组成,这些IMF满足以下2个条件[9]:① 极值点的数量和零点的数量相等,或者相差一个;② 任何时候根据信号的局部极大值与局部极小值定义的包络均值必须是零。EMD本质上是通过信号的特征时间尺度判断其包含的震荡模式,然后以此为依据将信号分解成若干个具有实际物理意义的IMF。
EMD算法的一般步骤如下:
步骤1????首先确定信号x(t)的所有极值点,再使用三次样条插值函数将所有极大值点作为上包络,所有极小值点作为下包络,设m1为上下包络的均值。
步骤2????计算信号x(t)和m1的插值:
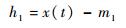 | (1) |
h1不一定满足IMF的条件,需要再将h1作为输入,重复上述过程,直至第k次提取出的信号h1k满足IMF条件,定义c1为第一阶IMF,记c1=h1k。
步骤3????将得到的第一阶IMF分量从信号x(t)中分离出来余量信号r1,即x(t)-c1=r1。
步骤4????将余量作为新的信号重复步骤1~步骤3,得到各阶IMF,直至满足终止条件,EMD终止。
信号经过EMD后可以表示为若干个IMF分量和一个余项rn的和:
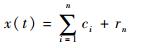 | (2) |
对于任意一个IMF分量c(t),其Hilbert变换定义为
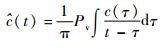 | (3) |
其中:Pv为柯西主值,则x(t)的解析信号z(t)形式为
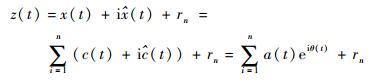 | (4) |
其中:a(t)和θ(t)分别为信号x(t)的瞬时幅度和瞬时相位,于是瞬时频率可以表示为
 | (5) |
将式(5) 代入式(4) 可以得到
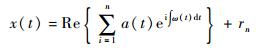 | (6) |
式中:将各个分量的幅度和瞬时频率表示为时间的函数,并可用能量曲线在时间-频率-幅度的三维空间上体现信号的时频特性。这种谱图称为Hilbert幅度谱,记为H(ω, t),简称Hilbert谱。相应地,幅度平方的时频分布就是Hilbert能量谱。
对H(ω, t)进行时间上的积分就可以得到Hilbert边际谱,记为h(ω)。
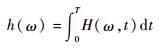 | (7) |
式中:T为信号持续时间。Hilbert边际谱与传统的FFT相似,可以体现信号在每个频点上的分布,并在统计意义上表示了在整个时间跨度上信号幅度的累积。
1.2 经典HHT变换存在的缺陷 经典HHT在对信号进行EMD时,由于信号中含有噪声和干扰信号,可能会使一个IMF中存在截然不同的若干种频率分量或者同一频率分量分配到不同的IMF中,这就是经典HHT的模态混叠问题[10]。这种模态混叠问题是信号的不连续性引起的,会导致得到的IMF并不具有真实的物理意义,也不能得到信号的瞬时频率等参数,最终引起信号的时频特性严重失真。为了直观地论述模态混叠问题,设定一个由正弦信号和小幅谐波信号叠加而成的仿真信号,如图 2(a)所示,其EMD结果如图 2(b)所示。从图中可以看出,模态混叠问题导致分解得到的2个IMF分量产生了严重的畸变。正弦信号和谐波信号被同时分配到了IMF1,且IMF2中也包含了正弦分量,从而使得2个IMF分量不能很好地反应信号的状态和特征,求其瞬时频率也就失去了该有的物理意义。
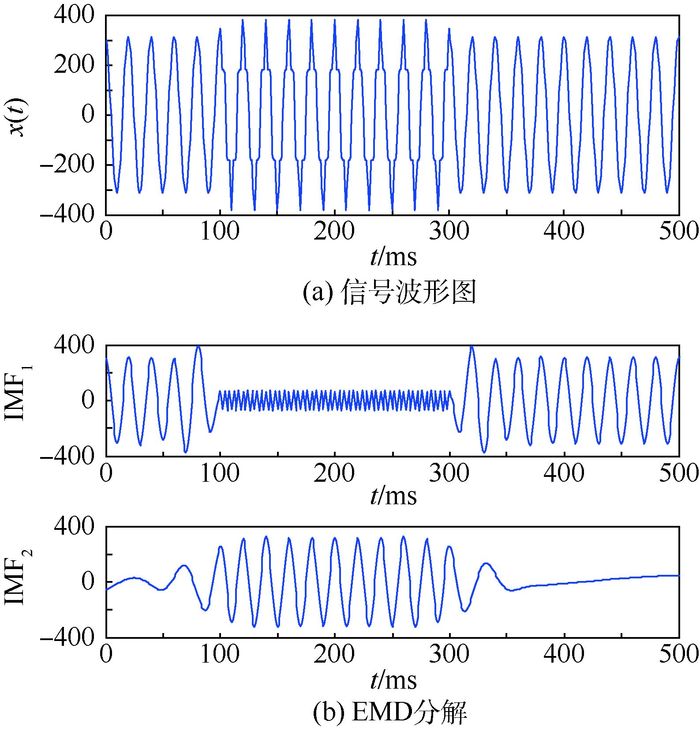 |
| 图 2 模态混叠示意图 Fig. 2 Sketch map of mode mixing |
| 图选项 |
此外,包含信号特征信息的IMF分量之间通常是正交的,与原始信号具有较高的相似性。但是使用经典HHT对信号进行分解时会产生相关性较低的IMF分量,这些分量会在能量谱中表现为虚假的频率分量,导致对信号的特征分析出现偏差。依旧使用图 2(a)中的信号进行分析,经过HHT得到其Hilbert能量谱如图 3所示。原始信号中包含50 Hz与250 Hz 2种频率分量,从图中可以看出其频率分量的能量大小和持续时间。但是由于虚假IMF分量的影响,在0~100 ms和300 ms以后都存在虚假频率的现象。
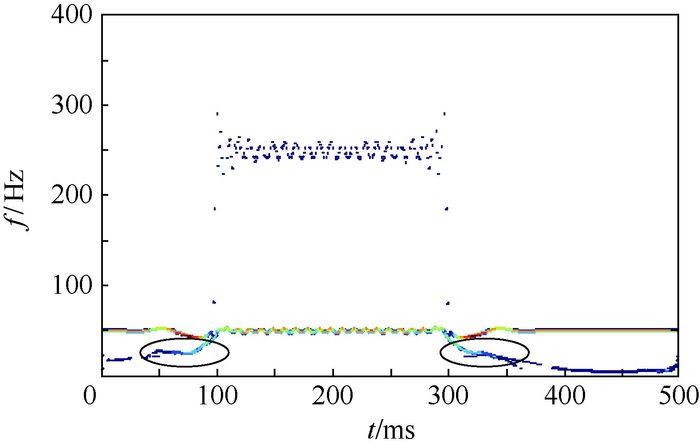 |
| 图 3 虚假频率示意图 Fig. 3 Sketch map of illusive frequency |
| 图选项 |
2 改进检测算法 文献[11]使用高阶分量重构瞬态信号进行判决,在一定程度上抑制噪声对信号的影响,但同时也会损失信号中包含的信息,对信号分析和识别造成影响。文献[4]中采用子波检测和局部瞬时能量密度双重降噪提高瞬态信号的信噪比,但其只对高频噪声具有良好的滤除效果,而对中低频噪声和非高斯噪声的效果并不理想。因此本文结合瞬态通信信号的特点、针对现有检测算法的缺陷,提出基于改进HHT和小波域Power-Law的检测算法。
模态混叠的根本原因是根据三次样条插值得到的包络为若干个不同频率分量叠加而成,造成一个IMF分量中含有不止一种频率成分。因此EEMD提出利用高斯白噪声具有频率平均分布的统计特性,通过加入白噪声对信号进行平滑,从而增强信号的连续性[12]。EEMD通过多次在信号中加入随机噪声改变信号处理的时间跨度,使EMD可以从更多的尺度分析信号成分,因此得到的平均IMF可以更加客观、全面地分析信号的特点,而加入的噪声可以通过多次叠加相互抵消。
此外,IMF分量是按照瞬时频率、幅值和能量呈递减的趋势排列,并且包含信号特征的IMF会与原信号具有较好的相关性[13]。而虚假IMF分量通常会在低频处出现,因此本文提出根据各IMF分量与原信号之间的能量差异和相关性筛选虚假IMF分量。第i级IMF分量IMFi与原信号s间的相关性可以根据能量系数δi衡量,计算公式为
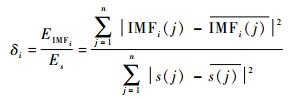 | (8) |
式中:EIMFi和Es分别为IMF各分量和原信号的能量值;
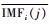
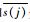
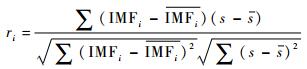 | (9) |
相关系数ri的阈值L可以通过式(10) 确定:
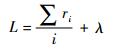 | (10) |
式中:λ的取值由检测算法所需IMF分量决定。当L的取值越大时,信号的高频特征就越突出,但同时也会损失部分特征信息;当L的取值越小时,信号的特征信息就越全面,混入虚假信息的风险也就越大。
基于以上理论,本文提出的改进检测算法原理如下:
步骤1????初始化EEMD的集合数Ns以及加入的白噪声幅度参数k。
步骤2????进行第n次EEMD,在信号中随机加入幅度系数为k的白噪声序列得到待处理信号sn(t)。对信号sn(t)使用EMD分解得到I个IMF,表示为IMFi, n(i=1, 2, …, I)。
步骤3????对Ns次分解得到的IMF分量计算平均值IMFi并将其作为第i个IMF分量。
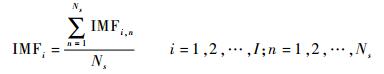 |
步骤4????根据式(8) 和式(9) 计算IMF与原信号的能量差异和相关系数,再根据判别方法剔除虚假IMF分量。
步骤5????使用得到的IMF分量对信号进行重构,得到信噪比增强后的待检测信号s′(t)。
步骤6????将信号s′(t)输入小波域Power-Law检测器判断是否存在瞬态信号,其检测算法为
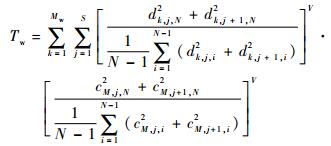 |
其中:dk, j, i2和cM, j, i2分别为信号在小波域的细节系数和近似系数; Mw为小波分解层数; S为小波系数长度;N为待检测信号等分的段数; V为一个非负实数,在检测中一般取2.5。
3 信号模型 3.1 瞬态信号模型 对于通信辐射源的个体识别主要从信号的瞬态和稳态两部分进行,瞬态信号由于包含更为丰富的个体特征而被广泛应用于个体识别。瞬态通信信号是指电台从不工作跳变到发射信号时产生的抖动信号,持续时间很短,通常只有几毫秒到几十毫秒。根据瞬态通信信号产生的物理机制,本文采用的通信信号模型为3个起始时刻、持续时间不同的指数衰减正弦信号叠加组成,可以用下面的公式表示:
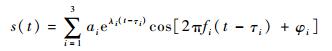 |
式中:ai和τi分别为对应信号分量的幅度参数和时间延时参数。a1=1.5,a2=0.3,a3=0.7,τ1=0.002 s,τ2=0.001 3 s,τ3=0.004 s。λi为各个信号分量幅度衰减快慢的度量,称为幅度衰减因子,λ1=700,λ2=850,λ3=600。采样频率fs=96 kHz,各个分量的信号频率为f1=5 kHz,f2=3 kHz,f3=7 kHz。初始信号相位φ1=π/3,π/6,π/4,信号持续时间为60 ms。信号波形如图 4所示。
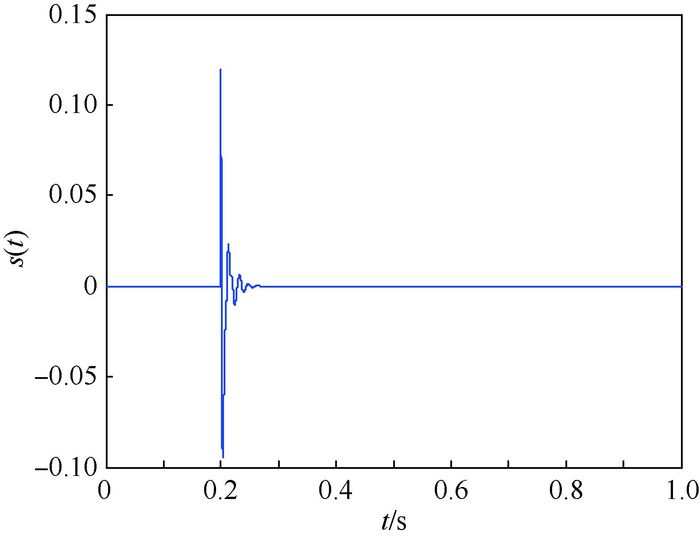 |
| 图 4 瞬态通信信号波形 Fig. 4 Waveform of transient communication signal |
| 图选项 |
3.2 非高斯信号模型 已有的理论和分析通常建立在干扰信号为高斯噪声的基础上,这对于一般的电子设备是适用的。但是在复杂电磁环境下,影响信号检测的许多噪声信号是非高斯的,这时如果仍作为高斯噪声进行处理就会造成信号的破坏和损失。因此,本节采用混合高斯模型对非高斯信号进行分析。混合高斯模型(Gaussian Mixture Model,GMM)是非高斯信号中一种重要的建模形式,具有结构简洁、易于实现的特点[14],其概率密度函数的表达式为
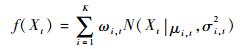 |
其中:ωi, t为t时刻第i个高斯分布在混合模型中所占的权值; K为高斯分布的个数;N(·)为高斯分布的概率密度函数;μi, t和σi, t2分别为第i个高斯分布的均值和方差。
因此,本文使用GMM对实际电磁环境中的背景噪声进行建模,并与瞬态通信信号混合构成待检测的信号模型。设高斯分布的个数K=3,函数的均值分别为:μ1=0,μ2=1,μ3=3;方差分别为:σ12=5,σ22=3,σ32=7。各个分量的权值随机生成,则GMM生成的非高斯噪声波形如图 5所示。
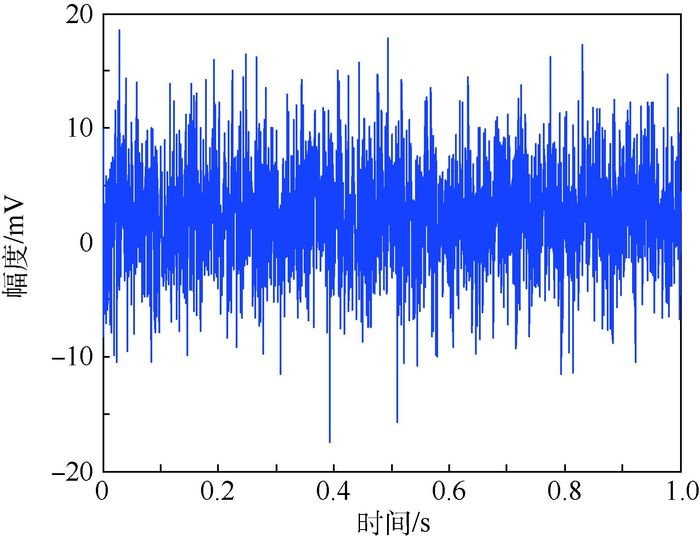 |
| 图 5 非高斯噪声波形 Fig. 5 Waveform of non-Gaussian noise |
| 图选项 |
4 仿真分析 仿真所采用的目标通信信号s(t)由两部分组成:用于传输信息的BPSK调制信号s1(t)和体现个体特征的瞬态信号s2(t),其波形如图 6所示。图 6中纵坐标为幅度,采样频率为20 kHz,图 6(c)中圆圈内为通信信号s(t)的个体特征。
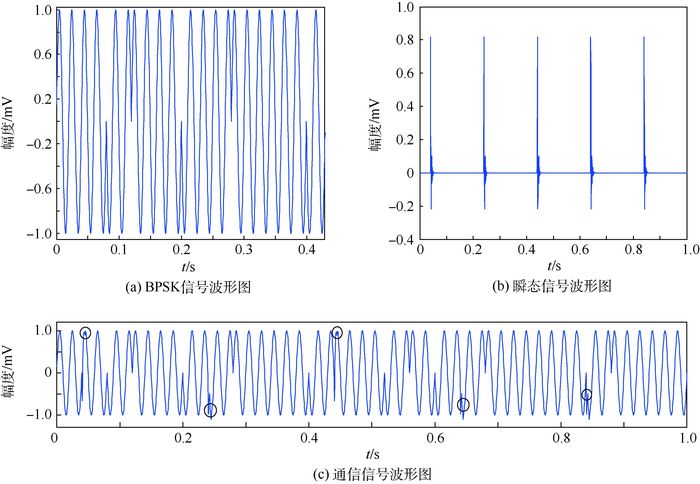 |
| 图 6 通信信号及其组成波形 Fig. 6 Waveform of communication signal and its components |
| 图选项 |
在信号s(t)中加入与3.2节参数一致的非高斯噪声序列,得到包含瞬态通信信号的待检测信号x(t),设信噪比为0 dB。首先使用经典HHT对信号x(t)进行分析,图 7为EMD分解得到的各个IMF分量IMF1~IMF6以及余量R,由于受非高斯噪声的影响,在高频部分的IMF分量IMF1和IMF2失真严重,无法分析其真实的物理含义。同时,在IMF3~IMF4明显存在一定程度的模态混叠。事实上,这2组IMF分量的混叠在瞬态信号产生的时刻(即在t=0.04,0.24,0.44,0.64,0.84 s处)更为突出,也就意味着在这些局部尺度内EMD无法将两部分信号有效地辨别出来。从能量角度来说,IMF3~IMF4中各有部分能量转换到IMF5~IMF6中,形成2组小参数IMF分量,但是这2组IMF并不包含实际通信信号具有的频率分量。
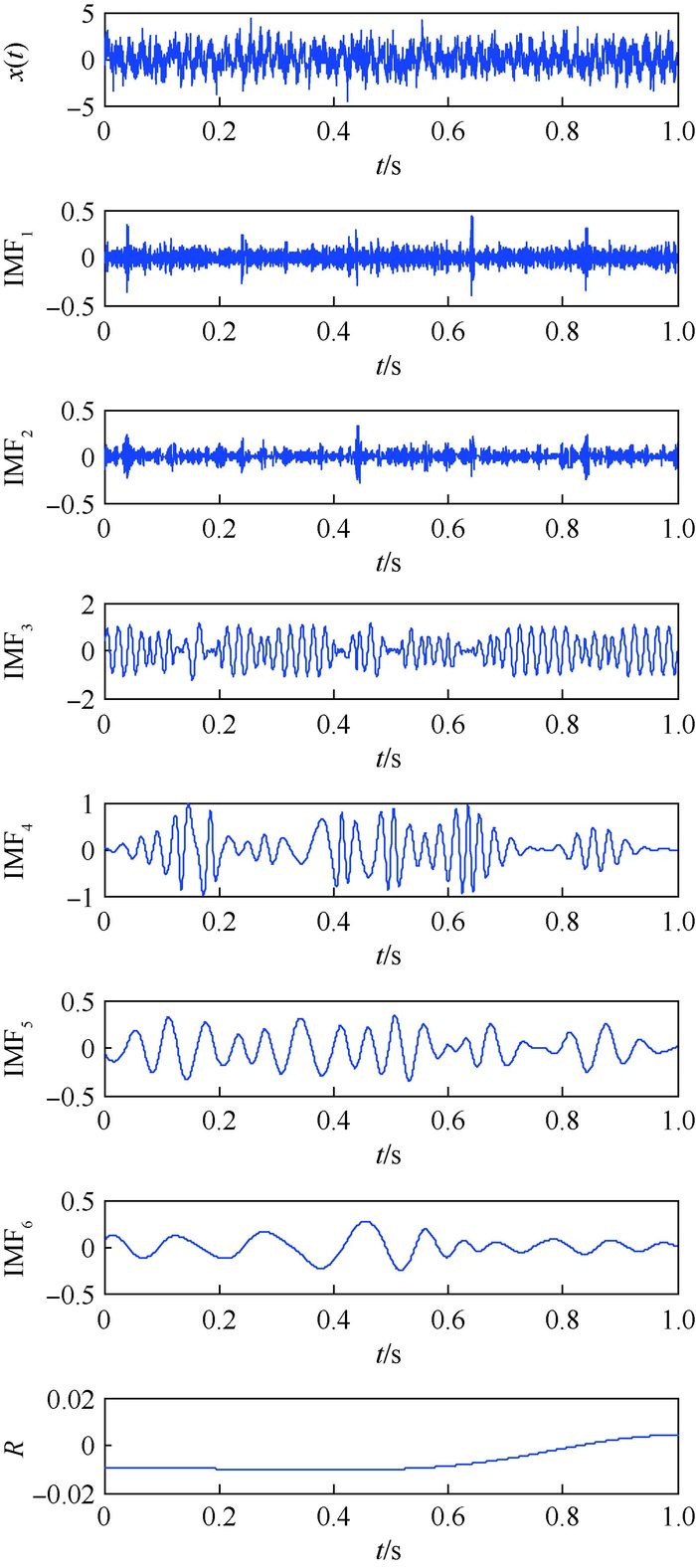 |
| 图 7 EMD分解结果 Fig. 7 Decomposition results of EMD |
| 图选项 |
图 8为各组IMF分量经过Hilbert谱变换得到的信号能量的时频分布图。由于采用BPSK信号作为信息传输方式,基带信号的变化会使通信信号相位发生反相。这种反相会导致经典HHT对信号的变化过于敏感,体现在时频图中即为瞬时频率的突变。根据通信信号模型可知共有5个时刻产生了瞬态信号,12个时刻发生了信号的反相,而这种BPSK信号反相时发生的频率抖动不利于对瞬态信号的检测,可能会导致检测器的虚检。此外,由于小参数IMF分量导致分布图中虚假频率的存在,导致对信号组成和特征的分析更为困难。因此,经典HHT对于瞬时通信信号的处理不够全面和深入,并且存在模态混叠和虚假频率等问题,不能实现对瞬时通信信号有效地检测。
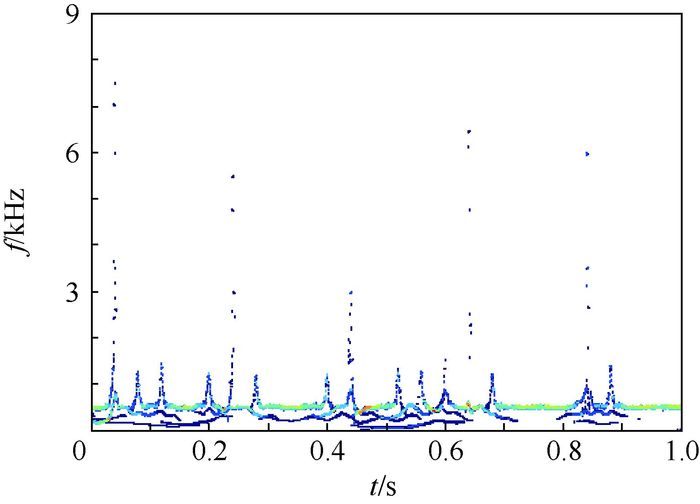 |
| 图 8 HHT能量时频分布 Fig. 8 Energy time-frequency distribution of HHT |
| 图选项 |
图 9为使用EEMD对待检测信号x(t)进行分解得到的各个IMF分量,其参数Ns=100、k=0.5。由于EEMD的核心算法仍是EMD,因此得到的IMF数目与EMD一致。IMF1和IMF2共同体现了瞬态通信信号的特点,这是由于瞬态通信信号为非线性非平稳信号,一个IMF分量无法包含其全部的频率成分和信号特点。对比图 7和图 9,EEMD通过加入随机白噪声对信号进行平滑,抑制了非高斯噪声对瞬态通信信号的影响,从而使瞬态信号的特征更加明显。IMF3的波形体现了EEMD的优越性,同时证明了EEMD理论的成立。在EMD分解时,IMF3是BPSK信号与瞬态通信信号混叠的结果,本质上可以等效为高频周期脉冲信号对低频BPSK信号的调制,但是受到分析尺度的限制,EMD并不能很好地把二者区分出来。而EEMD通过多次引入随机白噪声对信号进行多特征尺度的分析,最终通过平均得到IMF3的波形。这个过程实质上是幅度较低的瞬态通信信号受到噪声的影响而模糊,而幅度较高的BPSK信号相当于载频信号被保留下来。从能量的角度来看,IMF4正是由IMF3分出的能量产生的IMF分量,这也是IMF4幅值小于1的原因。因此,EEMD可以有效地分析处于非高斯噪声中的瞬态通信信号,抑制了经典HHT中存在的模态混叠的问题。
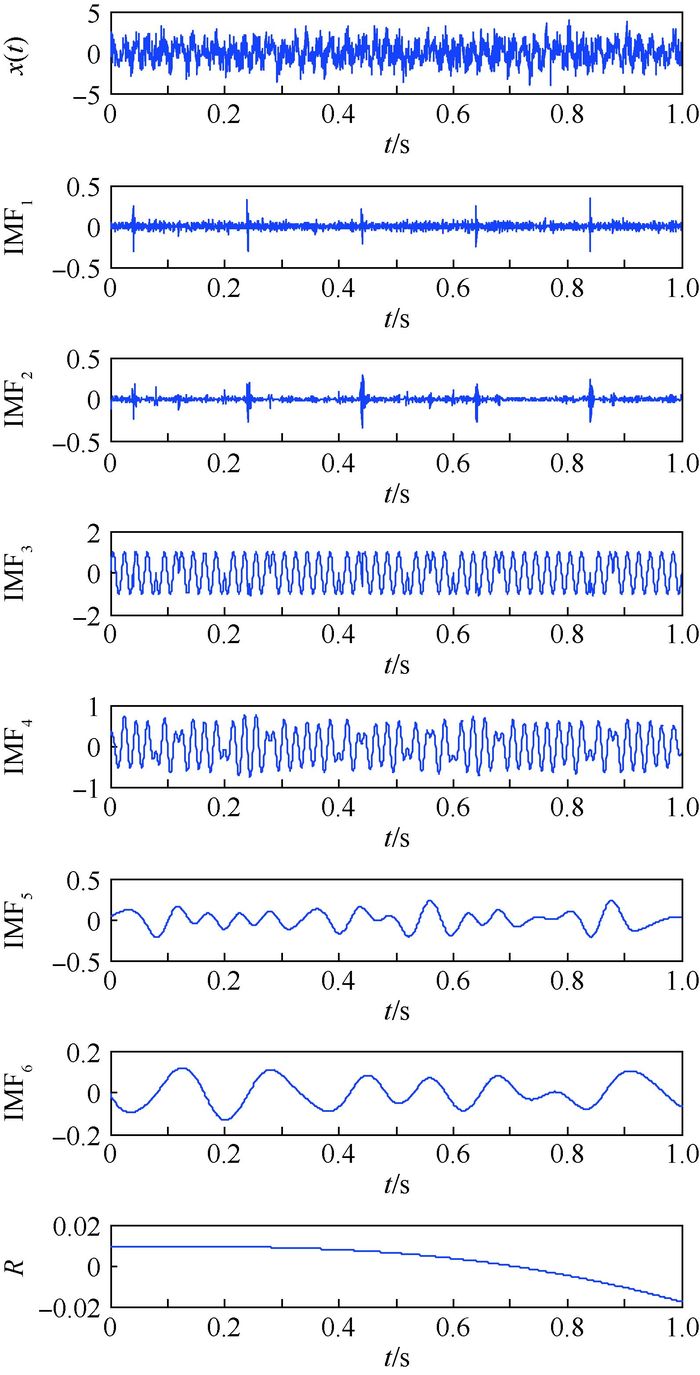 |
| 图 9 EEMD分解结果 Fig. 9 Decomposition results of EEMD |
| 图选项 |
但是从图 9中可以看出EEMD仍然存在虚假IMF分量的问题,因此本文提出结合能量与相关性对IMF分量进行筛选,剔除虚假频率对信号分析的影响。由式(8) 和式(9) 可得IMF5和IMF62组IMF分量为虚假分量,剔除后经过Hilbert变换得到信号的能量时频分布图,如图 10所示。从图中可以看出,BPSK信号的反相对于瞬态信号检测的影响已经大大降低,同时经过筛选后通信信号中幅度较低的虚假低频分量已经被剔除,在高频部分瞬态信号的特征也更为明显。由于减小了模态混叠和虚假频率分量的影响,使用本文提出的改进HHT算法得到的时频分布图可以更加有效地实现对瞬态通信信号的检测。
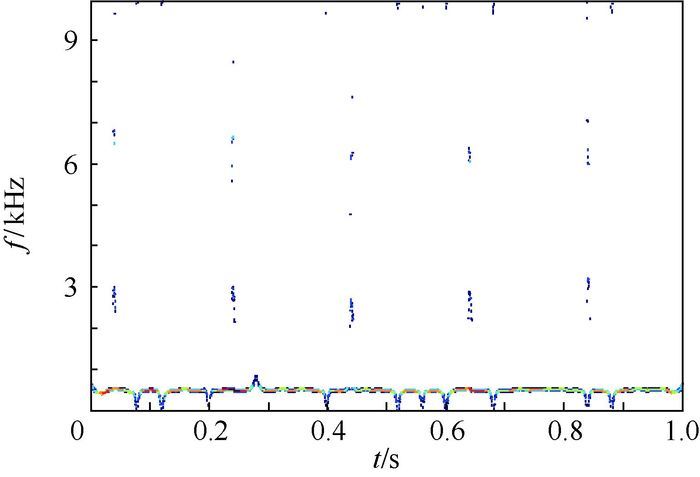 |
| 图 10 改进HHT能量时频分布 Fig. 10 Energy time-frequency distribution of improved HHT |
| 图选项 |
为了进一步研究本文算法(以下简称IHHT算法)的检测性能,采用正确检测率对比分析谱熵法(Spectrum Entropy,SE)[15]、HHT算法以及本文IHHT算法的实际检测效果。其中正确检测率的定义为
错误检测次数=瞬态信号判断为噪声的次数+噪声判断为瞬态信号的次数
正确检测率=正确检测次数/(正确检测次数+错误检测次数)
本文分别在信噪比为10、0和-10 dB的条件下对图 6中目标通信信号s(t)加入非高斯干扰噪声序列后进行检测,并使用3个方法各自独立进行200次的蒙特卡罗实验,得到如表 1的检测结果。
表 1 3种算法的正确检测率 Table 1 Correct detection rates of three algorithms%
| % | |||
| 检测算法 | 信噪比/dB | ||
| 10 | 0 | -10 | |
| SE | 90.13 | 86.94 | 81.27 |
| HHT | 92.67 | 89.71 | 86.83 |
| IHHT | 93.75 | 91.62 | 90.27 |
表选项
从表 1中可以看出,在信噪比较高时,3种检测算法都具有较好的检测效果,正确检测率都可以达到90%以上。但是随着噪声干扰信号的增强,SE算法的检测性能下降的最快,与之相比,HHT算法具有更好的鲁棒性。而本文提出的IHHT检测算法即使在-10 dB的条件下也能够达到90%以上的正确检测率,相较于经典HHT算法提高了3.44%。因此,本文算法在保留了HHT算法良好特性的基础上,克服其模态混叠和虚假IMF的缺点,进一步提高了对瞬态通信信号的检测能力。
5 结论 利用EEMD对非线性非平稳信号处理的优势并结合能量差异、相关性2种筛选方法,本文提出了改进HHT算法来实现对非高斯噪声中瞬态通信信号的有效检测。主要结论如下:
1) 通过EEMD引入白噪声从多个尺度分析信号成分,从而更加客观、全面地分析信号的特点;并通过对IMF的筛选避免模态混叠和虚假IMF对分析结果的影响。
2) 在信噪比较高时IHHT与其他检测算法都具有较好的检测效果,正确检测率都可以达到90%以上;但在信噪比为-10 dB的强干扰条件下IHHT算法相较于HHT算法能够提高3.44%的正确检测率。
在此基础上,下一步的研究中需要对其边界处理问题进行深入的研究。
参考文献
| [1] | KLEN R W, TEMPLE M A, MENOONHALL M J. Application of wavelet denoising to improve OFDM-based signal detection and classification[J].Security and Communication Networks, 2010, 3(1): 71–82. |
| [2] | CARROLL T L. A nonlinear dynamics method for signal identification[J].Chaos, 2007, 17(2): 023109–1.DOI:10.1063/1.2722870 |
| [3] | WACHOWSKI N, AZIMI-SADJADI M R. Detection and classification of nonstationary transient signals using sparse approximations and Bayesian networks[J].IEEE/ACM Transactions on Speech and Language Processing, 2014, 22(12): 1750–1764.DOI:10.1109/TASLP.2014.2348913 |
| [4] | 王燕, 邹男, 付进, 等. 基于局部瞬时能量密度级的瞬态信号检测方法[J].电子与信息学报, 2013, 35(7): 1720–1724. WANG Y, ZOU N, FU J, et al. Transient signal detection method based on partial instantaneous energy density level[J].Journal of Electronics & Information Technology, 2013, 35(7): 1720–1724.(in Chinese) |
| [5] | HUANG N E, WU Z H. A review on Hilbert-Huang transform:Method and its application to geophysical studies[J].Reviews of Geophysics, 2008, 46(6): 1029–1039. |
| [6] | HUANG N E, SHEN S S P. The Hilbert-Huang transform and its application[M].Kuala Lumpur: World Scientific Publishing Co.Pte.Ltd, 2005: 142-146. |
| [7] | DIVIN Y, LYATTI M, SNEZHKO A. THz Hilbert-transform spectrum analyzer based on high-Tc Josephson junction in stirling cryocooler[J].IEEE Transactions on Applied Superconductivity, 2013, 23(3): 4–7. |
| [8] | 杨振, 邹男, 付进. Hilbert-Huang变换在瞬态信号检测中的应用[J].声学技术, 2015, 34(2): 167–171. YANG Z, ZOU N, FU J. The application of Hilbert-Huang transform in transient signal detection[J].Technical Acoustics, 2015, 34(2): 167–171.(in Chinese) |
| [9] | 李明爱, 崔燕, 杨金福, 等. 基于HHT和CSSD的多域融合自适应脑电特征提取方法[J].电子学报, 2013, 41(12): 2479–2486. LI M A, CUI Y, YANG J F, et al. An adaptive multi-domain fusion feature extraction with method HHT and CSSD[J].Acta Electronicasinica, 2013, 41(12): 2479–2486.DOI:10.3969/j.issn.0372-2112.2013.12.025(in Chinese) |
| [10] | 程擂, 韩焱, 王鉴, 等. 基于改进HHT的水中爆炸冲击波信号时频特性分析方法[J].爆炸与冲击, 2011, 31(3): 326–331. CHENG L, HAN Y, WANG J, et al. Time-frequency representation analysis in underwater explosive shock wave signals based on an improved HHT method[J].Explosion and Shock Waves, 2011, 31(3): 326–331.(in Chinese) |
| [11] | 江向东, 杨德森, 时胜国. 基于高阶统计量的小波包去噪在瞬态信号检测中的应用研究[J].信号处理, 2005, 21(2): 126–130. JIANG X D, YANG D S, SHI S G. Wavelet packets de-noising based on high-order-statistic for transient detection[J].Signal Processing, 2005, 21(2): 126–130.(in Chinese) |
| [12] | 窦东阳, 赵英凯. 集合经验模式分解在旋转机械故障诊断中的应用[J].农业工程学报, 2010, 26(2): 190–196. DOU D Y, ZHAO Y K. Application of ensemble empirical mode decomposition in failure analysis of rotating machinery[J].Transactions of the CSAE, 2010, 26(2): 190–196.(in Chinese) |
| [13] | 谢静, 谭佐军, 陈阳, 等. Hilbert-Huang变换分析THz脉冲信号的时频特性[J].强激光与粒子束, 2014, 26(7): 131–135. XIE J, TAN Z J, CHEN Y, et al. THz time-frequency analysis with Hilbert-Huang transform[J].High Power Laser and Particle Beams, 2014, 26(7): 131–135.(in Chinese) |
| [14] | 韩明, 刘教民, 孟军英, 等. 一种自适应调整K-ρ的混合高斯背景建模和目标检测算法[J].电子与信息学报, 2014, 36(8): 2023–2027. HAN M, LIU J M, MENG J Y, et al. A modeling and target detection algorithm based on adaptive adjustment K-ρ for mixture Gaussian background[J].Journal of Electronics & Information Technology, 2014, 36(8): 2023–2027.(in Chinese) |
| [15] | 李荣荣, 胡昌奎, 余娟. 基于谱熵的语音端点检测算法改进研究[J].武汉理工大学学报, 2013, 35(7): 134–139. LI R R, HU C K, YU J. Research of speech endpoint detection based on spectral entropy algorithm[J].Journal of Wuhan University of Technology, 2013, 35(7): 134–139.(in Chinese) |
