位置姿态测量系统(Position and Orientation System,POS)是目前机载对地观测获取位置、速度、姿态等运动参数的主要手段[6-7],其组成包括惯性测量单元(Inertial Measurement Unit,IMU)、全球定位系统(Global Position System,GPS)接收机、导航计算机(POS Computer System,PCS)和后处理软件[8]。PCS中运行惯性/卫星组合估计算法。但是对于装备了多个或多种观测载荷的高性能综合机载对地观测系统,由于观测载荷安装在机体的不同位置,飞机的弹性变形会导致载荷间的空间相对关系发生变化。此时,单个POS显然无法满足不同安置点多载荷的高精度运动参数测量的需求。在该需求的牵引下,机载分布式POS系统应运而生,实现多点运动参数的同时测量。
机载分布式POS系统一般由一个高精度主POS、多个分布在机体不同位置的低精度子IMU、PCS和后处理软件4部分组成。其中,高精度主POS一般安装于载机机舱内,以GPS的位置和速度为量测信息进行惯性/卫星组合导航。将主系统的高精度位置、速度、姿态等运动信息作为时空基准信号,通过传递对准给子IMU,从而实现子IMU所在处运动信息的精确测量[9-11]。
由于机载对地观测要求载机做理想的匀速直线飞行,此时分布式POS系统的主POS因没有直接姿态观测信息,其姿态误差状态变量的可观测度较低,导致姿态测量误差缓慢积累。将主POS的姿态信息传递给子IMU后,子IMU的姿态估计结果也将存在缓慢积累的误差。因此,在应用分布式POS系统进行机载对地观测时,必须根据测区形状进行飞行轨迹设计,通过载机有目的、适当的机动动作,来提高运动参数的估计精度[12],从而满足对地观测成像的需要。
目前,国外已开发出多款POS产品,但在最优飞行轨迹方面的研究鲜见公开报道。瑞士Leica公司曾在其产品IPAS10的说明书中提供了一个参考的飞行轨迹,包括进入测区前机动方式的选择和离开测区后机动方式的选择[13],但是其对完成机动所需的时间、机动后系统达到稳定所需的时间以及直线段飞行时长等未给出明确的说明。
而国内主要是针对惯性导航系统初始对准用机动方式的研究[14-16]。例如,文献[15]通过对比水平运动、S型机动及拐弯运动,为飞行器在初始对准时最佳机动方案的确定提供依据。通常初始对准的时间较短,而对地观测用分布式POS系统要实现整个测区内的运动参数测量,必须对整个飞行轨迹过程中的机动方式等进行全面考虑。文献[16]提出一种利用载机爬升段进行分布式POS系统传递对准的方法,并与多种机动方式进行对比,但该方法没有考虑机体的弹性变形,也未对机动后滤波稳态时间等进行测试分析。
针对上述问题,本文根据实际飞行试验经验,首先,在分析机载分布式POS系统误差源的基础上,综合考虑多种因素的影响,给出几种飞行轨迹的详细设计方案和待测参数;然后,采用目前较为常用的二阶Markov过程模拟机体的弹性变形以及“速度+姿态”的匹配方式进行基于卡尔曼滤波的传递对准仿真,对设计的飞行轨迹方案进行对比验证与分析。
1 飞行轨迹方案设计 1.1 分布式POS系统误差分析 从分布式POS系统的组成来看,其对运动参数的测量精度主要受主子系统IMU器件精度、GPS定位精度、时间同步精度、传递对准精度的影响。其中,在差分定位模式下,GPS的定位精度受基站和流动站之间基线距离的影响。在结合机载对地观测应用时,载机不同的机动方式将改变分布式POS系统状态变量的可观测度,进而影响系统的估计精度。由于时间同步和传递对准属于分布式POS系统内部误差因素,在用户端无法调节。因此,本文主要考察其他在用户端影响运动参数测量精度的误差因素。
此外,在载机机动后,分布式POS系统的传递对准滤波器需要一定时间来达到稳态,在稳态之前运动参数估计精度不稳定,不能进入测区;而在进入测区后,平飞段(进行成像的直线段)的姿态测量精度将随时间下降。即从机动结束至进测区之前的飞行时间过短或过长都无法在测区内获得最佳的运动参数估计精度。因此,还需要对载机进入测区前和直线段的最佳时间长度进行测试,以保证整个测区内运动参数的测量精度。
1.2 飞行轨迹设计 根据1.1节确定的误差因素进行飞行轨迹设计。
为保证测区内运动参数的测量精度,分别在首次进入测区前、出测区与再次进测区之间设置机动区。机载对地观测飞行轨迹基本方案示意图如图 1所示。
 |
| 图 1 机载对地观测飞行轨迹基本方案 Fig. 1 Basic scheme of airborne earth observation flight trajectory |
| 图选项 |
图 1中:T1为出机动区1后、进入测区前的飞行时长;T2为测区直线段飞行时长。整个飞行轨迹流程为:起飞后,在进入测区前需在机动区1内进行机动以保证进入测区后的测量精度;结束机动后需要T1时间来稳定滤波估计器,然后进入测区进行时长为T2的直线飞行,为避免长时间直线飞行后测量精度下降的问题,直线飞行后需要出测区进入机动区2或机动区3进行机动,然后再次进入测区。子IMU惯性器件——陀螺仪和加速度计的分类和具体性能参数如表 1所示。
表 1 惯性器件性能参数 Table 1 Performance parameters of inertial sensors
| 器件水平 | 陀螺仪漂移/((°)·h-1) | 加速度计偏置/μg |
| 高精度 | 0.01 | 10 |
| 中精度 | 0.05 | 50 |
| 低精度 | 0.1 | 100 |
表选项
机动方式选取:根据目前实验室所进行的百余次机载对地观测飞行试验经验,首次进入测区前(机动区1)较为可行的机动方式主要有水平的S型、O型、8字型以及起飞的曲线爬升过程;机动区2和机动区3的机动方式选为U型。
T1设置:从机动后直接进入测区开始,即T1=0,以100 s间隔逐渐增大T1,统计不同T1下分布式POS系统在直线成像段的精度,为出机动区1后何时进入测区提供依据。
T2设置:分别选取100、200和400 s的时间,为测区成像段与U型轨迹规划提供依据。
GPS基线长度L0设置:分别选取20、40和60 km的基线长度,为GPS基站的合理架设提供依据。
飞行轨迹影响因素与参数选取如表 2所示。
表 2 飞行轨迹影响因素与参数选取 Table 2 Influencing factors and parameter selection of flight trajectory
| 子IMU惯性器件水平 | 测区前机动方式 | 测区前飞行时长/s | 直线段飞行时长/s | GPS基线长度/km |
| 高精度 | 无机动 | 0 | 100 | 20 |
| 中精度 | S型 | 100 | 200 | 40 |
| 低精度 | O型 | 200 | 400 | 60 |
| 8字型 | 300 | |||
| 曲线爬升 | 400 |
表选项
2 传递对准数学模型 机载分布式POS系统中子IMU依靠主POS的高精度位置、速度、姿态等运动参数对其进行传递对准,以实现所在处运动信息的精确测量。由于飞机机体存在弹性变形,主、子系统间除了确定性的杆臂误差和安装误差角以外,还存在随时间变化的随机杆臂误差和弹性变形角[17]。因此在传递对准数学模型中必须考虑挠曲变形。
本文采用的传递对准数学模型包括状态方程和量测方程。其中,状态方程以子系统惯导误差模型为基础,主要包括姿态角误差方程、速度误差方程、位置误差方程、惯性器件误差方程、安装误差角方程和弹性变形角方程。弹性变形角采用二阶Markov过程描述。量测方程基于“速度+姿态”的匹配方式[18]进行建立。
2.1 状态方程 机载分布式POS系统中的相关参考坐标系定义为:i为地心惯性坐标系;e为地球坐标系;主POS和子IMU导航坐标系均为东北天地理坐标系,分别用nm和ns表示;主POS和子IMU的载体坐标系分别用bm和bs表示。
1) 姿态角误差方程
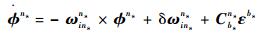 | (1) |
式中:
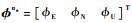

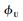
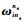
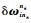
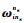
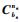
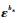
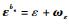
2) 速度误差方程
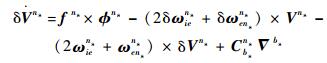 | (2) |
式中:
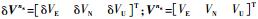
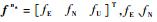
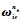
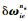
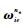
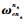

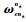
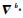
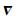
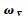

3) 位置误差方程
 | (3) |
式中:L、λ、H和δL、δλ、δH分别为子IMU的纬度、经度、高度和纬度误差、经度误差、高度误差;

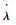
4) 惯性器件误差方程
实际工程应用中,通常将经过标定补偿后的陀螺仪和加速度计的误差近似为随机常值和白噪声[19]。随机常值可由微分方程式(4)描述:
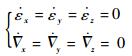 | (4) |
式中:εx、εy和εz分别为子IMU载体系x轴、y轴和z轴的陀螺仪常值漂移;
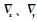
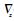
5) 安装误差角方程
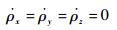 | (5) |
式中:ρx、ρy和ρz分别为子IMU载体系x轴、y轴和z轴安装误差角。
6) 弹性变形角方程
对于机体弹性变形角,在此以阵列天线SAR为例,分布式POS系统中子IMU安装在机翼两侧。飞行过程中,绕机体x轴、y轴和z轴均存在弹性变形角,其中绕y轴的弹性变形最大。在后续仿真中,也是基于此情况进行弹性变形角方程的参数设置。
弹性变形角用二阶Markov过程来描述[20]:
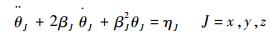 | (6) |
式中:θJ为弹性变形角;βJ=2.146/τJ ,τJ为二阶Markov过程相关时间;x、y和z分别代表b坐标系的3个轴;ηJ为零均值高斯白噪声,其方差QηJ满足:
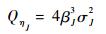 | (7) |
其中:Qη=[Qηx Qηy Qηz]T;σ2J为弹性变形角θJ的方差。
根据式(1)~式(6),建立如下系统状态方程:
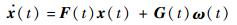 | (8) |
式中:F(t)和G(t)分别为状态转移矩阵和系统噪声驱动阵;ω(t)为系统噪声;x(t)为21维系统状态变量:
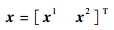 | (9) |
其中:x1为15维子惯导系统状态变量,包括平台失准角
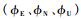
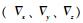
系统噪声ω(t)=[wεx wεy wεz w▽x w▽y w▽z ηx ηy ηz]T假定为零均值白噪声,其方差阵Q由陀螺仪常值漂移、加速度计常值偏置和弹性变形角二阶Markov过程参数Qη决定。
2.2 量测方程
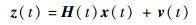 | (10) |
式中:
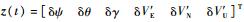
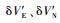
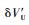
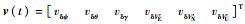


3 仿真验证 根据第1节设计的飞行轨迹方案,进行基于卡尔曼滤波的机载分布式POS系统实时传递对准仿真验证。
3.1 仿真条件 1) 轨迹与运动参数设置
设计以下5种运动方式进行仿真:①运动方式1:无机动+U型机动;②运动方式2:S型+U型机动;③运动方式3:O型+U型机动;④运动方式4:8字型+U型机动;⑤运动方式5:曲线爬升+U型机动。
5种运动方式的初始位置均为北纬40°、东经116°,运动方式1~运动方式4的初始高度均为7 000 m,运动方式5的初始高度为0 m;初始航向角(北偏东)、俯仰角、横滚角分别为40°、0°、0°;整个飞行过程中飞机速度为100 m/s。5种运动方式的轨迹参数如表 3所示。
表 3 5种运动方式的轨迹参数 Table 3 Trajectory parameters of five modes of motion
| 运动方式 | 时间/s | 运动状态 |
| 1 | 0~400 | 匀速直线 |
| 400~600 | 顺时针转180° | |
| 600~1 000 | 匀速直线 | |
| 2 | 0~100 | 匀速直线 |
| 100~800 | S型机动 | |
| 800~1 200 | 匀速直线 | |
| 1 200~1 400 | 顺时针转180° | |
| 1 400~1 800 | 匀速直线 | |
| 3 | 0~100 | 匀速直线 |
| 100~500 | O型机动 | |
| 500~900 | 匀速直线 | |
| 900~1 100 | 顺时针转180° | |
| 1 100~1 500 | 匀速直线 | |
| 4 | 0~100 | 匀速直线 |
| 100~1 000 | 8字型机动 | |
| 1 000~1 400 | 匀速直线 | |
| 1 400~1 600 | 顺时针转180° | |
| 1 600~2 000 | 匀速直线 | |
| 5 | 0~500 | 曲线爬升 |
| 500~900 | 匀速直线 | |
| 900~1 100 | 顺时针转180° | |
| 1 100~1 500 | 匀速直线 |
表选项
5种运动方式的飞行轨迹如图 2所示,其中AB直线段和CD直线段为测区成像段。
 |
| 图 2 5种运动方式的飞行轨迹 Fig. 2 Flight trajectory of five modes of motion |
| 图选项 |
2) 数据生成与滤波参数设置
首先设置一个预定的飞行轨迹,然后采用轨迹发生器模拟该轨迹下的位置、速度、姿态参数,以及陀螺仪和加速度计的理论输出。在轨迹发生器输出的速度、位置和姿态上叠加主POS的量测噪声作为主POS的真实输出;将陀螺仪和加速度计的理论输出通过安装误差角和弹性变形角进行转换,并在转换后的结果上叠加惯性器件的常值噪声和随机噪声作为子IMU陀螺仪和加速度计的真实输出。
主POS运动参数的精度根据商业产品POS/AV610的实时差分组合精度进行选取[20]。其中,航向角、俯仰角和横滚角精度分别为0.02°(1σ)、0.005°(1σ)和0.005°(1σ);速度精度为0.03 m/s(1σ);纬度、经度和高度精度分别为0.1 m(1σ)、0.1 m(1σ)和0.2 m(1σ)。
子IMU的陀螺仪常值、随机漂移均为0.1(°)/h,加速度计常值偏置为50 μg、随机偏置为50 μg。子IMU与主POS之间的杆臂在主POS的载体坐标系下表示为rbm=[5 m 0.1 m 0.1 m]T;子IMU的固定安装误差角均为0.5°;机翼弹性变形规律符合二阶Markov过程,二阶Markov过程的时间参数和弹性变形角均方差分别为τx=τz=2 s,τy=5 s和σx=σz=0.01°,σy=0.15°;子IMU捷联解算周期为0.01 s,滤波周期为1 s。
3.2 仿真结果与分析 1) 不同机动方式下子IMU运动参数估计精度结果与分析
图 3分别给出无机动、S型、O型、8字型和曲线爬升机动方式下得到的子IMU在成像段内姿态估计误差曲线和标准差(STD)统计,其中标准差统计结果为两段成像段AB和CD统计结果的平均值(本文运动参数的标准差均按此方法计算)。
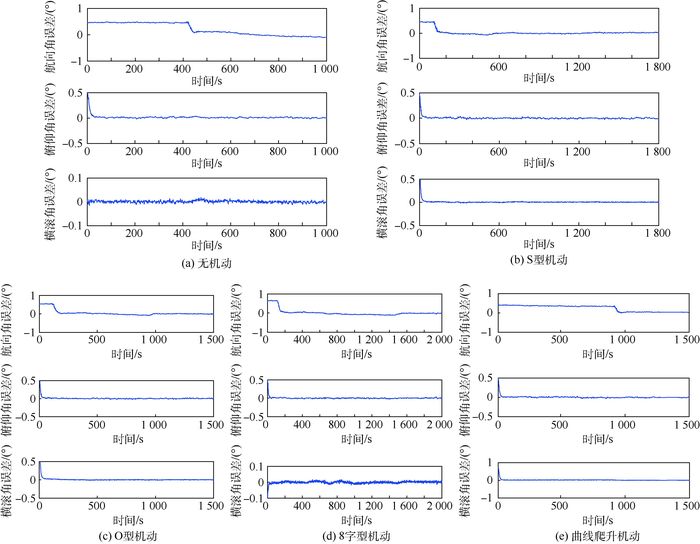 |
| 图 3 无机动、S型、O型、8字型和曲线爬升机动情况下姿态误差 Fig. 3 Attitude error of no maneuver、S type maneuver、O type maneuver、8 type maneuver and curve climb maneuver |
| 图选项 |
不同机动方式下得到的子IMU在成像段内姿态估计误差标准差统计如表 4所示。
表 4 不同机动方式下成像段姿态误差统计(STD) Table 4 Statistics of imaging segment attitude error under different maneuvering modes (STD)
| 机动方式 | 航向角估计误差/(°) | 俯仰角估计误差/(°) | 横滚角估计误差/(°) |
| 无机动 | 0.248 3 | 0.037 6 | 0.040 4 |
| S型 | 0.012 0 | 0.008 2 | 0.004 1 |
| O型 | 0.020 9 | 0.008 2 | 0.004 1 |
| 8字型 | 0.011 6 | 0.008 4 | 0.004 0 |
| 曲线爬升 | 0.152 1 | 0.009 2 | 0.003 8 |
表选项
从图 3和表 4可以看出,相比于无机动直接进入测区段飞行相比,其他4种机动方式均提高了航向角的估计精度,S型机动和8字型机动的航向角误差估计速度相近,其中8字型机动估计效果较好,4种机动方式俯仰角和横滚角的估计速度和估计误差差别不大。
2) 出机动区1后、进入测区前的飞行时长测试与分析
以8字型机动为例,完成该机动后、进入测区直线段之前,分别设置出机动区1后、进入测区前的匀速直线运动段飞行时长T1为0、100、200、300、400和500 s。重复进行10次仿真,子IMU姿态估计误差平均值统计如表 5所示。
表 5 不同T1下成像段姿态误差统计(STD) Table 5 Statistics of imaging segment attitude error with different T1 (STD)
| T1/s | 航向角估计误差/(°) | 俯仰角估计误差/(°) | 横滚角估计误差/(°) |
| 0 | 0.011 6 | 0.008 4 | 0.004 0 |
| 100 | 0.011 6 | 0.008 3 | 0.004 0 |
| 200 | 0.009 1 | 0.008 5 | 0.003 8 |
| 300 | 0.009 3 | 0.008 2 | 0.003 8 |
| 400 | 0.009 9 | 0.008 1 | 0.003 8 |
| 500 | 0.010 2 | 0.008 2 | 0. 0038 |
表选项
从表 5可以看出,载机完成8字型机动方式后,航向角的估计精度随飞行时间的增长呈现先提高后逐渐下降的趋势,而俯仰角和横滚角的估计误差变化微小。其中,当载机在进入测区前进行200 s的匀速飞行后,AB和CD成像段的航向角估计精度最高。
3) 测区直线段飞行时间测试与分析
在载机完成8字型机动方式后,进入测区前稳定时间为200 s的基础上,改变测区直线段飞行时长T2,分别取为100、200和400 s,重复进行10次仿真,并将结果进行平均来统计子IMU姿态估计的误差,统计结果如表 6所示。
表 6 不同T2下成像段姿态误差统计(STD) Table 6 Statistics of imaging segment attitude error with different T2 (STD)
| T2/s | 航向角估计误差/(°) | 俯仰角估计误差/(°) | 横滚角估计误差/(°) |
| 100 | 0.008 3 | 0.007 6 | 0.003 8 |
| 200 | 0.008 6 | 0.007 7 | 0.003 9 |
| 400 | 0.009 1 | 0.008 5 | 0.003 8 |
表选项
从表 6可以看出,姿态估计误差随着测区直线段飞行时间的增长而缓慢增大,特别是航向角的估计误差。因此,在实际飞行时,需要根据飞行速度和测区形状合理设计测区的飞行轨迹。
4) GPS基线长度对运动参数精度影响的测试与分析
针对实时成像飞行试验,GPS移动站接收机可实时接收基站的差分校正数据进行差分定位。改变GPS基线长度,将直接影响GPS的定位精度。而GPS测速是基于多普勒测速原理,所以其精度不受基线距离的影响。GPS的位置和速度是主系统进行惯性/卫星组合的量测信息,因此GPS基线长度的改变将直接影响主系统的定位精度。
目前,测量型GPS接收机定位精度为10 mm+1 ppm,但是该公式仅适用于10 ~15 km以内短基线范围[21]。当GPS基线更长时,定位精度迅速下降,当基线长度大于50 km时,一般只能达到分米级的精度[21]。本文结合多次飞行试验的经验,对GPS基线长度分别为20、40、60 km时的定位精度取值,如表 7所示。
表 7 不同GPS基线长度下GPS定位精度 Table 7 GPS positioning accuracy under different baseline lengths of GPS
| GPS基线长度/km | 水平定位精度/m | 高度定位精度/m |
| 20 | 0.1 | 0.2 |
| 40 | 0.5 | 1 |
| 60 | 1 | 2 |
表选项
主系统进行实时惯性/卫星组合导航后,定位精度要优于GPS的定位精度。随着GPS基线长度的增长,主系统的定位精度逐渐下降。在此假设3种GPS基线长度下,主系统的定位精度与GPS相同,测试子系统运动参数的变化。
3种GPS基线长度下成像段内子系统运动参数统计结果如表 8所示。
表 8 不同GPS基线长度下成像段子系统运动参数误差统计(STD) Table 8 Statistics of motion parameter error of imaging segment subsystem under different baseline lengths of GPS (STD)
| 运动参数 | GPS基线长度/km | ||
| 20 | 40 | 60 | |
| 航向角/(°) | 0.010 1 | 0.009 8 | 0.009 8 |
| 俯仰角/(°) | 0.008 0 | 0.008 0 | 0.008 1 |
| 横滚角/(°) | 0.003 7 | 0.003 8 | 0.003 8 |
| 东向速度/(m·s-1) | 0.013 7 | 0.016 2 | 0.018 1 |
| 北向速度/(m·s-1) | 0.016 2 | 0.017 1 | 0.018 9 |
| 天向速度/(m·s-1) | 0.019 4 | 0.019 4 | 0.020 1 |
| 纬度/m | 0.205 7 | 0.244 5 | 0.246 5 |
| 经度/m | 0.168 8 | 0.230 8 | 0.278 2 |
| 高度/m | 0.494 2 | 0.484 9 | 0. 519 2 |
| 基线长度/m | 0.218 0 | 0.597 2 | 1.275 7 |
表选项
从表 8可以看出,不同GPS基线长度对子系统测区成像段的姿态估计精度影响较小;速度和位置估计误差随GPS基线长度的增加而缓慢变大。这是由于主、子系统传递对准中采用“速度+姿态”的匹配方式,不同GPS基线长度下主系统的姿态和速度精度差异不大,因此在完成传递对准后,子系统的姿态和速度精度差异也不大。在子系统中采用速度积分来计算位置,因此不同GPS基线长度下子系统的位置精度也相近。但是增加GPS基线长度,主系统定位精度将下降,从而导致主、子系统之间的基线长度误差增大。
以上仿真结果是在对主、子系统之间的挠曲变形精确建模的基础上得到的,估计结果较为理想。而实际环境中,无法对挠曲变形进行精确建模,主系统的高精度姿态和速度就无法精确地传递给子系统,因此子系统的所有运动参数的精度均会明显下降。
综上可知:①与载机不做任何机动直接进入测区相比,进入测区前的4种机动方式均有效提高了测区直线段内子IMU的姿态精度,其中8字型机动由于机动方式更为充分达到的效果最好。②载机在完成有效机动进入测区段飞行前滤波需要一段时间达到相对稳定的状态。针对8字型机动,其稳定时间为200 s较为合适,随着飞行时间的增加,测区内子IMU的运动参数估计精度会逐渐下降。③测区直线段姿态估计误差随直线成像段飞行时间的增长而缓慢变大。④改变GPS基线长度对子系统的姿态、速度和位置精度影响较小,但主、子系统间的基线误差随GPS基线长度的增大而增大。
4 结 论 1) 本文针对机载对地观测载机长时间匀速直线飞行时分布式POS系统姿态误差随时间积累的问题,综合考虑实际飞行中的多种误差因素,设计4种飞行轨迹方案并进行仿真验证。
2) 在仿真验证中详细分析了不同滤波稳定时间、测区直线段飞行时间和GPS基线长度下运动参数的估计精度,为实际工程应用中合理规划飞行轨迹提供了有力的理论参考。
参考文献
| [1] | ZUFFADA C,LI Z,NGHIEM S V,et al.The rise of GNSS reflectometry for Earth remote sensing[C]//Proceedings of IEEE Geoscience and Remote Sensing Symposium.Piscataway,NJ:IEEE Press,2015. |
| [2] | 韦立登, 向茂生, 吴一戎. POS数据在机载干涉SAR运动补偿中的应用[J].遥感技术与应用, 2007, 22(2): 188–194. WEI L D, XIANG M S, WU Y R. The application of POS data in airborne interferometric SAR imaging processing[J].Remote Sensing Technology and Application, 2007, 22(2): 188–194.DOI:10.11873/j.issn.1004-0323.2007.2.188(in Chinese) |
| [3] | LI S S,ZHONG M Y,QIN J.The internal model control design of three-axis inertially stabilized platform for airborne remote sensing[C]//Proceedings of IEEE International Symposium on Instrumentation and Control Technology.Piscataway,NJ:IEEE Press,2012:1-9. |
| [4] | GONG X L, ZHANG R, FANG J C. Application of unscented R-T-S smoothing on INS/GPS integration system post processing for airborn earth observation[J].Measurement, 2013, 46(3): 1074–1083.DOI:10.1016/j.measurement.2012.11.028 |
| [5] | KIM T J.Motion measurement for high-accuracy real-time airborne SAR[C]//Proceedings of SPIE-The International Society for Optical Engineering.Bellingham,WA:SPIE,2004:36-44. |
| [6] | GROVES P D. Principles of GNSS,inertial,and multisensor integrated navigation systems[M].London: Artech House, 2013. |
| [7] | FANG J C, CHEN L, YAO J F. An accurate gravity compensation method for high-precision airborne POS[J].IEEE Transactions on Geoscience & Remote Sensing, 2014, 52(8): 4564–4573. |
| [8] | FANG J C, GONG X L. Predictive iterated Kalman filter for INS/GPS integration and its application to SAR motion compensation[J].IEEE Transactions on Instrumentation & Measurement, 2010, 59(4): 909–915. |
| [9] | CHATTARAJ S, MUKHERJEE A, CHAUDHURI S K. Transfer alignment problem:Algorithms and design issues[J].Gyroscopy and Navigation, 2013, 4(3): 130–146.DOI:10.1134/S2075108713030036 |
| [10] | 李四海, 王珏, 刘镇波, 等. 快速传递对准中机翼弹性变形估计方法比较[J].中国惯性技术学报, 2014, 22(1): 38–44. LI S H, WANG J, LIU Z B, et al. Comparison of wing distortion estimation methods in transfer alignment[J].Journal of Chinese Inertial Technology, 2014, 22(1): 38–44.(in Chinese) |
| [11] | GROVES P D. Optimising the transfer alignment of weapon INS[J].Journal of Pediatric Psychology, 2003, 56(2): 323–335. |
| [12] | 王新龙, 申亮亮, 马闪. 摇摆基座SINS快速精确传递对准方法[J].北京航空航天大学学报, 2009, 35(6): 728–731. WANG X L, SHEN L L, MA S. Transfer alignment of strapdown inertial navigation system on rolling bases[J].Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(6): 728–731.(in Chinese) |
| [13] | Technical reference manual IPAS10[EB/OL].[2016-07-01].http://www.leica.com. |
| [14] | 万德钧, 房建成. 惯性导航初始对准[M].南京: 东南大学出版社, 1998: 152-155. WAN D J, FANG J C. Initial alignment of inertial navigation[M].Nanjing: Publishing House of Southeast University, 1998: 152-155.(in Chinese) |
| [15] | 姜军, 杨亚非. SINS/GPS组合导航系统初始对准的可观测度分析[J].哈尔滨工业大学学报, 2007, 39(7): 1025–1027. JIANG J, YANG Y F. The analysis on the degree of observability to initial alignment of SINS/GPS integrated navigation system[J].Journal of Harbin Institute of Technology, 2007, 39(7): 1025–1027.(in Chinese) |
| [16] | 宫晓琳, 房建成. 一种机载遥感成像用分布式POS传递对准方法[J].北京航空航天大学学报, 2012, 38(4): 491–496. GONG X L, FANG J C. Method of transfer alignment of distributed POS for airborne remote imaging[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(4): 491–496.(in Chinese) |
| [17] | AKCA T,DEMIREKLER M.An adaptive unscented Kalman filter for tightly coupled INS/GPS integration[C]//IEEE Position Location & Navigation Symposium.Piscataway,NJ:IEEE Press,2012:389-395. |
| [18] | ZHOU N X,WANG S,DENG Z L.Comparison of three transfer alignment methods in marine missile SINS[C]//Proceeding of the 25th Chinese Control Conference.Piscataway,NJ:IEEE Press,2006:27-31. |
| [19] | 李端昌,钟麦英,郭丁飞.分布式POS传递对准中的误差检测与补偿[C]//第25届中国控制与决策会议论文集.沈阳:东北大学出版社,2013. LI D C,ZHONG M Y,GUO D F.Error detection and compensation in transfer alignment for the distributed POS[C]//Proceeding of the 25th Chinese Control and Decision Conference.Shenyang:Northeasten University Press,2013. |
| [20] | JONES D,ROBERTS C,TARRANT D,et al.Transfer alignment design and evaluation environment[C]//Proceeding of the IEEE Regional Conference on Aerospace Control Systems.Piscataway,NJ:IEEE Press,1993:753-757. |
| [21] | 吴北平.GPS网络RTK定位原理与数学模型研究[D].武汉:中国地质大学,2003. WU B P.Principle and mathematical model research for GPS network RTK[D].Wuhan:China University of Geosciences,2003. |
