战场复杂电磁环境对无线电引信的抗干扰能力提出了更高的要求，要求无线电引信必须能够对抗压制式与欺骗式干扰。研究调频引信的抗干扰性能对这类体制引信的发展都具有重要的意义。
目前国内外文献中，有很多关于无线电引信及其抗干扰性能的研究^[1-10]。文献[11]利用模糊函数来研究调频连续波引信的抗干扰性能，文献[12-13]提出了采用处理增益方法分析伪码体制以及伪码复合体制引信的抗干扰性能，文献[14-15]采用信干比(SJR)增益方法定量分析了超宽带引信和脉冲多普勒引信的抗干扰性能。信干比增益是基于干扰波形的表征参量，可以方便对比不同干扰样式信号的干扰效果，从而为抗干扰设计提供理论依据。目前大多数文献都是针对噪声干扰下引信的抗干扰性能研究，而对调幅干扰环境下调频多普勒引信抗干扰性能量化分析还未提及。并且较之其他样式干扰调频多普勒引信对调幅式干扰敏感，因此研究调幅干扰环境下调频多普勒引信抗干扰性能有很大意义。
本文以谐波定距三角波调频多普勒引信为例，以信干比增益作为衡量标准，详细推导了调频多普勒引信在正弦波调幅干扰、方波调幅干扰和三角波调幅干扰条件下接收机至检波端各级的时域信号表达式，得到了检波端输出信号与接收机输入信号之间的总信干比增益，建立了相应模型，并对其进行了仿真验证。定量研究了调频多普勒引信抗3种干扰的性能，获取了不同干扰下调频多普勒引信处理增益的量化表达式，仿真并对比分析了调频多普勒引信抗调幅干扰的性能。
1 调频多普勒引信时域分析 调频多普勒引信的工作原理如图 1所示。首先，载波振荡器产生三角波调频信号，经功率放大器放大后，由天线发射出去。发射信号碰到探测目标之后被反射，形成回波信号。回波信号经收发共用天线接收后，与本振线性调频信号经混频、放大，并经前置低通滤波器后，输出中频信号。中频信号被送入带通滤波器，得到的信号与m次谐波进行二次混频，并经多普勒滤波器后，输出检波信号(即多普勒信号)。此多普勒信号被送入信号处理电路，最后根据门限判决产生启动信号来引爆战斗部。

图 1 调频多普勒引信原理框图 Fig. 1 Principle diagram of FM Doppler fuze

图选项

没有干扰的情况下，三角波调频多普勒引信目标回波信号可表示为

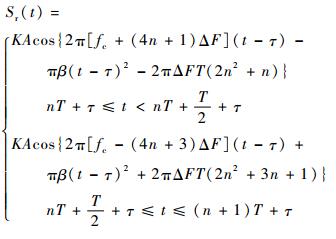(1)

式中：τ=2(R₀-v_rt)/c为动态延迟, R₀为初始弹目距离, v_r为弹与目标的径向速度, c为光速；K为信号从天线发射到接收过程中的衰减系数，它与探测目标的反射能力、方位和弹目距离有关；A为发射信号的振幅；f_c为载波频率；ΔF为调制频偏；T为三角波调制周期；β=4ΔF/T为调频率；n为周期数。
由其功率谱密度可知，回波信号S_r(t)的平均功率(即输入功率)为

(2)

接收到的回波信号S_r(t)经过前置带通滤波器后，与发射信号混频，再送入前置低通滤波器，得到中频信号S_i(t)。令t_n=t-nT，则S_i(t)可表示为

(3)

式中：A_B1和A_L1分别为前置带通滤波器和前置低通滤波器的增益。因为τ?t，可以忽略间隔为τ的两段，中频信号可以近似为调制周期为T的周期信号。这样，中频信号S_i(t)可以表示成调制频率f_m的傅里叶级数的形式，有

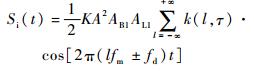(4)

(5)

式中：f_m=1/T为调制频率；f_d=2f_cv_r/c为多普勒频率；k(l, τ)为中频信号的傅里叶系数。
带通滤波后的中频信号与谐波发生器产生的m次谐波cos(2πmf_mt)进行二次混频，并送入多普勒滤波器，输出m次谐波的多普勒信号S_d(t)为

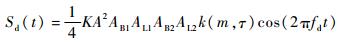(6)

式中：A_B2和A_L2分别为带通滤波器和多普勒滤波器的增益。
由式(6) 可知，接收机输出的多普勒信号S_d(t)的平均功率(即回波信号的输出功率)为

(7)

式中：为m次谐波系数k(m, τ)的关于参数τ的均方根值的平方。
2 抗调幅干扰理论分析 将三角波调频发射信号S_t(t)表示成傅里叶级数的形式，可表示为

(8)

(9)

式中：l为谐波次数；a_l为发射信号的傅里叶系数；μ=ΔF/f_m为调频指数；a=(μ-l)/(2μ)^0.5；b=(μ+l)/(2μ)^0.5；C(a)、C(b)、S(a)、S(b)表示菲涅尔积分。
调幅类干扰信号载频应与调频多普勒引信发射信号载频近似一致，且干扰信号调幅频率应尽可能地模拟调频多普勒引信系统的多普勒频率，这样才能对引信造成尽可能大的干扰。本文分析的调幅类干扰信号均基于上述原则。
2.1 正弦波调幅干扰下信干比增益定量推导 正弦波调幅干扰环境下引信接收机接收到的干扰信号J_r^sin(t)为

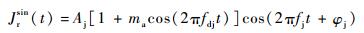(10)

式中：A_j为干扰信号的振幅；m_a为调幅指数；f_dj为调制信号的频率；f_j为载波频率；φ_j为载波的初始相位。
由式(10) 可知，干扰信号J_r^sin(t)的输入功率为

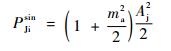(11)

干扰信号J_r^sin(t)经过前置带通滤波器后，与发射信号混频，再送入前置低通滤波器，可得到中频信号J_i^sin(t)。由于f_c加f_j和频项被前置低通滤波器滤除，则中频输出信号可表示为

(12)

式中：为发射信号通过前置低通滤波器通带内的所有谐波。
中频信号J_i^sin(t)被送入中心频率为mf_m的带通滤波器。提取出主要频率成分mf_m，则输出信号J_m^sin(t)可表示为

(13)

谐波信号J_m^sin(t)与谐波发生器产生的m次谐波cos(2πmf_mt)进行二次混频，并送入多普勒滤波器。经多普勒滤波后获得多普勒通带内的输出信号J_d^sin(t)：

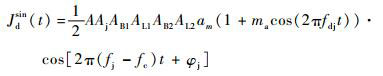(14)

由式(14) 可知，接收机输出的检波信号J_d^sin(t)的平均功率(即干扰信号的输出功率)为

(15)

因此，正弦波调幅干扰环境下，接收机的总信干比增益为

(16)

式中：SJR_I为输入信干比；SJR_O为输出信干比。
2.2 方波调幅干扰下信干比增益定量推导 方波调幅干扰环境下，引信接收机接收到的干扰信号J_r^squ(t)为

(17)

式中：a_nrj^squ为方波调制信号的傅里叶系数；n_r为谐波次数。
由式(17) 可知，干扰信号J_r^squ(t)的输入功率为

(18)

同理，干扰信号J_r^squ(t)经过前置带通滤波器后，与发射信号混频，再送入前置低通滤波器，可得到中频信号J_i^squ(t)，其表示为

(19)

式中：为干扰信号通过前置低通滤波器通带内的所有谐波。
中频信号J_i^squ(t)被送入中心频率为mf_m带通滤波器，因为f_m?f_dj，带通滤波器通带范围内的交叉项频率成分可忽略不计，故输出信号J_m^squ(t)可表示为

(20)

式中：为带通滤波器通带内的所有谐波。
谐波信号J_m^squ(t)与谐波发生器产生的m次谐波cos(2πmf_mt)进行二次混频，并送入多普勒滤波器，输出m次谐波的多普勒信号J_d^squ(t)为

(21)

式中：为多普勒滤波器通带内的谐波。
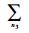
由式(21) 可知，接收机输出的检波信号J_d^squ(t)的平均功率(即干扰信号的输出功率)为

(22)

因此，方波调幅干扰环境下，接收机的总信干比增益为

(23)

2.3 三角波调幅干扰下信干比增益定量推导 三角波调幅干扰环境下，引信接收机接收到的干扰信号J_r^tri(t)为

(24)

式中：a_nrj^tri为三角波调制信号的傅里叶系数。由式(24) 可知，干扰信号J_r^tri(t)的输入功率为

(25)

同理，干扰信号J_r^tri(t)经过前置带通滤波器后，与发射信号混频，再送入前置低通滤波器，可得到中频信号J_i^tri(t)，其表示为

(26)

中频信号J_i^tri(t)被送入中心频率为mf_m带通滤波器，同样忽略带通滤波器通带范围内的交叉项频率成分，输出信号J_m^tri(t)可表示为

(27)

谐波信号J_m^tri(t)与谐波发生器产生的m次谐波cos(2πmf_mt)进行二次混频，并送入多普勒滤波器，输出m次谐波的多普勒信号J_d^tri(t)为

(28)

由式(28) 可知，接收机输出的检波信号J_d^tri(t)的平均功率(即干扰信号的输出功率)为

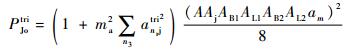(29)

因此，三角波调幅干扰环境下，接收机的总信干比增益为

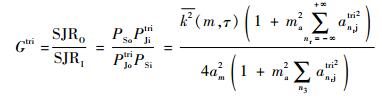(30)

2.4 抗调幅干扰结果分析 根据上述正弦波调幅干扰、方波调幅干扰和三角波调幅干扰下调频多普勒引信信干比增益的定量推导结果，分别得出这3种干扰环境下的输入信干比SJR_I、输出信干比SJR_O和总信干比增益G，如表 1所示。
表 1 调幅干扰下调频多普勒引信信干比增益理论分析结果 Table 1 Theoretical analysis results of SJR gain of FM Doppler fuze under AM jamming

干扰信号样式	SJRI	SJRO	G
正弦波调幅
方波调幅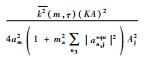
三角波调幅

表选项






从表 1可以看出，对比其总信干比增益表达式，调幅指数m_a的取值范围为(0, 1]，而以及值均介于0到1之间，所以对总信干比增益起决定性影响，因此可以得出调频多普勒引信抗正弦波调幅、三角波调幅以及方波调幅干扰的能力相当。经计算，调幅指数m_a在(0, 1]之间取值对总信干比增益影响较小。调频多普勒引信系统抗调幅干扰的总信干比增益G与调频多普勒引信的参数(调制频率f_m和调制频偏ΔF)和系统滤波器带宽有关。
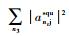
3 仿真与讨论 依据调频多普勒引信的工作原理，基于MATLAB构建了调频多普勒引信仿真模型。假设引信和目标在相距30 m的位置以500 m/s的相对速度互相接近。该调频多普勒引信的工作频率为3 GHz，最大频偏为15 MHz，其发射信号的振幅为1 V，初始相位为0，调制频率为150 kHz，多普勒频率为10 kHz，衰减系数为0.5。本文的3种调幅干扰采用相同的仿真参数，其中以接收机接收到的干扰信号功率为参考。理想情况下，干扰信号载波频率应与引信载波频率相同，此时干扰效果最佳。而在实际干扰中，由于干扰机精度等因素的影响，干扰机发射的干扰信号载波频率与引信载波频率可能会有微弱偏差，但干扰效果和在理想情况下有着相同的规律，为了更好地模拟真实干扰情况，在仿真中设置干扰信号的载波频率比引信载波频率大1 kHz，初始相位为0，调制频率为10 kHz，输入功率为0.5 W，调幅指数为1。本仿真系统采用30 GHz的采样频率，各级滤波器增益默认为1，选取的谐波次数为2次。图 2给出了正弦波调幅干扰模型图。

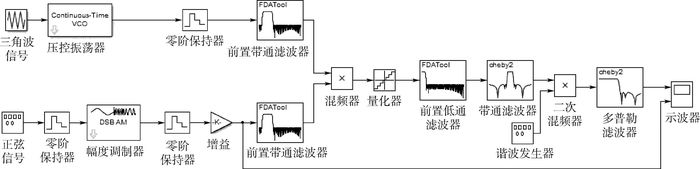图 2 正弦波调幅干扰模型 Fig. 2 Model of sine wave AM jamming

图选项

表 2给出了信干比增益的仿真结果与理论计算结果比对情况。根据仿真结果以及理论计算结果，调频多普勒引信在调幅信号干扰下总信干比增益在10 dB量级，因此调频多普勒引信具有一定的抗调幅干扰性能。对比3种干扰信号样式下总信干比增益结果，它们的总信干比增益值相差无几，因此针对各类调制样式的调幅干扰信号，调频多普勒引信系统的抗干扰能力相当。表 3给出在各类干扰波形样式下对某型引信两发样品(1^#和2^#)的干扰效果，结果表明不同调幅干扰样式下，使引信启动的最小干扰功率相当，验证了理论计算以及仿真结果。实际测试中调幅指数m_a从50%变化到100%，使引信启动的最小干扰功率保持一致，与理论分析中调幅指数对调频多普勒引信系统总信干比增益影响较小的结论相吻合。其中两发引信最小干扰功率的不同，在于两发引信的接收灵敏度个体差异。
表 2 调频多普勒引信抗调幅干扰仿真结果 Table 2 Simulation results of anti-AM jamming for FM Doppler fuze

干扰 信号样式	输入功率 仿真值/W	输出功率 仿真值/(10-4W)	总信干比 增益仿真值/dB	总信干比 增益理论值/dB	总信干比 增益表达式
正弦波调幅	0.501 2	5.349 5	9.797 3	8.104 1
方波调幅	0.499 0	3.677 3	11.406 1	9.696 5
三角波调幅	0.500 0	4.571 2	10.469 8	8.179 0

表选项






表 3 实验中各类干扰波形样式下使引信启动最小干扰功率 Table 3 Minimum experimental jamming power of fuze actuation under different jamming waves

干扰波形 样式	干扰信号 调幅指数/%	使1#引信启动最小 干扰功率/dBm	使2#引信启动最小 干扰功率/dBm
正弦波 调幅扫频	50 100	-15 -15	-17 -17
方波 调幅扫频	50 100	-15 -15	-23 -23
三角波 调幅扫频	50 100	-14 -14	-18 -18
锯齿波 调幅扫频	50 100	-14 -14	-16 -16

表选项






图 3(a)和图 3(b)分别给出了在相同干扰功率下，调频多普勒引信总信干比增益G与带通滤波器带宽F_b(中心频率为谐波频率)和多普勒滤波器带宽F_d的关系图。从中可以看出带通滤波器带宽在满足系统要求的范围内变化时对总信干比增益基本无影响，因为带通滤波器保留了通带内的特定次谐波，抑制了其他次谐波的能量，同时抑制了附着在其他次谐波上的干扰信号。由于干扰信号调幅频率与调频多普勒引信的多普勒频率相近，带通滤波器对附着在其通带内特定次谐波上的干扰信号抑制能力较弱，它会和真实信号一同通过带通滤波器进入调频多普勒引信系统的下一级。而当信号进入多普勒滤波器模块时，多普勒滤波器带宽越小，或值越小，总信干比增益越大。因此多普勒滤波器可以对干扰信号起到有效的抑制，在满足引信多普勒带宽的条件下，多普勒滤波器带宽越小，对干扰信号的抑制效果越好。所以在基于谐波定距原理的调频多普勒引信系统中，带通滤波器和多普勒滤波器共同对干扰信号起抑制作用，带通滤波器抑制了附着在其通带外谐波信号上的干扰信号，而多普勒滤波器抑制了带通滤波器通带内的干扰信号。

图 3 调频多普勒引信总信干比增益与带通滤波器带宽和多普勒滤波器带宽的关系 Fig. 3 Relationship between total SJR gain of FM Doppler fuze and bandpass filter bandwidth as well as Doppler filter bandwidth

图选项

仿真值与理论值存在一定误差，其主要来源为以下2个方面：① 仿真时高阶数字滤波器带来的延迟；② 理论推导时忽略的频率交叉项功率谱成分以及仿真系统中的噪声功率。
4 结论 1) 以信干比增益作为表征参量，定量研究了谐波定距三角波调频多普勒引信抗正弦波调幅、方波调幅和三角波调幅干扰的性能，根据对3种调幅式干扰下调频多普勒引信的总信干比增益分析，调频多普勒引信在调幅干扰下总信干比增益在10 dB量级，具有一定的抗调幅干扰性能。
2) 在相同的干扰功率下，调频多普勒引信系统抗各种调幅类干扰信号能力相当，对调幅干扰调制波形样式不敏感。调幅指数对调频多普勒引信系统的总信干比增益也基本无影响。
3) 基于谐波定距的调频多普勒引信系统，对干扰信号起主要抑制作用的是带通滤波器模块和多普勒滤波器模块。带通滤波器抑制了附着在其通带外谐波上的干扰信号，而对附着在其通带内特定次谐波上的干扰信号抑制能力较弱，多普勒滤波器则对其有一定抑制作用。
4) 在带通滤波器带宽一定的条件下，多普勒滤波器带宽对调频多普勒引信系统的总信干比增益有一定影响。带宽越小，总信干比增益越大。
5) 建立相应的仿真模型对其进行仿真，并用某型引信两发样品进行硬件实验。仿真、实验结果与理论分析相符，对未来调频多普勒引信抗调幅干扰研究有指导性意义。

参考文献

[1]	BROWN L. The proximity fuze[J].IEEE Aerospace and Electronic Systems Magazine, 1993, 8(7): 3–10.DOI:10.1109/62.223933
[2]	WILLIS C M.Method and apparatus for controlling a biphase modulation to improve autocorrelation in pseudorandom noise coded systems:US 5646627[P].1997-07-08.
[3]	PAN X, CUI Z Z. Full digital smart fuze on air target[J].Journal of Beijing Institute of Technology, 2010, 19(4): 386–389.
[4]	涂友超, 赵惠昌, 周新刚. 伪码体制引信抗瞄准式噪声调幅干扰性能研究[J].南京理工大学学报(自然科学版), 2008, 32(3): 350–355. TU Y C, ZHAO H C, ZHOU X G. Performance of anti-noise AM spot jamming of pseudo-random code fuzes[J].Journal of Nanjing University of Science and Technology (Natural Science), 2008, 32(3): 350–355.(in Chinese)
[5]	周新刚, 赵惠昌, 涂友超. 脉冲多普勒引信抗干扰性能评判方法和仿真[J].系统仿真学报, 2011, 23(1): 207–211. ZHOU X G, ZHAO H C, TU Y C. ECCM evaluation and simulation of pulse Doppler fuze[J].Journal of System Simulation, 2011, 23(1): 207–211.(in Chinese)
[6]	涂友超, 赵惠昌, 邓建平. 伪码调相正弦调频复合引信抗瞄准式噪声调幅干扰性能研究[J].探测与控制学报, 2008, 30(1): 29–33. TU Y C, ZHAO H C, DENG J P. Performance research on anti-noise AM spot jamming of PRBC-SFM combined fuze[J].Journal of Detection & Control, 2008, 30(1): 29–33.(in Chinese)
[7]	熊刚, 杨小牛, 赵惠昌. 伪码调相与正弦调频复合引信抗噪性能分析[J].现代雷达, 2007, 29(12): 12–17. XIONG G, YANG X N, ZHAO H C. Performance analysis of anti-noise of pseudo-random PM and sine frequency modulation combined fuze[J].Modern Radar, 2007, 29(12): 12–17.DOI:10.3969/j.issn.1004-7859.2007.12.004(in Chinese)
[8]	涂友超, 赵惠昌, 周新刚. 伪码调相与正弦调频复合引信抗噪声调频干扰性能研究[J].中国工程科学, 2009, 11(9): 68–73. TU Y C, ZHAO H C, ZHOU X G. Performance research on anti-noise FM jamming of pseudo-random code phase modulation and sine FM combined fuze[J].Engineering Sciences, 2009, 11(9): 68–73.(in Chinese)
[9]	HONG S, CHOI S, SHIN D, et al. Development of tracking technique against FMCW proximity fuze[J].Journal of the Korea Institute of Military Science and Technology, 2010, 13(5): 910–916.
[10]	ZHOU X G, ZHAO H C, XU Y Y. Theory and method for evaluation of anti-jamming capability of phase modulated by pseudorandom code combined with pulse Doppler fuze[J].Journal of Nanjing University of Science and Technology, 2010, 34(2): 176–181.
[11]	赵慧昌, 周新刚. 基于模糊函数切割法的线性调频连续波引信抗干扰性能测度[J].兵工学报, 2009, 30(12): 1591–1595. ZHAO H C, ZHOU X G. Anti-jamming performance evaluation of linear frequency-modulated continuous wave fuze based on ambiguity function incision[J].Acta Armamentarii, 2009, 30(12): 1591–1595.DOI:10.3321/j.issn:1000-1093.2009.12.005(in Chinese)
[12]	周新刚, 赵惠昌, 涂友超, 等. 基于多普勒效应的伪码调相及其与PAM复合引信的抗噪声性能分析[J].电子与信息学报, 2008, 30(8): 1874–1877. ZHOU X G, ZHAO H C, TU Y C, et al. Performance analysis concerning anti-noise for pseudo-random code phase modulation and pulse amplitude modulation combined fuze based on Doppler effect[J].Journal of Electronics & Information Technology, 2008, 30(8): 1874–1877.(in Chinese)
[13]	刘己斌, 赵惠昌, 陆建伟. 几种伪码体制引信的抗噪声性能分析[J].兵工学报, 2005, 26(1): 20–24. LIU J B, ZHAO H C, LU J W. Performance analysis concerning anti-noise for several pseudo-random code fuzes[J].Acta Armamentarii, 2005, 26(1): 20–24.(in Chinese)
[14]	闫岩, 崔占忠. 超宽带无线电引信抗干扰性能研究[J].兵工学报, 2010, 31(1): 13–17. YAN Y, CUI Z Z. Anti-jamming performance of ultra wideband radio fuze[J].Acta Armamentarii, 2010, 31(1): 13–17.(in Chinese)
[15]	李泽, 栗萍, 郝新红, 等. 脉冲多普勒引信抗有源噪声干扰性能研究[J].兵工学报, 2015, 36(6): 1001–1008. LI Z, LI P, HAO X H, et al. Anti-active noise jamming performance of pulse Doppler fuze[J].Acta Armamentarii, 2015, 36(6): 1001–1008.(in Chinese)