并网同步是新能源发电系统通过换流器允许接入电网的基本条件之一。同步即保证换流器输出电压与电网电压频率相同、相角相同和幅值相同。锁相环(Phase-Locked Loop，PLL)被广泛应用于并网同步方案中^[1-2]。
理想的PLL应该在电网电压扰动的情况下仍然能够准确和快速地跟踪到电网基波相位信号。三相电网与单相电网不同之处在于：三相电网存在电压不平衡情况，本质原因为存在负序扰动^[3-4]。因此，如何消除负序干扰、提高对电网正序分量的跟踪能力成为当前研究的热点。开环PLL常用过零检测原理，具有方法简单、实现容易特点，但是该方法需要计算反三角函数获得相位角，响应延迟长，且对谐波和负序分量干扰敏感，畸变电压下无法准确锁相^[5]。闭环PLL主要采用基于同步旋转坐标系的PLL实现同步跟踪。如文献[6]中提出基于双同步旋转坐标系的锁相环(Double Synchronous Rotating Frame-PLL, DSRF-PLL)方法，通过坐标运算实现dq轴坐标解耦，可以准确地从畸变电压中分离出正负序分量，但由于解耦过程增加了坐标运算量和滤波结构，系统的动态响应速度仍未提高；文献[7]提出双二阶广义积分器-锁频环(Double Second-Order Generalized Integrator based on Frequency-Locked Loop, DSOGI-FLL)，使得同步过程不再受电网畸变相位的干扰，FLL能够快速地估计到电网基波频率，提高了电网电压正负序分离的相位/频率跟踪能力。为了简化DSOGI分离电压正负序分量的结构，文献[8-9]提出一种降阶的广义积分器(ROR)，利用极性频率选择性特点，正负序分离结构输入、输出端的传递函数由实部二阶降为虚部一阶，简化的滤波环节明显提升了电压正负序分离速度，然而该方法利用PLL跟踪电网相位，对电网电压不平衡引起的相位跳变仍然很敏感，且一阶复数滤波环节无法消除电网存在的直流分量。
综合文献[7-9]各自的优势并考虑消除电网直流分量干扰，本文提出一种改进的一阶广义积分器锁频环(First-Order Generalized Integrator based on Frequency-Locked Loop，FOGI-FLL)方法。分析FOGI滤波环节的原理，在此基础上给出基于FOGI的FLL实现方法，改进之处在于在FOGI结构上引入积分环节，消除电网不平衡下的直流分量，并对本文所提方法的可行性进行了仿真验证。
1 电压不平衡状态对换流器的影响 三相电压源型逆变器的并网结构如图 1所示^[10]。图中：V_dc为直流母线电压；S_a、S_b和S_c分别为逆变器三相桥臂开关符号；u_a~u_c、i_a~i_c分别为逆变器端口三相输出电压和电流；R和L分别为滤波电阻和电感；U_c和U_f分别为逆变器端口电压和电网电压。并网结构的前级DC/DC部分为Boost升压电路，主要为换流器提供最大功率点；后级DC/AC部分为三相全桥换流电路，通过正弦PWM调制将前级直流部分转换成交流送入电网；换流器输出接LC滤波器，消除入网电流的谐波分量；电网用三相理想电压源和电网阻抗(电感和电阻串联组成)等效代替。

图 1 PWM调制的光伏逆变器并网主电路[10] Fig. 1 Main circuit of grid-connected photovoltaic inverter based on PWM modulation[10]

图选项

当电网电压出现不平衡波动时，三相三线制输电线路中会出现负序分量，计及直流分量，根据对称分量原理，三相电压的数学表达式为

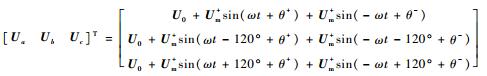(1)

式中：U_m⁺、ω和θ⁺分别为正序电压幅值、角频率和相位角；U_m^-、-ω和θ^-分别为负序电压幅值、角频率和相位角；U₀为直流分量。
式(1) 表明，负序分量与正序相比，大小不等、旋转角频率相反，而直流分量大小相等，相位相同。为了实现正负序分量的分离和独立控制，式(1) 进行克拉克变换，得αβ静止坐标系电压，如式(2) 所示：

(2)

由式(2) 可知，电网电压正负序分量的频率幅值相同，但方向相反，即极性相反，若采用谐振滤波方法提取正序分量，应满足谐振频率处幅值无穷大，相频为0，其他频率处幅值衰减为0。
2 电网同步方法 换流器主要通过PLL跟踪电网基频信号，但是在不平衡电网电压下，换流器中PLL的跟踪性能会降低甚至失效，导致并网输出电流出现严重畸变^[11]。为解决极端电网下的跟踪速度和精度问题，本文采用一种FOGI作为FLL的前置滤波环节，为其提供快速精确的电网电压基频正序信号。
2.1 一阶广义积分器 FOGI是通过引入复数因子将比例积分器(Proportional Integrator，PI)的传递函数改为2个极性不同的一阶形式，此方法无需利用过多的旋转坐标转换，能在电网电压不平衡下准确地分离出电压正负序分量，其传递函数如下：

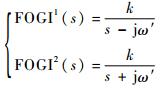(3)

式中：ω′为FOGI的谐振频率；k为增益系数，k值越小，滤波效果越好，但是系统的动态响应速度会变慢，理论上k取时滤波效果和响应速度最佳^[12]。
实现正负序基频分量分离的结构如图 2所示。图中：U_abc为电网输入电压；U_αβ⁺和U_αβ^-为输出基频分量。

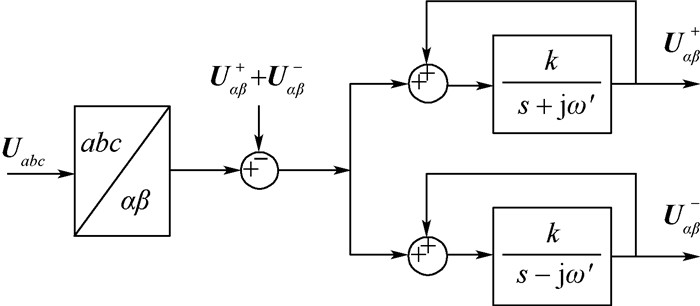图 2 正负序基频分量分离结构 Fig. 2 Separation structure of fundamental positive and negative sequence components

图选项

FOGI是正负序基频分量分离结构的核心模块，其实现结构如图 3所示。

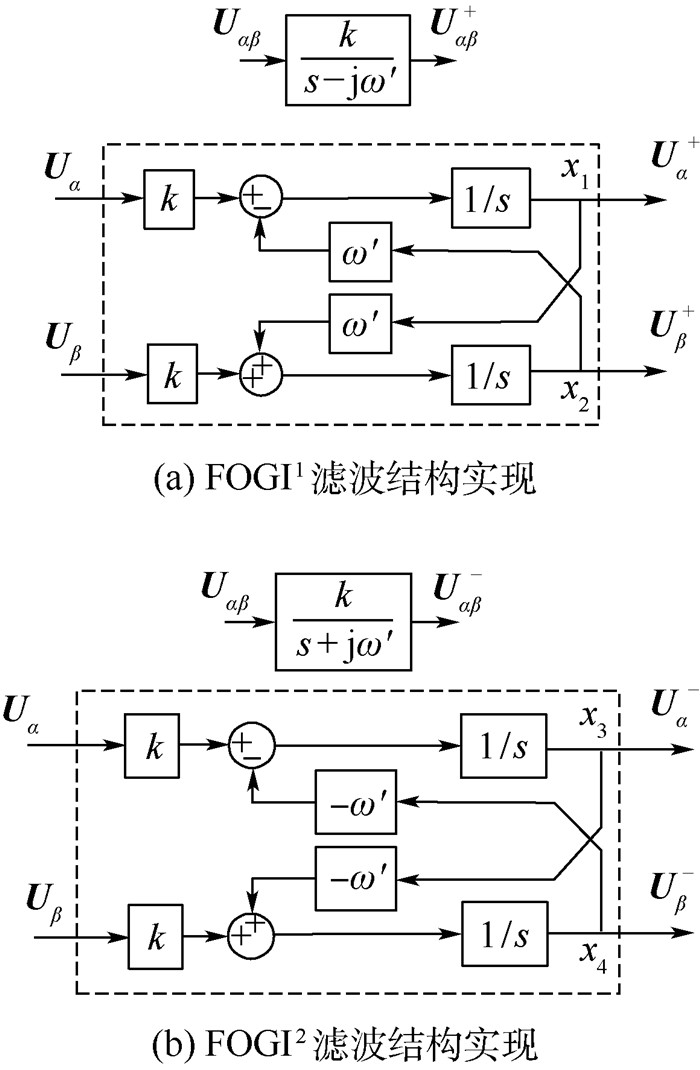图 3 正负极性FOGI滤波结构实现 Fig. 3 Structure of positive and negative pole FOGI filter

图选项

由图 3可知，FOGI中复数算子j通过α轴超前β轴90°的特性来实现，由于FOGI结构简单无三角函数和坐标运算，因此可以精确快速地分离出目标分量。由图 2可以得出，正负序基频分量输出传递函数为

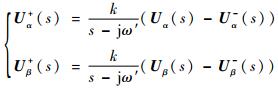(4)

FOGI既能对正负序分量直接进行分离，还增加了正负极性频率分离的功能。从图 4的幅频特性曲线可以看出，当设定的谐振频率为50 Hz时，只有+50 Hz的输入极性频率才可以无衰减地通过FOGI，而在-50 Hz输入极性频率被过滤掉，由于FOGI结构简单，对正负序分量和极性分量都可以进行分离，因此FOGI是逆变器并网暂态过程快速准确提取电网基波角频率的理想结构。

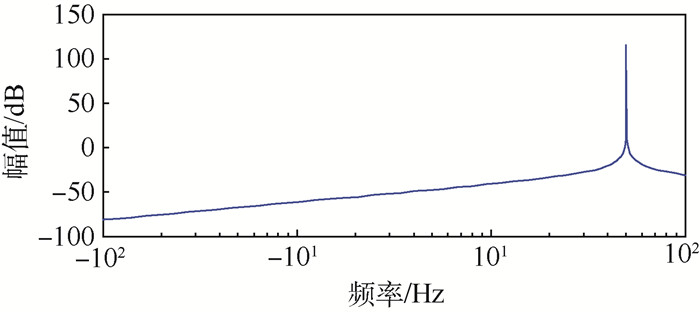图 4 FOGI分离+50 Hz幅频图 Fig. 4 Amplitude frequency diagram of separating +50 Hz based on FOGI

图选项

由图 4可知，FOGI在基波正序分量处增益频带很窄，即使电网频率在允许波动范围内，控制器也会作为频率突变情况进行动态调节。为了降低FOGI对允许运行频率的敏感度，解决办法是引入截止频率ω_c，增加FOGI控制器增益频带带宽。引入截止频率ω_c后的传递函数为

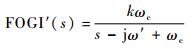(5)

从图 5可以看出，ω_c=10 rad/s的增益频带明显比ω_c=0的宽，FOGI结构考虑了一定范围的电网允许频率，因此该结构可以为FLL提供不含负序分量的基本角频率。

图 5 ωc为不同值时的Bode图 Fig. 5 Bode diagram of varing ωc

图选项

2.2 锁频环 FOGI是实现FLL结构的重要基础，FOGI的误差信号ε_v与其输入信号U_α之间的传递函数为

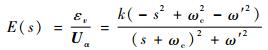(6)

根据式(6) 做出误差信号ε_v、输出正交信号U_β⁺对输入信号U_α的Bode图，如图 6所示。可知，输入相位ω在ω′附近出现了180°突变，当输入信号频率ω小于谐振频率ω′，误差信号ε_v和输出正交信号U_β⁺同相位，即为同相；当ω大于谐振频率ω′时，ε_v和U_β⁺相位相差180°，即为反相。为此引入变量偏差频率ε_f为ε_v和U_β⁺的乘积，当ω < ω′时，ε_v和输出正交信号U_β⁺同相，此时ε_f>0；当ω>ω′时，ε_v和U_β⁺反相，此时ε_f < 0；当ω=ω′时，谐振频率ω′增益为0，即ε_v=0，此时ε_f=0。FLL实现了对电网基波信号的实时跟踪与控制，由于反馈信息是角频率而非相位，故称为FLL。FLL积分器的增益取负增益系数-γ，目的是通过自动调节谐振频率ω′，抵偿掉误差信号ε_v，实现频率自适应跟踪。频率偏差经过负比例积分后与额定频率ω₀相加，最终获得电网基波频率ω′，FLL结构如图 7所示。

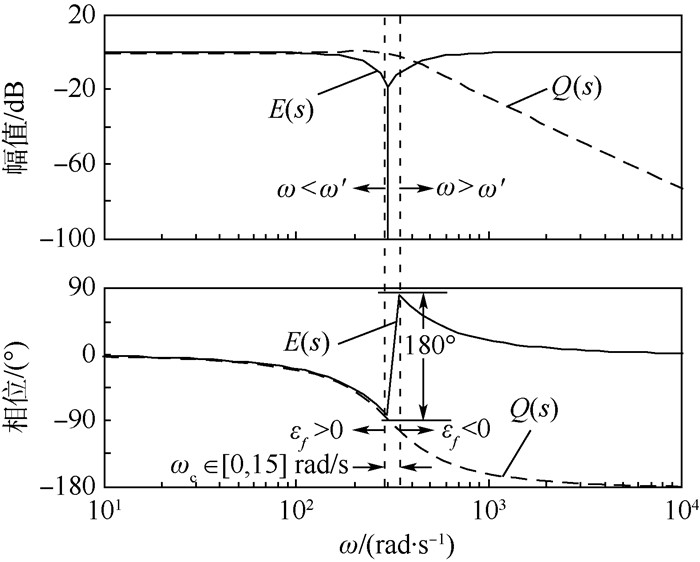图 6 E(s)和Q(s)的Bode图 Fig. 6 Bode diagram of E(s) and Q(s)

图选项

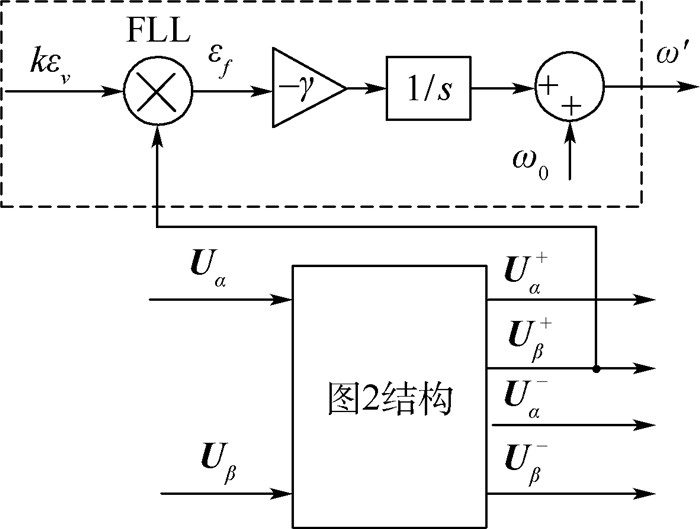图 7 FLL结构 Fig. 7 Configuration of FLL

图选项

3 FLL优化方法 换流器在换流期间会不可避免地引入直流分量，其危害在于引起FOGI正交信号出现偏差，进而影响FLL跟踪精度，因此有必要考虑消除换流过程中直流分量对锁频的干扰^[13]。由于FOGI本身的低通滤波特性不能直接消除直流分量^[14]，因此在此结构上引入积分补偿环节，其传递函数为

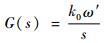(7)

式中：k₀为比例系数。通过对时间的积分，补偿环节能够可靠地消除直流分量。图 8和图 9分别为含直流分量抵偿的FOGI-FLL结构图和积分补偿环节阶跃响应比较图。

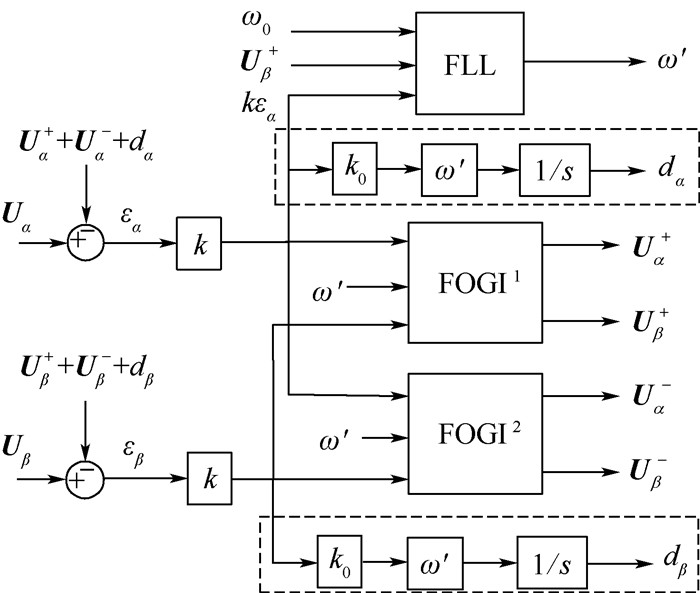图 8 含直流分量抵偿的FOGI-FLL结构 Fig. 8 FOGI-FLL structure with free DC component

图选项

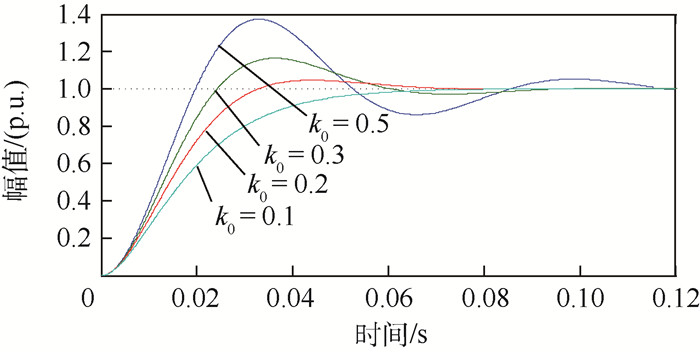图 9 积分补偿环节阶跃响应比较 Fig. 9 Comparison of step response of integral compensation

图选项

k₀的大小影响系统的稳定性和响应速度^[15]。根据劳斯判据，若k₀≥0，锁频可以维持稳定，但是k₀过大易引起较大的超调量，因此，k₀应有最佳值。根据图 9可以看出，k₀=0.5时的超调时间将超过0.12 s，0.1 s时响应速度缓慢，而k₀=0.3动态响应效果较好。
为简化传递函数分析，不计对幅频和相频特性影响较小的截止频率ω_c，引入直流分量消除环节后的系统的传递函数改写为

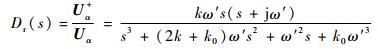(8)

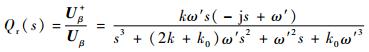(9)

(10)

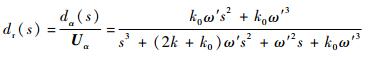(11)

由式(8)~式(11) 可知，当ω=ω′时，D_r(s)幅频值为1，相位角为0，D_r(jω)相位角为0，Q_r(jω)相位角为-90°，E_r(jω)和d_r(jω)幅频值为0。对于ω=0的直流输入分量，除d_r幅频值为1，其他皆为0，这表明积分补偿环节可以消除直流分量且不对基波正负序分离环节构成干扰。
4 仿真分析 为了验证本文方法对电网电压不平衡下的动态响应，进行了电网电压正负序分离仿真、相位跟踪仿真和频率自适应跟踪分析。换流器额定功率为15 kW，电网近似于无穷大系统，稳态时电网相电压为220 V，频率为50 Hz，电压不平衡度为0.7。为了便于参数的观察和比较，所有仿真参数进行标幺值(p.u.)处理。U_b和U_c两相电压由1.0 p.u.跌落至0.7 p.u.，不平衡运行时段为0.3~0.4 s。图 10为不平衡扰动量注入后的电网电压不平衡波动情况。

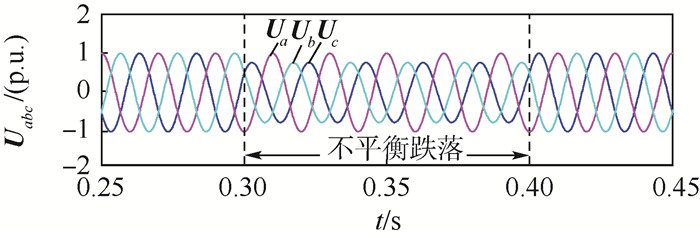图 10 两相电网电压跌落波形 Fig. 10 Waveforms of two-phase grid voltage fall

图选项

1) 正负序分离仿真
为了验证FOGI结构的正负序分量分离性能，本文首先将三相电压转换到αβ坐标系下，然后观察电压正负序分量输出情况。对比图 11(a)、(b)可以看出，由于没有进行负序分量分离，αβ相电压幅值不相等，电压不平衡问题未解决，而FOGI结构可以快速精确地分离出不平衡电压的正负序分量，且正负序电压的αβ轴分量相位一致，正负电压分离过程几乎不存在延时，满足动态响应要求。

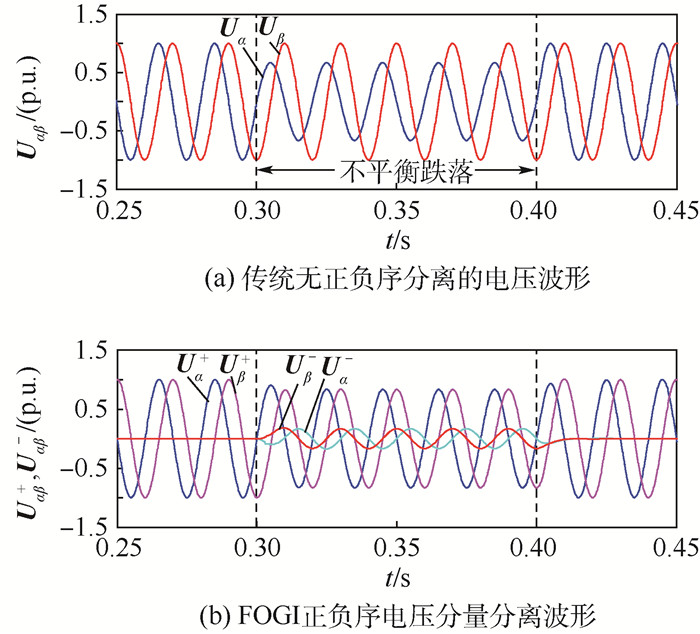图 11 正负序电压分量分离波形 Fig. 11 Separation waveforms of positive and negative sequence voltage component

图选项

2) 相位跟踪仿真
图 12比较了采用经典DSRF-PLL估计电网相位和FOGI-FLL估计电网相位情况。可以看出，二者都可以准确地估计到电网基波相位信息，而不受负序干扰，但是在检测速度上DSRF-PLL稍逊于FOGI-FLL，这是由于较二阶滤波系统，FOGI和FLL同时具有一阶频率自适应特性，相位响应缩短了20 ms。检测出相位波形近似直角三角形，表明分离出的正序电压分量正弦度高，且U_α⁺滞后U_β⁺ 90°，与理论分析相吻合。

图 12 相位检测波形 Fig. 12 Waveforms of phase detection

图选项

3) 频率自适应跟踪分析
图 13比较了传统DSRF-PLL和本文提出的FOGI-FLL频率估计情况。可以看出，采用传统DSRF-PLL方法估计的电网相位暂态响应时间长，且频率跳变不稳定，而FOGI-FLL频率估计时间缩短到20 ms，且频率波动小。对于实际的电网频率变化，该动态响应时间可以不计。

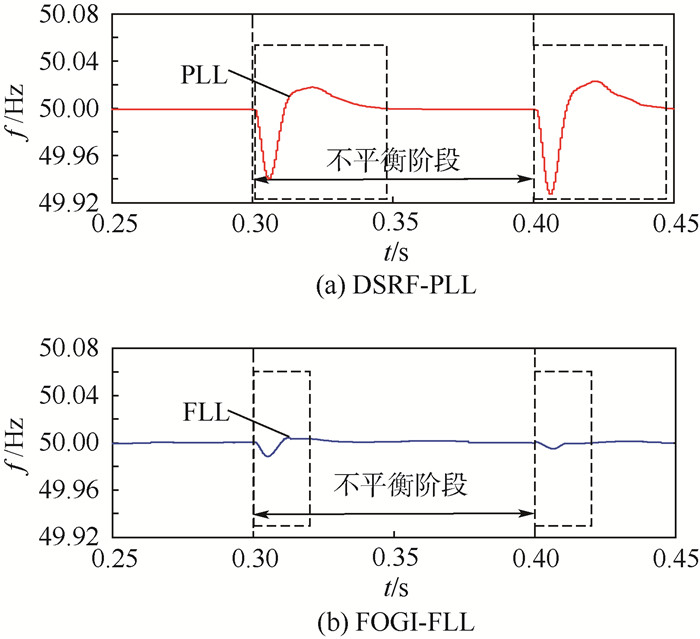图 13 频率检测波形 Fig. 13 Waveforms of frequency detection

图选项

4) 直流分量变化
为验证FOGI-FLL与直流分量之间的关系，在0.3~0.4 s时，设置电网单相电压不平衡，且电网注入直流电压分量为0.1 p.u.，输出结果如图 14所示。从图中虚线可以看出，在含有不平衡直流分量的电网电压中，经典的DSRF-PLL提取的U_αβ未能消除直流分量，且估计的频率中含有近似50 Hz的交流分量，电网同步跟踪效率不理想；本文的FOGI-FLL可以滤除直流分量，且电网估计频率也不含交流分量，在30 ms内恢复稳定，同步跟踪性能良好。本测试表明了换流器同步跟踪信号中FOGI-FLL消除直流分量的必要性和可行性，与理论分析情况相吻合。

图 14 输出的电压、角频率和相位检测波形 Fig. 14 Waveforms of voltage, angular frequency and phase detection

图选项

5 结论 本文在不平衡电网电压下建立了含不平衡分量和直流分量的换流器并网数学模型，提出了一种改进的FOGI-FLL频率自适应同步跟踪方法。
1) FOGI省掉坐标运算环节实现了正负极性频率分离，一阶滤波结构简单、动态响应快。
2) 利用FOGI输出正交信号和误差信号建立了FLL结构，由于频率比相位更稳定，所以FLL适用于变频场合。
3) 改进了FOGI-FLL结构，给出了消除直流分量的FLL优化结构，该模型依靠积分补偿环节增加了FOGI对直流分量的抗干扰能力，因此换流器抗电网各种扰动能力增强。
本文所提方法对提高并网换流器同步跟踪能力具有一定的参考价值。

参考文献

[1]	KARIMI G M, MOJIRI M, SAFAEE A, et al. A new phase-locked loop system for three-phase applications[J].IEEE Transactions on Power Electronics, 2013, 28(3): 1208–1218.DOI:10.1109/TPEL.2012.2207967
[2]	ESCOBAR G, PETTERSSON S, HO C N M.Phase-locked loop for grid synchronization under unbalanced operation and harmonic distortion[C]//IECON 2011-37th Annual Conference on IEEE Industrial Electronics Society.Piscataway, NJ:IEEE Press, 2011:675-680.
[3]	REYES M, RODRIGUEZ P, VAZQUEZ S, et al. Enhanced decoupled double synchronous reference frame current controller for unbalanced grid-voltage conditions[J].IEEE Transactions on Power Electronics, 2012, 27(9): 3934–3943.DOI:10.1109/TPEL.2012.2190147
[4]	黎金英, 艾欣, 邓玉辉. 微电网电压不平衡的分层补偿控制策略[J].哈尔滨工业大学学报, 2016, 48(3): 46–52. LI J Y, AI X, DENG Y H. Hierarchical control strategy for voltage unbalance compensation in micro-grid[J].Journal of Harbin Institute of Technology, 2016, 48(3): 46–52.DOI:10.11918/j.issn.0367-6234.2016.03.008(in Chinese)
[5]	丁稳房, 李志鹏, 余佳佳, 等. 基于光伏并网逆变器锁相环技术研究[J].湖北工业大学学报, 2015, 30(1): 5–7. DING W F, LI Z P, YU J J, et al. On the phase-locked loop technology based on photovoltaic grid inverters[J].Journal of Hebei University of Technology, 2015, 30(1): 5–7.(in Chinese)
[6]	RANI B I, ARAVIND C K, ILANGO G S, et al. A three phase PLL with a dynamic feed forward frequency estimator for synchronization of grid connected converters under wide frequency variations[J].International Journal of Electrical Power & Energy Systems, 2012, 41(1): 63–70.
[7]	RODRIGUEZ P, LUNA A, MUNOZ R S, et al. A stationary reference frame grid synchronization system for three-phase grid-connected power converters under adverse grid conditions[J].IEEE Transactions on Power Electronics, 2012, 27(1): 99–112.DOI:10.1109/TPEL.2011.2159242
[8]	赵新, 金新民, 周飞, 等. 采用降阶谐振调节器的并网逆变器锁频环技术[J].中国电机工程学报, 2013, 33(15): 38–44. ZHAO X, JIN X M, ZHOU F, et al. A frequency-locked loop technology of grid-connected inverters based on the reduced order resonant controller[J].Proceedings of the CSEE, 2013, 33(15): 38–44.(in Chinese)
[9]	GUO X, WU W, CHEN Z. Multiple-complex coefficient-filter-based phase-locked loop and synchronization technique for three-phase grid-interfaced converters in distributed utility networks[J].IEEE Transactions on Industrial Electronics, 2011, 58(4): 1194–1204.DOI:10.1109/TIE.2010.2041738
[10]	郭小强, 邬伟扬, 漆汉宏. 电网电压畸变不平衡情况下三相光伏并网逆变器控制策略[J].中国电机工程学报, 2013, 33(3): 22–28. GUO X Q, WU W Y, QI H H. Control strategies of three-phase PV grid-connected inverter under distorted and unbalanced voltage conditions[J].Proceedings of the CSEE, 2013, 33(3): 22–28.(in Chinese)
[11]	RODRIGUEZ P, LUNA A, MU?OZ-AGUILAR R S, et al. A stationary reference frame grid synchronization system for three-phase grid-connected power converters under adverse grid conditions[J].IEEE Transactions on Power Electronics, 2012, 27(1): 99–112.DOI:10.1109/TPEL.2011.2159242
[12]	BUSADA C A, JORGE S G, LEON A E, et al. Current controller based on reduced order generalized integrators for distributed generation systems[J].IEEE Transactions on Industrial Electronics, 2012, 59(7): 2898–2909.DOI:10.1109/TIE.2011.2167892
[13]	刘鸿鹏, 王卫, 吴辉. 光伏逆变器的调制方式分析与直流分量抑制[J].中国电机工程学报, 2010, 30(9): 27–32. LIU H P, WANG W, WU H. Modulation mode analysis and suppressing DC current of PV inverter[J].Proceedings of the CSEE, 2010, 30(9): 27–32.(in Chinese)
[14]	CIOBOTARU M, TEODORESCU R, AGELIDIS V G.Offset rejection for PLL based synchronization in grid-connected converters[C]//IEEE Applied Power Electronics Conference and Exposition.Piscataway, NJ:IEEE Press, 2008:1611-1617.
[15]	KARIMI G M, KHAJEHODDIN S A, JAIN P K, et al. Addressing DC component in PLL and notch filter algorithms[J].IEEE Transactions on Power Electronics, 2012, 27(1): 78–86.DOI:10.1109/TPEL.2011.2158238