删除或更新信息，请邮件至freekaoyan#163.com(#换成@)

基于灰色理论的复杂系统多故障模糊诊断*

本站小编 Free考研考试/2021-12-25
近年来，随着航天、核电、军工等领域的飞速发展，大型复杂系统的应用也越发普遍，随之而来的系统安全可靠性问题引起了人们的广泛关注。作为保护生命财产安全的有效手段，故障诊断一直在上述领域肩负着重要使命，但解决复杂系统的故障诊断问题绝非易事，通常需要一套可靠并具系统性的解决方案[1]。故障诊断就是检测和隔离故障的过程，其通常以系统可测试性设计为基础，用测试的方法获得故障现象，进而确定故障原因并开展维修[2]。传统的故障诊断一般以单故障模型为基础，然而对于工作于特定环境的空间站、月球车、战机等系统，测试维修的不及时可造成多故障并存的情况，系统的复杂性也加剧了多故障并发的可能。因此有必要对复杂系统多故障诊断问题展开探索研究。
故障检测是故障诊断的基础，信息流模型、多信号模型等基于图论的系统可测性模型[3-7]为复杂系统的故障检测提供了有效方法。上述模型充分利用图论方法的内在简化特性，将故障与测试间的因果关系以图形的方式表示，并最终建立了故障-测试相关矩阵，用二值化测试结果序列实现了对故障现象的统一表述。基于上述方法，国内外****围绕复杂系统可测性分析设计、多故障诊断等问题进行了深入研究[4, 8-13]。其中，连可等[8]提出了一种基于有向图模型的模糊多故障诊断算法，该算法计算测试向量与故障特性向量的空间向量夹角，并以夹角大小作为判定故障发生的依据，算法的有效性在航天工程领域得到了初步验证。但该算法未考虑故障诊断分优先级的情形，不利于对重点关注故障的快速筛查；以空间向量夹角大小作为故障判定指标损失了各测试传感器间的关联信息，降低了诊断结论的精细度，并且无法支持对诊断指标权重调整。
本文在考虑故障测试传感器的故障检测率和故障虚警率条件下提出了一种多故障模糊诊断方法，通过建立故障-测试相关矩阵，生成有排序的测试报警概率矩阵，并利用灰色关联度衡量故障测试结果向量与故障特征向量的接近度，避开了故障先验概率获取的难题。实验结果表明，与文献[8]相比，本文方法的首选结论诊断正确率和故障覆盖率均可达100%，并且在诊断指标权重调整、诊断精细度、重点关注故障检出等方面表现更优。
1 相关矩阵与灰色关联模型 1.1 故障-测试相关矩阵 相关矩阵(又称相关性矩阵)是一种表述2组对象序列间多重因果关系的有效方法。通过建立故障与测试(又称观测)间的相关矩阵，可将“直接判定某个故障是否产生的问题”转化为“判定获得的测试结果向量是否符合某故障的特征向量问题”，实现了对系统多逻辑层次故障问题的统一诊断求解。可以证明，相关矩阵可作为信息流、多信号等图论模型进行故障诊断的内在依据[9]。下面给出相关矩阵的基本概念定义[14]。
定义1??相关性：是指某个对象与另一对象之间的因果关系。这种相关性是有指向性的，若由x可推出y，则称y与x相关；若x与y可以互推，则称二者是互相关的。
定义2??N阶相关：是指两对象间因果关系的紧密程度。例如由x可直接推出y，则称y与x 1阶相关。若由x可推出y，再由y可推出z，则称z与x为2阶相关，y与x、z与y为1阶相关。同理可推得两对象间的N阶相关关系。
定义3??相关矩阵：是反映各对象间全阶相关(即包含各阶相关)关系的布尔矩阵。若矩阵中某列对象与某行对象相关，则矩阵相应行列的元素取值为1，否则为0。
故障-测试相关矩阵DFT如式(1) 所示：
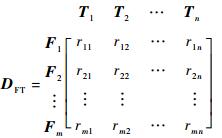(1)

式中：F表示故障; T表示测试; r表示故障与测试的相关关系。当故障Fi可被测试Tj检测到，则矩阵元素rij=1，否则rij=0。矩阵行向量Fi=[ri1, ri2, …, rin]T为故障特征向量，描述了第i个故障发生时系统中全部测试的输出表现。矩阵列向量Tj=[r1j, r2j, …, rmj]T描述了第j个测试可检出的全部故障，反映了其故障检测能力。
因故障特征可完全由测试向量定义，故障-测试相关矩阵又称之为依赖矩阵。在工程应用中，通过对系统进行可测性建模，建立故障-测试相关矩阵，可获得系统故障与测试间的完整依赖关系。
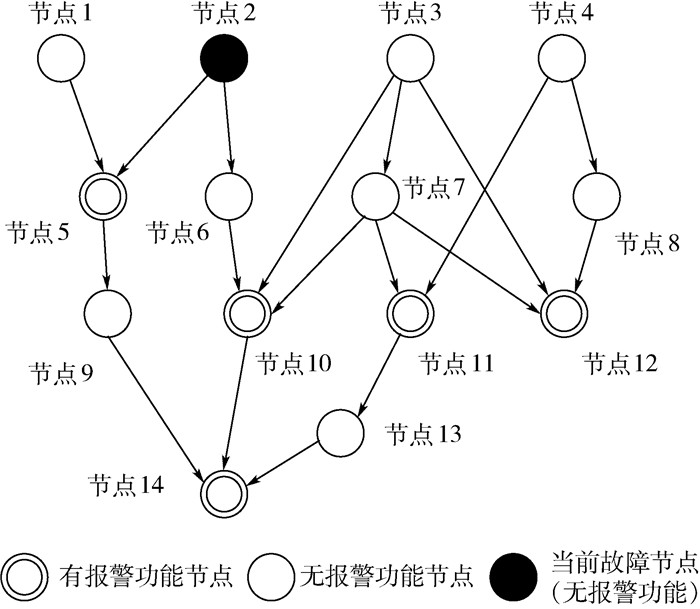
下面以一个用有向无环图描述的系统[15]示例说明DFT矩阵的建立方法。
图 1为某系统的有向信息流图[15]，图中以节点表示系统的各组成模块，以有向边表示节点间的故障传播方向。示例中节点5、10、11、12和14同时设置了测试报警功能，其既可对本节点的故障进行监测，也可通过特征参数判断实现对下级节点的故障报警，例如当图示的节点2故障时，节点5、10、14将产生报警。系统的上述故障报警功能分别体现了故障-测试的1阶相关及N(N>1) 阶相关特性。通过遍历系统所有节点，可建立故障-测试相关矩阵，如表 1所示。
图 1 示例系统有向信息流图 Fig. 1 Directed information flow for sample system
图选项




表 1 示例系统的DFT矩阵 Table 1 DFT matrix for sample system
故障节点 测试/报警节点号
1/5 2/10 3/11 4/12 5/14
1 1 0 0 0 1
2 1 1 0 0 1
3 0 1 1 1 1
4 0 0 1 1 1
5 1 0 0 0 1
6 0 1 0 0 1
7 0 1 1 1 1
8 0 0 0 1 0
9 0 0 0 0 1
10 0 1 0 0 1
11 0 0 1 0 1
12 0 0 0 1 0
13 0 0 0 0 1
14 0 0 0 0 1


表选项






1.2 灰色关联分析 灰色关联分析方法是灰色系统理论的一个重要分支，其由邓聚龙教授在文献[16]中提出，可面向样本数量贫乏或影响系统特征的因素间不独立的情况下进行数据关联分析。灰色关联分析的基本思想是根据序列曲线几何形状的相似程度来判断不同序列之间的联系是否紧密，具体实现思路是通过线性插值的方法将系统因素的离散行为观测值转化为分段连续的折线，进而根据折线的几何特征构造测度关联程度的模型。折线几何形状越接近，相应序列之间的关联度就越大，反之就越小[17]。
公理1??灰色关联公理。设X0=(x0(1), x0(2), …, x0(n))为系统特征行为序列，且Xi=(xi(1), xi(2), …, xi(n))(i=0，1, …, m)为相关因素序列。给定实数γ(x0(k), xi(k))，若实数满足条件
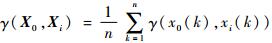
1) 规范性：0 < γ(X0, X1)≤1，γ(X0, X1)=1?(X0=Xi)。
2) 接近性：|x0(k)－xi(k)|越小，γ(x0(k), xi(k))越大。
则称上述条件1) 和2) 为灰色关联公理。
定理1??灰色关联度。设系统行为序列Xi=(xi(1), xi(2), …, xi(n))(i=1, 2, …, m)，对于ε∈(0, 1)，令

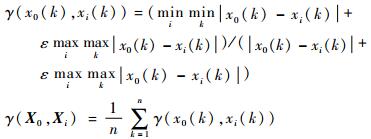则γ(X0, Xi)满足灰色关联公理，其中ε为分辨系数。γ(X0, Xi)称为X0与Xi的灰色关联度(又称邓氏灰色关联度[16])。
对于系统故障诊断而言，每个故障都可视为一个系统特征因素，且均可由测试空间中的一个序列表征，所以基于DFT矩阵的故障诊断问题在灰色关联公理的适用范围内。公理1的条件1) 表明系统中任何2个故障都不可能是严格无关的，不同故障的测试结果间具有相关性。公理1的条件2) 给出了相关性度量的依据。定理1则具体给出了符合公理1框架约束的一种有效形式。
为从测试空间推理故障，可将实际得到的测试向量结果序列对应为系统特征行为序列，将故障特征向量对应为系统相关因素序列，以此考察测试向量与故障特征向量的关联度。灰色关联度在故障诊断中的应用在第2节具体介绍。
2 多故障模糊诊断方法 在系统故障诊断工作中，DFT矩阵支持由测试现象推理故障，理论上能做到对故障的准确识别。但在实际工作中，受限于测试传感器固有特性及环境影响，测试不能达到理想无误状态。故障与测试的逻辑关系可存在4种情况的不确定性，下面用条件概率P(tj|fi)的形式具体说明。
1) P(tj=0|fi=0)：故障fi不发生、测试tj不报警，此时tj指示正确。
2) P(tj=1|fi=1)：故障fi发生、测试tj报警，此时tj正确检出了故障fi。
3) P(tj=0|fi=1)：故障fi发生、测试tj不报警，此时tj漏检了故障fi。
4) P(tj=1|fi=0)：故障fi不发生，测试tj报警，此时tj虚报了故障fi。
上述第2)~4) 种情况分别表示测试对故障的检测概率、漏检概率和虚警概率。除在测试tj与故障fi不相关的情况下P(tj|fi)为0，否则P(tj|fi)取值不为0。
不难看出，测试报警是故障诊断的触发条件，从测试传感器的故障检测概率和虚警概率指标中能够提取出模糊的故障信息，并且获取测试传感器的概率数据比之复杂系统的故障先验概率更容易，因此在测试空间上进行故障诊断具有可行性。
下面从测试不确定性角度重新考虑故障诊断问题，给出了多故障模糊诊断的具体流程，如图 2所示。
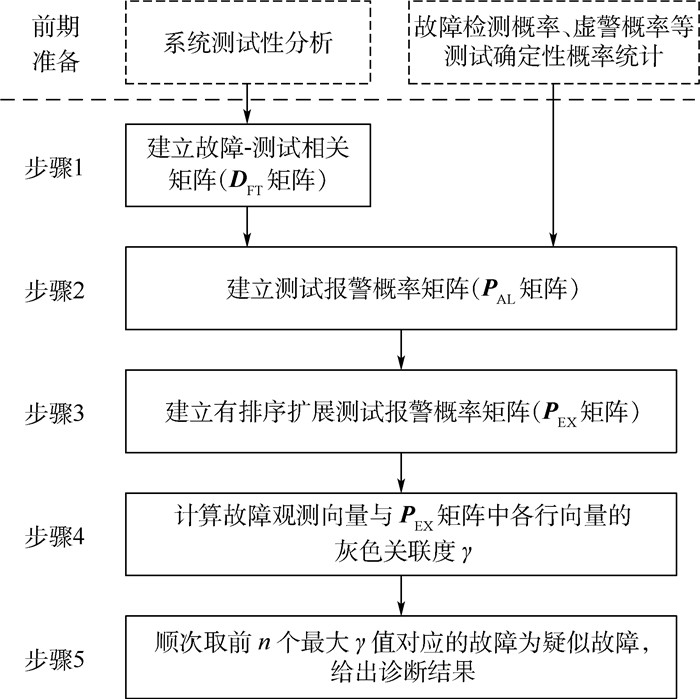图 2 多故障模糊诊断的实施流程 Fig. 2 Implementation process of multi-fault fuzzy diagnosis
图选项




在对系统进行可测性分析并建立DFT矩阵后，可基于DFT矩阵构建测试报警概率矩阵PAL=[pij]m×n，该矩阵包含了测试不确定性因素影响，矩阵元素pij表示概率值。PAL矩阵具体构造方式为：将DFT矩阵中rij=1的元素替换为测试Tj对故障Fi的故障检测概率值，并将rij=0的元素替换为测试Tj对故障Fi的故障虚警概率值。PAL矩阵考虑了在最坏情况下测试传感器以故障虚警概率对非故障节点进行报警的情形。一般来说，信息多层级传递将导致故障模糊性增强，故障与测试的相关阶数N值越大，存在测试虚警的可能性越大。为适于工程实用并简化计算，可选用式(2)~式(4) 定义的更新方法对PAL矩阵中各故障虚警概率值进行更新。
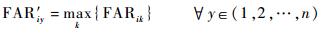(2)

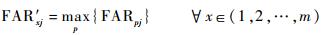(3)

(4)

式中：变量FAR和FAR′分别表示更新前后的矩阵元素中故障虚警概率。
当统一考虑第i个故障特征向量的测试虚警概率时可采用式(2) 计算，当统一考虑第j个测试对其各阶相关故障的虚警概率时可采用式(3) 计算，当统一考虑所有虚警概率并选取其最大值时可采用式(4) 计算。下面以图 1所示的系统为例，假设按式(3) 进行数据更新、节点3上的所有测试FAR值均为最大，构建PAL矩阵如表 2所示，其中变量FDR表示故障检测概率。
表 2 示例系统的PAL矩阵 Table 2 PAL matrix of sample system
故障节点 测试/报警节点号
1/5 2/10 3/11 4/12 5/14
1 FDR11 FAR32 FAR33 FAR34 FDR15
2 FDR21 FDR22 FAR33 FAR34 FDR25
3 FAR31 FDR32 FDR33 FDR34 FDR35
4 FAR31 FAR32 FDR43 FDR44 FDR45
5 FDR51 FAR32 FAR33 FAR34 FDR55
6 FAR31 FDR62 FAR33 FAR34 FDR65
7 FAR31 FDR72 FDR73 FDR74 FDR75
8 FAR31 FAR32 FAR33 FDR84 FAR35
9 FAR31 FAR32 FAR33 FAR34 FDR95
10 FAR31 FDR10, 2 FAR33 FAR34 FDR10, 5
11 FAR31 FAR32 FDR11, 3 FAR34 FDR11, 5
12 FAR31 FAR32 FAR33 FDR12, 4 FAR35
13 FAR31 FAR32 FAR33 FAR34 FDR13, 5
14 FAR31 FAR32 FAR33 FAR34 FDR14, 5


表选项






对于系统多故障的情况，可基于PAL矩阵构造有排序的扩展测试报警概率PEX矩阵。假定有两故障的组合{p, q}，首先在PAL矩阵上新插入1行来存储故障组合的特征向量，并将故障p和故障q所在行的元素按列序号逐个比较，选择值较大的放入扩展行的对应位置。上述处理方式对其他故障组合具有普适性。在不考虑多故障并发后出现故障消减或衍生条件下，m个故障最多可有2m－1种故障组合，考虑到实际系统的故障多集中在少数关键节点上，对上述经扩展后的矩阵按设定的诊断优先级重新进行故障行排序(优先级越高，则故障行号越小)，即可得到PEX矩阵。依据PEX矩阵可优先实现对重点关注故障的诊断，进而提高诊断效能。
对于表 2给出的PAL矩阵示例，假设节点号顺序即为诊断优先级、且优先级高的节点的FDR值较大，在考虑最多两故障并存的条件下，可构建如表 3所示的PEX矩阵示例。
表 3 示例系统的PEX矩阵 Table 3 PEX matrix of sample system
故障节点 测试/报警节点号
1/5 2/10 3/11 4/12 5/14
1 FDR11 FAR32 FAR33 FAR34 FDR15
1, 2 FDR11 FDR22 FAR33 FAR34 FDR15
1, 3 FDR11 FDR32 FDR33 FDR34 FDR15
1, 14 FDR11 FAR32 FAR33 FAR34 FDR15
2 FDR21 FDR22 FAR33 FAR34 FDR25
2, 3 FDR21 FDR22 FDR33 FDR34 FDR25
2, 14 FDR21 FDR22 FAR33 FAR34 FDR25
13 FAR31 FAR32 FAR33 FAR34 FDR13, 5
13, 14 FAR31 FAR32 FAR33 FAR34 FDR13, 5
14 FAR31 FAR32 FAR33 FAR34 FDR14, 5


表选项






从空间投影角度讲，基于PEX矩阵进行故障模糊诊断的实质是确定哪个故障在测试空间的投影向量(反映了故障特征)与实测结果向量更接近。本文以灰色关联度γ作为衡量故障实测结果向量T与该故障特征向量F接近程度的指标，γ值越大，诊断结果为“发生故障”的可信度越高。假定有实测结果向量为X0(向量元素值为1或0，分别表示“报警”或“不报警”)，PEX矩阵某行的故障特征向量为Xi，下面给出灰色关联度γ的计算步骤。
步骤1??对X0序列元素进行非零化处理。设X0=(x0(1), x0(2), …, x0(n))，?x0(j)=0，令x0(j)=0.01, j=1, 2, …, n。
步骤2??对各序列Xi进行初值归一化，令，i=0, 1, …, m。
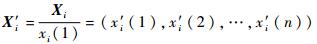
步骤3??求X′0与X′i对应分量之差的绝对值序列，记Δi(k)=|x′0(k)－x′i(k)|，Δi=(Δi(1), Δi(2), …, Δi(n)), i=1, 2, …, m。
步骤4??求Δi(k)在Xi全序列范围内的最大值和最小值，分别记为，m= ，k=1, 2, …, n，i=1, 2, …, m。
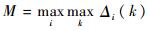
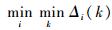
步骤5??计算序列元素的关联系数γ，，ε∈(0, 1)，k=1, 2, …, n，i=1, 2, …, m。
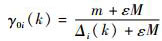
步骤6??求序列X′0与X′i(亦是X0与Xi)间的关联度，, i=1, 2, …, m。
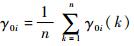
对各序列Xi做初值归一化处理可将各向量元素均转化为初值可比的无量纲数据，便于后续计算分析。对X0序列元素做非零化处理可防止进行初值归一化时分母为0，本文将非零值选取为0.01不会造成计算结果的符号改变和非线性。参数M、m和ε的引入使得关联系数γ具有多分辨特性，可根据各序列元素的实际取值情况进行诊断精度调优。通常情况下，M和m取值会分别从各测试的FDR和FAR中产生，否则与工程实际不符，此时ε取值的大小将反映FDR与FAR2种因素在故障诊断中的权重分配。
需要说明的是，考虑到基于FDR和FAR的故障诊断具有一定的模糊性，在实际应用中，可按由灰色关联度γ最大取值递减的次序选取n个故障或故障组合状态候选，以此提高诊断正确率。另外，前期工作涉及的系统测试性模型、测试确定性概率统计均属于诊断前准备，具体方法可参见相关文献，本文不做赘述。
3 应用实例及评估 下面以阿波罗飞船发射前系统状态[18]为例说明本文诊断方法的有效性。该系统考虑了10个故障状态和15个故障观测传感器，对其建立的DFT矩阵如表 4所示。
表 4 阿波罗飞船发射前系统状态DFT矩阵 Table 4 System state matrix DFT before launch of Apollo spacecraft
故障节点 测试节点
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 0 0 0 1 0 0 0 1 0 1 1 1 1 0 0
2 0 0 1 0 1 0 0 0 0 0 1 1 0 1 0
3 0 0 0 0 1 1 1 0 1 1 1 1 0 0 1
4 0 1 0 0 0 1 1 0 0 0 0 0 0 1 1
5 0 1 0 1 0 1 1 1 1 1 0 0 1 1 0
6 0 0 0 1 1 0 0 1 1 1 0 1 1 1 1
7 1 0 0 1 1 0 0 1 0 0 1 0 1 0 1
8 1 1 1 0 0 1 1 0 1 1 1 0 0 1 0
9 1 0 0 1 1 0 0 0 0 0 0 1 0 1 1
10 1 1 1 1 0 0 1 0 0 0 1 0 1 1 0


表选项






为了便于结果比较, 本文采用与文献[8]相同的实验条件：
1) 假设各传感器故障检测概率均为90%，虚警概率均为1%。
2) 假设传感器报警为理想状态，则PEX矩阵的行向量即为故障特征向量。
3) 假设系统最多同时发生2个故障，则PEX矩阵共有55个故障特征向量。
4) 备选诊断结论中包含的最大疑似故障数n取值为3。
进一步地，本文将故障状态编号次序作为故障诊断优先级排序；选用式(4) 对所得PAL及PEX矩阵进行数值更新，本例中所有测试的FAR值均为1%；均衡考虑FDR和FAR的影响权重，选取灰色关联度分辨系数ε=0.5。基于文献[8]方法和本文方法的实验结果比较如表 5所示，需要说明的是，表中2种方法所用的诊断指标(相似度与接近度)之间并无量值比较意义。
表 5 理想输入条件下的诊断结果 Table 5 Diagnosis results under ideal input condition
故障状态 报警传感器 文献[8]方法诊断结论 本文方法诊断结论
输出排序 故障序号 诊断判据 判据结果 输出排序 故障序号 诊断判据 判据结果
1 4, 8, 10, 11, 12, 13 最可能 1 相似度 0.996 3 最可能 1 接近度 0.933 3
次可能 1, 2 相似度 0.906 9 次可能 1, 2 接近度 0.805 3
第三可能 1, 7 相似度 0.906 9 第三可能 1, 6 接近度 0.762 6
3 5, 6, 7, 9, 10, 11, 12, 15 最可能 3 相似度 0.997 8 最可能 3 接近度 0.911 1
次可能 2, 3 相似度 0.946 1 次可能 2, 3 接近度 0.825 7
第三可能 3, 4 相似度 0.946 1 第三可能 3, 4 接近度 0.825 7
5 2, 4, 6, 7, 8, 9, 10, 13, 14 最可能 5 相似度 0.998 3 最可能 5 接近度 0.900 0
次可能 4, 5 相似度 0.973 2 次可能 4, 5 接近度 0.857 3
第三可能 1, 5 相似度 0.951 4 第三可能 1, 5 接近度 0.814 6
7 1, 4, 5, 8, 11, 13, 15 最可能 7 相似度 0.997 2 最可能 7 接近度 1.000 0
次可能 1, 7 相似度 0.939 5 次可能 1, 7 接近度 0.997 1
第三可能 7, 9 相似度 0.939 5 第三可能 7, 9 接近度 0.997 1
9 1, 4, 5, 12, 14, 15 最可能 9 相似度 0.996 3 最可能 9 接近度 1.000 0
次可能 2, 9 相似度 0.931 1 次可能 2, 9 接近度 0.997 1
第三可能 4, 9 相似度 0.906 9 第三可能 4, 9 接近度 0.995 7
2, 4 2, 3, 5, 6, 7, 11, 12, 14, 15 最可能 2, 4 相似度 0.998 3 最可能 2, 4 接近度 0.900 0
次可能 3, 8 相似度 0.932 5 次可能 2, 3 接近度 0.781 4
第三可能 2, 3 相似度 0.925 8 第三可能 3, 4 接近度 0.781 4
4, 6 2, 4, 5, 6, 7, 8, 9, 10, 12, 13, 14, 15 最可能 4, 6 相似度 0.999 4 最可能 4, 6 接近度 0.866 7
次可能 5, 6 相似度 0.999 4 次可能 5, 6 接近度 0.866 7
第三可能 3, 5 相似度 0.980 0 第三可能 3, 5 接近度 0.824 0
6, 8 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 最可能 6, 8 相似度 1.000 0 最可能 6, 8 接近度 1.000 0
次可能 3, 10 相似度 0.986 3 次可能 3, 10 接近度 0.998 6
第三可能 6, 10 相似度 0.986 3 第三可能 6, 10 接近度 0.998 6
8, 10 1, 2, 3, 4, 6, 7, 9, 10, 11, 13, 14 最可能 8, 10 相似度 0.999 1 最可能 8, 10 接近度 1.000 0
次可能 5, 8 相似度 0.978 1 次可能 5, 8 接近度 0.998 6
第三可能 5, 10 相似度 0.978 1 第三可能 5, 10 接近度 0.998 6
1, 10 1, 2, 3, 4, 7, 8, 10, 11, 12, 13, 14 最可能 1, 10 相似度 0.999 1 最可能 1, 10 接近度 1.000 0
次可能 1, 8 相似度 0.959 6 次可能 1, 8 接近度 0.997 1
第三可能 6, 10 相似度 0.943 0 第三可能 2, 10 接近度 0.995 7


表选项






实验结果表明，本文方法的首选结论诊断正确率和故障覆盖率均可达到100%。与文献[8]相比，本文方法在以下方面具有特别优势：
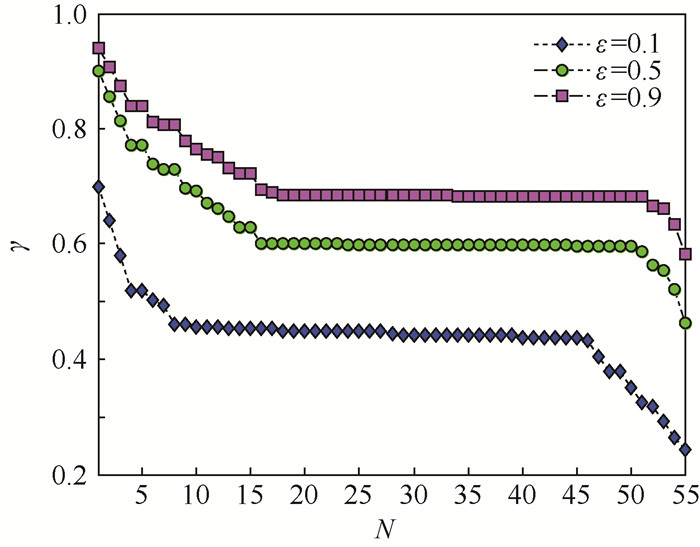
1) 支持通过改变灰色关联度分辨系数ε值来调整FDR和FAR值在诊断中的权重。对复杂系统而言，在不同工况条件下获得的测试指标FDR和FAR的可信度也将存在不确定性。在考虑FDR值大于FAR值的情况下，当认定测试的FDR值更可信时，可令ε取值大于0.5；当认定测试的FAR值更可信时，可令ε取值小于0.5；否则可令ε取值等于0.5。下面以表 5中的故障状态5为例，令ε取值分别为0.1, 0.5, 0, 9，保持其他实验条件不变，可获得如图 3所示的γ值结果分布。其中，纵轴为灰色关联度γ值计算结果；横轴数字代表按可能性递减次序给出的诊断结论次序N，例如N值为1、2、3的情况分别对应第1次序结论“最可能-故障5”、第2次序结论“次可能-故障4，5”、第3次序结论“第三可能-故障1，5”。
图 3 不同ε取值情况下故障状态5的灰色关联度 Fig. 3 Grey correlation degrees of fault state 5 at different ε values
图选项




图 3中数据表明：相同实验条件下，诊断结论的γ值与ε取值整体上表现为正比例关系。赋予FDR的权重越高(即认定其更可信)，诊断获得的γ值就越大，并逐渐向1逼近；反之，则γ取值越小。进一步计算可知，ε的上述不同取值并未对诊断结论正确得出造成影响。可变参数ε为工程人员进行多故障模糊诊断提供了一定的灵活性，对于不确定因素较多的复杂系统而言，支持诊断指标权重动态调整是非常必要的。文献[8]中基于空间向量间夹角的计算方式仅可算得固定值，不具备权重调整特性。
2) 同等条件下，本文方法的故障诊断精细度更优。因诊断给出的n个最大疑似故障状态将作为后续维修工作的直接参考，故可通过指标“维修建议正确率SCR”对诊断精细度进行结果导向性评价。本文定义DFT矩阵中各行向量对应的故障为“元故障”，PEX矩阵中的组合故障均可分解为元故障，则可得到如式(5) 所示的SCR算式：
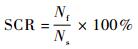(5)

式中:Nf为实际发生的元故障总数; Ns为诊断给出的n个最大疑似故障中包含的元故障总数。实际应用中，系统维护人员只需排查Ns个元故障即可完成对n个检出故障的覆盖。以表 5中的故障组合(6，8) 为例，易知其Nf值为2，Ns值为4，SCR值为50%。
图 4 表 5中故障状态的SCR取值 Fig. 4 SCR values of fault states in Table 5
图选项




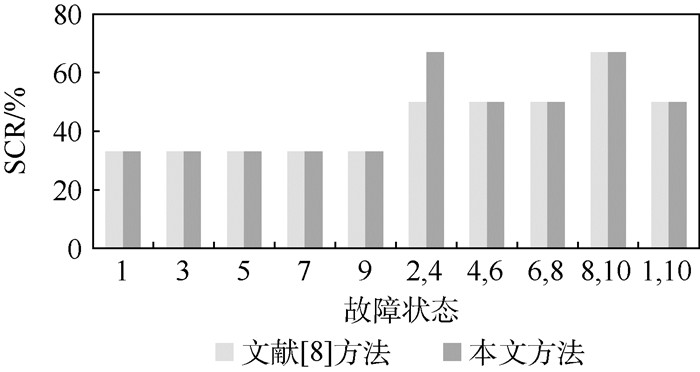
图 4给出了表 5中列出的全部故障状态的SCR值。结果表明，本文方法比文献[8]方法表现更优。
3) 本文采用故障诊断次序分级的策略，同等条件下，支持将重点关注故障优先检出，与工程中对故障按影响度分级的思路相吻合。在复杂系统故障组合数目庞大、多个故障或故障组合具有同等疑似程度的情况下，本文方法的优先级排序方式与文献[8]中任意选定的排序方式相比，具有更高的故障检出及排查效率。一个直观的例子是表 5中的故障组合(1，10)，本文计算得到接近度取值同为0.995 7的疑似故障共有5个，如表 6所示。按实验条件中设定的诊断优先级，本文方法可首选筛选出含故障2(优先级较高)的故障组合。容易证明，当诊断优先级改变时，例如以故障状态编号“逆序”作为诊断优先级排序，本文方法筛出的重点关注故障实例数将显著增多。
表 6 故障组合(1, 10) 的接近度量值与候选诊断结论示例 Table 6 Example of approximate measurement value and candidate diagnosis result of fault combination (1, 10)
接近度量值 候选诊断结论(疑似故障/故障组合)
0.995 7 2, 10 5, 8 5, 10 6, 10 10


表选项






总体而言，对于上述故障-测试简单组合的实验场景，本文方法已表现出基于小样本数据的多项诊断优势，在多故障组合、大实验数据量的情况下将可获得更优的诊断结果，可为复杂系统的多故障模糊诊断提供新的解决思路。
4 结论 1) 本文方法无需获取复杂系统先验故障概率即可完成测试不确定性条件下多故障模糊诊断。
2) 本文方法可通过改变灰色关联度分辨系数支持诊断指标权重动态调整，为工程实用中多故障模糊诊断提供了灵活性。
3) 本文方法与文献[8]方法性能表现相当，例如在单故障和双故障组合情况下，首选结论诊断正确率及故障覆盖率均可达100%，但本文方法具有更优的诊断精细度及重点关注故障筛选效果。

参考文献
[1] HASHTRUDIZAD S, KWONG R H, WONHAM W M. Fault diagnosis in discrete-event systems:Framework and model reduction[J].IEEE Transactions on Automatic Control, 2003, 48(7): 1199–1212.DOI:10.1109/TAC.2003.814099
[2] 田仲, 石君友. 系统测试性设计分析和验证[M].北京: 北京航空航天大学出版社, 2003: 4-8.
TIAN Z, SHI Z Y. System testability design analysis and verification[M].Beijing: Beihang University Press, 2003: 4-8.(in Chinese)
[3] DE PAUL R.A logic modeling as a tool for testability[C]//Proceedings of IEEE International Automatic Testing Conference.Piscataway, NJ:IEEE Press, 1985:203-207.
[4] DEB S, PATTIPATI K R, RAGHAVAN V. Multi-signal flow graphs:A novel approach for system testability analysis and fault diagnosis[J].IEEE Aerospace & Electronic Systems Magazine, 1995, 10(5): 14–25.
[5] RAO N S V. On parallel algorithms for single-fault diagnosis in fault propagate on graph systems[J].IEEE Transactions on Parallel and Distributed Systems, 1996, 7(12): 1217–1223.DOI:10.1109/71.553268
[6] KOKAWA M, MIYAZAKI S, SHINGAI S. Fault location using digraph and inverse direction search with application[J].Automatic, 1983, 19(6): 729–735.DOI:10.1016/0005-1098(83)90039-0
[7] 尹园威, 尚朝轩, 马彦恒, 等. 层次测试性模型的评估方法[J].北京航空航天大学学报, 2015, 41(1): 90–95.
YIN Y W, SHANG C X, MA Y H, et al. Method of testability evaluation using hierarchical testability model[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(1): 90–95.(in Chinese)
[8] 连可, 黄建国, 龙兵. 一种基于有向图模型的模糊多故障诊断算法[J].系统工程与电子技术, 2008, 30(3): 568–571.
LIAN K, HUANG J G, LONG B. Fuzzy multiple fault diagnosis algorithm based on digraph models[J].Systems Engineering and Electronics, 2008, 30(3): 568–571.(in Chinese)
[9] 杨鹏, 邱静, 刘冠军. 基于扩展的关联模型的测试性分析技术研究[J].系统工程与电子技术, 2008, 30(2): 371–374.
YANG P, QIU J, LIU G J. Research on extended dependency model-based testability analysis[J].Systems Engineering and Electronics, 2008, 30(2): 371–374.(in Chinese)
[10] 梁爽, 于劲松, 唐荻音, 等. 基于多信号流图与分支定界算法的故障诊断[J].北京航空航天大学学报, 2016, 42(1): 180–186.
LIANG S, YU J S, TANG D Y, et al. Research on fault diagnosis based on multi-signal flow graph and branch and bound algorithm[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(1): 180–186.(in Chinese)
[11] 方甲永, 肖明清, 王学奇, 等. 测试不可靠条件下多故障诊断方法[J].北京航空航天大学学报, 2011, 37(4): 433–438.
FANG J Y, XIAO M Q, WANG X Q, et al. Multiple fault diagnosis method with unreliable test[J].Journal of Beijing University of Aeronautics and Astronautics, 2011, 37(4): 433–438.(in Chinese)
[12] 沈琳, 于劲松, 唐荻音, 等. 图模型与学习算法结合的贝叶斯网络自动建模[J].北京航空航天大学学报, 2016, 42(7): 1486–1493.
SHEN L, YU J S, TANG D Y, et al. Automatic learning of Bayesian network structure using graph model and learning algorithm[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(7): 1486–1493.(in Chinese)
[13] SHAKERI M, RAGHAVAN V, PATTIPATI K R, et al. Sequential testing algorithms for multiple fault diagnosis[J].IEEE Transactions on Systems, Man and Cybernetics, 2000, 30(1): 1–14.
[14] U.S.Department of Defense.Basic dependency modeling terminology[EB/OL].Washington, D.C.:Office of the Secretary of Defense, DoD, 2008(2008-06-16)[2016-09-02].http://www.testability.com/Reference/Glossaries.aspx?Glossary=DependencyModeling.
[15] CHESSA S, SANTI P. Operative diagnosis of graph-based systems in multiple faults[J].IEEE Transactions on Systems, Man and Cybernetics, 2001, 31(2): 112–119.DOI:10.1109/3468.911368
[16] DENG J L. Introduction to grey system theory[J].Journal of Grey System, 1989, 1(1): 1–24.
[17] 刘思峰, 杨英杰, 吴利丰, 等. 灰色系统理论及其应用[M].北京: 科学出版社, 2014: 63-75.
LIU S F, YANG Y J, WU L F, et al. The grey system theory and its application[M].Beijing: Science Press, 2014: 63-75.(in Chinese)
[18] WOHL J G. Information automation and the Apollo program:A retrospective[J].IEEE Transactions on Systems, Man and Cybernetics, 1982, 12(4): 469–478.DOI:10.1109/TSMC.1982.4308851


相关话题/测试 系统 概率 序列 计算
  • 领限时大额优惠券,享本站正版考研考试资料!
    大额优惠券
    优惠券领取后72小时内有效，10万种最新考研考试考证类电子打印资料任你选。涵盖全国500余所院校考研专业课、200多种职业资格考试、1100多种经典教材，产品类型包含电子书、题库、全套资料以及视频，无论您是考研复习、考证刷题，还是考前冲刺等，不同类型的产品可满足您学习上的不同需求。 ...
    考试优惠券 本站小编 Free壹佰分学习网 2022-09-19
  • 空间站大气环控系统应急运行策略优化*
    大气环控系统(ECS)是载人航天器重要的组成系统[1-2]。该系统主要通过控制舱室五大环境参数(总压、氧分压、二氧化碳分压、温度和湿度)，为航天员提供适宜的舱室生存环境。许多****开展了载人航天器舱室环境仿真与优化研究，以改进大气环控系统的运行性能[3-5]。能源系统为空间站提供连续电能[6]，然 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 基于多模型的不等长序列数据关联算法*
    作为一种时间序列，不等长序列数据的关联是异类传感器融合必须解决的问题，其根本方法是对不等长度序列数据相似度的挖掘和度量，特别是干扰条件下量测序列出现突变点的情况。文献[1-15]相继研究了时间序列相似度的查询，形成了一系列序列度量的方法，离散傅里叶变换[1-3]、奇异值分解[4]、离散小波变换[5- ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 冲压空气涡轮泵的温控节流孔计算方法*
    冲压空气涡轮(RAT)应急系统是飞机安全的最后保障，在飞机发动机和电源功能全部丧失的情况下，RAT应急能源系统将空气的动能转换为电能/液压能，提供飞机基本操纵所需能源。RAT系统一般由冲压涡轮、液压泵/发电机和收放装置组成，共有2个工作状态：①收回状态，液压泵静止，不输出功率；②伸出状态，RAT弹出 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 基于遗传算法的飞行管理系统余度配置优化方法*
    飞行管理系统(以下简称飞管系统)是现代航空装备电子系统的基本组成部分，其实现了飞机飞行过程中全过程控制与管理，是保障飞机安全性的重要系统[1]。飞管系统安全性设计过程中，预算和后续维修保障成本是2个主要制约因素[2]。航空装备研制、装备使用、维护过程中，在保证多种约束条件同时满足的情况下，如何尽可能 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 电路测试响应信号的GP-KSVD稀疏重构算法*
    傅里叶变换、小波变换、奇异值分解等方法在信号处理领域中得到了广泛的应用与发展[1]，与此同时，信号的稀疏表示理论也逐渐成为研究热点，在信号去噪[2]、数据压缩[3]、盲源分离以及特征提取等领域都有应用。傅里叶变换以及小波变换中的信号表示是基于正交基的，因此需要保证基函数系的完备性和正交性，保证固有最 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 一种航天器太阳电池阵供电能力计算方法*
    航天器依靠太阳电池阵为设备供电，电池阵供电能力是影响航天器方案设计以及飞行任务规划的重要因素[1-3]。在航天器设计阶段，太阳电池阵供电能力分析可以优化帆板构型和布局，运营阶段，结合航天器轨道和姿态进行供电能力分析，可优化飞行任务规划，确保航天器能量平衡[4-5]。航天器电池阵供电能力受太阳光入射角 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 重点区域入侵安防设备系统可靠性建模方法*
    当前安防系统应用广泛，正在形成完整的产业价值链。在经历了模拟监控、数字监控、网络监控以及智能监控4个发展阶段后[1]，安防系统的复杂度越来越高，与此同时也带来了故障率升高的问题，最终影响系统的防范效果。随着用户对安防效果要求的提高，许多****针对防范效果进行研究，逐渐将可靠性分析和计算应用于各种安 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • AVB网络流量整形帧模型端到端延迟计算*
    音视频桥接技术(AVB)是由IEEE802.1AVB工作组(AVBTG)[1]定义的音视频流服务技术，已被车载电子系统等关键嵌入式领域考虑采用[2-4]，是很具潜力的下一代实时网络标准[5-8]。AVB采用基于信用量的整形(CBS)算法对音视频流量进行整形，通过对不同类型流量设定统一的逻辑带宽进行限 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 动态系统失效的不确定性分析及其高效算法*
    在航空航天、核反应堆控制、汽轮机械等工程领域，系统的安全性能越来越受到工程技术人员的关注。与此同时，系统设计也日趋大型化和复杂化。这些都对系统的可靠性设计分析提出了更高的要求。系统由多个元器件按照特定关系连接构成，系统工作状态与元器件工作状态密切相关。一般情况下，元器件失效率为定值。然而，系统设备中 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25
  • 输入输出受限的无人机防滑刹车系统容错控制*
    近20年来，无人机容错技术得到了长足的发展，特别针对大中型轮式起降无人机的机电系统容错理论也进行了深入的研究。刹车系统作为无人机的起飞着陆子系统的组成部分，对于保障无人机安全起飞、着陆及纠偏起到重要的作用。防滑刹车系统的可靠与否，直接关系到无人机载具的起降安全和任务完成程度。执行机构部分失效型故障普 ...
    北京航空航天大学论文文献 本站小编 Free考研考试 2021-12-25

Free考研考试FreeKaoYan.Com
欢迎来到Free考研考试，"为实现人生的Free而奋斗"

© 2020 FreeKaoYan! . All rights reserved.