本文在研究雷达角度欺骗干扰信号一般特性的基础上,根据线性调频(Linear Frequency Modulation,LFM)信号在分数阶傅里叶域的能量聚集特性,提出了一种压缩感知框架下的数字射频存储(Digital Radio Frequency Memory,DRFM)干扰机模型。干扰机通过对雷达信号压缩采样可在较低采样频率下获取欺骗干扰信号,在对单脉冲相干两点源干扰的研究基础上,通过控制干扰信号强度比,在实现角度拖引干扰基础上,考虑了闪烁干扰的实现问题,实现了对单脉冲雷达的有效角度欺骗干扰。仿真实验表明,本文提出的干扰机模型能够产生较好的欺骗干扰信号,同时干扰机具有产生稳定的角度拖引干扰和闪烁干扰能力。
1 理论基础 1.1 压缩感知基本理论 压缩感知(Compressed Sensing,CS)理论由Candes和Tao[8]于2006年正式提出,其证明了信号只要在某一个正交空间具有稀疏性,就能以较低的频率采样信号高概率地重构该信号。压缩感知的实现过程主要包括3步:① 如果信号x∈RN在某个正交变换Ψ下是可稀疏表示的,稀疏表示结果为x=Ψθ;② 设计一个平稳的与变换基不相关的M×N(M?N)维观测矩阵Φ,对信号x进行观测得到观测值y=Φx=ΦΨθ;③ 利用0-范数意义下的优化问题,使用重构算法优化求解得到精确θ或近似逼近
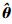
 | (1) |
对于压缩感知理论,信号的可稀疏表示是其可压缩感知的前提。压缩感知的感知过程实际上是对信号的采样过程。感知矩阵是获取信号结构化表示的手段;重构算法是实现信号重构的保证。
1.2 分数阶傅里叶变换基本概念 分数阶傅里叶变换(Fractional Fourier Transform,FRFT)是一种拓展的分数阶傅里叶变换,可以理解为信号在时频平面内坐标轴绕原点逆时针旋转任意角度后构成FRFT域上的表示方法。从积分核的角度给出p阶FRFT的基本定义:
 | (2) |
式中:Kp(μ, t)为FRFT的积分核函数;Aα =

1.3 单脉冲雷达相干干扰原理 单脉冲雷达,顾名思义,即根据单个雷达回波脉冲即可以得到目标角位置的全部信息。对于单脉冲雷达而言,目前常用的角度欺骗干扰技术主要包括非相干干扰、相干干扰等。图 1为相干干扰原理图。图中:θ0为等强信号方向;Δθ为两干扰机张角;θ为等强信号方向与目标夹角。θ3为目标偏离雷达等强信号方向的夹角,AJ1、AJ2和Ar分别为干扰源J1、J2和目标回波信号的幅度,φ1和φ2分别为干扰源J2的信号和回波信号相对于干扰源J1的信号相位差,则雷达天线1、2接收到的信号分别为
 |
| 图 1 相干干扰原理 Fig. 1 Principle of coherent jamming |
| 图选项 |
 | (3) |
式中:F为天线增益;ω为雷达载波频率。
2 基于DRFM的单脉冲雷达角度欺骗干扰机 2.1 欺骗干扰信号分析 雷达回波信号的一般形式如下:
 | (4) |
式中:φR和φT分别为雷达接收和发射信号;K为信号增益,与天线增益、发射机增益等有关,可由雷达方程计算得到;τ=2R/c为信号时延,R为目标与雷达距离,c为光速;fd=-2v/λ为多普勒频移,v为雷达径向速度,λ为发射波长;f0为雷达发射载频。对雷达欺骗干扰的基本条件是:所产生的欺骗干扰信号的全部参数落入雷达目标检测范围内,这就要求所产生的干扰信号大部分特征参数等于或近似目标特征参数,同时改变另一部分参数以达到迷惑敌方雷达的目的[9]。对于距离欺骗干扰信号,应使干扰信号包含的距离信息不同于真目标,而其他参数与真目标相同或相似;对于速度欺骗信号,应与目标的多普勒频移信息不同,而其他参数与真目标参数相同或相似;而对于角度欺骗干扰信号,应使目标的方位角或俯仰角与真目标不同,而其他参数与真目标相同或相似,即干扰信号的时延、多普勒参数应与真目标相同或相似。
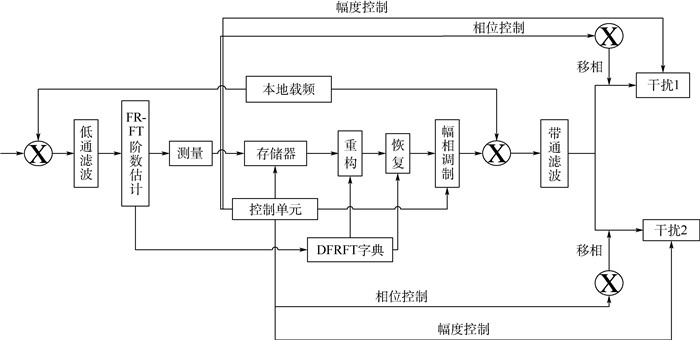
2.2 DRFM压缩感知角度欺骗干扰机 DRFM是一种可以存储一定带宽范围内的射频信号并对其进行精确复制输出的电子战设备,其关键技术在于对信号的量化存储和重构。DRFM一般有全脉冲存储转发、短脉冲存储循环转发和间歇采样存储转发3种工作方式。相比于后2种存储方式,全脉冲存储信号具有良好的相干性,处理复杂信号的能力较强[10]。但是全脉冲存储时数据量较大,对存储器、采样器等都具有极高的要求。DRFM技术的重点是实现信号的精确采样与恢复,因此,笔者设计了一种基于压缩感知框架的DRFM系统,在保留信号相干性的同时,降低DRFM系统对存储器、采样器等的需求。图 2为本文所提出的DRFM压缩感知交叉眼干扰机模型。图中:DFRFT为离散分数阶傅里叶变换。
 |
| 图 2 DRFM压缩感知相干干扰机模型 Fig. 2 Model of CS-DRFM coherent jammer |
| 图选项 |
图 2中的干扰机模型主要包含变频模块、压缩感知模块、存储单元、滤波模块等。变频模块实现对信号的上下变频;压缩感知模块包含FRFT阶数估计模块、测量模块、重构模块等,实现对信号的压缩采样与重构恢复。当雷达射频信号被接收并且传入DRFM信号处理单元时,通过下变频,低通滤波可以得到雷达中频信号;然后,FRFT阶数估计模块用于获取LFM雷达信号的最优变换阶以及LFM信号在FRFT域的稀疏表示结果;之后,测量模块获取雷达信号的压缩采样结果,采样数据送入高速存储器中。另一方面,DFRFT字典模块根据所获取的最优变换阶构建DFRFT正交基字典。在输出端,重构和恢复模块将存储器中存储的数据信息恢复得到源信号;再对恢复后信号进行一定干扰调制得到角度欺骗干扰信号;最后经过上变频,带通滤波后,通过移相器产生两路具有稳定相位关系的干扰射频信号;两路信号分别经由干扰发射机1和干扰发射机2中。干扰发射机对两路信号增益、放大后再转发给目标雷达,以实现对敌方雷达的角度欺骗干扰。
2.2.1 欺骗干扰信号的构建方法 2.1节中分析了角度欺骗干扰信号应具有的一般特性,为了能够得到较好的欺骗干扰信号,本文干扰机根据LFM信号在分数阶傅里叶域的能量聚集特性,采用压缩感知算法得到欺骗干扰信号,在精准重构信号的同时,可以降低DRFM对高速采样器和存储器的需求。根据FRFT理论可知,调频率相同的LFM信号所对应的最佳能量聚集阶次相同。
式(2) 给出了FRFT变换的变换式, FRFT的逆变换式为
 | (5) |
则信号x(t)可以看作是以逆变换核函数K-p(μ, t)为基的函数空间上展开的,则x(t)是以Xp(u)为权系数的正交基函数K-p(μ, t)所表征,即为所需的FRFT正交基字典。本文考虑使用离散化核矩阵作为FRFT正交基字典,选用Pei采样型DFRFT算法[11],具有最低的运算复杂度,文献[12]中给出了基于Pei采样型DFRFT算法的正反变换的矩阵表示形式。逆离散分数阶变换的矩阵表示形式为
 | (6) |
式中:x为原信号向量;Xp为p阶分数阶变换后信号向量;F-p为一个N×N的离散分数阶变换核矩阵。变换矩阵中的元素为
 | (7) |
式中:



Pei采样型算法能够保证离散分数阶变换的正交性和可逆性。由于LFM信号在FRFT域的能量聚集特性,Xp应为一个稀疏信号。对比式(4) 与式(1),可以得到Xp是源信号x在分数阶傅里叶域的稀疏表示结果,则逆变换矩阵F-p可以看作正交基字典。而压缩恢复算法可以根据正交基字典从压缩采样信号中得到恢复信号。
由上可知,干扰机产生欺骗干扰信号流程如下:当干扰机接收到敌方雷达发射的信号后,通过FRFT阶数估计模块获取雷达信号的变换阶数,以及LFM信号在分数阶傅里叶域的稀疏表示结果;然后,测量模块实现对信号的压缩采样,压缩采样信息存入高速存储设备;最后,信号重构与恢复模块通过压缩恢复算法以及DFRFT字典模块中的正交基字典实现对信号的重构与恢复,得到信号的精确恢复值,经过变频,相移得到两路具有稳定相位差的干扰射频信号。
2.2.2 干扰机工作方式 在利用DRFM干扰机实现相干干扰的基础上,本文研究了各干扰因素(如干扰信号强度比、干扰信号相位差等)对干扰性能的影响;通过控制两干扰源发射信号的强度,实现对单脉冲雷达的角度拖引干扰。采用DRFM干扰机进行角度拖引干扰的方法如下:当干扰机接收到信号时,DRFM产生角度欺骗干扰信号;DRFM控制模块控制干扰信号回波比不断增大,以使测角误差不断增大,诱使单脉冲雷达角跟踪系统沿着错误的角度轨迹跟踪目标,以达到角度拖引欺骗干扰的目的。在达到最大拖引角度后,通过干扰机控制强度比实现对目标雷达的闪烁干扰。
角度拖引欺骗干扰具有3个阶段:① 捕获期,干扰机接收到雷达信号后,获取雷达信号信息,产生欺骗干扰信号;② 拖引期,欺骗干扰机通过控制干扰参数(如干扰信号幅度比、相位差、回波信号强度比),使角度欺骗干扰信号不断偏离目标信号,诱使单脉冲雷达角跟踪系统沿着错误的角跟踪轨迹跟踪假目标信号;③ 闪烁期,在达到预定最大的拖引干扰角度Δθ后,调整干扰机两干扰信号强度比,可以使误差角度接近-Δθ,通过周期性控制干扰信号强度比, 可以使雷达跟踪天线在2Δθ角度范围内追摆,以达到对单脉冲雷达的角度欺骗干扰。
3 仿真实验与分析 3.1 LFM压缩感知性能分析 接收机接收到的LFM雷达回波信号如下:
 | (8) |
式中:A为信号增益,与发射机增益、天线增益等有关;k为LFM信号的调频率。
参照文献[13]对LFM信号参数进行设置,取载频f0=0,带宽B=200 MHz,脉冲宽度T=2 μs,采样频率fs=512 MHz。采用二维峰值搜索算法对干扰机接收到的信号进行FRFT阶数估计。二维峰值搜索算法的基本思想是:以变换阶数p为变量,对回波信号进行FRFT,得到信号在分数阶傅里叶域的二维分布,二维峰值对应的变换阶数即为信号的最优FRFT变换阶。本文的仿真实验中,设置阶数范围p∈[-1, 1],阶数步长为0.01。图 3为LFM源信号。图 4为使用二维峰值搜索算法得到的LFM信号在FRFT域的二维分布。图 5为LFM信号在FRFT域的稀疏表示结果。图 6为使用压缩采样匹配追踪(Compressed Sampling Match Pursuit,CoSaMP)重构算法[14]得到的稀疏重构结果。图 7为压缩恢复信号。
 |
| 图 3 LFM源信号(SNR=5 dB) Fig. 3 LFM source signal (SNR=5 dB) |
| 图选项 |
 |
| 图 4 LFM信号在FRFT域二维分布(SNR=5 dB) Fig. 4 Two-dimensional distribution of LFM signal in FRFT domain (SNR=5 dB) |
| 图选项 |
 |
| 图 5 LFM信号稀疏表示结果(SNR=5 dB) Fig. 5 Sparse representation of LFM signal (SNR=5 dB) |
| 图选项 |
 |
| 图 6 稀疏系数重构结果(SNR=5 dB) Fig. 6 Reconstruction of sparse coefficient (SNR=5 dB) |
| 图选项 |
 |
| 图 7 压缩恢复信号(SNR=5 dB) Fig. 7 Compressive recovery signal (SNR=5 dB) |
| 图选项 |
根据图 3~图 7可知,在低信噪比(Signal Noise Rate,SNR)情况下,基于FRFT的LFM压缩感知仍具有很好的恢复效果。同时,恢复信号中的噪声分量在压缩恢复过程中也得到了一定的消除,这是因为噪声信号在FRFT域不具备能量聚集特性。
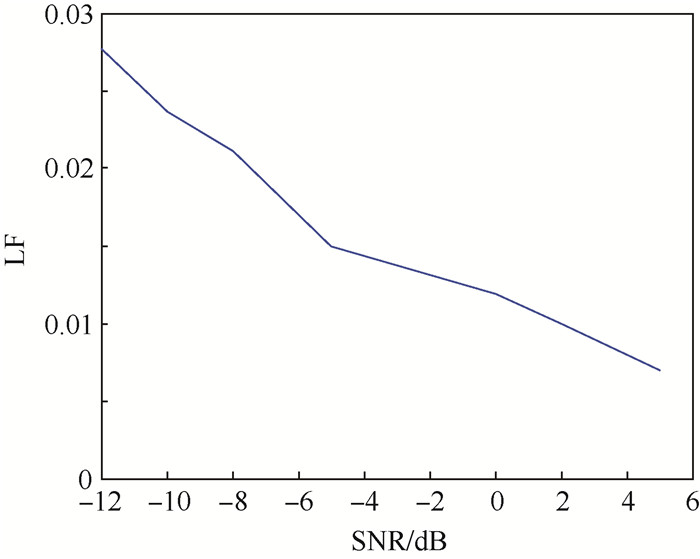
为了描述信号的重构性能,本文定义损耗因子(Loss Factor, LF)为
 | (9) |
式中:θ为回波信号在FRFT域的稀疏表示;
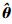
 |
| 图 8 压缩感知损耗因子 Fig. 8 Loss factor of compressed sensing |
| 图选项 |
由图 8可知,随着信噪比的升高,损耗因子不断减小,表明压缩恢复后的信号保留了原信号更大部分的能量,则压缩恢复后的信号能够更精确地表示原信号。
3.2 干扰机干扰效果仿真
3.2.1 单脉冲雷达系统仿真模型 为了验证本文所提出的干扰机模型的干扰效果,根据文献[15-17]等构建了单脉冲雷达测角系统,通过建立的单脉冲雷达测角系统,验证干扰机对单脉冲测角所产生的影响。图 9为单脉冲雷达测角系统的模型框图。
 |
| 图 9 单脉冲雷达测角系统框架 Fig. 9 Framework of monopulse radar system |
| 图选项 |
单脉冲雷达向目标发射LFM信号,当机载干扰机接收到雷达发射信号后,欺骗干扰机对干扰机接收信号进行处理并产生欺骗干扰信号,并通过干扰发射机发射出去。此时,单脉冲雷达接收机会接收到包含噪声、目标回波以及干扰信号的混合信号,经过雷达信号处理与数据处理最后得到角度信息。
表 1为单脉冲雷达测角系统各主要模块所使用的模型。
表 1 单脉冲雷达测角系统各模块模型 Table 1 Module models of monopulse radar system
| 系统模块 | 模块参数模型 |
| 天线模块 | 改进sinc函数模型 |
| 噪声模块 | 高斯白噪声 |
| 目标模块 | 点目标 |
| 信号模块 | LFM信号 |
| 测角模块 | 比幅测角 |
表选项
3.2.2 干扰机干扰性能仿真分析 对于相干干扰(交叉眼干扰),采用机载干扰机,2个干扰源一般设置于机翼两端,若两干扰源间距离为d,则两干扰源相对于雷达电轴的夹角为
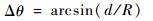 | (10) |
令两信号干扰源信号幅度比为b,回波信号与干扰信号的幅度比为a,如下:
 | (11) |
文献[12]中给出了相干干扰的理论干扰角度:
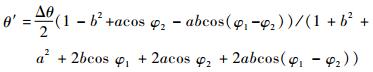 | (12) |
式中:θ′为雷达跟踪的天线误差指向角。
本文采用点目标模型,按照3.2.1节所示构建仿真模型,参照F-16战机翼展9.45 m为例设置两干扰源,令点目标距离雷达10 km,则可计算得到两干扰源张角为0.000 945 rad,设置目标方位角0.5 rad(28.64°),目标俯仰角0.4 rad (22.92°),两干扰源产生的干扰信号相位差为φ。需要注意的是,下列1)~3) 中的仿真未考虑噪声的影响。
1) 干扰信号强度比对干扰效果的影响
图 10为不同干扰信号强度比下的单脉冲雷达系统测角结果。令两干扰源间的相位差φ=π,回波信号强度比a=1/100。图 10中:红色星型线是采用式(11) 的理论仿真结果,蓝色三角型线是采样压缩感知恢复信号构建的角度干扰信号进行相干干扰的角度欺骗干扰结果。可以看出,随着干扰信号强度比b不断趋向于1,干扰误差角度越来越大,且干扰机干扰效果基本可以达到理论仿真的最大角度。
 |
| 图 10 不同干扰信号强度比下测角误差 Fig. 10 Angle measurement error at different interference signal intensity ratios |
| 图选项 |
2) 相位差对测角结果的影响
本文研究了两路干扰信号之间的相位差对于测角误差的影响。取两干扰源之间的干扰信号强度比为b=0.99,回波信号强度比a=1/100,仿真实验结果如图 11所示。图中:φ为相位差。
 |
| 图 11 不同相位差下测角误差 Fig. 11 Angle measurement error under different phase offset |
| 图选项 |
图 11为不同相位差下的测角误差仿真结果。图中:红色星型线表示根据式(12) 仿真所得到的理论测角误差结果,蓝色三角型线表示使用本文所提出的干扰机所得的测角误差结果。由图 11可知,两干扰源相位差越接近π,仿真得到的测角误差越大,即欺骗干扰效果越好。同时,测角误差具有相对于π对称的效果,且在测角误差相位差较为接近π时,变化十分明显,相位差远离π时,几乎无影响,且干扰效果很弱。同时,从图中还可以看出,采用压缩感知恢复信号作为角度欺骗干扰信号时,角误差十分接近理论角误差仿真结果。
3) 回波信号强度比对测角结果的影响
本文研究了回波信号强度比对相干干扰的影响。图 12为不同回波信号强度比下的单脉冲雷达系统测角结果。
 |
| 图 12 不同回波信号强度比下测角误差 Fig. 12 Angle measurement error under different echo signal intensity ratios |
| 图选项 |
图 12中:红色星型线表示根据式(12) 仿真所得到的理论测角误差结果,蓝色三角型线表示使用本文所提出的干扰机所得测角误差结果。取两干扰源间的强度比b=0.99,两干扰源间的相位差φ=π。由图 12可知,随着回波信号强度比a不断增大,即回波信号强度不断增强,角度测量结果越来越接近目标角度,即角度干扰效果越来越弱。干扰机在回波信号强度较小时,可以达到理论测角误差,且当回波信号强度比a>0.1时,干扰误差就非常小了。
4) 噪声对交叉眼干扰的影响
图 13为不同信噪比下的测角误差。两干扰源间的相位差φ=π,两干扰源之间的干扰信号强度比为b=0.99,回波信号强度比a=1/100。由图 13可知,噪声影响下的相干干扰,干扰误差角在无噪声基准误差角附近波动,同时波动值呈下降趋势。这是因为由干扰机转发的信号在幅度上远远大于雷达目标的回波信号,相比回波信号,干扰信号不容易淹没在噪声中,而更容易被雷达接收机探测得到;另一方面,噪声是同时作用于雷达干扰信号与雷达目标信号的,因此噪声对干扰误差角的影响并没有那么敏感,而是会引起误差角度在误差基准角(无噪声情况)附近波动。
 |
| 图 13 不同信噪比下测角误差 Fig. 13 Angle measurement error under different SNR |
| 图选项 |
3.3 角度拖引和闪烁干扰分析
3.3.1 角度拖引干扰 图 14为一种单脉冲拖引干扰示意图[12]。这种方法通过将干扰机在一定范围依次排开,按照一定顺序轮流开关机,将雷达的指向角逐渐拖引开。
 |
| 图 14 拖引干扰示意图[12] Fig. 14 Schematic diagram of pull-off jamming[12] |
| 图选项 |
如图 14所示,这种方法需要在空间投入多部干扰机才能实现较好的角度干扰,本文在研究图 10~图 12中干扰信号、回波信号强度比等因素对角度干扰效果的影响的基础上,提出了一种基于回波信号强度比控制的单脉冲雷达角度拖引干扰。
由图 10可知,误差角度随着干扰信号强度比增大而增大,且增长速度也越来越快。因此,为了实现近似匀速拖引,对干扰信号强度比进行分段处理,使误差角的增加速度在每一个干扰强度区间段内接近保持匀速增大。将干扰信号强度比的区间段范围设置为[0~0.6]、[0.6~0.9]、[0.9~ 0.99]3个区间段,每个区间段对应的拖引时间分别为T1、T2、T3。在每个区间段内,令干扰信号强度比匀速增加。本文采用卡尔曼跟踪滤波器[18]作为单脉冲雷达角度跟踪模型。设置T1=1 s,T2=3 s,T3=2 s,所得的角度跟踪结果如图 15所示。
 |
| 图 15 角度跟踪滤波仿真结果 Fig. 15 Simulation results of angle tracking filter |
| 图选项 |
图 15中:蓝色三角型线为相干干扰的角度仿真结果,红色圆型线为卡尔曼跟踪滤波器的滤波输出。从图中可以看出,卡尔曼滤波器能够很好地跟随角度误差角稳步增大,可以拖引达到的最大角度为1.97°,拖引时间约为6 s。
3.3.2 角度闪烁干扰 在3.3.1节角度拖引达到最大干扰角度时,进入闪烁干扰期,闪烁干扰方式是通过控制干扰信号强度比周期性的变化来实现的,令bI为3.2.2节中干扰信号强度比b的倒数,则有bI=1/b, 干扰信号强度比按周期ΔT来变化:
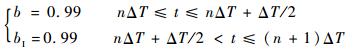 | (13) |
对于单脉冲雷达,闪烁周期ΔT一般为1~6 s[19]。文献[20]分析了选取不同闪烁频率对角跟踪回路的影响。
表 2为角闪烁干扰仿真结果。干扰机强度为相对回波信号强度,设置回波信号强度为1,根据文献[20]设置闪烁周期ΔT=2 s,误差角度为正表示目标向干扰机1方向偏离,反之则表示目标向干扰机2方向偏离。由表 2可知,目标的闪烁角度可以达到4°左右,相当于最大拖引角度的2倍。
表 2 角闪烁干扰仿真结果 Table 2 Simulation results of angle glint jamming
| 闪烁时间 | 干扰机1相对强度 | 干扰机2相对强度 | 干扰信号强度比 | 误差角度/(°) |
| nΔT≤t≤nΔT+ΔT/2 | 100 | 99 | b=0.99 | 1.97 |
| nΔT+ΔT/2 < t≤(n+1)ΔT | 98 | 99 | bI=0.99 | -2.03 |
表选项
3.4 干扰机性能分析 相比于多干扰机协同角度拖引方式,采用机载干扰机分布方式简单,无需在空间中投入多部干扰机,因此,干扰机的投入成本小,且本文在角度拖引干扰的基础上,控制干扰信号强度比,可以在拖引干扰完毕后直接引入闪烁干扰,相当于增强了角度拖引的角度,提升了干扰机性能。另一方面,当目标朝着雷达运动时,随着距离接近,干扰机张角会随之增大,则干扰误差角会越来越大。同时,本文采用压缩感知框架对DRFM进行了优化,实现了欠采样条件下的干扰信号重构,提高了DRFM干扰机处理高频宽带信号的能力。
4 结论 为了降低DRFM设备对于高速采样器与存储器的要求,本文根据LFM信号在FRFT域的能量聚集特性,设计了一种压缩感知框架下的DRFM单脉冲雷达欺骗干扰机模型,实现了对雷达信号压缩采样,同时,本文以相干干扰原理为基础,通过控制干扰信号强度比实现了稳定的角度拖引干扰以及闪烁干扰,然后设计单脉冲雷达系统,对欺骗干扰机的干扰性能进行了仿真实验。仿真实验结果表明,干扰机可以很好地产生欺骗干扰信号。通过干扰强度控制,能够实现对雷达的稳定拖引以及闪烁干扰。
参考文献
| [1] | SHERMAN S M. Monopulse principles and techniques[M].Dedham: Artech House, 1985: 362-380. |
| [2] | PAIK H, SASTRY N N, SANTIPRABHA I. Effectiveness of repeat jamming using LFM interference signal in monopulse receivers[J].Procedia Computer Science, 2015, 57: 296–304.DOI:10.1016/j.procs.2015.07.489 |
| [3] | SHANG Z, BAI W, FU X. Analysis of cross-eye jamming[J].International Proceedings of Computer Science & Information Tech, 2012, 55: 8–12. |
| [4] | LIU S Y, DONG C, XU X J, et al. Analysis of rotating cross-eye jamming[J].IEEE Antennas & Wireless Propagation Letters, 2015, 14: 939–942. |
| [5] | 刘松杨, 董春曦, 朱颖童, 等. 基于角度参数特定边界值的旋转交叉眼干扰容限研究[J].电子与信息学报, 2016, 38(4): 906–912. LIU S Y, DONG C X, ZHU Y T, et al. Tolerance analysis of rotating cross-eye jamming based on angle factor specific boundary value[J].Journal of Electronics and Information Technology, 2016, 38(4): 906–912.(in Chinese) |
| [6] | PLESSIS W P D, ODENDAAL J W, JOUBERT J. Tolerance analysis of cross-eye jamming systems[J].IEEE Transactions on Aerospace & Electronic Systems, 2010, 47(1): 740–745. |
| [7] | 张曦, 王星, 王红卫, 等. 单脉冲雷达的相干干扰研究[J].现代雷达, 2013, 35(12): 21–26. ZHANG X, WANG X, WANG H W, et al. A study on Mono-pulse radar coherent jamming[J].Modern Radar, 2013, 35(12): 21–26.(in Chinese) |
| [8] | CANDES E J, TAO T. Near-optimal signal recovery from random projections:Universal encoding strategies?[J].IEEE Transactions on Information Theory, 2006, 52(12): 5406–5425.DOI:10.1109/TIT.2006.885507 |
| [9] | ALMSLMANY A, CAO Q, WANG C. A new airborne self-protection jammer for countering ground radars based on sub-Nyquist[J].IEICE Electronics Express, 2015, 12(10): 2015–2091. |
| [10] | 董创业. 基于DRFM的雷达干扰技术研究[D]. 西安: 西安电子科技大学, 2007: 5-10. DONG C Y.Researching on radar jamming technology based on DRFM[D].Xi'an:Xidian University, 2007:5-10(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10701-2007048783.htm |
| [11] | PEI S C, DING J J. Closed-form discrete fractional and affine Fourier transforms[J].IEEE Transactions on Signal Processing, 2000, 48(5): 1338–1353.DOI:10.1109/78.839981 |
| [12] | 陶然. 分数阶傅里叶变换及其应用[M].北京: 清华大学出版社, 2009: 390-391. TAO R. Fractional Fourier transform and its application[M].Beijing: Tsinghua University Press, 2009: 390-391.(in Chinese) |
| [13] | 方标, 黄高明, 高俊, 等. FRFT域LFM雷达回波信号的压缩采样模型[J].西安电子科技大学学报, 2015, 42(1): 200–206. FANG B, HUANG G M, GAO J, et al. Compressive sensing of LFM echo signals in FRFT domains[J].Journals of Xidian University, 2015, 42(1): 200–206.(in Chinese) |
| [14] | FERREIRA J C, FLORES E L, CARRIJO G A. Quantization noise on image reconstruction using model-based compressive sensing[J].IEEE Latin America Transactions, 2015, 13(4): 1167–1177.DOI:10.1109/TLA.2015.7106372 |
| [15] | MAHAFZA B R. Radar systems analysis and design using MATLAB[M].2nd edBoca Raton: CRC Press, 2000. |
| [16] | 陈明嗣. 雷达系统仿真与角度干扰技术研究[D]. 成都: 电子科技大学, 2011: 30-32. CHEN M S.Simulation of radar system and research on angle jamming technology[D].Chengdu:University of Electronic Science and Technology of China, 2011:30-32(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10614-1011192495.htm |
| [17] | 徐喜安. 单脉冲雷达系统的建模与仿真研究[D]. 成都: 电子科技大学, 2006: 26-28. XU X A.Modeling and simulation analysis of monopulse radar[D].Chengdu:University of Electronic Science and Technology of China, 2006:26-28(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10614-2006113147.htm |
| [18] | KULIKOV G Y, KULIKOVA M V. The accurate continuous-discrete extended Kalman filter for radar tracking[J].IEEE Transactions on Signal Processing, 2015, 64(4): 948–958. |
| [19] | 王国玉, 汪连栋, 王国良. 雷达电子战系统数学仿真与评估[M].北京: 国防工业出版社, 2004: 295-298. WANG G Y, WANG L D, WANG G L. Mathematical simulation and evaluation of radar ew system[M].Beijing: National Defence Industry Press, 2004: 295-298.(in Chinese) |
| [20] | 闫晓鹏, 栗苹, 耿小明. 同步闪烁干扰中闪烁频率的选取[J].北京理工大学学报, 2008, 28(6): 553–556. YAN X P, LI P, GENG X M. Study on blinking frequency selection in non-coherent blinking jamming[J].Transactions of Beijing Institute of Technology, 2008, 28(6): 553–556.(in Chinese) |
