长期以来，多足步行机器人是国内外机器人领域研究的热点之一。相对于轮式机器人和履带式机器人，多足步行机器人由于其非连续支撑的特点，具有极强的地形适应性和运动灵活性^[1]。相对于双足机器人，四足机器人具有更好的承载能力和稳定性，且比六足机器人结构简单，易于控制^[2]。从工程角度，综合研发成本、制作难易度、控制方法和系统稳定性等各个方面，四足机器人是最好的足式机器人形式^[3]，从而受到了国内外研究人员的广泛重视。
当今足式机器人的研究多偏重于实际应用，与运动特性相比，可操作性也越来越多地受到研究人员的关注。为了实现可操作性，一方面，可采用在机器人机身上安装操作臂的方法。最早的移动操作臂^[4-5]是由一个可移动的基座和与之连接的一个操作臂组成，基座可以利用轮子、轨道或机械腿进行移动，而操作臂可以实现快速和精准的操作。波士顿动力公司研发的带有操作臂的BigDog^[6]和SpotMini机器人^[7]，在机身上安装了2或3自由度的操作臂，但操作臂增加了机身质量，且对机身运动的稳定性造成了影响。另一方面，多足步行机器人的其中的1条、2条或3条腿可充当操作臂，进行操作。东京工业大学的Kato和Hirose^[8]研制了四足机器人TITAN-IX，该机器人不仅可以正常行走，还可以使用足端进行操作，并可自动更换足端工具。NASA研发的六足地外探测机器人ATHLETE^[9-10]，在每一个足端轮子的侧方均可快速安装和更换不同的工具，实现不同的操作功能。
5自由度的操作臂，由于其本身的欠自由度结构，很难保证末端执行器同时达到期望的位置和姿态，而且由于机构构型的不同，也无法得到一个统一的逆运动学建模方法。Essex大学的Gan等^[11]针对5自由度Pioneer2机器人提出了一种逆运动学模型，该方法能给出任何可达到位置和姿态的逆运动学解，而且对99%以上不可达位姿也能给出近似解。随后针对该机器人，Xu等^[12]又提出了一种在保证期望位置的同时，保持其中一轴姿态正确逆运动学模型。国内，为了解决5自由度采摘机械手的轨迹规划问题，卢君宜等^[13]利用D-H参数法得到了该机器人的正运动学模型，并综合利用解析法和几何图解法得到了逆运动学解析解。
本文针对移动操作任务设计了一种腿臂融合四足机器人，对其中1条腿分支进行腿臂融合的特殊设计，实现腿臂功能复用。该分支在折叠时为普通腿分支实现行走功能，展开后变成5自由度的操作臂，可实现操作功能。首先，利用指数积公式建立了机器人的单腿运动学模型和整体逆运动学模型；其次，针对所设计的腿臂融合机器人操作臂构型，提出了保证位置和姿态的2种逆运动学最优求解方法；然后，在此基础上建立了本体与操作臂组成的串并混联机构的运动学模型，利用本体位移补偿操作臂末端位置偏差，使操作臂末端可同时达到期望的位置和姿态，实现精确操作；最后，对机器人本体、操作臂和串并混联机构的工作空间进行了仿真，并利用实验验证了机器人的腿行走和臂操作功能。
1 腿臂融合四足机器人机构与结构设计 四足机器人一般由机器人本体和4条串联机械腿组成。机械腿按照关节布置方式可分为仿爬行动物式和仿哺乳动物式2种。为了提高机器人在不平整地面的灵活性和稳定性，同时为了使得机器人在操作臂模式时有更高的稳定性和更大的活动范围，本文设计的四足机器人采用仿爬行动物式腿部结构^[14-15]。图 1为机器人整体机构简图。图 2为机器人样机整体结构图。机器人4个髋关节舵机在机器人本体上对称布置，髋关节、大腿关节、小腿关节采用单自由度铰链连接，足部采用球铰连接。其中1条腿被设计为腿臂融合分支，包含有5个转动关节，如图 3所示。当机器人行走时，腿臂融合分支折叠，实现正常的腿部功能，进行行走；当使用手臂末端执行器进行操作时，利用其他3条腿支撑本体，腿臂融合分支展开后成为以机器人本体为基座的5自由度操作臂，进行相应操作。

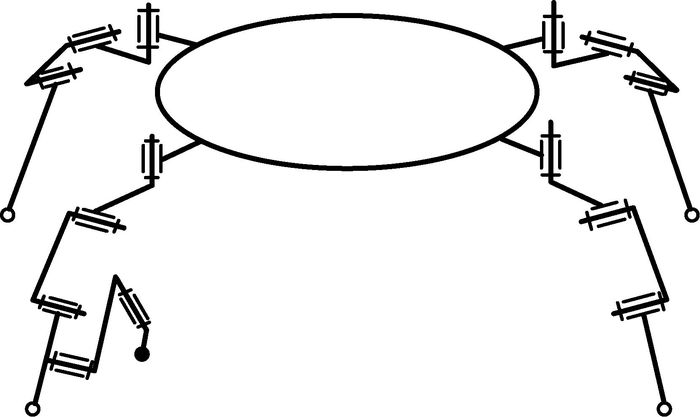图 1 腿臂融合四足机器人机构简图 Fig. 1 Mechanism sketch of integrated leg-arm quadruped robot

图选项

图 2 腿臂融合四足机器人结构 Fig. 2 Structure of integrated leg-arm quadruped robot

图选项

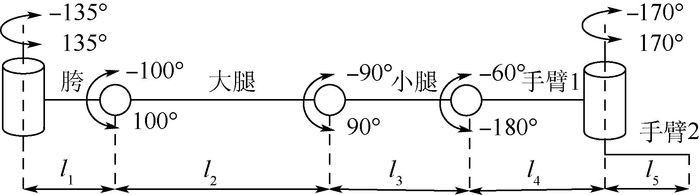图 3 含手臂的腿部机构简图 Fig. 3 Mechanism sketch of leg with arm

图选项

2 行走模式运动学模型分析 2.1 单腿运动学 在行走模式下，机器人腿部等价于一个三关节串联机构，本文采用指数积公式^[16]方法对机器人进行运动学建模。
图 4为行走模式下的单腿机构简图。为求解单腿的正向运动学，首先建立4个坐标系：全局坐标系{O}、本体坐标系{C}、髋关节坐标系{B_i}以及足端坐标系{A_i}。全局坐标系{O}建立在地面上；本体坐标系{C}建立在机器人本体的几何中心，如图 5所示；髋关节坐标系{B_i}的z轴与髋关节旋转轴线重合，x轴沿l₁方向；足端坐标系{A_i}与髋关节坐标系{B_i}平行且原点位于足末端，取机器人腿完全展开时为初始位形。

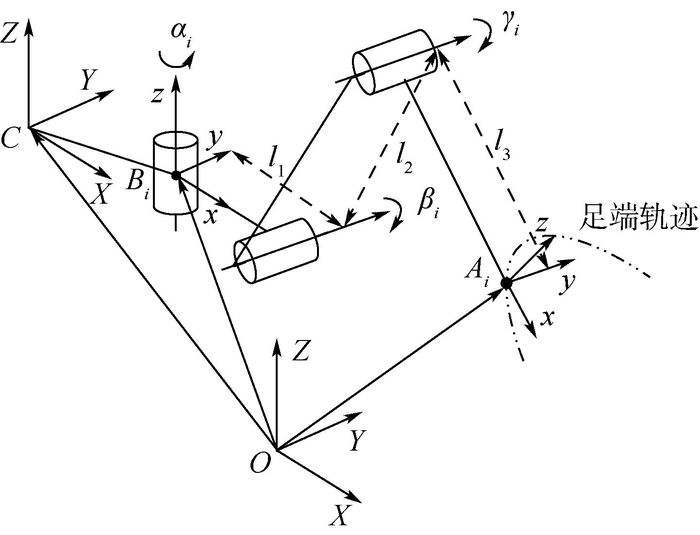图 4 腿部机构简图 Fig. 4 Mechanism sketch of leg

图选项

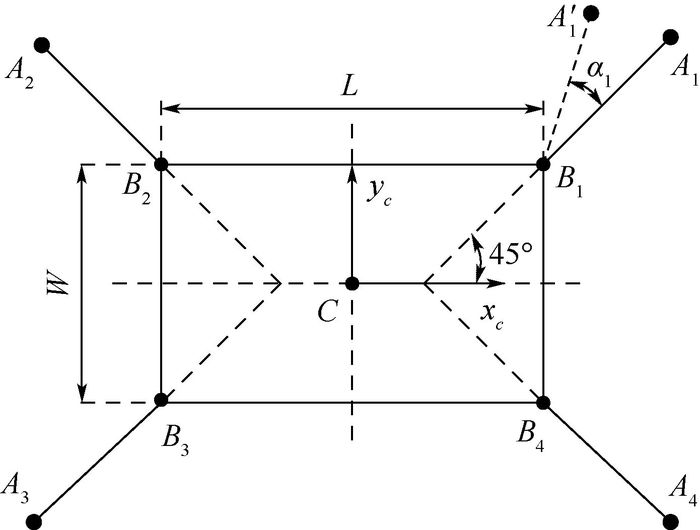图 5 机器人本体平面投影图 Fig. 5 Plane projection drawing of robot body

图选项

本体坐标系{C}和髋关节坐标系{B_i}都固连在机器人本体上，故本体坐标系{C}到髋关节坐标系{B_i}的变换矩阵固定不变，可以描述为

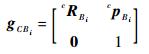式中：^cR_Bi为3×3的旋转矩阵；^cp_Bi为3×1的位置向量。


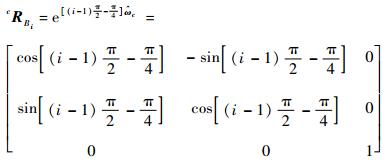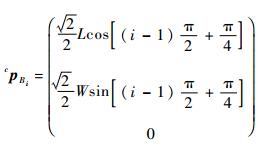对于机器人的第i条腿来说，初始位形下，髋关节坐标系{B_i}到足端坐标系{A_i}的变换为

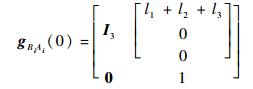运动旋量ξ_ij描述的是第i条腿的第j个关节的旋量运动，根据旋量理论^[17]，对于转动关节，运动旋量可以表示为

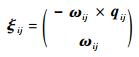式中：ω_ij∈R³为运动旋量运动轴线上的单位矢量；q_ij∈R³为轴线上任意一点。
各个关节的运动旋量计算如下：

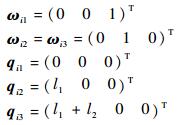因此

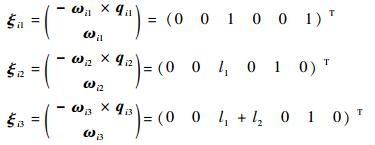单腿的正运动学用指数积公式表示为

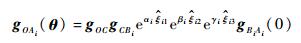(1)

式中：α_i为髋关节变量；β_i为大腿关节变量；γ_i为小腿关节变量；g_OC为从全局坐标系{O}到本体坐标系{C}的变换矩阵，即

其中：^oR_C为旋转矩阵，表示机器人本体在全局坐标系中的姿态；^oP_C为位置矢量，表示机器人本体在全局坐标系中的位置。
单腿的逆运动学问题是给定足端的位置后，求解各个关节变量，即在g_OAi(θ)已知的情况下求解α_i、β_i和γ_i。
由式(1) 可以得到

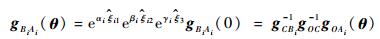而且

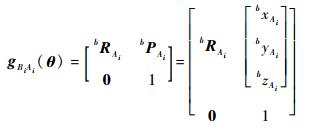由前述正运动学可以得到

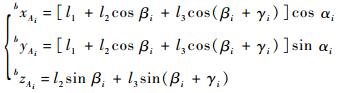(2)

方程组(2) 的求解方法可参考文献[18-19]，从而可以得到α_i、β_i和γ_i。具体结果如下：

式中：

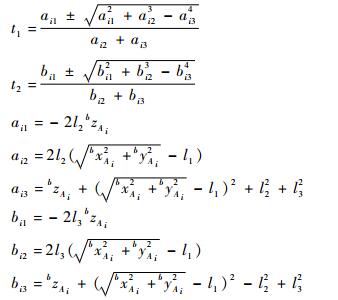通常方程组求得的解有2个，几何意义如图 6所示(情形Ⅰ：t₁取负号，t₂取正号；情形Ⅱ：t₁取正号，t₂取负号)。

图 6 不同解的几何意义 Fig. 6 Geometric meaning for different solutions

图选项

2.2 整体逆运动学 四足机器人整体可看作一个并联机构，本体是该并联机构的动平台，4条腿是该并联机构的串联支链。对于并联机构而言，由于各支链的运动参数互相耦合，其正运动学问题求解非常复杂且结果不唯一，目前尚未有求解并联机构正运动学问题的一般方法。并联机构逆运动学问题的求解则相对简单，可根据机器人本体的位姿和各足端点的位置，通过求解逆运动学问题来获得相应的关节转角值，以实现期望的运动。
按照图 4的方式建立参考坐标系，本体的位姿用g_oc∈SE(3) 表示，第i(i=1, 2, 3, 4) 条腿足端在全局坐标系{O}中的坐标用^oP_Ai∈R³表示，第i条腿足端在髋关节坐标系{B_i}中的坐标用^bP_Ai∈R³表示。
由式(1) 可得到

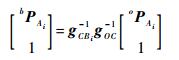(3)

如果给定^oP_Ai和g_OC，可通过式(3) 求出^bP_Ai。再根据2.1节求解方程组(2)，即可得到第i条腿的关节转角向量θ_i=(α_i β_i γ_i)^T。
3 操作模式运动学模型分析 机器人在操作模式时，腿臂融合分支展开成为5自由度操作臂，其余3条腿支撑机器人本体。本节先对操作臂进行正运动学建模，在此基础上分析逆运动学求解方法。由于机器人操作臂只有5自由度，而空间刚体运动包含6个自由度，因而对于给定的期望位置和姿态，操作臂不能保证同时完全满足。这里针对足式机器人本体位置比姿态更容易调整的特点，将位置和姿态的影响分开，提出2种逆解方法：保证位置和保证姿态，并给出每种方法下的姿态或位置偏差。在保证操作臂达到期望姿态的前提下，利用本体位移补偿位置偏差，这样可以使操作臂同时达到期望的位置和姿态，实现精确操作。最后对操作臂和与本体联合的操作臂工作空间进行仿真和分析。
3.1 操作臂的正运动学 操作臂的机构简图如图 7所示。使用指数积方法，取θ=0对应于机构完全展开时的位形，并建立基础坐标系{S}和工具坐标系{T}。其中，基础坐标系{S}的z轴与手臂关节1的转轴重合，x轴沿l₁方向，工具坐标系{T}与基础坐标系{S}平行且原点位于操作臂末端。

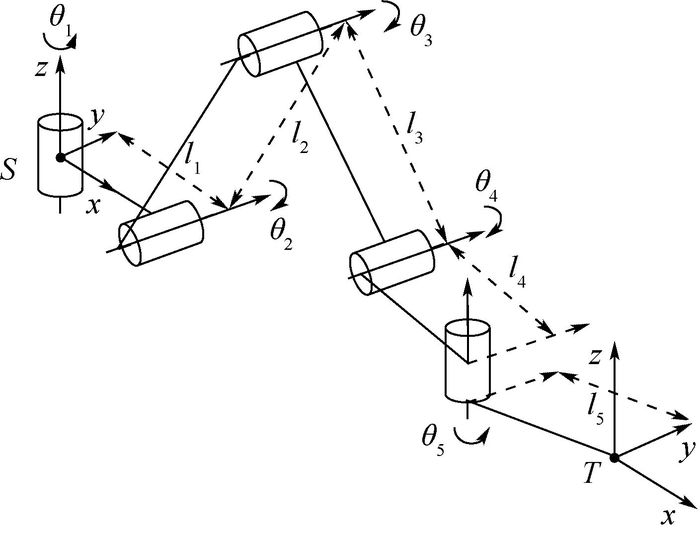图 7 操作臂机构简图 Fig. 7 Mechanism sketch of operating arm

图选项

θ=0时，基础坐标系与工具坐标系的变换为

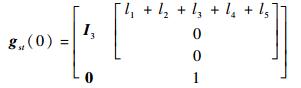为了构造转动关节的旋量，注意到

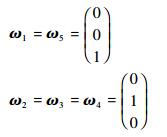操作臂正解的指数映射具有如下形式：

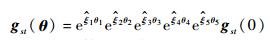用指数积公式展开得

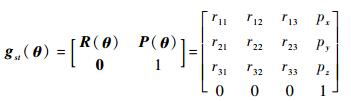该矩阵描述了末端工具坐标系在基础坐标系中的位置和姿态，其中：

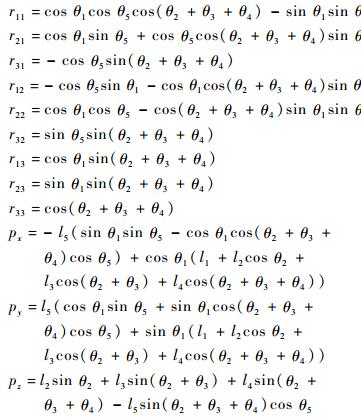3.2 操作臂的逆运动学 为了求解方便，通过观察，令

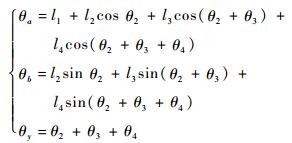(4)

并代入g_st(θ)得到

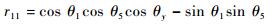(5)

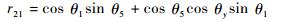(6)

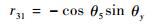(7)

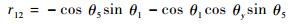(8)

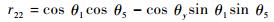(9)

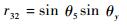(10)

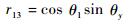(11)

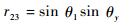(12)

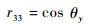(13)

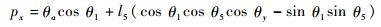(14)

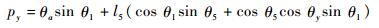(15)

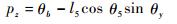(16)

进一步，将式(5) 代入式(14)，并将式(6) 代入式(15)，得到

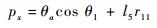(17)

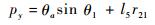(18)

通过观察可知，R(θ)与θ₁、θ₅、θ_y相关，P(θ)与θ₁、θ_a、θ_b相关。为了保证位置，需要由P(θ)求解θ₁，而为了保证姿态，θ₁则需要由R(θ)求解。

3.2.1 保证位置的逆解方法 1) 求解θ_a
由式(17)、式(18) 得

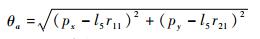2) 求解θ_b
由式(16) 得

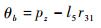3) 求解θ₁
由式(17) 和式(18) 得

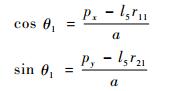从而

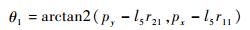4) 求解θ₅
由式(5)、式(6) 得

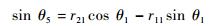从而

5) 求解θ_y
由式(5)、式(6) 得

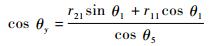又由式(7) 得到

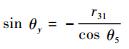从而

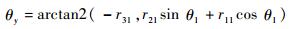6) 求解θ₂、θ₃、θ₄
解方程组(4)，得到

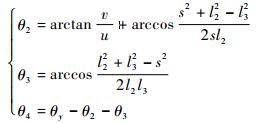式中：

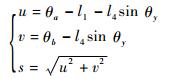7) 姿态偏差计算
将θ₁、θ₅、θ_y代入R(θ)，得到实际的姿态为R_a(θ)。定义旋转矩阵R_e(θ)为姿态偏差，则R(θ)=R_e(θ)R_a(θ)，从而得到

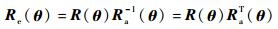此即是在保证位置逆解方法下的姿态偏差。

3.2.2 保证姿态的逆解方法 1) 求解θ₁
由式(11)、式(12) 可得

从而

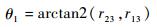2) 求解θ_y
由式(13) 直接可得

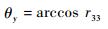3) 求解θ₅
由式(7)、式(10) 可得

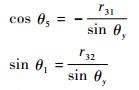从而

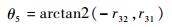4) 求解θ_a
观察P(θ)可知，p_x、p_y与θ_a、θ₁相关，而θ₁已经由R(θ)求出。由于在机器人手臂操作时，位置精度有着更重要的意义，而且误差也很容易通过机身的位移来补偿，故虽然不能保证p_x、p_y与期望值相同，但可以通过优化θ_a来使得p_x、p_y的误差达到最小。这里提出目标函数

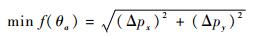由式(17)、式(18)，令f₁₁=cos θ₁, f₁₂=l₅r₁₁，f₂₁=sin θ₁, f₂₂=l₅r₂₁, 则

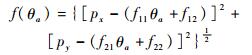展开上式得

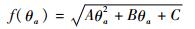式中：

易知，该目标函数在θ_a=B/(2A)时取得最小值。将A、B、C及f₁₁、f₁₂、f₂₁、f₂₂代入得

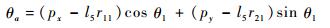5) 求解θ_b
由式(16) 得

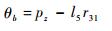6) 求解θ₂、θ₃、θ₄
解方程组(4) 得

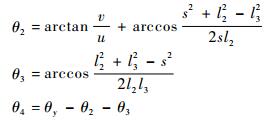式中：

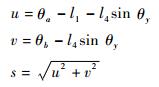7) 位置偏差计算
将θ₁、θ_a、θ_b代入P(θ)，得到实际的位置齐次坐标P_a(θ)。定义P_e(θ)为位置偏差，且P(θ)=P_e(θ)+P_a(θ)，则

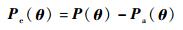(19)

此即是在保证姿态逆解方法下的位置偏差。
3.3 串并混联机构逆运动学 当机器人操作臂联合本体运动时，两者可等效为一个冗余自由度串并混联机构，按照传统方法，其逆运动学求解较为复杂。这里利用机器人本体位置可移动范围较大的特点，使用操作臂保证姿态的逆解方法求得位置误差，然后使用机身补偿位置误差，从而可实现腿臂融合分支的位姿精确控制。
给定腿臂融合分支期望位置和姿态后，由式(19) 可得到位置偏差P_e(θ)。根据2.2节，将P_e(θ)代入式(3)，可得到^bP_Ai，令

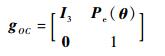再根据2.1节，求解方程组(2)，即可得到每条腿的关节转角θ_i=(α_i β_i γ_i)^T。
3.4 本体固定时操作臂工作空间分析 操作臂的主要尺寸和关节活动范围如表 1所示。根据3.1节建立的操作臂正运动学, 可以得到本体固定时操作臂的工作空间，如图 8和图 9所示。
表 1 腿臂融合四足机器人主要参数 Table 1 Basic parameters for integrated leg-arm quadruped robot

参数	数值
l1 /mm	48
l2/mm	190
l3/mm	166
l4/mm	110
l5/mm	65
θ1/(°)	(-135, 135)
θ2/(°)	(-100, 100)
θ3/(°)	(-170, 170)
θ4/(°)	(-60, -180)
θ5/(°)	(-170, 170)

表选项

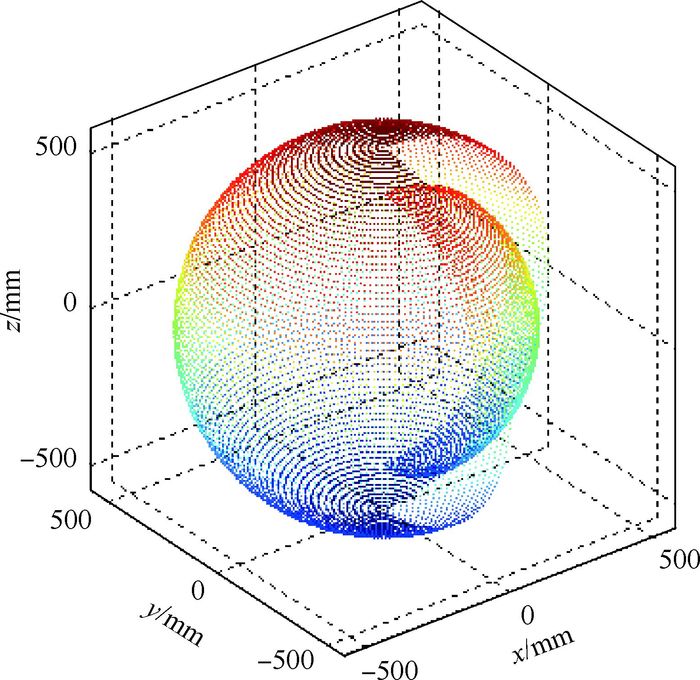图 8 本体固定时操作臂工作空间 Fig. 8 Workspace of operating arm with body fixed

图选项

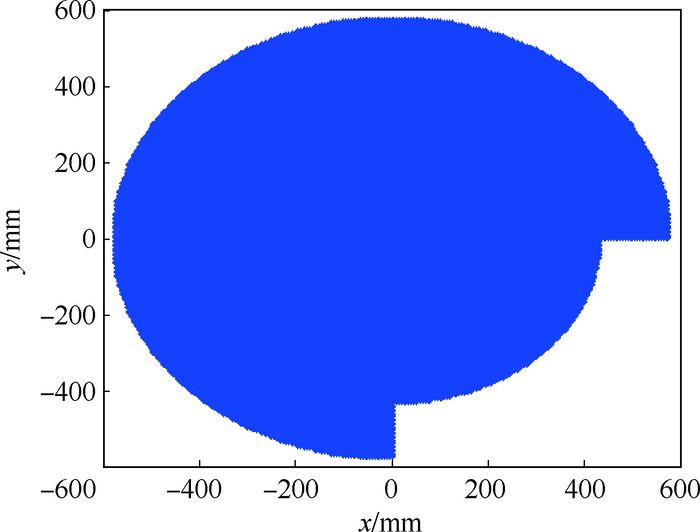图 9 本体固定时操作臂XOY平面的工作空间 Fig. 9 Workspace of operating arm in XOY plane with body fixed

图选项

3.5 本体可移动时操作臂工作空间分析 当机器人处于操作模式时，其中1条腿伸出作为操作臂，其他3条腿作为支撑腿。此时操作臂可以联合本体运动，从而可以拓展操作臂的工作空间。为此首先分析本体的工作空间。如图 10所示，A₂、A₃、A₄为机器人支撑足的立足点，此时机器人本体的可移动范围位于直角支撑三角形△A₂A₃A₄内。利用机器人整体逆运动学结合边界法仿真出本体姿态固定下的工作空间，如图 11所示。

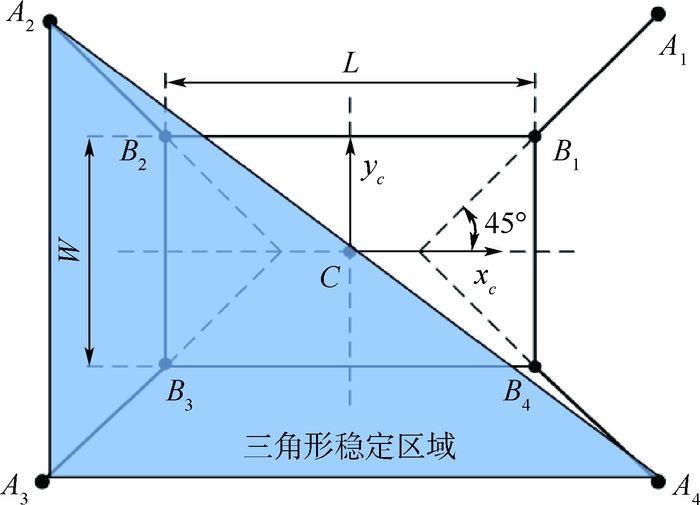图 10 3条腿支撑时机器人本体稳定区域 Fig. 10 Stability zone of robot body supported by three legs

图选项

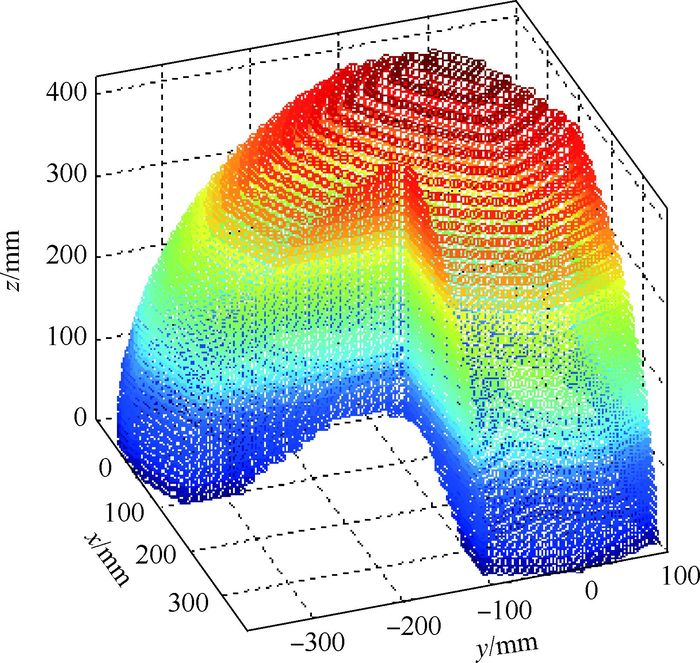图 11 姿态固定下的机器人本体工作空间 Fig. 11 Workspace of robot body when gesture is fixed

图选项

结合操作臂单独的工作空间，最终可以得到联合本体操作臂工作空间，如图 12和图 13所示。对比图 8与图 12可以看到，当与本体联合运动时，可以很大程度上拓展操作臂的工作空间。

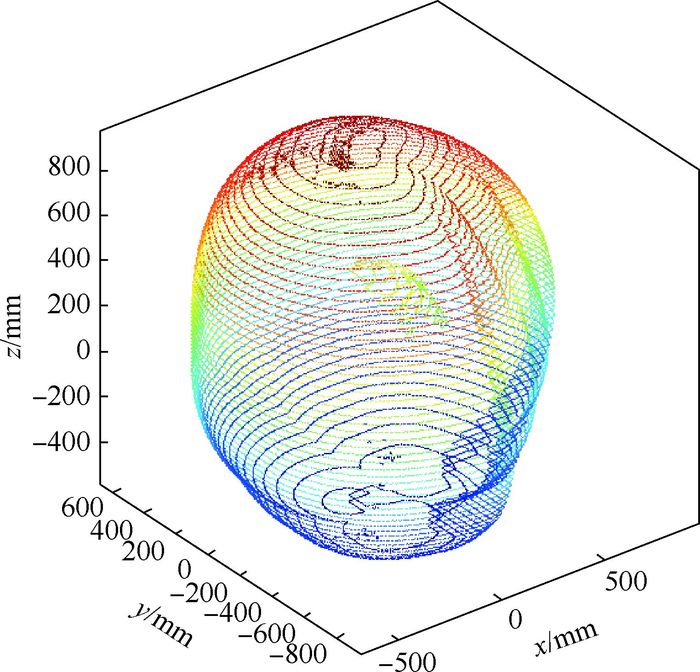图 12 本体可移动时操作臂工作空间 Fig. 12 Workspace of operating arm with body mobile

图选项

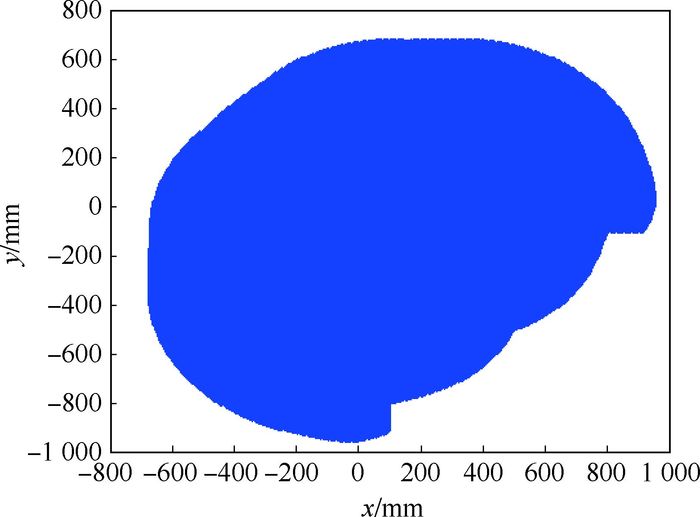图 13 本体可移动时操作臂XOY平面的工作空间 Fig. 13 Workspace of operating arm in XOY plane with body mobile

图选项

4 实验验证 对腿臂融合四足机器人的腿行走和臂操作功能分别进行实验验证。图 14为机器人行走模式实验。

图 14 机器人行走模式 Fig. 14 Walking mode of robot

图选项

图 15为机器人操作模式实验。以图 7中基础坐标系{S}为参考系，分别控制机器人操作臂末端摄像头达到不同的期望位置和姿态，其中姿态以ZYZ顺序的欧拉角表示。从图 15可见，为了保持操作臂末端达到期望位置，机器人本体会不断移动来补偿位置偏差。

图 15 机器人操作模式 Fig. 15 Operating mode of robot

图选项

5 结论 本文设计了一种腿臂融合的四足机器人，其腿臂融合分支具有腿行走和臂操作2种功能。
1) 对机器人腿行走和操作臂2种模式分别进行了正运动学和逆运动学分析，在欠自由度机构的基础上给出了5自由度操作臂保证位置和保证姿态的2种逆运动学求解方法，并给出了相应的姿态误差和位置误差。
2) 提出了一种串并混联机构的逆解方法，可以实现操作臂末端位姿的精确控制。
3) 进行相应的仿真和实验，验证了机器人行走和操作功能。
研究结果为下一步机器人和操作臂的轨迹规划及运动控制研究奠定了基础。

参考文献

[1]	HIROSE S.Three basic types of locomotions in mobile robots[C]//Proceedings of the 5th International Conference on Advanced Robotics 1991.Piscataway, NJ:IEEE Press, 1991, 1:12-17.
[2]	徐轶群, 万隆君. 四足步行机器人腿机构及其稳定性步态控制[J].机械科学与技术, 2003, 22(1): 86–91. XU Y Q, WAN L J. Leg mechanism of a quadruped walking robot and its stability gait control[J].Mechanical Science and Technology for Aerospace Engineering, 2003, 22(1): 86–91.(in Chinese)
[3]	HIROSE S, KATO K.Study on quadruped walking robot in Tokyo institute of technology-past, present and future[C]//Proceedings of the 2000 IEEE International Conference on Robotics & Automation.Piscataway, NJ:IEEE Press, 2000, 1(7):414-419.
[4]	YAMAMOTO Y, YUN X. Coordinating locomotion and manipulation of a mobile manipulator[J].IEEE Transactions on Automatic Control, 1994, 39(6): 1326–1332.DOI:10.1109/9.293207
[5]	KHATIB O, YOKOI K, CHANG K, et al.Vehicle/arm coordination and multiple mobile manipulator decentralized cooperation[C]//Proceedings of the 1996 IEEE/RSJ International Conference on Intelligent Robots and Systems(IROS 96).Piscataway, NJ:IEEE Press, 1996, 4-8:546-553.
[6]	ACKERMAN E.BigDog throws cinder blocks with huge robotic face-arm[EB/OL].[2013-03-01].http://spectrum.ieee.org/automaton/robotics/military-robots/bigdog-throws-cinder-blocks-with-huge-robotic-facearm.
[7]	ACKERMAN E.Boston dynamics’SpotMini is all electric, agile, and has a capable face-arm[EB/OL].[2016-06-23].http://spectrum.ieee.org/automaton/robotics/home-robots/boston-dynamics-spotmini.
[8]	KATO K, HIROSE S. Development of the quadruped walking robot, TITAN-IX-Mechanical design concept and application for the humanitarian demining robot[J].Advanced Robotics, 2001, 15(2): 191–204.DOI:10.1163/15685530152116227
[9]	WILCOX B H.ATHLETE:A cargo and habitat transporter for the moon[C]//Proceedings of the 2009 IEEE Conference on Aerospace.Piscataway, NJ:IEEE Press, 2009, 7-14:1-7.
[10]	WILCOX B H, LITWIN T, BIESIADECKI J, et al. ATHLETE:A cargo handling and manipulation robot for the moon[J].Journal of Field Robotics, 2007, 24(5): 421–434.DOI:10.1002/(ISSN)1556-4967
[11]	GAN J Q, OYAMA E, ROSALES E M, et al. A complete analytical solution to the inverse kinematics of the Pioneer2 robotic arm[J].Journal of Robotica, 2005, 23(1): 123–129.DOI:10.1017/S0263574704000529
[12]	XU D, CARLOS A, ACOSTA C, et al. An analysis of the inverse kinematics for a 5-DOF manipulator[J].International Journal of Automation and Computing, 2005, 2(2): 114–124.DOI:10.1007/s11633-005-0114-1
[13]	卢君宜, 杨庆华, 高峰, 等. 五自由度农业采摘机器人轨迹规[J].机电工程学报, 2010, 27(12): 1–6. LU J Y, YANG Q H, GAO F, et al. Trajectory planning of a 5-DOF agricultural picking robot[J].Journal of Mechanical Electrical Engineering, 2010, 27(12): 1–6.(in Chinese)
[14]	丁希仑, 徐坤. 一种新型变结构轮腿式机器人的设计与分析[J].中南大学学报, 2009, 40(S1): 91–101. DING X L, XU K. Design and analysis of a novel metamorphic wheel-legged rover mechanism[J].Journal of Central South University, 2009, 40(S1): 91–101.(in Chinese)
[15]	陈浩, 丁希仑. 四足变结构机器人的运动学分析[J].北京科技大学学报, 2012, 34(1): 53–58. CHEN H, DING X L. Kinematics analysis of a quadruped robot with variable structure[J].Journal of University of Science and Technology Beijing, 2012, 34(1): 53–58.(in Chinese)
[16]	BROCKETT R W. Mathematical theory of networks and systems[M].Berlin: Springer, 1984: 120-129.
[17]	于靖军, 刘辛军, 丁希仑, 等. 机器人机构学的数学基础[M].北京: 机械工业出版社, 2008: 60-78. YU J J, LIU X J, DING X L, et al. Mathematic foundation of mechanisms and robotics[M].Beijing: China Machine Press, 2008: 60-78.(in Chinese)
[18]	陈学东, 郭鸿勋. 四足机器人爬行步态的正运动学分析[J].机械工程学报, 2003, 39(2): 8–12. CHEN X D, GUO H X. Direct kinematics analysis of crawl gait for a quadruped robot[J].Chinese Journal of Mechanic Engineering, 2003, 39(2): 8–12.(in Chinese)
[19]	陈学东, 孙翊, 贾文川. 多足步行机器人运动规划与控制[M].武汉: 华中科技大学出版, 2006: 31-35. CHEN X D, SUN Y, JIA W C. Motion planning and control of mutilegged walking robots[M].Wuhan: Huazhong University of Science and Technology Press, 2006: 31-35.(in Chinese)