现有公开发表的关于锥体目标微动形式分类的文献大多是基于散射源微多普勒差异来实现微动分类的。文献[11]利用从锥体目标时频分布提取出的时频图宽度、时频平均熵值、频谱熵及自相关函数峰值比这4类特征实现了章动、进动及自旋锥体目标微动形式的分类。文献[12-14]分析了锥体目标微多普勒谱的分布差异,分别指出应用微多普勒域熵及波形标准差来区分微动以及应用特征谱来识别微动的方法,但文献[12-14]中回波模型采用的是理想散射点模型,并未考虑锥体目标锥底滑动型散射源对微动分类的影响,而且也未考虑散射源散射强度随雷达视角的变化,不过文献[12-14]中利用微多普勒谱的差异来寻求微动识别特征是值得借鉴的,本文尝试在此基础上进一步寻求章动、进动及自旋这3类锥体目标散射源微多普勒及其频谱的差异,进而实现微动分类。
1 空间锥体目标散射源微多普勒及其频谱分析 首先考虑不同微动形式下锥顶及锥底滑动型强散射源在时频分布中的理论轨迹。建立如图 1所示的空间锥体目标微动模型,以锥体质心O为坐标原点,以锥旋角速度矢量的方向为z轴,y轴与z轴及雷达视向η共面并垂直于z轴,x轴由右手螺旋定则确定,设锥旋角为φ,章动角为θ,雷达视向与z轴的夹角为α,简称雷达视角。锥体目标在高频电磁波照射下的散射主要由锥顶A及锥底滑动型散射源B、C组成。
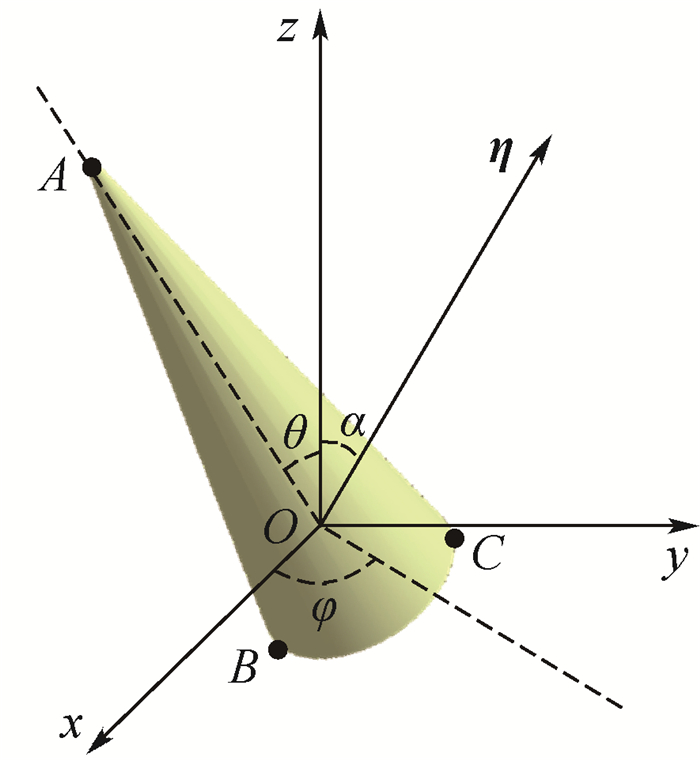 |
| 图 1 空间锥体目标微动模型 Fig. 1 Micro-motion model of spatial cone target |
| 图选项 |
设锥体质心O到锥顶A的距离为
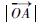
 | (1) |
雷达视向η可表示为
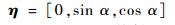 | (2) |
那么锥顶散射源A在雷达视向上的投影为
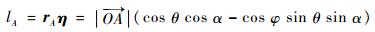 | (3) |
相应的微多普勒频移可表示为
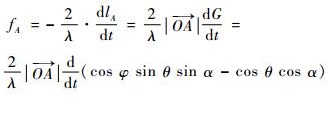 | (4) |
式中:G=cos φ sin θ sin α-cos θ cos α;λ为波长。
下面继续分析锥底滑动型散射源微多普勒频移的理论分布。首先得到雷达视向η与锥体极轴所构成的平面的单位法向为
 | (5) |
式中:
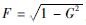
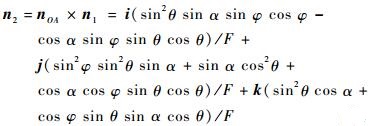 | (6) |
那么锥底滑动型强散射源B(C)在雷达坐标系下的坐标为
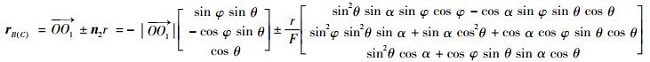 | (7) |
式中:
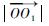
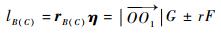 | (8) |
相应的微多普勒为
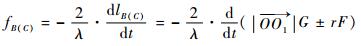 | (9) |
下面依据式(4) 及式(9) 分析不同微动形式下锥体目标强散射源微多普勒谱谱线分布规律。
1.1 自旋锥体目标散射源微多普勒谱 自旋锥体目标的锥旋角φ及章动角θ均为常数,所以其锥顶及锥底微多普勒频移均为0,即
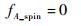 | (10) |
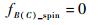 | (11) |
那么自旋锥体目标在时频分布中只在0Hz处有散射源分布,且其微多普勒频谱谱线为幅值为0的一条直线。
1.2 进动锥体目标散射源微多普勒谱 进动锥体目标的章动角θ为常数,也称为进动角,锥旋角φ满足:
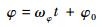 | (12) |
式中:ωφ为锥旋角速率;φ0为初始锥旋角。此时G和F均为以锥旋角φ为变量的函数,其中G直接由角频率为ωφ的分量合成,无需继续分解,由式(4) 知进动锥体目标锥顶散射源的微多普勒为
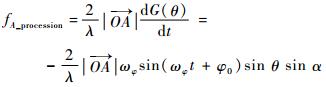 | (13) |
由式(13) 知相应的进动锥体目标锥顶散射源微多普勒谱谱线位于fφ处。又知F可分解为
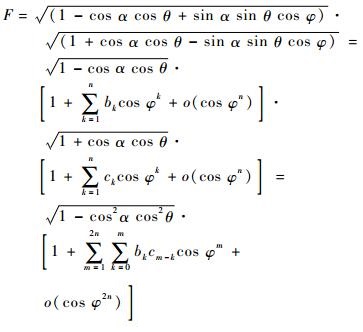 | (14) |
式中:符号bk及ck的定义为
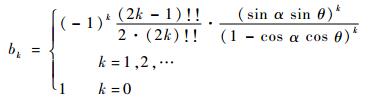 | (15) |
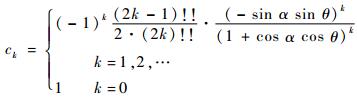 | (16) |
那么进动锥体目标锥底滑动型散射源的微多普勒可表示为
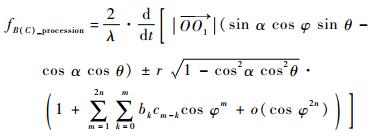 | (17) |
由三角函数积化和差可知,式(17) 可整理为
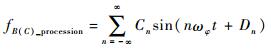 | (18) |
式中:Cn及Dn分别为微多普勒频移fB(C)_procession在角频率分量为nωφ上的幅值及相位,其表达式较为复杂,由于本文仅考虑进动锥体目标散射源微多普勒谱谱线处的频率分量,对其不再深究。所以进动锥体目标锥底滑动型散射源多普勒频移由频率分量为nωφ的三角函数构成,相应的微多普勒谱谱线位于nfφ处。
1.3 章动锥体目标散射源微多普勒谱 章动锥体目标的锥旋角φ及章动角θ均为时间的变量,分别满足
 | (19) |
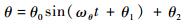 | (20) |
式中:θ0为摆动幅度;ωθ为摆动角速率;θ1为初始摆动相位角;θ2为初始摆动角。考虑到θ0 < π,由贝塞尔函数的性质[15]有
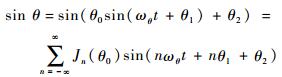 | (21) |
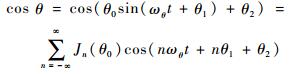 | (22) |
那么系数G可简化为三角函数的线性组合,即
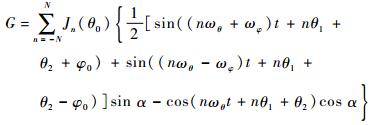 | (23) |
由式(4) 知章动锥体目标锥顶散射源的多普勒频移可表示为
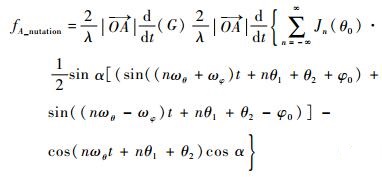 | (24) |
所以章动锥体目标锥顶散射源的微多普勒频移由角频率分量为nωθ±ωφ及nωθ的三角函数构成,相应的微多普勒谱谱线位于nfθ±fφ及nfθ处。对于锥底滑动型散射源而言,式(9) 中的F可由泰勒分解分解为
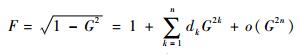 | (25) |
式中:系数dk=(-1)k(2k-1)!!/[2·(2k)!!],而G2的三角函数分解为
 | (26) |
将式(23)、式(25) 及式(26) 代入式(9) 中,经因式分解及三角函数的积化和差,不难发现章动锥体目标锥底滑动型散射源微多普勒频移可整理为
 | (27) |
式中:Em, n及Fm, n分别为微多普勒频移fB(C)_nutation在角频率分量为mωθ±nωφ上的幅值及相位,其表达式较为复杂,由于本文仅考虑章动锥体目标散射源微多普勒谱谱线处的频率分量,故对其不再深究。所以章动锥体锥底滑动型散射源微多普勒频移可分解为频率分量为mfθ±nfφ的三角函数的线性组合,相应的微多普勒谱谱线位于mfθ±nfφ处。至此,自旋、进动及章动这3类微动下锥体目标强散射源微多普勒谱谱线分布特性均已分析完毕,进而可知其各阶谱线出现位置,并将其列于表 1中(表中:m, n∈Z)。
表 1 不同微动下锥体目标强散射源微多普勒谱谱线峰值位置 Table 1 Micro-Doppler spectrum's peak position of strong scattering source of cone target under different micro-motions
| 微动形式 | 谱线峰值位置/Hz | |
| 锥顶散射源 | 锥底滑动型散射源 | |
| 自旋 | 无峰值 | 无峰值 |
| 进动 | fφ | nfφ |
| 章动 | nfθ±fφ, nfθ | mfθ±nfφ |
表选项
2 微动分类方法 由表 1分析发现,不同微动形式下微多普勒及其频谱谱线分布差异明显,微多普勒及其频谱谱线分布特征可作为微动分类的有效依据。因此能否从时频分布中提取出各散射源微多普勒脊线是区分微动的关键。
2.1 各散射源微多普勒脊线提取 微动分类的前提是从目标时频分布中提取出强散射源微多普勒脊线。本文引入一种手动提取多普勒脊线的方法,由于多普勒脊线是连续光滑的,不同散射源的多普勒脊线极易由人工辨识,可利用MATLAB中的ginput函数提取时频图中强散射源微多普勒脊线的控制点,该函数在读入的图像上方利用一个十字光标精确地寻找目标位置,本文对该函数做了较小改进,每读入一个控制点后,即利用3次样条插值生成插值后的曲线,具体的步骤如下:
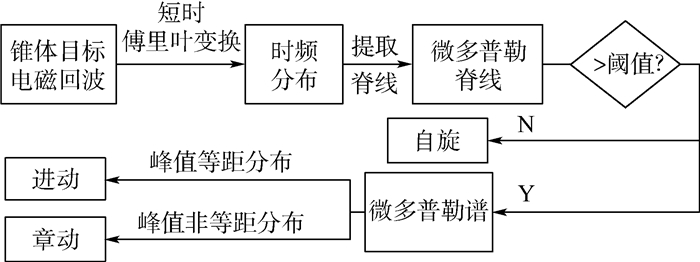
1) 选出散射源j的多普勒脊线作为待提取脊线,并选出起始时刻的多普勒脊线控制点(
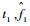
2) 继续选择控制点(
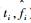
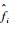
3) 比较差值后新生成的曲线是否与原来时频分布中的曲线相吻合。如果吻合的不好,i=i+1,在不吻合的地方继续添加控制点,并擦除原有的插值曲线,重复步骤2),直至曲线吻合为止。
4) j=j+1,重复步骤1)~3),直至没有剩余的散射源多普勒脊线可以提取为止。
5) 对所有提取的多普勒脊线做傅里叶变换以获得其频谱特征。
2.2 微动分类准则 在获取散射源微多普勒脊线后,如果微多普勒频移值小于等于指定阈值,则为自旋目标;对于微多普勒频移值大于指定阈值的微动目标,如果微多普勒谱峰值等间距分布(将单峰值分布也看成等间距),则目标微动形式为进动;相反地,如果微多普勒谱峰值非等间距分布(忽略锥旋角速率与摆动角速率互为整数倍的情况),则为章动。
至此,基于微多普勒的空间锥体目标微动分类方法分析完毕,图 2给出了本文微动目标分类方法的流程图。
 |
| 图 2 基于微多普勒的微动目标分类方法流程图 Fig. 2 Flow chart of micro-motion target classification method based on micro-Doppler |
| 图选项 |
3 仿真验证 首先验证表 1中结论的正确性。图 3~图 5中给出了不同微动下的锥体目标强散射源的微多普勒谱,仿真时不同微动形式下的锥体目标使用同一结构参数,具体参数设置如下:质心到锥顶的距离
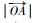
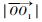
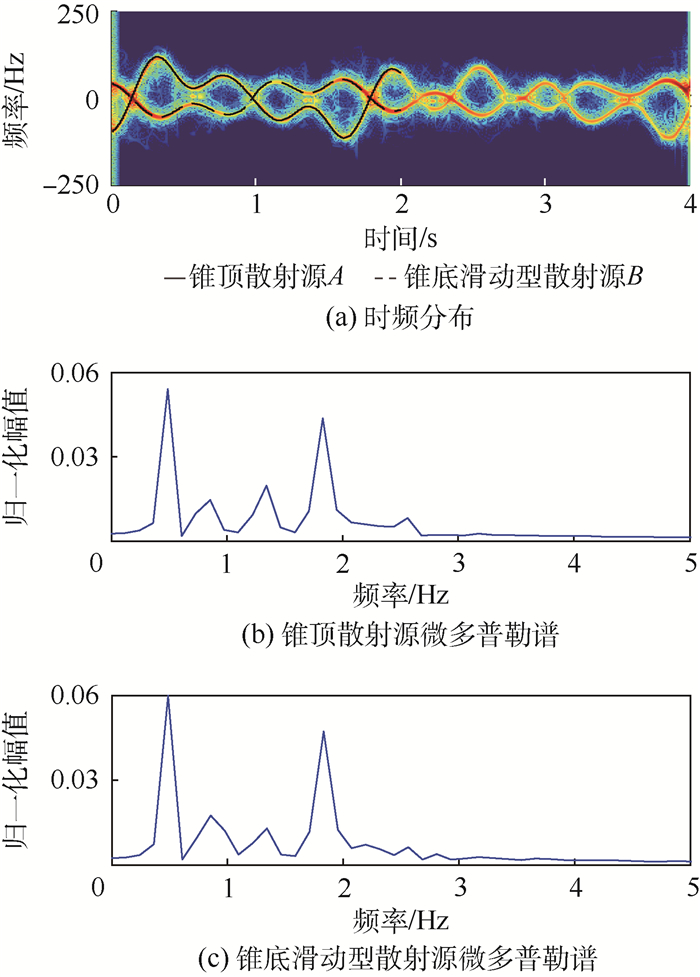 |
| 图 3 章动目标散射源微多普勒脊线及其微多普勒谱 Fig. 3 Micro-Doppler ridge and micro-Doppler spectrum of scattering sources of nutation target |
| 图选项 |
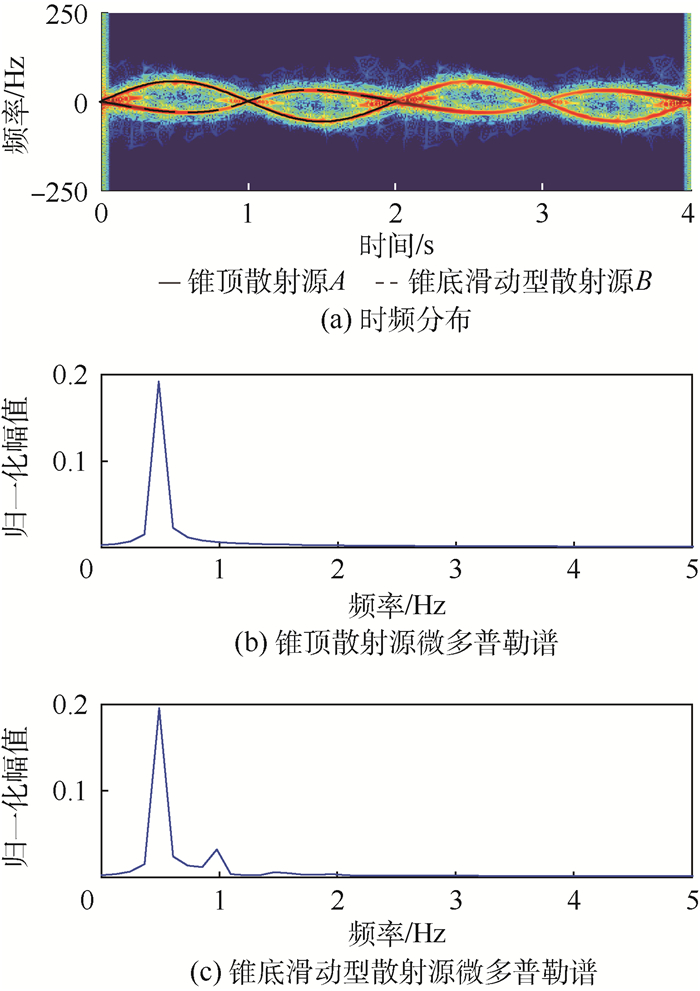 |
| 图 4 进动目标散射源微多普勒脊线及其微多普勒谱 Fig. 4 Micro-Doppler ridge and micro-Doppler spectrum of scattering sources of precession target |
| 图选项 |
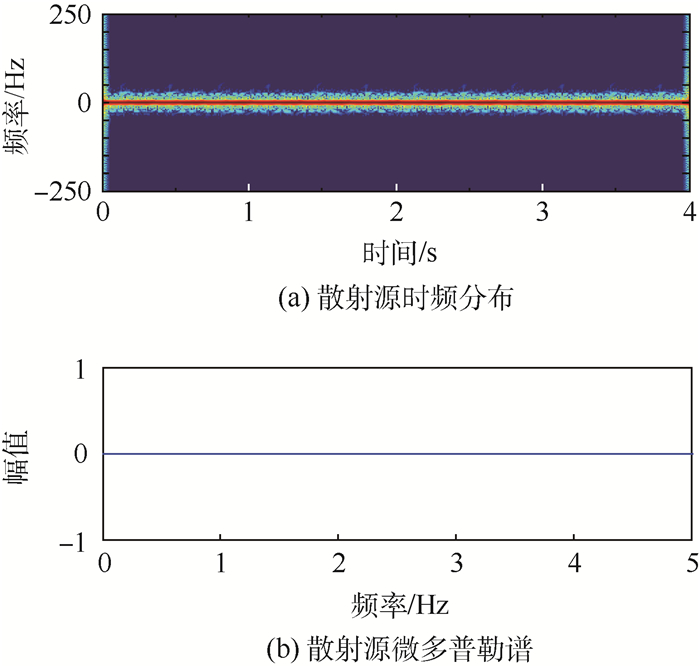 |
| 图 5 自旋目标散射源微多普勒脊线及其微多普勒谱 Fig. 5 Micro-Doppler ridge and micro-Doppler spectrum of scattering sources of spinning target |
| 图选项 |
从图 3(b)中发现章动目标锥顶散射源微多普勒谱的峰值位于0.5、1.3、1.3±0.5、1.3×2Hz附近处,峰值非等距分布,从图 3(c)中发现章动目标锥底滑动型散射源微多普勒谱的峰值位于0.5、1.3、1.3±0.5、1.3+0.5×2、1.3×2、1.3+0.5×3Hz附近处,峰值非等距分布;从图 4(b)中发现进动目标锥顶散射源微多普勒谱的谱线峰值位于0.5Hz附近处,峰值等距分布,从图 4(c)中发现进动目标锥底滑动型散射源微多普勒谱的谱线峰值位于0.5、0.5×2Hz附近处,峰值等距分布;从图 5(b)中发现自旋目标散射源微多普勒谱的谱线峰值位于0Hz处,不难发现不同微动形式下散射源微多普勒谱谱线分布与表 1中归纳的结果一致,同时也与2.2节中的微动分类准则一致。
下面继续验证本文提取微多普勒方法的可行性。以本节仿真中的3种情况为例,图 6给出了提取的控制点以及拟合后的微多普勒脊线,图 6(a)和图 6(b)中的三角形及圆形分别表示手动提取的锥顶及锥底滑动型散射源多普勒脊线的控制点,相应的实线及虚线表示3次样条插值后的曲线;由于自旋目标的锥顶锥底散射源重叠在一起,图 6(c)中以圆形表示手动提取的控制点,相应的实线表示3次样条插值后的曲线。此外还可以发现,在曲率较大处以及平缓段的中点和两端放置适当的控制点可以有效获取目标强散射源微多普勒脊线。
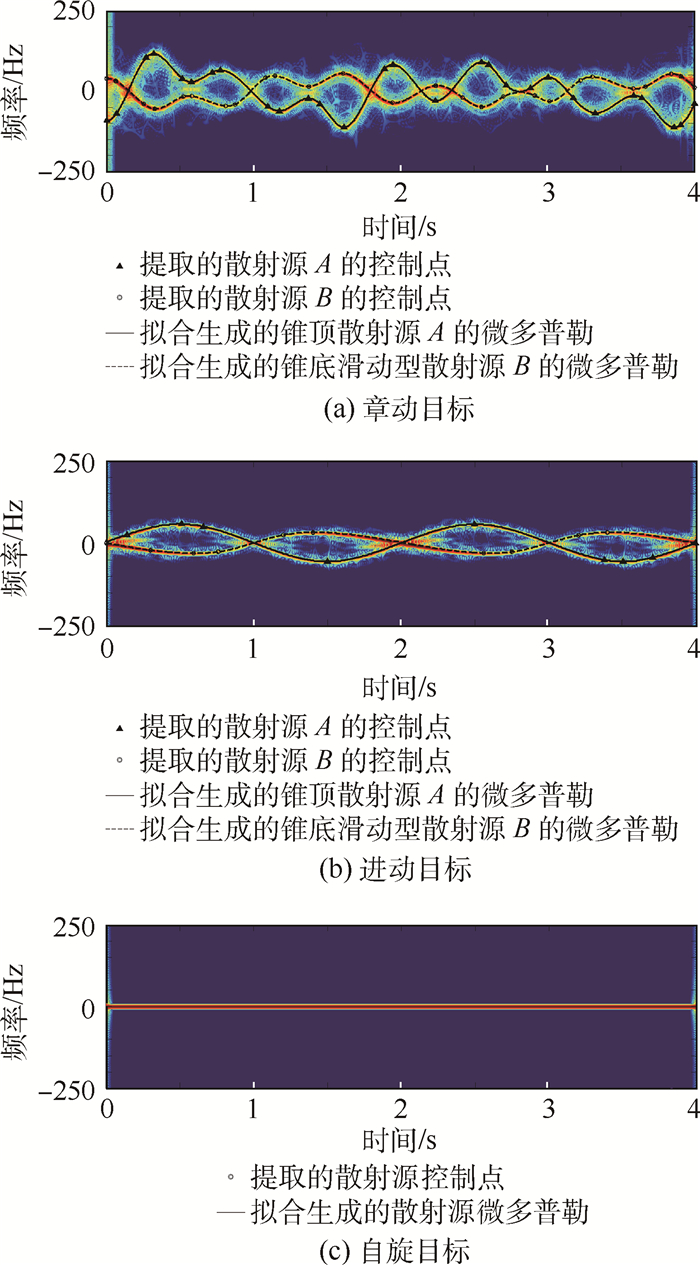 |
| 图 6 章动目标、进动目标及自旋目标微多普勒脊线提取 Fig. 6 Micro-Doppler ridge extraction of nutation target, precession target and spinning target |
| 图选项 |
综上所述,不难发现本文方法提取的散射源微多普勒脊线与时频分布图中散射源吻合的较好,这说明了本文微动分类特征提取方法是可行的。
下面继续分析本文所提分类方法的有效性,设定微动分类所用的微多普勒阈值为10Hz,由于锥体目标旋转对称,自旋运动对其电磁散射没有影响,可忽略自旋运动。分别改变其他微动参数,相应的参数设置范围如表 2所示(对自旋及进动目标而言,表中θ0的表示进动角)。
表 2 微动仿真参数设置范围 Table 2 Micro-motion simulation parameter setting range
| 微动形式 | fφ/Hz | φ/(°) | fθ/Hz | θ0/(°) | θ1/(°) | θ2/(°) | α/(°) |
| 自旋 | 0~360 | 5~20 | 0~180 | ||||
| 进动 | 0.3~1.5 | 0~360 | 5~20 | 0~180 | |||
| 章动 | 0.3~1.5 | 0~360 | 0.4~1.2 | 5~20 | 0~360 | 0~180 | 0~180 |
表选项
考虑在上述参数设置下的3类目标微动识别率随信噪比变化的情况,从表 2中每种微动下的参数范围中随机生成50组微动参数,信噪比(SNR)设置范围为[0, 5, 10, 15, 20, 25]dB,将其在不同信噪比下的识别结果绘于图 7中。
 |
| 图 7 各类微动锥体目标的识别率随信噪比的变化 |
| 图选项 |
可以看出自旋目标的识别率最高,这是由于自旋锥体目标散射源散射位置及强度恒定,只要总的散射强度未被噪声淹没即可提取出散射源微多普勒脊线,即可对自旋做出判定,而且自旋目标在时频分布上强散射源脊线处的能量分布是整个锥体目标散射能量的总和(章动及进动锥体目标在时频分布上散射源脊线处的能量是锥顶或锥底单独的贡献),因此自旋目标识别抗噪性较好,经仿真发现在信噪比低至0dB时,几乎所有仿真参数下的时频分布中目标总的散射强度仍较突出;章动及进动目标的辨识仅需一个散射源的微多普勒谱,但部分微动参数下可能存在遮挡及散射强度变小引起的散射源消隐,且随着信噪比的降低,微动周期内部分时段散射源可能被噪声淹没,从而无法提取出微多普勒,进而降低了识别率。
总的说来,当信噪比大于20dB时各类目标的微动识别都在90%以上,说明本文所提分类方法是有一定效果的。
4 结论 空间锥体目标微动识别是对其进行微动及结构参数估计的前提,对弹道目标防御具有重要意义。本文提出了一种空间锥体目标的微动分类方法,主要结论如下:
1) 本文建立了不同微动形式下锥顶及锥底滑动型散射源微多普勒的数学模型,归纳了不同微动形式下锥体目标散射源微多普勒谱的峰值分布形式,指出利用微多普勒阈值识别自旋、利用微多普勒谱峰值是否等间距分布识别章动及进动的微动分类方法。
2) 利用电磁仿真对本文算法进行验证,发现在信噪比大于20 dB时各类目标的微动识别效果都在90%以上。
参考文献
| [1] | 韩勋, 杜兰, 刘宏伟, 等. 窄带雷达观测下的锥体目标参数估计方法[J].西安电子科技大学学报, 2015, 42(6): 43–48. HAN X, DU L, LIU H W, et al. Parameter estimation method for the cone-shaped target under narrow-band radar observation[J].Journal of Xidian University, 2015, 42(6): 43–48.(in Chinese) |
| [2] | 杨有春, 童宁宁, 冯存前, 等. 利用最强散射点信息的平动补偿与微多普勒提取[J].西安电子科技大学学报, 2012, 39(6): 147–153. YANG Y C, TONG N N, FENG C Q, et al. Translation compensation and micro-Doppler extraction by using the information on the strongest scatter[J].Journal of Xidian University, 2012, 39(6): 147–153.(in Chinese) |
| [3] | 宁超, 黄璟, 黄培康. 基于HRRP的进动锥体目标特征参数求解方法[J].系统工程与电子技术, 2014, 36(4): 650–655. NING C, HUANG J, HUANG P K. Solution for characteristic parameters of precession cone-shaped target using HRRP[J].Systems Engineering and Electronics, 2014, 36(4): 650–655.(in Chinese) |
| [4] | 黄璟, 宁超, 朱勇. 基于最优路径的弹道目标径向长度提取方法[J].系统工程与电子技术, 2015, 37(7): 1499–1503. HUANG J, NING C, ZHU Y. Estimation method for ballistic target range profile length based on the optimal route algorithm[J].Systems Engineering and Electronics, 2015, 37(7): 1499–1503.DOI:10.3969/j.issn.1001-506X.2015.07.06(in Chinese) |
| [5] | 邵长宇, 杜兰, 韩勋, 等. 基于双视角距离像序列的空间锥体目标参数估计方法[J].电子与信息学报, 2015, 37(11): 2735–2741. SHAO C Y, DU L, HAN X, et al. Estimation method for space coning target parameters based on two-aspect range profile sequences[J].Journal of Electronics & Information Technology, 2015, 37(11): 2735–2741.(in Chinese) |
| [6] | 洪灵, 戴奉周, 刘宏伟. 基于三维重构的空间目标进动参数估计方法[J].电波科学学报, 2015, 30(2): 237–243. HONG L, DAI F Z, LIU H W. Precession parameters estimation for space target based on 3D reconstruction[J].Chinese Journal of Radio Science, 2015, 30(2): 237–243.(in Chinese) |
| [7] | WANG Z L, YAN F X, HE F, et al. Missile target automatic recognition from its decoys based on image time-series[J].Pattern Recognition, 2010, 43(6): 2157–2164.DOI:10.1016/j.patcog.2009.12.016 |
| [8] | 金光虎, 高勋章, 黎湘, 等. 基于ISAR像序列的弹道目标进动特征提取[J].电子学报, 2010, 6(6): 1–6. JIN G H, GAO X Z, LI X, et al. Precession feature extraction of ballistic targets based on dynamic image sequence[J].Acta Electronica Sinica, 2010, 6(6): 1–6.(in Chinese) |
| [9] | 高红卫, 谢良贵, 文树梁, 等. 弹道导弹目标微动特性的微多普勒分析与仿真研究[J].系统仿真学报, 2009, 21(4): 954–961. GAO H W, XIE L G, WEN S L, et al. Micro-Doppler analysis and simulation study of micro-motion performance of ballistic missile targets[J].Journal of System Simulation, 2009, 21(4): 954–961.(in Chinese) |
| [10] | 高红卫, 谢良贵, 文树梁, 等. 基于微多普勒特征的真假目标雷达识别研究[J].电波科学学报, 2008, 23(4): 775–780. GAO H W, XIE L G, WEN S L, et al. Research on radar target identification of warhead and decoys based on micro-Doppler signature[J].Chinese Journal of Radio Science, 2008, 23(4): 775–780.(in Chinese) |
| [11] | 韩勋, 杜兰, 刘宏伟, 等. 基于时频分布的空间锥体目标微动形式分类[J].系统工程与电子技术, 2013, 35(4): 684–691. HAN X, DU L, LIU H W, et al. Classification of micro-motion form of space cone-shaped objects based on time-frequency distribution[J].Systems Engineering and Electronics, 2013, 35(4): 684–691.(in Chinese) |
| [12] | 关永胜, 左群声, 刘宏伟, 等. 空间锥体目标微动特性分析与识别方法[J].西安电子科技大学学报, 2011, 38(2): 105–111. GUAN Y S, ZUO Q S, LIU H W, et al. Micro-motion characteristic analysis and recognition of cone-shaped targets[J].Journal of Xidian University, 2011, 38(2): 105–111.(in Chinese) |
| [13] | 关永胜, 左群声, 刘宏伟. 基于微多普勒特征的空间锥体目标识别[J].电波科学学报, 2011, 26(2): 209–215. GUAN Y S, ZUO Q S, LIU H W. Micro-Doppler signature based cone-shaped target recognition[J].Chinese Journal of Radio Science, 2011, 26(2): 209–215.(in Chinese) |
| [14] | 关永胜, 左群声. 基于特征谱的空间锥体目标识别方法[J].中国电子科学研究院学报, 2014, 9(2): 161–168. GUAN Y S, ZUO Q S. Eigenvalue spectrum signature based cone-shaped target recognition[J].Journal of CAEIT, 2014, 9(2): 161–168.(in Chinese) |
| [15] | 王竹溪, 郭敦仁. 特殊函数概论[M].北京: 北京大学出版社, 2012: 260-264. WANG Z X, GUO D R. Introduction to special function[M].Beijing: Peking University Press, 2012: 260-264.(in Chinese) |
