然而,真实大气密度的变化非常复杂,临近空间同时受来自下部的对流层活动以及太阳辐射和宇宙射线的影响,多种影响因素使得临近空间大气密度除了随高度、地理纬度、经度和季节变化的气候特性以外,还存在其他多种时间、空间尺度上的复杂变化。这些变化主要起源于周期为几天到一月的行星波、24 h周期及其高阶谐波的潮汐波、几分钟到10多个小时的大气重力波、更短时间尺度的大气湍流以及某些其他具有随机特性因素引起的大气扰动。当前国际上常用的包含临近空间大气密度的经验模式,包括美国标准大气(US76) 模式、CIRA系列模式、MSIS系列模式等,可输出大气密度的气候平均值,用于研究大气的气候变化特性。例如,凌超和陈泽宇[7]基于NRLMSISE-00分析了中国上空过渡流区大气温度和大气密度的月平均状态,但这些模式缺少对大气扰动的表征。美国宇航局/马歇尔空间飞行中心针对飞行器设计使用研发了大气模式GRAM系列,包括了大气气候态和大气扰动态,并随着数据源的逐步完善而不断地升级版本,目前的最新版本是GRAM-2010。俄罗斯科学院应用数学所在早些年制定了偏差大气模型并得到了实际应用[8]。
中国目前飞行器设计可以使用GJB 365.1—87[9](等同于国际标准ISO 2533—1975) 和GJB 366.1—87[10](等同于国际标准ISO 5878—1982),高度范围只到80 km。而事实上,真实大气密度可能与这2个标准存在较大偏差,该偏差对于飞行器的设计和指导飞行不能忽略,或者导致不必要的大余量。因此,基于实测数据建立高精度的大气模型是非常有意义的,开展基于大量实测数据的建模技术研究是有必要的。中国现阶段已累计获取了一定量的临近空间大气数据,其中一个很重要的应用需求是在已有的探测数据和在大气参量间已知的物理关系与某些假设的基础上,建立临近空间大气最“接近真实”的仿真模型,以在地面上仿真复杂多变的临近空间大气环境。
本文以临近空间大气密度的表征方法为牵引,针对20~100 km高度范围的临近空间大气密度,基于TIMED卫星上SABER探测器11年的大气密度数据,以38°N为例,统计分析临近空间大气密度的变化规律,探索建模的技术方法,并对该模型进行仿真测试,与地基激光雷达探测大气密度进行对比验证。
本文的创新点主要表现在:① 首次基于长达11年的TIMED/SABER卫星数据统计分析得到了38°N临近空间大气密度的气候平均态和大气扰动态的定量变化特性;② 明确提出了临近空间大气密度可表征为静态缓变气候平均量和动态瞬变大气扰动量之和,气候平均量可由基于大量实测数据的网格统计得到,大气扰动量可通过建立扰动模型(如自回归模型)得到。
1 数据来源与处理方法 SABER是一个放置于TIMED卫星上的10通道宽带辐射计,在卫星沿轨道飞行过程中采用临边测量CO2的红外辐射信号,反演生成低平流层到低热层包括各种大气参量(温度、气压和密度等)的垂直廓线。TIMED/SABER从2002年1月22日开始获取观测数据,至今仍在轨运行,在时间上具有非常好的连续性。该数据在纬度覆盖从一个半球的53°到另一个半球的82°,大约每60 d变换一次;在经圈方向全部覆盖,分布较均匀;地方时覆盖每天集中在2个时间点上,每天迁移约12 min,约60 d可覆盖24 h。每个正常工作日约有15个轨道数据,每个轨道大约96个事件,SABER每天可获取一千多根廓线数据,垂直分辨率约为0.4 km。本文中选用SABER版本V1.07数据,该版本温度数据在100 km以下已经作过许多比较和验证[11-12],并广泛应用于科学研究中[13-18],数据可信。在中纬地区30、60、80、90、100 km,SABER温度测量误差分别约为0.8、1.6、2.3、5.4、8.4 K[11]。万田等[19]利用SABER大气密度数据分析评估了100 km附近大气密度模型的误差带和置信度。
本文主要采用全球网格化和数学统计计算的方法,即对大气密度数据作质量控制和野值剔除之后,在垂直方向、纬度方向、经度方向、时间上采用网格划分,在网格内作数学统计平均值和标准差,具体方法可参考文献[20]对大气温度的处理方法。
1) 在垂直方向,对于每个探测剖面,在20~100 km高度范围,密度参量采用对数线性插值,纬度、经度和地方时采用最近点插值的方法,插值间隔为1 km。
2) 在纬度方向,以38°N为中心,查找半径为2°。
3) 在经度方向,在经度范围为0°~360°,格距为5°划分网格,查找半径为2.5°。
4) 在时间上,不计年份,以月为单位作统计,统计网格内平均值和标准差。
由此,便可得到基于大量卫星观测数值的临近空间大气密度随经度、高度和月份变化的月平均和标准差统计值,平均值表征大气密度的静态缓变气候值,标准差表征动态瞬变大气扰动量(不含大气定常行星波)[20]。
2 大气密度变化特性 基于TIMED/SABER 2002年1月至2013年1月共11年大气密度数据,统计计算得到了38°N临近空间大气密度气候平均值和标准差在经度0°~360°(分辨率为5°)、高度20~100 km(分辨率为1 km)、1~12月份(分辨率为1月)的定量值。基于该气候平均值和标准差数据集,本文将分析38°N临近空间大气密度的静态缓变气候平均态和动态瞬变大气扰动态的变化特性。
表 1和表 2分别给出了38°N、90°E在1月份和8月份随高度变化的大气平均密度、密度标准差以及平均密度相对美国US76的偏差百分比、密度标准差相对US76的百分比。
表 1 38°N、90°E大气密度在1月份的统计特征 Table 1 Statistical characteristics of atmospheric density at 38°N, 90°E in January
| 高度/km | 平均密度/(kg·m-3) | 密度标准差/(kg·m-3) | 平均密度相对US76偏差/% | 密度标准差相对US76百分比 |
| 20 | 0.085 25 | 0.001 968 | -4.118 | 2.214 |
| 25 | 0.038 1 | 0.000 926 5 | -4.934 | 2.312 |
| 30 | 0.017 31 | 0.000 539 3 | -5.967 | 2.93 |
| 35 | 0.008 003 | 0.000 293 1 | -5.448 | 3.463 |
| 40 | 0.003 826 | 0.000 168 8 | -4.247 | 4.224 |
| 45 | 0.001 921 | 8.461×10-5 | -2.294 | 4.304 |
| 50 | 0.001 008 | 4.928×10-5 | -1.874 | 4.799 |
| 55 | 0.000 543 3 | 3.343×10-5 | -4.343 | 5.886 |
| 60 | 0.000 284 5 | 2.015×10-5 | -8.115 | 6.508 |
| 65 | 0.000 141 4 | 1.059×10-5 | -13.37 | 6.487 |
| 70 | 6.53×10-5 | 4.467×10-6 | -21.16 | 5.393 |
| 75 | 2.935×10-5 | 2.663×10-6 | -26.49 | 6.672 |
| 80 | 1.329×10-5 | 1.395×10-6 | -28.02 | 7.557 |
| 85 | 5.984×10-6 | 6.546×10-7 | -27.19 | 7.965 |
| 90 | 2.707×10-6 | 2.839×10-7 | -20.63 | 8.325 |
| 95 | 1.249×10-6 | 1.361×10-7 | -10.23 | 9.788 |
| 100 | 5.39×10-7 | 7.51×10-8 | -3.652 | 13.43 |
表选项
表 2 38°N、90°E大气密度在8月份的统计特征 Table 2 Statistical characteristics of atmospheric density at 38°N, 90°E in August
| 高度/km | 平均密度/(kg·m-3) | 密度标准差/(kg·m-3) | 平均密度相对US76偏差/% | 密度标准差相对US76百分比 |
| 20 | 0.095 14 | 0.001 27 | 7.006 | 1.428 |
| 25 | 0.041 36 | 0.000 390 3 | 3.187 | 0.973 9 |
| 30 | 0.019 09 | 0.000 183 5 | 3.682 | 0.996 9 |
| 35 | 0.008 991 | 8.957×10-5 | 6.23 | 1.058 |
| 40 | 0.004 309 | 5.803×10-5 | 7.835 | 1.452 |
| 45 | 0.002 152 | 3.312×10-5 | 9.461 | 1.685 |
| 50 | 0.001 126 | 1.897×10-5 | 9.659 | 1.847 |
| 55 | 0.000 605 6 | 1.151×10-5 | 6.626 | 2.026 |
| 60 | 0.000 323 4 | 9.916×10-6 | 4.442 | 3.203 |
| 65 | 0.000 164 5 | 6.453×10-6 | 0.768 8 | 3.954 |
| 70 | 8.006×10-5 | 3.916×10-6 | -3.329 | 4.728 |
| 75 | 3.724×10-5 | 1.984×10-6 | -6.714 | 4.971 |
| 80 | 1.626×10-5 | 1.061×10-6 | -11.93 | 5.746 |
| 85 | 6.64×10-6 | 6.488×10-7 | -19.22 | 7.894 |
| 90 | 2.71×10-6 | 3.082×10-7 | -20.52 | 9.038 |
| 95 | 1.156×10-6 | 1.457×10-7 | -16.92 | 10.48 |
| 100 | 4.922×10-7 | 7.302×10-8 | -12.01 | 13.05 |
表选项
从结果可以看到,1月份38°N、90°E的大气平均密度与US76相比偏小,偏差百分比幅度在80 km高度上达最大,可达-28.02%,之后随高度逐渐减小;密度标准差相对US76的百分比随高度的增加总体呈现增大趋势,在100 km高度上可达13.43%。在8月份,大气平均密度与US76相比,在20~65 km高度范围偏大,最大偏差幅度出现在50 km,可达9.659%,在66~100 km高度范围偏小,最大偏差幅度出现在90 km,可达-20.52%;密度标准差相对US76的百分比随高度也呈现增加趋势。与1月份的百分比相比,8月份的标准差百分比数值在85 km以下较小,尤其是在55 km高度上,8月份为2.026%,1月份却高达5.886%,在85~100 km高度范围,8月份标准差百分比与1月份数值相当,在100 km高度上可达13.05%。这些特征与引起临近空间大气扰动的波源特性一致,包括大气重力波、定常行星波、传播性行星波以及大气潮汐、湍流等过程,反映的是大气扰动的总体效果[20]。
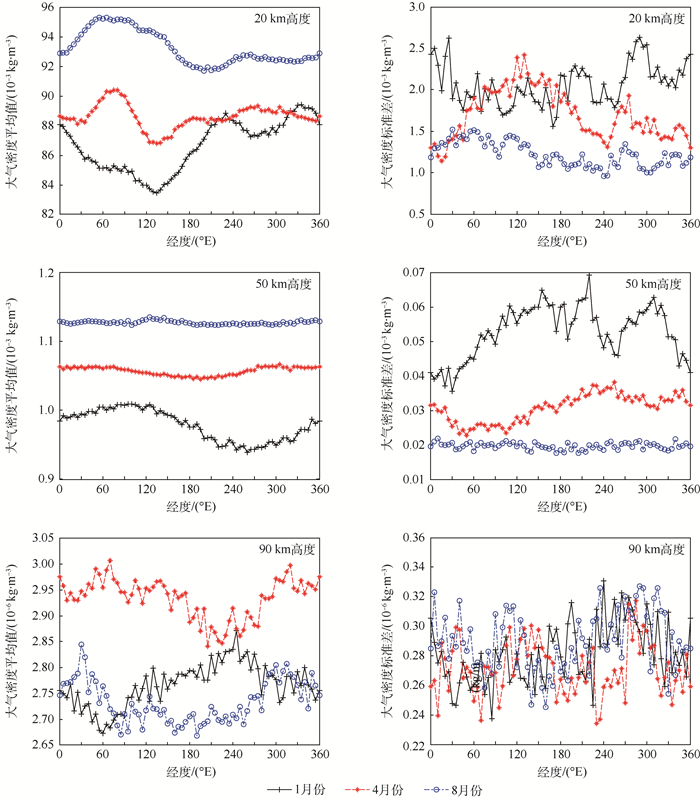
由大气密度的统计值可知,大气密度平均值和标准差除了随高度和季节变化外,沿水平方向(即经度)也是变化的,其变化特征在不同高度与季节各异。图 1给出了大气密度平均值和标准差在20、50、90 km高度上不同季节(1月代表冬季、4月代表春秋季、8月代表夏季)随经度的变化廓线。
 |
| 图 1 38°N大气密度平均值和标准差随经度的变化 Fig. 1 Longitudinal variations of averages and standard deviations of atmospheric density at 38°N |
| 图选项 |
从图 1可以看到,在20 km高度上,大气平均密度在8月份最大,1月份最小,4月份居中,随经度都有变化,幅度相当;大气密度标准差在8月份最小,1月份总体较大,4月份居中,其中,4月份随经度最为显著。在50 km高度上,大气平均密度和标准差在各个月份数值差别较大,变化范围没有交叠,大气平均密度在8月份最大,1月份最小,4月份居中,随经度变化较缓慢,尤其是在8月份,随经度基本不变;大气密度标准差在8月份最小,1月份最大,4月份居中,1月份随经度显著。在90 km高度上,大气平均密度和标准差在各个月份随经度的变化变得复杂,总体而言,大气平均密度在4月份最大,8月份最小,1月份居中,随经度变化都显著,幅度相当;大气密度标准差在各个月份数值相当,随经度变化非常复杂,呈现局地扰动特征。
3 建模技术和仿真试验 3.1 建模技术 根据本文中对大气密度变化规律的统计和分析,其物理状态与随纬度、经度、高度、季节变化的气候平均态有关,同时也与某些具有周期变化特性或者随机特性的大气扰动因素有关。因此,临近空间大气密度可表征为静态缓变气候平均分量和动态瞬变大气扰动分量之和,即
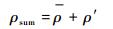 | (1) |
式中:ρsum为总的大气密度值;ρ为大气密度的气候平均分量;ρ′为大气密度的扰动分量。气候平均分量可由基于大量实测数据的网格统计,加上一定的插值方法得到;扰动分量可通过建立扰动模型得到。
从数据的分布规律中可以看到,当统计样本数足够多时,相对于统计月平均值的随机偏差量基本满足具有统计标准差的高斯分布。在实际情况中,沿航迹或者廓线,连续轨迹点之间是存在相关性的。本文采用自回归模型描述实际大气的随机扰动量,即从前一个相关联位置的扰动值计算新位置的小尺度扰动量。
假定2个连续轨迹点,记为位置1和位置2,两者的水平距离为Δx,垂直距离为Δz,假设位置1的随机扰动量是已知的,则位置2的扰动量可用式(2) 计算得到:
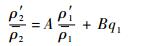 | (2) |
式中:q1为平均值为0、标准差为1的高斯分布随机数;A和B为系数,由位置1和位置2的相关性决定。假设σρ1和σρ2分别表示ρ′2/ρ2与ρ′1/ρ1的标准差,r表示它们之间的相关性,则
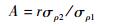 | (3) |
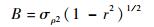 | (4) |
标准差σρ1和σρ2可由本文中大量数据统计得到,连续轨迹点间的自相关系数r可采用指数函数式(5) 表示:
 | (5) |
式中:Lh和Lz分别为水平方向和垂直方向的尺度因子,由随机扰动产生源的尺度特征决定。这里采用随高度增加的线性关系,20~100 km高度范围内垂直尺度因子Lz的变化范围为6~10 km,水平尺度因子Lh的变化范围为900~1 500 km[21]。当式(5) 中指数部分接近于0时,函数值会很大,因此须作修正。当
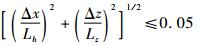
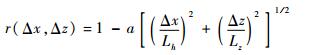 | (6) |
式中:a为修正系数,可根据经验设定,本文选取a=19.5。
当开始一次大气仿真时,初始位置大气密度的随机扰动值可从具有标准差σρ的高斯分布中随机给定,也可以由观测数据计算得到符合实际大气观测的初值扰动量,再由式(2) 即可得到下一个位置的扰动量,联合式(1) 可计算得到实际大气的一次仿真密度。
3.2 仿真试验 根据式(1)~式(6),联合利用第2节的统计分析结果,开展38°N大气密度的仿真试验,包括单站廓线的仿真以及假定航迹的仿真。
图 2给出了38°N、90°E大气密度分别在1月份和8月份的100个仿真实例,图中画出的是大气密度相对于月平均值的扰动量,粗黑色实线表示3倍标准偏差。可以看到,仿真值绝大部分都落在3倍标准差的包络线内。
 |
| 图 2 38°N、90°E大气密度的100个仿真实例 Fig. 2 100 simulated examples of atmospheric density at 38°N, 90°E |
| 图选项 |
图 3给出了大气密度在38°N、90°E的单次仿真结果,大气密度偏差指的是大气密度相对于US76的偏差。仿真结果与中国科学院国家空间科学中心在2014年野外科考实验中的瑞利激光雷达(LIDAR)在该地的大气密度实际观测结果进行对比,闫召爱等[22]介绍了该激光雷达的详细参数。图 3还给出了激光雷达在2014年8月7日05:40(北京时间)观测的大气密度相对于US76的偏差随高度的分布廓线。对比结果表明,模型仿真结果与实测大气的变化特性一致。在实际应用中,若借助蒙特卡罗方法通过足够多次的仿真试验可模拟实际大气的变化特性。
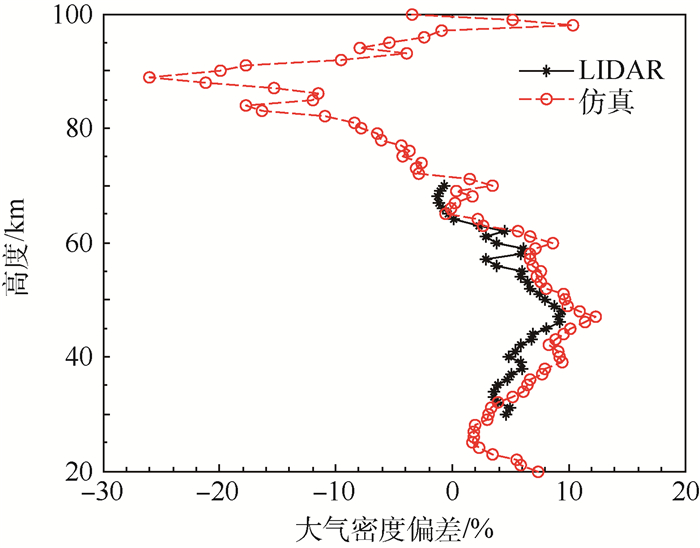 |
| 图 3 38°N、90°E仿真大气密度与激光雷达实测大气密度的比较 Fig. 3 Comparison of simulated atmospheric density with LIDAR-observed atmospheric density at 38°N, 90°E |
| 图选项 |
任意假定航迹如图 4(a)所示,在开始和降落区域作类似抛物线运动,形式为y=ax2+b,在中间段作水平运动,采用式(2) 扰动模型,仿真大气密度的扰动量,加上航迹上大气密度的平均值,由式(1) 可计算得到航迹上的大气密度。图 4(b)给出了8月份某次仿真的结果,图中显示大气密度与US76偏差,具体数值可在表 3中查询。仿真试验结果表明,该仿真模型可以结合实际需要使用,建模方法可行,可推广到别的纬度。
 |
| 图 4 沿假定航迹的仿真个例 Fig. 4 A simulation example along supposed flight trace |
| 图选项 |
表 3 38°N假定航迹8月份某次大气密度的仿真数据 Table 3 Simulation data of atmospheric density along supposed flight trace at 38°N in August
| 序号 | 经度/(°E) | 高度/km | 平均密度/(kg·m-3) | 密度标准差/(kg·m-3) | 仿真密度扰动量/(kg·m-3) | 仿真密度总和/(kg·m-3) | US76标准密度/(kg·m-3) | 大气密度偏差/% |
| 1 | 90 | 20 | 0.095 14 | 0.00127 | 0.000 194 6 | 0.095 33 | 0.088 91 | 7.225 |
| 2 | 85 | 35.56 | 0.008 304 | 8.674×10-5 | 0.000 125 | 0.008 429 | 0.007 794 | 8.151 |
| 3 | 80 | 50.22 | 0.001 096 | 1.941×10-5 | -1.411×10-5 | 0.001 082 | 0.001 | 8.207 |
| 4 | 75 | 64 | 0.000 188 4 | 6.354×10-6 | -1.692×10-6 | 0.000 186 7 | 0.000 18 6 | 0.373 |
| 5 | 70 | 76.89 | 2.717×10-5 | 1.615×10-6 | 1.123×10-6 | 2.829×10-5 | 2.999×10-5 | -5.661 |
| 6 | 65 | 88.89 | 3.344×10-6 | 3.336×10-7 | -2.023×10-7 | 3.141×10-6 | 4.162×10-6 | -24.53 |
| 7 | 60 | 100 | 4.997×10-7 | 7.820×10-8 | 1.066×10-7 | 6.064×10-7 | 5.594×10-7 | 8.397 |
| 8 | 55 | 100 | 5.058×10-7 | 7.763×10-8 | 1.373×10-7 | 6.432×10-7 | 5.594×10-7 | 14.97 |
| 9 | 50 | 100 | 5.028×10-7 | 7.943×10-8 | 1.045×10-7 | 6.073×10-7 | 5.594×10-7 | 8.557 |
| 10 | 45 | 100 | 4.943×10-7 | 7.739×10-8 | 1.044×10-7 | 5.987×10-7 | 5.594×10-7 | 7.032 |
| 11 | 40 | 100 | 5.019×10-7 | 8.076×10-8 | 1.450×10-8 | 5.164×10-7 | 5.594×10-7 | -7.684 |
| 12 | 35 | 100 | 5.012×10-7 | 7.309×10-8 | 7.436×10-8 | 5.756×10-7 | 5.594×10-7 | 2.898 |
| 13 | 30 | 100 | 4.936×10-7 | 8.246×10-8 | 4.283×10-9 | 4.979×10-7 | 5.594×10-7 | -11 |
| 14 | 25 | 100 | 4.927×10-7 | 6.966×10-8 | 3.191×10-8 | 5.246×10-7 | 5.594×10-7 | -6.215 |
| 15 | 20 | 100 | 4.864×10-7 | 7.377×10-8 | 4.104×10-10 | 4.868×10-7 | 5.594×10-7 | -12.98 |
| 16 | 15 | 100 | 4.889×10-7 | 7.340×10-8 | 9.052×10-8 | 5.794×10-7 | 5.594×10-7 | 3.583 |
| 17 | 10 | 100 | 4.864×10-7 | 6.865×10-8 | -3.041×10-9 | 4.834×10-7 | 5.594×10-7 | -13.59 |
| 18 | 5 | 100 | 4.910×10-7 | 7.274×10-8 | 5.459×10-8 | 5.456×10-7 | 5.594×10-7 | -2.464 |
| 19 | 0 | 100 | 4.884×10-7 | 7.715×10-8 | -3.546×10-8 | 4.529×10-7 | 5.594×10-7 | -19.03 |
| 20 | 355 | 100 | 4.874×10-7 | 7.358×10-8 | -7.477×10-8 | 4.126×10-7 | 5.594×10-7 | -26.24 |
| 21 | 350 | 100 | 4.839×10-7 | 8.645×10-8 | -9.498×10-8 | 3.889×10-7 | 5.594×10-7 | -30.48 |
| 22 | 345 | 100 | 4.853×10-7 | 8.262×10-8 | -9.750×10-8 | 3.878×10-7 | 5.594×10-7 | -30.68 |
| 23 | 340 | 100 | 4.899×10 | 8.115×10-8 | 4.824×10-8 | 5.381×10-7 | 5.594×10-7 | -3.8 |
| 24 | 335 | 100 | 4.880×10-7 | 8.184×10-8 | 1.240×10-9 | 4.892×10-7 | 5.594×10-7 | -12.54 |
| 25 | 330 | 100 | 5.026×10-7 | 8.033×10-8 | -1.913×10-8 | 4.835×10-7 | 5.594×10-7 | -13.57 |
| 26 | 325 | 100 | 4.969×10-7 | 7.662×10-8 | -6.842×10-8 | 4.285×10-7 | 5.594×10-7 | -23.4 |
| 27 | 320 | 100 | 4.883×10-7 | 7.899×10-8 | -4.075×10-8 | 4.475×10-7 | 5.594×10-7 | -20 |
| 28 | 315 | 89.7 | 2.973×10-6 | 3.369×10-7 | 2.661×10-7 | 3.239×10-6 | 3.611×10-6 | -10.31 |
| 29 | 310 | 78.18 | 2.239×10-5 | 1.412×10-6 | -1.841×10-6 | 2.055×10-5 | 2.458×10-5 | -16.41 |
| 30 | 305 | 65.45 | 0.000 155 1 | 6.633×10-6 | -9.634×10-6 | 0.000 145 4 | 0.000 154 | -5.547 |
| 31 | 300 | 51.52 | 0.000 929 1 | 1.755×10-5 | -3.237×10-6 | 0.000 925 8 | 0.000 854 7 | 8.327 |
| 32 | 295 | 36.36 | 0.007 313 | 7.660×10-5 | -7.940×10-5 | 0.007 233 | 0.006 886 | 5.037 |
| 33 | 290 | 20 | 0.092 51 | 0.001 049 | -0.000 174 2 | 0.092 33 | 0.088 91 | 3.851 |
表选项
4 结论 本文基于TIMED/SABER 2002年1月至2013年1月共11年的密度数据,分析了38°N大气密度的变化规律,探索了临近空间大气建模的方法。
1) 通过网格化和数学统计得到了38°N大气密度的平均值和标准差在经度0°~360°(分辨率为5°)、高度20~100 km(分辨率为1 km)、1~12月份(分辨率为1月)的定量数值,用于表征大气密度的静态缓变气候平均态以及动态瞬变大气扰动态。
2) 通过分析38°N大气密度的变化规律,结果表明,大气平均密度随高度、季节变化显著,在水平方向(即经度方向)反映了定常行星波的变化特性;大气密度扰动随高度的增加而迅速增大,在80 km以上变化特征非常复杂,在各个季节扰动量都比较大,反映了临近空间复杂多种来源波动和过程的综合作用。
3) 提出了临近空间大气密度可表征为气候平均量和大气扰动量之和的建模方法。基于统计气候平均量和大气扰动量的统计结果,建立了自回归扰动模型,并开展了仿真及与观测数据的比较试验。结果表明,该建模方法可用于初步仿真实际大气,对于别的纬度带可作一定的推广。
本文中TIMED/SABER数据来源虽然长达11年,但是由于探测技术本身的制约,网格统计量所能表征的物理含义仍受到一定的限制,即使该数据源时间范围再长,也无法突破这一问题,主要表现在2个方面:① 由于SABER探测器采用与TIMED卫星运动方向以夹角90°作临边扫描,沿视线方向积分的方式,可探测的最小水平波长受到技术限制,只可探测到水平尺度大于100~200 km的波动[23]。因此,网格内大气密度标准差参量不包含小尺度重力波以及湍流等其他小尺度过程的贡献,而主要是由大气重力波、传播性行星波以及大气潮汐引起的波扰动引起的偏离平均量。大气定常行星波的影响包含于网格内密度平均量[16],网格内统计标准差对大气扰动总量略有低估,主要是未包含水平尺度小于100~200 km的大气扰动。② 受设计的约束,SABER探测数据在地方时分布上的正午附近2~3 h内无探测,这对网格统计参量的表征范围会有一定的影响。地方时分布不匀主要影响大气潮汐波的表征,也会影响别的扰动量的提取。文献[15]采用模拟仿真的方法估计了SABER采用在地方时和经度上的不均匀性对提取定常行星波成分的影响,结果表明,波动的提取效率大于96%。因此,初步估计本文中SABER在地方时分布的不均匀性对网格内大气密度平均量和标准差的统计影响程度不大,定量的估计需要后续更多的仿真工作。
此外,本文中建立了一阶的自回归模型表征临近空间的大气扰动量,该模型简单,主要用于模拟大气随机扰动量。然而,临近空间大气扰动除了随机扰动之外,有些扰动源,例如来自于大气重力波、定常行星波、传播性行星波以及大气潮汐波等的扰动是有物理过程和周期、规律的,后续可根据这些物理扰动源的统计特征改进大气密度扰动模型。对于其他大气参量(大气温度、压强、风场),需发展互相关模型,约束各参量间的物理关系,解决其中的关键技术问题,发展全套的临近空间大气环境仿真模型,在实际应用中借助蒙特卡罗方法,就可在地面仿真实际复杂变化的临近空间大气。该建模的方法和结果可在实际应用中加以对比验证,再反馈修正模型,最终建立更符合实际观测的更适合应用部门需求的临近空间大气模型。
致谢
感谢TIMED/SABER工作组提供的探测数据(http://saber.gats-inc.com/data_services.php)
参考文献
| [1] | TSIEN H S. Superaerodynamics, mechanics of rarefied gases[J].Journal of the Aeronautical Sciences, 1946, 13(12): 653–664.DOI:10.2514/8.11476 |
| [2] | 姚伟, 李勇, 王文隽, 等. 平流层飞艇热力学模型和上升过程仿真分析[J].宇航学报, 2007, 28(3): 603–607. YAO W, LI Y, WANG W J, et al. Thermodynamic model and numerical simulation of a stratospheric airship take-off process[J].Journal of Astronautics, 2007, 28(3): 603–607.(in Chinese) |
| [3] | 刘强, 武哲, 祝明, 等. 平流层气球热动力学仿真[J].北京航空航天大学学报, 2013, 39(12): 1578–1583. LIU Q, WU Z, ZHU M, et al. Thermal-dynamic simulation of stratospheric balloon[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(12): 1578–1583.(in Chinese) |
| [4] | 张智超, 高振勋, 蒋崇文, 等. 高超声速气动热数值计算壁面网格准则[J].北京航空航天大学学报, 2015, 41(4): 594–600. ZHANG Z C, GAO Z X, JIANG C W, et al. Grid generation criterions in hypersonic aeroheating computations[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(4): 594–600.(in Chinese) |
| [5] | 黄飞, 张亮, 程晓丽, 等. 连续流失效对近空间飞行器气动特性的影响[J].空气动力学学报, 2013, 31(5): 623–628. HUANG F, ZHANG L, CHENG X L, et al. Effects of continuum breakdown on aerodynamics of near space vehicle[J].Acta Aerodynamica Sinica, 2013, 31(5): 623–628.DOI:10.7638/kqdlxxb-2012.0002(in Chinese) |
| [6] | 邓帆, 焦子涵, 付秋军, 等. 面向总体性能的高速飞行器布局优化研究[J].北京航空航天大学学报, 2016, 42(12): 2587–2595. DENG F, JIAO Z H, FU Q J, et al. Research of hypersonic vehicle shape optimal design based on overall performance[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(12): 2587–2595.(in Chinese) |
| [7] | 凌超, 陈泽宇. 中国上空过渡流区大气月平均状态的模拟结果[J].航天器环境工程, 2015, 32(3): 236–242. LING C, CHEN Z Y. Monthly averaged atmospheric conditions in the transition flow region of China based on the NRLMSISE-00 model[J].Spacecraft Environment Engineering, 2015, 32(3): 236–242.(in Chinese) |
| [8] | 季蓉芬. 地球扰动大气模型[J].航天返回与遥感, 1995, 16(1): 66–81. JI R F. The disturbed atmospheric model of the earth[J].Spacecraft Recovery and Remote Sensing, 1995, 16(1): 66–81.(in Chinese) |
| [9] | 陈昭. 北半球标准大气(-2~80公里): GJB 365. 1-87[S]. 北京: 国防科学技术工业委员会, 1987. CHEN Z.Standard atmosphere in northern hemisphere(-2-80 km):GJB 365.1-87[S].Beijing:Commission of Science Technology and Industry for National Defense, 1987(in Chinese). |
| [10] | 陈昭. 航空与航天用参考大气(0~80公里): GJB 366. 1-87[S]. 北京: 国防科学技术工业委员会, 1987. CHEN Z.Reference atmosphere for aerospace use (0-80 km):GJB 366.1-87[S].Beijing:Commission of Science Technology and Industry for National Defense, 1987(in Chinese). |
| [11] | REMSBERG E E, MARSHALL B T, GARCIA-COMAS M, et al. Assessment of the quality of the version 1.07 temperature-versus-pressure profiles of the middle atmosphere from TIMED/SABER[J].Journal of Geophysical Research:Atmospheres, 2008, 113(D17): D17101.DOI:10.1029/2008JD010013 |
| [12] | GARCIA-COMAS M, LOPEZ-PUERTAS M, MARSHALL B T, et al. Errors in sounding of the atmosphere using broadband emission radiometry (SABER) kinetic temperature caused by non-local-thermodynamic-equilibrium model parameters[J].Journal of Geophysical Research:Atmospheres, 2008, 113(D24): D24106.DOI:10.1029/2008JD010105 |
| [13] | CHEN Z Y, LU D R. Global structures of the DE3 tide[J].Chinese Science Bulletin, 2009, 54(6): 1073–1079. |
| [14] | XU J, SMITH A K, LIU H L, et al. Seasonal and quasi-biennial variations in the migrating diurnal tide observed by thermosphere, ionosphere, mesosphere, energetics and dynamics (TIMED)[J].Journal of Geophysical Research:Atmospheres, 2009, 114(D13): D13107.DOI:10.1029/2008JD011298 |
| [15] | XIAO C Y, HU X, TIAN J H. Global temperature stationary planetary waves extending from 20 to 120 km observed by TIMED/SABER[J].Journal of Geophysical Research:Atmospheres, 2009, 114(D17): D17101.DOI:10.1029/2008JD011349 |
| [16] | 张云, 熊建刚, 万卫星. 中层大气重力波的全球分布特征[J].地球物理学报, 2011, 54(4): 427–435. ZHANG Y, XIONG J G, WAN W X. Analysis on the global morphology of middle atmospheric gravity waves[J].Chinese Journal Geophysics, 2011, 54(4): 427–435.(in Chinese) |
| [17] | HUANG Y Y, ZHANG S D, YI F, et al. Global climatological variability of quasi-two-day waves revealed by TIMED/SABER observations[J].Annales Geophysicae, 2013, 31(6): 1061–1075.DOI:10.5194/angeo-31-1061-2013 |
| [18] | PANCHEVA D, MUKHTAROV P, SMITH A K. Climatology of the migrating terdiurnal tide (TW3) in SABER/TIMED temperatures[J].Journal of Geophysical Research, 2013, 118(4): 1755–1767. |
| [19] | 万田, 刘洪伟, 樊菁. 100 km附近大气密度模型的误差带和置信度[J].中国科学:物理学力学天文学, 2015, 45(12): 124706. WAN T, LIU H W, FAN J. Error band and confidence coefficient of atmospheric density models around altitude 100 km[J].Scientia Sinica-Physica, Mechanica & Astronomica, 2015, 45(12): 124706.(in Chinese) |
| [20] | 肖存英, 胡雄, 王博, 等. 临近空间大气扰动变化特性的定量研究[J].地球物理学报, 2016, 59(4): 1211–1221. XIAO C Y, HU X, WANG B, et al. Quantitative studies on the variations of near space atmospheric fluctuation[J].Chinese Journal Geophysics, 2016, 59(4): 1211–1221.DOI:10.6038/cjg20160404(in Chinese) |
| [21] | JUSTUS C G, WOODRUM A W, ROPER R G, et al.Four-D global reference atmosphere technical description.Part 1:NASA-TM-X-64871[R].Huntsville:George C.Marshall Space Flight Center, 1974:54-60. |
| [22] | YAN Z A, HU X, GUO W J, et al. Development of a mobile Doppler lidar system for wind and temperature measurements at 30-70 km[J].Journal of Quantitative Spectroscopy and Radiative Transfer, 2017, 188: 52–59.DOI:10.1016/j.jqsrt.2016.04.024 |
| [23] | PREUSSE P, ECKERMANN S D, ERN M. Transparency of the atmosphere to short horizontal wavelength gravity waves[J].Journal of Geophysical Research:Atmospheres, 2008, 113(D24): D24104.DOI:10.1029/2007JD009682 |
