拖曳式诱饵干扰是一种针对采用单脉冲测角技术雷达的有效干扰方法，被保护飞机通过拖曳线将动力和调制信号传送到诱饵。诱饵与目标均处于雷达探测主波束内，形成双点源非相干干扰^[1]，实现对单脉冲雷达的角度欺骗干扰。诱饵通过拖曳线与飞机相连，能够逼真模拟目标的飞行及散射特征，且与目标同处于雷达分辨单元内，使得雷达通过常规处理手段无法在时域、频域及空域进行分辨^[2]。
针对拖曳式诱饵干扰的对抗研究，主要分为诱饵与目标的分辨^[3-5]和诱饵干扰检测^[6-7]2个方面。目前，关于拖曳式诱饵干扰的检测研究主要从诱饵存在与否时单脉冲雷达接收回波幅度特征、极化特性^[8-11]等方面进行了分析。宋志勇等^[6-7]借鉴Blair和Brandt-Pearce^[12-15]在群目标检测中利用目标回波幅度变化的特点，提出了基于回波幅度特征及回波单脉冲比特征的拖曳式诱饵干扰检测方法。上述基于回波幅度特征的检测方法，均需多个探测脉冲相互独立，对于不满足探测脉冲独立的相参雷达，并没有探讨相应的处理方法。文献[8-11]以诱饵干扰信号极化特性与目标间的差异为前提，研究利用极化域特征差异对诱饵进行检测，但该方法不能鉴别具有目标极化散射矩阵模拟能力的全极化复杂调制假目标。
本文根据诱饵与目标信号间的多普勒频率差异，在平衡鉴相器输出端增加低通滤波器(LPF)，利用减法器提取出误差信号中包含多普勒频率差的部分，进而利用这一信号通过门限判别实现对拖曳式诱饵干扰的检测。首先，分析了有无拖曳式诱饵干扰时，平衡鉴相器输出角误差信号的表达式；其次，分析了拖曳式诱饵干扰下，单脉冲雷达导引头接收到的载机回波与诱饵干扰信号间的多普勒频率差；然后，推导了诱饵干扰条件下误差信号中包含多普勒频率差部分的表达式，并提出了目标检测方法；最后，仿真验证了本文方法的有效性。
1 单脉冲雷达测角分析 1.1 单点源情况 如图 1所示为一维单脉冲雷达测角系统框图。图中：AGC为自动增益控制；1、2分别表示经混频处理后得到的中频和信号y₁、差信号y₂；3、4分别表示经AGC处理后得到的和信号y₃、差信号y₄；5表示平衡鉴相器输出信号y₅。

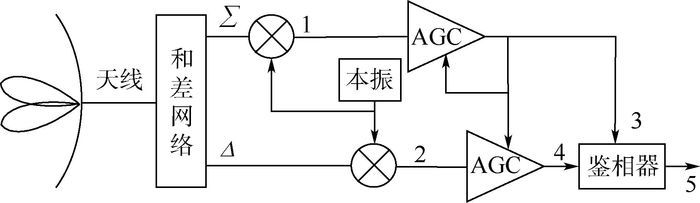图 1 单脉冲雷达测角系统框图 Fig. 1 Angle measure block diagram of monopulse radar system

图选项

单点源情况下，单脉冲雷达收到的和差信号为

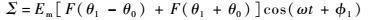(1)

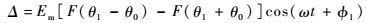(2)

式中：F(θ-θ₀)和F(θ+θ₀)分别为2个与天线等信号轴偏离±θ₀的天线波束方向图；E_m为信号振幅；θ₁为点源相对天线等信号轴的角位置；φ₁为点源在雷达天线口面处的相位；ω为接收信号高频频率。
经混频后

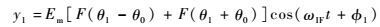(3)

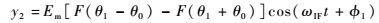(4)

式中：ω_IF为混频后中频信号频率。
令

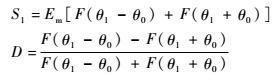式中：S₁为和波束接收信号的幅度；D为和差波束接收信号的比，在主波束范围内，D的大小与目标偏离等信号轴的大小成正比。
经增益为G=V₀/S₁(V₀为AGC自身的增益控制电压)的AGC处理后：

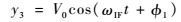(5)

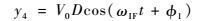(6)

经平衡鉴相器处理，输出角误差信号为

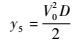(7)

经低通滤波器处理后：

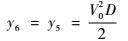(8)

由式(7) 可知，角误差信号与目标偏离等信号轴的大小成正比，即目标角位置与等信号轴重合时，D=0，输出角误差信号亦为0；若目标偏离等信号轴越大，则D越大，输出角误差亦越大。由式(8) 可知，单点源情况下，角误差信号经低通滤波器处理后，其值无变化。
1.2 拖曳式诱饵干扰情况 拖曳式诱饵干扰下，接收信号为

(9)

(10)

式中：S₂为诱饵干扰信号幅度；D₁为和差波束接收目标信号的比；D₂为和差波束接收诱饵干扰信号的比；φ₂(t)=φ₁+ψ(t)为诱饵信号在天线口面处的相位；ψ(t)=Δφ(t)+2πΔFt为由快变量诱饵转发相位不稳定Δφ(t)与慢变量两点源多普勒频率差ΔF引起的诱饵与目标回波相位差异。

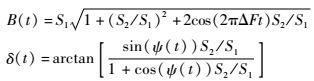y₁信号矢量合成如图 2所示。

图 2 信号矢量合成图 Fig. 2 Diagram of phasor summation analysis of signals

图选项

拖曳式诱饵干扰情况下，AGC的增益G=V₀/B(t)，则

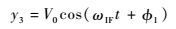(11)

(12)

式中：R=S₂/S₁为诱饵与目标信号的幅度比。
经平衡鉴相器处理后，输出角误差信号为

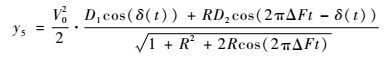(13)

由式(13) 可知，当存在拖曳式诱饵干扰时，输出角误差信号受目标与诱饵的角位置、能量比、相位差、多普勒频率差等影响，此时单脉冲雷达获得的为受欺骗的角度，使得天线等信号轴指向目标与诱饵连线的能量中心处。
式(13) 所示平衡鉴相器输出角误差信号表达式含有两点源多普勒频率差部分，与现有文献[1-2]分析存在差异。这主要是由于现有文献[1-2]在分析平衡鉴相器输出时，将多普勒频率差等效为影响两点源相位差的一个因素，从而在平衡鉴相器输出端消除了多普勒频率差。而实际上两点源多普勒频率差远小于平衡鉴相器输入端中频信号频率，相对于两点源初始相位差异、路程差等引起的快变相位差，多普勒频率差引起的相位变化是一个慢变量，而这一慢变量经平衡鉴相器处理后不会被转换为直流电压输出，而是保留其交流特性^[16-17]。
2 载机回波与拖曳式诱饵干扰信号多普勒频率差分析 当载机检测到来袭导弹时，可以选择释放拖曳式诱饵干扰欺骗雷达导引头。虽然在较远的距离上探测载机和诱饵信号，其多普勒频率差会很小，但随着导引头与目标越来越接近，其多普勒频率差会不断增大，这将会给识别目标信号和诱饵信号带来机会。
图 3为计算多普勒频率差的示意图，其中载机在A点、诱饵在B点、导弹在C点，拖曳线长度为L(AB之间的线段长度)，导弹距离载机为R₀，导弹飞行速度为V₁，载机飞行速度为V，导弹与载机连线方向与载机飞行方向的夹角为β，攻击角为α，α=β+θ，Δθ为载机和诱饵对导弹形成的张角。

图 3 多普勒频率差计算示意图 Fig. 3 Schematic of derivation of Doppler frequency difference

图选项

根据图 3可得，导弹和载机相对运动产生的多普勒频率为

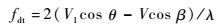(14)

式中：λ为雷达波长。
由于诱饵被拖曳飞行，且质量较轻，加之载机速度快，远距离时诱饵的速度大小和运动方向近似与载机相同，则导弹和诱饵相对运动产生的多普勒频率为

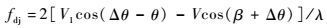(15)

则载机与诱饵之间的多普勒频率差为

(16)

3 拖曳式诱饵干扰检测 分析比较式(7) 和式(13)2种情况下平衡鉴相器输出角误差信号，在拖曳式诱饵干扰下，角误差信号受目标与诱饵干扰信号间多普勒频率差的调制，设计能够滤除这一多普勒频率差的低通滤波器，则拖曳式诱饵干扰下，经滤波处理前后的角误差电压会发生变化；而在单点源情况下，由式(8) 知滤波前后角误差信号无变化。如图 4所示，通过设立门限来实现对这一误差电压变化情况的检测，则可实现对拖曳式诱饵干扰的告警。

图 4 拖曳式诱饵干扰检测框图 Fig. 4 Block diagram of towed radar active decoy jamming detection

图选项

下面推导出拖曳式诱饵干扰下平衡鉴相器输出角误差信号经低通滤波器后的表达式，并给出拖曳式诱饵干扰检测的表达式。
由信号矢量图 2可知：

(17)

(18)

将式(17)、式(18) 以及三角恒等式cos(M－N)=cos Mcos N+sin Msin N代入式(13) 得

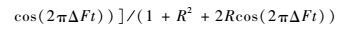(19)

误差电压y₅经低通滤波器处理后，其直流分量被提取出来，等效于保留式(19) 进行傅里叶级数展开时的第1项。对于一个周期为T的周期函数f(t)，其直流分量可表示为

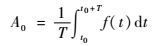(20)

则式(19) 的直流分量可表示为

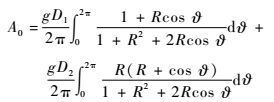(21)

式中：g=V₀²/2；?=2πΔFt。
式(21) 中，令

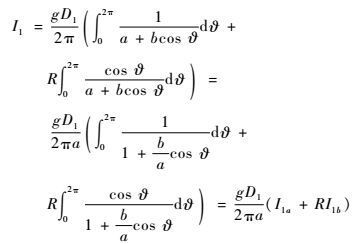(22)

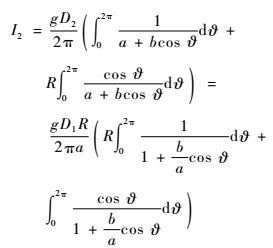(23)

又由三角函数积分式

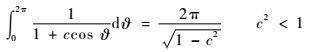(24)

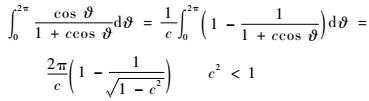(25)

对于任意R＞0(R≠1)，有1+R²＞2R，即，则

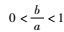
(26)

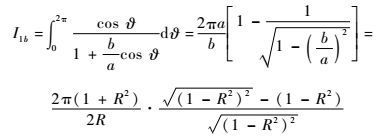(27)

当R＞1时，

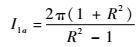(28)

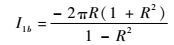(29)

当R＜1时，

(30)

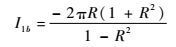(31)

综上可知：

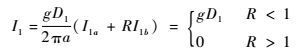(32)

对于式(23)，同理可得如下结论：
当R＞1时，

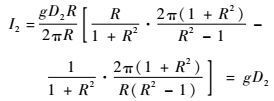(33)

当R＜1时，

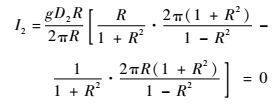(34)

即

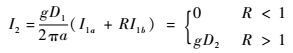(35)

当R=1时，式(21) 为

(36)

将式(32)、式(35)、式(36) 代入式(21) 得

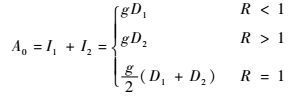(37)

拖曳式诱饵干扰下，诱饵干扰信号强于目标回波信号^[1]，即S₂＞S₁R=S₂/S₁＞1，经低通滤波器处理后，减法器输出信号为

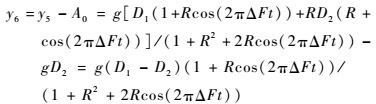(38)

由式(38) 可知，拖曳式诱饵干扰检测信号y₆为经AGC处理后的角误差信号滤除直流后的部分，其值主要受两点源间张角、能量比及多普勒频率差的影响，而回波信号振幅起伏不会对检测信号形成影响。因此，根据适当的条件，设定一定检测概率下的门限值η，可实现对诱饵干扰的检测。拖曳式诱饵干扰门限检测的表达式为

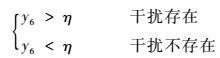(39)

式中：η为干扰检测门限，其值主要由单点源情况下目标回波信噪比及和差通道的幅相不一致性确定。
4 仿真分析 4.1 多普勒频率差仿真分析 根据式(16) 对拖曳式诱饵干扰下导弹攻击过程中载机与诱饵的多普勒频率差进行仿真分析，通过设定不同的攻击角、导弹速度、载机速度、拖曳线长度以及载机与诱饵信号的功率比，仿真分析载机与诱饵多普勒频率差的变化曲线。仿真参数设置如下：诱饵干扰功率为目标回波功率的2倍，拖曳线长度为100 m载机从10 km远处向导弹靠近，载机速度为300 m/s，导弹速度为800 m/s，导弹攻击角范围为0°~180°, 对应图 5，假定0°~90°范围为尾追攻击，90°~180°范围为迎头攻击。

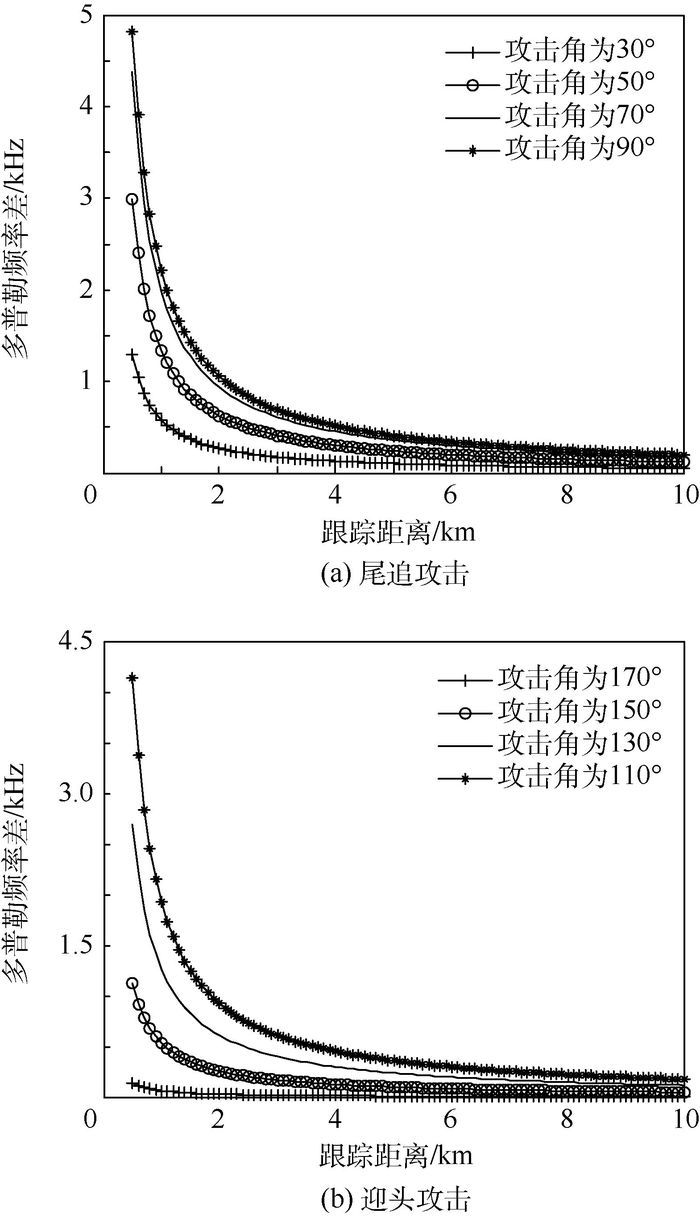图 5 典型参数下多普勒频率差 Fig. 5 Doppler frequency difference under typical parameters

图选项

从图 5可以看出，导弹从不同角度攻击时，载机与诱饵的多普勒频率差不同。由图 5可知，典型参数下，在不考虑方向时迎头攻击和尾追攻击情况类似，导弹攻击方向与载机飞行方向夹角越小，载机与诱饵的多普勒频率差越小，反之越大；特别是当攻击角为90°时，此时多普勒频率差最大，从仿真结果可以看出，在10 km距离时，多普勒频率差为250Hz左右。当攻击角较小时(30°)时，多普勒频率差较小，但也达到50 Hz左右。
4.2 拖曳式诱饵干扰检测仿真分析 雷达对拖曳式诱饵干扰的检测是一个时变、动态的过程，影响检测因素较多。下面根据式(38)、式(39) 仿真分析典型干扰条件下检测电压y₆及诱饵检测概率随目标与诱饵间两点源张角Δθ、功率比ISR及多普勒频率差ΔF的变化情况。设g=20，信噪比SNR=5 dB，雷达波束宽度θ_BW=1.6°，对振幅和差单脉冲天线方向图作线性化近似，单脉冲误差斜率k_m=1.3。门限η为单点源情况下，信噪比SNR=5 dB，和差通道幅相不一致性为5%时，平衡鉴相器的输出值。图 6~图 8为不同条件下进行1 000次Monte Carlo仿真的结果。

图 6 两点源张角变化(ISR=30 dB，ΔF=250 Hz) Fig. 6 Variation of dual-source field angle (ISR=30 dB, ΔF=250 Hz)

图选项

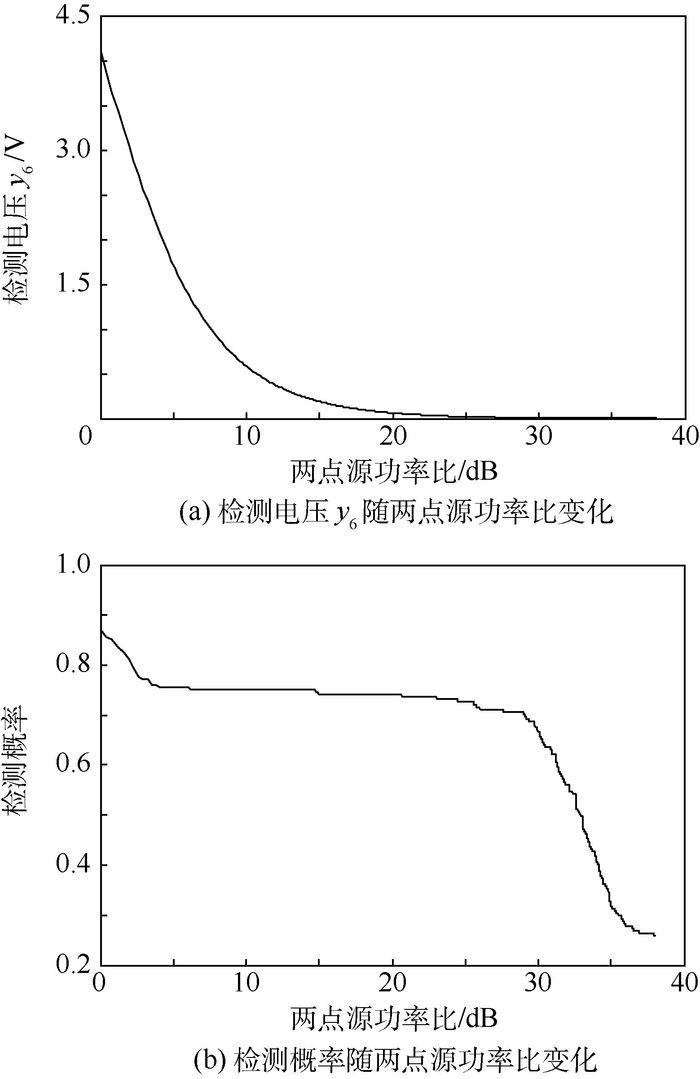图 7 两点源功率比变化(Δθ=0.4°，ΔF=250 Hz) Fig. 7 Variation of dual-source jam-to-signal ratio(Δθ=0.4°, ΔF=250 Hz)

图选项

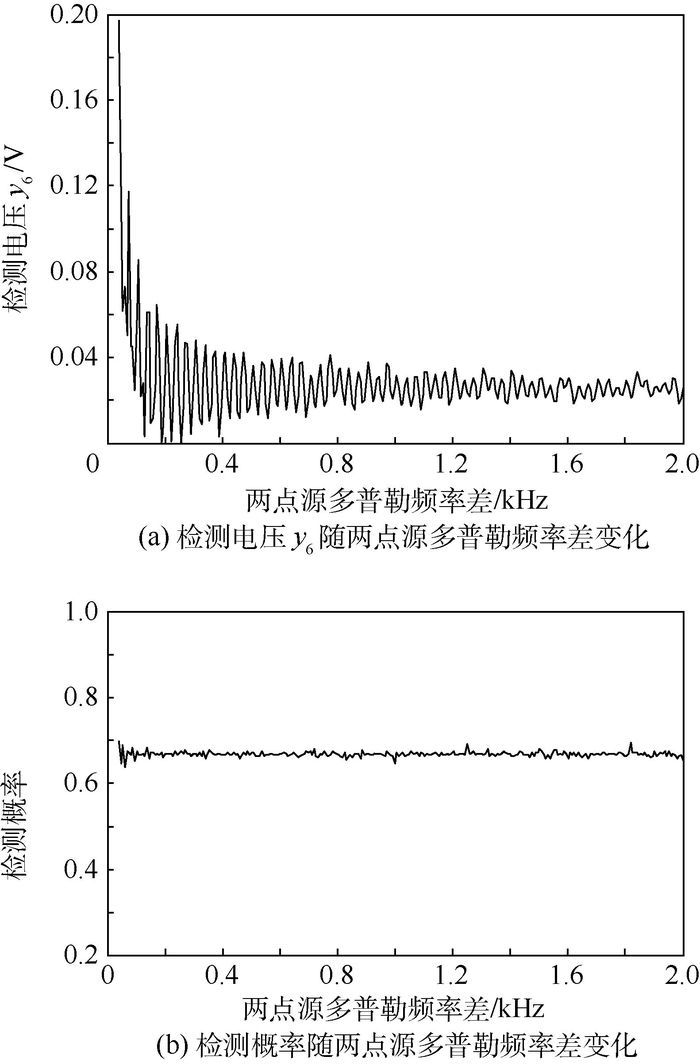图 8 两点源多普勒频率差变化(ISR=30 dB，Δθ=0.4°) Fig. 8 Variation of dual-source Doppler frequency difference(ISR=30 dB, Δθ=0.4°)

图选项

由图 6(a)可知，检测电压随着两点源张角的增大而增大。这是由于当两点源间功率比、多普勒频率差固定后，在主波束范围内，随着两点源张角增大，两点源间差波束增益差亦增大，故检测电压增大。当两点源张角继续增大到超出主瓣范围后，主波束内只有一个信源，此时检测电压会迅速减小。同时从图 6(b)可以看出，检测概率亦随着张角的增大而增大，当张角增大超过一定角度后，检测概率不再增大。
图 7表明，随着两点源功率比的增加，检测电压逐渐减小。这是由于随着两点源中干扰功率的增大，AGC的增益逐渐减小，其输出角误差信号中由两点源多普勒频率差引起的交流分量亦逐渐减小，故检测电压减小。随着两点源功率比的增大，检测概率亦减小，当两点源功率比小于30 dB时，检测概率不小于0.67。当两点源功率比大于30 dB时，检测概率急剧下降，可通过在接收机前端增加限幅器来降低两点源功率比，从而提高强干扰下诱饵检测概率。
图 8表明，随着多普勒频率差的增大，检测电压在一定范围内波动。这是由于在不同的多普勒频率差下，AGC的增益会有起伏变化，使得平衡鉴相器输出误差电压发生变化波动，从而使得检测电压发生波动。随着多普勒频率的变化，检测概率亦在一定范围内波动，其平均检测概率在0.67左右。
5 结论 拖曳式诱饵干扰情况下，单脉冲平衡鉴相器输出信号中包含由诱饵和目标多普勒频率差异引起的交流分量。基于这一差异，本文得出以下结论：
1) 推导了拖曳式诱饵干扰下经平衡鉴相器处理后输出角误差信号交流分量的表达式。
2) 根据有无拖曳式诱饵干扰时，平衡鉴相器输出角误差交流分量的大小，利用门限检测实现了对转发式拖曳式诱饵干扰的检测。
3) 多种条件下的仿真分析表明，通过这一差异，能够实现对拖曳式诱饵干扰较高的检测概率。

参考文献

[1]	白渭雄, 唐宏, 陶建峰. 拖曳式诱饵对单脉冲雷达的干扰分析[J].电子信息对抗技术, 2007, 22(6): 39–42. BAI W X, TANG H, TAO J F. Analysis of towed decoy jamming on monopulse radar[J].Electronic Information Warfare Technology, 2007, 22(6): 39–42.(in Chinese)
[2]	白渭雄, 焦光龙, 付红卫. 拖曳式诱饵对抗技术研究[J].系统工程与电子技术, 2009, 31(3): 579–582. BAI W X, JIAO G L, FU H W. Study on antagonistic technology of towed decoys[J].Systems Engineering and Electronic, 2009, 31(3): 579–582.(in Chinese)
[3]	宋志勇, 肖怀铁, 付强, 等. 一种波束内目标与诱饵DOA联合估计新方法[J].国防科技大学学报, 2012, 34(5): 96–101. SONG Z Y, XIAO H T, FU Q, et al. A novel approach to jointly estimate the DOA of the target and decoy within the radar beam[J].Journal of National University of Defense Technology, 2012, 34(5): 96–101.(in Chinese)
[4]	宋志勇, 肖怀铁, 祝依龙, 等. 基于改进MCMC的波束内目标与诱饵联合参数估计[J].宇航学报, 2012, 33(4): 451–459. SONG Z Y, XIAO H T, ZHU Y L, et al. Joint parameter estimation of the target and decoy within the radar beam based on improved MCMC[J].Journal of Astronautics, 2012, 33(4): 451–459.(in Chinese)
[5]	宋志勇, 肖怀铁, 祝依龙, 等. 末制导雷达目标与诱饵的联合参数估计和辨识[J].系统工程与电子技术, 2012, 34(4): 644–651. SONG Z Y, XIAO H T, ZHU Y L, et al. Joint parameter estimation and identity recognition of targets and decoys in terminal guidance[J].Systems Engineering and Electronics, 2012, 34(4): 644–651.(in Chinese)
[6]	宋志勇, 肖怀铁. 基于回波幅度特征的拖曳式诱饵存在性检测[J].电子与信息学报, 2011, 33(6): 1515–1519. SONG Z Y, XIAO H T. Detection of presence of towed radar active decoy based on amplitude characteristic[J].Journal of Electronics & Information Technology, 2011, 33(6): 1515–1519.(in Chinese)
[7]	宋志勇, 肖怀铁, 祝依龙, 等. 基于扩展单脉冲比的拖曳式诱饵存在性检测[J].航空学报, 2011, 32(9): 1656–1668. SONG Z Y, XIAO H T, ZHU Y L, et al. Detection of presence of towed radar active decoy based on extended monopulse ratio[J].Acta Aeronautica et Astronautica Sinica, 2011, 32(9): 1656–1668.(in Chinese)
[8]	李永祯, 王雪松, 王涛, 等. 有源诱饵的极化鉴别研究[J].国防科大学报, 2004, 26(3): 83–88. LI Y Z, WANG X S, WANG T, et al. Polarization discrimination algorithm of active decoy and radar target[J].Journal of National University of Defense Technology, 2004, 26(3): 83–88.(in Chinese)
[9]	李永祯, 王雪松, 肖顺平, 等. 基于IPPV的真假目标极化鉴别算法[J].现代雷达, 2004, 26(9): 38–42. LI Y Z, WANG X S, XIAO S P, et al. A new polarization discrimination algorithm for active decoy and radar target based on IPPV[J].Modern Radar, 2004, 26(9): 38–42.(in Chinese)
[10]	王涛, 王雪松, 肖顺平. 随机调制单极化有源假目标的极化鉴别研究[J].自然科学进展, 2006, 26(5): 611–617. WANG T, WANG X S, XIAO S P. Study on discrimination of random modulated single polarization decoy[J].Progress in Nature Science, 2006, 26(5): 611–617.(in Chinese)
[11]	宋立众, 乔晓林, 孟宪德. 脉冲多普勒雷达导引头角欺骗干扰的极化抑制[J].电波科学学报, 2005, 20(3): 353–357. SONG L Z, QIAO X L, MENG X D. Polarization suppression of angle cheating interference in pulse Doppler radar seeker[J].Chinese Journal of Radio Science, 2005, 20(3): 353–357.(in Chinese)
[12]	BLAIR W D, BRANDT-PEARCE M. Unresolved Rayleigh target detection using monopulse measurements[J].IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(2): 543–552.DOI:10.1109/7.670335
[13]	BLAIR W D, BRANDT-PEARCE M.Discrimination of targets and RGPO echoes using frequency diversity[C]//Proceeding of the 28th Southeastern Symposium on System Theory, 1996:280-284.
[14]	BLAIR W D, BRANDT-PEARCE M.Estimation and discrimination for swerling targets[C]//Proceeding of the 29th Southeastern Symposium on System Theory, 1997:509-513.
[15]	BLAIR W D, BRANDT-PEARCE M.Monopulse processing for tracking unresolved targets:DINSWCDD/TR-A655033[R].Dahlgren:Naval Surface Warfare Center, 1997.
[16]	列昂诺夫A A. 单脉冲雷达[M]. 黄虹, 译. 北京: 国防工业出版社, 1974: 55-58. LEONOV A A.Monopulse radar[M].HUANG H, translated.Beijing:National Defense Industry Press, 1974:55-58(in Chinese).
[17]	栾华东, 李道清. 高频电子线路[M].武汉: 华中科技大学出版社, 2013: 137-139. LUAN H D, LI D Q. High frequency electronic circuits[M].Wuhang: Huang Zhong University of Science and Technology Press, 2013: 137-139.(in Chinese)