考虑实际生产中的等待时间约束正成为学术界和工业界的研究热点。Tu和Chen[1]将设备的平均失效时间(Mean Time Between Failure, MTBF)和平均修复时间(Mean Time To Repair, MTTR)整合进GI/G/m排队模型,为带等待时间约束的串行工作站作了能力规划,并研究了不同控制策略下各工作站能力规划水平的变化。Ono等[2]基于M/M/1模型和利特尔法则(Little’s law),根据缓冲区WIP的阈值大小,建立了一种基于风险的评估方法。更多关于排队模型在这类问题上的应用可参见文献[3]。Wu等[4]基于马尔可夫决策过程,通过最小化持有成本和废弃成本之和,为一个等待时间约束(含加工时间)呈指数分布的串行系统建立了最优控制策略;之后又将模型扩展至工作站内含多台并行机的情形[5]。Shi和Gershwin[6]假设上下游设备的MTBF和MTTR均服从几何分布,基于离散时间马尔可夫链推导出了WIP等待时间的概率分布。文献[7]同样考虑设备的随机故障,借鉴经济订货批量(Economic Order Quantity, EOQ)思想,通过权衡WIP的返工成本和下游瓶颈工作站的能力损失,推导出了缓冲区容量的最优控制限。上述文献从多种角度对带等待时间约束的生产系统进行了分析研究,如能力规划、风险、缓冲区控制等,并且大都考虑了设备的随机故障。但是,仍存在2个问题:一是仅选用MTBF和MTTR 2个参数对设备的劣化过程及修复进行刻画,与实际偏差较大;二是就其维护方式而言,属于事后维修,这一假设在自动化程度较高的行业里并不合理,如半导体制造。
关于生产设备的退化和可靠性问题一直是学术界研究的热点。Peng等[8]综合考虑系统的连续劣化过程和受到的突发性外界冲击,建立了可靠性和维护模型。王严等[9]分析保障设备故障对装备保障活动的影响, 建立了保障设备站点内的保障过程模型。张卓琦等[10]则考虑了系统中部件间存在的故障相关性,提出了一种年龄预防性维修与机会维修相结合的维修策略。上述文献从设备故障的不同内在机理出发,建立故障模型,但并未将设备的退化过程与实际生产活动(如引起的产品质量问题)相联系起来。
综合以上2点,本文针对一个带等待时间约束的生产系统,用更为准确的劣化模型来刻画其劣化过程,并考虑其劣化过程引起的质量损失问题,通过引入预防性维护(Preventive Maintenance, PM)策略和M/G/1/K排队模型对预防性维护阈值和中间缓冲区容量作联合优化,以最大化系统的有效产出。
1 问题描述 考虑如图 1所示的一个由2个工作站串联的带缓冲区的生产系统。其中,上游工作站1为非能力约束资源(Non-Capacity Constraint Resources, NCCR),下游工作站2为能力约束资源(Capacity Constraint Resources, CCR),即瓶颈工作站。每一工作站前面都有一定数量的WIP,分别组成队列Q1、Q2,由工作站1加工后的WIP在Q2中的等待时间不得超过某一设定的时间上限,即存在“等待时间约束TC”。
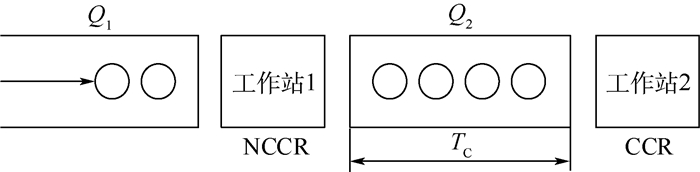 |
| 图 1 带等待时间约束的串行生产系统 Fig. 1 A serial production system with queue time constraints |
| 图选项 |
定义1 有效产出:以图 1所示的生产系统为研究对象,将总期望产出去除质量损失、被阻塞未进入Q2的潜在工件以及因超出TC被废弃的WIP后剩余的产出,如图 2所示。
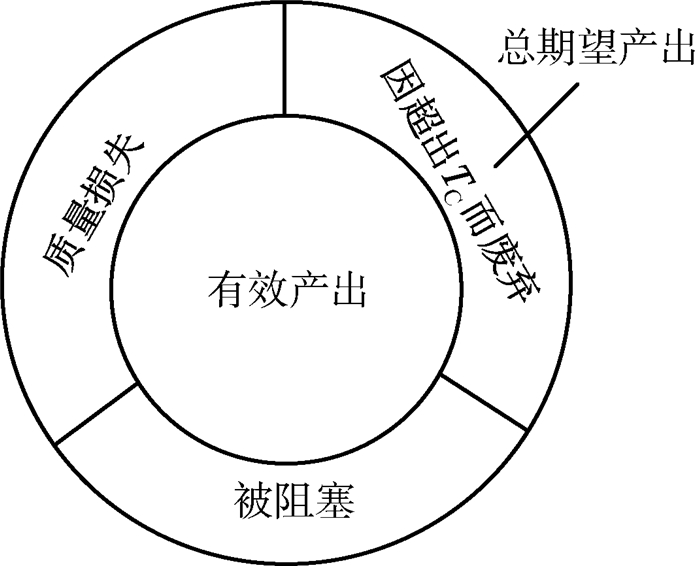 |
| 图 2 “有效产出”示意图 Fig. 2 Schematic diagram of "effective throughput" |
| 图选项 |
为进一步描述研究问题域,作如下假设:① 工作站1和2一次均只能加工一个工件。工作站1前面的缓冲区容量为无限大,为方便后文计算,工作站2前面的缓冲区容量设为K-1;② 工件到达工作站1的时间间隔服从指数分布,经工作站1加工后进入缓冲区Q2, 当Q2已满时,则关停工作站1以阻止新的WIP加入队列,直至Q2中WIP数量小于K-1;③ 若Q2中WIP的等待时间超过“等待时间约束TC”,则直接废弃;④ 随着生产活动的进行,工作站1和2都不可避免地发生劣化。对非瓶颈工作站1采取事后维修(替换)策略,替换后恢复至全新状态,并且替换时间忽略不计;瓶颈工作站2服从连续的劣化过程,并对其状态进行连续监测,在其劣化量达到失效阈值DF之前对其进行PM,并且每次PM均不能使其恢复至初始全新状态;⑤ 经工作站2加工出的产品并非全都是完美的,存在质量损失,并且质量损失随着其劣化量的增大而增大。
基于以上假设,本文的决策目标是:在瓶颈工作站2的预期寿命范围TL内,综合决策工作站2的PM阈值DP和缓冲区Q2容量的控制上限K-1,以最大化系统的有效产出。
2 模型构建 2.1 生产系统的劣化过程及维护建模 考虑到工作站1为NCCR,仅对到达的工件进行初步的预处理,因此对其进行事后维修(替换),该工作站内一般均为通用型设备,较易获得,忽略其替换时间。
基于约束理论(Theory of Constraints, TOC),瓶颈决定系统产能,为此选用更为准确的劣化模型对工作站2的劣化过程进行刻画。伽马过程具有非负的独立增量特性,被广泛应用于模拟单调累积增长的渐变式退化过程,如磨损、疲劳、腐蚀、裂纹生长、蠕变等[11]。更多关于伽马过程在设备劣化及维护领域的应用可参见文献[12]。文献[11]对金属表面点蚀生长过程的研究表明:点蚀坑深的增量与时间呈非线性关系。为此本文选取非定态伽马过程来对工作站2的连续劣化过程进行建模,假设其形状参数α(t)=αtq(q>0),尺度参数β>0。设工作站2在初始时刻为全新状态,即X(0)=0,则其t时刻劣化量X(t)的概率密度函数(PDF)为
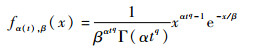 | (1) |
式中:
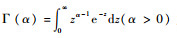
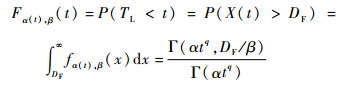 | (2) |
式中:Γ(t, x)为上不完全伽马函数,Γ(t, z)=
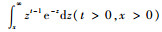
定理1 如果某设备(系统)的劣化过程服从伽马过程,并存在一个失效阈值(上界),则其失效率函数是关于时间的增函数。
证明 不失一般性,考虑如下伽马过程X(t):初始状态X(0)=0,形状参数α(t)>0,尺度参数β>0,失效阈值为DF。根据定义,失效率函数可表示为
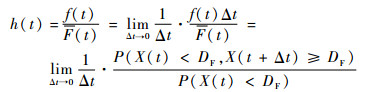 |
式中:f(t)为失效时间的概率密度函数;F(t)为可靠度函数。
令ΔX=X(t+Δt)-X(t)表示在区间[t, t+Δt]内的劣化增量,设其概率密度函数为g(y, Δt), y∈(0, DF)。于是有
 |
式中:
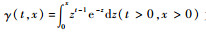
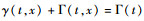
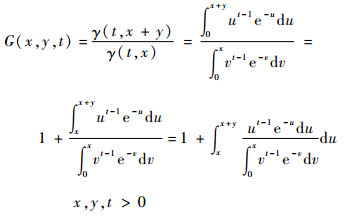 |
对t求偏导,可得
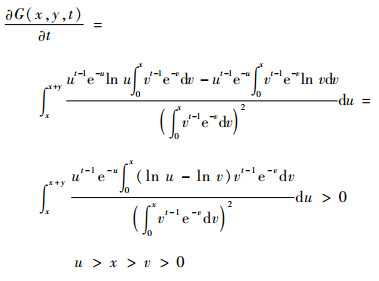 |
于是,G(x, y, t)是关于t的增函数,那么
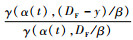
定义2 设X,Y是2个随机变量,若对任意正数a,有P(X>a)≥P(Y>a),则称X随机的大于Y,记作X≥stY[13]。
进一步地,设{Xn, n=1, 2, …}表示某一随机过程,若对所有的n=1, 2, …,均满足Xn≥st(≤st)Xn+1,则称{Xn, n=1, 2, …}是随机递减(递增)的。
定理2 设X(Mi)表示第i次PM后,系统劣化量恢复至的中间某一水平。假设对
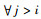
证明 由文献[11]可知,若X≤stY,φ(u)是一个单调增函数并且φ(u)≥0,则有E[φ(X)]≤E[φ(Y)]。根据定理2中的前提条件,易得hj(t)=E[hj(t)X(Mj)]≥E[hi(t)X(Mi)]=hi(t)其中:hk(t)|x显然恒为正数。设Fi+1(t)为系统第i+1个运行周期Ti+1的寿命分布函数,Ri+1(t)为其可靠度函数,则
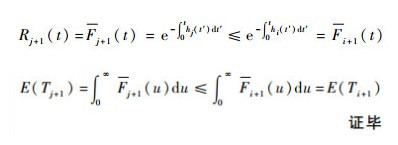 |
工作站2从初始全新状态第1次运行达到PM阈值所经历时间的期望值为
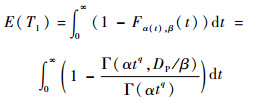 | (3) |
第i次PM后(i=1, 2, …,N-1),第i+1个运行周期的期望长度为
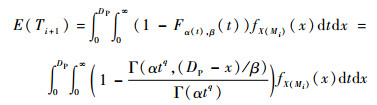 | (4) |
式中:fX(Mi)为第i次PM后,工作站2的劣化量恢复至X(Mi)(0 < X(Mi) < DP)的概率密度函数。
假设第i次PM时间Mi(i=1, 2,…, N-1) 是关于维护阈值和维护次数的增函数,Mi服从参数为λi的指数分布(其期望

由以上分析可知,将工作站2的整个预期寿命TL划分为N个维护周期。随着N的增大,运行周期的期望长度越来越短,而每个运行周期结束后进行PM所花费的时间越来越长,直至达到预期寿命对其进行更新(替换)。
2.2 质量损失建模 由第1节假设⑤,随着工作站2劣化程度的加剧,其所生产出产品的质量性能也随之下降,即存在质量损失。根据文献[14],可以用田口质量损失函数(二次损失函数)衡量质量损失的相关成本:
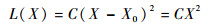 | (5) |
式中:L(X)为质量损失函数;X0为系统全新状态时的劣化量(本文X0=0);C为相关的成本系数。
在工作站2的整个寿命周期内,总质量损失为
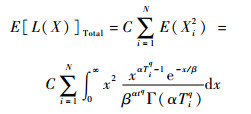 | (6) |
为描述产品质量损失与产出损失L(O)间的关系,在文献[15]基础上,构造两者间函数关系如下:
 | (7) |
式中:k1、k2为比例系数。于是,在工作站2的整个寿命周期内,由质量损失引起的总产出损失为
 | (8) |
2.3 基于M/G/1/K排队模型的缓冲区建模 如图 1所示,工件经工作站1加工后进入队列Q2,按照到达的先后顺序依次在工作站2进行加工,可以视为一排队系统。设α(n)表示在工作站2加工某工件期间,有n个新工件进入Q2的概率,则
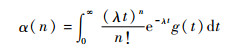 | (9) |
式中:λ为工件的到达率;g(t)为工作站2加工单位产品所需时间s2的概率密度函数。由第1节假设②,工作站1和2之间的缓冲区最多可容纳K-1个WIP。设缓冲区的状态i表示在工作站2加工完某一工件的瞬间,队列中恰好存在i个WIP(i=0, 1,…, K-1)。pi, j表示图 3所示马尔可夫链从状态到状态的转移概率,pi, j定义为
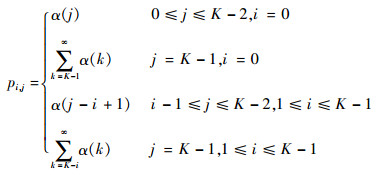 |
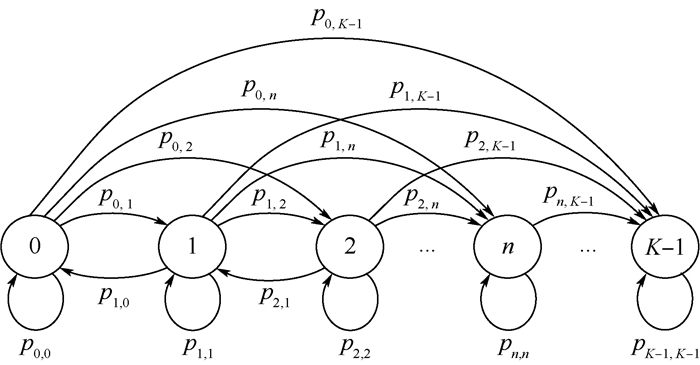 |
| 图 3 排队系统的状态转移示意图 Fig. 3 Schematic diagram of state transition for queuing systems |
| 图选项 |
设pn(n=0, 1, …, K-1) 表示当系统处于稳态时,在工作站2加工完某工件的瞬间Q2中恰好有n个工件的稳态概率。pn可以通过式(10) 求解:
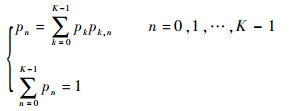 | (10) |
式(10) 中2个公式分别表示状态平衡方程和归一化等式。在工作站2加工完工件的瞬间,系统有0, 1,…, K-1共K种可能状态,即共有K个独立变量。但式(10) 中平衡方程只有K-1个是相互独立的,因此必须加入归一化等式才能求解。选取前K-1个平衡方程以及归一化等式,并改写成以下形式:
 |
设向量p=[p0, p1, …, pK-1]T,b=[0, 0, …, 1]T,A为一个K×K的矩阵:
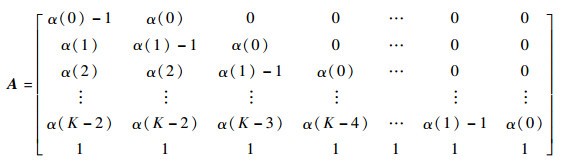 |
根据式(10) 中K个相互独立的线性方程组,可将问题转化为求解线性方程组Ap=b,其解为p=A-1b。注意到此时的pn(n=0, 1,…, K)表示在工作站2加工完某工件的瞬间,Q2中存在n个WIP的稳态概率,而非任意时刻系统中存在n个WIP的概率。根据泊松过程的PASTA性质,任意时刻系统中恰好有n个WIP的稳态概率pn(n=0, 1,…, K)可通过式(11) 计算:
 | (11) |
式中:
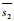
 | (12) |
缓冲区WIP超出TC而废弃的概率为
 | (13) |
式中:gk(t)为工作站2加工完k个WIP所需时间的概率密度函数,可由其加工单个WIP时间的概率密度函数g(t)求得。
3 数值实例 本节通过一个数值实例来对所提模型进行演示。工作站2的预期寿命TL=650 h,失效阈值DF=150 μm,工件的到达率服从参数λ=5.5的指数分布,工作站2的加工单位产品的时间s2服从[0.1, 0.2]的均匀分布,中间缓冲区WIP的等待时间约束TC=1.2 h。参考文献[11]中对点蚀生长过程所服从非定态伽马过程的参数估计方法,用最大似然法对参数α、β和q进行估计。假设进行了n次不同时段的观测,似然函数为
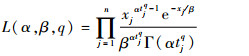 | (14) |
对式(14) 取对数,得
 | (15) |
最大化式(15),利用MATLAB编程得到各参数的估计值:α=3.2,β=4.3,q=0.5。选取PM阈值DP=120 μm,工作站2劣化量达到PM阈值所经历时间的累积概率函数(CDF)和概率密度函数如图 4所示。可以看到:在160 h以后,工作站2劣化量达到PM阈值的概率将稳定趋近于1。
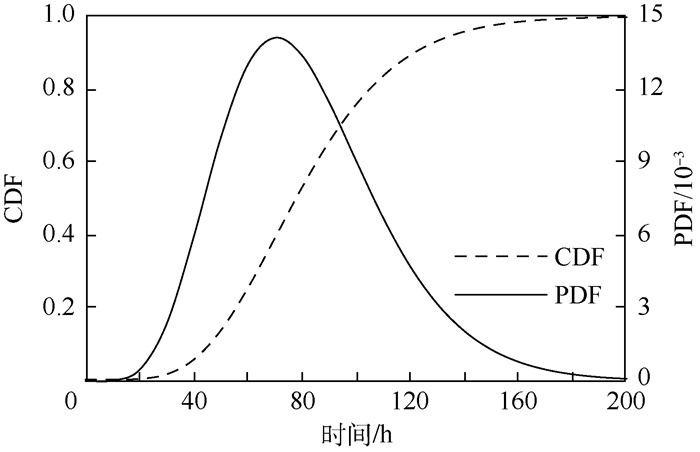 |
| 图 4 工作站2达到DP经历时间的CDF和PDF Fig. 4 CDF and PDF of service time of station 2 until DP |
| 图选项 |
根据第2节构建的劣化及维护模型,当DP=120 μm时,工作站2在前5个维护周期(N=1~5) 内失效率函数的变化如图 5所示,可以得出以下结论:① 在任一维护周期内,其失效率函数是关于时间的增函数;② 随着维护周期的增大,同一时刻工作站2的失效率越来越大。图 5验证了定理2的正确性,并且可以得出推论:随着维护周期个数的增大,工作站2的期望运行时间越来越短。
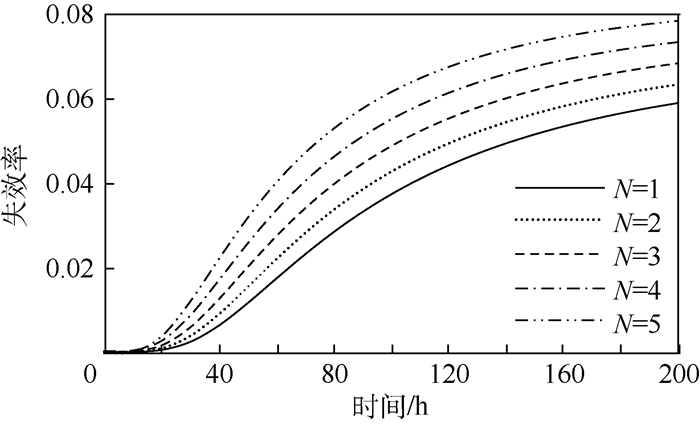 |
| 图 5 不同维护周期里失效率函数随时间的变化 Fig. 5 Variation of failure rate function with time in different maintenance periods |
| 图选项 |
图 6验证了上述推论的正确性,并且可以看到:当PM阈值DP分别取为[110,115,120,125,130] μm时,对应工作站2在寿命范围内的维护周期个数分别为[12, 11, 10, 10, 9],这是由于DP值设置的越大,则对应的运行时间和PM时间均越长,则在有限的寿命范围内总维护周期个数越少。图中,DP=125 μm和130 μm对应的2条曲线在最后一个维护周期快速下降的原因是最后一个维护周期是不完整的,分别运行了5.4 h和22.2 h便达到了预期寿命TL(更新点)。
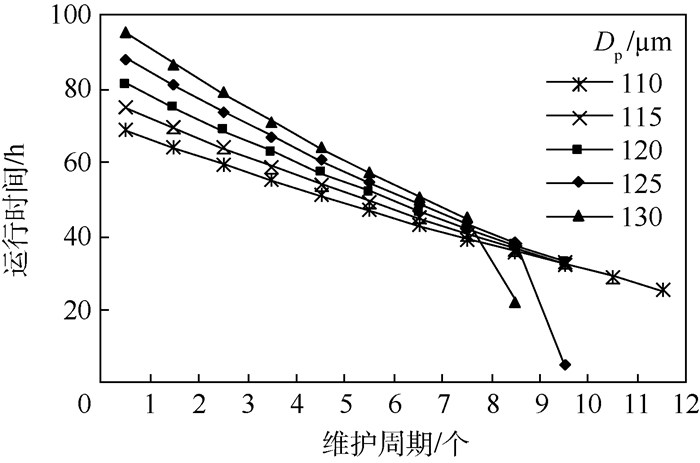 |
| 图 6 不同DP下各维护周期的期望运行时间 Fig. 6 Expected service time of each maintenance period under different DP |
| 图选项 |
图 7表明了在理想情况下(即不考虑质量损失、阻塞及WIP等待时间超出TC),不同的PM阈值对应的总期望产出及质量损失。可以看到:随着PM阈值的增大,系统在理想情况下的总期望产出也越大,原因在于总运行时间相对变长,总PM时间相对变短;但是引起的质量损失成本也随之增大,这是因为系统在进行PM前的劣化程度加剧,而2.2节的质量损失模型表明:质量损失成本与劣化量的二次方成正比关系。
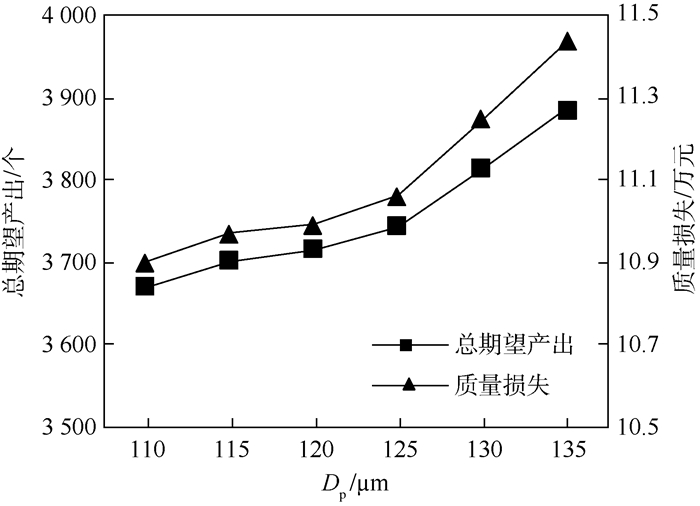 |
| 图 7 不同DP对应的的总期望产出及质量损失 Fig. 7 Expected total throughput and quality loss under different DP |
| 图选项 |
工件的阻塞概率(PB)及因超出TC而废弃的概率(PS)随缓冲区容量K-1的变化情况如图 8所示。随着K值的增大,工件的阻塞概率变小,但缓冲区内WIP超出TC约束的概率变大。容易理解:将缓冲区容量设置的越大,则经工作站1加工后的工件有更大的概率加入队列Q2;但同时意味着Q2中WIP在被工作站2加工前的等待时间更长,则超出TC的概率越大。
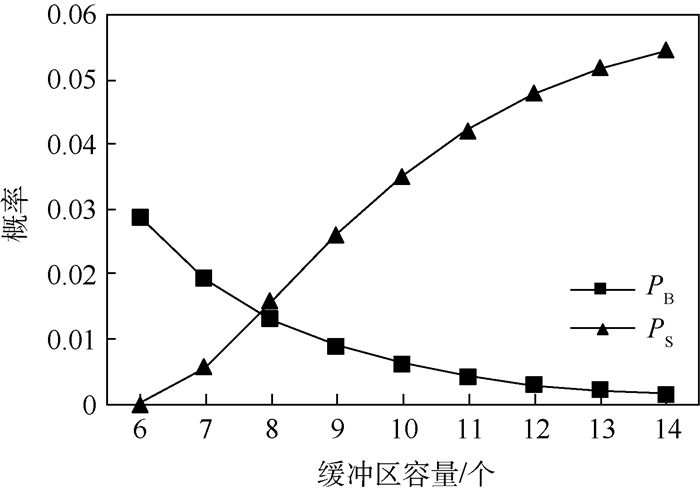 |
| 图 8 PB、PS随缓冲区容量的变化 Fig. 8 Variation of PB and PS with buffer capacity |
| 图选项 |
DP及K的变化均会影响系统的有效产出,但是难以将两者整合进一个数学模型中,以寻求最大化目标函数对应的最优组合。为此采用数值迭代算法寻找两者的最优组合[DP*, K*],见表 1。
表 1 不同的[DP, K]对应的系统有效产出 Table 1 Effective throughput of systems under different combinations of [DP, K]
| K/个 | 有效产出/个 | |||||
| DP=110μm | DP=115μm | DP=120μm | DP=125μm | DP=130μm | DP=135μm | |
| 6 | 3365 | 3378 | 3386 | 3393 | 3400 | 3393 |
| 7 | 3378 | 3390 | 3398 | 3405 | 3412 | 3406 |
| 8 | 3365 | 3377 | 3386 | 3393 | 3399 | 3392 |
| 9 | 3346 | 3358 | 3367 | 3373 | 3380 | 3372 |
| 10 | 3328 | 3340 | 3348 | 3355 | 3361 | 3353 |
| 11 | 3312 | 3324 | 3332 | 3338 | 3344 | 3336 |
| 12 | 3299 | 3311 | 3319 | 3325 | 3331 | 3323 |
| 13 | 3290 | 3301 | 3309 | 3316 | 3321 | 3313 |
| 14 | 3283 | 3295 | 3303 | 3309 | 3314 | 3306 |
表选项
可以看到:当[DP, K]取值为[130,7]时,对应的系统有效产出最大,为3412个。
4 结论 1) 定义“有效产出”这一概念,使制造企业关注实际生产过程中由于设备劣化引起的质量损失、缓冲区的阻塞以及由于WIP等待时间过长而废弃等问题,避免盲目追求生产率。
2) 对工作站2全寿命周期内劣化过程及预防性维护的建模,能较好地符合生产实际,为制造企业开展维护活动提供参考。
3) 在结论2) 的基础上考虑由于设备劣化引起的质量损失,进而提出了一种基于状态的预防性维护策略,减少系统因产品质量而损失的产出。
4) 引入M/G/1/K排队模型求解缓冲区WIP的阻塞及超出等待时间约束的概率,为存在等待时间约束的实际生产系统的缓冲区控制提供了一种新的优化思路,进而提高系统的有效产出。
数值实例表明:本文所提模型是切实、有效的,对于制造企业的设备维护、缓冲区控制以及产出提高有一定的指导意义。为使模型更符合实际生产情况,可进一步考虑实际生产成本、维护成本等。
参考文献
| [1] | TU Y M, CHEN H N. Capacity planning with sequential time constraints under various control policies in the back-end of wafer fabrications[J].Journal of the Operational Research Society, 2010, 61(8): 1258–1264.DOI:10.1057/jors.2009.36 |
| [2] | ONO A, KITAMURA S, MORI K.Risk based capacity planning method for semiconductor fab with queue time constraints[C]//Proceedings of IEEE International Symposium on Semiconductor Manufacturing, 2006.Piscataway, NJ:IEEE Press, 2006:49-52. |
| [3] | WU K. Classification of queueing models for a workstation with interruptions:A review[J].International Journal of Production Research, 2014, 52(3): 902–917.DOI:10.1080/00207543.2013.843799 |
| [4] | WU C H, LIN J T, CHIEN W C. Dynamic production control in a serial line with process queue time constraint[J].International Journal of Production Research, 2010, 48(13): 3823–3843.DOI:10.1080/00207540902922836 |
| [5] | WU C H, LIN J T, CHIEN W C. Dynamic production control in parallel processing systems under process queue time constraints[J].Computers & Industrial Engineering, 2012, 63(1): 192–203. |
| [6] | SHI C, GERSHWIN S B. Part waiting time distribution in a two-machine line[J].IFAC Proceedings Volumes, 2012, 45(6): 457–462.DOI:10.3182/20120523-3-RO-2023.00114 |
| [7] | WU K, ZHAO N, GAO L, et al. Production control policy for tandem workstations with constant service times and queue time constraints[J].International Journal of Production Research, 2016, 54(21): 6302–6316.DOI:10.1080/00207543.2015.1129468 |
| [8] | PENG H, FENG Q, COIT D W. Reliability and maintenance modeling for systems subject to multiple dependent competing failure processes[J].ⅡE Transactions, 2010, 43(1): 12–22. |
| [9] | 王严, 马麟, 文佳, 等. 考虑保障设备故障的装备维修保障模型[J].北京航空航天大学学报, 2012, 38(1): 123–127. WANG Y, MA L, WEN J, et al. Maintenance-support model of materiel considering support equipment failure[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(1): 123–127.(in Chinese) |
| [10] | 张卓琦, 吴甦, 李斌锋. 考虑故障相关的两部件系统机会维修策略[J].清华大学学报(自然科学版), 2012, 52(1): 122–127. ZHANG Z Q, WU S, LI B F. Opportunistic maintenance policy for a two-unit system with failure interactions[J].Journal of Tsinghua University(Science and Technology), 2012, 52(1): 122–127.(in Chinese) |
| [11] | 翟子青. 基于随机过程的蒸汽发生器传热管腐蚀失效寿命分析[D]. 上海: 上海交通大学, 2011: 34-38. ZHAI Z Q.Stochastic modeling for the degradation of steam generator tubes due to pitting corrosion[D].Shanghai:Shanghai Jiao Tong University, 2011:34-38(in Chinese). |
| [12] | VAN NOORTWIJK J M. A survey of the application of gamma processes in maintenance[J].Reliability Engineering & System Safety, 2009, 94(1): 2–21. |
| [13] | CHENG G, ZHOU B, LI L. Joint optimisation of buffer size and preventive maintenance for a deteriorating upstream machine[J].International Journal of Systems Science:Operations & Logistics, 2015, 2(4): 199–210. |
| [14] | SUN J W, XI L F, DU S C, et al. Tool maintenance optimization for multi-station machining systems with economic consideration of quality loss and obsolescence[J].Robotics and Computer-Integrated Manufacturing, 2010, 26(2): 145–155.DOI:10.1016/j.rcim.2009.07.005 |
| [15] | ZHOU B, LIU Z. Optimizing preventive maintenance:A deteriorating system with buffers[J].Industrial Management & Data Systems, 2016, 116(8): 1719–1740. |
