20世纪末以来，随着微型飞行器(MAV)的发展，昆虫高超飞行能力的研究为人们广泛关注^[1]。作为仿生机械力学，其涉及复杂的空气动力学问题。目前，****对昆虫飞行的空气动力学原理的研究主要分为实验和数值计算研究，通过大量研究揭示昆虫的升力产生原理。最早Weis-Fogh^[2]通过观察台湾小黄蜂，他提出了“合拢/打开”机制。随后Ellington等^[3]通过制作鹰蛾的自动拍动模型并分析流场，发现翅膀上方一个螺旋形涡，该涡不随着运动脱落，这个机制被命名为“不失速机制”。Dickinson等^[4]以果蝇模型翼的拍动运动为对象，发现翅膀拍动过程中产生的升力持续保持较高值，与Ellington等^[3]的不失速机制所推测相符，此外，他们解释了升力中的2个峰值，并提出“转动环量”机制和“尾迹捕获”机制。Sun和Tang^[5]对果蝇翅膀的拍动运动进行了数值计算研究，对升力峰值提出不同的解释，他们认为拍动起始阶段和结束阶段中的2个升力峰值分别是由于翅的快速加速运动和翅的快速上仰产生的。
与前面提到的昆虫不同，蜻蜓有2对翅膀，而且蜻蜓翅的拍动频率不高，约有30 Hz左右(果蝇约为250 Hz)；另外翅的展弦比较大，一般在7.9左右(果蝇约为3.0)。这些特点也许蕴含着新的气动机制。Azuma^[6]、Ellington^[7-9]、Russell^[10]及Dong^[11]等曾对多种蜻蜓的飞行作过观测研究，但是对于蜻蜓飞行时非定常运动气动力特性的研究工作却很少，人们对于蜻蜓飞行的空气动力学原理还不是很了解。
本课题组使用高速摄影技术对一种蜻蜓-黄蜻的自由飞行进行观测实验^[12]。实验观测发现蜻蜓匀速爬升过程中出现一种特殊的现象：蜻蜓扑翼时出现周期性停止拍动的飞行状况，而停止拍动时身体质心的位移与加速度均未受影响。间歇性拍动飞行不仅不影响爬升飞行，由于扑翼次数更少，还可能节省飞行能耗。蜻蜓的间歇性飞行是否具有特殊的意义。由于实验中无法获得流场细节，亟需通过计算进一步探究间歇性拍动飞行的机理。
本文采用浸入式边界法非定常计算程序对间歇性拍动运动流场进行模拟，并围绕蜻蜓爬升状态下间歇性飞行的气动特征展开研究。文中系统地对比分析了推力系数和升力系数的结果，并对不同间歇时长下的气动特性进行分析，从而初步揭示了蜻蜓间歇性拍动飞行的机理。
1 数值方法 1.1 方法简述 本文采用的浸入式边界法非定常计算程序为课题组编程。程序采用Fadlun等^[13]在Mohd-Yusof^[14]的基础上发展的方法，用于昆虫扑翼飞行的数值模拟。方程建立在完全正交的笛卡儿坐标中，计算过程中不需要进行坐标变换。
昆虫扑翼飞行二维非定常流动控制方程，即二维不可压Navier-Stokes方程为

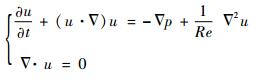(1)

式中：t为时间; u为流体速度, 速度在x方向和y方向的分量分别记为u和v; p为流体压力; Re为雷诺数。
给定计算域条件为：大小为20×20的正方形网格作为计算域，网格数为176 400，雷诺数为157，进口边界条件为均匀来流，上下边界给定无剪切边界条件，出口边界给定第二类边界条件。
1.2 方法验证 静止圆柱绕流是二维流动中的经典问题。本文选定计算域为30×15的矩形区域，雷诺数较低时采用均匀网格，网格数为300×150，随着雷诺数的提高，需要在圆柱附近局部加密网格，本文在计算Re=300时将网格数相应增加至315×165。圆柱在计算域中的相对位置如图 1所示，圆柱直径D=1。计算域左侧边界为入口边界，设置远前方来流速度U_∞=1, V_∞=0；右侧边界为出口边界，出口压力p=1;上下边界采用无剪切边界条件，即边界上有

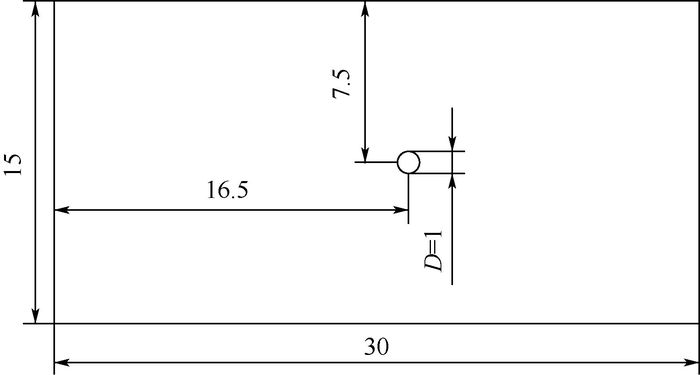图 1 圆柱在计算域中的相对位置 Fig. 1 Relative position of circular cylinder in computational domain

图选项

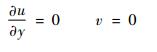(2)

本文的数值模拟计算获得了与前人数值(Gresho^[15], Saiki^[16])和实验研究(Coutanceau^[17])基本相同的结果。
取Re=25的圆柱绕流的流场细节与文献[15-17]中的数据进行对比，其结果如表 1所示。
表 1 Re=25圆柱绕流流场细节对比 Table 1 Comparison of flow field details around a circular cylinder at Re=25

结果来源	尾迹 长度	尾迹最宽处 x轴坐标	尾涡中心 x轴坐标	两尾涡中心点的 y方向距离
本文	1.20	0.89	1.04	0.42
Gresho[15]	1.15	0.81	0.88	0.47
Saiki[16]	1.41		1.03	0.50
Coutanceau[17]	1.22	0.85	0.94	0.51

表选项






阻力系数C_D是衡量圆柱绕流的关键参数，将本文计算得到的阻力系数C_D随雷诺数Re的变化曲线与前人数值(Silva^[18], Park^[19])或实验研究(Wieselsberger^[20], Relf^[21])的结果进行对比，吻合度较高，如图 2所示。

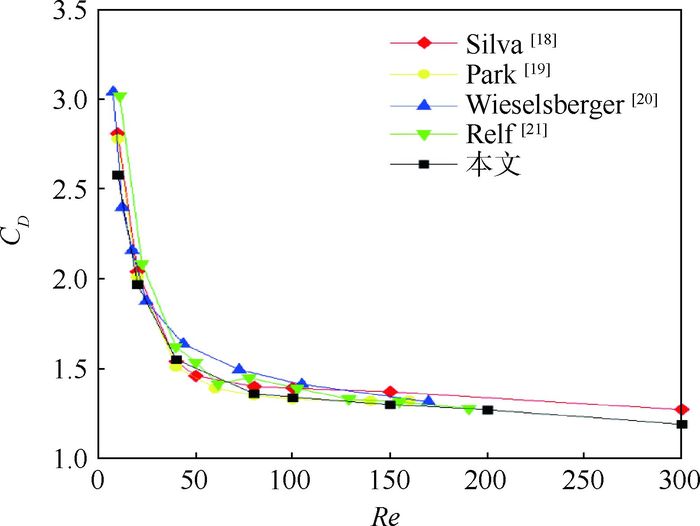图 2 圆柱绕流阻力系数对比 Fig. 2 Comparison of drag coefficient of flow around a circular cylinder

图选项

2 运动规律的数理模型 2.1 翅膀模型 蜻蜓通过上下拍动的叠加完成飞行。一个下挥行程和一个上拍行程组成一个完整的拍动周期。
昆虫扑翼飞行时，可近似认为翅膀是在同一平面内，拍动平面与身体轴向的夹角成为拍动平面倾斜角β。图 3展示了一个椭圆翼型横截面沿拍动平面的“8字形”运动^[22]。该运动可以转化为有2个方向的自由度，一个是翼型剖面中心点沿拍动平面的周期性平动，另一个是翅膀弦长绕弦中心的转动(转角记为α)。

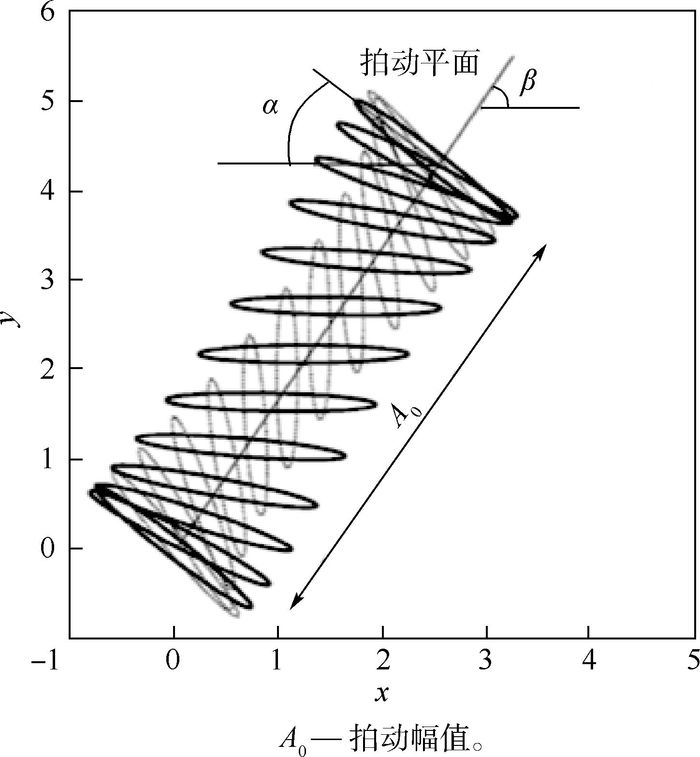图 3 单翼在一个周期内的扑翼规律 Fig. 3 Wing flapping law of single wing in a stroke

图选项

本文选用的椭圆模型翼如图 3所示。选用2个长短轴之比为10的椭圆来模化蜻蜓的前后翅展向中间位置的翼型剖面。椭圆的长轴即翅膀的弦长，尺寸为2a=1。
2.2 运动方程
2.2.1 平动运动方程 翼型中心点沿拍动平面的平动与实际飞行中蜻蜓的拍动角对应，平动速度用表示，如图 4所示，定义为

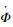
图 4 φ为0°时拍动幅度Φ和翻转角α在一个周期内随时间变化运动函数 Fig. 4 Time-dependent motion function of flapping amplitude Φ and pitching angle α in a stroke (φ=0°)

图选项

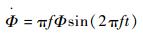(3)

式中：f为拍动频率; Φ为拍动幅度。实际计算时，程序通过给定拍动幅度Φ来控制翼型剖面的运动规律。根据实验结果发现蜻蜓爬升过程中前后翅的连续周期性平动运动规律近似正弦规律，定义如下：

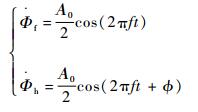(4)

式中：和分别为前翅和后翅的拍动幅度；?为前后翅相位差。

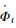
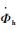
2.2.2 转动运动方程 根据拍摄实验得到的真实蜻蜓翅膀攻角变化规律，发现实际蜻蜓扑翼过程中，翅膀弦线在拍动的开始和结束进行快速翻转，而在上下拍动的中间位置有一段稳定值。翼型的转动运动规律用α来描述，α的大小为翼型长轴与水平面的夹角。对于α随时间变化的规律，以翅膀在一个拍动周期内翻转为例描述如下：

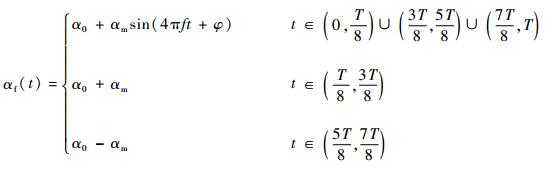(5)

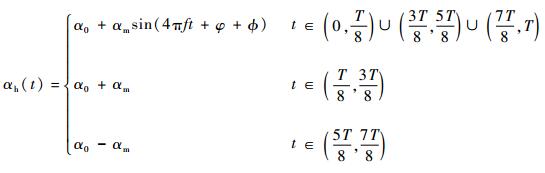(6)

式中：α_f和α_h分别为前翅和后翅的翻转角；α₀为初始转动角；α₀+α_m和α₀－α_m分别为下拍和上拍时中间段的稳定迎角值，α_m为翻转角极小值；T为拍动周期；φ为前翅转动运动和平动运动的相位差，如图 4所示。
3 间歇性拍动飞行的机理分析 3.1 间歇性拍动飞行的实验观测 间歇性拍动飞行在蜻蜓的匀速爬升过程中普遍存在。在蜻蜓观测实验中，发现243组蜻蜓观测实验中存在28组间歇性飞行现象，占比12%，且几乎所有的间歇性飞行都出现在匀速爬升过程中。
图 5为蜻蜓某次实际飞行中前后翅的拍动角随时间变化曲线图，后翅拍动角超前于前翅。通过分析可知前后翅相位差范围在70°~100°，该结果与其他组实验中测量的结果都一致。

图 5 蜻蜓爬升过程中翼面拍动幅度随时间变化曲线 Fig. 5 Time-dependent flapping amplitude of dragonfly wings during climbing

图选项

观察图 5发现：翅膀每拍动2~4个周期就短暂滑翔一段时间，滑翔时翅膀微微抖动。这种飞行称之为“间歇性拍动飞行”。短暂滑翔过程定义为：起始于后翅拍动角停止上拍节点，终止于后翅拍动角开始正常下拍节点，如图 5黑框所示。短暂滑翔时长参数与拍动周期时长之比，用τ表示。
分析实验得到的蜻蜓间歇性拍动飞行数据，发现蜻蜓在间歇性拍动飞行时短暂滑翔的时间长度并不一致。针对8组图像清晰完整的实验测量进行分析发现间歇性拍动飞行主要有3种滑翔时长：1倍拍动周期出现6例，占75%；1.5倍拍动周期出现1例，占12.5%；2倍拍动周期也出现1例，占12.5%。
根据实验观察结果，本文通过模拟双翅拍动规律，使翅膀每2个拍动周期后进行一次间歇滑翔，这个过程定义为一个“间歇飞行周期”。则滑翔时长占间歇飞行周期比为τ/(2+τ)，简称间歇占比，用λ表示。本文设置τ分别为:0，0.5，1，1.5，2，3，则对应的λ分别为：0，0.2，0.3，0.4，0.5，0.6。
一个间歇飞行周期内的平动规律定义如下：

(7)

(8)

间歇性飞行上下拍动时的转动规律同2.2.2节所述，翅膀停止拍动时的转动角定义如下:

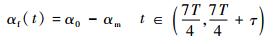(9)

3.2 间歇性拍动飞行的气动特性分析
3.2.1 不同间歇占比对平均力系数的影响 首先，取连续拍动算例与间歇占比不同的5个间歇拍动算例为对象做对比分析。
对于扑翼飞行来说，由于一个拍动周期中翅膀运动规律呈周期性变化，翅膀拍动产生的推力和升力也会随之进行周期性变化，因此对于翅膀气动力的研究，通常关注一个间歇飞行周期中产生气动力的平均值。
如图 6为计算出的前后翅平均推力系数和平均升力系数随间歇占比变化的折线图。前后翅平均推力系数和平均升力系数定义如下：

图 6 平均力系数随间歇占比的变化 Fig. 6 Variation of average force coefficient with different gliding time proportions

图选项

(10)

式中：C_Df、C_Dh和C_Lf、C_Lh分别为前后翅的推力系数和前后翅的升力系数。
从图 6中可以看出：平均推力系数和平均升力系数随着间歇时长占间歇飞行周期比例的增大而减小。总体趋势为前段下降较快，中段下降平缓，末端快速下降为接近0。当间歇占比从0转变为0.2时，平均推力系数与平均升力系数均出现大坡度下滑现象。随后，当间歇占比为0.2~0.5时，平均推力系数随间歇占比的增大而缓慢减小。升力系数的变化规律与推力系数相类似，但在间歇占比为0.2~0.5时，平均升力系数下降的斜率绝对值比推力系数小。当间歇占比增大至0.6时，平均推力系数与升力系数均下降至接近0。这说明蜻蜓在进行间歇占比为0.6的间歇性飞行时，升力与推力均不足以支持蜻蜓的飞行。因此以间歇占比为0.6进行的间歇性飞行是不合理的，这也与实验统计结果吻合。
综上所述，间歇性拍动飞行会导致平均推力系数和平均升力系数的减小，且对平均推力系数的影响相对平均升力系数更大。

3.2.2 不同间歇占比对推力系数的影响 为了探究间歇性拍动飞行为什么对平均推力系数的影响相对平均升力系数更大，本文对瞬时推力系数和升力系数进行分析。
图 7为计算结果稳定后截取的4个拍动周期内瞬时推力系数随时间变化的曲线图。图 7(a)~图 7(d)分别是连续拍动，以及间歇占比λ分别为0.3、0.4和0.5的间歇性拍动飞行。令截取点的飞行时间为0，横坐标所示是飞行时间与拍动周期之比，用t/T表示；纵坐标表示瞬时推力系数。

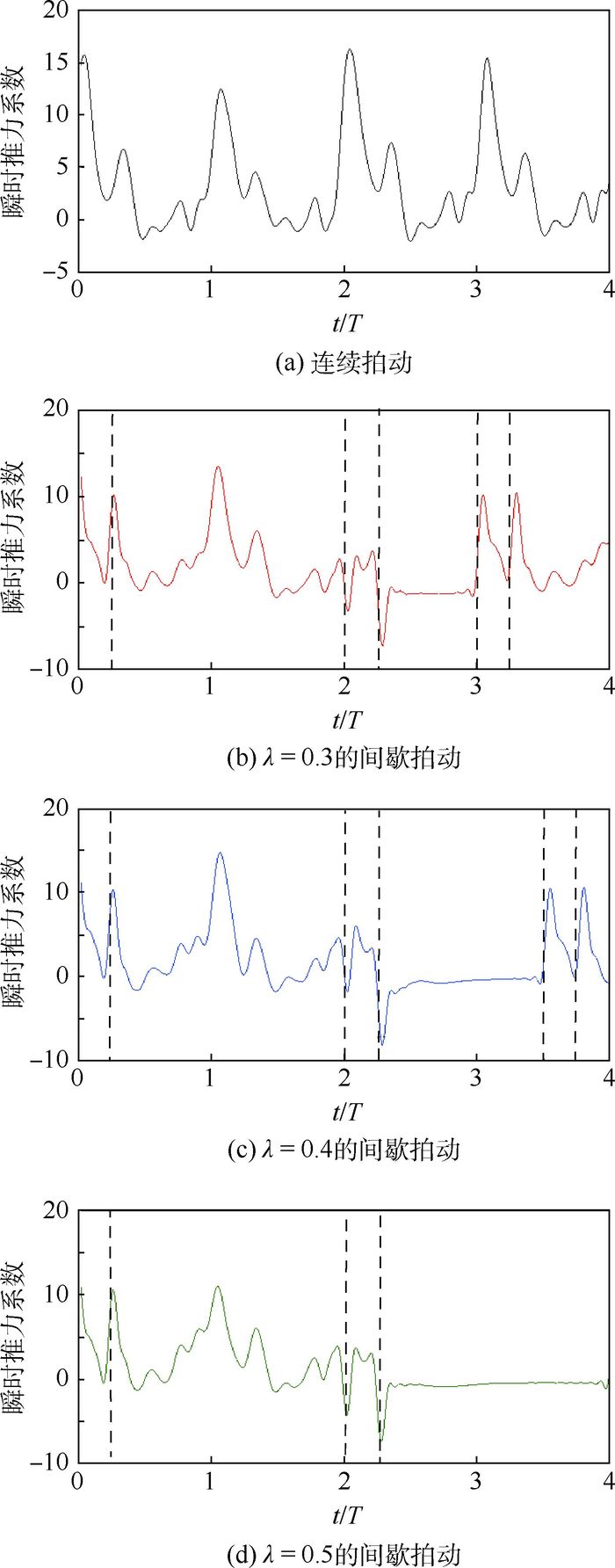图 7 不同间歇占比的间歇拍动飞行的瞬时推力系数 Fig. 7 Time-dependent thrust coefficient with different gliding time proportions of intermittent flapping flight

图选项

在图 7(b)虚线分段中可以看到，模型翼在一个间歇飞行周期内的运动过程可以分为4个阶段，按时间发展顺序分别为：启动拍动阶段(t/T∈(0, 0.25))，稳定拍动阶段(t/T∈(0.25, 2))，短暂滑翔初期(t/T∈(2, 2.25))，短暂滑翔稳定期(t/T∈(2.25, 2.25+τ))。短暂滑翔稳定期之后，进入下一个拍动周期的启动拍动阶段，形成一个周期性循环运动。
对比图 7(a)~图 7(d)可见，在稳定拍动阶段和短暂滑翔稳定期，连续拍动与间歇占比为0.3、0.4和0.5的间歇性拍动飞行的推力系数曲线差别不大；而在启动拍动阶段和短暂滑翔初期，连续拍动和间歇性拍动的推力系数存在较大差异。
首先，为了分析启动拍动阶段的推力系数特征，图 8展示了几种不同飞行方式的推力系数在t/T∈(0, 1) 期间随时间的变化规律。

图 8 不同间歇占比的间歇拍动飞行的瞬时推力系数在t/T∈(0, 1) 期间的变化规律对比 Fig. 8 Comparison of change laws of time-dependent thrust coefficient with different gliding time proportions of intermittent flapping flight during t/T∈(0, 1)

图选项

在t/T∈(0, 0.25) 期间，启动拍动阶段的模型翼运动规律为：后翅先开始向上拍动，前翅从中点位置滞后π/4相位差随之上拍。在此期间的推力系数变化特征为：连续拍动飞行的推力系数存在一个峰值，随后降至约为0。间歇性飞行的推力峰值与连续飞行的峰值相当，但是前者的推力系数迅速下降，在t/T=0.25处又产生一个峰值。图 8中标注的阴影区面积表示推力系数之和削弱的值。对于间歇占比为0.3的间歇拍动飞行，该阶段对平均推力系数的削弱作用占8.7%。
其次，为了分析短暂滑翔初期的推力系数特征，图 9展示了几种不同飞行方式的推力系数在t/T∈(2, 3) 期间随时间的变化规律。在t/T∈(2, 2.25) 期间，短暂滑翔初期的模型翼运动规律为：后翅已经停止拍动，前翅从最低位置上拍到最高位置后也停止拍动。在此期间的力系数变化特征为：连续拍动飞行的推力系数存在一个峰值，随后降至0；间歇性拍动飞行的推力系数线下降后上升，其峰值仅约为连续飞行的峰值的1/4，且不同间歇占比的间歇性飞行的推力峰值几乎相等。图 9中标注的阴影区面积表示推力系数之和削弱的值。对于间歇占比为0.3的间歇拍动飞行，该阶段对平均推力系数的削弱作用占20.2%。

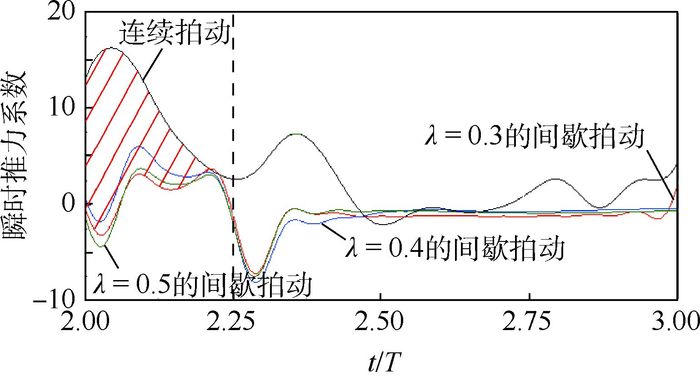图 9 不同间歇占比的间歇拍动飞行的瞬时推力系数在t/T∈(2, 3) 期间的变化规律对比 Fig. 9 Comparison of change laws of time-dependent thrust coefficient with different gliding time proportions of intermittent flapping flight during t/T∈(2, 3)

图选项

最后，在短暂滑翔稳定阶段，即图 9所示t/T∈(2.25, 3) 期间，间歇拍动飞行的推力系数保持约为0，连续拍动的推力系数值也在0附近波动。对于间歇占比为0.3的间歇拍动飞行，该阶段对平均推力系数的削弱作用占22.5%。
可以认为，连续飞行转变为间歇拍动飞行时，短暂滑翔初期和短暂滑翔稳定阶段对平均推力系数的减小影响重大，而启动拍动阶段对推力系数的影响相对较小。

3.2.3 不同间歇占比对升力系数的影响 图 10分别是连续拍动与间歇占比λ为0.3、0.4和0.5的间歇拍动飞行在一个间歇飞行周期内的瞬时升力系数随时间的变化曲线图。

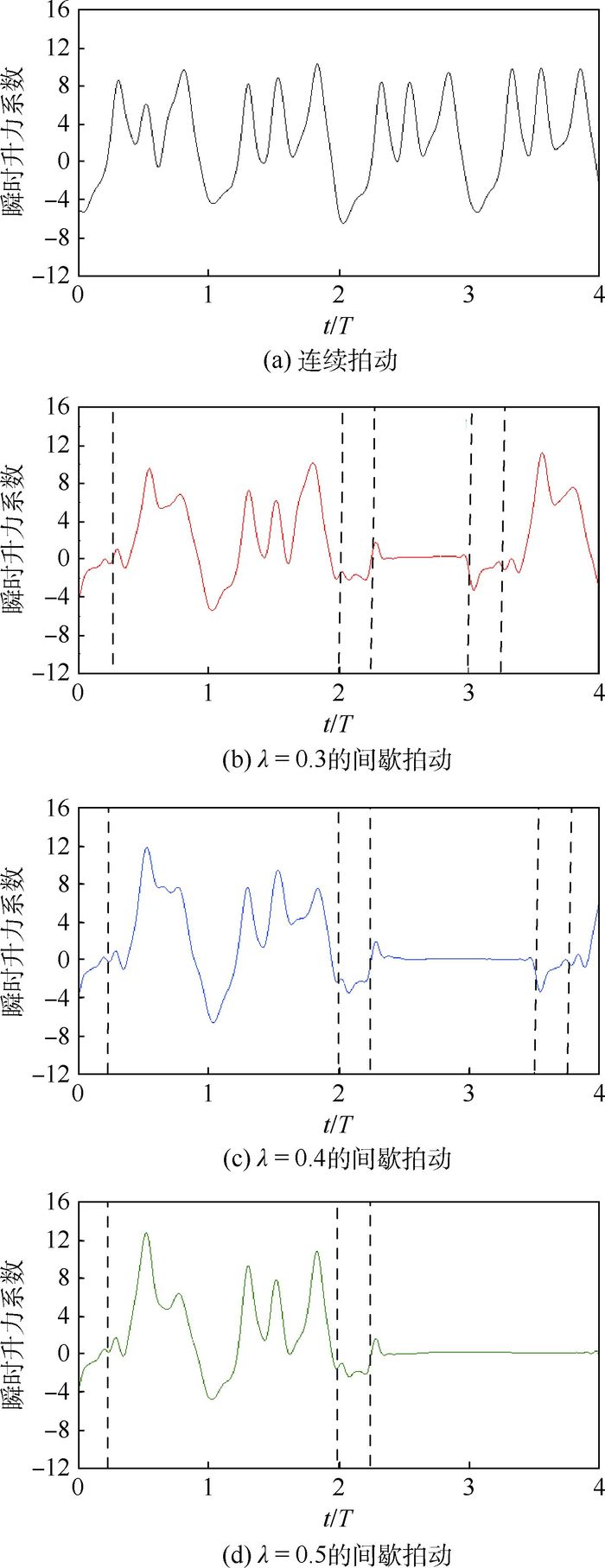图 10 不同间歇占比的间歇拍动飞行的瞬时升力系数 Fig. 10 Time-dependent lift coefficient with different gliding time proportions of intermittent flapping flight

图选项

从图 10可以看到，在稳定拍动阶段t/T∈(0.25, 2) 和短暂滑翔稳定阶段t/T∈(2.25, 3)，不同间歇占比的间歇拍动飞行的升力系数曲线波动趋势相似。在短暂滑翔稳定阶段，间歇性拍动飞行的升力系数保持约为0。对于间歇占比为0.3的间歇拍动飞行，该阶段对平均升力系数的削弱作用占41.4%。
首先，分析启动拍动阶段的升力系数。图 11为不同间歇占比的推力系数在t/T∈(0, 1) 期间随时间的变化规律。在t/T∈(0, 0.25) 期间，连续拍动飞行和间歇性拍动飞行的升力系数具有相同的谷值，且均为负值并随着时间的增大而增大，约在t/T=0.25时相交。图 11中标注的阴影区面积表示升力系数之和削弱的值。对于间歇占比为0.3的间歇拍动飞行，该阶段对平均升力系数的提高作用占8.1%。

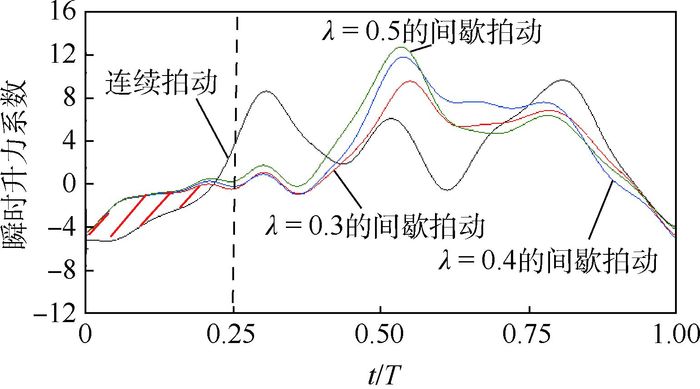图 11 不同间歇占比的间歇拍动飞行的瞬时升力系数在t/T∈(0, 1) 期间的变化规律对比 Fig. 11 Comparison of change laws of time-dependent lift coefficient with different gliding time proportions of intermittent flapping flight during t/T∈(0, 1)

图选项

随后，分析短暂滑翔初期的升力系数。图 12为不同间歇占比的推力系数在t/T∈(2, 3) 期间随时间的变化规律。在t/T∈(2, 2.25) 期间，连续拍动飞行和间歇性拍动飞行的升力系数均为负值并随着时间的增大而增大，约在t/T=2.25时相交，但是前者的升力系数谷值与后者相比减小了2/3。图 12中标注的阴影区面积表示升力系数之和增加的值。对于间歇占比为0.3的间歇拍动飞行，该阶段提高了平均升力系数，对平均升力系数的提高贡献8%。

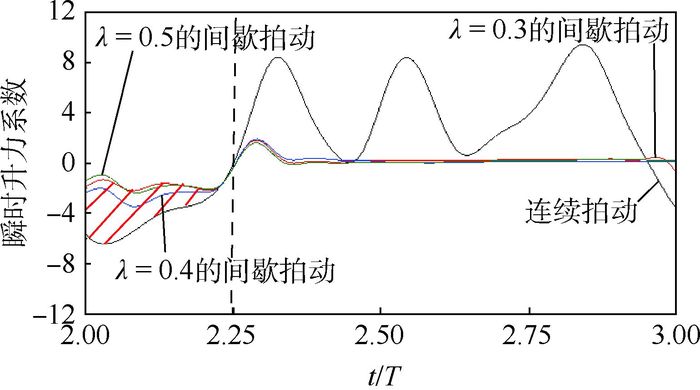图 12 不同间歇占比的间歇拍动飞行的瞬时升力系数在t/T∈(2, 3) 期间的变化规律对比 Fig. 12 Comparison of change laws of time-dependent lift coefficient with different gliding time proportions of intermittent flapping flight during t/T∈(2, 3)

图选项

综上所述，稳定短暂滑翔期间双翅停止拍动对平均升力系数的影响最大，而启动拍动阶段对其影响较小，然而，短暂滑翔初期却在一定程度上对平均升力系数的提高产生贡献。
3.3 不同间歇占比对间歇性拍动飞行的影响 通过以上分析，发现由于间歇性飞行对平均推力系数的影响相对平均升力系数更大，直接产生的结果为：间歇性飞行提高了蜻蜓飞行的升推比。
图 13为间歇占比为0.2~0.5的间歇拍动飞行和连续拍动飞行的平均升推比。

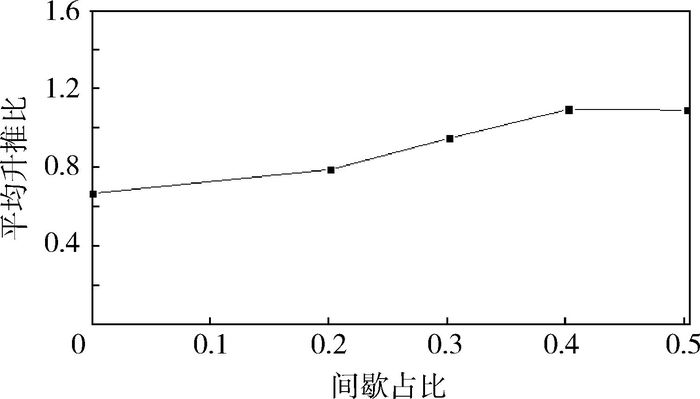图 13 平均升推比随间歇占比的变化 Fig. 13 Variation of average lift-thrust ratio with different gliding time proportions

图选项

从图 13中可以看出：平均升推比随着间歇占比的增大先增大后趋于稳定。当间歇占比为0.3时，平均升推比接近为1。
结合图 6所示的平均推力系数和平均升力系数，可以得知：蜻蜓在间歇性拍动飞行时短暂滑翔时长间歇占比为0.3、0.4、0.5的间歇性拍动飞行有助于提高升推比，实现了对升力、推力的重新分配，同时保持一定的推力系数和升力系数。
并且，间歇占比为0.3的间歇拍动飞行在保证大升推比的同时，与间歇占比为0.4、0.5的飞行方式相比，具有更高的平均推力和升力，这可以解释为何实验中观测到的间歇占比为0.3的间歇性拍动飞行情况占了75%。
4 结论 本文采用二维浸入式边界法非定常计算程序，以间歇飞行的间歇占比为变量，围绕蜻蜓爬升状态下连续飞行和间歇性飞行的气动特征展开研究，得到如下结论：
1) 通过统计蜻蜓观测实验中的间歇性飞行规律，发现间歇性拍动飞行在蜻蜓的爬升过程中普遍存在，出现概率约占总实验数的12%。
2) 揭示了间歇性飞行对平均推力系数和平均升力系数都有重要影响，但对平均推力系数的影响更大。在连续飞行转变为间歇性飞行时，短暂滑翔初期和短暂滑翔稳定阶段均大幅度减小了推力系数；而对于升力系数，短暂滑翔初期却在一定程度上对平均升力系数的提高产生贡献。
3) 揭示了间歇占比为0.3的间歇拍动飞行能够在保证大升推比的情况下，具有更高的推力和升力。从而说明了蜻蜓实际飞行中多发生间歇占比为0.3间歇拍动飞行的原因。
本文的工作是基于对间歇性飞行的二维计算。为了分析三维不同翅膀翼型的影响和径向涡的影响，将会开展三维工作，进一步解释其中的机制。

参考文献

[1]	SUN M. Insect flight dynamics:Stability and control[J].Reviews of Modern Physics, 2014, 86(2): 615–646.DOI:10.1103/RevModPhys.86.615
[2]	WEIS-FOGH T. Quick estimates of flight fitness in hovering an-imals, including novelmechanism for lift production[J].Journal of Experimental Biology, 1973, 59(1): 169–230.
[3]	ELLINGTON C P, VAN DEN BERG C, WILLMOTT A P. Leading edge vortices in insect flight[J].Nature, 1996, 384(6610): 626–630.DOI:10.1038/384626a0
[4]	DICKINSON M H, LEHMANN F O, SANE S P. Wing rotation and the aerodynamic basis of insect flight[J].Science, 1999, 284(5422): 1954–1960.DOI:10.1126/science.284.5422.1954
[5]	SUN M, TANG J. Unsteady aerodynamic force generation by a model fruit flywing in flappingmotion[J].Journal of Experimental Biology, 2002, 205(1): 55–70.
[6]	AZUMA A, WATANABE T. Flight performance of a dragonfly[J].Journal of Experimental Biology, 1988, 137(1): 221–252.
[7]	WAKELING J M, ELLINGTON C P. Dragonfly flight.Ⅱ.Velocities, accelerations and kinematics of flapping flight[J].Journal of Experimental Biology, 1997, 200(3): 557–582.
[8]	WAKELING J M, ELLINGTON C P. Dragonfly flight.I.Gliding flight and steady-state aerodynamic forces[J].Journal of Experimental Biology, 1997, 200(3): 543–556.
[9]	WAKELING J, ELLINGTON C. Dragonfly flight.Ⅲ.Lift and power requirements[J].Journal of Experimental Biology, 1997, 200(3): 583–600.
[10]	WANG Z J, RUSSELL D. Effect of forewing and hindwing interactions on aerodynamic forces and power in hovering dragonfly flight[J].Physical Review Letters, 2007, 99(14): 12243–12254.
[11]	DONG H, KOEHLER C, LIANG Z, et al.An integrated analysis of a dragonfly in free flight:AIAA-2010-4390[R].Reston:AIAA, 2010.
[12]	高倩, 郑孟宗, 李志平, 等. 蜻蜓爬升过程飞行特征实验研究[J].北京航空航天大学学报, 2016, 42(6): 1271–1278. GAO Q, ZHENG M Z, LI Z P, et al. Experimental study on flight performance of dragonfly during climbing[J].Journal of Beijing University of Aeronautics and Astronsutics, 2016, 42(6): 1271–1278.(in Chinese)
[13]	FADLUN E A, VERZICCO R, ORLANDI P, et al. Combined immersed-boundary finite-difference methods for three-dimensional complex flow simulations[J].Journal of Computational Physics, 2000, 161(1): 35–60.DOI:10.1006/jcph.2000.6484
[14]	MOHD-YUSOF J.Combined immersed-boundary/B-spline methods for simulations of flow in complex geometries[C]//Annual Research Briefs, 1997:317-327.
[15]	GRESHO P M, CHAN S T, LEE R L, et al. A modified finite element method for solving the time-dependent, incompressible Navier-Stokes equations.Part 2:Applications[J].International Journal for Numerical Methods in Fluids, 1984, 4(7): 619–640.DOI:10.1002/(ISSN)1097-0363
[16]	SAIKI E M, BIRINGEN S. Numerical simulation of a cylinder in uniform flow:Application of a virtual boundary method[J].Journal of Computational Physics, 1996, 123(2): 450–465.DOI:10.1006/jcph.1996.0036
[17]	COUTANCEAU M, BOUARD R. Experimental determination of the main features of the viscous flow in the wake of a circular cylinder in uniform translation.Part 2.Unsteady flow[J].Journal of Fluid Mechanics, 1977, 79(2): 257–272.DOI:10.1017/S0022112077000147
[18]	SILVA L E, SILVEIRA-NETO A, DAMASCENO J J R. Numerical simulation of two-dimensional flows over a circular cylinder using the immersed boundary method[J].Journal of Computational Physics, 2003, 189(2): 351–370.DOI:10.1016/S0021-9991(03)00214-6
[19]	PARK J, KWON K, CHOI H. Numerical solutions of flow past a circular cylinder at Reynolds numbers up to 160[J].KSME International Journal, 1998, 12(6): 1200–1205.DOI:10.1007/BF02942594
[20]	WIESELSBERGER C. New data on the laws of fluid resistance[J].Physikalische Zeitschrift, 1921, 22: 321–328.
[21]	RELF E F. An electrical method for tracing stream lines in the two-dimensional motion of a perfect fluid[J].Philosophical Magazine, 1924, 29(285): 535–539.
[22]	JANE W Z. Two dimensional mechanism for insect hovering[J].Physical Review Letters, 2000, 85(10): 2216–2219.DOI:10.1103/PhysRevLett.85.2216