由于基于线性系统理论的设计方法存在建模与实际被控对象差距较大的缺点,尤其对于高超声速飞行器这一类具有强非线性特点的被控对象,线性系统方法已不再适用。因此,近年来在高超声速飞行器控制系统设计方面国内外文献大多采用非线性控制方法。文献[7]利用非线性动态逆方法设计鲁棒控制器,并利用随机鲁棒性分析其稳定性。文献[8]将自适应方法应用于动态逆控制器设计。文献[9]将滑模方法应用于高超声速飞行器控制,并利用有限时间积分方法证明稳定性。文献[10]将反步法引入高超声速飞行器控制系统设计,文献[11]在其基础上,设计在线自适应律,提出了高超声速飞行器的自适应反步法。文献[12-13]将反步法结合自适应神经网络,进一步提高系统鲁棒性。
在以上针对高超声速飞行器的控制系统设计方案中,反步法不仅对系统不确定性具有较强鲁棒性,且对系统非线性项不需附加约束、适应性强,因此得到了更为广泛的应用。
为解决传统反步法所带来的“微分爆炸”问题,文献[14]中提出了一种动态面控制方法,该方法通过引入若干一阶低通滤波器避免了对虚拟控制指令的直接微分,并在高超声速飞行器控制中得到广泛应用[15-16]。文献[15]运用动态面方法,并考虑执行机构饱和问题,设计高超声速飞行器控制器。文献[16]提出一种带有积分项的动态面控制器。
然而动态面方法中一阶滤波器的引入同样带来一些问题。首先,高超声速飞行器高度子系统相对阶为3,在运用反步法框架下的动态面方法时,需要3个设计步骤,且需设计2个低通滤波器。这在很大程度上增加了控制器复杂度。其次,动态面方法中一阶滤波器的引入不可避免的改变了名义虚拟控制指令,因此会带来一定误差。本文利用高阶跟踪微分器能够精确估计给定信号任意阶导数的能力[17],完成反步法中第1步虚拟控制量导数及二阶导数的精确计算,同时根据俯仰角与俯仰角速率之间简单的导数关系,可以直接在第2步中得到实际控制量的指令值。相比于传统动态面方法,将设计步骤从3步减少为2步。且省略了2个一阶滤波器的设计,在简化设计复杂度的同时,消除了滤波器所带来的误差,跟踪精度高于传统动态面方法。另外,在每一步设计中,将参数不确定和外部扰动带来的系统偏差视作等效干扰。采用扩张状态观测器对每一步等效干扰进行估计,并在控制器设计过程中进行干扰补偿。通过对比仿真,说明了本文所提方法的优越性。
1 模型建立及问题描述 1.1 飞行器动力学模型 考虑文献[18]中提出的面向控制的吸气式高超声速飞行器纵向动力学模型为
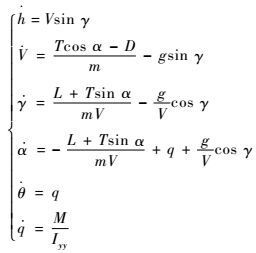 | (1) |
式中:m、Iyy、g分别为飞行器质量、绕机体系y轴转动惯量、重力加速度。高超声速飞行器纵向运动模型包含6个状态:高度(h)、速度(V)、弹道倾角(γ)、迎角(α)、俯仰角(θ)、俯仰角速率(q);2个控制输入:燃料当量比(Φ)、升降舵偏角(δe)。T、D、L、M分别为高超声速飞行器发动机推力、气动阻力、升力、俯仰力矩,且具有以下形式:
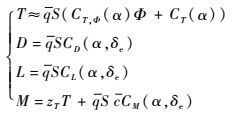 | (2) |
其中:q=0.5ρV2为动压,ρ为大气密度;S为飞行器参考面积;c为平均气动弦长;zT为推力对俯仰力矩的耦合系数;CT, Φ、CT、CL、CD及CM为推力及气动力相关系数,其定义如下:
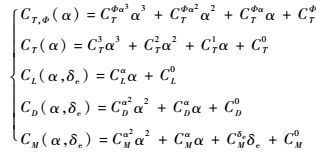 | (3) |
式中:带上标的各变量为曲线拟合系数,其取值可参考文献[18]。
1.2 控制问题描述 高超声速飞行器的控制目标为跟踪给定的高度指令(hd)与速度指令(Vd)。现有文献中,通常将飞行器纵向动力学模型划分为高度子系统与速度子系统[8, 19],并分别以升降舵偏角(δe)及燃料当量比(Φ)为控制输入。这样,将问题转化为2个单输入单输出非线性系统的跟踪控制问题。
在高度子系统设计中,以弹道倾角指令γd代替高度指令hd作为高度子系统的跟踪信号[20]。定义高度跟踪误差为zh=h-hd, 对其求导可得
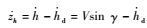
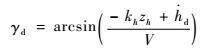 | (4) |
式中:kh>0为控制增益。
在下面的设计中,均以弹道倾角指令代替高度指令。为了将高度子系统变换为严反馈形式,对模型作以下假设:
假设1??弹道倾角方程和俯仰角速率方程中的推力项的影响均视作干扰考虑。
针对高度子系统,将状态变量定义为x=[x1, x2, x3]T=[γ, θ, q]T。基于上述假设,建立如下严反馈形式的高度子系统模型:
 | (5) |
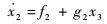 | (6) |
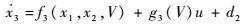 | (7) |
式中:
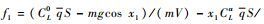
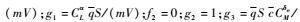
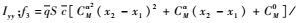
针对速度子系统,建立如下模型:
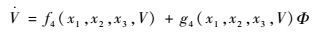 | (8) |
式中:
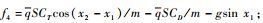
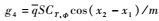
从式(8) 给出的整理后的速度子系统模型可以看出,该子系统相对阶为1,本文中采用动态逆方法设计控制器。从式(5)~式(7) 给出的整理后的高度子系统可以看出,该子系统相对阶为3,通常的动态面控制方法,需要分3步设计。本文提出一种基于跟踪微分器的减步控制方案,可有效减少控制器的设计步骤,并提高跟踪精度。
2 高阶跟踪微分器设计 设计如下跟踪微分器(Tracking Differentiator, TD):
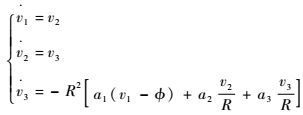 | (9) |
式中:R、a1、a2、a3为待设计的正常数;φ为TD的输入信号;v1、v2、v3为TD的状态变量,且分别为
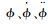
引理1[21]??对于式(9) 中给出的线性高阶跟踪微分器,若矩阵
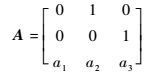 |
为正定矩阵,且输入信号φ:[0, ∞)→R满足
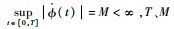
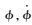
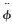
根据引理1,对于有界输入信号φ,式(9) 中所设计的TD在保证矩阵A正定前提下,满足:
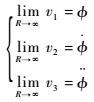 | (10) |
3 控制器设计 3.1 高度子系统干扰抑制减步控制方案 在1.2节中,已经通过变换将高度子系统表达为相对阶为3的严反馈形式,跟踪信号为弹道倾角。本节采用基于高阶跟踪微分器的减步方案,设计控制器。
步骤1??为了实现对弹道倾角指令的跟踪,定义该步的动态面为S1=x1-γd,由式(5) 可得
 | (11) |
以x2为该步的虚拟控制输入,设计名义虚拟控制指令x2d为
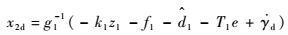 | (12) |
式中:k1>0为待设计增益常数;z1=S1-e,
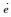

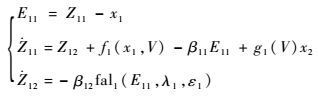 | (13) |
式中:Z11和Z12为ESO状态;
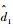
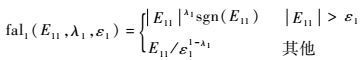 | (14) |
将步骤1中的名义虚拟控制指令x2d通过式(9) 中设计的跟踪微分器,即
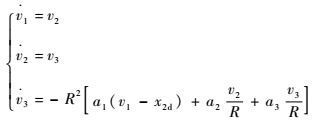 | (15) |
在后续设计中,采用v1作为实际虚拟控制指令,因此δ1=v1-x2d。跟踪微分器的收敛性由引理1保证,因此δ1能在很短时间内趋近于0。
步骤2??本步的设计目标为实现对实际虚拟控制指令v1的跟踪。定义该步的动态面为S2=x2-v1,由式(6) 可得
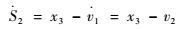 | (16) |
以x3为该步的虚拟控制输入,设计名义虚拟控制指令x3d为
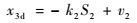 | (17) |
式中:k2>0为待设计增益常数。对x3d直接求导可得
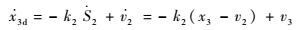 | (18) |
从式(18) 可以看出,借助微分器的作用,x3d的导数可以精确获得,而不需要重新设计一个微分器或滤波器去获得该步名义虚拟控制律的导数,这给控制设计带来了较大便利。
在得到
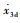
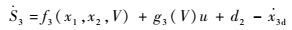 | (19) |
与步骤1中类似,采用ESO获得对未知干扰的估计值
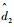
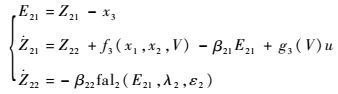 | (20) |
式中:Z21和Z22为ESO状态;
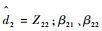
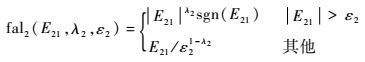 | (21) |
由上述ESO获得等效干扰估计值
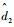
 | (22) |
式中:k3>0为控制器增益。
显然本节中所给出的减步控制方案从设计步骤上对传统动态面方法进行了简化。进一步分析,传统动态面方法通常在每个设计步骤最后,将各名义虚拟控制指令通过一阶惯性环节,获得实际虚拟控制指令及其一阶导数。此方法虽然解决了反步法中的“微分爆炸”问题,然而一阶惯性环节的加入使得实际虚拟控制指令与名义虚拟控制指令间存在一定误差,因此动态面方法在一定程度上牺牲了收敛速度与控制精度。本文中的减步控制方案采用跟踪微分器跟踪名义控制指令,并获得其精确导数值,因此在收敛速度与跟踪精度上优于动态面方法。
3.2 速度子系统动态逆控制器设计方案 速度子系统控制器采用动态逆设计方法。定义速度跟踪误差为zV=V-Vd。考虑式(8),则速度跟踪误差的导数为
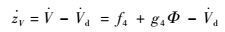 | (23) |
设计速度子系统控制律如下:
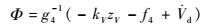 | (24) |
式中:kV>0为控制器增益。
4 稳定性证明 4.1 高度子系统稳定性证明 在3.1节中,采用干扰抑制减步方案设计了高度子系统控制器,本小节对该方法进行稳定性证明。
定义Lyapunov函数为
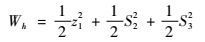 | (25) |
对其求导可得
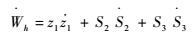 | (26) |
实际的系统状态x2和x3可以表示为
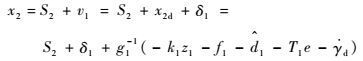 | (27) |
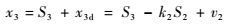 | (28) |
依据式(27) 和式(28) 计算得到z1,S2和S3的导数分别为
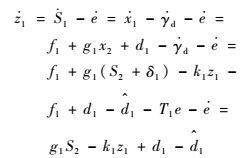 | (29) |
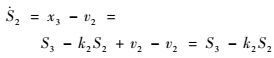 | (30) |
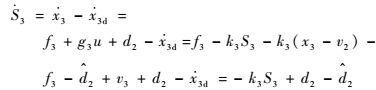 | (31) |
将式(29)~式(31) 代入式(26),得到沿着系统轨迹的Lyapunov函数的导数如下:
 | (32) |
利用Young不等式,可以得到以下不等式关系:
式中:b11>0和b12>0均为可设计的常数。将上述不等式关系代入式(32) 可以得到
 | (33) |
选择
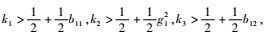
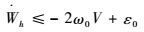 | (34) |
式中:ω0=
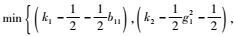
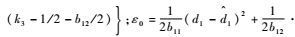
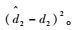
通过合理选择2个扩张状态观测器的参数,可以实现对γ回路及q回路等效干扰的快速精确估计,从而使的ε0在很短时间内收敛到原点附近的很小邻域内。控制增益ki(i=1, 2, 3) 的设计保证了ω0>0,ω0越大,对于干扰的抑制效果越好,跟踪精度越高。由以上关于ω0和ε0的分析结果可知,z1、S2和S3一致毕竟有界稳定。又由引理1,在参数选择合理的情况下,高阶跟踪微分器所带来的第1步虚拟控制指令的改变δ1有限时间收敛到0,因此S1也是一致毕竟有界稳定的。从上面分析可以看出,闭环系统所有信号稳定,且通过选择参数,能快速收敛到原点的领域内。
4.2 速度子系统稳定性证明 在3.2节中,采用动态逆方法设计了速度子系统控制器,本小节对该方法进行稳定性证明。
定义如下Lyapunov函数:
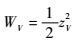 | (35) |
对其求导可得
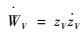 | (36) |
将式(23) 及式(24) 代入式(36),可得
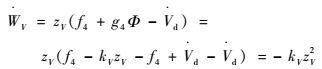 | (37) |
因此,速度子系统一致渐进稳定。
5 仿真验证 为了验证所提控制方案,本节对该方案开展数值仿真验证。仿真模型采用式(1) 及式(2) 给出的全量非线性模型。控制目标是实现对给定速度和高度信号的跟踪,其中高度指令信号为通过2个二阶指令滤波器的两次阶跃信号,2个指令滤波器的自然频率和阻尼比分别为ωfh=0.3,ξfh=0.95。速度指令为通过2个二阶指令滤波器的一次阶跃信号,2个指令滤波器的自然频率和阻尼比分别为ωfV=0.1,ξfV=0.95。飞行器初始状态为V0=2 347.6 m/s,h0=25 908 m, γ0=0°。在此状态进行配平计算可得α0=0.92°, θ0=0.92°, q0=0 (°)/s, δe=3.36°, Φ=0.08。
选择控制器增益为k1=0.8, k2=2.5, k3=2.8,kV=1.1;选择跟踪微分器增益为a1=0.5, a2=0.2, a3=0.3, R=0.05;选择扩张状态观测器参数为β11=β12=30, β21=β22=10, λ1=λ2=0.8, ε1=ε2=0.001。仿真中考虑系统参数不确定性为等效干扰,假设实际气动参数CLα, CT3, CT2, CT1, CT0, CTΦα3, CTΦα2, CTΦα, CTΦ各自与其名义值之间相差25%,实际气动参数CMα, CMα2, CMδe各自与其名义值之间相差30%,并加入0.5°的风干扰附加迎角。仿真结果如图 1~图 5所示。
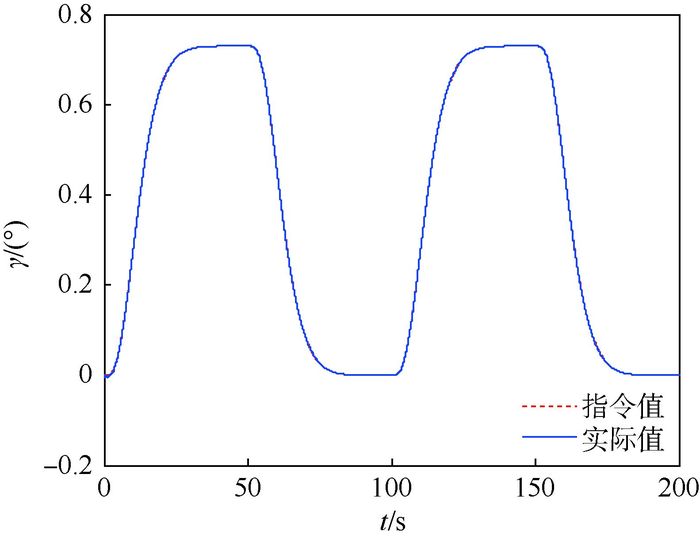 |
| 图 1 减步控制方案弹道倾角跟踪曲线 Fig. 1 Flight path angle tracking curves with reduced step control scheme |
| 图选项 |
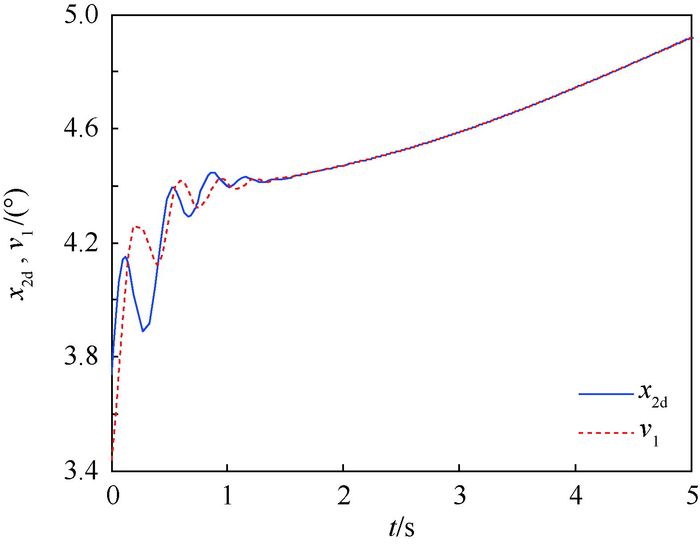 |
| 图 2 减步控制方案虚拟控制指令曲线 Fig. 2 Virtual control signal curves with reduced step control scheme |
| 图选项 |
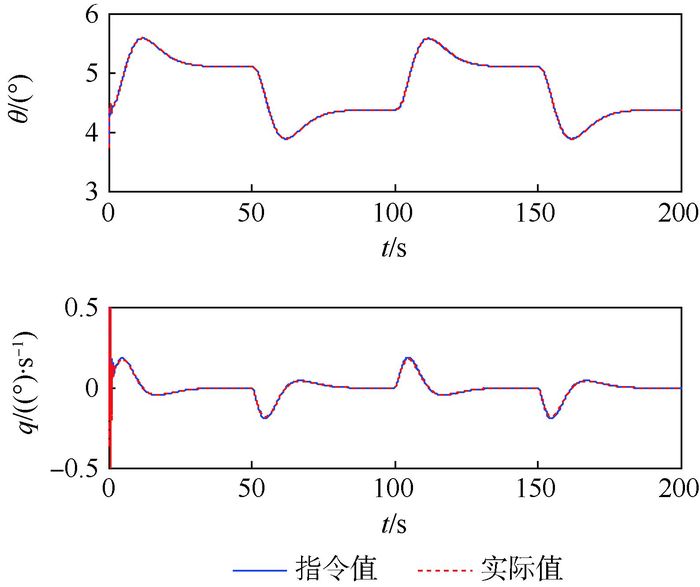 |
| 图 3 减步控制方案俯仰角与俯仰角速率跟踪曲线 Fig. 3 Pitch angle and pitch angle rate tracking curves with reduced step control scheme |
| 图选项 |
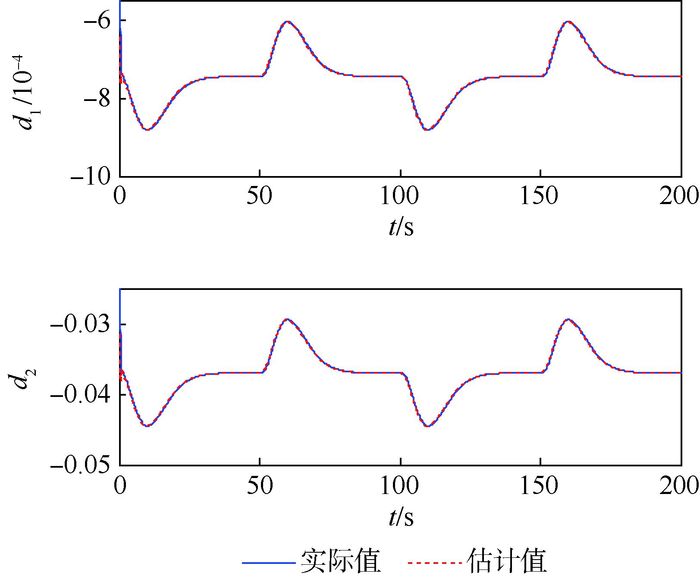 |
| 图 4 等效干扰观测曲线 Fig. 4 Observed curves of equivalent disturbances |
| 图选项 |
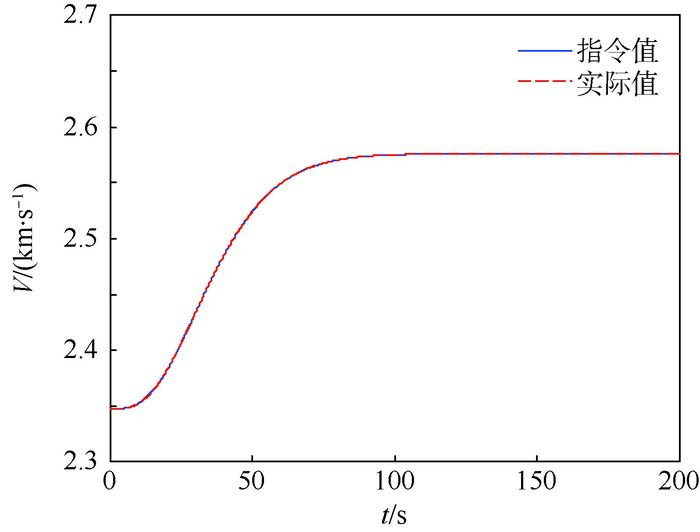 |
| 图 5 速度跟踪曲线 Fig. 5 Velocity tracking curves |
| 图选项 |
图 1给出了弹道倾角跟踪曲线,可以看出本文提出的减步控制方案实现了闭环系统对弹道倾角指令的精确跟踪。对弹道倾角跟踪精度影响较大的因素主要包括2个:一是将步骤1名义指令通过微分器计算导数所带来的步骤2名义指令信号的改变;二是不确定及干扰带来的影响。从图 1结合图 2及图 4可以看出,由于跟踪微分器对名义指令信号及其导数的精确估计,以及扩张状态观测器对干扰信号的精确估计,这两方面影响都得到了很好的抑制,从而实现了对弹道倾角指令的精确跟踪。图 2给出了步骤1虚拟控制指令名义值和实际值(即x2d和v1)的对比曲线。可以看出,微分器状态v1在很短时间内就精确收敛到x2d上,从而验证了跟踪微分器的效果。图 3给出了俯仰角与俯仰角速率跟踪曲线,仿真结果说明这2个变量均实现了对指令信号的精确跟踪。图 4给出了等效干扰d1和d2的估计曲线,通过扩张状态观测器,实现了对等效干扰的精确估计。图 5为速度跟踪曲线,可以看出速度回路对参考信号具有很快的响应能力,实现了对速度参考指令的精确跟踪。
通过上述数值仿真,验证了本文所提减步控制方案完成了预设的控制目标,实现了对给定指令信号的精确跟踪。为了对比本文所提方法与基于一阶滤波器的传统动态面控制方法的性能,下面开展对比仿真验证。在对比仿真验证中,步骤1与步骤2的名义虚拟控制指令分别为x2d和x3d,实际虚拟控制指令
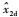
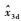
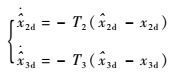 | (38) |
式中:T2、T3分别为滤波器时间常数,仿真中选取T2=T3=8。对比仿真中考虑的动力学模型不确定性与上一步仿真中相同。在传统动态面控制方案中,同样采用扩张状态观测器实现对不确定、干扰以及忽略项所组成的等效干扰的估计并在每一步控制器设计中消除等效干扰的影响。另外传统动态面仿真中每一步所采用的控制增益与减步控制仿真方案中相同。
图 6~图 8给出了减步控制方案与传统动态面控制方案的对比仿真结果。
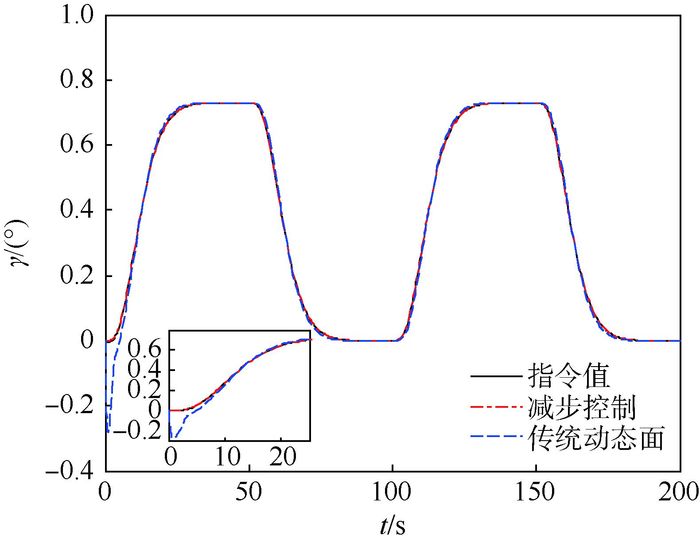 |
| 图 6 弹道倾角跟踪对比 Fig. 6 Comparison of flight path angle tracking |
| 图选项 |
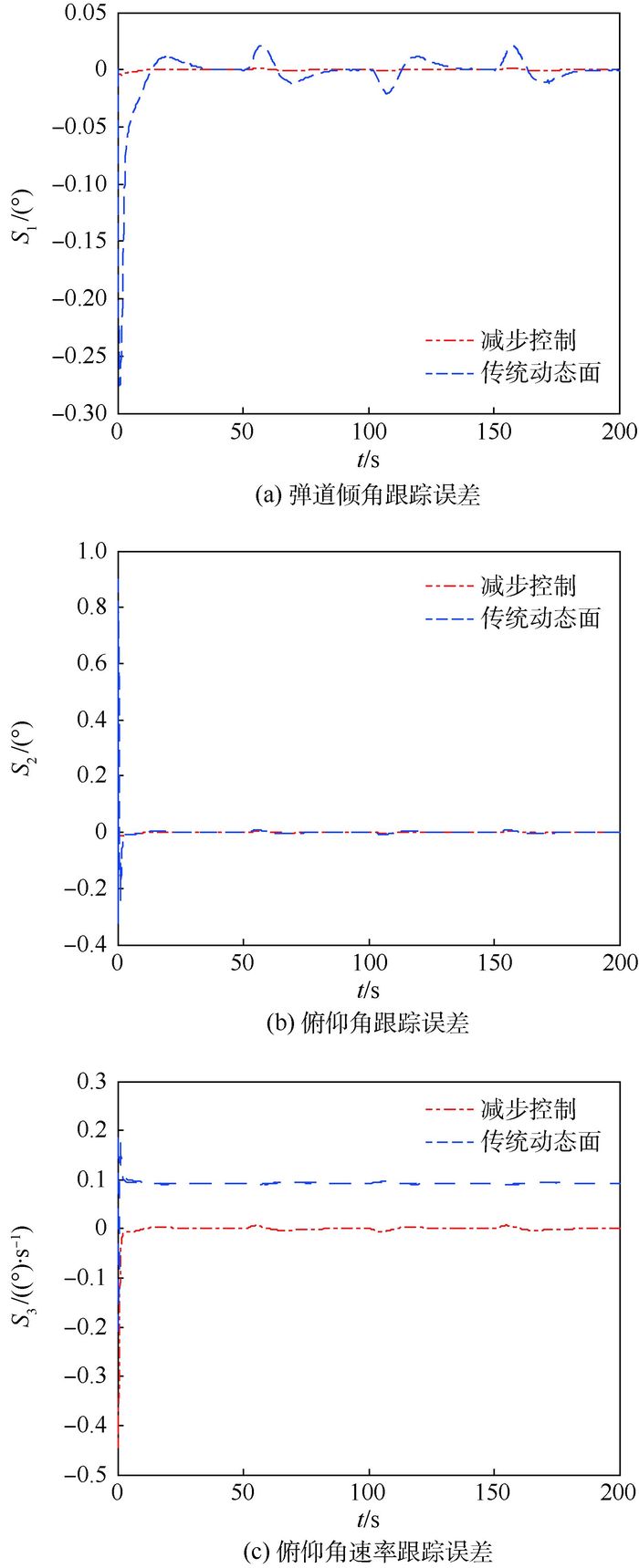 |
| 图 7 弹道倾角、俯仰角与俯仰角速率跟踪误差对比 Fig. 7 Comparison of flight path angle, pitch angle and pitch angle rate tracking error |
| 图选项 |
 |
| 图 8 升降舵偏角对比 Fig. 8 Comparison of elevator deflection |
| 图选项 |
图 6给出了弹道倾角跟踪的对比曲线,图 7为弹道倾角、俯仰角与俯仰角速率跟踪误差对比曲线。图 8给出了2种方案下升降舵偏角的对比曲线。从对比仿真结果可以看出,由于减步控制方案中跟踪微分器对名义指令信号及其导数的精确估计,使得该方案的收敛速度和跟踪精度均高于传统动态面控制方案。另外从图 8中可以看出,采用减步控制方案所需的升降舵偏角略大于传统动态面控制,但均处于最大舵偏允许范围之内。
6 结论 1) 通过在传统动态面方法中加入高阶跟踪微分器,避免每一步都需要计算上一步名义虚拟控制变量导数的问题,将设计步骤从3步减小为2步,有效降低了控制系统复杂度。
2) 所提控制方案避免引入传统动态面控制中的低通滤波器。从而避免了实际虚拟控制量与名义虚拟控制量改变所带来的误差,提高了跟踪精度。
3) 将气动参数不确定性,外部扰动以及忽略项视作等效干扰,利用扩张状态观测器对其进行精确估计,并在控制中进行补偿。有效提高了控制器对不确定与干扰抑制能力。
4) 利用Lyapunov理论给出了闭环系统一致毕竟有界稳定的证明,并通过数值仿真说明了所提方案的优越性。
参考文献
| [1] | RODRIGUEZ A A, DICKESON J J, CIFDALOZ O, et al. Modeling and control of scramjet-powered hypersonic vehicles:Challenges, trends, & tradeoffs:AIAA-2008-6793[R].Reston:AIAA, 2008. |
| [2] | LAMORTE N, FRIEDMANN P P, DALLE D J, et al. Uncertainty propagation in integrated airframe-propulsion system analysis for hypersonic vehicle[J].Journal of Propulsion and Power, 2015, 31(1): 54–68.DOI:10.2514/1.B35122 |
| [3] | DICKESON J J, RODRIGUEZ A A, SRIDHARAN S, et al.Control-relevant modeling, analysis, and design for scramjet-powered hypersonic vehicle:AIAA-2009-7287[R].Reston:AIAA, 2009. |
| [4] | KARLGARD C D, MARTIN J G, TARTABINI P V, et al.Hyper-X Mach 10 trajectory reconstruction:AIAA-2005-5920[R].Reston:AIAA, 2005. |
| [5] | MORELLI E A. Flight test experiment design for characterizing stability and control of hypersonic vehicles[J].Journal of Guidance, Control, and Dynamics, 2009, 32(3): 949–959.DOI:10.2514/1.37092 |
| [6] | 孙长银, 穆朝絮, 余瑶. 近空间高超声速飞行器控制的几个科学问题研究[J].自动化学报, 2013, 39(11): 1901–1913. SUN C Y, MU Z X, YU Y. Some control problem for near space hypersonic vehicles[J].Acta Automatica Sinica, 2013, 39(11): 1901–1913.(in Chinese) |
| [7] | WANG Q, STENGEL R F. Robust nonlinear control of a hypersonic aircraft[J].Journal of Guidance, Control, and Dynamics, 2000, 23(4): 577–585.DOI:10.2514/2.4580 |
| [8] | FIORENTINI L, SERRANI A, BOLENDER M A, et al. Nonlinear robust adaptive control of flexible air-breathing hypersonic vehicles[J].Journal of Guidance, Control, and Dynamics, 2009, 32(2): 401–416. |
| [9] | SUN H B, LI S H, SUN C Y. Finite time integral sliding model control of hypersonic vehicles[J].Nonlinear Dynamics, 2013, 73(1/2): 229–244. |
| [10] | 刘燕斌, 陆宇平. 基于反步法的高超音速飞机纵向逆飞行控制[J].控制与决策, 2007, 22(3): 313–317. LIU Y B, LU Y P. Longitudinal inversion flight control based on backstepping for hypersonic vehicle[J].Control and Decision, 2007, 22(3): 313–317.(in Chinese) |
| [11] | 黄喜元, 王青, 董朝阳. 基于Backstepping的高超声速飞行器鲁棒自适应控制[J].系统工程与电子技术, 2011, 33(6): 1321–1326. HUANG X Y, WANG Q, DONG C Y. Robust adaptive control of hypersonic vehicles via Backstepping method[J].Systems Engineering and Electronics, 2011, 33(6): 1321–1326.(in Chinese) |
| [12] | XU B, GAO D X, WANG S X. Adaptive neural control based on HGO for hypersonic flight vehicles[J].Science China Information Sciences, 2011, 54(3): 511–520.DOI:10.1007/s11432-011-4189-8 |
| [13] | XU B, FAN Y H, ZHANG S M. Minimal-learning-parameter technique based adaptive neural control of hypersonic flight dynamics without back-stepping[J].Neurocomputing, 2015, 164(C): 201–209. |
| [14] | SWAROOP D, HEDRICK J K, YIP P P, et al. Dynamic surface control for a class of nonlinear systems[J].IEEE Transactions on Automatic Control, 2000, 45(10): 1893–1899.DOI:10.1109/TAC.2000.880994 |
| [15] | XU B, HUANG X Y, WANG D W, et al. Dynamic surface control of constrained hypersonic flight models with parameter estimation and actuator compensation[J].Asian Journal of Control, 2014, 16(1): 162–174.DOI:10.1002/asjc.2014.16.issue-1 |
| [16] | WASEEM A B, LIN Y, KENDRICK A S. Adaptive integral dynamic surface control of a hypersonic flight vehicle[J].International Journal of Systems Science, 2015, 46(10): 1717–1728.DOI:10.1080/00207721.2013.828798 |
| [17] | 韩京清, 王伟. 非线性跟踪微分器[J].系统科学与数学, 1994, 14(2): 177–183. HAN J Q, WANG W. Nonlinear tracking-differentiator[J].Journal of Systems Science and Mathematical Science, 1994, 14(2): 177–183.(in Chinese) |
| [18] | PARKER J T, SERRANI A, YURKOVICH S, et al. Control-oriented modeling of an air-breathing hypersonic vehicle[J].Journal of Guidance, Control, and Dynamics, 2007, 30(3): 856–869.DOI:10.2514/1.27830 |
| [19] | XU B, SHI Z K. An overview on flight dynamic and control approaches for hypersonic vehicles[J].Science China Information Sciences, 2015, 58(7): 1–19. |
| [20] | FIORENTINI L, SERRANI A. Adaptive restricted trajectory tracking for a non-minimum phase hypersonic vehicle model[J].Automatic, 2012, 48(7): 1248–1261.DOI:10.1016/j.automatica.2012.04.006 |
| [21] | GUO B Z, ZHAO Z L. On convergence of tracking differentiator[J].International Journal of Control, 2001, 84(4): 693–701. |
