Masutani等[6]基于C-W解析解提出了一种双椭圆拼接绕飞构型,并设计了反馈控制策略进行构型维持;赵书阁和张景瑞[7]在此基础上研究了快速绕飞问题。罗建军等[8-9]研究了利用多脉冲控制进入和退出绕飞构型的方法。朱彦伟[10]进行了单脉冲“水滴”形、多脉冲受限圆形和“田径场”形等多种绕飞构型的设计,并分析了能量消耗。Straight[11]提出了一种在圆形标称轨迹上设置导航点的多脉冲绕飞策略,并进行了优化。Hope和Trask[12]提出一种“水滴”形脉冲轨迹实现航天器悬停任务;Lovell和Tollefson[13]利用一组轨道要素参数进一步对“水滴”构型几何描述进行了研究。饶殷睿等[14]利用相对轨道要素法研究了“水滴”形悬停构型描述和控制问题;悬停任务设计方法可拓展至绕飞构型设计中。王功波等[15]基于连续推力技术,推导了满足快速绕飞条件的空间圆编队动力学模型。朱小龙等[16]利用基于同伦法思想的推力幅值延拓方法,得到了有限推力以及脉冲推力绕飞的燃料最优绕飞轨迹。
上面提到的方法可以实现航天器相对运动的受迫绕飞,但大多关注快速绕飞问题,未验证慢速绕飞的适用性问题;缺乏对绕飞构型的设计与参数描述研究。针对上述情况,本文设计了伴随航天器相对近圆轨道参考航天器轨道平面内的4种绕飞构型:双椭圆拼接绕飞、单水滴绕飞、双水滴拼接绕飞和基于标称轨迹的多脉冲绕飞构型,推导了伴随航天器初始状态变量与绕飞构型形状参数的关系,给出了不同绕飞构型的解析表达式和脉冲控制策略。数值仿真显示4种受迫绕飞构型可同时解决快速绕飞和慢速绕飞问题。
1 绕飞运动研究基础 1.1 坐标系及运动方程 参考航天器为近圆轨道,伴随航天器的相对运动模型采用C-W方程(也称为Hill方程)。首先建立以参考航天器质心为坐标原点的LVLH(当地水平当地垂直)坐标系OXYZ,如图 1所示。XY平面为参考航天器轨道平面,X轴由地心指向参考航天器质心,Z轴沿参考航天器角动量方向,Y轴由右手法则确定,n为参考航天器轨道角速度。
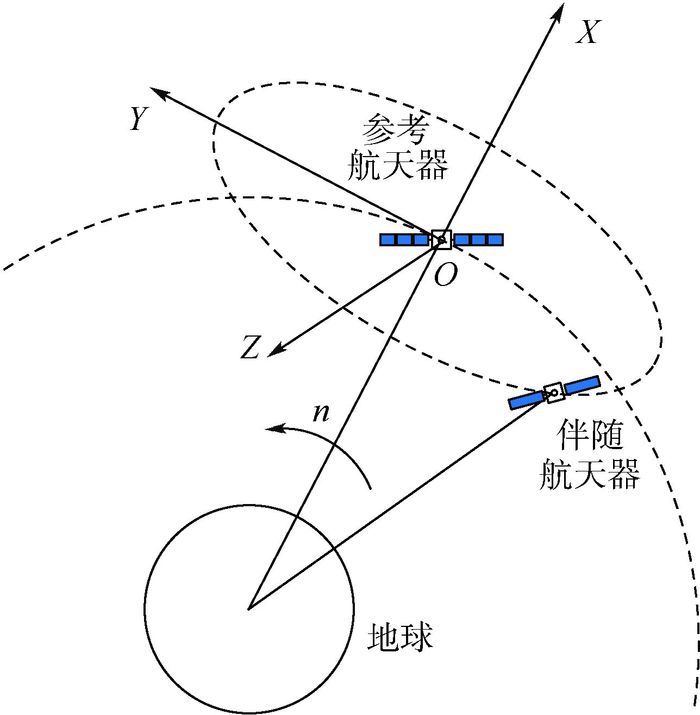 |
| 图 1 参考航天器LVLH坐标系 Fig. 1 Reference spacecraft LVLH coordinate system |
| 图选项 |
当参考航天器运行于圆或近圆轨道,且伴随航天器与参考航天器距离很近时,两航天器之间的引力差可线性化处理,得到伴随航天器在参考航天器LVLH坐标系中的相对运动方程为
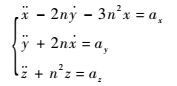 | (1) |
式中:x、y、z为伴随航天器的质心在LVLH坐标系中的位置;ax、ay、az分别为伴随航天器在X、Y、Z轴3个方向的控制加速度。
将
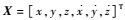
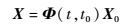 | (2) |
式中:Φ(t, t0)为状态转移矩阵,具体形式见式(3);X0为t0时刻的状态量。
注意到平面内变量x、y和平面外变量z的运动是解耦的,本文主要研究在参考航天器轨道平面内的相对运动。
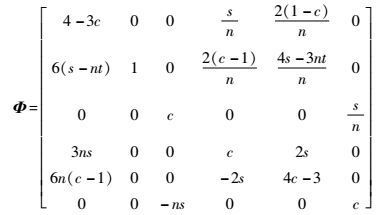 | (3) |
式中:s=sin(nt);c=cos(nt)。
1.2 自然绕飞构型 当伴随航天器的初始状态满足

自然绕飞构型如图 2所示,将OA的距离l作为描述自然绕飞构型的几何参数。
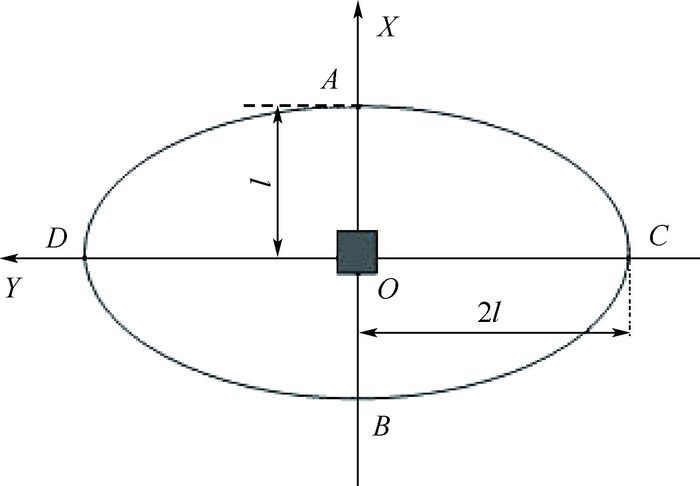 |
| 图 2 自然绕飞构型示意图 Fig. 2 Schematic diagram of natural fly-around formation |
| 图选项 |
A点作为初始点,伴随航天器的初始状态变量为
 | (4) |
自然绕飞构型相对位置的解析表达式为
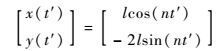 | (5) |
式中:t′=mod(t, T),mod为时间t对绕飞周期T进行取余操作。
1.3 双椭圆拼接绕飞构型 一些****在自然绕飞构型基础上提出了双椭圆拼接受迫绕飞构型[5-6]。双椭圆拼接绕飞构型是由关于X轴对称的2个镜面对称的自然绕飞椭圆的部分轨迹拼接形成的封闭轨迹,如图 3所示。伴随航天器按照粗实线箭头方向围绕参考航天器绕飞,根据2个椭圆的对称性,只要在A、B两点施加径向(X轴方向)脉冲,就能形成拼接绕飞构型。
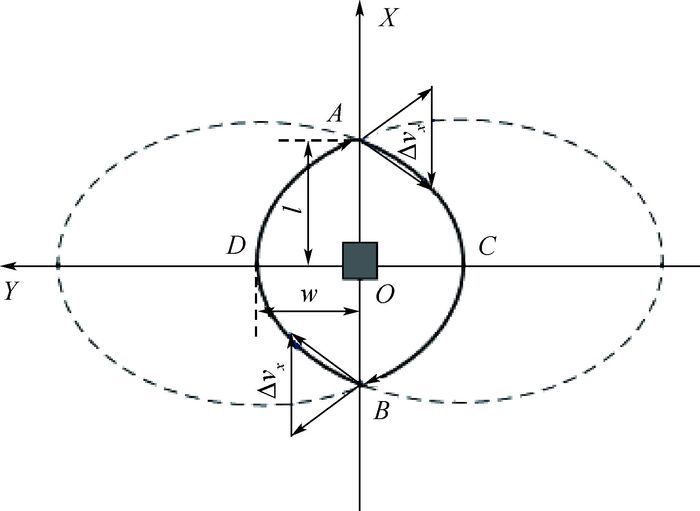 |
| 图 3 双椭圆拼接绕飞构型示意图 Fig. 3 Schematic diagram of bi-elliptic joint fly-around formation |
| 图选项 |
双椭圆拼接绕飞构型可用l、w和T等参数描述,w为OD的长度,T为伴随航天器绕飞周期。3个变量中,只有2个是独立变量,选取l和T来描述绕飞轨迹,w可表示为
 | (6) |
A点作为初始点,伴随航天器的初始状态变量为
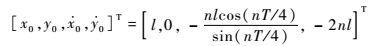 | (7) |
双椭圆拼接绕飞构型的解析式为
 | (8) |
双椭圆拼接绕飞构型中伴随航天器在A点和B点施加的脉冲为
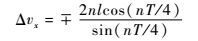 | (9) |
两次脉冲均沿径向方向,脉冲施加时刻分别为t′=0和t′=T/2。
参考航天器的轨道周期为T0,绕飞周期T=kT0,k为绕飞周期系数,对于双椭圆拼接绕飞构型,k的取值范围为(0, 2)。当k逼近0或2时,式(6) 和式(7) 中分母逼近零,出现奇点情况,此时绕飞脉冲趋于无穷。后文若不加特殊说明,本文研究的绕飞构型绕飞周期系数取值范围为(0, 2)。
2 水滴受迫绕飞构型设计 水滴形状的相对运动构型最早应用于航天器悬停任务中,通过调整控制周期还可扩展至绕飞运动中。本节首先描述了一种单水滴绕飞构型,接着设计了一种双水滴拼接绕飞构型。
2.1 单水滴绕飞构型 当伴随航天器的半长轴与参考航天器不同时,即
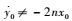
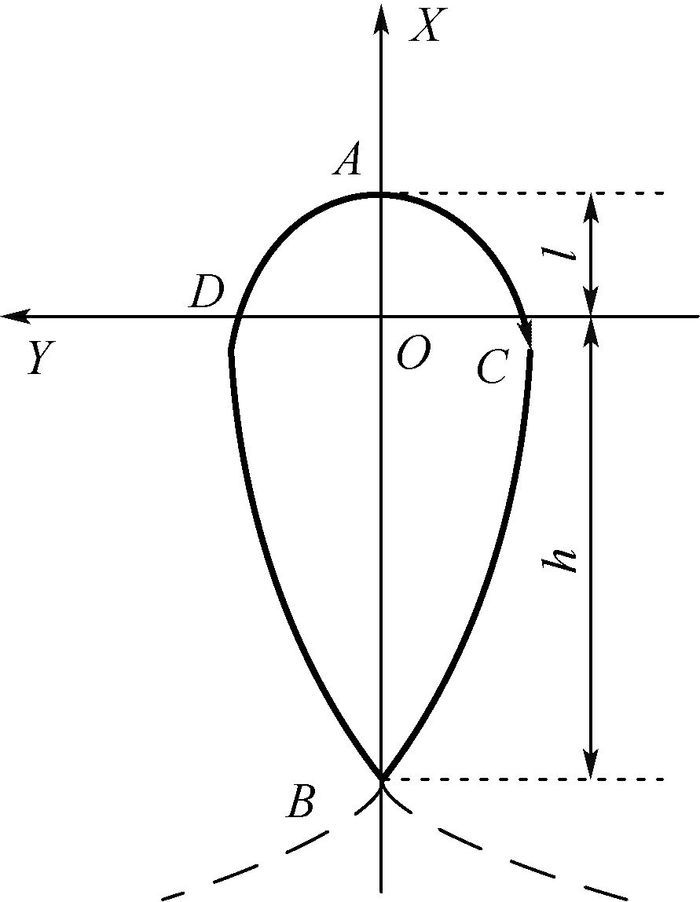 |
| 图 4 水滴绕飞构型示意图 Fig. 4 Schematic diagram of teardrop fly-around formation |
| 图选项 |
用l、h和T来描述水滴绕飞构型,h为OB的长度,同样只有2个变量是独立的。选取l和T为独立变量,则h可表示为
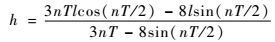 | (10) |
选A点为初始点,伴随航天器的初始状态变量为
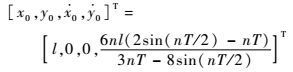 | (11) |
水滴绕飞构型的解析式为
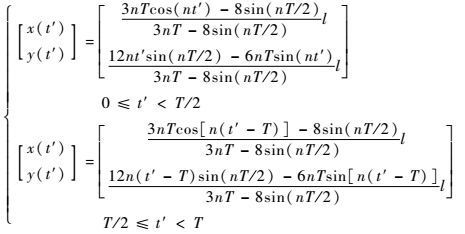 | (12) |
伴随航天器在水滴尖点B处需要施加的径向脉冲为
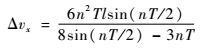 | (13) |
脉冲施加时刻为t′=T/2。
对于水滴绕飞,当k取值较小时,A、B两点位于Y轴同侧;要形成绕飞构型,要求A、B位于Y轴两侧,即l与h异号,计算可得k的取值范围为(0.406, 1.406 7)。当k<0.406,A、B点位于Y轴同侧,形成文献[12-14]提到的悬停构型。当k逼近0.406时,式(10) 和式(13) 中分母逼近零,出现奇点,绕飞构型半径和脉冲特别大。注意到,对于慢速绕飞(1.406 7>k>1),水滴绕飞构型的形状与图 4形状不同,呈现出倒立的“心”形,见图 5;随着k的不断增大,水滴尖点B不断上移,直至逼近甚至超越Y轴。当k>1.406 7时,A、B两点再次同侧,绕飞构型形状比较复杂,如图 5点划线所示,一个完整的构型中伴随航天器实际上绕参考航天器飞行了2周,不符合慢速绕飞要求。
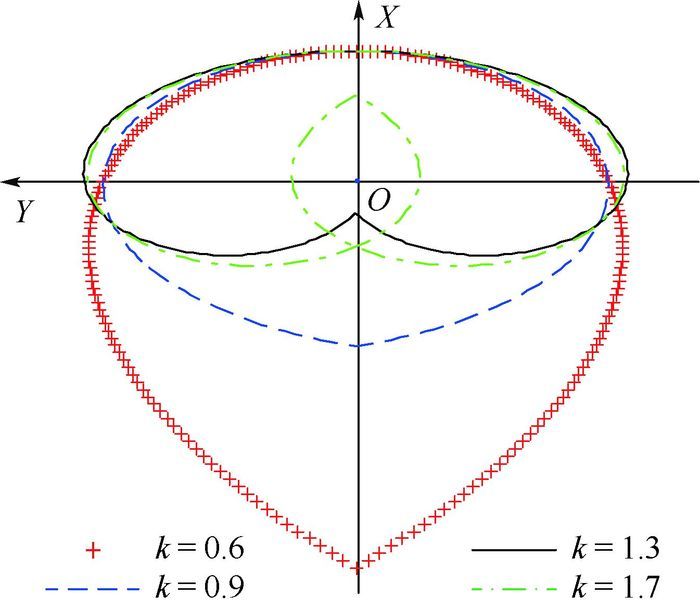 |
| 图 5 不同绕飞周期系数的水滴绕飞形状 Fig. 5 Teardrop fly-around shapes with different fly-around period coefficients |
| 图选项 |
2.2 双水滴拼接绕飞构型 借鉴双椭圆拼接绕飞构型的设计思路,由关于Y轴镜面对称的2个单水滴轨迹拼接可以形成双水滴拼接绕飞构型,如图 6所示。2个水滴构型与Y轴各有2个相同的交点C、D,在这两点施加脉冲可实现周期性绕飞轨迹。
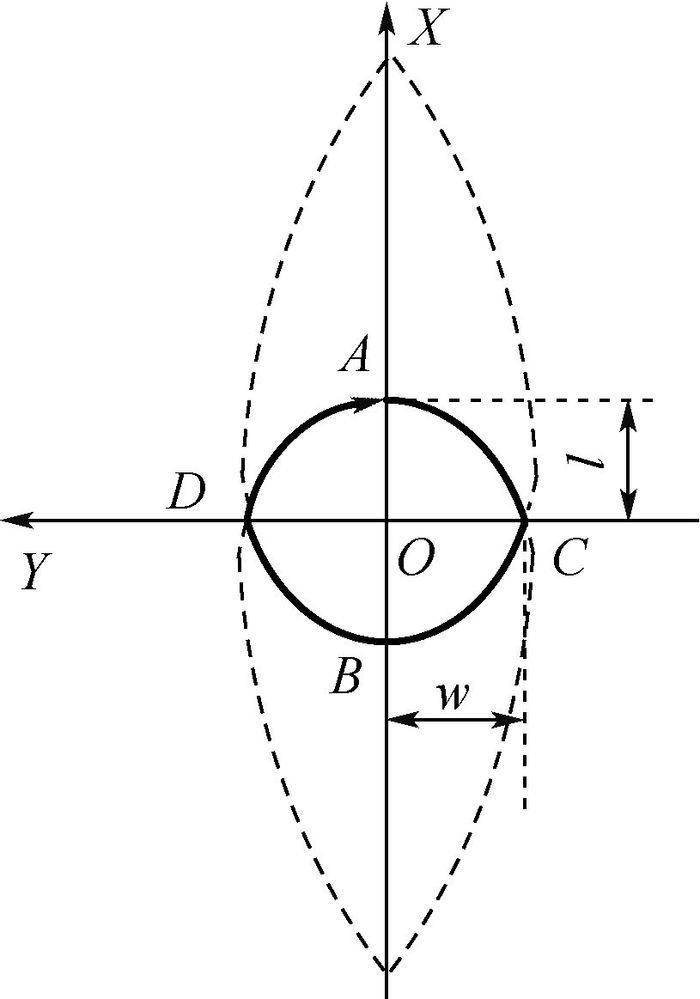 |
| 图 6 双水滴拼接绕飞构型示意图 Fig. 6 Schematic diagram of bi-teardrop joint fly-around formation |
| 图选项 |
用l、w和T来描述双水滴拼接绕飞构型,只有2个变量是独立的。选取l和T来描述绕飞构型,则w可表示为
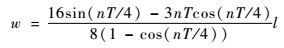 | (14) |
A点作为初始点,伴随航天器的初始状态变量为
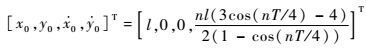 | (15) |
双水滴拼接绕飞构型解析式为
 | (16) |
根据双水滴绕飞构型的对称性,在C和D点需要施加迹向(Y轴方向)脉冲为
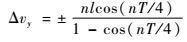 | (17) |
脉冲施加时刻为t′=T/4和t′=3T/4。
双水滴拼接绕飞构型中k的取值范围为(0, 2),绕飞构型形状随k的变化不大。
3 基于标称轨迹的多脉冲绕飞构型 1.3节和第2节提出的3种受迫绕飞构型利用了相对运动的规律,用单次或两次脉冲控制实现受迫绕飞,本节研究用三脉冲以及以上的多脉冲策略实现受迫绕飞任务。在圆形标称轨迹上设置导航点,如图 7所示,在每个导航点施加脉冲,使伴随航天器依次经过每个导航点。根据相邻两个导航点的相对位置,可以计算每次变轨脉冲的大小和方向。用绕飞半径ρ、绕飞周期T和总变轨次数b(整数)等参数来描述多脉冲绕飞构型。图 7中:A、B、C分别为3个导航点;θ1、θ2和θ3分别为相邻2个导航点AB、BC、CA之间的圆心夹角;σ为初始点A的初始相位角;Δv1、Δv2和Δv3分别为A、B、C3点的脉冲矢量;Δt1、Δt2和Δt3分别为相邻2个导航点AB、BC、CA之间的变轨时间间隔。
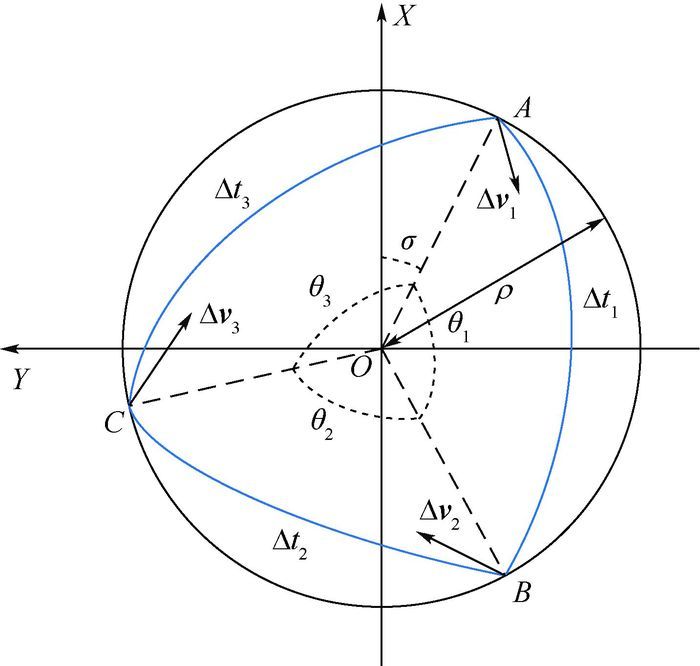 |
| 图 7 多脉冲绕飞构型示意图 Fig. 7 Schematic diagram of multi-impulse fly-around formation |
| 图选项 |
3.1 EAET方法 首先采用导航点等角度等时间(EAET)分布的假设,即脉冲位置在标称圆轨迹上等间隔分布。相邻2个导航点的圆心夹角为θi=2π/b,相邻2个导航点的时间间隔为Δti=T/b。
各导航点的相对位置为
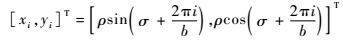 | (18) |
式中:i∈[0, b-1]且为整数。
当σ=0°,利用文献[17]中相对运动Lambert问题的解析解,可以计算第i个导航点的脉冲为
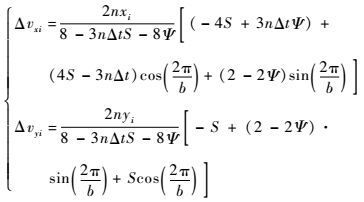 | (19) |
式中:Δt为2次脉冲的时间间隔;S=sin(nΔt);Ψ=cos(nΔt)。
基于标称轨迹的多脉冲绕飞构型每个周期所需总脉冲为
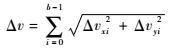 | (20) |
各脉冲的施加时刻为t′=iT/b,i∈[0, b-1]。影响多脉冲绕飞构型总脉冲大小的因素包括脉冲次数b和A点初始相位角σ等变量。
3.2 燃料最优多脉冲绕飞 以导航点的位置和脉冲时刻为优化变量,可以研究基于圆标称轨迹的燃料最优多脉冲绕飞构型。以三脉冲绕飞为例,待优化变量为
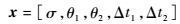 | (21) |
优化目标函数为
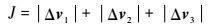 | (22) |
优化变量x要满足的约束条件包括:
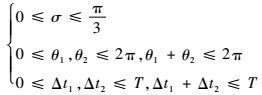 | (23) |
以EAET方法的结果作为优化变量的初值,基于圆标称轨迹的燃料最优多脉冲绕飞问题本质是一个参数优化问题。
4 数值仿真 设参考航天器轨道为绕地球运行的1 000 km圆轨道,轨道周期约为6 307 s。在初始时刻,伴随航天器位于参考航天器径向上方1 km处。
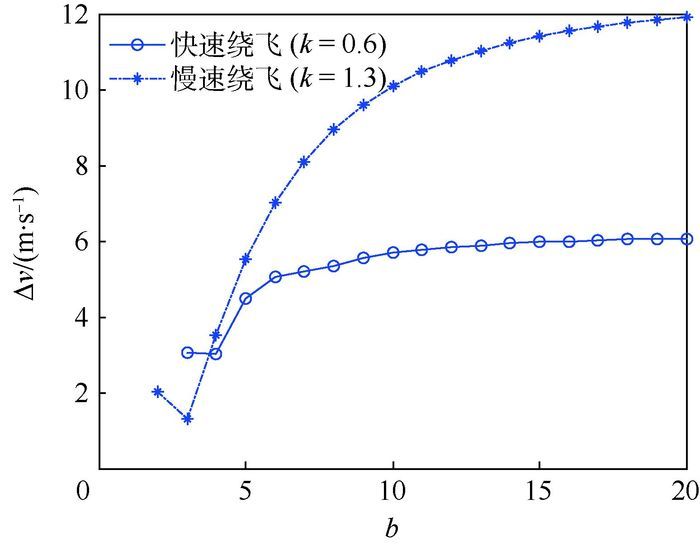
4.1 多脉冲绕飞数值仿真与分析 基于圆标称轨迹的多脉冲绕飞构型设计中,脉冲次数b对绕飞构型形状和总脉冲大小有影响。对于伴随航天器的慢速绕飞运动,设定绕飞周期为8 200 s,即k=1.3。脉冲次数对于脉冲大小和构型形状的影响如图 8和图 9所示。当脉冲次数为3时,总脉冲消耗最小;随着脉冲次数增大,总脉冲变大,最终趋于连续推力控制的总脉冲值。随着脉冲次数增加,绕飞轨迹与标称圆轨迹相比的偏差减小。
 |
| 图 8 受迫绕飞总脉冲随脉冲次数曲线 Fig. 8 Curves of forced fly-around total impulse with numbers of impulse |
| 图选项 |
 |
| 图 9 不同脉冲次数慢速绕飞构型形状示意图 Fig. 9 Schematic diagram of slow fly-around formation shape with different numbers of impulse |
| 图选项 |
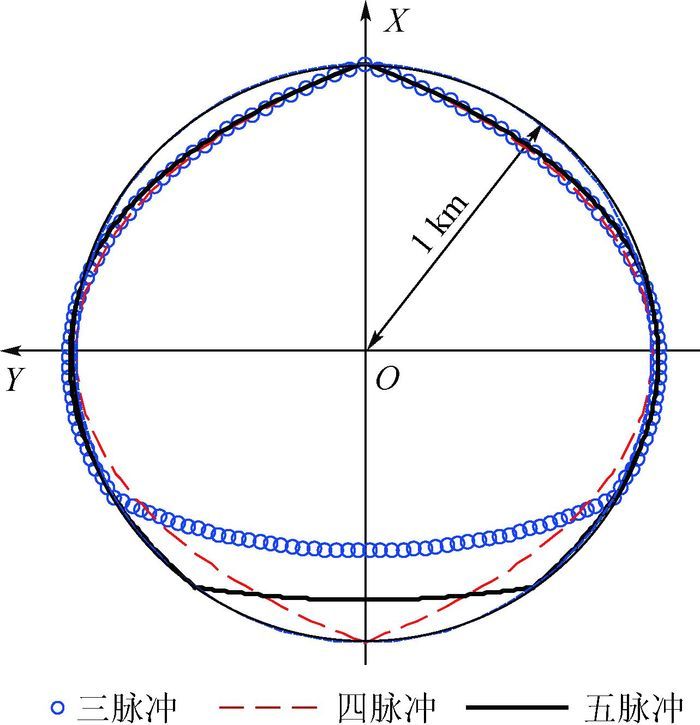
对于伴随航天器的快速绕飞运动,设定绕飞周期为3 800 s,即k=0.6。同样分析快速绕飞脉冲次数b对于绕飞构型形状和总脉冲的影响。如图 8所示,脉冲次数为3~4时,总脉冲大小接近,为最小值;随着脉冲次数增多,总脉冲逐渐增大,并渐渐接近连续推力总脉冲值。图 10为脉冲次数对于快速绕飞轨迹形状的影响,四脉冲绕飞构型与双椭圆拼接绕飞构型形状非常接近。
 |
| 图 10 不同脉冲次数快速绕飞构型形状示意图 Fig. 10 Schematic diagram of fast fly-around formation shape with different numbers of impulse |
| 图选项 |
无论是快速绕飞还是慢速绕飞,三脉冲消耗的总脉冲较小,因此燃料最优多脉冲绕飞研究中脉冲次数选为3。采用MALTAB的优化工具箱,得到优化变量的取值为
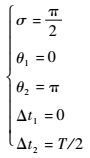 | (24) |
三脉冲退化为两脉冲绕飞,根据优化变量的取值可得到以下结论:燃料最优三脉冲受迫绕飞的优化结果为两脉冲的双水滴拼接绕飞构型。
4.2 慢速绕飞构型比较 研究伴随航天器的慢速绕飞,设定绕飞周期为8 200 s,即k=1.3。对于基于标称轨迹的多脉冲绕飞构型,采用EAET方法,选取脉冲次数b=3。
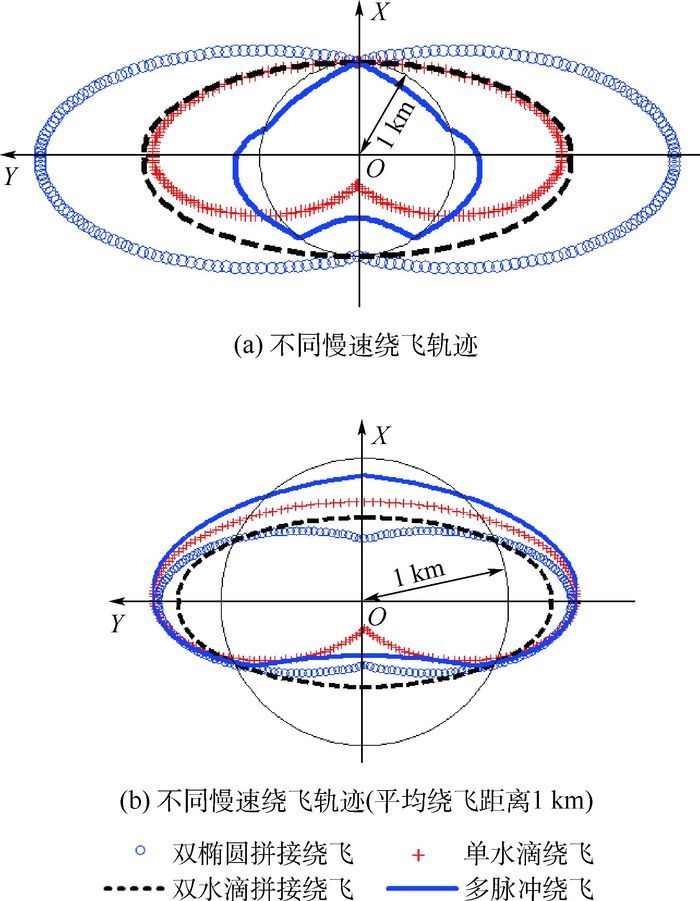
4种慢速绕飞构型如图 11(a)所示,其中细实线表示的是半径为1 km的标称圆。算例中,水滴绕飞构型的形状近似翻转的“心”形。注意到,图 11(a)中,不同绕飞构型中伴随航天器离参考航天器的平均距离不同,其中双椭圆拼接绕飞距离最大,三脉冲绕飞距离最小。由式(9)、式(13)、式(17) 可知,总脉冲与距离成正比。在比较各种绕飞构型的燃料消耗时,绕飞距离不应成为影响权衡的因素。定义一个新变量
 | (25) |
式中:d为一个绕飞周期的平均绕飞距离;Δv为单位化脉冲,表示每单位平均绕飞距离需要的脉冲总量,m/(s·km)-1。
图 11(b)为平均绕飞距离为1 km的4种慢速绕飞构型形状。4种慢速绕飞构型的脉冲消耗情况如表 1所示,第4列总脉冲大小为图 11(a)所示由相同初始点出发每个周期所需脉冲大小,第5列单位化脉冲为平均绕飞距离为1 km每个周期所需脉冲。双椭圆拼接绕飞需要2次径向脉冲,2次脉冲大小相同,方向相反;单水滴绕飞构型每个绕飞周期仅需1次径向脉冲;双水滴拼接绕飞需要2次迹向脉冲,大小相同,方向相反;基于标称轨迹的多脉冲绕飞构型中,每1次脉冲均包含径向和迹向分量。慢速绕飞算例中,双水滴拼接绕飞构型总脉冲最小;双椭圆拼接绕飞构型和单水滴绕飞构型单位化总脉冲非常接近。
 |
| 图 11 不同慢速绕飞构型示意图 Fig. 11 Schematic diagram of different slow fly-around formations |
| 图选项 |
表 1 慢速绕飞总脉冲比较 Table 1 Comparison of slow fly-around total impulse
| 绕飞 构型 | 次数 | 方向 | 总脉冲大小/ (m·s-1) | 单位化脉冲/ (m·s-1·km-1) |
| 双椭圆 拼接绕飞 | 2 | 径向 | 2.03 | 0.893 |
| 单水滴 绕飞 | 1 | 径向 | 1.275 | 0.891 |
| 双水滴 拼接绕飞 | 2 | 迹向 | 0.622 | 0.366 |
| 多脉冲 绕飞 | 3 | 混合 | 1.299 | 1.145 |
表选项
4.3 快速绕飞构型比较 快速绕飞仿真中,设定伴随航天器的绕飞周期为3 800 s,即k=0.6。对于基于标称轨迹的多脉冲绕飞构型,采用EAET方法,选取脉冲次数b=3。
4种快速绕飞构型如图 12所示,图 12(a)为伴随航天器由相同的初始点出发点形成的4种不同绕飞构型,图 12(b)为平均绕飞距离为1 km的绕飞轨迹。
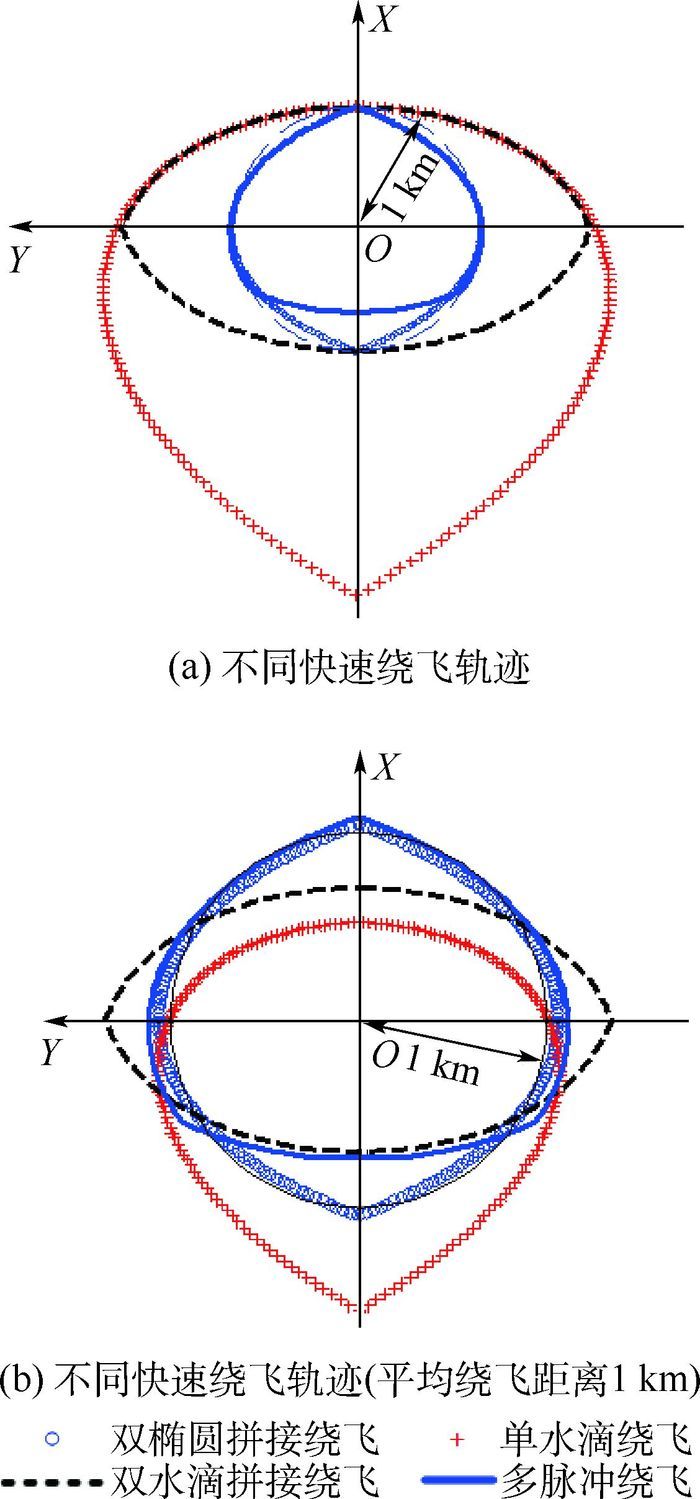 |
| 图 12 不同快速绕飞构型示意图 Fig. 12 Schematic diagram of different fast fly-around formations |
| 图选项 |
4种快速绕飞构型的脉冲消耗情况如表 2所示。快速绕飞算例中,双水滴拼接绕飞构型单位化脉冲最小;双椭圆拼接绕飞构型和单水滴绕飞构型单位化脉冲非常接近。三脉冲绕飞所需总脉冲最大。
表 2 快速绕飞总脉冲比较 Table 2 Comparison of fast fly-around total impulse
| 冲绕飞 构型 | 次数 | 方向 | 总脉冲大小/ (m·s-1) | 单位化脉冲/ (m·s-1·km-1) |
| 双椭圆 拼接绕飞 | 2 | 径向 | 2.895 | 3.019 |
| 单水滴 绕飞 | 1 | 径向 | 5.79 | 2.997 |
| 双水滴 拼接绕飞 | 2 | 迹向 | 2.841 | 2.00 |
| 多脉冲绕飞 | 3 | 混合 | 3.049 | 3.315 |
表选项
4.4 不同周期绕飞构型比较 本节主要从燃料消耗和绕飞距离误差2个角度分析不同绕飞构型的优缺点。燃料消耗指数用伴随航天器绕飞一个周期需要的总脉冲来考量;绕飞距离误差的定义为δerror=(d-d0)/d0,d0为期望绕飞距离,d为实际绕飞距离,绕飞距离误差反映了绕飞构型的形状,对于一些近距离观测任务,绕飞距离误差不能太大。
绕飞周期是影响不同绕飞构型总脉冲的重要因素,图 13以绕飞周期系数k为横轴,分析了不同绕飞构型单位化脉冲随绕飞周期的变化情况。本文研究的绕飞周期系数变化范围为(0, 2),单水滴绕飞构型仅适合绕飞周期系数在(0.406, 1.406 7) 的情况,另外3种绕飞构型满足(0, 2) 的变化范围。
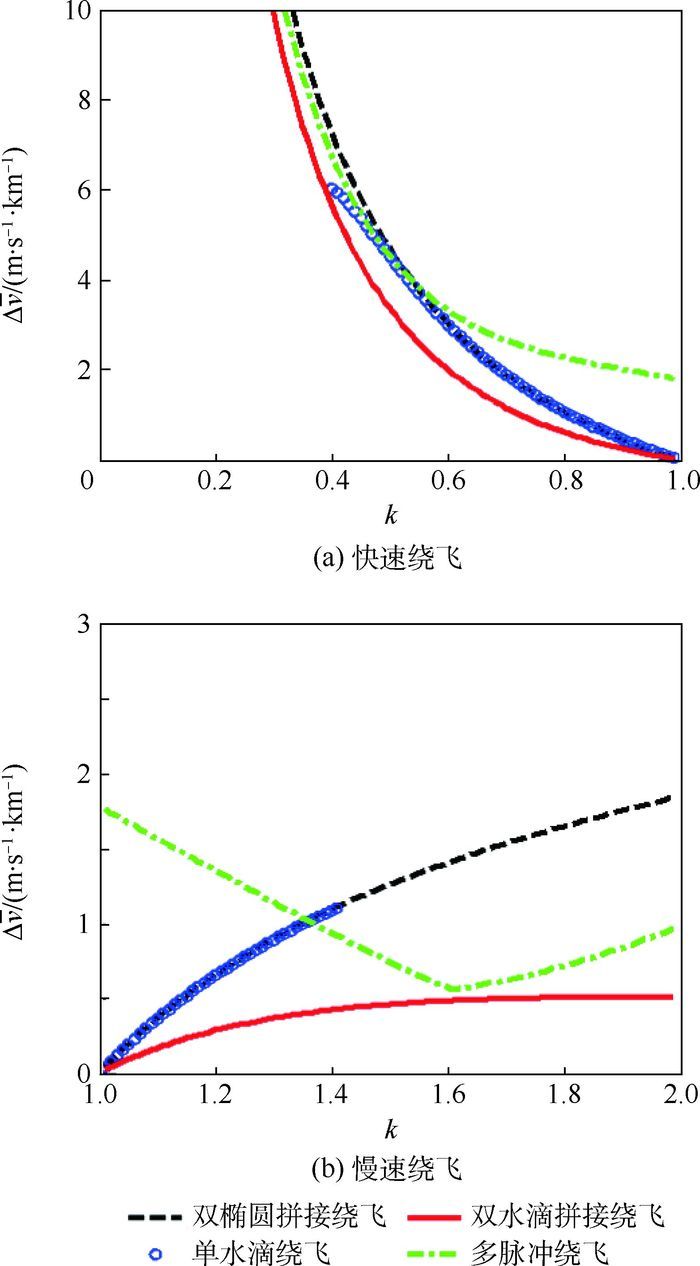 |
| 图 13 绕飞单位化脉冲随绕飞周期变化曲线 Fig. 13 Curves of fly-around unitized impulse with different fly-around periods |
| 图选项 |
图 13结果显示,双水滴拼接绕飞构型的燃料消耗总体处于较低的水平;单水滴绕飞和双椭圆拼接绕飞构型具有比较接近的燃料消耗。当k=1时,对应自然绕飞构型;只有多脉冲绕飞(此处选择三脉冲)燃料消耗不是零,这是因为圆标称轨迹的要求改变了绕飞轨迹形状,需要消耗额外的燃料。当快速绕飞周期较短时,保持受迫快速绕飞所需的总脉冲较大;随着绕飞周期逐渐增大,总脉冲值迅速减小。
图 14反映了一个绕飞周期内绕飞距离误差δerror随绕飞周期系数的变化曲线,其中多脉冲绕飞的脉冲次数为4。从曲线中可以得到以下结论:多脉冲绕飞构型的绕飞距离误差比较小,总体上低于10%,适合对绕飞观测距离有严格限制的任务;快速绕飞模式中,当绕飞周期系数较小时,双椭圆拼接构型和双水滴拼接构型均为狭长的封闭曲线,绕飞距离误差比较大,随着绕飞周期系数的增大,平均距离误差逐渐减小,在k=0.5附近达到最小值;此后,随着绕飞周期继续增大,双椭圆拼接绕飞构型距离误差迅速增大,而双水滴拼接构型距离误差保持平缓,变化不大。单水滴绕飞构型的距离误差比较大。
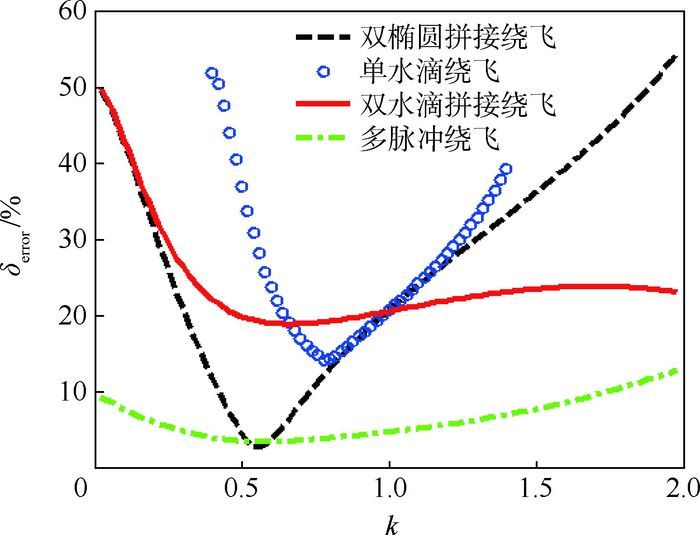 |
| 图 14 绕飞距离误差随绕飞周期变化曲线 Fig. 14 Curves of fly-around distance errors with different fly-around periods |
| 图选项 |
从燃料消耗的角度分析,双水滴拼接构型所需脉冲最小,每个绕飞周期内采用2次切向脉冲,变轨效率最高;当绕飞周期比较小时(k<0.3),双椭圆拼接绕飞、双水滴拼接绕飞、多脉冲绕飞构型的燃料消耗差距并不大,相对差距不超过12%。当绕飞周期逐渐增大,双水滴拼接绕飞构型燃料消耗小的优势体现出来。从绕飞距离误差的角度分析,多脉冲绕飞构型误差最小,适合对观测绕飞距离有严格限制的场景,其次是双水滴拼接构型,总体上误差变化较为平缓;单水滴绕飞构型误差最大。这些结论对于工程应用有很强的指导意义,在选择绕飞构型时需要综合权衡燃料消耗和绕飞距离误差2个因素。
5 结论 基于C-W方程对航天器受迫绕飞问题进行了研究,提出了受迫绕飞设计方法和脉冲控制策略,得到:
1) 设计了双水滴拼接绕飞等4种受迫绕飞构型,给出伴随航天器初始变量与轨迹形状参数的关系,推导了绕飞构型的解析表达式。
2) 提出的双水滴拼接绕飞构型使用2次迹向脉冲实现“慢速”或“快速”绕飞,燃料消耗较其他3种绕飞构型小。
3) 采用脉冲式控制策略,可以实现伴随航天器相对于参考航天器的慢速绕飞和快速绕飞,控制策略简单,工程上易于实现。
参考文献
| [1] | WALTZ D M. On-orbit servicing of space systems[M].Malabar: Krieger Publishing Company, 1993: 193-227. |
| [2] | 崔乃刚, 王平, 郭继峰, 等. 空间在轨服务技术发展综述[J].宇航学报, 2007, 28(4): 805–811. CUI N G, WANG P, GUO J F, et al. A review of on-orbit servicing[J].Journal of Astronautics, 2007, 28(4): 805–811.(in Chinese) |
| [3] | 陈小前, 袁建平, 姚雯, 等. 航天器在轨服务技术[M].北京: 中国宇航出版社, 2009: 153-168. CHEN X Q, YUAN J P, YAO W, et al. Spacecraft on orbit service technology[M].Beijing: China Aerospace Press, 2009: 153-168.(in Chinese) |
| [4] | SABOL C, BURNS R, MCLAUGHLIN C A. Satellite formation flying design and evolution[J].Journal of Spacecraft and Rockets, 2001, 38(2): 270–278.DOI:10.2514/2.3681 |
| [5] | CLOHESSY W H, WILTSHIRE R S. Terminal guidance system for satellite rendezvous[J].Journal of the Areospace Sciences, 1960, 27(9): 653–658.DOI:10.2514/8.8704 |
| [6] | MASUTANI Y, MATSUSHITA M, MIYAZAKI F.Flyaround maneuvers on a satellite orbit by impulsive thrust control[C]//IEEE International Conference on Robotics and Automation.Piscataway, NJ:IEEE Press, 2001:421-426. |
| [7] | 赵书阁, 张景瑞. 航天器共面圆型快速绕飞控制研究[J].航天控制, 2014, 32(1): 68–72. ZHAO S G, ZHANG J R. A study on trajectory control of spacecraft in-plane circular fast fly-around[J].Aerospace Control, 2014, 32(1): 68–72.(in Chinese) |
| [8] | 罗建军, 周文勇, 袁建平. 卫星快速绕飞轨迹设计与制导[J].宇航学报, 2007, 28(3): 628–632. LUO J J, ZHOU W Y, YUAN J P. A general method of trajectory design and guidance for fast satellite circumnavigation[J].Journal of Astronautics, 2007, 28(3): 628–632.(in Chinese) |
| [9] | 罗建军, 杨宇和, 袁建平. 共面快速受控绕飞轨迹设计与控制[J].宇航学报, 2006, 27(6): 1389–1392. LUO J J, YANG Y H, YUAN J P. Trajectory design and control of in-plane fast controlled flyaround[J].Journal of Astronautics, 2006, 27(6): 1389–1392.(in Chinese) |
| [10] | 朱彦伟. 航天器近距离相对运动轨迹规划与控制研究[D]. 长沙: 国防科学技术大学, 2009. ZHU Y W.Trajectory planning and control for spacecraft proximity relative motion[D].Changsha:National University of Defense Technology, 2009(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-90002-2009213058.htm |
| [11] | STRAIGHT S D.Maneuver design for fast satellite circumnavigation[D].Dayton:Air Force Institute of Technology, 2004. |
| [12] | HOPE A S, TRASK A J. Pulsed thrust method for hover formation flying[J].Advances in the Astronautical Sciences Series, 2003, 116: 2423–2434. |
| [13] | LOVELL T A, TOLLEFSON M V. Calculation of impulsive hovering trajectories via relative orbit elements[J].Advances in the Astronautical Sciences, 2006, 123(3): 2533–2548. |
| [14] | RAO Y R, YIN J F, HAN C. Hovering formation design and control based on relative orbit elements[J].Journal of Guidance, Control, and Dynamics, 2016, 39(2): 360–371.DOI:10.2514/1.G001238 |
| [15] | 王功波, 孟云鹤, 郑伟, 等. 快速绕飞卫星空间圆编队设计方法[J].宇航学报, 2010, 31(11): 2465–2470. WANG G B, MENG Y H, ZHENG W, et al. Fast fly around satellite space circle formation design[J].Journal of Astronautics, 2010, 31(11): 2465–2470.DOI:10.3873/j.issn.1000-1328.2010.11.005(in Chinese) |
| [16] | 朱小龙, 刘迎春, 高扬. 航天器最优受控绕飞轨迹推力幅值延拓设计方法[J].力学学报, 2014, 46(5): 756–769. ZHU X L, LIU Y C, GAO Y. Thrust-amplitude continuation design approach for solving spacecraft optimal controlled fly-around trajectory[J].Chinese Journal of Theoretical and Applied Mechanics, 2014, 46(5): 756–769.(in Chinese) |
| [17] | MULLINS L D. Initial value and two point boundary value solutions to the Clohessy-Wiltshire equations[J].Journal of the Astronautical Sciences, 1992, 40(4): 487–501. |
