自20世纪70年代以来,研究者一直对共轴刚性旋翼直升机的旋翼控制相位角问题进行研究[8-13],Halley[9]通过风洞试验,分析了共轴刚性旋翼直升机在前进比为0~0.1范围内时旋翼控制相位角为40°(与挥舞响应滞后角近似相等)和70°(明显高于挥舞响应滞后角)2种情况下的配平特性与操纵功效。分析发现旋翼控制相位角为40°时,相比于旋翼控制相位角70°能够提高周期变距的操纵功效,降低不同速度下的配平纵向周期变距。Ruddell和Macrino[10-11]通过风洞和飞行试验研究了共轴刚性旋翼直升机以前进比在0~0.4之间时不同旋翼控制相位角对桨毂处弯矩和配平特性的影响。发现当旋翼控制相位角为40°时,上、下旋翼桨毂弯矩都随着前飞速度的增加而增加,当前进比大于0.25时,上、下旋翼桨毂弯矩已经超过了结构强度限制。但当旋翼控制相位角为60°时,该速度范围内的上、下旋翼桨毂弯矩明显降低,且改善了直升机俯仰姿态。上述研究表明,若利用挥舞响应滞后角来确定共轴刚性旋翼直升机的旋翼控制相位角,虽然能够保证周期变距的操纵功效,但随着飞行速度的增加,上、下旋翼桨毂处弯矩明显增大,影响桨毂的结构强度。若比照常规旋翼将旋翼控制相位角设定为接近90°,虽然能通过操纵抑制上、下旋翼桨毂处弯矩,但也降低了全机的纵向操纵功效,增大配平所需的纵向配平操纵量,甚至超出限幅值。
到目前为止,人们对旋翼控制相位角的研究主要局限于上、下旋翼桨毂弯矩及纵向配平特性,但对旋翼控制相位角影响俯仰姿态导致的直升机废阻功率变化以及旋翼控制相位角对需用功率的影响尚未开展实质性研究。通过旋翼控制相位角对纵向配平特性,上、下旋翼桨毂弯矩和直升机需用功率影响进行分析,并进行旋翼控制相位角合理配置,有助于提高共轴刚性旋翼直升机的设计技术。
针对以上问题,本文利用课题组建立的XH-59A共轴刚性旋翼直升机飞行动力学模型[14],研究旋翼控制相位角对纵向配平特性、需用功率以及上、下旋翼桨毂弯矩的影响。基于上述分析,本文以直升机需用功率最小为目标,以上、下旋翼最大桨毂弯矩限制和配平纵向周期变距限幅为约束条件,提出一种共轴刚性旋翼控制相位角配置方法。
1 飞行动力学模型概述 本文利用课题组建立的飞行动力学模型对旋翼控制相位角问题进行分析,模型所选用的机型为XH-59A共轴刚性旋翼直升机,基本参数见表 1[15],其中:Ω为旋翼转速。
表 1 XH-59A共轴刚性旋翼直升机参数[15] Table 1 Parameters of XH-59A coaxial rigid rotor helicopter[15]
| 参数 | 数值 |
| 旋翼半径/m | 5.5 |
| 桨叶片数 | 3×2 |
| 预扭角/(°) | -10 |
| 旋翼速度/(rad·s-1) | 36.1 |
| 桨叶根梢比 | 2 |
| 一阶挥舞固有频率 | 1.4Ω |
| 上、下旋翼轴间距/m | 0.77 |
| 平尾面积/m2 | 5.57 |
| 垂尾面积/m2 | 2.79 |
| 起飞重量/kg | 5 500 |
| 下旋翼坐标/m | (0, 0, -0.89) |
| 重心坐标/m | (0, 0, 0) |
| 平尾坐标/m | (-6.80, 0, 0.20) |
| 垂尾坐标/m | (-6.80, 0, -0.50) |
表选项
XH-59A共轴刚性旋翼直升机飞行动力学模型包含18个运动自由度。分别为机身的6个刚体运动自由度,上、下旋翼挥舞运动的6个自由度以及上、下旋翼动态入流的6个自由度。模型的状态空间形式如下:
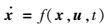 | (1) |
式中:x=[E, F, G]T,E=[u, v, w, p, q, r, Φ, Θ, ψ],u、v、w为机身运动速度,p、q、r为机身运动的角速度,Φ、Θ、ψ为机身运动的欧拉角,F=
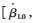
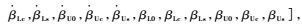
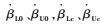
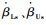
旋翼控制相位角是旋翼设计中的重要参数。旋翼控制相位角确定了旋翼周期变距所产生桨毂力矩的方向。因此,对于单旋翼常规直升机而言,为了降低周期变距操纵耦合,旋翼控制相位角一般与挥舞响应滞后角相等。对于共轴刚性旋翼直升机,如图 1所示(以纵向周期变距为例)。图中A与A′点分别为施加纵向周期变距后的变距最高点和最低点;B和B′点分别为施加纵向周期变距后的桨叶挥舞最高点和最低点;MB为纵向周期变距所产生的桨毂力矩方向;Ψ为旋翼方位角。根据图 1,当旋翼控制相位角Γ与挥舞响应滞后角θcp不同时,周期变距操纵所产生的上、下旋翼耦合桨毂力矩MBX可以相互抵消。
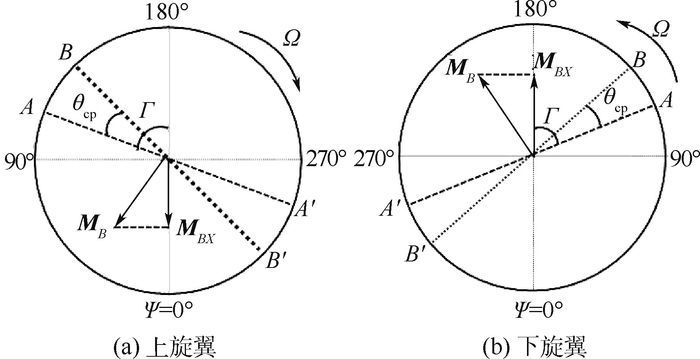 |
| 图 1 共轴刚性旋翼纵向周期变距操纵挥舞 Fig. 1 Control flapping of longitudinal cyclic pitch on coaxial rigid rotor |
| 图选项 |
根据图 1,对于共轴刚性旋翼直升机来说,旋翼控制相位角的改变不会引起过大的操纵耦合。但共轴刚性旋翼直升机的旋翼控制相位角会对包括纵向配平特性、需用功率和桨毂弯矩等产生较大影响。因此本文根据XH-59A直升机飞行动力学模型,通过对0~80 m/s速度范围内的配平研究稳定飞行状态旋翼控制相位角对纵向配平特性、需用功率以及上、下旋翼桨毂弯矩的影响。
2 旋翼控制相位角对纵向配平特性的影响 2.1 对纵向周期变距的影响 根据共轴刚性旋翼直升机的操纵原理,其上、下旋翼的变距可分别表示为
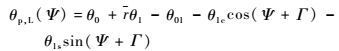 | (2) |
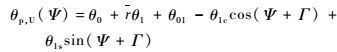 | (3) |
式中:r为无量纲桨叶剖面距桨毂中心的位置;θ1为桨叶扭度。
图 2给出了XH-59A共轴刚性旋翼直升机旋翼控制相位角Γ分别为20°、40°、60°和80°时,配平纵向周期变距θ1c随前飞速度v的变化。
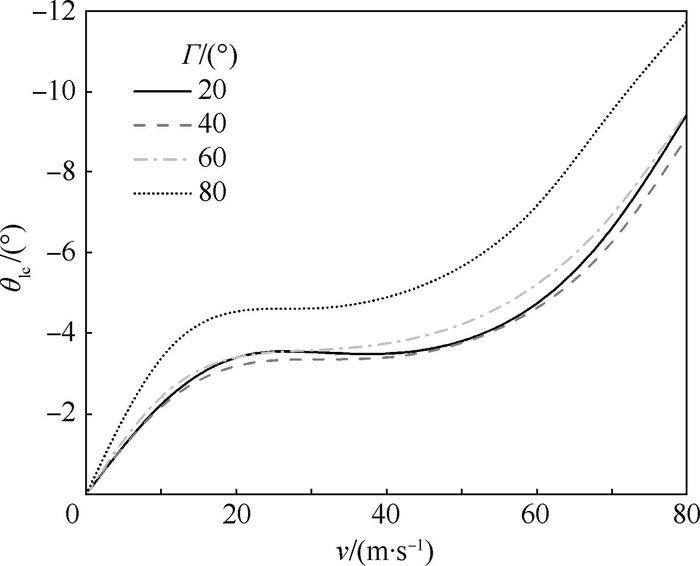 |
| 图 2 稳定平飞时的纵向周期变距 Fig. 2 Longitudinal cyclic pitch in steady level flight |
| 图选项 |
从图 2可以看出,当旋翼控制相位角Γ为20°、40°及60°时,纵向周期变距随飞行速度的变化趋势和量值大小基本一致,其中40°对应的纵向周期变距在整个飞行包线内均为最小,该旋翼控制相位角与XH-59A所采用刚性旋翼的挥舞响应滞后角近似相等。当旋翼控制相位角为80°时,纵向周期变距急剧增加,甚至超出其限幅。这表明,采用旋翼挥舞响应滞后角作为旋翼控制相位角可降低纵向周期变距操纵。
2.2 对俯仰姿态的影响 图 3给出了XH-59A共轴刚性旋翼直升机旋翼控制相位角Γ分别为20°、40°、60°和80°时,俯仰姿态θ随前飞速度v的变化。
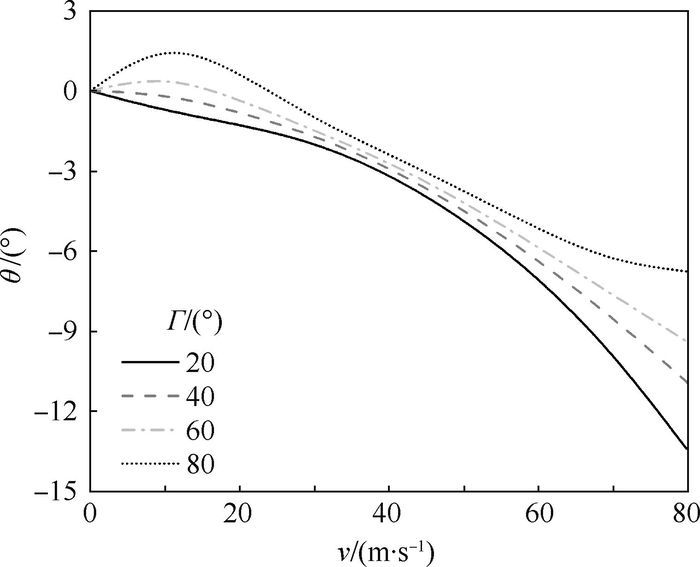 |
| 图 3 稳定平飞时的俯仰姿态 Fig. 3 Pitch attitude in steady level flight |
| 图选项 |
由图 3可以看出,随着旋翼控制相位角的增加,直升机的低头姿态随前飞速度的变化逐渐趋缓。这表明,过小的旋翼控制相位角会显著增加直升机的低头姿态,进而增加直升机废阻功率。有关旋翼控制相位角对需用功率的影响,将在第3节中分析。
3 旋翼控制相位角对需用功率的影响 图 4给出了旋翼控制相位角Γ分别为20°、40°、60°和80°时XH-59A共轴刚性旋翼直升机需用功率Ptotal随前飞速度v的变化。
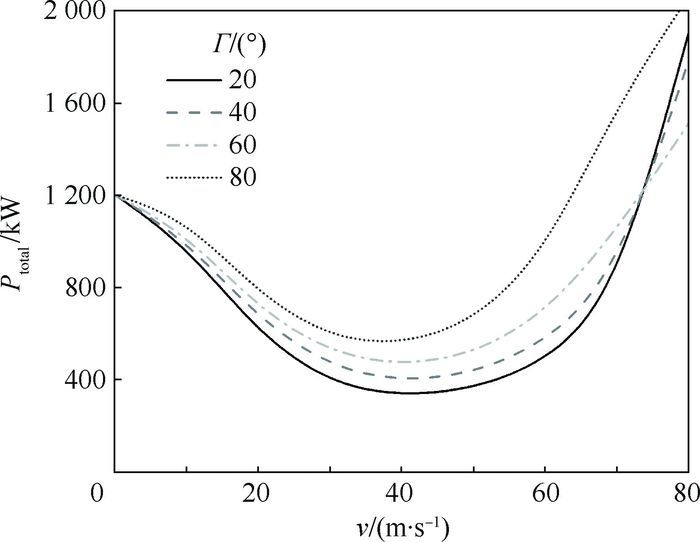 |
| 图 4 稳定平飞时的需用功率 Fig. 4 Power required in steady level flight |
| 图选项 |
由图 4可以看出,在悬停附近,旋翼控制相位角对直升机的需用功率影响不大,但随着前飞速度的增加,旋翼控制相位角越小,直升机需用功率随前飞速度的变化越剧烈,需用功率马鞍形曲线的凹点值越小,随着前飞速度的进一步增加,需用功率显著增加,当前飞速度达到75 m/s时,旋翼控制相位角越小(Γ=20°)所对应的需用功率反超其他旋翼控制相位角所对应的需用功率。由图 4可知,悬停小速度附近的需用功率不随旋翼控制相位角的变化而变化,较低的旋翼控制相位角对降低久航速度的需用功率是有利的,但增加了大速度飞行时的需用功率。
为了分析旋翼控制相位角对直升机需用功率的影响原因,可利用需用功率系数mk估算公式[16],其表达式如下:
 | (4) |
式中:μ为前进比;Cx7为桨叶特征剖面阻力系数;σ为旋翼实度;KP为旋翼型阻功率修正系数;CT为旋翼拉力系数;vdx为等效桨盘处的轴向诱导速度;J0为桨尖损失修正系数;CQ为废阻系数;V0为无量纲前飞速度。
当共轴刚性旋翼直升机前飞时,前行桨叶处动压大于后行桨叶处。此时较低的旋翼控制相位角会增加前行桨叶处的桨距,充分发挥前行桨叶处的升力潜力,提高旋翼的气动效率,降低Cx7[17],减小需用功率。随着前飞速度的提高,废阻功率CQV0占总功率的比重逐渐增大。较低的旋翼控制相位角会降低直升机俯仰姿态角(见图 3),增加机身迎风面积,增大CQ,导致需用功率提高。因此在图 4中,在直升机处于小速度前飞时,选择较低的旋翼控制相位角有利于降低需用功率。在高速前飞时,为降低需用功率,应适当提高旋翼控制相位角。
4 旋翼控制相位角对桨毂弯矩的影响 根据旋翼挥舞运动方程[18],可得共轴刚性旋翼的上、下旋翼在稳定飞行时俯仰和滚转桨毂力矩分别为
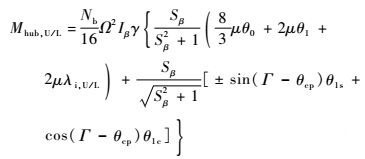 | (5) |
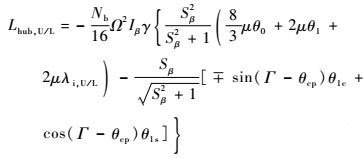 | (6) |
上、下旋翼的桨毂处最大弯矩为
 | (7) |
式中:Iβ为桨叶挥舞惯性矩;γ为桨叶洛克数;λi, U/L为上、下旋翼的无量纲垂向速度;Sβ为旋翼的刚度数;Nb为桨叶片数。对XH-59A共轴刚性旋翼直升机,Sβ≈0.8~1.4(常规单旋翼带尾桨直升机Sβ≈0~0.2)。
图 5给出了旋翼控制相位角Γ为20°、40°、60°和80°时,上、下旋翼的最大桨毂弯矩Wmax随前飞速度v的变化。
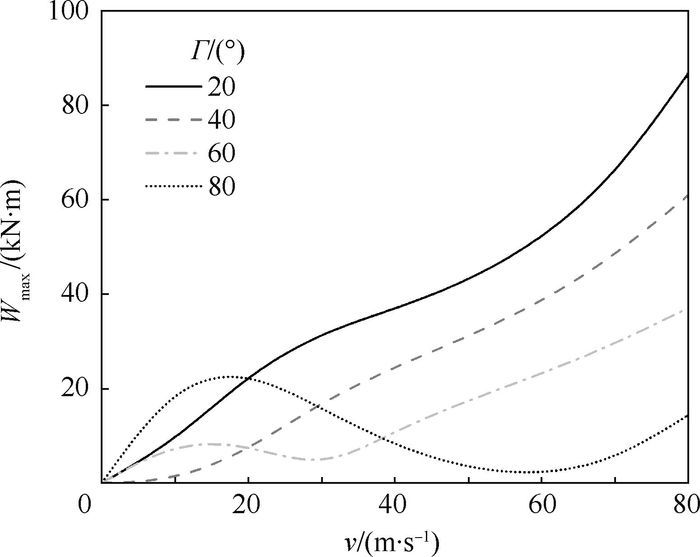 |
| 图 5 稳定平飞时的上、下旋翼最大桨毂弯矩 Fig. 5 Maximum hub bending moment of upper and lower rotor in steady level flight |
| 图选项 |
由图 5可以看出,当旋翼控制相位角为20°和40°时,上、下旋翼最大桨毂弯矩随速度的增加而增加,但此时旋翼控制相位角越小,上、下旋翼最大桨毂弯矩的幅值越大。当旋翼控制相位角为60°和80°时,上、下旋翼最大桨毂弯矩随速度的变化呈现先增大、后减小、再增大的过程。在小速度时,采用与挥舞响应滞后角近似相等的旋翼控制相位角(Γ=40°)时,对应的上、下旋翼最大桨毂弯矩最小。随着前飞速度的增加,在20 m/s以后,采用与挥舞响应滞后角近似相等的旋翼控制相位角的上、下旋翼最大桨毂弯矩明显增大。此时采用较高的旋翼控制相位角(Γ=60°,80°)有利于降低上、下旋翼最大桨毂弯矩。综合上述分析可以发现,随着前飞速度逐渐增加旋翼控制相位角有利于降低上、下旋翼最大翼桨毂弯矩。
5 旋翼控制相位角配置 通过第2~4节的研究发现,为避免纵向周期变距超出其限幅,在大速度前飞时,降低旋翼控制相位角使其接近旋翼挥舞响应滞后角有利于降低配平纵向周期变距,但过小的旋翼控制相位角会增加直升机的低头俯仰姿态,增加大速度飞行时直升机的废阻功率;为减小需用功率和上、下旋翼的桨毂弯矩,旋翼控制相位角应在小速度时相对较小,在大速度情况下随着前飞速度的提高而增加。由此可见,旋翼控制相位角直接影响共轴刚性旋翼直升机的性能、配平及载荷。需通过合理配置旋翼控制相位角随飞行速度的变化关系,使共轴刚性旋翼直升机的性能、配平及载荷随飞行速度在合理的范围内变化。
为了综合考虑旋翼控制相位角对共轴刚性旋翼直升机的性能、配平及载荷的影响,本文提出了一种合理配置旋翼控制相位角的方法,该方法以直升机需用功率最小为目标,以纵向周期变距处于限幅内,上、下旋翼的桨毂弯矩小于结构所能够长时间承受的最大值为约束条件,即
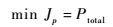 | (8) |
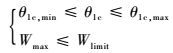 | (9) |
式中:Jp为配置目标函数;θ1c, min和θ1c, max分别为纵向操纵的最低和最高限幅值;Wlimit为结构所能够长时间承受的最大桨毂弯矩值。图 6为XH-59A共轴刚性直升机旋翼控制相位角配置流程图,vmax为直升机的最大平飞速度;med表示三者取中间值。
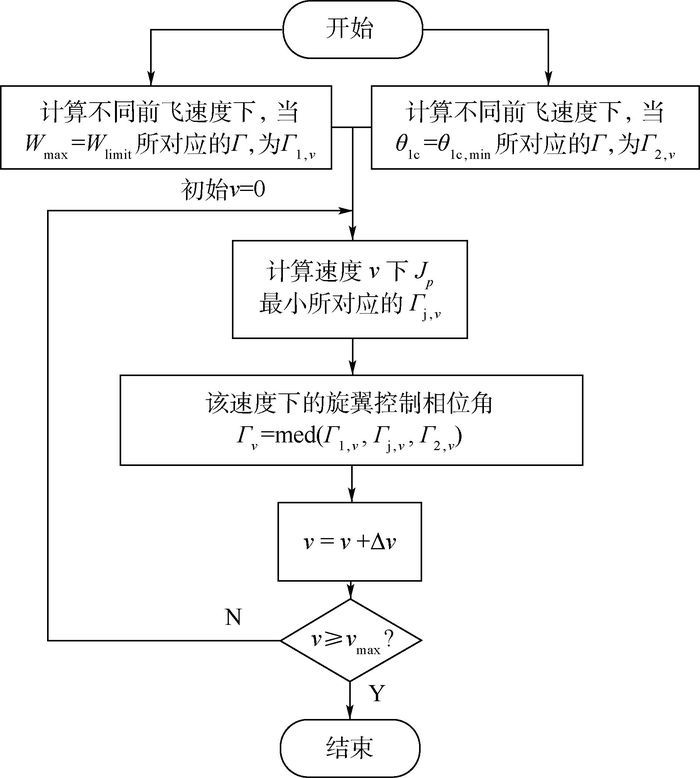 |
| 图 6 旋翼控制相位角配置流程图 Fig. 6 Flowchart of rotor control phase angle allocation |
| 图选项 |
XH-59A共轴刚性直升机旋翼能够长时间承受桨毂弯矩大小为Wlimit=39 170 N·m[19],纵向周期变距的限幅值为θ1c, min/max=±9.6°[11]。根据这些条件可得XH-59A共轴刚性旋翼直升机在0~80 m/s速度范围内旋翼控制相位角Γ随速度的变化关系,以及对应的纵向周期变距θ1c、俯仰姿态角θ、直升机需用功率Ptotal和上、下旋翼桨毂最大弯矩Wmax随前飞速度v的变化趋势,如图 7所示。并加入了XH-59A在飞行试验中的旋翼控制相位角设定作为比对。
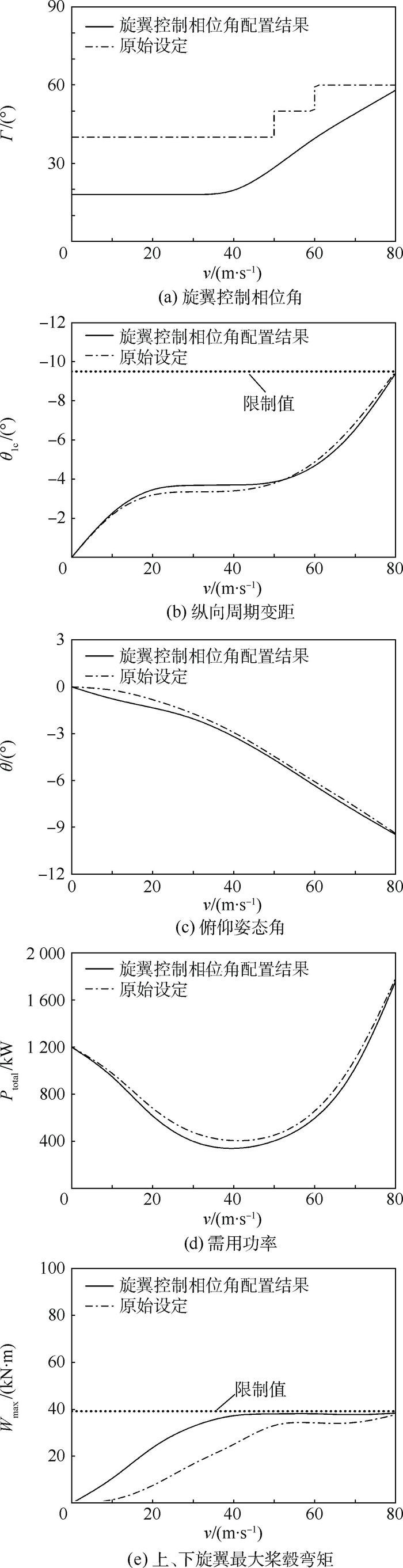 |
| 图 7 旋翼控制相位角配置结果 Fig. 7 Results of rotor control phase angle allocation |
| 图选项 |
由图 7可以看出,通过旋翼控制相位角配置,能够使纵向周期变距和上、下旋翼桨毂弯矩满足对应的限幅要求。在0~80 m/s飞行速度范围内,能够有效降低需用功率,与文献[11]结果相比,需用功率最大可降低8%左右。
6 结论 本文研究了共轴刚性旋翼的旋翼控制相位角对纵向配平特性、需用功率以及上、下旋翼桨毂弯矩配平结果的影响。在此基础上,提出了一种旋翼控制相位角的配置方法。通过上述研究,得到:
1) 旋翼控制相位角直接影响共轴刚性旋翼直升机的性能、配平及载荷。为避免纵向周期变距超出其限幅,取旋翼挥舞响应滞后角作为旋翼控制相位角能获得最佳的纵向周期变距随飞行速度的变化关系。为了改善俯仰姿态角,降低大速度飞行时需用功率,旋翼控制相位角不应在高速时过小。在小速度飞行时,为减小久航速度附近区域的需用功率,旋翼控制相位角不宜过大;为降低上、下旋翼桨毂弯矩,旋翼控制相位角应随着前飞速度而逐渐提高。
2) 提出的合理配置旋翼控制相位角的方法以直升机需用功率最小为目标,以纵向周期变距处于限幅内,上、下旋翼的最大桨毂弯矩小于结构所能长时间承受的最大值为约束条件。该方法能够使纵向周期变距和上、下旋翼的最大桨毂弯矩满足对应的限幅要求。同时,在0~80 m/s的飞行速度范围内,能够有效降低需用功率,与文献[11]结果相比,需用功率最大可降低8%左右。
参考文献
| [1] | YEO H, JOHNSON W. Investigation of maximum blade loading capability of lift-offset rotors[J].Journal of the American Helicopter Society, 2014, 59(1): 1–12. |
| [2] | JOHNSON W, MOODIE A M, YEO H.Design and performance of lift-offset rotorcraft for short-haul missions:ARC-E-DAA-TN4611[R].Moffett Field:NASA AMES Research Center, 2012. |
| [3] | JOHNSON W.NDARC-NASA design and analysis of rotorcraft-Theoretical basis and architecture:NASA/TP-2009-215402[R].Washington, D.C.:NASA, 2010. |
| [4] | WALSH D, WEINER S, ARIFIAN K, et al.High airspeed testing of the Sikorsky X2 technology demonstrator[C]//Proceedings of the 67th American Helicopter Society Annual Forum.Washington, D.C.:American Helicopter Society, 2011:2057-2066. |
| [5] | 高正, 陈仁良. 直升机飞行动力学[M].北京: 科学出版社, 2003: 31-32. GAO Z, CHEN R L. Helicopter flight dynamics[M].Beijing: Science Press, 2003: 31-32.(in Chinese) |
| [6] | LEISHMAN G J. Principles of helicopter aerodynamics with CD extra[M].Cambridge: Cambridge University Press, 2006: 142-144. |
| [7] | BURGESS R K.The ABC rotor:A historical perspective[C]//Proceedings of the 60th Annual Forum of American Helicopter Society.Washington, D.C.:American Helicopter Society, 2004:7-10. |
| [8] | FERGUSON K M.Towards a better understanding of the flight mechanics of compound helicopter configurations[D].Glasgow:University of Glasgow, 2015. |
| [9] | HALLEY D H.ABC helicopter stability, control, and vibration evaluation on the Princeton dynamic model track[C]//Proceedings of the 29th Annual National Forum of American Helicopter Society.Washington, D.C.:American Helicopter Society, 1973:740-752. |
| [10] | RUDDELL A J. Advancing blade concept (ABCTM) development[J].Journal of the American Helicopter Society, 1977, 22(1): 13–23. |
| [11] | RUDDELL A J, MACRINO J A.Advancing blade concept(ABC)high speed development[C]//Proceedings of the 36th Annual Forum of American Helicopter Society.Washington, D.C.:American Helicopter Society, 1980:274-283. |
| [12] | COLEMAN C P.A survey of theoretical and experimental coaxial rotor aerodynamic research:NASA TP-3675[R].Washington, D.C.:NASA, 1997. |
| [13] | CHI Z, TODD R Q, HOSSEIN S, et al.Aeromechanics of the coaxial compound helicopter[C]//Proceedings of the 56th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference.Reston:AIAA, 2015:1-19. |
| [14] | 袁野, 陈仁良, 李攀. 共轴刚性旋翼飞行器配平特性及验证[J].南京航空航天大学学报, 2016, 48(2): 186–193. YUAN Y, CHEN R L, LI P. Trim characteristics and verification of coaxial rigid rotor aircraft[J].Journal of Nanjing University of Aeronautics & Astronautics, 2016, 48(2): 186–193.(in Chinese) |
| [15] | PHELPS A E, MINECK R E.Aerodynamic characteristics of a counter-rotating, coaxial, hingeless rotor helicopter model with auxiliary propulsion:NASA-TM-78705[R].Washington, D.C.:NASA, 1978. |
| [16] | 王适存. 直升机空气动力学[M].北京: 国防工业出版社, 1985: 123-124. WANG S C. Helicopter aerodynamics[M].Beijing: National Defense Industry Press, 1985: 123-124.(in Chinese) |
| [17] | BAGAI A.Aerodynamic design of the X2 technology demonstratorTM main rotor blade[C]//Proceedings of the 64th Annual Forum of American Helicopter Society.Washington, D.C.:American Helicopter Society, 2008:1565-1580. |
| [18] | PADFIELD G D. Helicopter flight dynamics:The theory and application of flying qualities and simulation modelling[M].London: Blackwell Science Ltd, 1996: 93-108. |
| [19] | ABBE J T L, BLACKWELL R H, JENNEY D S.Advancing blade concept (ABC)TM dynamics[C]//33rd American Helicopter Society Annual Forum.Washington, D.C.:American Helicopter Society, 1977:692-701. |
