目前,美军标AR-40A是舰载机自动着舰系统设计时所参考的重要准则[2-4],该准则采用经典控制理论中的以频域分析为主、时域仿真分析为辅的方法[5],按照自动着舰系统的总体结构,自内而外进行反馈参数选择和不同层级控制系统结构的设计。但该准则给出的频域特性边界要求主要针对F-4、F/A-18等Ⅳ类飞机,并没有说明该准则的边界要求是否适用于Ⅰ类飞机自动着舰系统的设计。而国内的自动着舰系统研究起步较晚,目前并没有形成成熟的针对Ⅰ类飞机的自动着舰系统设计准则。
自动着舰品质等级一般以登舰率、自动着舰品质等级、着舰误差规范三者作为评价指标[4],但由于登舰率涉及甲板堵塞、飞机故障等客观影响因素,自动着舰品质等级需要飞行员进行主观评价,二者无法通过仿真实现评价。因此,结合AR-40A准则,以着舰误差规范作为评价自动着舰系统设计的评价指标,进行小型飞机自动着舰系统设计评价,选取着舰效果良好的自动着舰系统频域特性曲线,与AR-40A准则给出的设计边界进行对比,可以验证AR-40A准则对于小型飞机自动着舰系统设计是否适用。
本文对比分析了小型(Ⅰ类)、中型(Ⅱ、Ⅳ类)飞机自动着舰系统设计结果的频域特性曲线,在此基础上,提出了AR-40A准则应用于小型飞机时应作出的相应修改建议。
1 自动着舰系统设计 1.1 研究对象运动特性分析 为对比验证AR-40A准则对于中型、小型飞机的适用性,选取某型飞机及其尺寸缩比率为4的缩比机作为研究对象,这样可以尽可能地减小气动外形对结果分析的影响,有利于分析准则对于尺寸、质量较小飞机的适用性[6]。飞机经过增稳后的等效系统模态特性如表 1所示。表 1中:ωn1为短周期模态自然频率;Tθ2为短周期模态分子时间常数;ζn1为短周期模态阻尼;ζn2为长周期模态阻尼;ωd、ζd分别为荷兰滚模态频率、阻尼;TR为滚转模态时间常数;TS为螺旋模态时间常数。
表 1 等效系统模态特性 Table 1 Modal characteristics of equivalent system
| 运动模态 | 参数 | 原型 | 缩比 |
| 短周期 | ωn1·Tθ2/rad ζn1 | 2.34 0.87 | 7.35 0.71 |
| 长周期 | ζn2 | 0.09 | 0.19 |
| 荷兰滚 | ωd/(rad·s-1) ζd | 1.04 0.51 | 1.52 0.49 |
| 滚转收敛 | TR/s | 0.34 | 0.17 |
| 螺旋 | TS/s | 30.5 | 22.8 |
表选项
原型机属于Ⅱ类飞机,缩比机为Ⅰ类飞机。经过增稳控制设计后,二者纵向、横航向响应特性均满足一级品质要求。由于本体特性的影响,增稳后飞机的模态特性仍能够在一定程度上反映缩比机相对原型机的运动特性变化。由表 1可知,缩比机俯仰姿态响应更快;荷兰滚模态频率更高;滚转收敛模态收敛速度更快;螺旋模态发散更快。由以上结果推广,一般的Ⅰ类飞机相比Ⅱ类飞机,其本体频率更高,对指令的响应更为迅速,运动状态改变更快。
1.2 自动着舰系统基本结构 本文采用的自动着舰系统如图 1所示,该系统主要由机载控制律和舰载导引律2部分组成。机载控制律由自动驾驶仪和进近动力补偿系统组成,自动驾驶仪接收航迹引导指令控制飞机着舰,进近动力补偿系统保证飞机进行着舰过程中的空速、迎角稳定[7]。舰载导引律由甲板运动补偿器和着舰引导控制律组成,甲板运动补偿保证飞机与航母甲板运动同步;着舰引导控制律解算出飞机的理想航迹,并将位置偏差量转换为飞机的航迹控制指令。
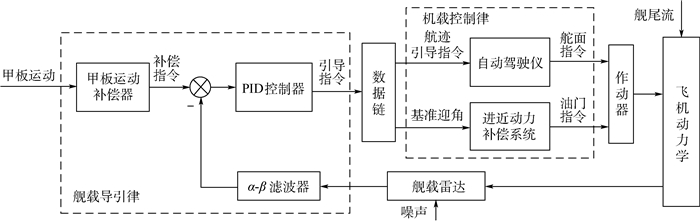 |
| 图 1 自动着舰系统引导控制结构图 Fig. 1 Structure chart of guidance and control of automatic carrier landing system |
| 图选项 |
自动着舰系统采用高度变化率
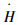
1.3 自动着舰系统设计准则 美军标AR-40A中给出的自动着舰系统设计要求主要应用于图 1中自动驾驶仪及舰载导引律中的PID控制器调参过程。一般来说,使自动着舰系统的频域特性满足准则的边界要求,即可获得较为满意的着舰效果[11],这些要求包括:①低频段幅值边界。低频段幅值边界反映了对系统稳态精度的要求。②幅值带宽频率。幅值带宽频率主要反映了系统对于指令响应的快速性要求。③中高频段幅值上边界。中高频段幅值上边界主要对系统谐振峰值大小进行限制,从而使其具有足够的阻尼特性,对指令的响应更加平稳,减小超调量。④相角带宽频率。相角带宽频率除了反映系统的快速性要求外,在该频率处的相位滞后要求也可以体现对系统的稳定性要求[12]。
表 2对频域特性指标的选取及验证目标进行了整理和说明。
表 2 频域特性设计指标选取 Table 2 Selection of design index for frequency-domain characteristics
| 频域特性 | 验证目标 |
| 高度变化率对高度变化率指令 | 纵向飞控系统响应特性 |
| 高度对高度指令 | 纵向着舰引导控制律 |
| 滚转角对滚转角指令 | 侧向飞控系统响应特性 |
| 侧向位移对侧向位移指令 | 侧向着舰引导控制律 |
表选项
全自动着舰需要系统在尽可能大的带宽内对指令的响应尽可能快速、精确,即幅值增益尽可能为0,相角滞后尽可能小,幅值带宽、相角带宽尽可能大,才能够保证飞机精确着舰并消除着舰过程中的外部扰动影响。实际系统往往只能在一定带宽内满足这种要求,但同样能够取得较好的着舰效果。因此,自动着舰需求与闭环飞机系统特性共同确定了AR-40A准则的边界要求。显然,对于不同类型的飞机,其闭环系统特性也存在较大差别,因此,该准则的边界应当做出适度调整。
通过自动着舰仿真,验证AR-40A准则的边界对小型飞机是否仍然有效,若无效或部分有效,则需要通过对比原型机、缩比机、F/A-18三者的频域特性变化规律,对原准则做出调整,以使该准则仍然能够指导不同种类飞机自动着舰系统的设计。
2 全自动着舰数学仿真 分别完成原型机、缩比机的自动着舰系统设计后,为了验证设计成功与否,进行了包含舰载机、航母、大气扰动在内的飞机-航母-大气环境自动着舰数学仿真验证[10-13]。主要以着舰点平均误差(着舰误差的算术平均值)与散布误差(着舰误差的方差)作为指标进行自动着舰系统的性能评价[10-14]。通过改变航母摇晃运动的初始相位,生成大气紊流数据的白噪声发生器的随机数种子,进行多组数学仿真验证,得到仿真数据并计算着舰误差的统计结果。仿真中的大气紊流强度在垂直方向、纵向、侧向分量的均方根(RMS)分别为0.6、1.0、0.7 m/s。航母垂荡运动振幅为±1.2 m/s;横滚运动振幅为±5.0°;纵摇运动振幅为±1.25°;艏摇运动振幅为±0.7°。设置条件的改变规则如表 3所示。
表 3 初始设置条件的改变规则 Table 3 Changing rules of initial settings
| 分组序号 | 随机数种子 | 垂荡位移初始相位集合/rad | 横滚角初始相位集合/rad | 纵摇角初始相位集合/rad | 艏摇角初始相位集合/rad |
| Set 1 | 23 341 |  | 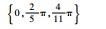 | 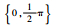 | 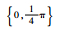 |
| Set 2 | 985 | 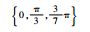 | 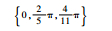 |  | 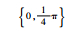 |
| Set 3 | 985 | 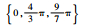 | 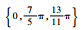 | 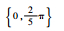 | 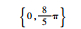 |
表选项
由表 3可知,样本数量共计108组,记录每次着舰的纵向误差xerr、侧向误差yerr后,得到的着舰误差分布如图 2所示,平均误差和散布误差的统计结果以及对应评价指标[15]如表 4和表 5所示。
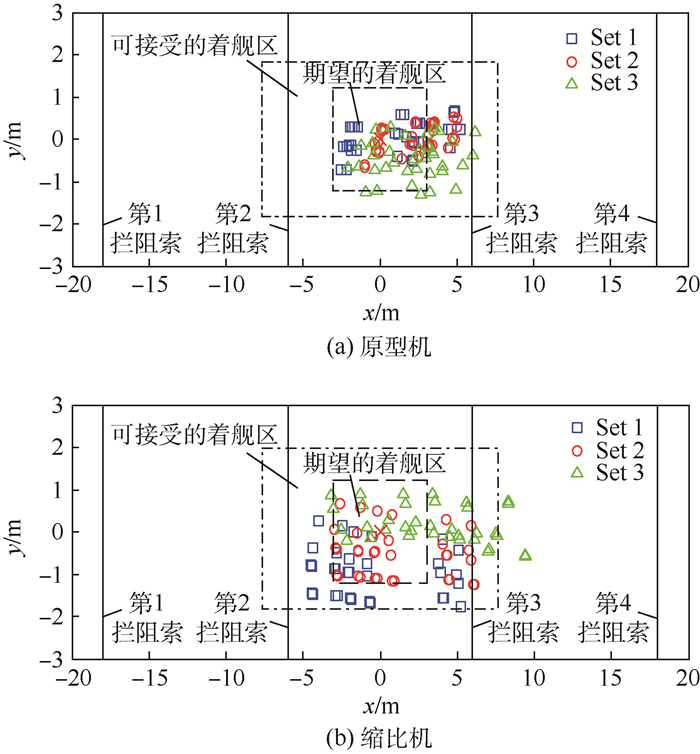 |
| 图 2 原型机和缩比机自动着舰点分布 Fig. 2 Touching point distribution of automatic carrier landing for prototype and shrinkage aircrafts |
| 图选项 |
表 4 原型机着舰误差的统计结果 Table 4 Statistical results of carrier landing errors for prototype aircraft
| 分组序号 | 纵向平均误差/m | 纵向散布误差/m | |xerr|<3.05 m | 侧向平均误差/m | 侧向散布误差/m | |yerr|<1.22 m |
| Set 1 | 1.144 0 | 2.424 8 | 30/36 | 0.040 3 | 0.225 5 | 36/36 |
| Set 2 | 2.153 3 | 1.872 4 | 20/36 | 0.006 3 | 0.311 0 | 36/36 |
| Set 3 | 2.117 3 | 2.161 7 | 20/36 | 0.430 5 | 0.499 8 | 35/36 |
| 均值 | 1.804 9 | 2.153 0 | 70/108 | 0.159 0 | 0.345 4 | 107/108 |
| 评价指标[15] | ±3.05 | <7.32 | ±1.22 | <1.52 |
表选项
表 5 缩比机着舰误差的统计结果 Table 5 Statistical results of carrier landing errors for shrinkage aircraft
| 分组序号 | 纵向平均误差/m | 纵向散布误差/m | |xerr|<3.05 m | 侧向平均误差/m | 侧向散布误差/m | |yerr|<1.22 m |
| Set 1 | -0.120 7 | 3.495 8 | 18/36 | -0.975 1 | 0.553 8 | 24/36 |
| Set 2 | 1.082 2 | 3.095 7 | 24/36 | -0.502 4 | 0.551 3 | 34/36 |
| Set 3 | 3.291 3 | 3.630 8 | 15/36 | 0.190 0 | 0.433 4 | 36/36 |
| 均值 | 1.417 6 | 3.695 8 | 57/108 | -0.429 2 | 0.703 6 | 94/108 |
| 评价指标[15] | ±3.05 | <7.32 | ±1.22 | <1.52 |
表选项
由图 2(a)、(b)可知,可接受的着舰区域位于第2、3根拦阻索之间,当飞机在该区域着舰能够保证尾钩钩到拦阻索并安全着舰。图 2(a)、表 4与图 2(b)、表 5中结果表明,原型机、缩比机的着舰效果良好;由于采用了相同的大气与甲板运动干扰条件,缩比机受到的影响更为明显,其着舰散布误差更大,但其平均误差与散布误差的均值仍满足要求,这说明原型机和缩比机的自动着舰系统设计均较为成功。
3 准则适用性分析 3.1 缩比机的运动特性 与描述飞机运动的一般微分方程相同,缩比机的方程也采取这种形式[6]。但缩比机方程中包含的飞机外形尺寸、运动特征参数需按照一定比例K缩放。
描述高阶增稳飞机运动,通常采用典型二阶振荡环节与一阶惯性环节。若考虑缩比机与原型机的相似性,根据相似准则,缩比机二阶振荡环节频率为原型机的K0.5倍,阻尼不变;一阶惯性环节动态特性时间常数为原型机的K-0.5倍[16]。闭环缩比机的系统自然频率为闭环原型机的K0.5倍,阻尼不变;动态特性时间常数为闭环原型机的K-0.5倍[16]。若不考虑缩比机与原型机的相似性,在进行控制系统设计时,仅将缩比机视为一架小型飞机,闭环缩比机与闭环原型机运动特性的关系仍然在很大程度上能够反映这种变化趋势。如表 1所示,缩比机短周期模态频率与姿态响应时间常数的乘积ωn1·Tθ2由2.34 rad增加至7.35 rad,阻尼由0.87小幅度减少至0.71;荷兰滚模态频率由1.04 rad/s增加至1.52 rad/s,阻尼由0.51减小至0.49;滚转收敛模态时间常数由0.34 s减小至0.17 s;螺旋模态时间常数由30.5 s减小至22.8 s。相比闭环原型机,闭环缩比机频率增大,阻尼近似不变,动态特性时间常数减小。
3.2 高度变化率准则 以第2节中自动着舰系统设计的数学仿真结果作为算例进行对比,原型机、缩比机的高度变化率对高度变化率指令的频域特性曲线如图 3所示。
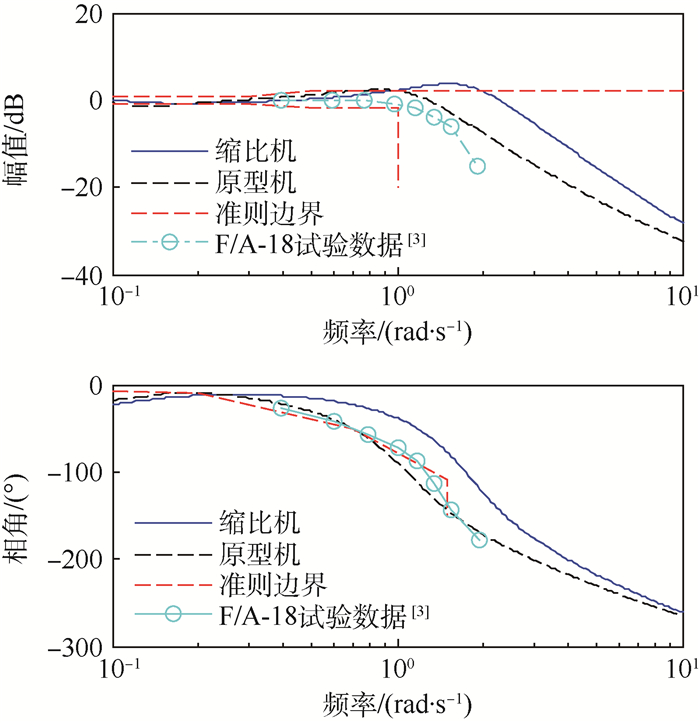 |
| 图 3 高度变化率对高度变化率指令的频域特性曲线 Fig. 3 Frequency-domain characteristic curves of altitude change rate to altitude change rate instruction |
| 图选项 |
图 3中红色虚线为高度变化率准则边界要求。高度变化率准则为:①对于幅值边界,在低频段(≤0.3 rad/s)为±1 dB,频率达到0.5 rad/s时,幅值边界逐步放宽至±2 dB,频率进一步增大后,幅值上边界不变,仍为+2 dB,但下边界在频率大于1 rad/s后不再加以限制。②对于相角边界,随着频率增大,相角滞后要求逐渐放宽,相角边界由4条斜率依次增大的直线段组成,关键转折点为:(0.2 rad/s,-10°)、(0.7 rad/s,-50°)、(1.5 rad/s,-110°)。图 3中数据点连线为F/A-18的海试验证结果[3],用于调参过程中的参考对比。
由图 3可知,原型机的高度变化率对高度变化率指令的频域特性曲线基本位于AR-40A准则所规定的边界内,且与F/A-18飞机响应结果近似,只在1~2 rad/s之间存在更大的相角滞后。这说明高度变化率准则对于原型机这类中型飞机是适用的。
缩比机开始产生幅值衰减、相角滞后的频率增大,幅值曲线在1~2 rad/s间会小幅超出边界要求,但相角滞后曲线的斜率近似不变。需要指出的是,缩比机的高度变化率对高度变化率指令频域特性曲线虽然基本仍位于高度变化率准则给出的边界内,但若参考F/A-18结果进行缩比机自动着舰系统设计,得到的结果无法完成全自动着舰,这说明现有的高度变化率准则边界对于缩比机已部分失效。相比原型机,缩比机为Ⅰ类飞机,其闭环系统频率更高,惯性更小,对中高频指令的响应更快,对外界中高频扰动的响应更为明显;其控制系统须具有更高的幅值带宽和相角带宽以保证自动着舰系统能够快速精确地控制飞机并抑制外界扰动的影响。对于缩比机,高度变化率准则中的幅值边界和相角边界频率过小,按高度变化率准则边界中的规定,对大于1 rad/s的中高频段控制能力不足,幅值衰减,相角滞后过大,无法实现对缩比机这类频率高、惯性小的飞机进行良好控制。经过多次数学仿真实验验证,缩比机产生幅值衰减的频率不能小于1.5 rad/s,但对幅值上边界的要求可适当放宽;开始产生相角滞后的频率不能小于0.2 rad/s,否则无法完成满足误差精度的自动着舰。根据以上分析结果,对高度变化率准则做出的修改如图 4所示,幅值边界均向右平移至2 rad/s处。由于缩比机惯性较小,响应更快,即使幅值特性曲线增加较大,超出现有边界,仍可通过指令调整使高度变化率达到期望值。因此,将上边界放宽至4dB,相角边界平移至3 rad/s处,其余边界不变。
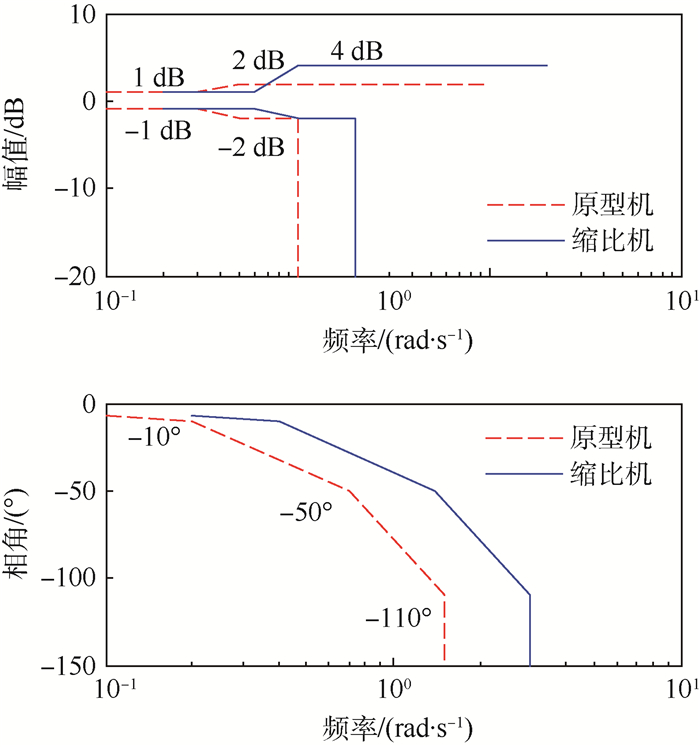 |
| 图 4 高度变化率对高度变化率指令的频域边界要求 Fig. 4 Frequency-domain boundary requirement of altitude change rate to altitude change rate instruction |
| 图选项 |
3.3 高度准则 原型机、缩比机的高度对高度指令的频域特性曲线如图 5所示。
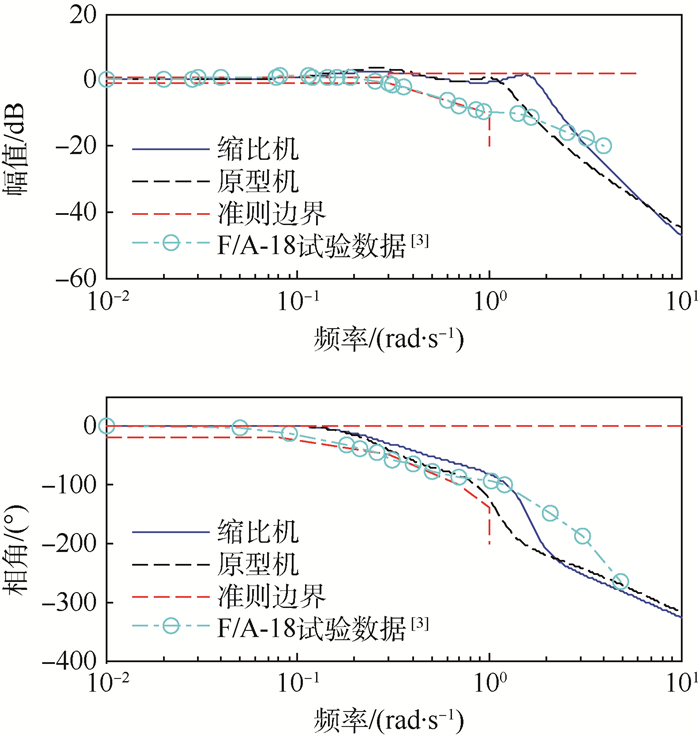 |
| 图 5 高度对高度指令的频域特性曲线s Fig. 5 Frequency-domain characteristic curves of altitude to altitude instruction |
| 图选项 |
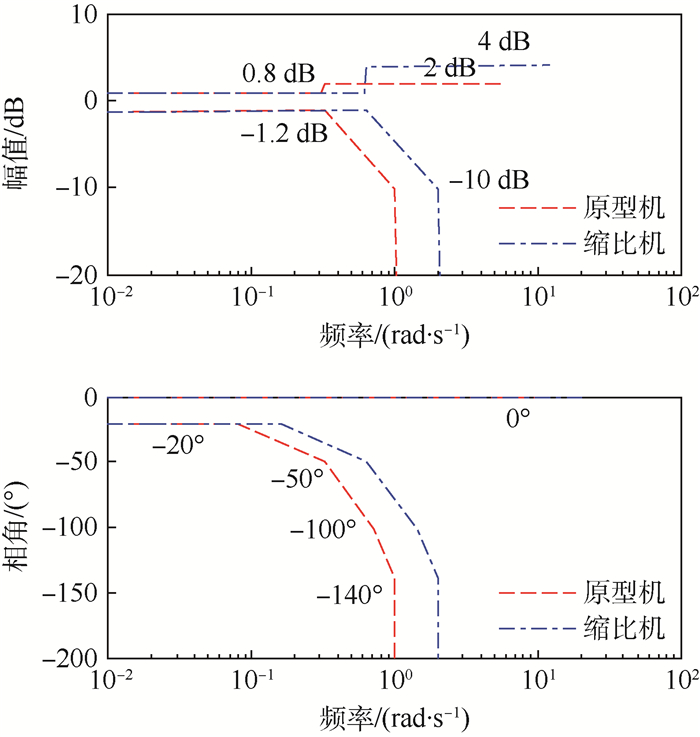
图 5中红色虚线为高度准则边界要求。高度准则边界为:①对于幅值边界,其低频段范围为0.01~0.3 rad/s,幅值上下边界分别为0.8和-1.2dB;在中高频段内,幅值上边界保持不变,一直为2 dB;但下边界与幅值带宽频率有关,在带宽频率处(1 rad/s)对应的幅值要求为小于-10 dB,因此在达到带宽频率前存在边界约束,超出后则无限制。②对于相角边界,随着频率增大,相角滞后要求逐渐放宽,相角边界由5条斜率依次增大的直线段组成,关键转折点为:(0.1 rad/s,-20°)、(0.3 rad/s,-50°)、(0.7 rad/s,-100°)、(1.0 rad/s,-140°)。此外,在关注的频段内相角上边界始终为0°,表明不期望控制系统存在相角超前。图 5中数据点连线为F/A-18的海试验证结果[3],用于调参过程中的参考对比。
原型机的高度指令频域特性曲线完全在边界内,其产生幅值衰减和相角滞后的频率与边界要求几乎一致。这说明高度准则对于原型机也完全适用。缩比机的高度指令频域特性曲线幅频增益较大,出现了峰值,超出AR-40A规定的边界;开始产生幅值衰减的频率由1.1 rad/s增加到了1.8rad/s,并且在0.2~2 rad/s间的相角滞后更小。这说明缩比机对高度指令的响应更快,更容易出现超调。由于高度准则是在高度变化率准则基础上形成的准则,两者的边界要求存在相关性。同样地,对于缩比机,高度准则中的幅值边界和相角边界频率过小,对大于1 rad/s的中高频段控制能力不足,幅值衰减,相角滞后过大,无法对缩比机这类频率高、惯性小的飞机进行较好控制。数学仿真实验结果表明,缩比机产生幅值衰减的频率不能小于1.5 rad/s,开始产生相角滞后的频率不能小于0.15 rad/s,否则无法完成满足误差精度的自动着舰。根据以上分析,对高度准则做出修改,如图 6所示,幅值边界向右移动至2 rad/s,中高频段的上边界变为放宽至4 dB以满足中高频段缩比机惯性较小,频率较高,对高度指令超调增大的特性;相角下边界向右平移1 rad/s,各边界分段斜率不变。
 |
| 图 6 高度对高度指令的频域边界要求 Fig. 6 Frequency-domain boundary requirement of altitude to altitude instruction |
| 图选项 |
3.4 滚转角准则 原型机、缩比机的滚转角对滚转角指令的频域特性曲线如图 7所示。
 |
| 图 7 滚转角对滚转角指令的频域特性曲线 Fig. 7 Frequency-domain characteristic curves of roll angle to roll angle instruction |
| 图选项 |
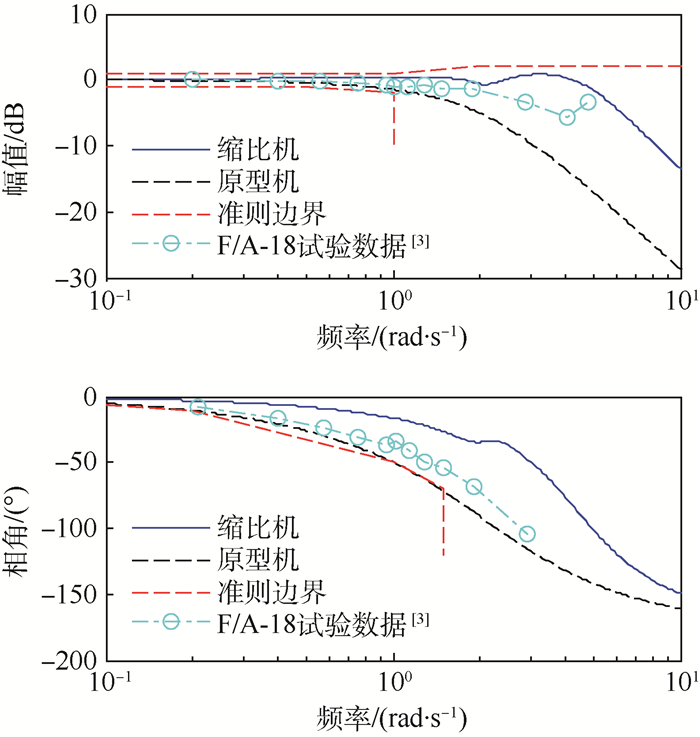
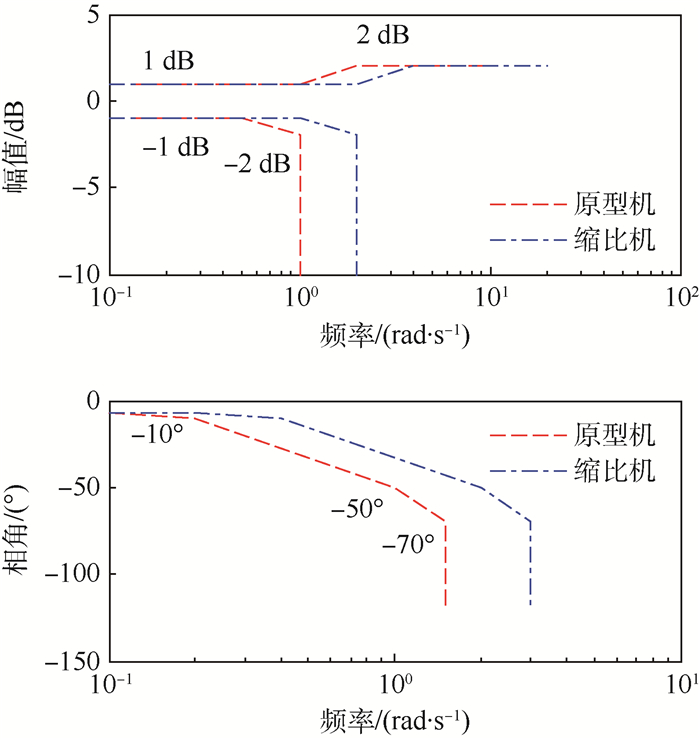
图 7中红色虚线为滚转角准则边界要求。滚转角边界准则为:①对于幅值边界,上边界在低频段(≤1 rad/s)为1 dB,频率达到2 rad/s时,幅值边界逐步放宽至2 dB,频率进一步增大后,幅值上边界要求不变;下边界在频率小于0.5 rad/s时为-1 dB,之后逐步放宽并在1 rad/s时达到-2 dB,频率大于1 rad/s后不再作要求。②对于相角边界,随频率增大,相角滞后要求逐渐放宽,相角边界由4条斜率依次增大的直线段组成,关键转折点为:(0.2 rad/s,-10°)、(1.0 rad/s,-50°)、(1.5 rad/s,-70°)。图 7中数据点连线为F/A-18的海试验证结果[3],用于调参过程中的参考对比。
原型机的滚转角频域特性曲线完全在边界内,产生幅值衰减和相角滞后的频率与F/A-18飞机近似,说明滚转角准则边界完全适用于原型机。缩比机开始产生幅值衰减的频率增加到了约3rad/s,开始产生相角滞后的频率增加到了约0.3 rad/s,且缩比机的幅值衰减和相角滞后明显小于原型机。由于缩比机的滚转轴惯性矩大幅度减小,对滚转角指令的响应更快,对外界扰动的响应也更加明显,滚转角控制系统也必须具有更高的幅值带宽和相角带宽来保证对缩比机滚转角的快速精确控制和对外界扰动影响的抑制。现有滚转角准则对于幅值带宽、相角带宽的要求过低,不能满足缩比机着舰过程中的控制要求。数学仿真实验结果表明,缩比机允许产生幅值衰减的频率不能小于2 rad/s,允许产生相角滞后的频率不能低于0.3 rad/s,否则不能完成着舰或着舰精度不满足要求。对滚转角准则做出修改,如图 8所示,幅值边界向右移动至2 rad/s,上下边界大小不变;相角边界向右平移至3 rad/s,下边界各分段斜率不变。
 |
| 图 8 滚转角对滚转角指令的频域边界要求 Fig. 8 Frequency-domain boundary requirement of roll angle to roll angle instruction |
| 图选项 |
3.5 侧向位移准则 原型机、缩比机的侧向位移对侧向位移指令的频域特性曲线如图 9所示。
 |
| 图 9 侧向位移对侧向位移指令的频域特性曲线 Fig. 9 Frequency-domain characteristic curves of lateral displacement to lateral displacement instruction |
| 图选项 |
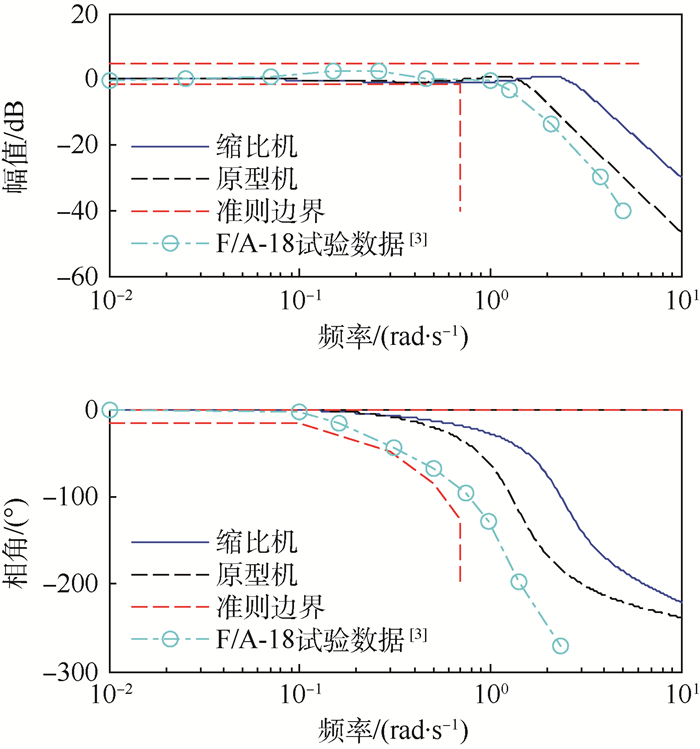
图 9中红色虚线为侧向位移准则边界要求。侧向位移边界准则为:①对于幅值边界,上边界始终为5 dB,下边界在到达带宽频率(0.7 rad/s)前为-2 dB,超出后则无限制约束。幅频响应特性在低频段应满足上下边界的要求,以保证系统满足稳态精度的要求。在中频段,幅频响应特性需要满足上边界的限制,以保证系统具有较好的阻尼特性。同时,幅频响应特性需要满足中频段下边界对于截止频率的要求。②对于相角边界,随频率增大,相角滞后要求逐渐放宽,其边界由5条斜率依次增大的直线段组成,关键转折点为:(0.1 rad/s,-15°)、(0.3 rad/s,-50°)、(0.5 rad/s,-90°)、(0.7 rad/s,-130°)。此外,在关注的频段内相角上边界始终为0°,表明不期望控制系统存在相位超前。图 9中数据点连线为F/A-18的海试验证结果[3],用于调参过程中的参考对比。
原型机的侧向位移频域特性曲线在0.8~1rad/s间略有超出,相角曲线则在0.2~1 rad/s间略有超出,侧向位移准则边界基本适用于原型机。缩比机产生幅值衰减的频率从0.4 rad/s增加到了约1 rad/s,产生相角滞后的频率从0.7rad/s增加到了约2 rad/s。侧向位移的响应特性主要与飞机的荷兰滚模态特性以及滚转收敛模态特性相关,即侧向位移准则与滚转角准则也存在相关性。由于缩比机滚转响应速度更快,荷兰滚频率更高,对于大于1 rad/s的中高频指令的响应更快速,对外界扰动的反应更明显。因此,侧向位移准则中对于中高频段边界要求也应做出修改,使之适用于缩比机频率高、惯性小的特点。数学仿真实验结果表明,缩比机允许幅值产生衰减的频率不能小于1.5 rad/s,允许产生相角滞后的频率不能小于0.2 rad/s。根据分析结果,对侧向位移准则做出修改,如图 10所示,幅值边界向右平移至约1.5rad/s,上下边界不变;相角下边界向右平移至约1.5 rad/s,各边界分段斜率不变,上边界不变。
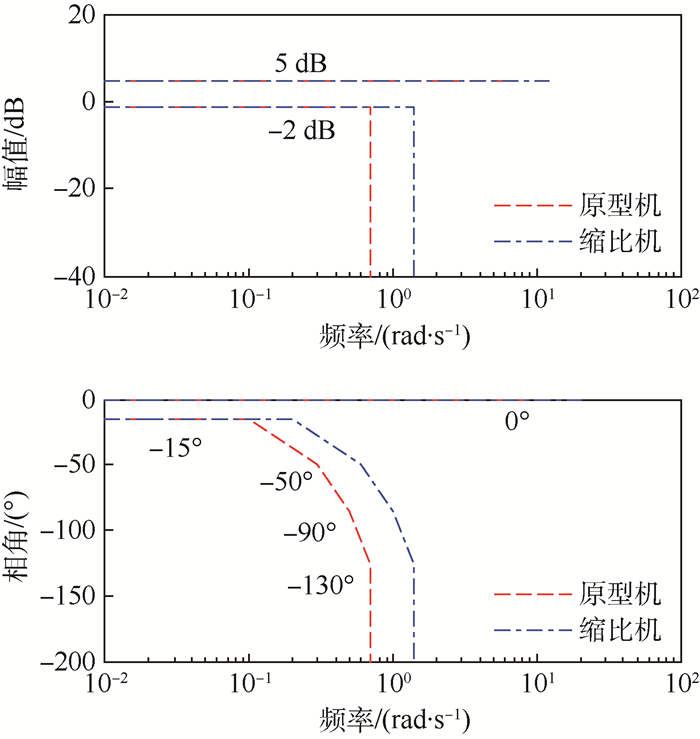 |
| 图 10 侧向位移对侧向位移指令的频域边界要求 Fig. 10 Frequency-domain boundary requirement of lateral displacement to lateral displacement instruction |
| 图选项 |
4 结论 本文研究了目前自动着舰系统设计中主要遵循的准则AR-40A对于小型飞机(Ⅰ类飞机)的适用性。研究结果表明,AR-40A准则中规定的幅值边界和相角边界并不完全适用于小型飞机的自动着舰系统设计,小型飞机的低频段、中高频段划分与准则中的划分存在差异。根据本文研究结果推广至一般小型飞机,建议对准则做如下修改:
1) 高度变化率准则。小型飞机的幅值带宽频率边界提高至约2 rad/s;幅值上边界在中高频段可放宽至约4 dB;允许产生相角滞后的频率边界应提高至0.2 rad/s,相角带宽频率提高至约3 rad/s。
2) 高度准则。小型飞机的低频段应大于0.5 rad/s,其幅值带宽频率应提高至2 rad/s;幅值上边界可放宽至4 dB;允许产生相位滞后的频率边界应提高至约0.2 rad/s,相角带宽频率边界应提高至约2 rad/s。
3) 滚转角准则。幅值带宽频率边界提高至2 rad/s;允许相角产生滞后的频率边界提高至0.3 rad/s;相角带宽频率边界提高至3 rad/s。
4) 侧向位移准则。幅值带宽频率边界提高至1.5 rad/s;允许相角产生滞后的频率边界提高至0.2 rad/s;相角带宽频率边界提高至1.5 rad/s。
参考文献
| [1] | 杨一栋. 无人机着舰制导与控制[M].北京: 国防工业出版社, 2013: 7-18. YANG Y D. Guidance and control of UAV carrier landing[M].Beijing: National Defense Industry Press, 2013: 7-18.(in Chinese) |
| [2] | URNES J M, HESS R K. Development of the F/A-18A automatic carrier landing system[J].Journal of Guidance, Control, and Dynamics, 1985, 8(3): 289–295.DOI:10.2514/3.19978 |
| [3] | PRICKETT A L, PARKES C J.Flight testing of the F/A-18E/F automatic carrier landing system[C]//2001 IEEE Aerospace Conference.Piscataway, NJ:IEEE Press, 2001:2593-2612.http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=931220 |
| [4] | SCHUST A P, YOUNG P N, SIMPSON W R.Automatic carrier landing system (ACLS) category Ⅲ certification manual:1506-01-1-2750[R].Annapolis:ARINC Research Corp., 1982.http://agris.fao.org/openagris/search.do?recordID=AV2012091979 |
| [5] | 郭锁凤, 申功璋, 吴成富. 先进飞行控制系统[M].北京: 国防工业出版社, 2013: 214-218. GUO S F, SHEN G Z, WU C F. Advanced flight control system[M].Beijing: National Defense Industry Press, 2013: 214-218.(in Chinese) |
| [6] | 杨一栋, 郑峰婴, 王新华. 舰载机等效模型及着舰控制规范[M].北京: 国防工业出版社, 2013: 5-18. YANG Y D, ZHENG F Y, WANG X H. Equivalent model of carrier-based aircraft and landing control specification[M].Beijing: National Defense Industry Press, 2013: 5-18.(in Chinese) |
| [7] | 张明廉, 徐军. 舰载飞机自动着舰系统的研究[J].北京航空航天大学学报, 1994, 20(4): 386–391. ZHANG M L, XU J. The research of automatic carrier-based aircraft landing system[J].Journal of Beijing University of Aeronautics and Astronautics, 1994, 20(4): 386–391.(in Chinese) |
| [8] | 章卫国, 王新民, 刘长林. 舰载飞机纵向自动着舰控制系统研究[J].西北工业大学学报, 1996, 14(4): 549–553. ZHANG W G, WANG X M, LIU C L. The research of longitudinal carrier-based aircraft automatic landing control system[J].Journal of Northwestern Polytechnical University, 1996, 14(4): 549–553.(in Chinese) |
| [9] | URNES J M, HESS R K, MOOMAW R F. H-dot automatic carrier landing system for approach control in turbulence[J].Journal of Guidance, Control, and Dynamics, 1981, 4(2): 177–183.DOI:10.2514/3.56069 |
| [10] | 杨一栋. 舰载机着舰引导技术译文集[M].北京: 国防工业出版社, 2004: 73-84. YANG Y D. Translation of carrier-guided technology of shipboard[M].Beijing: National Defense Industry Press, 2004: 73-84.(in Chinese) |
| [11] | RUDOWSKY T, HYNES M, LUTER M, et al.Review of the carrier approach criteria for carrier-based aircraft-Phase Ⅰ:Final report:NAWCADPAX/TR-2002/71[R].Maryland:Naval Air Warfare Center Aircraft Division Patuxent River, 2002.https://www.researchgate.net/publication/266579861_REVIEW_OF_THE_CARRIER_APPROACH_CRITERIA_FOR_CARRIER-BASED_AIRCRAFT_-PHASE_I_FINAL_REPORT |
| [12] | Department of Defense, US.Flying qualities of piloted aircraft:MIL-STD-1797A[S].Washington, D.C.:Department of Defense, US, 1995. |
| [13] | BUTTRILL C S, ARBUCKLE P D, HOFFLER K D.Simulation model of a twin-tail, high performance airplane:NASA TM 107601[R].Hampton:Langley Research Center, 1992.https://www.researchgate.net/publication/24296888_Simulation_model_of_a_twin-tail_high_performance_airplane |
| [14] | 杨一栋. 舰载飞机着舰引导与控制[M].北京: 国防工业出版社, 2007: 105-195. YANG Y D. Guidance and control of carrier-based aircraft[M].Beijing: National Defense Industry Press, 2007: 105-195.(in Chinese) |
| [15] | 杨一栋. 着舰安全与复飞技术[M].北京: 国防工业出版社, 2013: 33-36. YANG Y D. Landing and go-around technical security[M].Beijing: National Defense Industry Press, 2013: 33-36.(in Chinese) |
| [16] | 陈孟钢, 高金源. 缩比模型飞机极其飞控系统与原型机的相似关系[J].飞行力学, 2003, 21(2): 34–37. CHEN M G, GAO J Y. Similarity relationships between scaled-model aircraft with its flight control system and prototype aircraft[J].Flight Dynamics, 2003, 21(2): 34–37.(in Chinese) |
