中国在航空发动机性能寻优控制领域也开展了大量的探索性研究,先后将序列线性规划算法、线性规划与模型辅助模式搜索混合优化算法、序列二次规划(Sequential Quadratic Programming,SQP)算法等应用到性能寻优控制中[4-7]。这些算法属于规划算法,在一个初值的基础上,通过迭代的算法寻找最优解,算法通常不能跳出局部最优点。而近年来,群体智能算法(如遗传算法、粒子群算法等)由于其全局寻优能力,也被应用于航空发动机性能寻优中[8-9],相比于传统的规划算法,群体智能算法因具有结构简单、智能搜索等特点受到广泛关注。但是群体智能算法应用于性能寻优时每个个体均需要多次调用发动机稳态模型来获得其适应度,因而优化时间大大增加,影响了性能寻优的实时性。
相比于常规的涡扇和涡喷发动机,变循环发动机(Variable Cycle Engine, VCE)之所以能够获得优良的性能,得益于其具有较大的可调涵道比,因而能够适应发动机不同工作模式下对推力F及耗油率sfc的需求。变循环发动机相比常规涡扇发动机飞行包线更大,表现出更强的非线性变参数特征,具有更多的几何可调变量和控制回路,寻优过程更加复杂。经典的线性规划算法不适用于变循环发动机这样的强非线性系统,而SQP算法中QP子问题的约束条件是原问题约束的线性近似,因此在变循环发动机性能寻优控制中有可能陷入局部最优[10-11]。而对序列二次约束二次规划(Sequential Quadratically Constrained Quadratic Programming,SQCQP)算法而言,QCQP子问题采用二次近似的方法,对原问题的描述更精确[12],因而更适合强非线性的系统。
鉴于采用经典性能寻优算法不易获得最优解,而采用群体智能算法则实时性较差。为此本文针对变循环发动机的性能寻优控制中可调变量增多,使得最优解不易获得的问题,提出了一种结合群体智能和非线性规划的寻优算法——改进微分进化-序列二次约束二次规划(Improved Differential Evolution-Sequential Quadratically Constrained Quadratic Programming, IDE-SQCQP)算法,通过IDE算法求解QCQP子问题,获得最优搜索方向,提高了算法的全局寻优能力,同时利用SQCQP算法能够准确描述对象特性的特点,使得寻优过程耗时较少。
在变循环发动机数字仿真平台上开展了IDE-SQCQP算法的性能寻优控制效果验证,并与常用于性能寻优控制的SQP算法进行了对比,验证了算法的有效性。
1 变循环发动机性能寻优控制问题 变循环发动机有多种方案,采用核心驱动风扇级(CDFS)的变循环发动机的结构如图 1所示[11]。变循环发动机有2种工作模式:单外涵模式和双外涵模式。在双外涵模式下,模式选择活门(MSV)处于打开状态,前可调面积涵道引射器(FVABI)及后可调面积涵道引射器(RVABI)均打开;在单外涵模式下,MSV处于关闭状态,FVABI保持打开状态,RVABI关小。FVABI可改变通过主外涵道的气流流量并保持通过FVABI的气流压力大于通过MSV的气流压力,RVABI可调节外涵出口气流的分流。
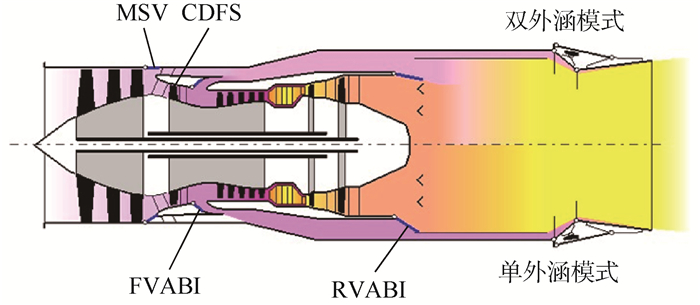 |
| 图 1 变循环发动机结构示意图[11] Fig. 1 Configuration schematic diagram of variable cycle engine[11] |
| 图选项 |
对于变循环发动机,性能寻优控制中可供选择的控制量有主燃烧室燃油流量Wfb、加力燃油流量Wfa、尾喷口面积A8、风扇导叶角αfan、CDFS导叶角αcdfs、压气机导叶角αcom、低压涡轮进口导叶角αturb、前可调面积涵道引射器开度Afvabi和后可调面积涵道引射器开度Arvabi等,不考虑加力状态,其他8个变量在2种工作模式下均可以调节,则2种工作模式下的寻优向量均为
 | (1) |
为了保证寻优过程获得可行解,上述寻优变量还必须满足:
 | (2) |
在寻优过程中,除了要考虑可调变量x的范围,还必须考虑发动机自身的安全约束,如转速、温度、喘振裕度等限制。因此,性能寻优过程的约束条件还包括:
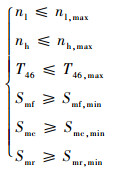 | (3) |
式中:nl为风扇相对转速;nh为压气机相对转速;T46为涡轮出口温度;Smf为风扇喘振裕度;Smc为CDFS喘振裕度;Smr为主外涵道再循环裕度。
将发动机的安全约束转化为式(4)所示约束函数,在寻优过程中满足gi(x)≥0(i=1, 2, …, 6)。
 | (4) |
根据飞行条件,研究变循环发动机性能寻优控制的2种模式:最大推力寻优控制模式和最小油耗寻优控制模式。其中,在起飞、加速、爬升等阶段需要发动机尽可能地提供最大推力,最大推力寻优控制模式的数学表达式可描述为
 | (5) |
在巡航状态下,在保持推力F基本恒定的前提下尽可能地降低发动机耗油率sfc,最小油耗寻优控制模式的数学表达式可描述为
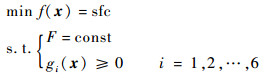 | (6) |
综合式(5)、式(6),发动机性能寻优如式(7)所示:
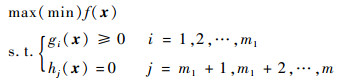 | (7) |
式中:gi(x)为不等式约束;hj(x)为等式约束。
在性能寻优控制过程中,寻优算法在线计算符合寻优目标的最佳可调参数组合,并保证发动机安全可靠工作。
2 SQCQP算法 用于航空发动机性能寻优控制的寻优算法应具有精度高、实时性好等特点。与其他非线性规划优化算法相比,SQCQP算法[12-14]所构造的QCQP子问题是原问题的二次近似,比SQP算法中的QP子问题能够更准确地描述原问题的非线性特征,从而使得在求解一些优化问题时,能够用比SQP算法更少的迭代次数寻到更优结果,因而其在航空发动机性能寻优控制中具有很好的应用前景。
考虑如式(7)所示的约束最优化问题,对于寻优变量x=[x1, x2, …, xn]T, xi, min<xi<xi, max, i=1, 2, …, n,其可行域如式(8)所示:
 | (8) |
SQCQP算法的迭代过程如下:
步骤1??初始化。令k=1,设置参数β, σ∈(0, 1),γ∈(0, +∞),0<ε?1,初始点x0∈Rn。
步骤2??求解子问题获得搜索方向。在当前迭代点xk,构造如式(9)所示的QCQP子问题并求解,得到xk处的可行搜索方向dk。
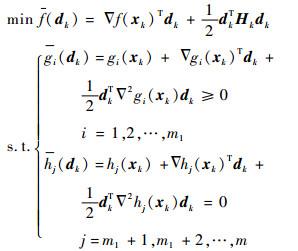 | (9) |
式中:g(xk)、h(xk)为g(xk)、h(xk)在xk处的二次近似函数;Hk为f(x)在xk处的Hesse矩阵,为了保证式(9)解的存在性及唯一性,Hk需为对称正定矩阵。
由于Hesse矩阵的直接计算比较困难,如果使用偏导数法,则非常耗费时间。一般设置Hk初值为单位阵I,并根据一定的校正方法逐渐校正,目前比较常用的校正方法有BFGS校正,其校正公式为
 | (10) |
式中:Bk为Hesse矩阵Hk的近似;sk=xk+1-xk;yk=Δf(xk+1)-Δf(xk)。
步骤3??步长搜索。得到当点xk的搜索方向dk后,乘以步长tk得到新的迭代点xk+1。
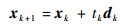 | (11) |
式中:tk为{1, β, β2, …}中满足式(12)条件的最大值。
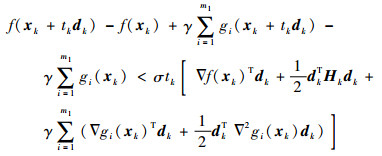 | (12) |
步骤4??采用式(10)修正Hesse矩阵Hk并返回步骤2,令k=k+1。迭代搜索直至tk≤ε或||dk||<ε,认为此时算法达到非线性规划问题的KKT点,停止迭代计算。
不同于QP子问题的求解,由于QCQP子问题中存在二次约束,因此解法较为困难,这也是影响SQCQP算法推广的重要因素。因此本文先将QCQP子问题转化为式(13)所示的罚函数,然后使用IDE算法通过智能搜索的方式求解QCQP子问题(笔者曾尝试使用经典的牛顿法求解该子问题,结果求解时间过长且不容易找到全局最优解)。
 | (13) |
式中:σI和σE分别为不等式约束和等式约束的罚因子。
3 基于IDE算法求解QCQP子问题 DE算法是1995年由美国****Storn和Price[15]提出的一种基于种群内个体相互协作的仿生智能计算方法。与遗传算法相比,DE算法直接用实数运算,在解决复杂优化问题时的性能更加突出,过程也更为简单,因而具有更快更强的全局寻优能力。本文对DE算法的改进包括以下几个方面:
1) 采用动态的缩放因子。DE算法主要通过变异操作产生新个体,变异操作中缩放因子Fdv过大或者过小都不是最好的选择。通常在寻优的初期,希望Fdv大一些,增强种群的全局搜索能力,在寻优的后期,希望Fdv小一些,增强种群的寻优精度,本文采用式(14)设定缩放因子:
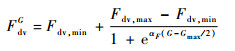 | (14) |
式中:FdvG为第G代的缩放因子;Fdv, max和Fdv, min分别为设置的最大和最小缩放因子;αF为调整Fdv下降的系数。
2) 变异操作。标准的DE算法在变异时个体随机选择,不能充分利用种群中最优个体信息,因此本文采用式(15)进行变异操作:
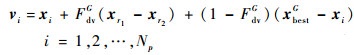 | (15) |
式中:vi为变异个体; r1、r2为[1, Np]之间的随机数,Np为种群数量;xbestG为上一代种群中的最优个体。
由式(15)可以看出,变异个体相对原个体位置的位移由2部分构成:一部分是随机的迁移;另一部分是向最优个体的迁移。这样可以在保证寻优能力的前提下加快种群的收敛速度。
3) 对新一代种群中适应度低的个体进行二次变异。通常采用将这部分个体(μNp个,μ为比例)重新初始化的变异方式,以增加种群的多样性,但对收敛速度和精度没有明显改善。本文提出依据一定的概率在最优个体附近或种群中心位置附近重新生成新个体,使得新变异获得的个体有更大的概率接近最优解。
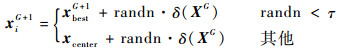 | (16) |
式中:xbestG+1为当前种群最优个体;xcenter为当前种群的中心位置,即个坐标分量的平均值;randn为服从均值为0、方差为1的正态分布的随机数;δ(XG)为种群的标准差;τ为[0, 1]之间的常数。
采用IDE算法求解QCQP子问题的步骤如下:
步骤1??G=0,在寻优空间内初始化种群X0,每个个体代表一个可行搜索方向dk,按式(13)计算种群的适应度J(X0)。
步骤2??按式(15)进行变异操作得到变异种群VG,交叉操作与标准DE算法相同,产生试验种群UG。
步骤3??贪婪选择。计算试验种群的适应度J(UG),并与上一代种群对比,择优产生下一代种群XG+1。
步骤4??对XG+1按照适应度进行排序,将适应度差的个体按式(16)进行二次变异,并再次进行贪婪选择。
步骤5??如果达到最大优化代数,则退出优化过程,否则令G=G+1,返回步骤2。
为验证采用IDE算法求解QCQP子问题的SQCQP算法的寻优能力,采用表 1中给出的测试函数进行SQP算法[16]与IDE-SQCQP算法的对比验证。Prob1、Prob2是低维简单非线性规划问题,Prob3、Prob4是高维复杂非线性规划问题。2种算法设定最大迭代次数为50次,寻优结束条件为||dk||<10-6或tk<10-6。寻优结果对比如表 2所示。
表 1 测试函数 Table 1 Test functions
| 编号 | 测试函数 |
| Prob1 | 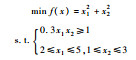 |
| Prob2 | 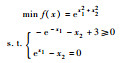 |
| Prob3 |  |
| Prob4 | 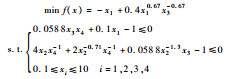 |
表选项
表 2 SQP算法与IDE-SQCQP算法的测试结果对比 Table 2 Comparison of test results between SQP and IDE-SQCQP algorithms
| 算法 | 测试函数 | x0 | Niter | 寻优结果f(x) | 参考最优值f(x) |
| SQP | Probl | [l, l] | 3 | 6.777 777 777 774 569 | 6.7 |
| [5, 5] | 4 | 6.777 777 777 777 770 | |||
| Prob2 | [1, 1] | l5 | l. 836 82l 753 924 569 | 1.836 82178 | |
| [2, 2] | 50 | 2.520 727 612 805 417 | |||
| Prob3 | [4, 2, l, l, 8, 7, l, 0.5] | 50 | 3.947 372 022 706 715 | 3.951 163 406 | |
| [l, l, l, l, 6.l, 6.l, l, l] | 50 | 3.950 744 454 322 580 | |||
| Prob4 | [7, l, 0.5, 8] | 50 | -5.689 567 423 597 13l | -5.739 820 386 | |
| [7, 0.l, 0.l, 7] | 50 | -5.740 096 689 116 705 | |||
| IDE-SQCQP | Probl | [1, 1] | 2 | 6.777 762 345 747 336 | 6.7 |
| [5, 5] | 2 | 6.777 762 347 781 540 | |||
| Prob2 | [1, 1] | 7 | 1.836 818 809 380 766 | 1.836 821 78 | |
| [2, 2] | 26 | 1.836 818 906 828 806 | |||
| Prob3 | [4, 2, l, l, 8, 7, l, 0.5] | 19 | 3.951 178 934 326 082 | 3.951 163406 | |
| [l, l, l, l, 6.l, 6.l, l, l] | ll | 3.951 176 013 300 333 | |||
| Prob4 | [7, l, 0.5, 8] | l3 | -5.739 763 870 783 301 | -5.739 820 386 | |
| [7, 0.l, 0.l, 7] | 2l | -5.739 771 048 390 224 | |||
| 注:x0—搜索的起始值;Niter—寻优过程的迭代次数。 | |||||
表选项
由表 2可以看出,无论是高维(8维)还是低维(2维)寻优问题,IDE-SQCQP算法均能在到达最大迭代次数前收敛,且搜索结果非常接近最优值。其寻优过程中的迭代次数明显小于SQP算法,且在维数较高时,优势更明显。SQP算法在Prob3和Prob4中均达到了最大迭代次数,这与文献[14]的研究结论相一致。同时从表 2中可以看出,SQP算法对问题的初始值敏感,不同的初始值,可能得到不同的搜索结果,如Prob2中,当初值为[2, 2]时,SQP算法达到最大迭代次数也没有搜索到最优点,而IDE-SQCQP算法则稳定性很强。
针对变循环发动机这种具有多个可调变量的强非线性对象,在性能寻优过程中,子问题的建立需要反复调用稳态模型,这是性能寻优控制过程中耗费时间较多的过程,同时不同工作点的寻优初始值有较大差异,因此如果一种算法能在保证寻优精度的情况下减少寻优迭代次数,且对寻优的初始值不是很敏感,则可以明显地提高性能寻优控制的实时性与准确性。
值得指出的是,采用IDE-SQCQP算法进行性能寻优的过程,与采用IDE算法进行性能寻优是不同的。前者只需在构造QCQP子问题时调用发动机稳态模型计算Δf(xk)、Δgi(xk)、Δhj(xk)即可,对于不同个体的适应度,则是通过式(13)计算得出,因而其在采用人工智能算法确保全局最优下降方向的同时,实时性也能够得到保证。
4 变循环发动机性能寻优控制仿真 4.1 性能寻优控制结构 变循环发动机性能寻优控制的结构如图 2所示,主要包括发动机闭环控制系统和性能寻优模块。其中,发动机闭环控制系统采用ALQR控制方法[17],以风扇相对转速nl、压气机相对转速nh、发动机压比πepr为被控量,燃油流量Wfb、尾喷口面积A8、后可调面积涵道引射器开度Arvabi为控制量,采用三输入三输出的闭环控制方式,其他可调变量采取开环控制模式(由于本文不研究变循环发动机的多变量控制问题,因而此部分内容不详述)。
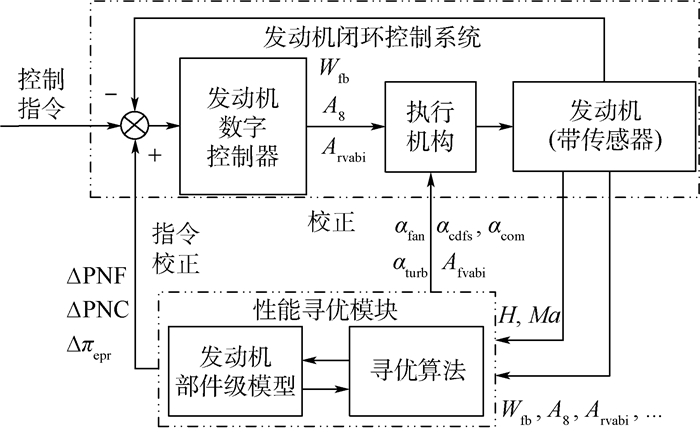 |
| 图 2 变循环发动机性能寻优控制结构 Fig. 2 Control structure of variabe cycle engine performance seeking |
| 图选项 |
性能寻优模块由寻优算法和发动机部件级模型组成。性能寻优模块寻找当前飞行条件下符合目标的发动机最佳输入组合,寻优过程结束后获得发动机的最佳工作状态,将此状态对应的3个闭环控制信号的调整量(ΔPNF、ΔPNC、Δπepr)作为指令校正值参与闭环控制,其他参与开环控制的可调变量[αfan, αcdfs, αcom, αturb, Afvabi]T作为各几何机构的指令信号传递给执行机构,使发动机运行到寻优得到的最佳工作点。
基于上述变循环发动机性能寻优控制结构,开展发动机性能寻优控制数字仿真。硬件平台是主频2.53 GHz的CPU和4 G内存的计算机,软件平台基于VC++开发,发动机模型动态仿真步长为20 ms。IDE算法参数设置如表 3所示。4.2节和4.3节将给出最大推力寻优控制模式及最小油耗寻优控制模式的仿真结果。
表 3 IDE算法参数设置 Table 3 Parameter setting of IDE algorithm
| 参数 | 数值或范围 |
| Fdv | 0.2~1.0 |
| Gmax | 50 |
| Np | 50 |
| αF | 0.3 |
| μ | 1/3 |
| τ | 0.5 |
表选项
4.2 最大推力寻优控制模式仿真 变循环发动机低空低马赫数状态下采用双外涵模式推力更高。在高度H=0 km,马赫数Ma=0,油门杆角度PLA=70°的中间状态进行最大推力寻优控制模式的仿真,如图 3所示,在t=0 s进入优化,图中同时给出了SQP算法的寻优结果,除导叶角参数和Smf、Smc、Smr外,其他参数均为相对优化前各参数的归一化量。
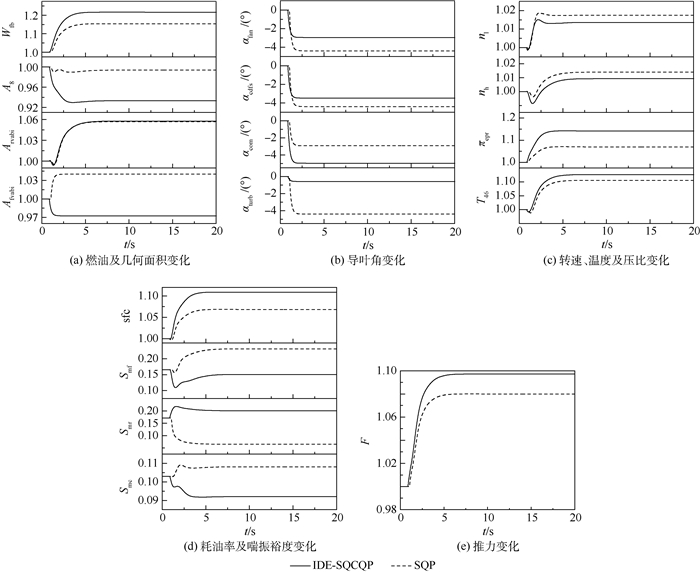 |
| 图 3 最大推力寻优控制模式仿真结果 Fig. 3 Simulation results of maximum thrust seeking control mode |
| 图选项 |
由图 3可以看出,为了增大推力,发动机的燃油流量Wfb增大,发动机压比与涡轮后温度增加,单位推力增加,同时发动机的耗油率也增加。2种算法都能保证优化后的发动机工作在约束范围内。SQP算法寻优时间为1.041 s,推力提高了8%,IDE-SQCQP算法寻优时间为0.866 s,推力提高了9.72%。IDE-SQCQP算法比SQP算法寻优时间减少16.81%,优化效果提升了21.50%,在实时性和寻优能力上具有明显的优势。
4.3 最小油耗寻优控制模式仿真 变循环发动机高空高马赫数状态下采用单外涵模式耗油率更低。在H=12 km,Ma=1.5,PLA=40°的单外涵巡航状态进行最小油耗寻优控制模式的仿真。t=0 s进入优化。图 4为2种算法进行寻优控制后的发动机状态参数变化及输入量变化的对比。图中除导叶角参数和Smf、Smc、Smr外,其他参数均为相对优化前各参数的归一化量。
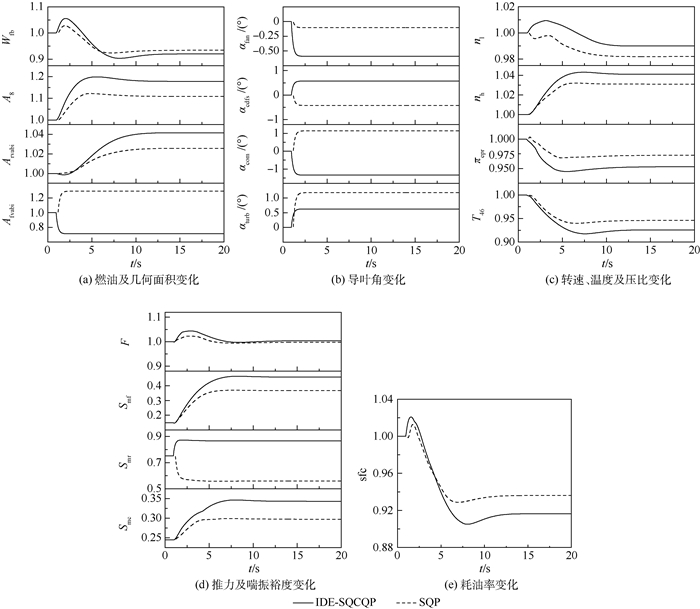 |
| 图 4 最小油耗寻优控制模式仿真结果 Fig. 4 Simulation results of minimum specific fuel consumption seeking control mode |
| 图选项 |
由图 4可以看出,最小油耗寻优控制模式下,因为需要保持推力恒定,为了降低耗油率sfc必须降低燃油流量Wfb,降低燃油流量会造成T46和πepr降低,这样会造成单位推力下降,为保持推力基本恒定,尾喷口面积增大,通过发动机的空气流量增加,由此保持推力基本恒定。以上寻优结果与文献[7, 9]一致。2种算法都能保证优化后的发动机工作在约束范围内,并且推力基本保持不变。SQP算法寻优时间为1.144 s,耗油率降低了6.38%,IDE-SQCQP算法寻优时间为0.948 s,耗油率降低了8.36%。IDE-SQCQP算法比SQP方法寻优时间减少17.13%,优化效果提升了31.03%,再次显示出明显的时间和精度优势。
5 结论 本文提出了一种IDE-SQCQP算法用于变循环发动机性能寻优控制,仿真结果表明:
1) 通过罚函数将QCQP子问题转化为适应度函数,以一种IDE算法求解QCQP子问题,解决了QCQP子问题的求解问题,同时确保了搜索方向的最优性。
2) 测试函数仿真表明,IDE-SQCQP算法对初值变化具有良好的稳定性,能够以较少的迭代次数搜索到最优值。
3) 将IDE-SQCQP算法应用于具有多个可调变量的变循环发动机性能寻优过程中,相比经典的SQP算法表现出更好的实时性和寻优能力。
由上可知,IDE-SQCQP算法具有较强的非线性寻优能力,在变循环发动机的性能寻优控制中具有较好的应用前景。
参考文献
| [1] | GILYARD G B, ORME J S.Performance seeking control:Program overview and future directions:AIAA-1993-3765[R].Reston:AIAA, 1993. |
| [2] | SMITH R H, CHISHOLM J D, STEWART J F. Optimizing aircraft performance with adaptive integrated flight/propulsion control[J].Journal of Engineering for Gas Turbines & Power, 1990, 113(1): 87–94. |
| [3] | SILVA V V R, KHATIB W, FLEMING P J. Performance optimization of gas turbine engine[J].Engineering Applications of Artificial Intelligence, 2005, 18(5): 575–583.DOI:10.1016/j.engappai.2005.01.001 |
| [4] | 任新宇, 杨育武, 樊思齐. 推进系统综合性能寻优控制研究[J].推进技术, 2010, 31(1): 61–64. REN X Y, YANG Y W, FAN S Q. Study on propulsion system overall performance seeking control algorithm[J].Journal of Propulsion Technology, 2010, 31(1): 61–64.(in Chinese) |
| [5] | ZHU Y B, FAN S Q, ZHANG X H, et al.A hybrid optimization method research for aeroengine performance seeking control[C]//Biennial Conference on Engineering Systems Design and Analysis.New York:ASME, 2006:145-149. |
| [6] | 孙丰诚, 孙健国. 基于序列二次规划算法的发动机性能寻优控制[J].航空动力学报, 2005, 20(5): 862–867. SUN F C, SUN J G. Aero-engine performance seeking control based on sequential quadratic programming algorithm[J].Journal of Aerospace Power, 2005, 20(5): 862–867.(in Chinese) |
| [7] | 王健康, 张海波, 孙健国, 等. 基于复合模型及FSQP算法的发动机性能寻优控制试验[J].推进技术, 2012, 33(4): 579–590. WANG J K, ZHANG H B, SUN J G, et al. Experimental verification of aero-engine performance seeking control based on the hybrid model and FSQP algorithm[J].Journal of Propulsion Technology, 2012, 33(4): 579–590.(in Chinese) |
| [8] | 刘楠, 黄金泉. 应用改进粒子群算法的涡轴发动机性能寻优[J].南京航空航天大学学报, 2013, 45(3): 303–308. LIU N, HUANG J Q. Performance seeking of turbo-Shaft engines based on improved particle swarm optimization algorithm[J].Journal of Nanjing University of Aeronautics and Astronautics, 2013, 45(3): 303–308.(in Chinese) |
| [9] | 王元, 李秋红, 黄向华. 基于DMOM算法的航空发动机性能寻优控制[J].航空动力学报, 2016, 31(4): 948–954. WANG Y, LI Q H, HUANG X H. Aero-engine performance seeking control based on DMOM algorithm[J].Journal of Aerospace Power, 2016, 31(4): 948–954.(in Chinese) |
| [10] | TAKESHI T, NANAHISA S.A performance optimization control of variable cycle engines:AIAA-2003-4984[R].Reston:AIAA, 2003. |
| [11] | 王元. 变循环发动机建模及性能寻优控制技术研究[D]. 南京: 南京航空航天大学, 2015. WANG Y.Research on modeling techniques and performance seeking control of variable cycle engine[D].Nanjing:Nanjing University of Aeronautics and Astronautics, 2015(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10287-1016752036.htm |
| [12] | 简金宝. 光滑约束优化快速算法[M].北京: 科学出版社, 2010. JIAN J B. Fast algorithm for smooth constrained optimization[M].Beijing: Science Press, 2010.(in Chinese) |
| [13] | JIAN J B, TANG C M, ZHENG H Y. Sequential quadratically constrained quadratic programming norm-relaxed algorithm of strongly sub-feasible directions[J].European Journal of Operational Research, 2010, 200(3): 645–657.DOI:10.1016/j.ejor.2009.01.052 |
| [14] | TANG C M, JIAN J B, LI G Y. A working set SQCQP algorithm with simple nonmonotone penalty parameters[J].Journal of Computational & Applied Mathematics, 2011, 236(6): 1382–1398. |
| [15] | STORN R, PRICE K. Differential evolution:A simple and efficient adaptive scheme for global optimization over continuous spaces[J].Journal of Global Optimization, 1995, 23(4): 341–359. |
| [16] | 马昌凤. 最优化方法及其Matlab程序设计[M].北京: 科学出版社, 2010. MA C F. Optimization method and its Matlab program design[M].Beijing: Science Press, 2010.(in Chinese) |
| [17] | 杨刚, 孙健国, 李秋红. 航空发动机控制系统中的增广LQR方法[J].航空动力学报, 2004, 19(1): 153–158. YANG G, SUN J G, LI Q H. Augmented LQR method for aeroengine control systems[J].Journal of Aerospace Power, 2004, 19(1): 153–158.(in Chinese) |
