飞机移动生产线是丰田生产方式/精益生产理论在飞机制造业的应用，对于降低飞机的装配成本、提升装配效率、缩短装配工期具有重要意义。
在飞机整个装配过程中，移动生产线上的飞机以平稳的速度从一个工作站移动到下一个并缓慢通过整个生产线，从而完成飞机所需的所有装配作业，而移动生产线速度的调整，可以设定生产线的不同生产节拍。为了保证生产线按需连续稳定生产，装配作业所需的物料及其准时配送也成为移动生产线正常运作的关键环节之一。通常在生产线旁会专门配置相关空间作为装配所需物料的存放区域，通过小车运送的方式将物料按时定量配送至相应的线边区域。事实上，飞机移动生产线上一架飞机的任意作业调度安排，不仅必须遵循工艺顺序约束及资源约束，还需同时考虑物料配送计划与物料的线边存储，为了获得更加有效可行的调度计划，其作业调度决策需要高度协调装配作业活动与物料配送活动。本文把飞机移动生产线装配作业调度问题抽象为一类特殊的资源受限项目调度问题(Resource-Constrained Project Scheduling Problem，RCPSP)。在这一问题中，各装配活动可以看作是项目的作业，装配所需的人力、设备工具、线边空间及物料配送能力等视为项目所需资源。其与一般RCPSP问题的主要区别在于：问题中引入了物料配送因素，问题的决策不仅需要优化决策各装配作业的开始时间，还必须同时决策安排装配所需物料的配送时间与物料存储位置。因此，可认为是一类集作业调度与物料配送调度问题于一体的联合决策问题，本文把这一问题称之为考虑物料配送的飞机移动生产线调度问题(Aircraft Moving Assembly Line Scheduling Problem Considering Material Delivery，AMALSP-CMD)。综上所述，飞机移动生产线中装配作业数量大、作业间的装配顺序复杂、资源共享、物料配送及存储能力受限等特点对装配作业的调度造成了极大困难，本文正是以此为背景，提出了AMALSP-CMD问题并对其进行优化研究。
现有文献已经对经典的RCPSP问题进行了较为充分的研究，目前的求解算法基本可以分为精确算法、启发式算法和元启发式算法3类。Chaleshtarti和Shadrokh^[1]采用分支定界法求解目标为最小化工期的累积资源受限项目调度问题(RCPSP-CU)。Berthold等^[2]整合了整数规划、约束规划和满意度测试法，提出了一种分支定界机制，并对下界的确定做了优化。RCPSP问题已被证明是一个NP-hard问题^[3]，启发式算法的效率相对精确算法较高，在求解大规模问题时更加有效。Tormos和Lova^[4]在RCPSP问题中引入随机抽样和混合多路径算法对作业进行优化，同时证明了这类算法的高效性。元启发式算法是对启发式算法的改进，主要包括禁忌搜索算法、模拟退火算法、遗传算法等。Bukata等^[5]采用并行禁忌搜索算法求解RCPSP问题的最小工期。Bouleimen和Lecocq^[6]在传统的模拟退火算法中考虑解空间的特异性重新设计了搜索机制，对单模式和多模式的RCPSP问题进行求解。Alcaraz和Maroto^[7]使用遗传算法对项目调度中的资源进行分配，并提出了新的交叉算子，在广泛的样本试验中取得了良好的效果。Hartmann^[8]提出了一类自适应遗传算法，通过任务列表对染色体进行编码，同时在染色体上增加了一个判定串并行解码方式的基因，数值实验证明了这类算法可以通过有效选择合适的解码方式产生较优解。Merkle等^[9]对蚁群算法进行优化，使用了双信息素组合评价方法搜索更优的项目调度计划。Kumar和Vidyarthi^[10]改进了传统的粒子群算法对RCPSP问题求解，提出了一种有效的粒子生成算子，避免了传统算法中粒子由于位置与速度的更新出现失效，提高了算法的效率。而针对飞机移动生产线的RCPSP问题，王琰和陆志强^[11]分析了飞机移动生产线的多重约束，建立了整数规划模型，并提出了基于WRST规则的启发式算法。郑倩和奚立峰^[12]对3种作业人数选择规则和9种作业优先顺序决策规则进行组合，构成了27种启发式算法，通过比较这些启发式算法在测试问题集中的表现选出最有效地解决此问题的方法。上述RCPSP问题的研究对于本文所研究的AMALSP-CMD问题中作业调度的建模与算法设计具有重要参考意义。而对于生产线的物料配送问题，葛茂根等^[13]针对机械产品总装过程中物料的JIT配送问题进行了研究，把产品生产计划和节拍时间作为已知参数，考虑了配送设备的容积约束和工位线旁库存的面积限制，建立了多目标数学模型，并采用了混合粒子群算法求解。Fathi等^[14-15]对汽车装配线物料配送中的多载量小车调度问题进行了研究，构建了最小化多载量小车出行次数与线边库存成本的多目标数学模型，并设计了相应的优化算法。
综上所述，目前的研究大多将装配系统和物料配送系统拆分为2个相对独立的系统，对线边物料配送的研究大部分都是基于已制定好的生产计划，但实际生产线上常出现由于物料配送能力受限等原因导致装配作业中断的情况。事实上，生产线中各装配作业的开始时间与物料配送时间等因素是相互影响的，通过联合决策可以更有效地为作业装配和物料配送提供协同性计划，保证生产线平稳运行，具有较高的理论研究意义。Khayat等^[16]在对车间内作业调度问题的研究中综合考虑了机器资源与搬运小车的数量约束，建立了以最小化作业加工完成时间为目标函数的数学规划模型，并通过CPLEX软件求解。Aguirre等^[17]对半导体制造中的加工与搬运问题进行了联合建模，并设计了基于混合整数规划的顺序启发式算法。现阶段，中国飞机装配车间的物料配送方式还停留在传统的“面向服务”模式，即工人根据装配计划到库房申请领料配送，然后进行装配作业，这种被动的物料供应模式容易导致物料管理混乱，并产生生产浪费、装配延误等问题。因此，采用主动的“面向装配”模式并将物料配送与装配调度相结合综合制订生产计划具有实际应用价值。本文所提出的AMALSP-CMD问题，基于实际生产背景，综合考虑了飞机装配过程的作业顺序约束、资源约束、物料配送能力上限和物料在线边空间的存放等因素，建立了以装配总工期最小化为目标函数的数学模型，并提出了相应的算法对作业开始时间、物料配送时间和线边空间存储位置进行联合决策。
1 问题描述及数学模型 1.1 问题描述 飞机移动生产线调度问题，是通过优化决策各作业的开始时间、物料配送时间及其相应的线边存储位置，以达到最小化装配总工期的目标。AMALSP-CMD问题的假设与说明如下：
1) 飞机装配作业项目包含n项作业，J={1, 2, …, n}，任意j∈J的执行工期为t_j，开始时间为T_j^S，完成时间T_j^F=T_j^S+t_j。P_j表示作业j的紧前作业集合，任意作业在其紧前作业全部完成后才能执行。增加作业0和作业n+1表示虚作业，虚作业执行时间为0，且不占用任何资源。
2) 可更新资源为R={1, 2, …, K}，任意时刻第k种资源总量为R_k，单位时间内作业j消耗资源k的数量用r_jk表示。
3) 将时间离散化，时间集合为D={1, 2, …, z}，z表示所有作业操作时间总和，任意d∈D表示离散的时间节点。
4) 将飞机上的作业空间离散化，如图 1所示，对于任意一架飞机，以飞机机尾作为零参考点，ψ表示飞机的长度。飞机上的作业空间集合为Γ={1, 2, …, ψ}，任意l_j∈Γ表示作业j在飞机上的固定装配位置。

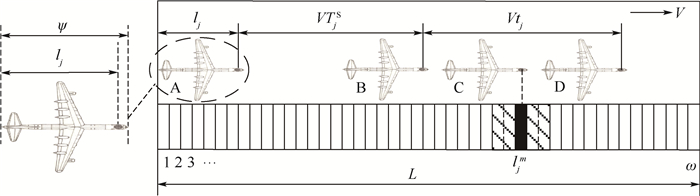图 1 飞机移动生产线作业装配点及物料摆放位置示意图 Fig. 1 Schematic of positions of assembly and material storage on aircraft moving assembly line

图选项

5) 假定飞机移动生产线的移动速度为V，作业j在移动生产线上的装配位置和物料摆放位置可通过图 1表示。离散化的线边空间集合为L={1, 2, …, ω}，l∈L。对于任意一架飞机，图中状态A表示飞机进入移动生产线的起始位置。在时刻T_j^S飞机移动到状态B位置时作业j开始装配，经过t_j时间段飞机移动到状态D所示位置时作业j装配完成。作业j开始执行到完成时间段内飞机在移动生产线上移动距离的中间位置，即状态C所示位置，定义该位置作业j的装配点所对应的线边空间位置为该作业所需物料的中心摆放位置l_j^m，用图中黑色部分表示。任意l_j^m∈L，l_j^m=「l_j+VT_j^S+Vt_j/2 ，表示向上取整。
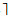
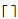
6) 线边空间的分配以将任意作业装配所需物料存放在距离装配中心位置较近区域为基本原则，可允许物料占用l_j^m左右两侧各m个单位的线边空间，用图 1中阴影部分表示。
7) 飞机装配作业j所需的物料主要包括4类：形状不规则、数量少的大型结构件，需求量大、体积小的通用标准件，体积中等、数量多的装配件和复杂昂贵的系统件。大型结构件由于线边空间容量不足，采用标准料架直接进行配送；通用标准件(如装配所需的螺母等紧固件)由于需求量较高且体积小，通常在各工位线边单独划定存放区域，通过定期补货的方式配送；因此本文重点考虑装配件和系统件2类物料的配送与存放。装配件和系统件均使用标准料箱由小车配送至线边空间，并在装配作业结束后以统一回收空料箱的方式进行供应，配送完成时间T_j^D≤T_j^S，配送提前期t_j^p≤p_max，物料占用线边空间时长为T_j^O=T_j^F-T_j^D。作业j对物料的需求为v_j。
8) 每个单位线边空间容量为S_u，假定任意时刻物料综合配送能力的上限为D_max，记项目总工期为T。
本文研究问题的3类决策变量如下：
1) x_jd。0, 1变量，当其为1时表示作业j在时刻d开始执行，否则为0。
2) y_jd。0, 1变量，当其为1时表示作业j所需物料在时刻d完成配送，否则为0。
3) v_jdl。非负整数变量，表示作业j在时刻d在线边空间l存放的料箱数量，取值范围为{0, 1, 2，…，S_u}。
1.2 数学模型 AMALSP-CMD的数学模型如下：

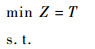(1)

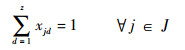(2)

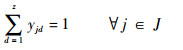(3)

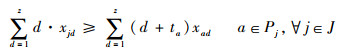(4)

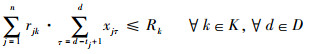(5)

(6)

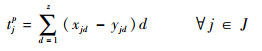(7)

(8)

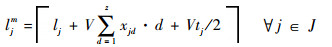(9)

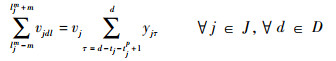(10)

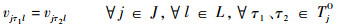(11)

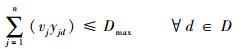(12)

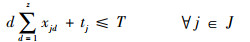(13)

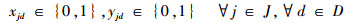(14)

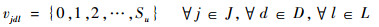(15)

式(1)为目标函数，表示要求飞机装配总工期最小化；式(2)表示作业一旦开始不允许抢占，必须连续执行直到完成；式(3)表示任意作业装配所需的物料必须一次性配送至线边空间；式(4)定义了作业间的时序约束关系，一项作业必须在其所有的紧前作业全部完成后才能执行；式(5)为资源约束，任意时刻所有执行的作业对任意资源的需求不得超过该资源的供应上限；式(6)表示任意单位线边空间存放的物料不得超过其上限；式(7)定义了作业所需物料的配送提前期；式(8)表示任意作业物料的配送时间应早于其装配时间且配送提前期不超过上限值；式(9)定义了某项作业的物料摆放中心位置与装配位置及时间的线性关系；式(10)和式(11)表示任意作业的物料应存放在该作业装配时对应线边空间的中间摆放位置且不得超出左右一定范围；式(12)表示任意时刻所有安排配送的物料数量不得超过物料综合配送能力上限；式(13)定义了项目的完成时间；式(14)和式(15)定义了决策变量的可行域。
2 算法设计 针对AMALSP-CMD问题的特点，本文设计了一类以遗传算法为框架的启发式算法(THBG)，其中结合了解生成算法和局部优化搜索算法。该算法的基本框架与主要思想为：通过遗传算法较强的全局搜索能力搜寻较优的作业执行顺序，为每一条包含作业执行顺序的染色体设计有效的算法(SCRDS)，对资源、配送能力和线边空间进行合理分配，从而获得各项作业的开始时间、物料配送时间和物料在线边空间的存储位置的初始解。在此基础上，基于上述初始解调度结果，通过考虑两作业间物料存放空间调整的局部优化算法对线边空间进行再分配，使得更多的作业能并行执行，进一步缩短装配总工期。
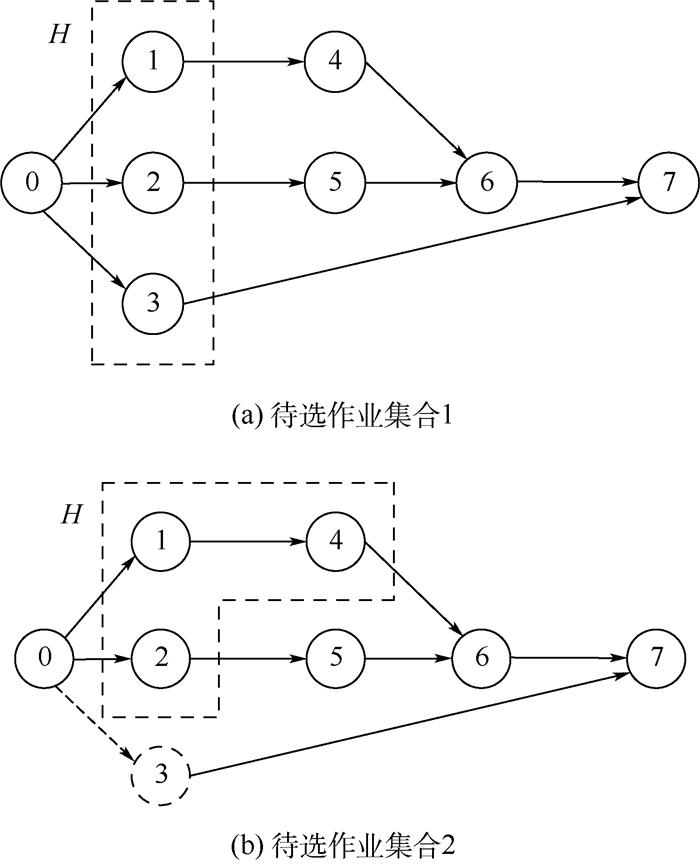
2.1 遗传算法框架 遗传算法采用作业列表表达方式(job list representation)编码，染色体I={λ}由作业列表λ组成，每一个基因位表示一个作业序号，则每一条染色体代表一个作业顺序列表。为了提高算法效率，本文借鉴了文献[8]中提出的针对作业列表部分染色体的初始化方式与交叉、变异算子，在染色体内部镶嵌了作业间的紧前紧后关系确保初始解及产生的后代染色体均为可行解。染色体的初始化方式如图 2所示。

图 2 染色体初始化示意图 Fig. 2 Schematic of chromosome initialization

图选项

图 2(a)为一包含虚作业共8个作业的项目网络图。首先安排虚作业0进入作业列表，将未安排的作业中紧前作业已全部执行完成的作业加入待选集合H，此时待选作业集合H={1, 2, 3}；然后在H中等概率随机挑选一个作业为下一个执行作业，例如选择作业3；此时更新H={1, 2, 4}，如图 2(b)所示。下一步在新的候选作业集合H中再随机挑选一个作业进行安排，依次直至所有作业被安排完。染色体的交叉方式为子代染色体保留部分父代I^F的染色体，交换部分的染色体继承父代I^M剔除I^F中重复的作业后按序保留下的作业列表，如将染色体λ^F =(0 1 2 3 4 5 6 7)与λ^M =(02315467)第4~6基因位的片段进行交叉，得到子代染色体λ^S=(0 1 2 3 5 4 6 7)与λ^D=(0 2 3 1 4 5 6 7)。变异算子通过交换或调整同一候选作业集合H中的作业顺序完成，例如对图 2(a)候选集合H={1, 2, 3}中的作业执行顺序进行重组，将父代染色体λ=(0 1 2 3 5 4 6 7)变异为λ_m=(0 2 3 1 5 4 6 7)。
设定遗传算法的种群大小为M，迭代次数为N，适应度函数fit为项目工期的倒数，η表示当前代数。算法框架如图 3所示。

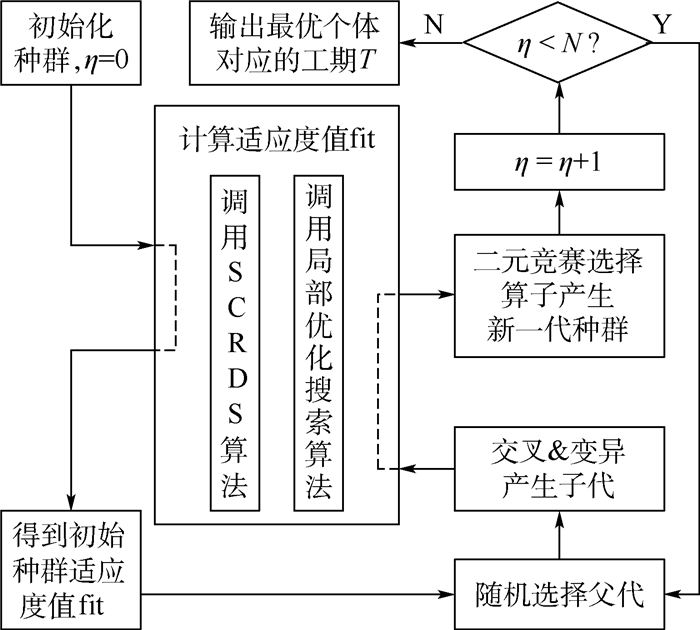图 3 遗传算法框架 Fig. 3 Genetic algorithm framework

图选项

2.2 基于作业顺序列表的解生成算法 在作业执行顺序确定的情况下，综合考虑作业的资源约束、物料配送能力约束和线边空间容量约束为各项作业安排开始时间、物料配送时间和物料存放空间。对于列表中的每一个作业，采用JIT配送方式。算法的设计以串行进度生成机制为核心，依次判定选定作业的各类资源、配送能力和线边空间容量在其紧前作业最晚完成时刻是否满足。在资源满足条件下，若在给定的最大配送提前期内某时刻配送能力满足且线边空间容量充足，可通过提前配送策略将该作业所需物料早于装配开始时间配送，并以暂存的形式存放在相应线边空间处，此时可以得到作业的开始时间、物料配送时间以及物料相应的线边空间存放位置。任意资源、配送能力或线边空间容量不足均将作业开始时间延期一单位执行。SCRDS算法的具体步骤如下：
步骤1??获取作业安排序列{j₁, j₂, …, j_n}，令i=1，k=1。
步骤2??选取作业j_i，将其紧前作业的最晚完成时间max{T_pj^F}作为拟开始安排时间T_j^ST, 则j_i的结束时间T_j^FT=T_j^ST+t_j，装配所需物料拟配送时间T_j^DT=T_j^ST。
步骤3??若j_i满足当d∈[T_j^ST, T_j^FT]，r_jk≤R_k，转步骤4，否则转步骤11。
步骤4??若j_i所需物料满足d = T_j^ST，v_j≤D_d^c，转步骤6，否则转步骤5。
步骤5??作业j_i的物料配送时间T_j^DT= T_j^DT-1，若T_j^ST-T_j^DT≤p_max且T_j^DT≥0，转步骤4，否则转步骤11。
步骤6??计算时刻T_j^ST作业j_i的物料摆放中心位置l_j^m，标记为l_c。若满足d∈[T_j^DT, T_j^FT]，v_j≤v_lc，则将j_i的物料存放于线边单元l_c中，v_lc=v_lc-v_j，转步骤12，否则先将空间l_c放满，v_j=v_j-v_lc，转步骤7。
步骤7??从l_c向左侧线边空间搜索k个单元，若d∈[T_j^DT, T_j^FT]，v_j≤v_lc-k，则将作业j_i的剩余物料存放在线边单元l_c-k内，v_lc-k=v_lc-k-v_j，转步骤12，否则转步骤8。
步骤8??从l_c向右侧线边空间搜索k个单元，若d∈[T_j^DT, T_j^FT]，v_j≤v_lc+k，则将作业j_i的剩余物料存放在线边单元l_c+k内，v_lc+k=v_lc+k-v_j，转步骤12，否则转步骤9。
步骤9??若d∈[T_j^DT, T_j^FT]，v_lc-k+v_lc+k≥v_j，则将作业j_i物料先放满线边l_c-k的空间，v_j=v_j-v_lc-k，余下物料存放在l_c+k中，v_lc+k=v_lc+k-v_j，转步骤12，否则，先将l_c-k和l_c+k空间放满，v_j=v_j-(v_lc-k+v_lc+k)，转步骤10。
步骤10??若k＜m，k=k+1，转步骤7，否则转步骤11。
步骤11??T_j^ST=T_j^ST+1，T_j^DT=T_j^ST，转步骤3。
步骤12??为作业j_i安排开始时间T_j^S =T_j^ST，物料配送时间T_j^D=T_j^DT。
步骤13??更新资源R_k、配送能力D^c和线边空间容量v_l。
步骤14??若j_i=j_n，转步骤15，否则i=i+1，转步骤2。
步骤15??输出调度计划S，作业j_n的完成时间即为项目工期D，算法结束。
2.3 基于物料摆放位置调整的局部优化搜索算法 在SCRDS算法安排作业物料摆放位置的过程中，为了使作业尽早开始执行，在满足资源约束和配送能力约束的前提下，作业会最大限度地占用周边的空间。因此可能会出现作业i占用了作业j的线边空间，导致作业j所需物料没有足够的存放空间必须延后执行的情况发生。本文设计了针对此类情况的两作业物料摆放位置调整的局部优化搜索算法，通过撤销作业i对作业j物料摆放位置的占用或改变作业i物料的摆放位置，可能使得作业j能够提前执行，缩短项目工期。局部优化搜索机理如图 4所示。

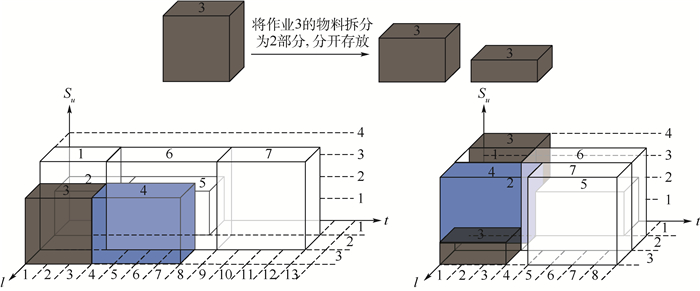图 4 基于物料摆放位置调整的局部优化搜索机理 Fig. 4 Local optimization search mechanism based on material position adjustment

图选项

对于一个包含7作业的项目，l轴表示线边空间单元，t表示时间轴，S_u表示单位线边空间的最大容量，图中方块代表作业的物料需求量。假定允许物料存放在中心摆放位置左右各一格的线边空间单元内，对于作业3的物料(设中心摆放位置l_j^m=2)，若将其拆分为2部分分开存放于线边单元1和单元3中，则作业4在不延期的情况下所需物料在线边单元3中有足够的空间可以存放。因此作业4和作业3可以并行执行，同时后续作业也能提前执行缩短整个项目的工期。
假定作业i的开始时间为T_i^S，完成时间为T_i^F，物料摆放中心位置为l_i^m，作业j的开始时间为T_j^S，完成时间为T_j^F，物料摆放中心位置为l_j^m，所有作业均允许物料占用摆放中心位置左右两侧各m个单位的线边空间。若作业j没有被延期执行，作业i开始时间为T_i^S′，完成时间为T_i^F′，作业j开始时间为T_j^S′，完成时间为T_j^F′。
性质1??在资源约束和配送能力满足的前提下，若作业i和作业j满足以下4个条件，则采用局部算法可以优化项目工期。
1) [l_j^m-m, l_j^m+m]∩[l_i^m-m, l_i^m+m]且i?P_j，表示作业i与作业j的物料线边摆放空间重叠，且作业i不是作业j的紧前作业。
2) T_j^S＞max{T_Pj^F}，表示作业j被延期执行。
3) T_i^S′≤T_j^S′≤T_i^F′，表示若不存在延期，作业i和作业j之间可以存在时间上的重叠，有并行执行的可能。
4) 当T_i^S′≤t≤max{T_i^F′, T_j^F′}，S_left[l_i^m-m, l_i^m+m]-S_uj^m≥S_left[l_i^m-m, l_i^m+m]∩S_left[l_j^m-m, l_j^m+m]，表示可以通过调整部分作业i的物料摆放位置使得作业j的物料能够在不拖期的情况下有足够的空间存放。
证明：
1) 对于作业1~i-1，其开始和结束时间不受影响。
2) 对于作业i与作业j之间的作业，由于只移动了作业i和作业j的物料，对其他作业的物料摆放没有任何改变，不会影响其开始和完成时间。
3) 对于作业j+1~n，由于T_j^F′≤T_j^F，因此T_j+1^F′≤T_j+1^F, …, T_n^F′≤T_n^F，使得总工期必定不会增加。
局部优化搜索算法的具体步骤如下：
步骤1??获取作业安排序列{j₁, j₂, …, j_n}，记优化前调度结果为S，工期为D。
步骤2??令i=1，k=2，选择初始作业1为j_i=j₁，初始作业2为j_k=j₂。
步骤3??若j_i和j_k满足可执行局部优化的4个条件，则标记j_i为作业1，j_k为作业2，否则转步骤7。
步骤4??撤销j_i、j_k及j_k+1~j_n的调度计划，并将作业1的部分物料移至l_i-l_i∩l_j的线边空间单元，将作业2的物料存放进l_i∩l_j线边空间单元。
步骤5??继续执行原来的调度计划，将作业j_k+1~j_n全部安排完, 得到新的调度计划S′，工期为D′。
步骤6??若D′＜D，转入步骤7；否则撤销步骤4和步骤5，并转步骤7。
步骤7??若i≤n且k＜n，k=k+1并转步骤3；若i＜n，k=n，则i=i+1，k=i+1，并转步骤3；若i=n且k=n，转步骤8。
步骤8??输出新的调度计划S′和新的项目工期D′，算法结束。
3 数值实验 本文基于PSPLIB问题库中的算例，根据AMALSP-CMD问题特点对数据进行扩充，为作业数量为10、20、30、60、90、120、480和1 200等8类规模的数据，分别生成10组算例。其中作业间的顺序约束、作业操作时间和所需各类资源量使用PSPLIB问题库中的原数据，同时为算例中的每个作业j随机生成l_j∈(1, 8)的装配位置和v_j∈(5, 10)的物料需求量，并设定飞机移动速度V=0.1，物料可占用左右两侧各2个单位的线边空间，单位时间综合配送能力上限D_max=25，允许物料最大配送提前期p_max=3。通过C#(VS2010)对算法编程进行测试与分析，实验平台为Intel i7-4790处理器，3.60 GHz主频，8 G内存。
3.1 与CPLEX结果对比 为了验证THBG算法的精确性，通过CPLEX软件对数学模型进行求解，将求得的解与THBG算法得到的结果进行对比。由于CPLEX不适用于求解大规模算例，因此表 1给出了作业规模分别为10、20、30各10组不同算例的求解结果。表 1中：Dur为项目的工期；T_CPU为CPU求解时间；GAP为THBG算法得到的工期与CPLEX求得结果的差值百分比，计算公式为GAP= 。
表 1 小规模算例数值实验结果 Table 1 Numerical experiment results of small-scale examples

作业规模	算例	Dur/TCPU		GAP/%
		CPLEX	THBG
10	1	16/0.58	16/0.54	0.00
	2	23/1.43	23/0.53	0.00
	3	13/1.61	13/0.53	0.00
	4	34/2.77	34/0.52	0.00
	5	20/1.11	20/0.50	0.00
	6	31/0.93	31/0.54	0.00
	7	20/0.92	20/0.52	0.00
	8	22/1.87	22/0.52	0.00
	9	22/0.58	22/0.49	0.00
	10	20/1.05	20/0.51	0.00
	平均值	22.1/1.29	22.1/0.52	0.00
20	1	24/66.67	24/0.83	0.00
	2	24/6.14	24/0.83	0.00
	3	33/126.88	35/0.83	5.71
	4	36/23.06	36/0.84	0.00
	5	24/13.29	24/0.83	0.00
	6	18/3.63	18/0.85	0.00
	7	24/21.36	24/0.84	0.00
	8	27/7.28	27/0.82	0.00
	9	22/3.58	22/0.83	0.00
	10	22/17.50	23/0.85	4.35
	平均值	25.4/28.94	25.7/0.84	1.01
30	1	43/810	43/1.52	0.00
	2	53/677	53/1.54	0.00
	3	37/3 478	37/1.46	0.00
	4	41/9 478	42/1.58	2.44
	5	46/25 007	47/1.49	2.17
	6	42/3 811	42/1.71	0.00
	7	61/14 967	62/1.48	1.64
	8	LB=52/-	57/1.47	9.62*
	9	LB=51/-	57/1.48	11.76*
	10	61/32 927	61/1.50	0.00
	平均值	48/11 394	50.1/1.52	0.78
注：CPLEX栏中数据，如16/0.58表示CPLEX求得的精确解和CPU时间，LB=52/-表示CPLEX在可接受时间(36 000 s)内无法求出问题可行解，记录其低界值LB=52；THBG栏中数据，如16/0.54表示THBG算法得到的解和CPU时间；GAP栏中“*”表示CPLEX得不到可行解时用低界计算GAP值。

表选项






通过与CPLEX实验对比可以发现，在小规模问题中，THBG算法在大多数算例中都能获得较好的解。在作业规模为10的算例下，均能得到最优解，当作业规模为20和30时，与最优解差值的均值分别为1.01%和0.78%，证明了THBG算法的有效性。随着作业规模增加，CPLEX求解所需的时间迅速上升，在作业规模为30下，平均计算时间达到了11 394 s，甚至无法在可接受时间内得到理想的低界。而THBG算法不仅能在较短时间内得到优质解，且求解时间稳定，说明THBG算法在求解时间上也具有巨大的优势。
3.2 大规模数据算法效果对比 为了测试本文算法在求解大规模数据的效果，选取作业规模为30、60、90、120、480和1 200的算例，并为每个算例增加3类对比实验，R-NMO表示作业物料只能存放在摆放中心位置不允许占用两侧线边空间规则，H-TD表示传统的先安排生产计划后考虑物料配送的两阶段决策算法，H-SCRDS表示基于SCRDS的启发式算法。其中，H-TD算法的具体规则为：
第1阶段，在不考虑物料配送能力与存储决策的情况下仅针对资源约束和作业间的顺序约束做出生产作业计划；第2阶段，对第1阶段做出的生产作业计划进行物料配送的安排。这类决策方式可能会出现厂内物料配送能力不足或线边空间容量无法满足原有生产作业计划的情况发生，此时需要将部分作业延期执行得到新的生产作业计划。在其余条件相同情况下，将上述3种算法的解与本文的THBG算法得到的项目工期进行对比，数值实验结果如表 2和图 5所示。表 2中:Dur表示各个数据规模下10组算例得到的项目工期均值，GAP表示不同算法得到工期结果的差值百分比，其中GAP_(R-NMO)=(Dur_R-NMO-Dur_THBG)/Dur_THBG, GAP_(H-TD)=(Dur_H-TD-Dur_THBG)/Dur_THBG, GAP_(H-SCRDS)=(Dur_H-SCRDS-Dur_THBG)/Dur_THBG。对上述数值实验结果分析可以得出以下结论：
表 2 不同算法工期结果和优化比例 Table 2 Durations and optimal proportion of different algorithms

作业规模	Dur					GAP/%
	R-NMO	H-TD	H-SCRDS	THBG		R-NMO	H-TD	H-SCRDS
30	54.86	56.24	50.17	50.10		9.79	12.38	0.14
60	74.70	73.45	61.89	61.40		21.81	19.19	0.80
90	91.70	93.65	76.03	75.00		22.80	23.78	1.37
120	137.30	156.05	111.53	108.90		26.48	41.75	2.42
480	395.48	393.37	305.24	296.37		33.44	32.73	2.99
1 200	981.50	1 033.62	739.00	709.44		38.35	45.70	4.17

表选项

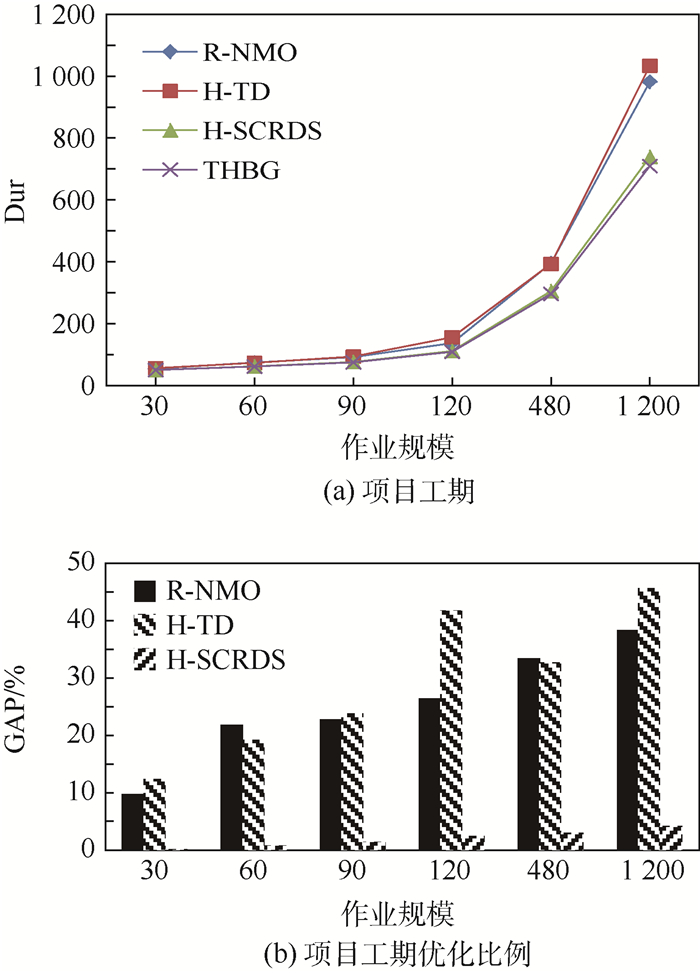图 5 不同算法计算工期结果比较 Fig. 5 Comparison of durations of different algorithms

图选项

1) 本文设计的SCRDS算法相比于物料不能占用两侧线边空间的规则对项目工期结果有很大的优化，SCRDS算法对飞机移动生产线边空间进行了有效的分配与利用，提高了线边空间的使用效率。在项目作业规模为30时，相比于R-NMO规则所得结果的优化比例为9.79%，当项目的作业规模为60、90和120时，优化比例分别为21.81%、22.80%和26.48%，均超过20%，作业规模为1 200时，平均优化比例可以达到38.35%。
2) THBG算法在各个规模的问题上得到的结果都优于H-TD算法得到的结果。当作业规模为1 200时，THBG算法相比H-TD算法得到的结果优化比例均值达到了45.70%，说明将AMALSP-CMD问题中的资源、物料配送能力等约束综合考虑对装配计划进行决策相比传统的两阶段调度方法具有优势。
3) 问题规模较小时，局部优化算法效果不明显，只有少数项目可以实现工期优化。随着问题规模的增大，局部优化算法效果逐渐变好。当问题规模为1 200时，平均优化比例超过4%。由于SCRDS算法对线边空间的利用率已经很高，在作业规模较小时，很难找到满足条件的作业通过微调物料摆放位置使其提前执行，因此该局部优化算法针对大规模算例效果较好。
4 结论 1) 以飞机移动生产线为实际背景，将其抽象为资源受限项目调度问题，并引入了物料配送能力约束和线边空间物料存放的约束，对AMALSP-CMD问题建立了相应的数学模型
2) 针对物料的JIT配送策略及线边空间物料的摆放设计了以遗传算法为框架的启发式算法，提高了线边空间利用率，减少了因物料存放空间不足无法配送导致的作业延期，优化了项目总工期。
3) 通过数值实验对算法进行了验证，结果证明了本文算法的有效性，与传统两阶段决策算法相比，将物料配送及其在线边空间的存放与装配中的资源等约束进行综合考虑，具有较高的理论与实际意义。

参考文献

[1]	CHALESHTARTI A S, SHADROKH S. Branch and bound algorithms for resource constrained project scheduling problem subject to cumulative resources[C]//International Conference on Information Management, Innovation Management and Industrial Engineering.Piscataway, NJ:IEEE Press, 2011:147-152.
[2]	BERTHOLD T, HEINZ S, LVBBECKE M E, et al.A constraint integer programming approach for resource-constrained project scheduling[M]//LODI A, MILANO M, TOTH P.Integration of AI and OR techniques in constraint programming for combinatorial optimization problems.Berlin:Springer, 2010:313-317.
[3]	BLAZEWICZ J, LENSTRA J K, KAN A H G R. Scheduling subject to resource constraints:Classification and complexity[J].Discrete Applied Mathematics, 1983, 5(1): 11–24.DOI:10.1016/0166-218X(83)90012-4
[4]	TORMOS P, LOVA A. An efficient multi-pass heuristic for project scheduling with constrained resources[J].International Journal of Production Research, 2003, 41(5): 1071–1086.DOI:10.1080/0020754021000033904
[5]	BUKATA L, ?ǔCHA P, HANZáLEK Z. Solving the resource constrained project scheduling problem using the parallel Tabu search designed for the CUDA platform[J].Journal of Parallel & Distributed Computing, 2014, 77(11): 58–68.
[6]	BOULEIMEN K, LECOCQ H. A new efficient simulated annealing algorithm for the resource-constrained project scheduling problem and its multiple mode version[J].European Journal of Operational Research, 2003, 149(2): 268–281.DOI:10.1016/S0377-2217(02)00761-0
[7]	ALCARAZ J, MAROTO C. A robust genetic algorithm for resource allocation in project scheduling[J].Annals of Operations Research, 2013, 102(1): 83–109.
[8]	HARTMANN S. A self-adapting genetic algorithm for project scheduling under resource constraints[J].Naval Research Logistics, 2002, 49(5): 433–448.DOI:10.1002/(ISSN)1520-6750
[9]	MERKLE D, MIDDENDORF M, SCHMECK H. Ant colony optimization for resource-constrained project scheduling[J].IEEE Transactions on Evolutionary Computation, 2002, 6(4): 333–346.DOI:10.1109/TEVC.2002.802450
[10]	KUMAR N, VIDYARTHI D P. A model for resource-constrained project scheduling using adaptive PSO[J].Soft Computing, 2015, 20(4): 1565–1580.
[11]	王琰, 陆志强. 基于多重约束的飞机移动装配线作业调度优化[J].工业工程与管理, 2011, 16(6): 115–120. WANG Y, LU Z Q. Job scheduling optimization of aircraft moving assembly line under multiple constraints[J].Industrial Engineering & Management, 2011, 16(6): 115–120.(in Chinese)
[12]	郑倩, 奚立峰. 飞机移动生产线作业调度问题的启发式算法[J].工业工程与管理, 2015, 20(2): 116–121. ZHENG Q, XI L F. Heuristics for aircraft moving assembly line scheduling problem[J].Industrial Engineering & Management, 2015, 20(2): 116–121.(in Chinese)
[13]	葛茂根, 刘明周, 钱芳, 等. 基于JIT的多目标总装准时物料配送方法研究[J].中国机械工程, 2011, 22(23): 2834–2838. GE M G, LIU M Z, QIAN F, et al. Research on multi-objective method on main assembly material delivery based on JIT[J].China Mechanical Engineering, 2011, 22(23): 2834–2838.(in Chinese)
[14]	FATHI M, ALVAREZ M J, MEHRABAN F H, et al. A multiobjective optimization algorithm to solve the part feeding problem in mixed-model assembly lines[J].Mathematical Problems in Engineering, 2014, 11(1): 809–812.
[15]	FATHI M, RODRíGUEZ V, FONTES D B M M, et al. A modified particle swarm optimization algorithm to solve the part feeding problem at assembly lines[J].International Journal of Production Research, 2016, 54(3): 1–16.
[16]	KHAYAT G E, LANGEVIN A, RIOPEL D. Integrated production and material handling scheduling using mathematical programming and constraint programming[J].European Journal of Operational Research, 2006, 175(3): 1818–1832.DOI:10.1016/j.ejor.2005.02.077
[17]	AGUIRRE A M, MéNDEZ C A, CASTRO P M. A hybrid scheduling approach for automated flowshops with material handling and time constraints[J].International Journal of Production Research, 2014, 52(9): 2788–2806.DOI:10.1080/00207543.2014.885664