随着航空航天技术的发展和电子系统应用的拓展，电子系统对于可靠性的要求越来越高。电子系统的可靠性是衡量系统工作性能的重要指标，同时也是指导系统结构设计的重要依据，因此，合理准确地分析电子系统的可靠性显得尤为重要。胚胎电子阵列(Embryonic Electronic Array, EEA)是一种基于多细胞生物生长和发育过程而设计的新型硬件结构，具有类似于生物的自组织、自检测和自修复功能^[1]，其具有的自修复能力能够有效地提高电子系统的可靠性，本文主要对胚胎电子阵列的可靠性进行了研究。
20世纪90年代，Garis^[2]和Mange等^[3]提出了仿生硬件的概念，仿生硬件分为进化型硬件和胚胎型硬件^[4]。胚胎电子阵列是胚胎型硬件的基础，一经提出就受到了国内外****的广泛关注，并取得了大量的研究成果。Ortega和Tyrrell研究了胚胎电子阵列的基本结构和故障自修复方法^[5]，并基于n/k系统理论对阵列的可靠性进行了分析^[6]，为后续研究打下了基础。文献[7]研究了基于总线的胚胎电子阵列结构，利用总线通信的优势简化了胚胎电子阵列的内部通信和自修复实现的复杂程度，并基于n/k系统模型建立了阵列的可靠性模型，与典型的胚胎电子阵列进行了对比分析^[7]。文献[8-9]研究了基于原核细胞的原核胚胎电子阵列，实现了故障自修复，并基于可靠性和硬件资源消耗2个指标，与真核胚胎电子阵列进行了深入对比分析。文献[10]研究了具有多种连接方式的胚胎电子阵列结构，有效地提高了阵列的自修复能力，基于可靠性指标对阵列内基因备份数目优选^[11]和阵列的性能进行了研究。南京航空航天大学的王友仁教授团队基于n/k系统理论及其改进模型对胚胎电子阵列在行(列)移除自修复和细胞移除自修复方式下的可靠性进行了深入研究，将可靠性作为胚胎电子阵列自修复策略选择的重要参考指标^[12-13]。在阵列可靠性研究的基础上，对胚胎电子阵列的布局进行了优化^[14]。考虑阵列中细胞粒度对于可靠性建模的影响^[15]，改进传统的可靠性模型，研究了应用设计过程的可靠性提高方法。文献[16]基于n/k系统模型分析了胚胎电子阵列的可靠性，并研究了n×n规模胚胎电子阵列的优化设计，为实际应用打下了基础。文献[17]基于可靠性指标，对演化硬件的性能进行了深入分析。
胚胎电子阵列的可靠性是衡量阵列结构和自修复能力的重要指标，同时也是衡量电子阵列工作性能的重要指标。现有关于胚胎电子阵列可靠性分析主要是基于n/k系统可靠性模型，该方法能够分析电子阵列可靠性随时间的变化，但是不能准确地将阵列的工作状态与阵列可靠性结合起来，更加透彻地分析阵列可靠性的规律。多态系统理论^[18]能够准确地定义部件的多态性，透彻地分析部件性能的变化对系统性能和可靠性的影响，以及系统失效的渐变过程，因此在复杂系统可靠性分析和优化设计领域有广阔的应用前景^[19]。
分析总线胚胎电子阵列(Bus-Based Embryonic Electronic Array, BBEEA)的结构特点和工作原理，将多态系统理论引入到总线胚胎电子阵列的可靠性分析中，利用通用生成函数(Universal Generating Function, UGF)方法建立总线胚胎电子阵列的可靠性分析模型。与基于n/k系统的电子阵列可靠性分析模型进行对比，对基于多态系统电子阵列可靠性分析模型的正确性和有效性进行验证。基于建立的多态系统阵列可靠性分析模型对总线胚胎电子阵列的可靠性进行分析，并根据阵列的可靠性要求指导阵列的结构设计。同时，对比不同规模总线胚胎电子阵列与典型胚胎电子阵列的可靠性，对总线胚胎电子阵列的性能进行分析。
1 总线胚胎电子阵列 1.1 总线胚胎电子阵列结构 现有胚胎电子阵列结构应用于大规模数字电路设计时，存在硬件资源消耗大、故障覆盖率低和资源利用率低等不足。为了使胚胎电子阵列技术适用于大规模数字电路的设计实现，从功能分解的角度设计了一种总线胚胎电子阵列结构，如图 1所示。

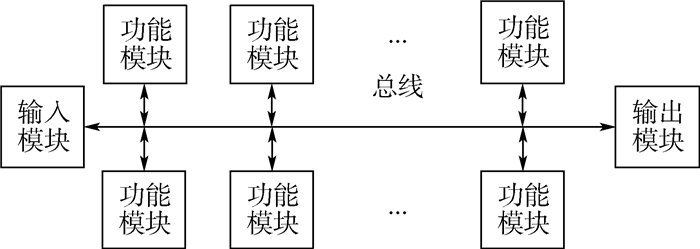图 1 总线胚胎电子阵列结构 Fig. 1 Structure of bus-based embryonic electronic array

图选项

总线胚胎电子阵列主要由输入模块、输出模块、功能模块和总线组成。其中输入模块完成外部输入信号到胚胎电子阵列的输入；输出模块将胚胎电子阵列的处理结果输出到外部；功能模块是胚胎电子阵列的核心部分，主要完成具体的电路功能；总线将阵列中所有的模块连接起来，完成各个模块间的信号传递。对于复杂的功能电路，首先将功能电路分解为若干简单子电路，将分解后的子功能电路映射到功能模块，由功能模块实现各个子功能电路。输入模块将输入信号输入到总线中，各个功能模块对数据进行处理，最后将处理后的信号由输出模块进行输出，所有的功能模块共同实现复杂的功能电路。
功能模块是总线胚胎电子阵列的核心部分，用于实现具体的功能电路。功能模块主要由胚胎电子细胞和检测控制模块组成，功能模块的具体结构如图 2所示。功能模块内的胚胎电子细胞分为工作细胞和空闲细胞2种，所有的工作细胞与空闲细胞成链状连接，胚胎电子细胞均与检测控制模块相连。工作细胞主要实现具体的电路功能，空闲细胞主要用于实现故障自修复。胚胎电子细胞由控制单元、基因配置存储单元、功能单元和输入输出单元构成。检测控制模块主要实现电路正常工作、故障自修复和故障检测的控制。功能模块内的空闲细胞和工作细胞数目可以根据电路的设计要求灵活选择。

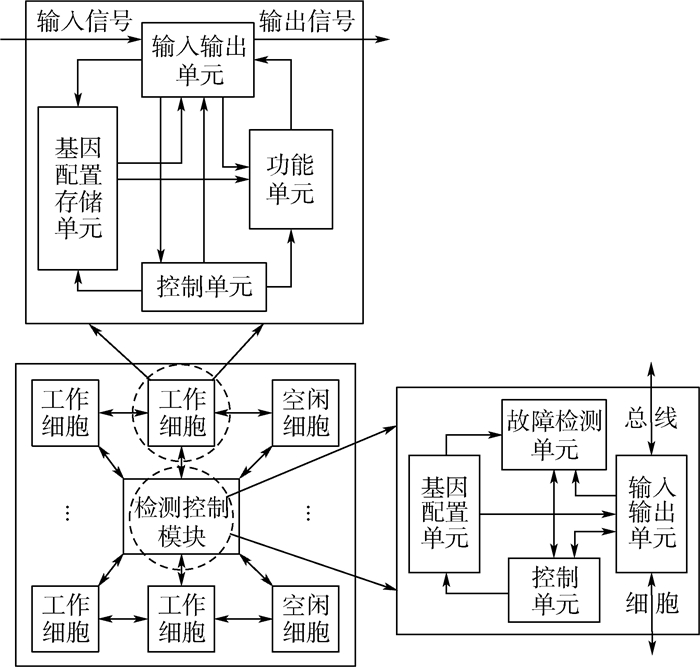图 2 功能模块结构 Fig. 2 Structure of functional block

图选项

1.2 循环移除故障自修复策略 总线胚胎电子阵列中所有的电路功能由功能模块进行实现，所以故障自修复仅在各个功能模块中进行。功能模块内所有的胚胎电子细胞成链状连接，所以采用一种循环移除的故障自修复策略，其基本原理如图 3所示。

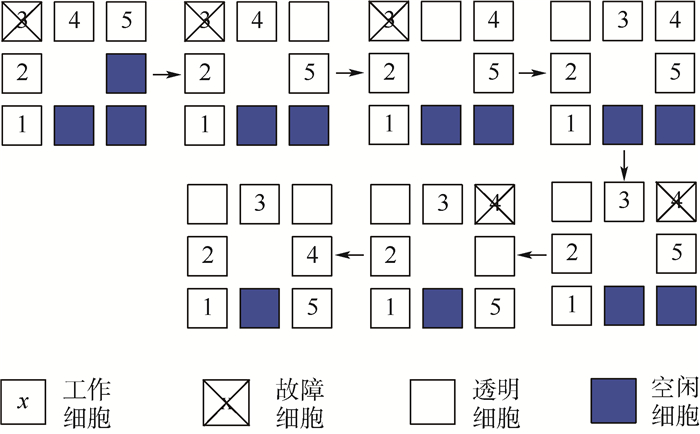图 3 循环移除故障自修复 Fig. 3 Cyclic elimination fault self-repair

图选项

当胚胎电子阵列中功能模块的功能出现故障时，并不知道故障细胞具体的位置。启动循环移除故障自修复功能，首先细胞5的基因向后移动1位并重新配置表达，细胞5变为透明状态，充当导线作用，此时电路功能仍不正常，说明细胞5无故障。以同样的步骤开始移动细胞4的基因，此时功能仍不正常，说明细胞4正常。移动细胞3的基因，当细胞3变为透明状态时，功能模块功能恢复正常，故障自修复完成。当细胞4出现故障，首先细胞5的基因向后移动1位并重新配置表达，细胞5变为透明状态，此时功能仍不正常，说明细胞5无故障。以同样的步骤开始移动细胞4的基因，细胞4变为透明状态，功能模块的功能恢复正常，故障自修复完成。
2 多态系统理论可靠性分析模型 2.1 多态系统理论 多态系统主要分为多工作(或失效)状态系统和多性能水平系统，其中多工作(或失效)状态系统是指系统除了“正常工作”和“完全失效”2种状态外，还具有多种工作(或失效)状态^[18]。
多态系统中一些部件失效或者性能衰退会导致系统部分失效或系统性能下降，从而引起整个系统呈现出多种工作(或失效)状态或性能水平^[19]。多态系统理论能够准确定义部件的多态性，能够透彻地分析部件性能变化对系统性能和可靠性的影响，以及系统失效的渐变过程，因此在复杂系统可靠性分析和优化设计领域有广阔的应用前景。
2.2 运算法则 通过UGF方法对部件在工作过程中的状态性能概率分布可表示为^[20]

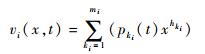(1)

式中：v_i(x, t)为部件i在t时刻处于状态x的概率；p_ki(t)为部件在状态k_i时的状态概率；h_ki为部件处于状态k_i时的状态性能；i为系统中的第i个部件，i=1, 2, …, n，n为系统中部件的总数；k_i为部件i的第k_i个状态，k_i=1, 2, …, m_i，m_i为部件i的状态总数。系统的通用生成函数可以通过如下运算获得：

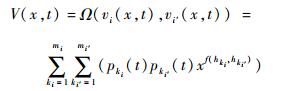(2)

式中：f(h_ki, h_ki′)为系统的状态性能。
根据系统内部部件连接的结构特点，定义如下运算符：
1) 当h_ks为h_ki和h_ki′的最小值时，定义φ₁运算符

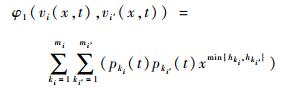(3)

2) 当h_ks为h_ki和h_ki′的和时，定义φ₂运算符

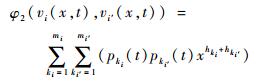(4)

定义多态系统的最小任务性能需求为w，则系统工作过程的可靠度为

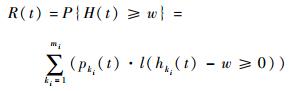(5)

式中：l(h_ki(t)－w≥0)为示性函数，当h_ki(t)－w≥0时，l(h_ki(t)－w)=1, 当h_ki(t)－w < 0时，l(h_ki(t)－w)=0；H(t)={h_mi(t), h_mi-1(t), …, h_ki(t), …, h₂(t), h₁(t)}。
可靠度的本质是概率，为了从时间角度给出系统可靠性明确的评价指标，故采用平均故障前时间(MTTF)来衡量系统的可靠性，则系统的MTTF为

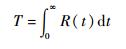(6)

3 总线胚胎电子阵列可靠性建模 3.1 总线胚胎电子阵列结构分析 总线胚胎电子阵列的各个功能模块独立完成各自的功能。阵列中每个功能模块都正常工作，整个阵列才能完成特定的电路功能，因此整个阵列可以近似为一个由功能模块组成的串联系统。功能模块工作过程中，模块中可正常工作胚胎电子细胞数目大于完成电路功能所需要的胚胎电子细胞数目，功能模块就可以正常工作。但是在这个过程中，根据功能模块内可正常工作胚胎电子细胞的数目不同，功能模块存在多个不同工作状态。
总线胚胎电子阵列作为一个系统，功能模块相当于系统中的部件，在工作过程中，若功能模块内出现故障，由于功能模块内存在空闲细胞用于故障自修复，仍能保证功能模块正常工作。功能模块的工作状态相对于最初的工作状态已经发生了变化，但是阵列仍可以正常工作，所以在阵列正常工作过程中，因为功能模块具有多种工作状态，从而总线胚胎电子阵列也就具有了多种状态。因此总线胚胎电子阵列属于多工作状态的多态系统，故可以借助多态系统理论对总线胚胎电子阵列的可靠性进行透彻的分析和建模。
3.2 基于多态系统的阵列可靠性建模 在总线胚胎电子阵列中，假设阵列中功能模块的数目为s，功能模块内工作细胞数目为g，总的细胞数目为m。则单一功能模块可划分为m-g+1个状态，如表 1所示。
表 1 功能模块的状态及概率 Table 1 States and probability of functional block

状态	0	1	…	xj	…	m-g+1
概率	p0(t)	p1(t)	…	pxj(t)	…	pm-g+1(t)

表选项






表 1中，0表示故障状态，即功能模块内可正常工作胚胎电子细胞数目小于g；1表示可正常工作胚胎电子细胞数目为g，功能模块刚好能正常工作；状态x_j表示可正常工作胚胎电子细胞数为x_j+g-1；状态m-g+1表示功能模块的胚胎电子细胞均可以正常工作。
假设电子细胞的失效率为λ，胚胎电子细胞的寿命分布服从指数分布。因此胚胎电子细胞的可靠度(失效概率分布函数)为e^－λt，功能模块各个工作状态对应的概率如下：
状态0即功能模块内可正常工作的胚胎电子细胞数目小于g，则可以正常工作的电子细胞数目可能为0, 1, …, g-1。电子细胞正常工作的概率为e^－λt，对应电子细胞不能正常工作的概率为1-e^－λt。功能模块内可正常工作胚胎电子细胞数目为0时，即功能模块内所有的胚胎电子细胞全都故障，对应的概率为(1－e^－λt)^m=C_m⁰e^－0λt(1－e^－λt)^m。功能模块内可正常工作胚胎电子细胞数目为1时，存在C_m¹种可能情况，对应的概率为C_m¹e^－1λt(1－e^－λt)^m－1。同理可知功能模块内可正常工作胚胎电子细胞数目为g-1时，存在C_m^g－1种可能选择，则对应的概率为C_m^g－1e^{－(g－1)λt}(1－e^－λt)^m－g+1，因此功能模块状态0对应的概率为

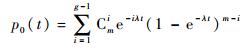(9)

状态1即功能模块内可正常工作的胚胎电子细胞数目为g，存在C_m^g种可能方式。g个胚胎电子细胞正常工作的概率为e^－gλt，剩下m-g个胚胎电子细胞故障的概率为(1－e^－λt)^m－g，因此功能模块状态1对应的概率为

(8)

状态x_j即功能模块内可正常工作的胚胎电子细胞数目为g+x_j-1，存在C_m^g+x_j－1种可能方式。g+x_j-1个胚胎电子细胞正常工作的概率为e^{－(g+x_j－1)λt}，剩下m-g-x_j+1个胚胎电子细胞故障的概率为(1－e^－λt)^{m－g－x_j+1}，因此功能模块状态x_j对应的概率为

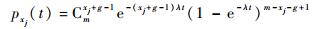(9)

状态m-g+1即功能模块内所有的胚胎电子细胞均可正常工作，这样就存在C_m^m种可能的方式，m个胚胎电子细胞正常工作的概率为e^－mλt，因此功能模块状态m-g+1对应的概率为

(10)

为简化计算的复杂程度，假设每个功能模块内的工作细胞和总的细胞数目相同，细胞的失效率也相同，则所有功能模块的状态数和各个状态对应的概率分布均相同。
对有s个功能模块的总线胚胎电子阵列，各个功能模块间以串联的形式连接。每个功能模块均有m-g+1个状态，则阵列中功能模块具有的状态可表示为x_s1=x_s2=…=x_ss={0, 1，…, m-g+1}，各个工作状态对应的概率可表示为p_s1=p_s2=…=p_ss={p₀(t), p₁(t), …, p_m-g+1(t)}，总线胚胎电子阵列的MTTF计算如下。
设集合A={a₁, a₂, …, a_y}，集合B={b₁, b₂, …, b_y}，定义States运算符。States(A, B)={A(i)×B(j)}(1≤i, j≤y)，即集合A中元素与集合B中元素依次相乘。
1) 阵列内功能模块间是串联结构，因此总线胚胎电子阵列具有的状态X为

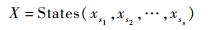(11)

2) 由定义的States运算可得总线胚胎电子阵列各个状态对应的概率P可表示为

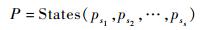(12)

3) 若要保证总线胚胎电子阵列正常工作，则所有功能模块必须正常工作。定义功能模块刚好正常工作的状态为1，要保证整个总线胚胎电子阵列正常工作，则必须保证阵列对应的状态X≥1，则整个阵列正常工作的概率可表示为

(13)

p_α即阵列中所有大于0状态对应的概率之和，总线胚胎电子阵列对应的可靠度R_α(t)=p_α。
4) 总线胚胎电子阵列的MTTF为

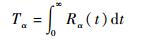(14)

4 可靠性分析模型仿真验证与应用分析 4.1 可靠性分析模型仿真验证 假设总线胚胎电子阵列内功能模块数目s=4，每个功能模块内的胚胎电子细胞数目m=10，功能模块正常工作所需胚胎电子细胞数目g=5，胚胎电子细胞的失效率λ=6×10^-5/h。每个功能模块均具有7个工作状态，为x_j={0, 1, 2, 3, 4, 5, 6}，每个状态对应的概率为p_xj={p₀(t), p₁(t), p₂(t), p₃(t), p₄(t), p₅(t), p₆(t)}。

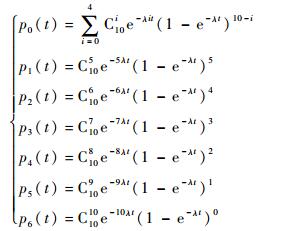(15)

由式(11)和式(12)可知，总线胚胎电子阵列共具有76个工作状态，为X={0, 1, 2, 3, 4, …, 900, 1 080, 1 296}, 各个工作状态对应的概率P={q₀(t), q₁(t), q₂(t), q₃(t), q₄(t), …, q₉₀₀(t), q_{1 080}(t), q_{1 296}(t)}，由第3节基于多态系统的可靠性分析模型计算可知，阵列的可靠度曲线如图 4所示。

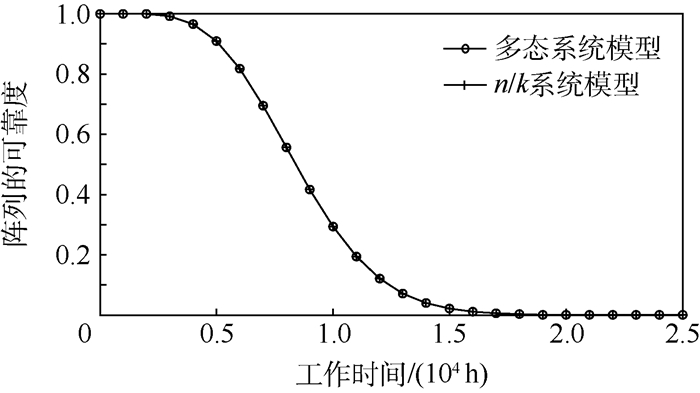图 4 2种可靠性分析模型下总线胚胎电子阵列的可靠度曲线 Fig. 4 Reliability curve of BBEEA with two kindsof reliability analysis model

图选项

为了验证本文模型的有效性，以文献[21]中基于n/k系统理论对总线胚胎电子阵列的可靠性分析为对比对象。阵列中每个功能模块的可靠度R_x(t)为

(16)

整个阵列的可靠度R_z(t)为

(17)

从而总线胚胎电子阵列的MTTF用T_z表示为

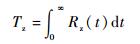(18)

基于n/k系统建立的可靠性分析模型，利用MATLAB对总线胚胎电子阵列的可靠性进行仿真分析，结果也如图 4所示。
图 4为总线胚胎电子阵列在2种不同可靠性分析模型下的可靠度曲线，阵列在某个时刻的可靠度即阵列在该时刻可以正常工作的概率。图 4中基于2种不同可靠性分析模型的阵列可靠度曲线几乎完全重合，表明基于多态系统的可靠性分析模型能够准确衡量阵列的可靠度变化。随着阵列时间的增加，2种可靠性分析模型计算的阵列可靠度曲线均从1变为0。0~0.12×10⁴ h，阵列的可靠度为1，阵列开始工作时，所有的部件均工作性能良好，阵列此时能够正常工作，可靠度为1。0.12×10⁴~0.52×10⁴ h，阵列的可靠度开始下降，仍高于0.9，随着工作时间的增加，部件发生失效，阵列的可靠度开始下降，但是因为功能模块中有空闲细胞可用于故障修复，因此阵列的可靠度处于较高水平。0.52×10⁴ h后，随着阵列工作时间的增加，阵列可靠度下降速率加快，阵列的可靠度逐渐下降为0。随着工作时间增加，阵列中故障细胞数目增加，而阵列的容错能力有限，且阵列内功能模块间组成串联系统，当功能模块内故障细胞数超过了空闲细胞数目，功能模块就将故障，从而导致阵列失效，阵列的可靠度降为0。
4.2 多态系统可靠性分析模型应用分析
4.2.1 总线胚胎电子阵列结构设计 利用多态系统可靠性分析模型对总线胚胎电子阵列的可靠性进行分析，根据阵列的可靠性设计要求指导阵列的结构设计。当功能模块内胚胎电子细胞数目一定时，可以改变功能模块内空闲细胞的数目，改变阵列的可靠性。当功能模块内空闲细胞数目一定时，可以改变功能模块内工作细胞数目，改变阵列的可靠性。
基于总线胚胎电子阵列设计实现某功能电路需要消耗12个工作细胞，为保证总线胚胎电子阵列的MTTF大于1.2×10⁴ h，应如何设计阵列的结构使之满足设计要求？
1) 功能模块内胚胎电子细胞数目一定
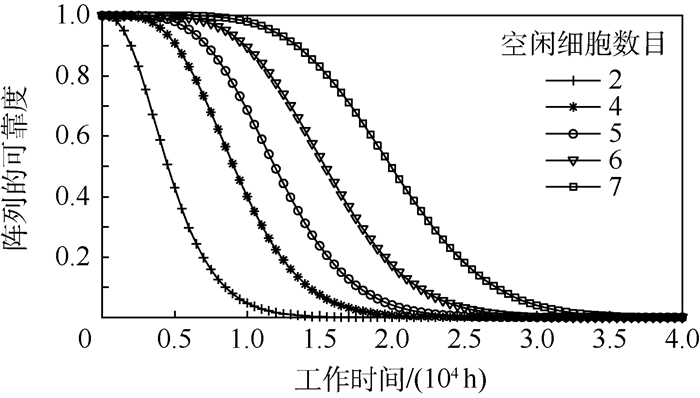
假设每个功能模块有8个胚胎电子细胞，通过改变功能模块中空闲细胞的数目改变阵列的MTTF。为保证每个功能模块内空闲细胞数相同，选择功能模块内空闲细胞数目分别为2、4、5、6和7，对应阵列的可靠度曲线如图 5所示，随功能模块内空闲细胞数目的变化, 阵列的MTTF如图 6所示，具体数值见表 2。

图 5 功能模块内选择不同空闲细胞数目时总线胚胎电子阵列的可靠度曲线 Fig. 5 Reliability curves of BBEEA with different numbers of spare cells chosen in functional block

图选项

图 6 功能模块内选择不同空闲细胞数目时总线胚胎电子阵列的MTTF曲线 Fig. 6 MTTF curve of BBEEA with different numbers of spare cells chosen in functional block

图选项

表 2 功能模块内选择不同空闲细胞数目时总线胚胎电子阵列的MTTF值 Table 2 MTTF of BBEEA with different numbers of spare cells chosen in functional block

空闲细胞数目	2	4	5	6	7
阵列的MTTF/h	4 967	9 455	12 251	15 667	20 160

表选项






图 5为功能模块内选择不同数目空闲细胞阵列的可靠度曲线。随着工作时间的增加，阵列的可靠度由1下降为0，功能模块内选择不同数目空闲细胞阵列的可靠度下降速度不一致。功能模块内空闲细胞数目为2时，阵列的可靠度下降最快；功能模块内空闲细胞数目为7时，阵列的可靠度下降最慢。随着功能模块内空闲细胞数目的增加，阵列的可靠度下降速度减缓。随着功能模块内空闲细胞数目的增加，功能模块能够自修复的次数也增加，阵列能够正常工作的时间更长，所以阵列的可靠度下降速度减缓。
图 6和表 2为功能模块内选择不同数目空闲细胞阵列的MTTF。功能模块内空闲细胞数目为2时，阵列的MTTF最小，功能模块内空闲细胞数目为7时，阵列的MTTF最大。随着功能模块内空闲细胞数目的增加，阵列的MTTF也不断增加，且增加的速度越来越快。实现功能电路需要工作细胞数目一定，当功能模块内总的细胞数目一定时，功能模块内空闲细胞数目越多，阵列的空闲细胞数目越多，阵列可自修复的次数越多，阵列的MTTF就越高，从而阵列可正常工作的时间就越长。当功能模块内空闲细胞数目为2、4、5、6和7时，阵列内总的空闲细胞数目为4、12、20、36和84。随着功能模块内空闲细胞数目的增加，阵列总的空闲细胞数目增加越来越多，所以随着功能模块内空闲细胞数目的增加，阵列MTTF增加速率不断增加。
阵列设计要求MTTF大于1.2×10⁴ h，根据分析当阵列功能模块内空闲细胞数目大于等于5时，阵列的MTTF满足设计要求。所以在设计阵列结构时，当功能模块内细胞数目固定为8时，选择阵列内空闲细胞数目大于等于5时，可满足设计要求。
2) 功能模块内空闲细胞数目一定
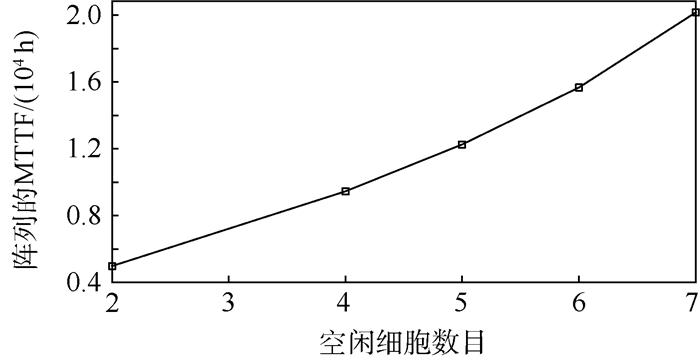
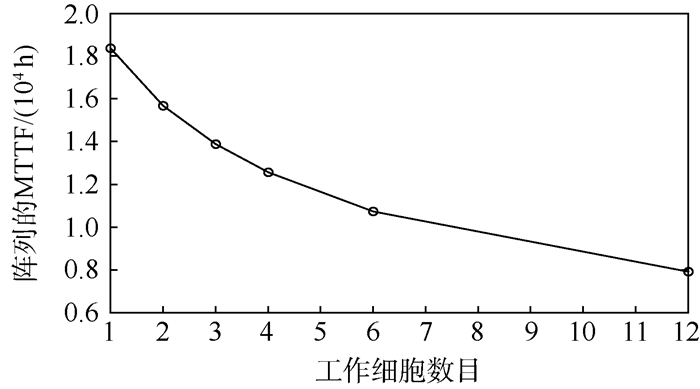
假设每个功能模块内空闲细胞的数目为6，改变功能模块内工作细胞的数目，改变阵列的MTTF。为保证每个功能模块内细胞数目相同，选择功能模块内工作细胞数目分别为1、2、3、4、6和12，对应阵列的可靠度曲线如图 7所示，随功能模块内工作细胞数目变化, 阵列的MTTF如图 8所示，具体数值见表 3。

图 7 功能模块内选择不同工作细胞数目时总线胚胎电子阵列的可靠度曲线 Fig. 7 Reliability curves of BBEEA with different numbers of work cells chosen in functional block

图选项

图 8 功能模块内选择不同工作细胞数目时总线胚胎电子阵列的MTTF曲线 Fig. 8 MTTF curve of BBEEA with different numbers of work cells chosen in functional block

图选项

表 3 功能模块内选择不同工作细胞数目时总线胚胎电子阵列的MTTF值 Table 3 MTTF of BBEEA with different numbers of work cells chosen in functional block

工作细胞数目	1	2	3	4	6	12
阵列的MTTF/h	18 359	15 667	13 870	12 558	10 734	7 921

表选项






图 7为功能模块内选择不同数目工作细胞阵列的可靠度变化曲线。随着工作时间的增加，阵列的可靠度均由1下降至0，其中功能模块内工作细胞数目为12时，阵列的可靠度下降最快，功能模块内工作细胞数目为1时，阵列的可靠度下降最慢。随着功能模块内工作细胞数目的减少，阵列的可靠度下降依次变慢。功能电路实现需要的工作细胞数目一定，功能模块中空闲细胞数目一定，功能模块中的工作细胞数目越少，阵列中功能模块数目就越多，整个阵列内空闲细胞数目就越多，阵列可自修复次数就越多，阵列能够正常工作的概率就大，阵列的可靠度曲线下降就越慢。
图 8和表 3为功能模块内选择不同数目工作细胞数目阵列的MTTF。当功能模块内工作细胞数目为1时，阵列的MTTF最大，当功能模块内工作细胞数目为12时，阵列的MTTF最小。随着功能模块内工作细胞数目的增加，阵列的MTTF依次下降，且下降的速度依次变缓。实现功能电路需要工作细胞的数目为12个，每个功能模块内空闲细胞的数目固定为6个，随着功能模块内工作细胞数目的增加，阵列中空闲细胞的数目不断下降，阵列可自修复的次数不断减少，阵列能够正常工作的时间也下降，阵列的MTTF也不断下降。当功能模块内工作细胞的数目分别为1、2、3、4、6和12时，阵列内空闲细胞的数目分别为72、36、24、18、12和6，阵列中功能模块的数目分别为12、6、4、3、2和1。随着功能模块内工作细胞数目的增加，阵列内空闲细胞数目减少的数目越来越少，所以阵列的MTTF下降速度不断变缓。
阵列设计要求MTTF大于1.2×10⁴ h，阵列中每个功能模块内的空闲细胞数目一定，可以通过改变功能模块内工作细胞数目的方法改变阵列的MTTF。根据上述分析，当功能模块中工作细胞数目小于等于4时，阵列的MTTF满足设计要求。

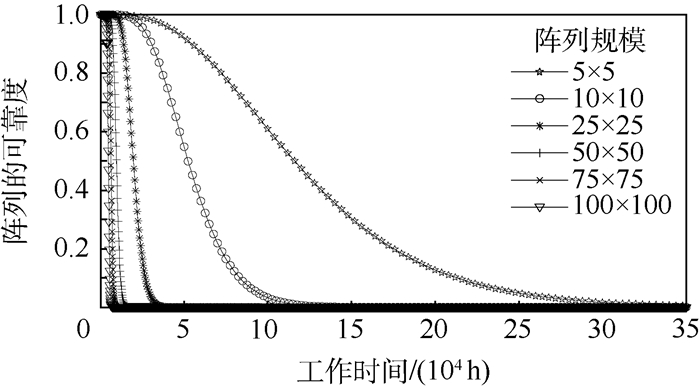
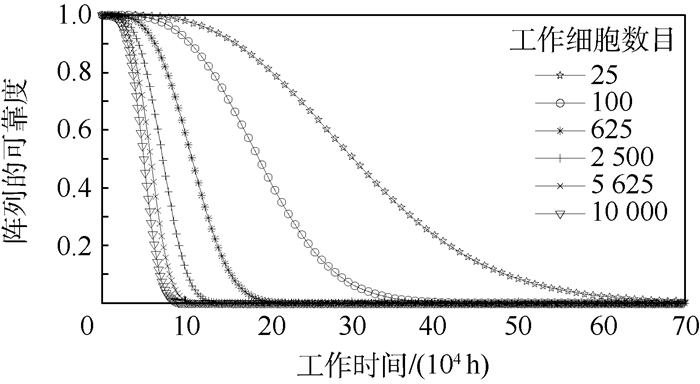
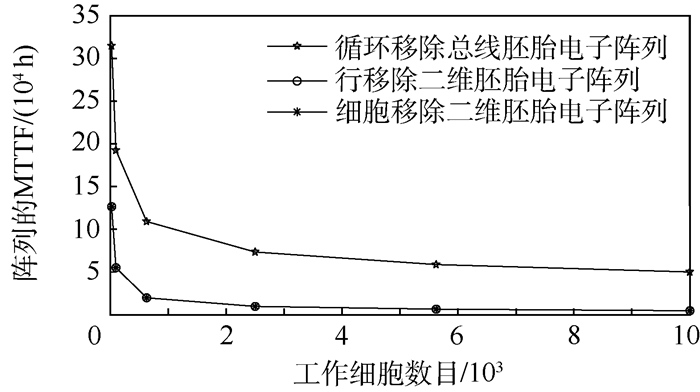
4.2.2 总线胚胎电子阵列性能分析 可靠性是衡量胚胎电子阵列性能的重要指标。为了对总线胚胎电子阵列的可靠性指标进行分析，选择典型的二维胚胎电子阵列进行对比分析，二维胚胎电子阵列的可靠性在文献[22]中进行了详细的分析。选取阵列工作细胞数目分别为25、100、625、2 500、5 625和10 000个，阵列中空闲细胞数目分别为15、60、375、1 500、3 375和6 000。二维胚胎电子阵列中工作阵列的规模分别为5×5、10×10、25×25、50×50、75×75和100×100，为使行移除自修复获得最大的可靠性，二维胚胎电子阵列的规模分别为8×5、16×10、40×25、80×50、120×75和160×100。总线胚胎电子阵列中，功能模块的结构都相同，每个功能模块由5个工作细胞和3个空闲细胞组成，胚胎电子细胞的失效率均相同为λ=1×10^-6/h。不同阵列规模下行移除自修复二维胚胎电子阵列的可靠度曲线如图 9所示，不同阵列规模下循环移除自修复总线胚胎电子阵列的可靠度曲线如图 10所示，不同阵列规模下细胞移除自修复二维胚胎电子阵列的可靠度曲线如图 11所示。不同阵列规模下总线胚胎电子阵列、行移除自修复二维胚胎电子阵列与细胞移除自修复二维胚胎电子阵列的MTTF如图 12所示，具体的阵列MTTF如表 4所示。

图 9 不同规模行移除二维胚胎电子阵列的可靠度曲线 Fig. 9 Reliability curves of different scales of two-dimensional EEA with row elimination

图选项

图 10 不同规模循环移除总线胚胎电子阵列的可靠度曲线 Fig. 10 Reliability curves of different scales of BBEEA with cyclic elimination

图选项

图 11 不同规模细胞移除二维胚胎电子阵列的可靠度曲线 Fig. 11 Reliability curves of different scales of two-dimensional EEA with cell elimination

图选项

图 12 不同阵列结构、自修复方式和规模下阵列MTTF曲线 Fig. 12 MTTF curves of array with different structures, self-repair strategies and scales

图选项

表 4 不同阵列结构、自修复方式和规模下阵列MTTF值 Table 4 MTTF of array with different structures, self-repair strategies and scalesh

104h
阵列结构与自修复方式	工作细胞数目
	25	100	625	2 500	5 626	10 000
循环移除总线胚胎电子阵列	31.459	19.248	10.905	7.342 7	5.874 3	5.027 6
行移除二维胚胎电子阵列	12.666	5.517 6	2.010 3	0.972 55	0.641 13	0.478 13
细胞移除二维胚胎电子阵列	12.666	5.517 6	2.010 3	0.972 55	0.641 13	0.478 13

表选项






图 9为不同阵列规模行移除二维胚胎电子阵列可靠度曲线。随着工作时间的增加，阵列的可靠度不断下降，其中阵列规模越大，阵列的可靠度下降越快。胚胎电子阵列只进行了行冗余以保证最大的自修复次数，阵列的规模越大，阵列中胚胎电子细胞数目越多，胚胎电子细胞的失效率相同，因此阵列越容易出现故障，阵列的失效率越高。阵列的冗余行数是固定的，所以阵列的规模越大，阵列的可靠度下降越快。
图 10为不同阵列规模循环移除自修复总线胚胎电子阵列可靠度曲线。随着工作时间的增加，阵列的可靠度都不断下降，且阵列的规模越大，阵列的可靠度下降越快。总线胚胎电子阵列中，功能模块的结构均相同，当阵列规模确定后，功能模块的数目也就确定。总线胚胎电子阵列中，所有的功能模块均必须正常工作，整个阵列才能正常工作，若某个功能模块完全故障无法修复，整个阵列就将失效。每个功能模块内的空闲细胞数目固定，功能模块的自修复次数也就固定，且胚胎电子细胞的失效率相同，阵列规模越大，功能模块数目越多，整个阵列的失效概率就越大，所以阵列的可靠度下降越快。
图 11为不同阵列规模细胞移除二维胚胎电子阵列可靠度曲线。随着工作时间的增加，阵列的可靠度不断下降，且阵列的规模越大，阵列的可靠度下降趋势就越快。已知阵列仅进行了行冗余，根据细胞移除自修复的修复原理，此时的细胞移除自修复与行移除自修复相同。该阵列仅进行了行冗余，所以在工作过程中，阵列中任意一行中出现故障都将进行行移除自修复。阵列中胚胎电子细胞的失效率均相同，阵列的规模越大，阵列某行的失效概率就越大，所以阵列规模越大，阵列的可靠度曲线下降越快。
图 12和表 4为3种不同阵列结构和自修复方式下，不同规模胚胎电子阵列的MTTF。随着阵列规模的增加，3种自修复方式下胚胎电子阵列的MTTF都呈下降趋势，且下降的速率由快变慢。总线胚胎电子阵列中，功能模块的结构均相同，功能模块内空闲细胞数目也是固定的，胚胎电子细胞的失效率相同。阵列的规模越大，阵列内功能模块数目越多，所以阵列的MTTF就会下降。在二维胚胎电子阵列中，阵列规模越大，阵列中每行胚胎电子细胞数目就越多，胚胎电子细胞的失效率均相同，则该行胚胎电子细胞的失效率就越大。阵列的规模固定，可自修复次数固定，所以阵列的MTTF随着阵列规模增加而下降。总线胚胎电子阵列中，由式(18)可知，功能模块数目越少，可靠度曲线下降越慢，且功能模块数目越小，每增加一个功能模块，阵列可靠度下降越快，对应阵列的MTTF也就下降越快；阵列内功能模块数目较大时，功能模块数目增加，对阵列的可靠度影响很小，所以阵列的MTTF减少较慢。同理，对于二维胚胎电子阵列，阵列的行(列)数越小时，阵列的行(列)数目增加1，阵列的可靠度曲线下降越多，对应阵列MTTF减少就越多，当阵列的行(列)数较大时，行(列)数目的增加，阵列的可靠度曲线下降开始减缓，对应阵列的MTTF下降就少。
循环移除自修复总线胚胎电子阵列的MTTF大于行移除自修复二维胚胎电子阵列和细胞移除自修复二维胚胎电子阵列，且行移除自修复二维胚胎电子阵列和细胞移除自修复二维胚胎电子阵列的MTTF完全相同。总线胚胎电子阵列中，阵列理论的最大可自修复次数为空闲细胞的数目，分别为15、60、375、1 500、3 375和6 000。行移除自修复二维胚胎电子阵列中理论最大可修复次数为冗余的行数，分别为3、6、15、30、45和60。细胞移除自修复二维胚胎电子阵列中，因为阵列仅对行进行了冗余，所以此时的细胞移除自修复方式与行移除自修复方式一致，理论最大可修复次数分别为3、6、15、30、45和60。所以循环移除自修复总线胚胎电子阵列的MTTF高于行移除自修复二维胚胎电子阵列和细胞移除自修复二维胚胎电子阵列，且行移除自修复二维胚胎电子阵列和细胞移除自修复二维胚胎电子阵列的MTTF相同。

4.2.3 总线胚胎电子阵列预防性维修 总线胚胎电子阵列具有故障自修复能力，但是故障自修复能力是有限的，为了保证电子系统长时间处于正常工作状态，必须研究阵列的预防性维修。基于多态系统的总线胚胎电子阵列可靠性分析模型可以通过计算得到阵列在任意时刻的工作状态及对应概率，通过阵列处于不同工作状态的概率可以衡量阵列的工作性能，从而为预防性维修提供指导。以4.1节中总线胚胎电子阵列在t=5 000 h时工作为例，阵列的状态及各个状态对应概率如表 5所示。
表 5 t=5 000 h时总线胚胎电子阵列工作状态及概率 Table 5 Work states and probability of BBEEA at t=5 000 h

状态	概率
0	0.090 9
1	0
2	0.000 2
3	0.000 3
4	0.000 9
5	0.000 2
6	0.002 1
8	0.003 2
9	0.001 7
10	0.001 4
12	0.009 0
15	0.002 3
16	0.007 9
18	0.008 8
20	0.005 9
24	0.023 0
25	0.000 8
27	0.004 4
30	0.011 5
32	0.013 5
36	0.027 0
40	0.014 5
45	0.009 0
48	0.040 0
50	0.003 8
54	0.013 1
60	0.034 6
64	0.016 5
72	0.043 3
75	0.006 1
80	0.024 4
81	0.004 3
90	0.024 9
96	0.043 1
100	0.011 0
108	0.025 0
120	0.052 2
128	0.012 9
135	0.017 7
144	0.043 6
150	0.015 8
160	0.024 6
162	0.003 3
180	0.046 2
192	0.028 1
200	0.015 6
216	0.011 9
225	0.011 9
240	0.049 2
250	0.003 3
256	0.005 7
270	0.006 8
288	0.012 8
300	0.028 4
320	0.014 4
324	0.001 0
360	0.015 4
375	0.005 4
384	0.004 1
400	0.013 7
432	0.002 2
450	0.004 6
480	0.007 8
500	0.005 8
540	0.001 3
576	0.001 3
600	0.005 0
625	0.000 9
648	0.000 1
720	0.001 4
750	0.001 1
864	0.000 1
900	0.000 5
1 080	0.000 1
1 296	0

表选项






此时阵列可正常工作概率为所有大于1的工作状态概率之和，即此时的可靠度为R(5 000)=0.909 1，此时阵列处于良好的工作状态。同时，由表 5可以看出，阵列以较高的概率处于状态24至状态400，表明随着阵列工作了5 000 h，阵列内某些部件失效的概率较高，阵列难以处于较好的工作状态，阵列处于状态400以上的概率为0.032 2。又因为阵列内仍有冗余的空闲细胞可以进行故障自修复，所以阵列此时也不会处于较差的工作状态，阵列处于状态24以下的概率为0.134 8。此时阵列的工作状态性能良好，可不进行预防性维修，但是此时阵列的性能相对于最初已经有了一定的下降，需要加强状态检测，当阵列处于较低状态的概率较大时，应立即采取预防性维修，保证阵列能够处于正常工作状态。因此，可以根据阵列在某一时刻所处工作状态的概率，近似衡量阵列的工作性能，为预防性维修决策提供指导。
基于多态系统的总线胚胎电子阵列可靠性分析模型能够非常直观地得到任意时刻总线胚胎电子阵列所处工作状态的概率，根据阵列所处各个状态的概率评估阵列此时的工作状态。如果阵列处于较高状态的概率很大，表明阵列此时的工作性能较好，可不进行维修；当阵列处于较低状态的概率较大时，表明阵列此时的工作性能较差，可以采取预防维修策略，防范阵列功能失效。所以基于多态系统理论的总线胚胎电子阵列可靠性分析模型可以为阵列预防性维修决策提供理论指导。
5 结论 通过分析总线胚胎电子阵列的结构特点和工作原理，将多态系统理论引入到总线胚胎电子阵列的可靠性分析建模中，并利用建立的可靠性模型对总线胚胎电子阵列的结构设计、性能评估和预防性维修决策进行研究。主要结论如下：
1) 通过与典型的n/k系统理论可靠性模型进行对比，基于多态系统理论的总线胚胎电子阵列可靠性分析模型能够准确地评估阵列的可靠性指标，同时可以将阵列的工作状态与可靠性结合起来，能够更透彻地分析阵列的可靠性。
2) 基于多态系统理论的总线胚胎电子阵列可靠性分析模型可以根据阵列的可靠性设计要求，对阵列的结构设计进行指导，能够更加合理地选择阵列内空闲细胞数目和工作细胞数目。
3) 基于多态系统理论的总线胚胎电子阵列可靠性分析模型将阵列的工作状态与可靠性相结合，可以对阵列的预防性维修决策提供指导。
总的来说，基于多态系统理论的总线胚胎电子阵列可靠性分析模型能够准确透彻地分析阵列的可靠性，为胚胎电子阵列技术的可靠性评估提供了一种新思路。同时，利用建立的阵列可靠性分析模型可以对阵列的结构设计、性能分析和预防性维修决策提供理论指导，对胚胎电子阵列技术的工程应用具有重要价值。

参考文献

[1]	蔡金燕, 朱赛, 孟亚峰. 一种新型的仿生电子细胞基因存储结构[J].电子学报, 2016, 44(8): 1915–1923. CAI J Y, ZHU S, MENG Y F. A novel gene memory structure for bio-inspired electronic cell[J].Acta Electronica Sinica, 2016, 44(8): 1915–1923.(in Chinese)
[2]	GARIS H D. Genetic programming: Artificial nervous systems, artificial embryos and embryological electronics[C]//Proceeding of the 1st Workshop on Parallel Problem Solving from Nature, 1990: 117-123.
[3]	MANGE D, GOEKE M, MADON D, et al. Embryonics: A new family of coarse-grained field-programmable gate array with self-repair and self-reproducing properties[C]//Proceeding of 1996 IEEE International Symposium on Circuits and Systems. Piscataway, NJ: IEEE Press, 1996: 25-28.
[4]	YAO X, HIGUCHI T. Promises and challenges of evolvable hardware[J].IEEE Transaction on Systems, Man and Cybernetics, Part C, 1999, 29(1): 87–97.DOI:10.1109/5326.740672
[5]	ORTEGA C, TYRRELL A. Biologically inspired reconfigurable hardware for dependable applications[C]//IEEE Half-day Colloquium on Hardware Systems for Dependable Applications. Piscataway, NJ: IEEE Press, 1997: 1-4.
[6]	ORTEGA C, TYRRELL A. Reliability analysis in self-repairing embryonic systems[C]//Proceeding of the 1st NASA/DoD Workshop on Evolvable Hardware. Piscataway, NJ: IEEE Press, 1999: 120-128.
[7]	李廷鹏. 基于总线结构的仿生自修复技术研究[D]. 长沙: 国防科学技术大学, 2012: 17-32. LI T P. Research on bio-inspired self-repairing technology based on bus structure[D]. Changsha: National University of Defense Technology, 2012: 17-32(in Chinese).
[8]	SAMIE M, DRAGFFY G, POPESCU A. Prokaryotic bio-inspired model for embryonic[C]//Proceedings of the 4th NASA/ESA Conference on Adaptive Hardware and Systems. Piscataway, NJ: IEEE Press, 2009: 163-170.
[9]	李岳, 王南天, 钱彦岭. 原核细胞仿生自修复电路设计[J].国防科学技术大学学报, 2012, 34(3): 154–157. LI Y, WANG N T, QIAN Y L. Self-healing circuit design inspired by prokaryotic cell[J].Journal of National University of Defense Technology, 2012, 34(3): 154–157.(in Chinese)
[10]	ZHU S, CAI J Y, MENG Y F. Partial-DNA cyclic memory for bio-inspired electronic cell[J].Genetic Programming and Evolvable Machines, 2016, 17(2): 83–117.DOI:10.1007/s10710-015-9248-2
[11]	朱赛, 蔡金燕, 孟亚峰, 等. 胚胎电子细胞中基因备份数目优选方法[J].北京航空航天大学学报, 2016, 42(2): 328–336. ZHU S, CAI J Y, MENG Y F, et al. Gene backup number selection method for embryonics cell[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(2): 328–336.(in Chinese)
[12]	ZHANG Z, WANG Y R. Method to self-repair reconfiguration strategy selection of embryonic cellular array on reliability analysis[C]//2014 NASA/ESA Conference on Adaptive Hardware and Systems(AHS). Piscataway, NJ: IEEE Press, 2014: 225-232.
[13]	张砦, 王友仁. 基于可靠性分析的胚胎硬件容错策略选择方法[J].系统工程理论与实践, 2013, 33(1): 236–242. ZHANG Z, WANG Y R. Guidelines to fault-tolerant strategy selection in embryonics hardware based on reliability analysis[J].Systems Engineering-Theory & Practice, 2013, 33(1): 236–242.DOI:10.12011/1000-6788(2013)1-236(in Chinese)
[14]	张砦, 王友仁. 基于可靠性优化的芯片自愈型硬件细胞阵列布局方法[J].航空学报, 2014, 35(12): 3392–3402. ZHANG Z, WANG Y R. Method to reliability improvement of chip self-healing hardware by array layout reformation[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(12): 3392–3402.(in Chinese)
[15]	张砦, 王友仁. 应用设计过程的胚胎硬件细胞单元粒度优化方法[J].航空学报, 2016, 37(11): 3502–3511. ZHANG Z, WANG Y R. Cell granularity optimization method of embryonic hardware in application design process[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(11): 3502–3511.(in Chinese)
[16]	林勇, 罗文坚, 钱海, 等. n×n阵列胚胎电子系统应用中的优化设计问题分析[J].中国科学技术大学学报, 2007, 37(2): 171–176. LIN Y, LUO W J, QIAN H, et al. Analysis of optimization design in n×n array embryonic system applications[J].Journal of University of Science and Technology of China, 2007, 37(2): 171–176.(in Chinese)
[17]	张峻宾, 蔡金燕, 孟亚峰. 基于EHW和RBT的电子电路故障自修复策略性能分析[J].北京航空航天大学学报, 2016, 42(11): 2423–2435. ZHANG J B, CAI J Y, MENG Y F. The performance of electronic circuit fault self-repair strategy based on EHW and RBT[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(11): 2423–2435.(in Chinese)
[18]	李春洋. 基于多态系统理论的可靠性分析与优化设计方法研究[D]. 长沙: 国防科学技术大学, 2010: 48-91. LI C Y. Research on reliability analysis and optimization based on the multi-state system theory[D]. Changsha: National University of Defense Technology, 2010: 48-91(in Chinese).
[19]	潘刚, 尚朝轩, 蔡金燕, 等. 基于Semi-Markov模型的多态系统不完全维修决策研究[J].航空学报, 2017, 38(2): 320178. PAN G, SHANG C X, CAI J Y, et al. Research on imperfect maintenance decision for multi-syatem based on Semi-Markov model[J].Acta Aeronautica et Astronautica Sinica, 2017, 38(2): 320178.(in Chinese)
[20]	LISNIANSKI A, FRENKEL I, DING Y. Multi-state system reliability analysis and optimization for engineers and industrial managers[M].Berlin: Springer, 2010: 143-198.
[21]	王涛, 蔡金燕, 孟亚峰. 总线细胞阵列中空闲细胞冗余数量研究[J].微电子学与计算机, 2016, 33(9): 1–5. WANG T, CAI J Y, MENG Y F. Research on the redundant number of spare cells in bus-based embryonic array[J].Microelectronics & Computer, 2016, 33(9): 1–5.(in Chinese)
[22]	王涛, 蔡金燕, 孟亚峰, 等. 胚胎电子阵列中空闲细胞的配置研究[J].航空学报, 2017, 38(4): 320266. WANG T, CAI J Y, MENG Y F, et al. Research on the configuration of idle cells in embryonics electronic cell array[J].Acta Aeronautica et Astronautica Sinica, 2017, 38(4): 320266.(in Chinese)