Mettas[6]结合加速试验数据利用极大似然估计方法,分析了简单时间-应力相关条件下产品的可靠性,但只分析了产品服从威布尔分布下的情况。Yang[5]引入真实贮存环境的温度和湿度变化曲线,分析真实贮存环境下的火工品的等效贮存期,但是没有评估产品的可靠性。洪东跑等[7]利用了比例风险模型将不同试验环境条件下的试验数据整合成相同环境应力下的试验数据,进而对系统进行可靠性综合评估。并利用了多种环境下的试验数据来确定基准失效率,评估模型参数给出了产品可靠度下限[8],但评估的各环境应力水平都是恒定的。Hong等[9]以一个对数正态分布为例,以斜坡应力加速试验为模型,评估在时变斜坡应力下的可靠性模型。
Benavides[10]利用累积故障模型研究得到时变应力下设备的可靠性模型,该模型只针对两参数威布尔分布。Bian和Gebraeel[11]提出了一个随机退化模型框架来计算在确定且周期变化的环境下部件的剩余寿命。张国龙等[12]在文献[8]的基础上利用比例风险模型评估多阶应力条件下的产品可靠性。González等[13]研究了在时变电压下的电子产品的可靠性模型,利用随机失效累积损伤模型和改良的逆幂律模型来描述时变电压下的电子产品的可靠性。
产品在工作或贮存过程中,为了安全和方便,往往直接暴露于外界的自然环境条件中,仅有极少部分产品工作或贮存于室内,遭受的温度等环境条件由空调等控温设备所控制。产品在生产、装配、运输和使用等阶段也往往处于不同的地理位置,自然环境条件差别较大,因此对于一个给定的产品来说,使用恒定的环境应力来进行可靠性评估是不可取的。
针对传统可靠性评估方法往往只考虑恒定环境应力的情况,引入典型地理位置的真实自然环境的时变应力,使用六参数多项式拟合方法得到环境应力变化趋势,并假定2种时变环境应力模式,在Nelson累积损伤模型的基础上,研究真实时变环境应力下的基于加速寿命试验数据的产品可靠性评估方法。
1 真实自然环境的时变应力 中国跨越热带、温带和寒带3个气候带,不同气候带下的气候环境条件差别较大。查阅资料可得到海口、敦煌和漠河等不同地区的典型地理位置的历史气温情况。图 1绘制了2016年海口每天的最高温度Tmax、最低温度Tmin和平均温度Tavg,可以看出相邻天数的温度变化是巨大的,且每周的温度变化数据是难以平滑的。多项式拟合方法常被用于数据拟合,可良好地反映数据的变化情况[5],拟采用六参数多项式拟合方法有效地平滑整个温度记录数据,可得到其变化趋势。
 |
| 图 1 海口的2016年气温情况 Fig. 1 Temperature condition in Haikou in 2016 |
| 图选项 |
为了便于后文的可靠性评估研究,利用六参数多项式拟合方法处理中国3个典型地理位置的日常平均温度数据,得到其拟合函数如图 2所示。海口的温度曲线拟合函数为
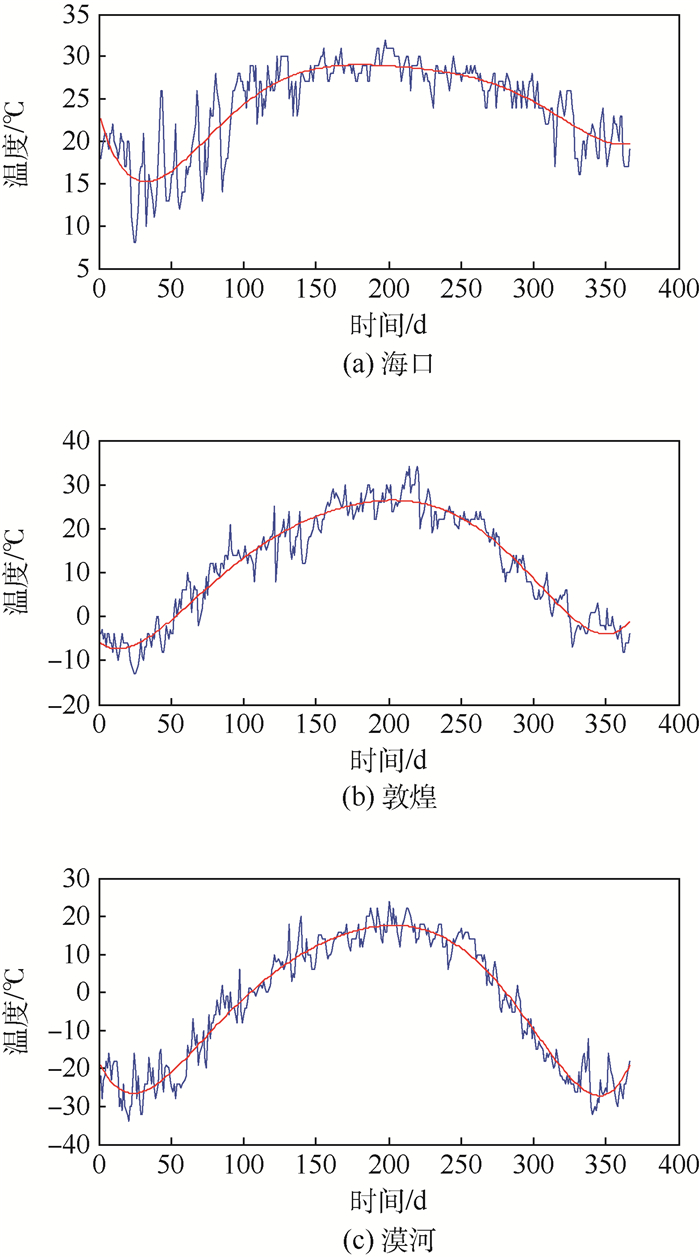 |
| 图 2 典型地理位置的日常平均温度曲线与拟合函数 Fig. 2 Daily average temperature curves and fitting function of typical geographical location |
| 图选项 |
 | (1) |
式中:T为日常平均温度,℃;x为时间,d。
可用日常平均温度来代表每天的温度变化,则产品遭受的环境应力水平S1, S2, …, Sn可由平均温度的拟合函数确定,Si=Tavgi,i=1, 2, …, n,Tavgi为第i天的日常平均温度。其相应的持续时间ti是确定的,ti=24 h,i=1, 2, …, n。其时变环境应力模式如图 3所示。
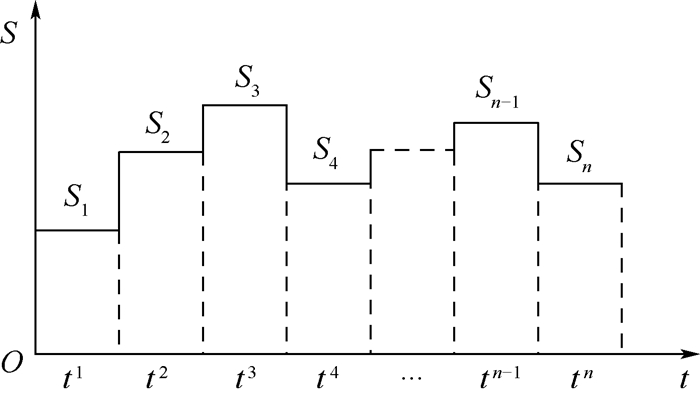 |
| 图 3 时变环境应力模式a Fig. 3 Mode a of time-varying environmental stress |
| 图选项 |
利用日常平均温度的方法是快捷方便的,但可能不太精确。日常昼夜的温度变化中,每天的温度变化表现为最高温度和最低温度之间的交替循环,可利用最高温度和最低温度之间的正弦曲线来表示日常昼夜的温度变化,如图 4所示。每天的温度环境应力成正弦变化趋势,即第k天的温度环境应力为
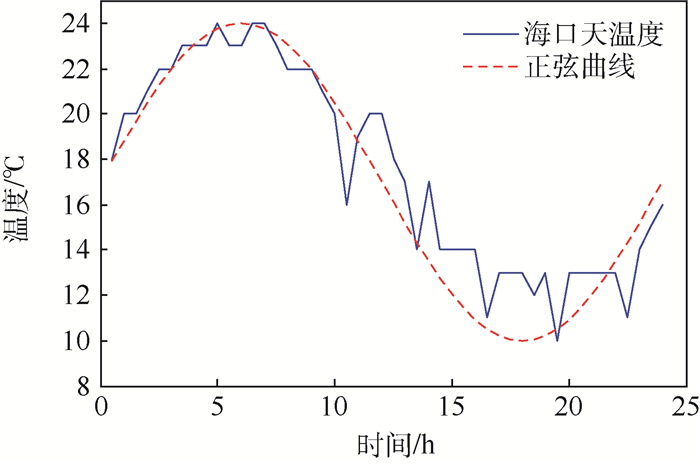 |
| 图 4 海口的天温度数据和正弦曲线 Fig. 4 Daily temperature data in Haikou and sinusoidal curve |
| 图选项 |
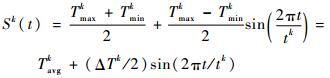 | (2) |
式中:Tmaxk和Tmink分别为第k天的最高温度和最低温度,可由最高温度拟合函数和最低温度拟合函数得到; Tavgk=(Tmaxk+Tmink)/2为第k天的日常平均温度; ΔTk=(Tmaxk-Tmink)/2,tk=24 h,k=1, 2, …, n。其时变环境应力模式如图 5所示。
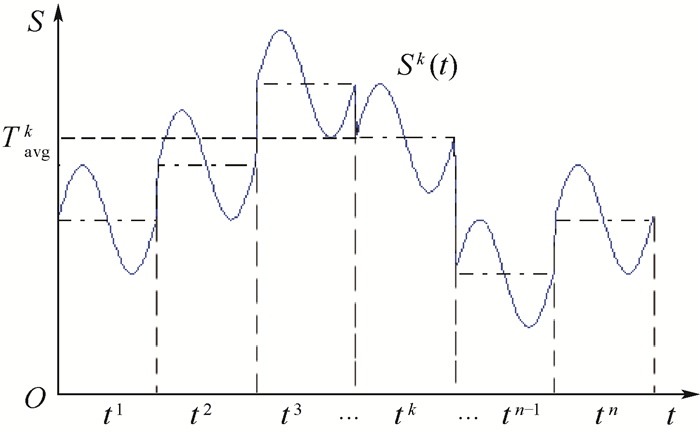 |
| 图 5 时变环境应力模式b Fig. 5 Mode b of time-varying environmental stress |
| 图选项 |
时变环境应力模式a和模式b都能反映产品所处地理位置的年度季节变化所导致的环境应力变化,同时模式b还反映出了所处地理位置每天昼夜变化所导致的环境应力变化。假定不同环境应力水平下产品的失效机理不变,且产品在工作过程中没有受到维修或修复。
2 可靠性评估 2.1 加速模型 加速模型表征了产品失效分布的寿命特征与产品所受应力水平之间的关系,常见的加速模型有Arrhenius模型、Eyring模型和Inverse Power模型等。
在恒定应力下系统失效可能服从指数、威布尔和对数正态等多种分布,其参数和寿命特征如表 1所示,其中参数λ、θ、η和μ随应力大小S而变化,威布尔分布的形状参数m和对数正态分布的形状参数σ被假定为恒定不变。联合考虑失效分布模型和加速模型,可以得到不同应力大小S下的失效分布。
表 1 常用失效分布模型 Table 1 Common failure distribution model
| 分布 | 参数 | 寿命特征 | 累积故障分布函数 |
| 指数 | λ | 平均寿命 |  |
| 威布尔 | m, η | 特征寿命η |  |
| 对数正态 | μ, σ | 中位寿命μ |  |
表选项
2.2 时变环境应力下的可靠性评估 对产品进行步进应力试验,每个应力水平S1, S2, …, Sk下试验持续时间依次为t1, t2-t1, …, tk-tk-1,在Nelson累积损伤模型的基础上,步进加速应力的累积故障分布函数[14]为
 | (3) |
式中:当t=ti时,F(τi, Si+1)=F(ti-ti-1+τi-1, Si),i=1, 2, …, k-1,且t0=τ0=0。以威布尔分布为例,则
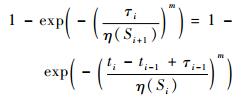 | (4) |
其中:时间
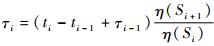
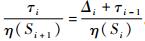
 | (5) |
 | (6) |
同理当产品失效服从指数分布时,
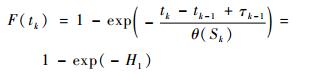 | (7) |
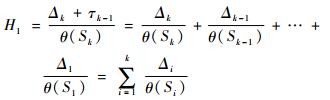 | (8) |
当产品失效服从对数正态分布时,
 | (9) |
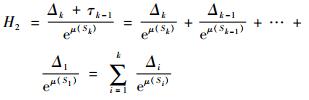 | (10) |
当复杂时变环境应力S(t)是关于时间的连续函数时,寿命特征η(S(t))也是一个关于时间的连续函数。当Δi→0时,威布尔分布下的累积函数为
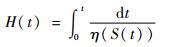 | (11) |
产品的累积故障分布函数为
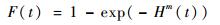 | (12) |
同理可得指数分布下的累积函数H1(t)=
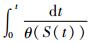
对数正态分布下的累积函数H2(t)=
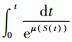
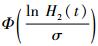
对于如图 3所示的时变环境应力模式a,则产品的累积故障分布函数如表 2所示。
表 2 时变环境应力模式a下的累积故障分布函数 Table 2 Cumulative failure distribution function under Mode a of time-varying environmental stress
| 分布 | 累积故障分布函数 |
| 指数 | 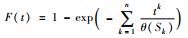 |
| 威布尔 | 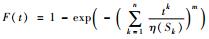 |
| 对数正态 | 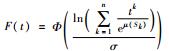 |
表选项
对于如图 5所示的时变环境应力模式b,设时间
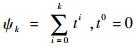
表 3 时变环境应力模式b下的累积函数 Table 3 Cumulative function under Mode b of time-varying environmental stress
| 分布 | 累积函数 |
| 指数 | 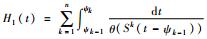 |
| 威布尔 |  |
| 对数正态 |  |
表选项
2.3 两种时变环境应力模式的比较 结合相应的加速模型,可得到产品在2种时变环境应力模式下的累积故障分布函数和可靠度函数。不妨假定产品的加速模型为Arrhenius模型,产品失效服从威布尔分布,则在恒定温度Tcons下,产品的可靠度函数为
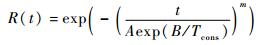 | (13) |
式中:A和B为Arrhenius模型的参数值。
时变环境应力模式a下的产品的可靠度函数为
 | (14) |
时变环境应力模式b下的产品的可靠度函数为
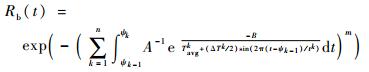 | (15) |
在已知tk=24 h,k=1, 2, …, n时,式(15)可化简得
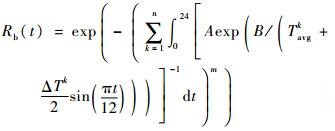 | (16) |
恒定温度下得到的可靠度函数并没有考虑到温度的变化情况,使用了一个定值来表示温度变化,其实是不符合实际的。比较2种模式的可靠度函数可知:当ΔTk=0时,Ra(t)=Rb(t)。当地理位置每天的昼夜温差变化不大时,即每天的最高温度Tmaxk和最低温度之间的差距Tmink很小,ΔTk≈0时,Ra(t)≈Rb(t)。当地理位置每天的温差变化较大时,ΔTk?0,则可知Rb(t)的计算相对较复杂,但计算结果较Ra(t)更精确。
2.4 多失效模式情况 当产品含有多种失效模式时,设TMi是第i种失效模式所导致的失效时间,则拥有N个相互独立失效模式的产品的失效时间为N个失效时间的最小值即min{TM1, TM2, …, TMN},时变环境应力下产品的可靠性[15]可表示为
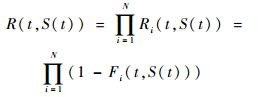 | (17) |
式中:Ri(t, S(t))和Fi(t, S(t))分别为时变应力下产品第i种失效模式的可靠度函数和累积故障分布函数。在相同的时变环境应力S(t)下,产品的不同失效模式可能服从不同失效分布,且对应的加速模型的参数也可能不同。
当产品含有2种失效模式,且2种失效模式分别服从于指数分布和威布尔分布,产品的加速模型为Arrhenius模型,模型参数分别为A1、B1和A2、B2时,时变温度应力T(t)下,产品的可靠度为
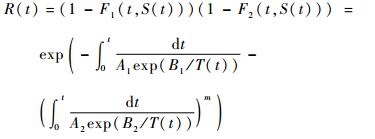 | (18) |
3 参数估计 运用加速试验方法评估模型参数,拟对产品进行恒定应力加速寿命试验。假定在试验中产品总共遭受了N个恒定应力水平,且在第k个恒定应力下的样本失效个数为sk,失效时间分别为t1(k), t2(k), …, tsk(k)。结合加速寿命试验数据,利用极大似然估计方法来估计函数参数[16]。所有样本的极大似然函数为
 | (19) |
式中:f(k)(t)和R(k)(t)分别为第k个应力水平下的概率密度和可靠度函数;tend和s0分别为截尾时间和未失效个数。使得函数L的值最大,进而得到模型参数的估计值。
4 实例分析 已知某型号红外传感器产品的失效分布为威布尔分布,现对传感器进行定时截尾下的恒定应力加速寿命试验,得到试验数据,截尾时间为750 h,如表 4所示。
表 4 加速寿命试验数据 Table 4 Accelerated life test data
| 温度/K | 失效时间/h |
| 383 | 238, 456, 513, 687 |
| 403 | 157, 182, 276, 311, 357 |
| 423 | 97, 115, 145, 177, 208 |
表选项
其加速模型为Arrhenius模型,得到威布尔分布下的参数ηk=ec+d/Tk。根据极大似然估计方法可得,模型参数为:c=-7.990 5;d=5 518.214;m=3.515 7。
当传感器所处地理位置为海口时,引入海口的日常平均温度、最高温度和最低温度的六参数多项式拟合函数,得到其在所处地理位置的真实时变环境应力下的模式a和模式b的可靠度曲线,并与在传统可靠性评估所使用的恒定环境应力22℃下的可靠度曲线比较,如图 6所示。可知使用恒定温度评估的可靠性与使用真实环境应力评估的可靠性差别较大。
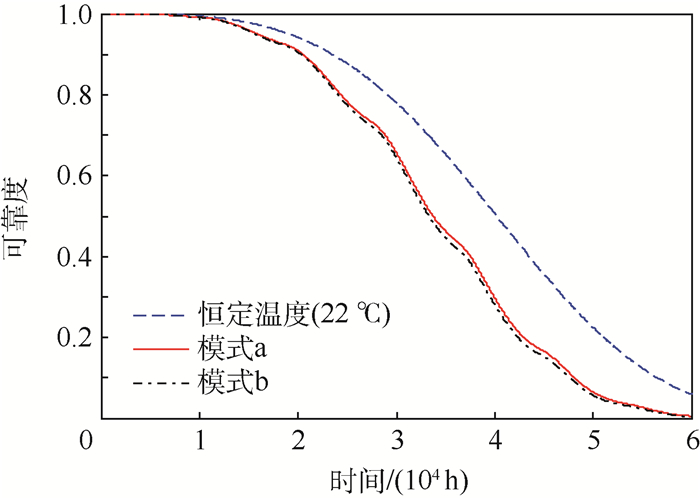 |
| 图 6 时变环境下的可靠度曲线 Fig. 6 Reliability curves of time-varying environment |
| 图选项 |
当可靠度R=0.9时,恒定温度下的可靠寿命为2.352 1×104 h,模式a的可靠寿命为2.059 2×104 h,模式b的可靠寿命为2.035 2×104 h。根据厂家提供的数据,当可靠度R=0.9时产品在海口的可靠寿命为2×104 h,则模式b的可靠寿命更加贴近实际情形下的可靠寿命。
当传感器位于不同的地理位置时,由图 7可知,其在不同地理位置的模式b的可靠度曲线差别较大。
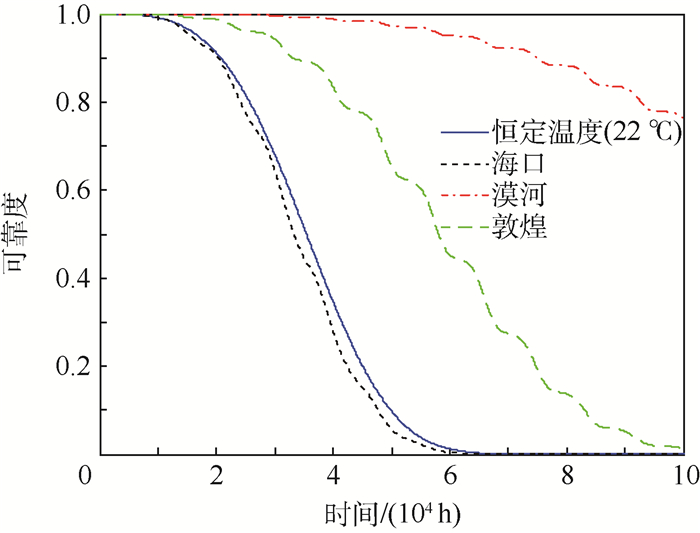 |
| 图 7 在不同地理位置的可靠度曲线 Fig. 7 Reliability curves at different geographical locations |
| 图选项 |
当可靠度R=0.9时,在漠河的可靠寿命为7.509 6×104 h,在敦煌的可靠寿命为3.326 4×104 h。
使用模式b的真实时变环境应力进行可靠性评估,可得产品在漠河、敦煌和海口的可靠寿命分别约为恒定温度下所评估的可靠寿命的3.2倍、1.4倍和0.87倍。
根据工程经验可得,漠河的气温条件相对于海口和敦煌的气温条件比较低,相同的可靠度水平下,位于漠河的传感器相对拥有着更高的可靠寿命,敦煌的传感器次之,海口的传感器的可靠寿命相对最低。
传统的使用恒定应力进行可靠性评估的方法在各个不同地理位置得到的产品的可靠性评估结果是相同的,而实际情况中位于不同地理位置的产品的可靠寿命差别较大。模式b下的可靠性评估结果更加地符合实际情形下的可靠性评估。使用恒定温度应力进行可靠性评估是不可取的,引入产品所处地理位置的真实环境应力,可更精确地评估产品的可靠度。
5 结论 引入典型地理位置的真实自然环境应力,研究真实时变环境应力下的基于加速寿命试验数据的产品可靠性评估方法。
1) 采用六参数多项式拟合方法处理其历史气候数据,得到其变化趋势,在此基础上假定了2种时变应力模式。
2) 时变环境应力模式a和模式b都能反映产品所处地理位置年度的环境应力变化,同时模式b还反映出了所处地理位置每天的环境应力变化。模式a方法快捷方便但模式b方法的结果更精确。
3) 在漠河、敦煌和海口的可靠寿命分别约为恒定温度下所评估的可靠寿命的3.2倍、1.4倍和0.87倍。
4) 与使用恒定环境应力的传统可靠性评估方法相比,引入产品所处地理位置的真实环境应力,可更精确地评估产品的可靠性。
参考文献
| [1] | FARD N, LI C. Optimal simple step stress accelerated life test design for reliability prediction[J].Journal of Statistical Planning & Inference, 2009, 139(5): 1799–1808. |
| [2] | HE Q, CHEN W, PAN J, et al. Improved step stress accelerated life testing method for electronic product[J].Microelectronics Reliability, 2012, 52(11): 2773–2780.DOI:10.1016/j.microrel.2012.04.003 |
| [3] | FAN T, HSU T. Constant stress accelerated life test on a multiple-component series system under weibull lifetime distributions[J].Communications in Statistics-Theory and Methods, 2014, 43(10): 2370–2383. |
| [4] | YANG G B. Optimum constant-stress accelerated life-test plans[J].IEEE Transactions on Reliability, 1996, 43(4): 575–581. |
| [5] | YANG L. Correlation between accelerated aging test and real world storage temperature[C]//Joint Propulsion Conference & Exhibit. Reston: AIAA, 2007: 5138-5150.http://arc.aiaa.org/doi/abs/10.2514/6.2007-5138 |
| [6] | METTAS A. Reliability predictions based on customer usage stress profiles[C]//Proceedings of the Annual Reliability and Maintainability Symposium. Piscataway, NJ: IEEE Press, 2005: 20-25.http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1408332 |
| [7] | 洪东跑, 赵宇, 马小兵. 利用变环境试验数据的可靠性综合评估[J].北京航空航天大学学报, 2009, 35(9): 1152–1155. HONG D P, ZHAO Y, MA X B. Integrated reliability assessment using varied environment test data[J].Journal of Beijing University of Aeronautics and Astronautics, 2009, 35(9): 1152–1155.(in Chinese) |
| [8] | 洪东跑, 马小兵, 赵宇. 基于比例风险模型的可靠性综合评估[J].系统工程与电子技术, 2010, 32(10): 2132–2135. HONG D P, MA X B, ZHAO Y. Integrated reliability assessment based on proportional risk model[J].Systems Engineering and Electronics, 2010, 32(10): 2132–2135.DOI:10.3969/j.issn.1001-506X.2010.10.25(in Chinese) |
| [9] | HONG Y, MA H, MEEKER W Q. A tool for evaluating time-varying-stress accelerated life test plans with log-location-scale distributions[J].IEEE Transactions on Reliability, 2010, 59(4): 620–627.DOI:10.1109/TR.2010.2083252 |
| [10] | BENAVIDES E M. Reliability model for step-stress and variable-Stress Situations[J].IEEE Transactions on Reliability, 2011, 60(1): 219–233.DOI:10.1109/TR.2010.2085574 |
| [11] | BIAN L, GEBRAEEL N. Stochastic methodology for prognostics under continuously varying environmental profiles[J].Statistical Analysis & Data Mining, 2012, 6(3): 260–270. |
| [12] | 张国龙, 蔡金燕, 梁玉英, 等. 时变环境下基于加速寿命试验的产品故障预测方法[J].海军工程大学学报, 2013, 25(1): 108–112. ZHANG G L, CAI J Y, LIANG Y Y, et al. Fault prediction method based on accelerated life test of products in time-varying conditions[J].Journal of Naval University of Engineering, 2013, 25(1): 108–112.(in Chinese) |
| [13] | GONZáLEZ L C M, BORBóN M I R, VALLES-ROSALES D J, et al. Reliability model for electronic devices under time varying voltage[J].Quality & Reliability Engineering International, 2015, 32(4): 1295–1306. |
| [14] | NELSON W. Accelerated life testing-step-stress models and data analyses[J].IEEE Transactions on Reliability, 1980, R-29(2): 103–108.DOI:10.1109/TR.1980.5220742 |
| [15] | NOOROSSANA R, SABRI-LAGHAIE K. System reliability with multiple failure modes and time scales[J].Quality & Reliability Engineering International, 2015, 32(3): 1109–1126. |
| [16] | METTAS A, VASSILIOU P. Modeling and analysis of time-dependent stress accelerated life data[C]//Proceedings of the Annual Reliability and Maintainability Symposium. Piscataway, NJ: IEEE Press, 2002: 343-348.http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=981665 |
