纤维金属层板的金属层伴有抵抗裂纹增长的纤维[5]。当疲劳裂纹在金属层中增长时,这些纤维不破坏,限制疲劳裂纹的张开行为。在疲劳裂纹萌生阶段和裂纹扩展初始阶段,纤维桥接机制不存在,即纤维没有限制金属层裂纹张开的作用。Alderliesten[6]研究指出,对于不同层板,纤维开始起作用的临界裂纹长度不同,一般在几毫米到十几毫米之间,取决于层板的结构及层间黏结情况。对于疲劳寿命的研究表明,在桥接机制起作用之前,金属层应力起主要作用;桥接机制起作用之后,金属层应力和桥接应力共同起作用[7-8]。为了预测疲劳寿命,需要考虑金属层板的实际应力水平。而对于多层结构层板(3/2及以上层板),层板内部金属层受到两侧界面黏结力作用,相应的金属层应力小于外部金属层应力[1],这也是外部金属层首先破坏的原因。故层板金属层应力的研究往往针对的是外部金属层应力。
层板中金属层应力的测定能为纤维金属层板的研制及应用提供重要参考指标,为理论应力求解模型的选取提供参照标准,对于研究纤维金属层板的疲劳寿命问题具有重要意义。然而,应力的测定不能直接通过试验方法实现,通常只能由试验测得材料表面应变情况,进而由理论公式计算得出。目前,国内外针对复合材料层板应变的测量方法较少。Murphy和Duke[9]成功地将信号臂埋置于环氧树脂内,使用光导纤维干涉仪实现了复合材料层板内应力的测量。马子广等[10]通过在复合材料层板试验件上粘贴应变片的方法,记录了应力-应变曲线。屈蓓[11]和耿红霞[12]等分别应用光学应变技术测定了铝板冲击振动情况及带孔铝板的拉伸弹性模量。传统的静态应力测量通过电阻应变片、光弹、钢弦振动、机械传动、液压传递等得出与应力相关的效应,计算应力值。其中应用最广泛的是电阻应变片法。以上测量方法,或使用条件受到限制、或操作繁琐、精度低,往往只能测量局部区域的平均应变情况。
为了估算纤维金属层板的疲劳裂纹萌生寿命及预测纤维金属层板疲劳寿命,实现纤维金属层板金属层应力的预测至关重要。目前国内外对于复合材料层板,均利用经典层板理论及派生方法来实现应力预测。闻柏承和顾震隆[13]用经典层板理论分析了复合材料层板中的面内应力;甄文强等[14]在经典层板理论的基础上,考虑到大载荷产生的拉剪损伤耦合效应的影响,实现了平纹编织复合材料偏轴下应力的预测;对于纤维金属层板材料,虽然组分材料不同导致了不同形式的应力分布及变形,但仍可考虑应用经典层板理论进行分析。Spronk等[15]和Homan[1]引入热膨胀系数的影响,修正经典层板理论,实现纤维金属层板金属层应力预测。经典层板理论及其派生方法中层板整体刚度矩阵的计算是各层刚度根据其组分的体积分数简单相加,均未考虑实际铺层情况及层间相互作用,所求层板整体刚度矩阵与实际情况有一定差异[16],使得金属层应力的预测存在较大误差。
本文采用光学应变法来实现纤维金属层板中外部金属层应变的测量;在不考虑层板固化产生的残余应力的情况下,利用子层刚度理论来修正经典层板理论,实现层板金属层应力更准确地预测。具体方法是,在经典层板理论的基础上,通过子层刚度理论获得层板整体等效刚度矩阵,对层板理论中的整体刚度矩阵进行修正。
1 光学应变法测量层板金属层应变 1.1 测试方法及原理 光学应变法是借助数字化光学应变仪,利用2个高清相机,基于双目立体视觉原理,采用三维数字图像相关方法,可对被测物体表面的三维形貌和载荷作用下的三维变形场进行测量。主要原理如下:首先,利用经过校验的标定板对双目相机系统进行标定,获得2个相机的内外参数;其次,利用相关匹配算法,得到左右相机采集图像中对应点的视差,从图像中各点的视差数据和预先获得的标定参数重建物体表面的三维形貌;再次,通过比较载荷作用下测量区域内各点的三维形貌的变化,得到被测物体全场三维位移分布及应变分布;最后,利用层板组分材料的弹性模量转换成试样表面的应力,即纤维金属层板金属层应力。数字化光学应变仪测试系统如图 1所示。
 |
| 图 1 数字化光学应变仪测试系统 Fig. 1 Testing system of digital optical strain gauge |
| 图选项 |
1.2 测试方法的优点 光学应变法能实时测量试样关键部位的全局应变,测量精度为0.01%,可以确定最大应变的位置及其周围应变情况,为试样的应变、应力分析提供可靠的保证。光学应变法相比于常用的传统的应变片测量法,有以下优势:①准备试验时,不损伤试样原表面,并且避免了胶的厚度、固化温度及粘贴压力的影响,保证了试验结果真实性。②应变片最大量程为4%~5%,往往因为量程的限制不能测量整个过程的应变,而光学应变法量程为0.05%~100%,则避免了此限制。③测量范围大:用同样的传感器测量不同的物体,尺寸范围为1~1000mm。④全场的图形化结果,结果包含大量的数据点,高密度的数据点和测量结果的图形化显示,可以帮助更好地了解零件性能。实现最大应变位置准确定位,在一定程度上可以代替并优于软件仿真,因为该方法是实际情况的真实测试。⑤具有先进的后处理模块,能显示各点的主应变方向和等值线以及各种过程参量,并分析计算各点的X向应变分量、Y向应变分量、Mises应变、厚度减薄率、Tresca应变、剪切应变、剪切角及各方向位移等。
1.3 测试操作步骤 具体测试过程如下:①用酒精擦拭清洁试样表面。②在试样表面喷涂一层亚光白色油漆,然后再用亚光黑色漆,以散点法落于试件表面。③根据所需观察试样的应变范围,选取标定板,标定应变仪。④开始试验,首先使用应变仪拍取基准状态(无载荷状态)试样表面照片,再拍取各加载状态下的试样表面照片,如图 2所示。⑤结束试验,对应变仪所拍摄的照片进行处理,选取所要观察应变的区域,去除不必要区域。⑥满足合理参考误差前提下设置参考点。⑦分析计算以获得试样表面应变情况,如图 3、图 4所示。⑧寻找最大应变部位并读取应变值,根据应力应变关系,获得金属层应力。
 |
| 图 2 原始试样及喷涂试样照片 Fig. 2 Photos of original and sprayed specimen |
| 图选项 |
 |
| 图 3 试样孔心截面Y向应变 Fig. 3 Y-direction strain of specimen section through pinhole center |
| 图选项 |
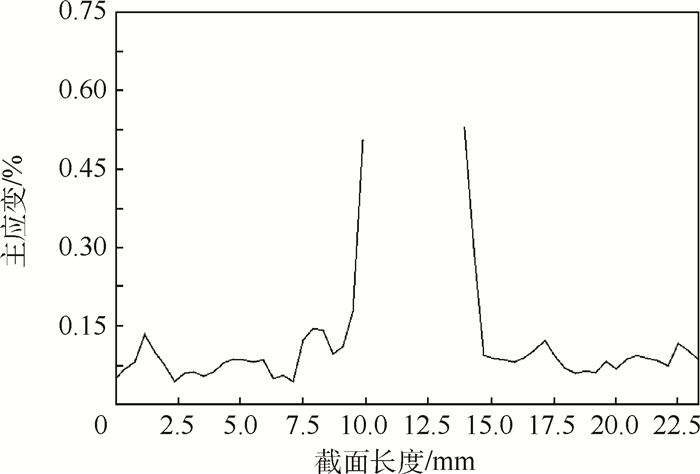 |
| 图 4 试样孔心水平截面应变 Fig. 4 Strain of specimen horizontal section through pinhole center |
| 图选项 |
2 层板金属层应力预测模型 2.1 经典层板理论 许多文献对经典层板理论做了概括。通过总结归纳,经典层板理论模型实现主要有3个步骤[17]:①各组分材料的本构关系;②层板的整体刚度矩阵;③计算各层材料应力。
2.1.1 各组分材料的本构关系 纤维金属层板结构由相互平行的金属及非金属组分材料交替叠加而成,层板中各组分材料本构关系的通用形式为[18]
 | (1) |
式中:(σx σy σz τyz τzx τxy)T为应力向量;(εx εy εz γyz γzx γxy)T为应变向量;刚度矩阵为
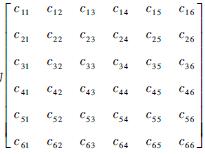
在求解实际问题或进行复合材料设计时,经常遇到整体坐标系与局部坐标系不重合的现象。这时,需要利用刚度矩阵坐标转换公式将局部坐标系下的刚度矩阵c转换为整体坐标系下的刚度矩阵c[19]:
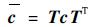 | (2) |
式中:
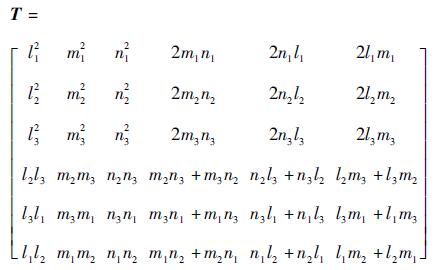 |
其中:li, mi, ni(i=1, 2, 3)为材料的局部坐标系(O123)和整体坐标系(Oxyz)中各个坐标轴的方向余弦,见表 1。
表 1 不同坐标系下坐标轴间的余弦值 Table 1 Cosine value between coordinate axes in different coordinate systems
| 坐标轴 | x | y | z |
| 1 | l1 | m1 | n1 |
| 2 | l2 | m2 | n2 |
| 3 | l3 | m3 | n3 |
表选项
利用转换公式将层板中各层局部坐标系下的刚度矩阵转换为整体坐标系下的刚度矩阵,其通用形式为
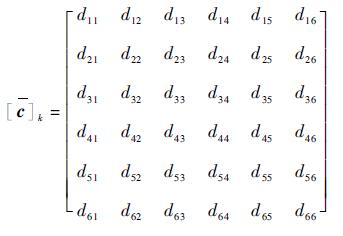 | (3) |
式中:k表示第k层材料。
考虑到纤维金属层板各层属性,其刚度矩阵可表示为
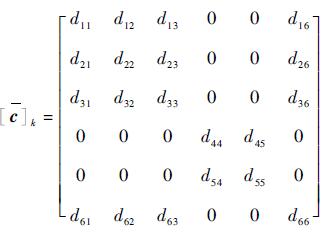 | (4) |
2.1.2 整体刚度矩阵 层板的整体刚度矩阵Q及柔度矩阵S为
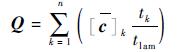 | (5) |
 | (6) |
式中:tk为第k层材料厚度;tlam为层板总厚度。
2.1.3 计算各层材料压力 外载荷下层合板中面应变为
 | (7) |
整体坐标系下张量应变转换为局部坐标系下张量应变,各层材料主方向应变通用形式为
 | (8) |
各层材料主方向应力为
 | (9) |
2.2 修正层板刚度矩阵 在2.1节经典层板理论实现过程中,层板整体刚度矩阵的计算是各层刚度根据其组分的体积分数简单相加,未能考虑到实际铺层情况及层间相互作用,造成所求层板整体刚度矩阵与实际情况有一定差异,从而使得金属层应力的预测存在较大误差。为了解决此问题,本文引入等效刚度矩阵的概念来对经典层板理论中整体刚度矩阵的求解方法进行修正。
2.2.1 层板材料性能等效及子层刚度法等效刚度理论 由于复合材料内部结构的多样性和多尺度性(即复合材料层合板是由多层单向板铺放而成,每一层单向板的铺放角度、铺放厚度不同),导致了各层材料在整体坐标系下不同的材料性能,从而使得复合材料整体层合板的材料性能复杂多样[20]。虽然试验方法可以对复合材料的有效性能进行测试,但进行材料力学性能的试验研究给出的一般都是经验公式,受加工条件、制备方法等因素的影响,给出的测试结果往往具有一定的局限性。因此,通过建立力学模型,用理论方法分析和预测复合材料的力学性能,最终把复合材料层合板的性能等效成各向异性材料的性能,对于复合材料结构性能分析及结构优化设计有重要的意义。
Sun和Li[16]基于界面连续性假设,提出的子层刚度法直接从组分的本构关系出发,以整体角度把弹性张量进行统一化处理,进一步应用统计平均思想推导出刚度公式,求解出材料的整体等效刚度矩阵[21]。文献[20]针对正交各向异性复合材料有3个正交的弹性性能对称面的特殊结构,以子层刚度法为理论基础,通过应变能密度守恒定律,推导出适用于正交各向异性复合材料的等效刚度矩阵:
 | (10) |
式中:相关刚度系数可根据子层刚度公式求出[16]
 |
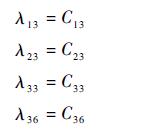 |
 |
其中:Vk为第k层材料的体积分数。
2.2.2 修正经典层板理论 通过子层刚度法理论求得层板的等效刚度矩阵后,代入到经典层板理论中。修正后的经典层板理论如下:①各组分材料在整体坐标系下的刚度矩阵,通过式(1)、式(2)、式(4)求解;②采用改进的子层刚度理论计算层板的等效刚度矩阵,见式(10);③等效刚度矩阵的逆矩阵式(6)代入到式(7),得到层板中面应变
 | (11) |
将式(11)代入到式(8)、式(9)中, 即可获得所求金属层应力。
3 实例验证 为了验证该光学应变法测量的准确性及预测模型的有效性,本文选取2060铝锂合金2/1结构及3/2结构的纤维金属层板进行加载试验。采用平板开孔试件,试件沿材料纵向取材,形式如图 5所示,层板结构如图 6所示,其组分材料属性见表 2。其中2/1及3/2层板应力集中系数分别为2.57和2.56。本文以层板受单向拉伸载荷情况为例。考虑到研究目标为材料的线弹性性能,边界条件为分别对层板施加50、60、70、80、90、100MPa远程应力。分别利用光学应变法对其进行金属层应变测量,使用ANSYS软件对其进行有限元仿真分析,采用经典层板理论及修正方法对其进行金属层应力预测。由于其试件所受载荷为试件长度方向,该方向应力、应变作用最大,则后文所指的金属层应力应变均为试件长度方向应力应变。
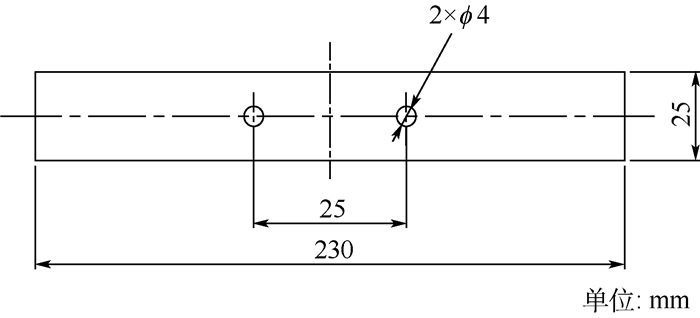 |
| 图 5 铝锂合金层板试件 Fig. 5 Test specimen of Al-Li alloy laminates |
| 图选项 |
 |
| 图 6 2/1及3/2层板结构 Fig. 6 Structure of 2/1 and 3/2 laminates |
| 图选项 |
表 2 层板组分材料属性及尺寸 Table 2 Material properties and sizes of laminates' components
| 材料 | 弹性模量/GPa | 泊松比 | 厚度/mm |
| 金属层 | 72.4 | 0.3 | 1.9 |
| 预浸料层 | 54.6 | 0.252 | 0.9 |
表选项
3.1 有限元仿真分析 以试件为研究对象,本文通过商用有限元软件ANSYS来实现有限元仿真分析。对于纤维金属层板试样各组分厚度影响其所受应力情况,采用三维实体建模方式,单元类型为SOLID185。由于主要研究对象为孔周部位,故对孔周边进行网格细化处理。层板厚度方向网格划分情况为:每层金属层划分成4个网格,每层纤维层划分成2个网格。其每层材料单元的材料属性赋予情况如表 2所示。为了模拟实际作用效果,在试件长度方向一端的底面施加全约束,另一端的2个侧平面施加相应载荷。其有限元模型如图 7~图 9所示。通过有限元仿真分析,获得不同应力下层板金属层的应变情况,见图 10。
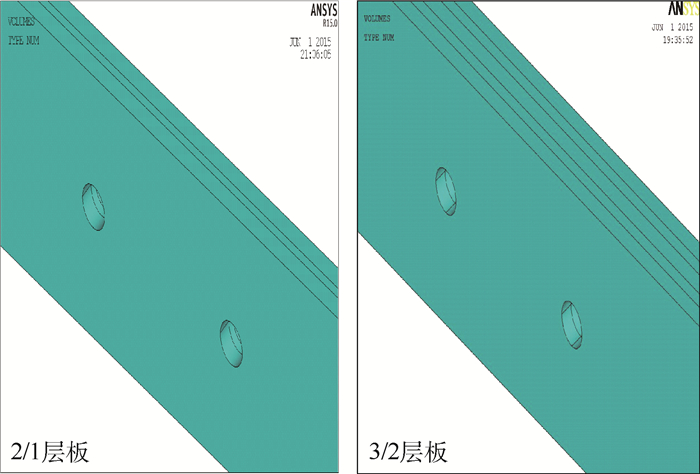 |
| 图 7 2/1及3/2层板几何模型 Fig. 7 Geometric models of 2/1 and 3/2 laminates |
| 图选项 |
 |
| 图 8 有限元模型网格划分情况 Fig. 8 Meshing case of finite element model |
| 图选项 |
 |
| 图 9 有限元模型边界条件 Fig. 9 Boundary conditions of finite element model |
| 图选项 |
 |
| 图 10 有限元模型应力分析结果 Fig. 10 Stress analysis results of finite element model |
| 图选项 |
3.2 光学应变法测量层板金属层应力 使用数字化光学应变测量仪,按照上述介绍的光学应变法试验步骤,分别测量2/1层板及3/2层板试样不同远程应力下的应变,取最大应变部位(孔周部位)为研究对象,其试验过程见图 2~图 4。由光学应变法获得孔周的应变情况,提取各应力下的最大应变。测试获得的应变数据根据胡克定律转换成应力张量,并对该试验数据进行线性拟合。2/1层板及3/2层板各应力下最大应力的有限元仿真结果及应变测试结果如图 11(a)、图 12(a)所示。
 |
| 图 11 2/1层板金属层最大应力测量及预测结果 Fig. 11 Measurement and prediction results of maximum stress in metal layer of 2/1 laminates |
| 图选项 |
 |
| 图 12 3/2层板金属层最大应力测量及预测结果 Fig. 12 Measurement and prediction results of maximum stress in metal layer of 3/2 laminates |
| 图选项 |
3.3 数学模型预测层板金属层应力 分别采用经典层板理论及修正后金属层应力预测模型,对2/1层板及3/2层板试件在不同远程应力下的金属层应力进行预测,考虑应力集中影响,所得结果如图 11(b)、图 12(b)所示。
3.4 结果对比分析 由图 11(a)、图 12(a)可知,数字化光学应变法结果与有限元仿真结果较吻合,2/1层板及3/2层板最大误差分别为2.12%和3.68%,从而证明了该测试方法的准确性及实用性。由图 11(b)、图 12(b)可知通过经典层板理论预测结果与光学应变结果比较,2/1层板及3/2层板最大误差分别为9.91%和13.15%;修正后的层板理论预测结果较经典层板理论与光学应变结果更接近,2/1层板及3/2层板最大误差分别为7%和7.32%,准确率分别提升了2.91%和5.83%,证明了该修正模型的有效性和先进性。
4 结论 1) 数字化光学应变法实现了纤维金属层板金属层应力的测量。通过实例应用及对比有限元仿真结果,分析表明:2/1层板及3/2层板最大误差分别为2.12%和3.68%,验证了该方法的准确性。
2) 利用子层刚度理论修正经典层板理论,实现了纤维金属层板金属层应力更准确的预测。通过实例分析并对比光学应变测量结果及经典层板理论预测结果,研究表明:2/1层板及3/2层板预测准确率分别提升了2.91%和5.83%,验证了该模型的有效性、先进性。
参考文献
| [1] | HOMAN J J. Fatigue initiation in fiber metal laminates[J].International Journal of Fatigue, 2006, 28(4): 366–374.DOI:10.1016/j.ijfatigue.2005.07.030 |
| [2] | 郭亚军, 吴学仁. 纤维金属层板疲劳裂纹扩展速率与寿命预测的唯象模型[J].航空学报, 1998, 19(3): 275–282. GUO Y J, WU X R. Phenomenological model for predicting fatigue crack growth in fiber reinforced metal laminates[J].Acta Aeronautica et Astronautica Sinica, 1998, 19(3): 275–282.(in Chinese) |
| [3] | CHANG P Y, YEH P C, YANG J M. Fatigue crack initiation in hybrid boron/glass/aluminum fiber metal laminates[J].Materials Science and Engineering A, 2008, 496: 273–280.DOI:10.1016/j.msea.2008.07.041 |
| [4] | FRIZZELL R M, MCCRATHY C T, MCCARTHY M A. An experimental investigation into the progression of damage in pin-loaded fiber metal laminates[J].Composites Part B:Engineering, 2008, 39(6): 907–925.DOI:10.1016/j.compositesb.2008.01.007 |
| [5] | MARISSEN R.Fatigue crack growth in ARALL:A hybrid aluminum-aramid composite material crack growth mechanisms and quantitative predictions of the crack growth rates[D].Delft:Delft University of Technology, 1988. |
| [6] | ALDERLIESTEN R C.Development of an empirical fatigue crack growth prediction model for the fibre metal laminate glare[D].Delft:Delft University of Technology, 1999. |
| [7] | 郭亚军. 纤维金属层板的疲劳损伤与寿命预测[D]. 北京: 北京航空材料研究院, 1997. GUO Y J. Fatigue damage and life prediction of fiber reinforced metal laminates[D].Beijing:Beijing Institute of Aeronautical Materials, 1997(in Chinese). |
| [8] | KIEBOOM O.Fatigue crack initiation and early crack growth in glare at different temperatures[D]. Delft:Delft University of Technology, 2000. |
| [9] | MURPHY K, DUKE J. A rugged optical fiber interferometer for strain measurements inside a composite material laminate[J].Journal of Composites, Technology and Research, 1988, 10(1): 11–15.DOI:10.1520/CTR10269J |
| [10] | 马子广, 陈庆童, 王卫卫. 复合材料层压板开孔拉伸力学性能探究[J].直升机技术, 2015(1): 64–69. MA Z G, CHEN Q T, WANG W W. The exploring of composite materials' mechanical properties under tensile loading[J].Helicopter Technique, 2015(1): 64–69.(in Chinese) |
| [11] | 屈蓓, 付小龙, 何俊武, 等. 非接触式光学应变测量技术研究进展[J].计测技术, 2013, 33(5): 10–15. QU B, FU X L, HE J W, et al. Research on optical non-contact strain measurement[J].Metrology & Measurement Technology, 2013, 33(5): 10–15.(in Chinese) |
| [12] | 耿红霞, 付朝华, 蒋小林, 等. 光学应变测量系统在研究生实验教学中的应用[J].实验室研究与探索, 2015, 34(3): 220–224. GENG H X, FU C H, JIANG X L, et al. Application of optical strain measurement system in experiment teaching for postgraduates[J].Re-search and Exploration in Laboratory, 2015, 34(3): 220–224.(in Chinese) |
| [13] | 闻柏承, 顾震隆. 带或不带脱层的复合材料层板强度的预报[J].复合材料学报, 1989, 2(1): 48–54. WEN B C, GU Z L. Probabilistic prediction of laminates with or without delamination[J].Acta Materiae Compositae Sinica, 1989, 2(1): 48–54.(in Chinese) |
| [14] | 甄文强, 王波, 李潘, 等. 平面编织C/SiC复合材料层合板偏轴拉伸性能研究[J].机械强度, 2014, 36(1): 856–861. ZHEN W Q, WANG B, LI P, et al. Study of off-axis tensile properties of plain-woven C/SiC composites[J].Journal of Mechanical Strength, 2014, 36(1): 856–861.(in Chinese) |
| [15] | SPRONK S W F, SEN I, ALEDRLIESTEN R C. Predicting fatigue crack initiation in fibre metal laminates based on metal fatigue test data[J].International Journal of Fatigue, 2015, 70: 428–439.DOI:10.1016/j.ijfatigue.2014.07.004 |
| [16] | SUN C T, LI S J. Three dimensional effective elastic constants for thick laminates[J].Composite Material, 1988, 22(7): 629–639.DOI:10.1177/002199838802200703 |
| [17] | BRUNBAUER J, PINTER G. Fatigue life prediction of carbon fibre reinforced laminates by using cycle-dependent classical laminate theory[J].Composites Part B:Engineering, 2015, 70: 167–174.DOI:10.1016/j.compositesb.2014.11.015 |
| [18] | 张振瀛. 复合材料力学基础[M].北京: 航空工业出版社, 1989: 10. ZHANG Z Y. Mechanical basis of composite[M].Beijing: Aviation Industry Press, 1989: 10.(in Chinese) |
| [19] | 赵美英, 陶梅贞. 复合材料结构力与结构设计[M].西安: 西北工业大学出版社, 2007: 12. ZHAO M Y, TAO M Z. Structural mechanics and structural design of composite[M].Xi'an: Northwestern Polytechnical University Press, 2007: 12.(in Chinese) |
| [20] | 孟维迎. 大型风机叶片复合纤维性能等效算法研究及应用[D]. 呼和浩特: 内蒙古工业大学, 2013. MENG W Y.Research and application of performance equivalence agorithm of composite for large scale wind turbine blade[D].Huhhot:Inner Mongolia University of Technology, 2013(in Chinese). |
| [21] | 孙鹏文, 岳彩宾, 张兰挺, 等. 基于子层刚度法性能等效的风机叶片分析研究[J].太阳能学报, 2013, 34(11): 1974–1977. SUN P W, YUE C B, ZHANG L T, et al. Research on wind turbine blade analysis of composite equivalent elastic constants based on sub-laminate stiffness method[J].Acta Energiae Solaris Sinica, 2013, 34(11): 1974–1977.(in Chinese) |
