在波长调制光谱法的免标定技术的基础上[8],又提出了扫描波长调制光谱法[7-12]。在使用扫描波长调制光谱法时,通常调谐激光波长使其扫描范围覆盖整个吸收光谱。在扫描波长调制光谱法中,包含气体吸收信息的激光测量信号通过锁相放大器后分离出二次谐波信号与一次谐波信号,二次谐波信号被一次谐波信号标准化后,其峰值点用来进一步计算气体参数。
值得注意的是,在扫描波长调制光谱法获得的标准化二次谐波信号中,峰值点是在谐波信号的中间部分。因此,可以适当地减少激光波长扫描范围,只扫描部分吸收光谱来获得峰值点。谐波信号的主峰扫描方法[13]就是通过只扫描谐波信号主峰部分对应的吸收光谱来提高测量速度。当然这样提高速度是以牺牲吸收光谱的信息量为基础的。虽然减少激光波长的扫描范围可以有效地提高速度,但是最后获得的峰值点很容易受到波长移动、电子噪声、探测器噪声和激光光强噪声的影响[14-16]。
本文提出了对吸收光谱谐波信号的主峰进行拟合的气体浓度测量方法。因为只扫描谐波信号主峰对应的吸收光谱部分,所以提高了测量速度。在对测量到的主峰信号进行拟合之后,可以有效降低随机测量噪声和激光随机波动带来的影响。称这种方法为谐波信号的主峰拟合方法,与谐波信号的主峰扫描方法相比,该方法在保证测量速度的基础上提高了测量精度。
1 方法 1.1 谐波信号的主峰拟合方法 在谐波信号的主峰拟合方法中,激光器的驱动电流被一个叠加了高频正弦波的斜坡信号驱动[14],激光器输出的激光波长与激光光强同时被其调制。在激光通过了吸收气体后,带有气体吸收信息的激光光强可以用It(t)表示,其遵循Beer-Lambert定律,
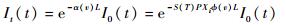 | (1) |
式中:α(v)为吸收系数;L为吸收路径长度;I0 (t)为初始的激光强度;P为总气压;T为温度,Xi为被测气体对应的摩尔分数;?(v)为被测气体的线型函数;S(T)为被测气体的线型强度,线型强度只与温度T相关。
在测得带有气体吸收信息的激光光强It(t)后,将该信号输入锁相放大器进行处理。在锁相放大器中,该信号分别与同频率但相位相差90°的2组正弦信号相乘,这里的正弦信号频率一组与驱动激光器的高频正弦信号相同,一组是驱动激光器的高频正弦信号的2倍。分别用来计算一次谐波信号和二次谐波信号。在通过低通滤波器后,锁相放大器输出了2个X分量信号(X1f, X2f)和2个Y分量信号(Y1f, Y2f),下标1f,2f分别对应一次谐波信号和二次谐波信号的分量。为了去除背景信号的影响,可以在使用一次谐波信号对二次谐波信号进行标准化处理后,减去无吸收气体时的谐波信号。用一次谐波信号标准化二次谐波信号的结果S2f/1f的具体公式如下[10]:
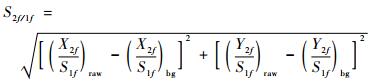 | (2) |
式中:下标raw和bg分别表示未处理的通过吸收气体的谐波信号和通过相同光学路径但无吸收气体的背景信号。背景信号包括了非吸收区间带来的吸收影响。一次谐波S1f可以通过式(3)算出:
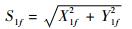 | (3) |
标准化后的二次谐波信号峰值点可以用来确定被测气体(如CO2)的参数。
图 1中描述了被测气体是CO2时在吸收中心为6 357.3 cm-1处的仿真的标准化谐波信号(WMS-2f/1f)和其对应的导数。可以看出标准化后的二次谐波的峰值点在谐波的主峰部分,并且该部分的导数单调递减,这一部分在图中用曲线AB描绘了出来。并且使谐波信号的峰值点大致在曲线AB的中点处。因为曲线AB描绘的主峰部分信噪比高,线型简单,因此在实验中只扫描这一部分信号对应的吸收谱线,并在多项式拟合之后测出峰值点。
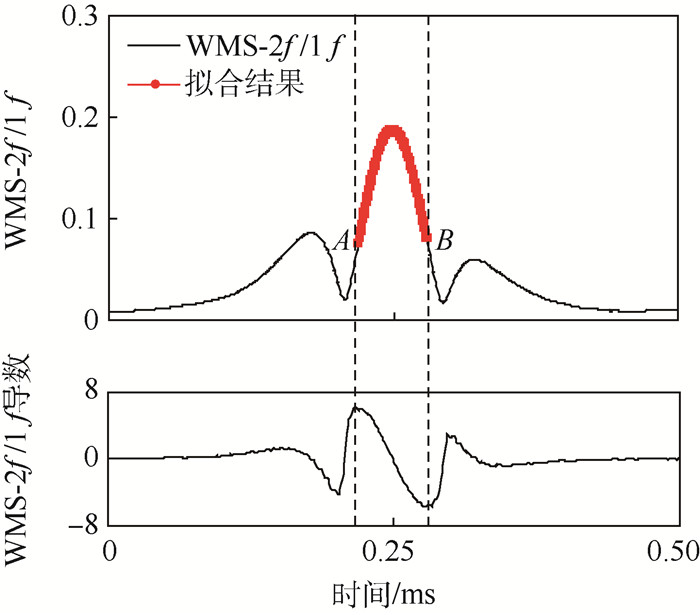 |
| 图 1 被测气体是CO2时在吸收中心为6 357.3 cm-1处仿真的WMS-2f/1f及其导数 Fig. 1 Simulated WMS-2f/1f and its derivative at absorption center of 6 357.3 cm-1 with CO2 as measured gas |
| 图选项 |
根据Stone-Weierstrass定理,任何复杂系统中的连续信号可以使用多项式进行无限逼近。因此,谐波信号中用曲线AB描绘的部分也可以使用多项式进行拟合,并进一步计算峰值点。
本文中,使用一个K阶的多项式拟合曲线AB,多项式为
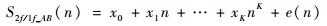 | (4) |
式中:xk (k=0, 1, …, K)为多项式系数;e(n)为拟合残差,n为采样点的序列数。
假设曲线AB处有个N采样点,则式(3)可以表示为
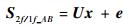 | (5) |
式中:S2f/1f_AB为曲线AB的向量表示形式,
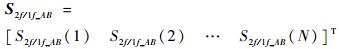 | (6) |
U为指数矩阵,其元素为采样点序列数n的不同次幂
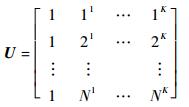 | (7) |
e为拟合残余向量,
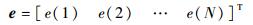 | (8) |
x为待求的系数向量,
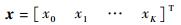 | (9) |
x可以通过最小二乘法算出[17]
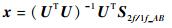 | (10) |
因为导数单调递减,所以峰值点可以在式(3)的导数为0时求得。曲线AB的导数在峰值点处可以表示为
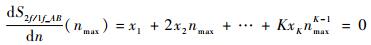 | (11) |
式中:nmax为峰值点的序列数。峰值大小可以通过式(12)算得:
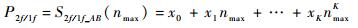 | (12) |
在计算得到峰值点后,将峰值与仿真的峰值进行比较从而计算得出气体浓度[9]。
1.2 多项式阶数的确定方法 在谐波信号的主峰拟合方法中,计算的复杂度和精确度由多项式的阶数K决定。为了找到合适的多项式阶数,对CO2在6 357.3 cm-1处的谐波信号进行了仿真计算,其中CO2的浓度从0.01变化到0.05。
在实际操作中,采集到的数据总是有无法避免的噪声,因此将白噪声加到了仿真的标准化二次谐波中。信噪比(SNR)分别设为80、65和50 dB。图 2描述了无噪声及信噪比分别为80、65和50 dB时,标准化二次谐波峰值的真值与测量值的绝对差与多项式阶数的关系。
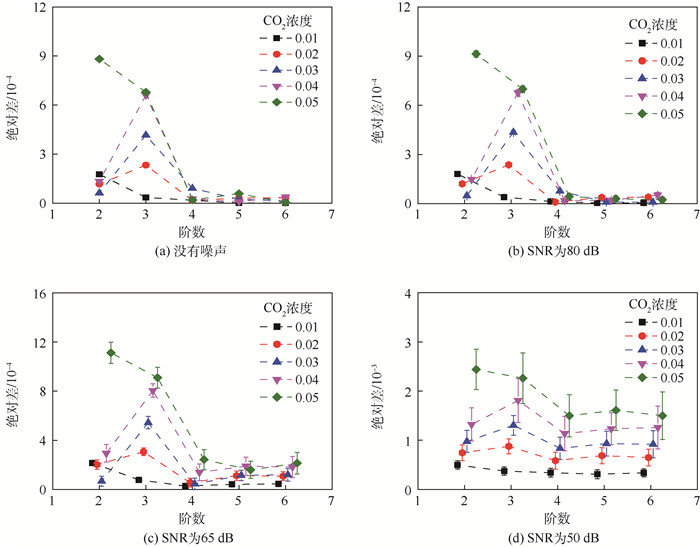 |
| 图 2 WMS-2f/1f峰值的真值与测量值的绝对差随着多项式阶数的变化 Fig. 2 Variation of absolute deviation between true peak value and measured peak value of WMS-2f/1f with degree of polynomial |
| 图选项 |
在图 2中,每个点的值与误差棒分别表示50次计算的绝对差的平均值与标准差。图中多项式的阶数相同的5个点被稍微水平移动了一些,这样可以更清楚地看出各个数值之间的不同。如图 2所示,尽管信噪比不一样,但是当多项式的阶数大于等于4时,绝对差没有明显的改变。因此,多项式的阶数定为4。
2 实验结果与讨论 为了降低噪声对谐波信号峰值测量的影响,本文中对标准化后的二次谐波的主峰部分进行了多项式拟合。从而提高了峰值的测量精度。在实验中,峰值测量的精度还与主峰部分参与拟合的数据长度有关。图 3描述了测量气体浓度信噪比随主峰部分参与拟合的数据长度的变化。参与拟合的数据都在图 1描述的曲线AB上,且其中点都在峰值位置。
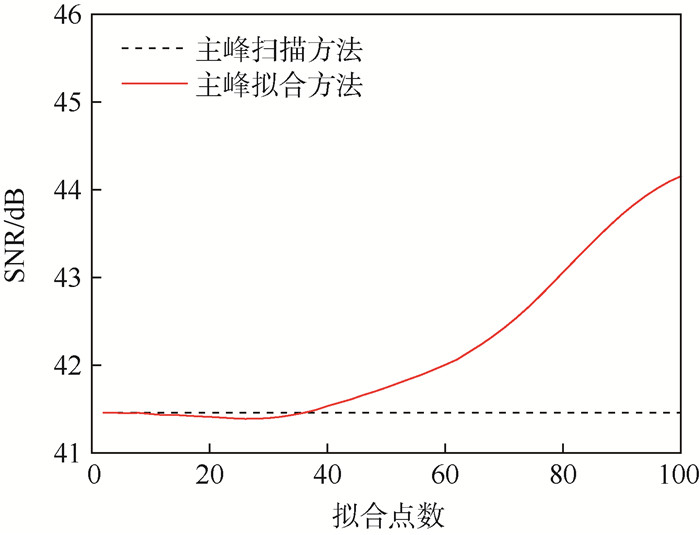 |
| 图 3 使用2种方法分别对谐波信号进行处理时,测量气体浓度信噪比与主峰部分参与拟合数据长度的变化 Fig. 3 Variation of gas concentration SNR with length of data involved in main peak fitting for two harmonic signal processing methods |
| 图选项 |
信噪比SNR的计算方式如下:
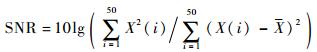 | (13) |
式中:X(i)为计算得的气体浓度;X为50个测量值的平均值。
可以看出,信噪比随着参与拟合数据长度的增加而提高。当拟合的数据少于曲线AB数据量(100)的40%时,谐波信号的主峰拟合方法结果的信噪比低于谐波信号的主峰扫描方法结果的信噪比。因此只要拟合数据足够多才能体现拟合方法的优点。当曲线AB上的数据全部用来拟合时,信噪比提高最多,达3 dB。在实验中,为了获得最高的信噪比,将曲线AB上的数据全部用来拟合。
为了更好地表现多项式拟合方法去除噪声的效果,图 4选择了噪声大的谐波信号进行拟合。当CO2气体浓度只有0.01时,电子噪声、探测器噪声和激光光强噪声会造成谐波信号的震荡,如图 4所示,从探测到的谐波信号中直接获得峰值与真值相差很远,而多项式拟合可以有效地平滑谐波信号中的噪声。因此可以认为拟合后的信号更加接近真实信号,获得的峰值点也更加接近真值。
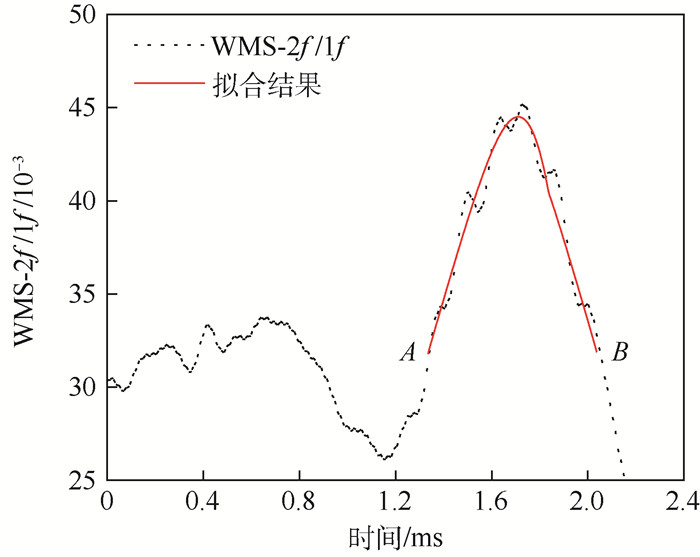 |
| 图 4 WMS-2f/1f以及主峰拟合后的结果 Fig. 4 Curve fitting results of standardized second harmonic signal WMS-2f/1f and main peak |
| 图选项 |
为了比较谐波信号的主峰扫描方法和谐波信号的主峰拟合方法在不同浓度下的结果,CO2浓度从0.01增加到0.05。高频正弦的频率是120 kHz,三角扫描的频率是1.25 kHz。在每个浓度值下,都重复测量了50次来计算信噪比。图 5展示了2种方法的测量信噪比随着气体浓度变化的情况。可以看出,2种方法的信噪比都随着气体浓度的增加而增加。在气体浓度相同时,本文提出的谐波信号的主峰拟合方法的信噪比要高出约2 dB。
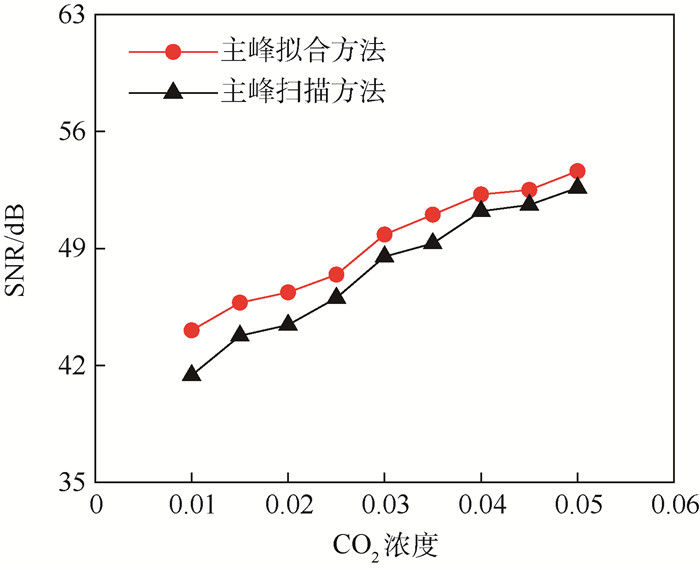 |
| 图 5 使用2种方法分别对谐波信号进行处理时,测量信噪比随气体浓度的变化 Fig. 5 Variation of measured SNR with gas concentration for two harmonic signal processing methods |
| 图选项 |
3 结论 1) 由于本文方法扫描的光谱范围缩减到谐波信号主峰部分,缩短了扫描时间,因此可以有效地提高测量速度。
2) 在CO2浓度从0.01变化到0.05的过程中,谐波信号的主峰扫描方法和谐波信号的主峰拟合方法在不同浓度下的结果证明,多项式拟合的过程可以有效提高测量的信噪比约2 dB。
3) 在要求气体测量的信噪比不低于45 dB的情况下,在固定高频正弦和低频三角扫描的频率分别为120和1.25 kHz时,谐波信号的主峰拟合方法可以测到低至0.015浓度的CO2气体。而谐波信号的主峰扫描方法则只可以测到0.025浓度的CO2气体。因此,谐波信号的主峰拟合方法可以在一定的信噪比要求下降低气体浓度测量的下限。但是谐波信号的主峰拟合方法进行浓度测量的实现基于主峰扫描方法,只有在主峰扫描方法可以探测到谐波信号的基础上,才能使用主峰拟合方法提高测量结果的信噪比。
参考文献
| [1] | PHILIPPE L C, HANSON R K. Laser diode wavelength-modulation spectroscopy for simultaneous measurement of temperature, pressure, and velocity in shock-heated oxygen flows[J].Applied Optics, 1993, 32(30): 6090–6103.DOI:10.1364/AO.32.006090 |
| [2] | LIU C, XU L, LI F, et al. Resolution-doubled one-dimensional wavelength modulation spectroscopy tomography for flame flatness validation of a flat-flame burner[J].Applied Physics B, 2015, 120(3): 407–416.DOI:10.1007/s00340-015-6150-9 |
| [3] | GOLDENSTEIN C S, SPEARRIN R M, SCHULTZ I A, et al. Wavelength-modulation spectroscopy near 1.4 μm for measurements of H2O and temperature in high-pressure and -temperature gases[J].Measurement Science and Technology, 2014, 25(5): 055101.DOI:10.1088/0957-0233/25/5/055101 |
| [4] | CAI W, KAMINSKI C F. A tomographic technique for the simultaneous imaging of temperature, chemical species, and pressure in reactive flows using absorption spectroscopy with frequency-agile lasers[J].Applied Physics Letters, 2014, 104(3): 034101.DOI:10.1063/1.4862754 |
| [5] | SPEARRIN R M, GOLDENSTEIN C S, JEFFRIES J B, et al. Quantum cascade laser absorption sensor for carbon monoxide in high-pressure gases using wavelength modulation spectroscopy[J].Applied Optics, 2014, 53(9): 1938–1946.DOI:10.1364/AO.53.001938 |
| [6] | NEETHU S, VERMA R, KAMBLE S S, et al. Validation of wavelength modulation spectroscopy techniques for oxygen concentration measurement[J].Sensors and Actuators B:Chemical, 2014, 192: 70–76.DOI:10.1016/j.snb.2013.10.070 |
| [7] | PENG Z M, DING Y J, CHE L, et al. Calibration-free wavelength modulated TDLAS under high absorbance conditions[J].Optics Express, 2011, 19(23): 23104–23110.DOI:10.1364/OE.19.023104 |
| [8] | SUN K, CHAO X, SUR R, et al. Analysis of calibration-free wavelength-scanned wavelength modulation spectroscopy for practical gas sensing using tunable diode lasers[J].Measurement Science and Technology, 2013, 24(12): 125203.DOI:10.1088/0957-0233/24/12/125203 |
| [9] | QU Z, GHORBANI R, VALIEV D, et al. Calibration-free scanned wavelength modulation spectroscopy-Application to H2O and temperature sensing in flames[J].Optics Express, 2015, 23(12): 16492–16499.DOI:10.1364/OE.23.016492 |
| [10] | RIEKER G B, JEFFRIES J B, HANSON R K. Calibration-free wavelength-modulation spectroscopy for measurements of gas temperature and concentration in harsh environments[J].Applied Optics, 2009, 48(29): 5546–5560.DOI:10.1364/AO.48.005546 |
| [11] | LIU J T C, JEFFRIES J B, HANSON R K. Wavelength modulation absorption spectroscopy with 2f detection using multiplexed diode lasers for rapid temperature measurements in gaseous flows[J].Applied Physics B, 2004, 78(3-4): 503–511.DOI:10.1007/s00340-003-1380-7 |
| [12] | SCHULTZ I A, GOLDENSTEIN C S, JEFFRIES J B, et al. Diode laser absorption sensor for combustion progress in a model scramjet[J].Journal of Propulsion and Power, 2014, 30(3): 550–557.DOI:10.2514/1.B34905 |
| [13] | GOLDENSTEIN C S, ALMODóVAR C A, JEFFRIES J B, et al. High-bandwidth scanned-wavelength-modulation spectroscopy sensors for temperature and H2O in a rotating detonation engine[J].Measurement Science and Technology, 2014, 25(10): 105104.DOI:10.1088/0957-0233/25/10/105104 |
| [14] | LIU J T C, RIEKER G B, JEFFRIES J B, et al. Near-infrared diode laser absorption diagnostic for temperature and water vapor in a scramjet combustor[J].Applied Optics, 2005, 44(31): 6701–6711.DOI:10.1364/AO.44.006701 |
| [15] | BAYRAKLI I, AKMAN H. Ultrasensitive, real-time analysis of biomarkers in breath using tunable external cavity laser and off-axis cavity-enhanced absorption spectroscopy[J].Journal of Biomedical Optics, 2015, 20(3): 037001.DOI:10.1117/1.JBO.20.3.037001 |
| [16] | SUN K, WANG S, SUR R, et al. Sensitive and rapid laser diagnostic for shock tube kinetics studies using cavity-enhanced absorption spectroscopy[J].Optics Express, 2014, 22(8): 9291–9300.DOI:10.1364/OE.22.009291 |
| [17] | XU L, ZHANG J Q, YAN Y. A wavelet-based multisensor data fusion algorithm[J].IEEE Transactions on Instrumentation and Measurement, 2004, 53(6): 1539–1545.DOI:10.1109/TIM.2004.834066 |
