1 研究方法 1.1 实验 本文装置为颗粒高速射流冲蚀实验循环装置。循环系统的动力源是功率1.5 kW水泵,蓄水箱中的液固两相流经由水泵打入管道中,经直径12 mm的喷嘴射流冲击实验样品。实验过程中管道流为满管流,以保证水流速度不发生变化,喷嘴由机械装置固定,以保证冲蚀角度不会因为水流冲击造成震动而发生变化。实验样品由固定装置固定,样品固定装置可变换角度,以改变液固两相流射流冲击角度。本次实验射流冲击样品角度选用30°。观察装置为高速摄像仪,可观察记录液固两相流中流态,以及颗粒速度。喷嘴冲击水流速度约为10.5 m/s。本文所用实验材料为奥氏体304不锈钢。表 1为304不锈钢化学成分。实验样品厚2 mm、直径为16 mm。实验样品在实验前依次经过180、400、600、800、1 200、2 000目碳化硅砂纸打磨,最后在仪器上抛光,以保证样品初始表面没有自然划痕。液固两相流中所使用的石英砂,选用粒径为50~60目石英砂颗粒,本次实验颗粒含量(质量分数)为0.5%。
表 1 304不锈钢化学成分 Table 1 Chemical composition of 304 stainless steel
| 成份 | C | Si | Mn | P | S | N | Cr | Ni | Fe |
| 质量分数/% | 约0.024 | 约0.550 | 约1.800 | 约0.030 | 约0.001 | 约0.049 | 约18.200 | 约8.200 | 剩余 |
表选项
1.2 数值计算 本文所应用的数值计算方法是建立在连续相的基础上进行计算,通过跟踪颗粒运动轨迹,利用磨损模型完成冲蚀量的预测和计算。连续相具有三维、不可压缩和湍流的特征,控制方程包括连续方程、动量方程,所使用的是RNG k-ε湍流模型[9-10]。
1.2.1 离散相控制方程 颗粒轨迹采用拉格朗日方程求解。流场中颗粒质量分数为0.5%,浓度非常小,连续相流体和离散相颗粒的密度相差大,因此,可忽略固体颗粒受到的绕流阻力、附加质量力、流场压力梯度引发的附加力、颗粒旋转升力等作用力一并不予考虑。固体颗粒运动方程为[9-11]
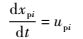 | (1) |
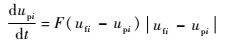 | (2) |
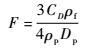 | (3) |
式中:下标f、p和i分别为连续相、离散相和空间方位;x为空间坐标位置;t为时间;u为运动速度;F为固体颗粒所受的拖曳力;D为固体颗粒的直径;ρ为密度;CD为固体颗粒雷诺数Rep定义的拖曳系数,其表达式为
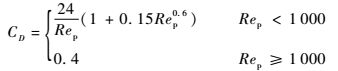 | (4) |
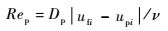 | (5) |
其中:ν为连续相的运动黏度。
1.2.2 磨损模型 应用Yao[12]和Finnie[13]等腐蚀与冲蚀研究中心的计算模型,完成冲蚀磨损的计算。方程式(6)和方程式(7)综合考虑了固体颗粒冲击速度、冲击角度、壁面材料硬度、固体颗粒形状等因素对冲蚀磨损的影响。
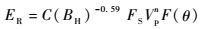 | (6) |
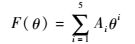 | (7) |
式中:ER为材料的冲蚀磨损率;BH为材料的布氏硬度;FS为颗粒的体型系数(尖锐颗粒取1.0, 半圆形颗粒取0.53, 圆形颗粒取0.2);Vp为颗粒的冲击速度;θ为冲击角度;C、n和Ai为经验常数。θ为根据壁面材料确定的经验常数。本实验使用样品304不锈钢硬度为187,假定颗粒为圆形颗粒,FS取0.2。
1.2.3 壁面反弹模型 固体颗粒撞击壁面时存在能量的转移和损失,表现形式为热传导、样品表面磨损等。本次模拟中确定的避免恢复方程如下:
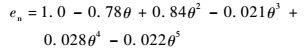 | (8) |
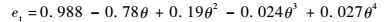 | (9) |
式中:en和et分别为法向和切向磨损系数。
1.2.4 几何模型 利用ANSYS GAMBIT软件创建几何模型,如图 1所示,包含喷嘴、样品区域、水箱底部和计算域。定义喷嘴壁面、箱体底部、样品冲击面为无滑移固体壁面,其他边界为压力出口边界条件,离散相边界类型为reflect,速度入口在喷嘴进口处。网格数目为185万,在冲击壁面附近加密处理。
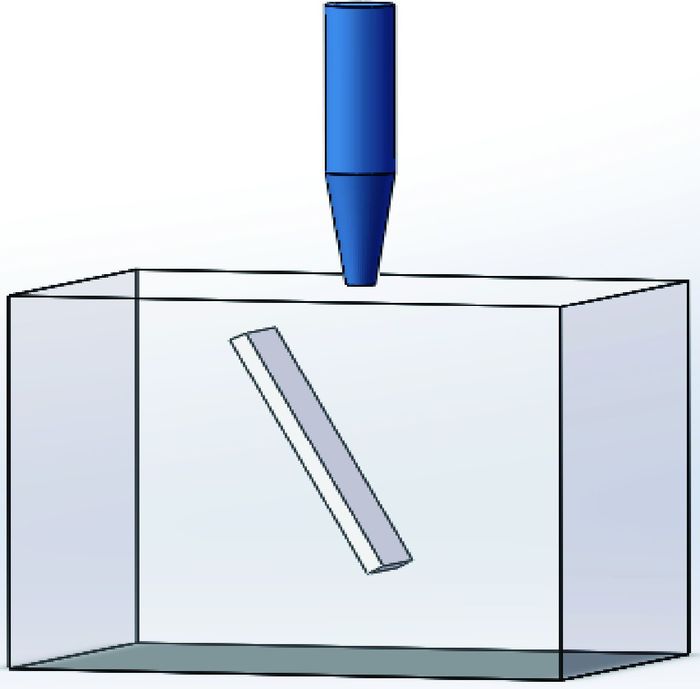 |
| 图 1 数值计算几何模型 Fig. 1 Geometric model of numerical calculation |
| 图选项 |
2 结果讨论 2.1 颗粒粒径对磨损行为的影响 实验所用颗粒为50~60目粒径的石英砂。图 2为石英砂颗粒的SEM形貌,图 2(a)和图 2(b)分别为石英砂初始粒径图与冲蚀48 h后的石英砂粒径图。由图 2可见,颗粒冲击样品表面后粒径变小。图 2中颗粒的平均直径可由表 2所示。
 |
| 图 2 颗粒SEM形貌 Fig. 2 Particle morphology of SEM |
| 图选项 |
表 2 石英砂不同时间段的粒径分布 Table 2 Particle size distribution with different time period
| 冲蚀 时间/h | 颗粒粒径质量分数/% | |||
| 粒径 50~60目 | 粒径 60~70目 | 粒径 70~80目 | 粒径 >80目 | |
| 0 | 100 | 0 | 0 | 0 |
| 12 | 36.3 | 45.8 | 10.9 | 7 |
| 48 | 25.6 | 29.8 | 32.5 | 12.1 |
表选项
表 2为石英砂颗粒粒径的质量分数分布。未冲蚀之前,颗粒粒径50~60目占100%。在冲蚀12 h后,50~60目粒径的石英砂质量分数减少至36.3%,60~70目粒径的石英砂质量分数增加至45.8%,70~80目粒径的石英砂质量分数增加至10.9%,大于80目粒径的石英砂质量百分数增加至7%。在冲蚀48 h后,50~60目粒径的石英砂质量分数减少至25.6%,60~70目粒径的石英砂质量百分数减少至29.8%,70~80目粒径的石英砂质量百分数增加至32.5%,大于80目粒径的石英砂质量百分数增加至12.1%。通过计算可知,在12 ~48 h冲蚀这段时间过程中,50~60目粒径的石英砂颗粒质量百分数减小量与60~70目粒径的石英砂颗粒质量百分数减小量之和约等于70~80目粒径的石英砂颗粒质量百分数增加量,并且随着冲蚀时间的增加,颗粒粒径有向70~80目集中的趋势。
图 3为304不锈钢长时间冲蚀48 h过程中的质量磨损随时间变化。图 3表明304不锈钢样品质量磨损随着冲蚀时间的增加而逐渐降低,最后趋于平缓。图 3中质量磨损在冲蚀时间39 h后,进入平缓区。该结果与Bitter[14]提出微切削理论(方程式(10)和式(11))的计算结果相吻合。
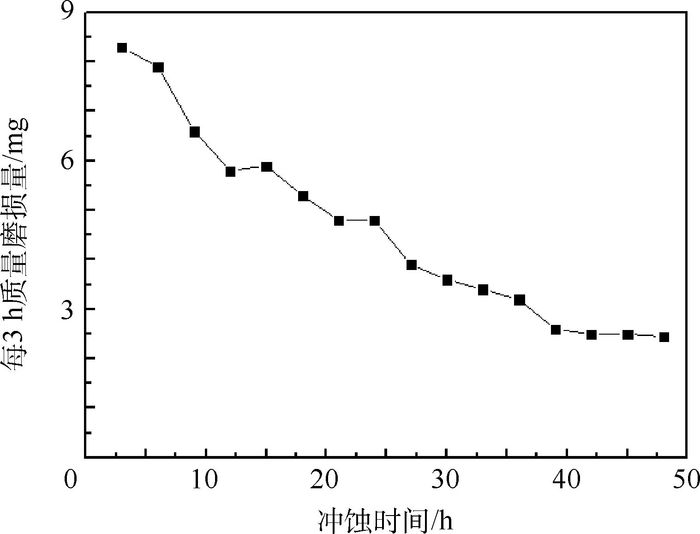 |
| 图 3 304不锈钢质量磨损随冲蚀时间变化 Fig. 3 Variation of 304 stainless steel mass loss with erosion time |
| 图选项 |
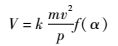 | (10) |
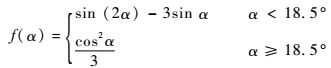 | (11) |
式中:V为样品质量冲蚀磨损量;m为单个颗粒质量;v为颗粒碰撞壁面速度;f(α)为颗粒碰撞角度函数,α为碰撞角度;p为靶材流动应力;k为常数。当冲蚀时间累计39 h后,颗粒粒径主要分布在60~80目之间,其中70~80目粒径的颗粒质量分数占大部分。实验中发现,样品质量磨损率随时间增加而逐渐降低,冲蚀39 h后趋于平缓。进行分析,可以发现。首先,在实验中,v不变,p不变,当颗粒粒径减小时,相当于减小了颗粒的体积,颗粒的密度不变,故而m减小,样品质量磨损量随时间增加而减小同时质量磨损率随时间增加而减小。其次,当颗粒粒径降低到70~80目后,相对于50~60目的单个颗粒质量减小,由牛顿第二定律公式可知,在加速度保持不变的前提下,颗粒质量减小颗粒与材料表面的撞击力减小。由于颗粒硬度基本不变,撞击力减小后,不足以使颗粒破裂,导致粒径不再减小即粒径分布趋于稳定。在本次实验冲蚀39 h后,由于颗粒含量较低且颗粒粒径高度集中在70~80目,在颗粒与样品表面撞击的频率较低情况下导致颗粒与样品表面的撞击力度与撞击频率趋于稳定,从而样品质量磨损率在39 h后趋于稳定。
2.2 颗粒运动轨迹对磨损行为的影响
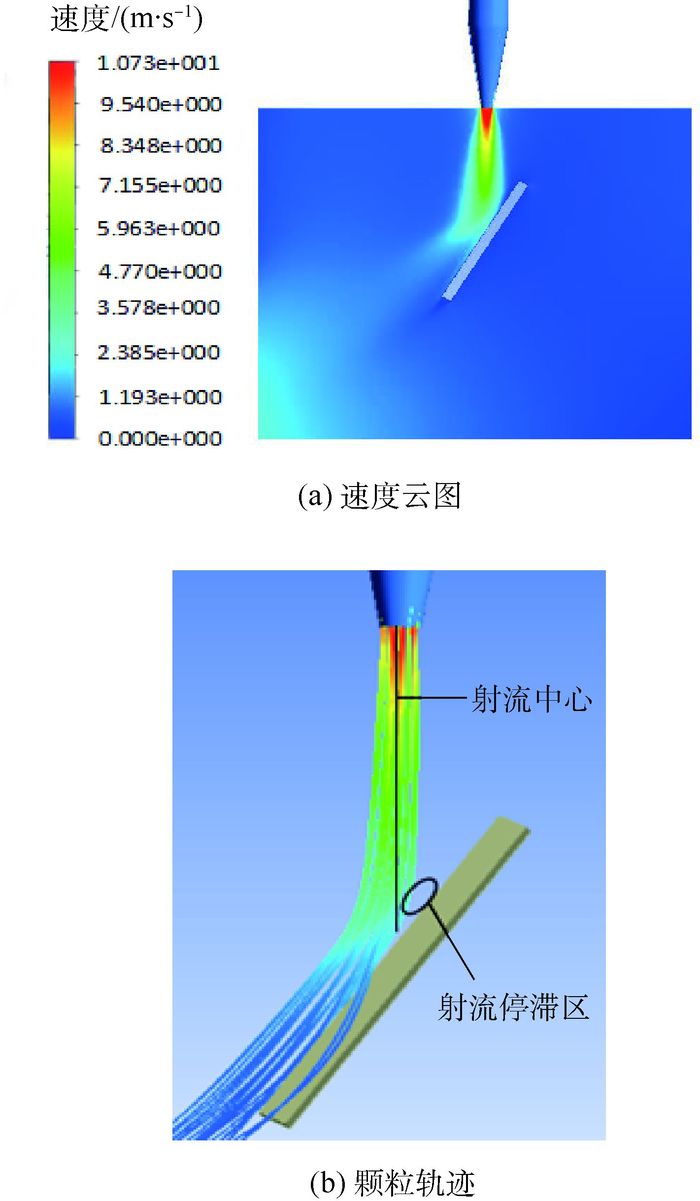
2.2.1 流场特征 颗粒在液流带动下运动并与304不锈钢板相碰,液流流场决定了颗粒碰撞壁面。图 4为连续相在计算域内的速度云图和颗粒迹线。由图 4(a)可知,射流最大的速度发生在射流中心线与喷嘴出口的交界处,数值大约为10.7 m/s,与实验喷嘴出口速度10.5 m/s相吻合。沿着射流中心线,连续相的速度有所降低,这是因为接近样品处的静压较高。从图 4(b)可知,由于高静压的存在,射流中心线与样品的交界处,连续相的速度较低且由于射流冲蚀角度较小,流场迹线显示样品表面与连续相的冲击点为非均匀分布,且在射流中心线处存在射流停滞点。
 |
| 图 4 流场数值计算 Fig. 4 Numerical calculation of flow field |
| 图选项 |
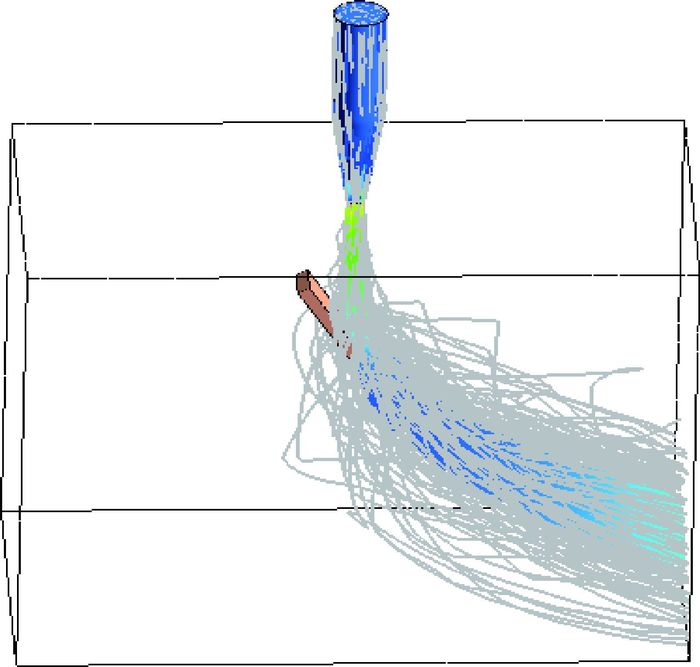
2.2.2 颗粒分布特征 图 5为数值计算的颗粒轨迹分布。大部分颗粒的轨迹沿着水流路径方向。在射流中心线与样品交界高静压区,即射流停滞区域,颗粒的运动轨迹趋于液流方向,远离射流中心区域;由于射流中心对应于样品中心,因而颗粒撞击样品表面中心区域,以及与液流方向相反区域的数目减少,沿着液流方向且远离中心射流区域的样品表面撞击数目增加。一个颗粒是否能撞击到样品,取决于液流。根据颗粒碰撞实验样品的分布情况,将样品工作表面划分3个区域(如图 6所示),区域①为停滞区域,区域②为切削过渡区域,冲击角度为15°~ 30°;区域③为贴壁射流区域,冲击角度小于15°。可以发现,区域①射流停滞且与液流方向相反,几乎没有颗粒撞击;区域②大部分颗粒运动轨迹沿液流冲击方向,与样品表面撞击角度在15°~30°区间内;区域③小部分颗粒运动轨迹沿水流方向贴壁射流,撞击角度小于15°。区域②颗粒的法向分力较大,刺入表面的深度较大,之后的切削作用可以顺利进行,致使样品表面发生较多材料脱落,磨损量较大;区域③颗粒的法向分力较小,不足以刺入表面或进入的深度较小,导致后续的切削作用不易进行,因而其磨损量较小。
 |
| 图 5 数值计算的颗粒轨迹分布 Fig. 5 Numerical calculation of particle tracking trajectories distribution |
| 图选项 |
 |
| 图 6 颗粒-壁面碰撞点(数值计算)分布及对应冲蚀后样品磨损分区 Fig. 6 Distribution diagram of particle-wall collision point (numerical calculation) and partition of tested sample wear after washout |
| 图选项 |
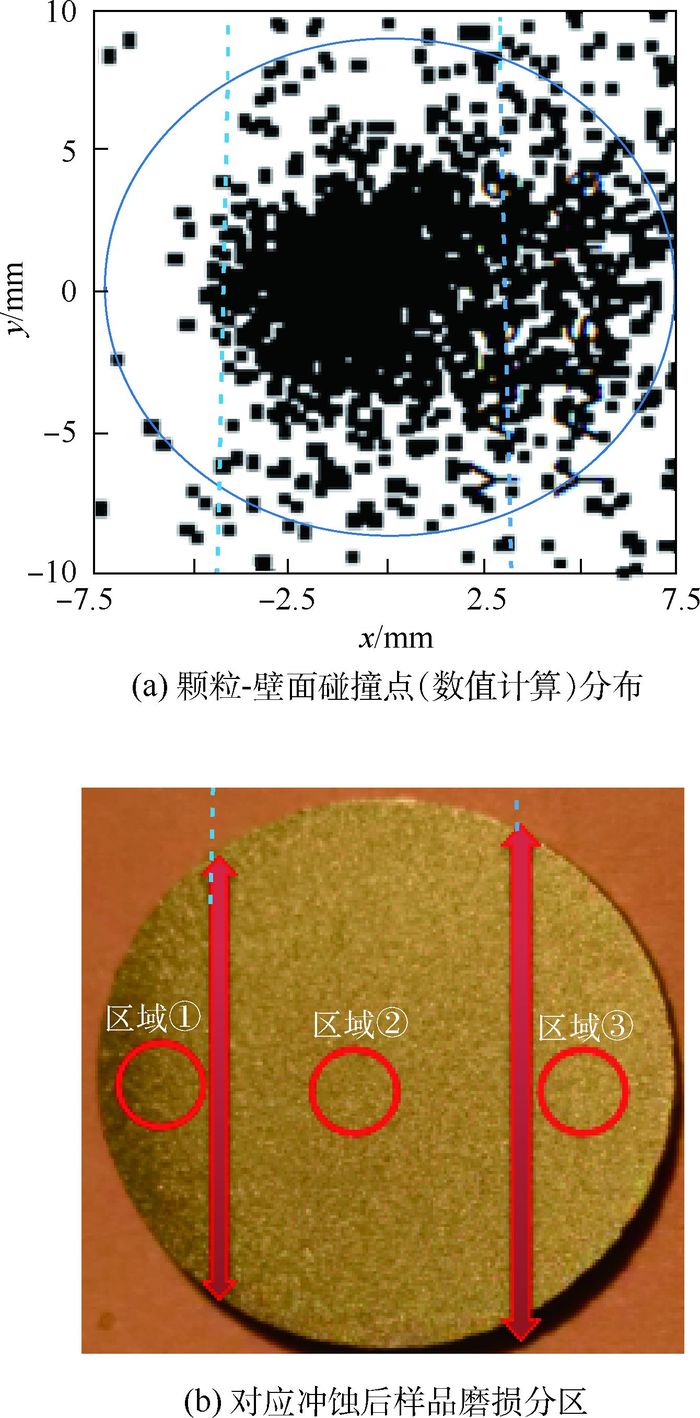
2.2.3 样品表面撞击点分布 射流流场的分布决定颗粒的运动轨迹,颗粒的运动轨迹决定了颗粒与实验样品表面的冲击角度以及撞击点在样品表面的分布,从而导致样品表面形貌存在磨损分区。样品表面形貌的磨损分区采用肉眼观察和SEM 2种观察方法。图 6 (b)表明了在肉眼观察情况下,样品表面形貌经过试验冲蚀后分为3个不同区域,这3个不同区域与数值计算获得的图 6(a)相似。图 6(a)是由样品表面与颗粒跟踪轨迹相交点组成。由图 6(a)可知,颗粒与样品的撞击点分布区域可以分为3个区域。由样品直径15 mm,可分为区域①(-7.5~-4.5 mm)、区域②(-4.5~3.5 mm)、区域③(3.5~7.5 mm)。区域①几乎没有撞击点,大部分的撞击点主要分布在区域②,区域③含有部分撞击点。这表明颗粒主要作用于样品表面的区域②。颗粒与样品的撞击点分布越密集的区域,表明该区域样品表面与颗粒撞击的次数多、撞击频率高,因而磨损大。图 6(b)中区域①明显比区域②、③要颜色暗淡,说明在该区域的颗粒-壁面碰撞次数比其他两区域的碰撞次数要少,更大程度保持材料原始的本色。
图 7显示的是样品表面撞击点分布。由图 7可知,在样品表面区域①(-7.5~-4.5 mm)内,撞击点占比(在此区域的碰撞次数占总碰撞次数的比例)为0.48%;区域②(-4.5~3.5 mm)内,撞击点占比为63.6%;区域③(3.5~7.5 mm)内,撞击点占比为13.9%。因此,颗粒与样品表面撞击主要集中在区域②,且在样品中心沿着水流方向约2.5 mm左右达到峰值。颗粒在样品表面区域①的撞击点非常少,这可能是由于颗粒轨迹沿液流方向。且在射流停滞区域上方,存在高静压区,使颗粒运动轨迹远离区域①,从而导致颗粒与样品撞击点分布稀少。由于样品直径较小,且只捕捉一次撞击点,所以在区域③发现的颗粒与样品撞击点占比小。
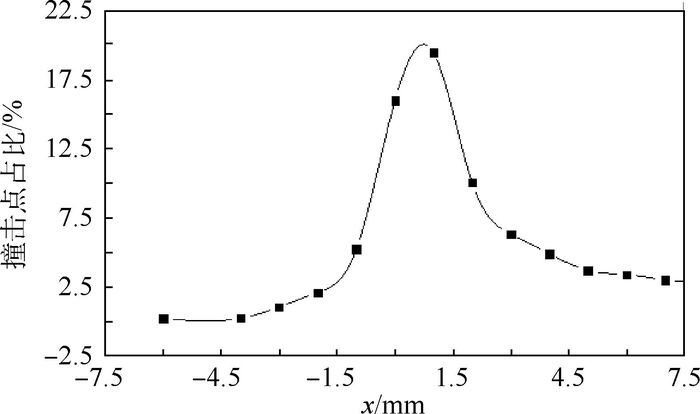 |
| 图 7 数值计算颗粒-壁面撞击点分布 Fig. 7 Numerical calculation of particle-wall collision point distribution |
| 图选项 |
2.3 材料物相 图 8中,A为奥氏体,M为马氏体,F为铁素体。初始抛光状态304不锈钢材料的X射线衍射(XRD)测试表明:样品未冲蚀之前存在少量的铁素体,可能是因为样品的奥氏体相质量分数并非100%。图 8中,抛光后304不锈钢在冲蚀21 h后的XRD曲线可发现,冲蚀21 h后,不锈钢样品由于冲蚀的作用,材料物相发生了相变,部分奥氏体由于颗粒撞击力的作用转变为马氏体,此结果与Aribo等[15]实验结果相吻合。颗粒撞击材料产生了足够的应力导致材料部分奥氏体转变为马氏体;在颗粒撞击材料行为发生后,材料的奥氏体大部分转变为马氏体与铁素体;马氏体相抗腐蚀性较奥氏体相弱,因此,冲蚀后的材料其腐蚀率将提高,继而磨损率加大。这可能是导致材料在冲蚀21 h之后,颗粒粒径减小的情况下,样品依然存在较高质量冲蚀损耗率的原因。
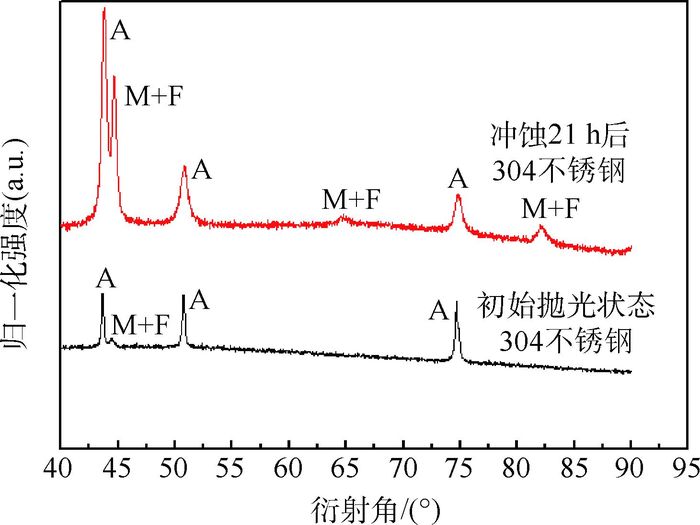 |
| 图 8 初始抛光状态以及冲蚀21 h后304不锈钢XRD测试的比较 Fig. 8 Comparison of 304 stainless steel XRD measurement between original polish and washout after 21 h |
| 图选项 |
3 结论 1) 颗粒粒径随着冲蚀时间的增加而逐渐减小,变化趋势逐渐平缓。随着颗粒粒径的减小,颗粒对材料产生的冲击作用减小,导致材料由于微切削产生的质量磨损变化区域平缓。
2) 材料表面磨损区域可分为3个区域:停滞区、切削过渡区域和贴壁射流区域。停滞区颗粒撞击少,撞击点占比0.48%;切削过渡区域为主磨损区,撞击点占比达到63.6%,且撞击角度在15°~30°;贴壁射流区域撞击点占比13.9%,撞击角度小于15°。
3) 304不锈钢材料物相结构由于颗粒撞击部分奥氏体会转变为马氏体和铁素体,马氏体相对于奥氏体抗腐蚀性较差,因此将促进腐蚀磨损行为。
参考文献
| [1] | 马志宏, 李运泽, 张华, 等. 砂尘环境试验设备中颗粒浓度场的实验研究[J].北京航空航天大学学报, 2005, 31(8): 884–887. MA Z H, LI Y Z, ZHANG H, et al. Experimental study on particle concentration in sand and dust equipment[J].Journal of Beijing University of Aeronautics and Astronautics, 2005, 31(8): 884–887.(in Chinese) |
| [2] | TRIBBLE A C, BOYADJIAN B, DAVIS J, et al.Contamination control engineering and design guidelines for the aerospace community-results:AIAA-1996-4375[R].Reston:AIAA, 1996. |
| [3] | ARNOLD G S. Spacecraft contamination model development[J].Proceedings of SPIE, 1998, 3427: 272–289.DOI:10.1117/12.328499 |
| [4] | BARENGOLTZ J.Molecular and particulate containments:A contamination data base within environment:AIAA-1988-0014[R].Reston:AIAA, 1988. |
| [5] | TRIBBLE A C. The space environment:Implications for spacecraft design[M].Princeton: Princeton University Press, 1995: 183. |
| [6] | THOMAS B S, GRAHAM S A, DAVID F H, et al. Photochemical spacecraft self-contamination:Laboratory results and system impacts[J].Journal of Spacecraft and Rockets, 1989, 26(5): 358–367.DOI:10.2514/3.26080 |
| [7] | 唐萍, 朱光武, 秦国泰, 等. 航天器表面污染物质沉积变化和控制因子评估[J].北京航空航天大学学报, 2015, 41(5): 891–896. TANG P, ZHU G W, QIN G T, et al. Changes of contamination deposition on spacecraft surface and evaluation of control factors[J].Journal of Beijing University of Aeronautics and Astronautics, 2015, 41(5): 891–896.(in Chinese) |
| [8] | ZHAO Y L, ZHOU F, YAO J, et al. Erosion-corrosion behaviour and corrosion resistance of AISI 316 stainless steel in flow jet impingement[J].Wear, 2015, 328-329: 464–474.DOI:10.1016/j.wear.2015.03.017 |
| [9] | FAN J R, YAO J, CEN K F. Antierosion in a 90° bend by particle impaction[J].AIChE Journal, 2002, 48(7): 1401–1412.DOI:10.1002/(ISSN)1547-5905 |
| [10] | FAN J, YAO J, ZHANG X Y. Experimental and numerical investigation of a new method for protecting bends from erosion in gas-particle fows[J].Wear, 2001, 251: 853–860.DOI:10.1016/S0043-1648(01)00742-6 |
| [11] | JIN T, LUO K, WU F, et al. Numerical investigation of erosion on astaggered tube bank by particle laden flows with immersed boundary method[J].Applied Thermal Engineering, 2014, 62(2): 444–454.DOI:10.1016/j.applthermaleng.2013.10.004 |
| [12] | YAO J, ZHOU F, ZHAO Y L. Investigation of erosion of stainless steel by two-phase jet impingement[J].Applied Thermal Engineering, 2015, 88: 353–362.DOI:10.1016/j.applthermaleng.2014.08.056 |
| [13] | FINNIE I, STEVICK G R, RIDGELY J R. The influence of impingement angle on the erosion of ductile metals by angular abrasive particles[J].Wear, 1992, 152(1): 91–98.DOI:10.1016/0043-1648(92)90206-N |
| [14] | BITTER J G. A study of erosion phenomena[J].Wear, 1963, 6(1): 5–21.DOI:10.1016/0043-1648(63)90003-6 |
| [15] | ARIBO S, BARKER R, HU X, et al. Erosion-corrosion behaviour of lean duplex stainless steel in 3.5wt% NaCl solution[J].Wear, 2013, 302(1-2): 1602–1608.DOI:10.1016/j.wear.2012.12.007 |
