互相关速度测量技术是以随机过程的相关理论和信息理论为基础发展起来的一种流动参数检测技术。根据互相关原理可以对2个相似信号求出它们之间的时间延迟,并可与不同的传感器进行结合,完成不同的参数测量任务,具有原理简单、实现方便的优点[15-16]。
在本文的测量中,将外加气泡作为水体的噪声,利用互相关测速原理,将速度测量转换为对时间间隔的测量。借助电磁检测方法和硬件装置,在垂直上升管道的2个平行截面分别安装激励线圈和接收线圈,由于被测液体和气泡的电导率差异较小,测量到的信号波动值微弱,易被背景信号淹没。为此可适当提高激励频率,使其达到1 MHz及以上。通过电磁测试系统对空气-水为工质的两相流中的气泡速度进行测量,并将上下2组接收线圈上的信号进行对比,利用MATLAB软件做互相关运算,最终得到2组信号间的时间差。
1 测速理论 1.1 电磁检测原理 在电磁检测系统中,电磁传感器阵列由若干个激励线圈和接收线圈构成,具体数目和结构根据测量条件和要求来确定。被测物场也称为敏感场通常用绝缘材料作为边界,外侧按照一定规律排列着传感器阵列。计算机控制激励信号发生单元对物场进行激励。被测物体具有导电性或导磁性(或两者兼具),当敏感场内电导率或磁导率的分布发生变化时,接收线圈的信号会感应到投影数据,即可以反映场内电学参数变化的边界信息[17]。检测信息由2种信号叠加而成:和激励线圈产生的主磁场(B)相关的信号以及和涡流产生的二次磁场(ΔB)相关的信号,B和ΔB的矢量关系如图 1所示。图中:Re为实部,Im为虚部,α为总磁场的相位。在检测系统中,磁场的波动ΔB反映为检测线圈接收电压的波动(ΔV)。
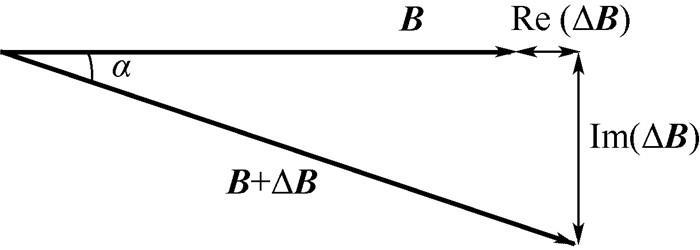 |
| 图 1 主磁场B和二次磁场ΔB的矢量图 Fig. 1 Vector diagram of primary magnetic field B and second scattered magnetic field ΔB |
| 图选项 |
在微扰动情况下,对于低电导率物体,有
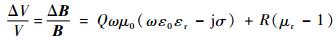 | (1) |
式中:ω为系统频率;ε0和εr分别为真空介电常数和相对介电常数;μ0和μr分别为真空磁导率和物体的相对磁导率;σ为物体的电导率;系数Q和R只与物体的几何参数有关。
当被测物体为生物溶液或其他导电性较弱的流体时,主磁场在被测溶液中产生的二次磁场以一个负虚部的形式存在,并且其幅值与激励频率和电导率有关[18]。一般情况下,当导电性较差时,检测到的信号较微弱,不易提取。为了提高测量精度,往往采用激励频率较高的检测系统[19-20]。
1.2 互相关测速原理 对于2个能量信号而言,互相关函数可用于了解它们之间的相似性以及时间关系,是一个有用的统计量。它给出了在频域内2个信号是否相关的一个判断指标,能用来确定输出信号有多大程度来自输入信号。若这2个信号波形具有相似性,那么互相关函数的峰值点处对应的时间即为它们之间的时间延迟。
本文将互相关测速方法和电磁传感器进行结合,在两相流垂直上升管道上相距为L的2个截面处分别安装结构和功能均相同的电磁传感器,根据流体流动方向,分别定义为上游传感器和下游传感器。当流体的随机噪声,即气泡经过2组传感器时,会对相应的接收信号造成扰动。记2组检测信号分别为p(t)和q(t),由于L是一个相对管道长度较小的值,故可认为流体在流经2组传感器时是一个匀速平稳的过程。根据Wang等的“凝固流动”假设[21],被测流体经过上游传感器时造成的扰动信号必然会在一定时间间隔后以相同的形式反映在下游传感器的输出信号中。即在理想情况下,q(t)的波形应与p(t)完全相似,仅仅在时间上滞后了τ0时刻,τ0称为渡越时间,表示如下:
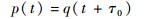 | (2) |
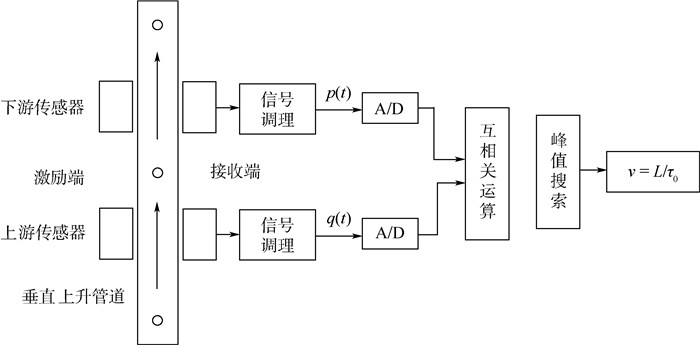
图 2为互相关测速的原理图。当气泡分别经过上游和下游传感器时,通过接收线圈得到相应的感应信号,经过信号放大、滤波和A/D转换,计算出p(t)和q(t)的互相关函数为[22]
 |
| 图 2 互相关测速原理图 Fig. 2 Schematic diagram of velocity measurement based on cross correlation |
| 图选项 |
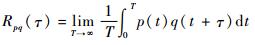 | (3) |
将式(2)代入式(3)得
 | (4) |
由自相关函数的性质可知,p(t)的自相关函数Rpp(τ)在τ=0时取得最大值,故Rpp(τ-τ0)在τ=τ0时取得峰值,通过提取峰值点即可得到渡越时间τ0。在理想的匀速流动状态下,可求气泡速度为
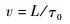 | (5) |
基于以上的电磁检测理论和互相关运算,本文提出的测速方法采用电磁检测系统作为硬件平台,对采集到的感应信号求互相关函数,以期得到和速度相关的参数值。
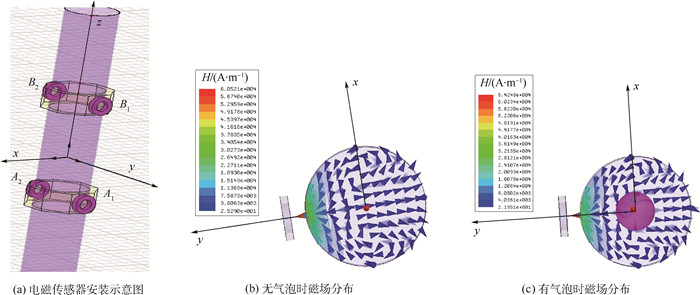
2 电磁检测系统仿真及实验 2.1 基于MAXWELL Ansoft仿真 图 3为有限元仿真软件MAXWELL Ansoft中电磁传感器安装的示意图和无气泡、有气泡通过时磁场分布图。从图 3(a)中可以看出,该检测系统一共有2组传感器,每组传感器均包括一个激励线圈和一个接收线圈,它们的位置关于xz平面对称。上游传感器中线圈记为A1和A2,下游传感器中线圈记为B1和B2。字母A和B代表传感器的位置,下标数字1和2分别表示激励线圈和接收线圈。激励线圈产生主磁场,并作用于流体,同时流体对其有反作用,产生二次磁场。如此提取的检测信号便与工质密切相关。当气泡混入水流并经过传感器时,由于流体导电性发生了变化,磁场分布发生变化(xy平面分布特征如图 3(b)和图 3(c)所示,H为磁场强度),检测信号也随之改变。
 |
| 图 3 MAXWELL Ansoft电磁仿真示意图 Fig. 3 Diagram of electromagnetic simulation based on MAXWELL Ansoft |
| 图选项 |
气液两相流自下往上垂直流动,当气泡经过上游传感器的接收线圈A2时,A2上的信号波形会发生变化。接着,气泡经过下游传感器的接收线圈B2,在B2的信号中产生同样的波动,这2个波动的时间差即气泡通过这2组传感器所在平面的时间差。据此建立简化模型,假设气泡尺寸均匀,呈单列分布,忽略流体静力学压力和电磁场的影响,流过程中形状大致不变且无击穿,气泡之间以及气泡与管壁之间无力的作用。待速度稳定后,再启动信号采集过程。
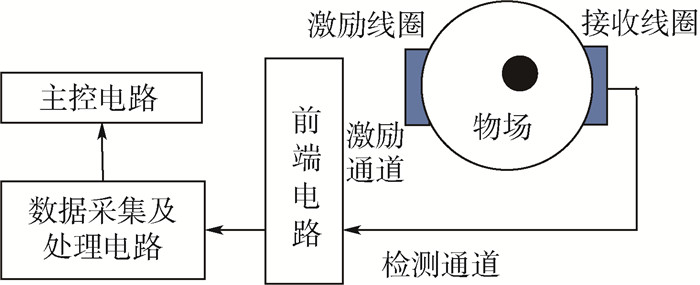
2.2 实验平台 该实验的原理是气体和液体之间存在电导率差异,经过2个线圈之间时会对线圈间互感信号的相位造成不同影响。目的是通过辨别其中的气相因素对检测信号造成的影响,实现对其速度的测量。根据实验原理进行实验设计,检测系统结构如图 4所示。
 |
| 图 4 电磁检测系统结构 Fig. 4 Structure of electromagnetic testing system |
| 图选项 |
实验平台如图 5所示,循环水自下而上流过管道,利用气泡发生装置产生不同速度的气泡。气泡呈单列依次向上运动,为使结果具有较强的对比性,气泡速度设置为3种:0.64、0.42及0.30 m/s。同时,通过设计对称性良好的传感器线圈,达到减小误差的目的。针对实验对象的低导电性,激励信号频率采用8.3 MHz,以便得到较好的测量值。上下游传感器纵向距离设置为200 mm,每隔1 ms保存一组相位解调数据,对每组检测信号共保存2 000个数据。
 |
| 图 5 测速实验平台 Fig. 5 Experimental platform of velocity measurement |
| 图选项 |
2.3 实验结果及数据分析 重复性实验一共安排6组,实验条件基本相同。对所测数据进行总结,发现6组数据波动不大,故可取其平均值,作为最终数据进行分析。
由检测信号可得,由检测信号提取的相位信息与气泡的速度有一定的关联,可用来辨识不同速度的气泡。为了简化计算,首先对相位做归一化处理并进行滤波,如图 6所示。
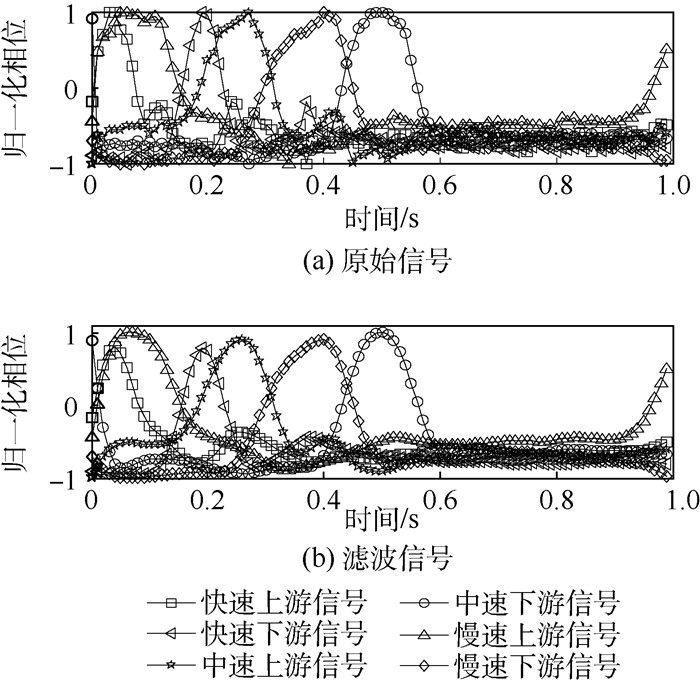 |
| 图 6 滤波前后的归一化相位信号 Fig. 6 Normalized phase signal before and after smoothing |
| 图选项 |
由图 6可以看出,当气泡通过上游传感器所在截面时,接收线圈上的信号会出现明显波动,该波动呈马鞍形,且会在一定时间间隔后以相似的特征出现在下游接收信号中,这样即可实现无需标定的自动测量。无论从气泡通过单个截面传感器所经历的时间,还是从气泡在2个截面间经历的时间,都可以明确区分出3种速度。对滤波后的相位信号进行互相关运算,分别求出3种速度时2组检测信号的互相关函数,并提取峰值。
根据互相关函数的定义,可知峰值点对应的时间即为2个波形相似的信号之间的延时时间。互相关函数波形如图 7所示,其为时间的函数。
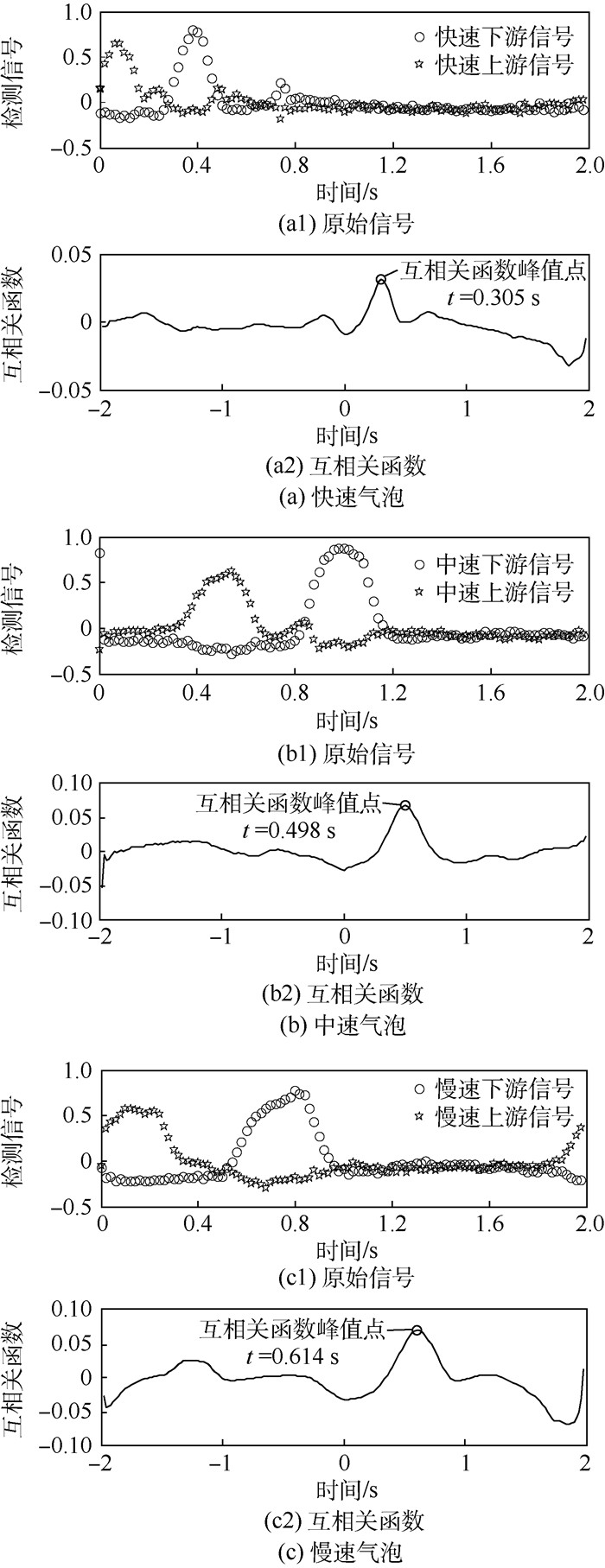 |
| 图 7 2组检测信号及其互相关函数 Fig. 7 Two groups of testing signals and their cross correlation functions |
| 图选项 |
由图 7可知,对于快、中和慢速气泡而言,2组检测信号的时间间隔分别为0.305、0.498和0.614 s。由于2组传感器的垂直距离为200 mm,故由式(5)可得快、中和慢速气泡速度分别为
 | (6) |
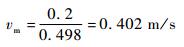 | (7) |
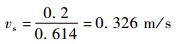 | (8) |
快、中和慢速气泡测量的相对误差分别为
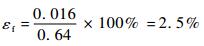 | (9) |
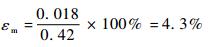 | (10) |
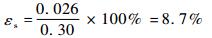 | (11) |
由计算结果可知,根据电磁检测原理测量的信号计算出的速度与理论速度比较吻合。同时,气泡速度越小时,测量结果误差越大。分析原因为,气泡经过两截面传感器时,速度越大,越符合匀速运动的假设,测量结果越接近于理论值。
3 结论 1) 基于电磁参数测量的气液两相流中气泡速度的检测方法中,相位信息可作为气泡速度的特征信号。结合互相关运算,得到不同速度下2组检测信号的时间间隔。
2) 在气泡匀速经过传感器的假设下,计算出3种气泡的速度,实验数据可清晰辨识出3种速度。相对误差分别为2.5%、4.3%和8.7%。
3) 经分析可知,该方法的测量在气泡速度较大时更准确,在气泡速度较小时,误差较大。同时,具有非接触非侵入的优点。
参考文献
| [1] | WALKE S M, SATHE V S. Experimental study on comparison of rising velocity of bubbles and light weight particles in the bubble column[J].International Journal of Chemical Engineering and Applications, 2012, 3(1): 25–30. |
| [2] | LUCAS G P, MISHRA R. Measurement of bubble velocity components in a swirling gas-liquid pipe flow using a local four-sensor conductance probe[J].Measurement Science and Technology, 2005, 16(3): 749–758.DOI:10.1088/0957-0233/16/3/018 |
| [3] | KULKARNI A A, JOSHI J B. Bubble formation and bubble rise velocity in gas-liquid systems:A review[J].Industrial & Engineering Chemistry Research, 2005, 44(16): 5873–5931. |
| [4] | TASSIN A L, NIKITOPOULOS D E. Non-intrusive measurements of bubble[J].Experiments in Fluids, 1995, 19(3): 121–132. |
| [5] | XIE J L, AL-DAHHAN M, DUDUKOVIE M P. Bubble velocity, size, and interfacial area measurements in a bubble column by four-point optical probe[J].AIChE Journal, 2008, 54(2): 350–363.DOI:10.1002/(ISSN)1547-5905 |
| [6] | ONG B.Experimental investigation of bubble column hydrodynamics:Effect of elevated pressure and superficial gas velocity[D].Saint Louis:Washington University, 2003:37-59.http://adsabs.harvard.edu/abs/2003PhDT........19O |
| [7] | LIU T J, BANKOFF S G. Structure of air-water bubbly flow in a vertical pipe-Ⅱ.Void fraction, bubble velocity and bubble size distribution[J].International Journal of Heat and Mass Transfer, 1993, 36(4): 1061–1072.DOI:10.1016/S0017-9310(05)80290-X |
| [8] | ZENIT R, KOCH D L, SANGANI A S. Impedance probe to measure local gas volume fraction and bubble velocity in a bubbly liquid[J].Review of Scientific Instruments, 2003, 74(5): 2817–2827.DOI:10.1063/1.1569391 |
| [9] | HIBIKI T, HOGSETT S, ISHⅡ M. Local measurement of interfacial area, interfacial velocity and liquid turbulence in two-phase flow[J].Nuclear Engineering and Design, 1998, 184(2-3): 287–304.DOI:10.1016/S0029-5493(98)00203-9 |
| [10] | SAMET N, MARECHAL P, DUFLO H. Ultrasound monitoring of bubble size and velocity in a fluid model using phased array transducer[J].NDT & E International, 2011, 44(7): 621–627. |
| [11] | SOUSA R G, PINTO A M F R, CAMPOS J B L M. Effect of gas expansion on the velocity of a Taylor bubble:PIV measurements[J].International Journal of Multiphase Flow, 2006, 32(10-11): 1182–1190.DOI:10.1016/j.ijmultiphaseflow.2006.06.002 |
| [12] | ZHANG C, ECKERT S, GERBETH G. Experimental study of single bubble motion in a liquid metal column exposed to a DC magnetic field[J].International Journal of Multiphase Flow, 2005, 31(7): 824–842.DOI:10.1016/j.ijmultiphaseflow.2005.05.001 |
| [13] | YIN W L, KARIMIAN N, LIU J, et al. Measurement of electromagnetic properties of power station steels[J].NDT & E International, 2012, 51: 135–141. |
| [14] | YIN W L, PEYTON A J, ZYSKO G, et al. Simultaneous noncontact measurement of water level and conductivity[J].IEEE Transactions on Instrumentation and Measurement, 2008, 57(11): 2665–2669.DOI:10.1109/TIM.2008.926054 |
| [15] | 陈敏, 何俊华, 季延俊, 等. 基于互相关的气泡速度的测量方法研究[J].光子学报, 2005, 34(8): 1253–1256. CHEN M, HE J H, JI Y J, et al. Researches on the measurement of bubble velocity based on cross correlation[J].Acta Photonica Sinica, 2005, 34(8): 1253–1256.(in Chinese) |
| [16] | CHENG W, MURAI Y, SASAKI T, et al. Bubble velocity measurement with a recursive cross correlation PIV technique[J].Flow Measurement and Instrumentation, 2005, 16(1): 35–46.DOI:10.1016/j.flowmeasinst.2004.08.002 |
| [17] | ZHAO Q, CHEN G, HAO J N, et al. Numerical approach for the sensitivity of a high-frequency magnetic induction tomography system based on boundary elements and perturbation method[J].Metallurgical and Materials Transactions A, 2013, 24(7): 074004. |
| [18] | SCHARFETTER H, CASANAS R, ROSELL J. Biological tissue characterization by magnetic induction spectroscopy(MIS):Requirements and limitations[J].IEEE Transactions on Biomedical Engineering, 2003, 50(7): 870–880.DOI:10.1109/TBME.2003.813533 |
| [19] | YANG T M, CHEN G, YIN W L, et al. A high frequency digital induction system for conductive flow level measurements[J].Flow Measurement and Instrumentation, 2014, 37: 83–91.DOI:10.1016/j.flowmeasinst.2013.11.002 |
| [20] | YIN W L, CHEN G, CHEN L J, et al. The design of a digital magnetic induction tomography (MIT) system for metallic object imaging based on half cycle demodulation[J].IEEE Sensors Journal, 2011, 11(10): 2233–2240.DOI:10.1109/JSEN.2011.2128866 |
| [21] | WANG J, FAUTRELLE Y, NGUYEN-THI H, et al. Thermoelectric magnetohydrodynamic flows and their induced change of solid-liquid interface shape in static magnetic field-assisted directional solidification[J].Metallurgical and Materials Transactions A, 2016, 47(3): 1169–1179.DOI:10.1007/s11661-015-3277-6 |
| [22] | 胡广书. 数字信号处理——理论、算法与实现[M].3版北京: 清华大学出版社, 2012: 33-38. HU G S. Digital signal processing-Theory, algorithm and implementation[M].3rd edBeijing: Tsinghua University Press, 2012: 33-38.(in Chinese) |
