对于微结构光栅的辐射特性求解,传统的辐射传输理论不再适用,这时需要求解Maxwell方程组获得光栅内电磁场。常用的求解方法有严格耦合波分析(Rigorous Coupled Wave Analysis,RCWA)法、时域有限差分、等效介质理论等[6],其中RCWA法的推导过程是严格的,能得到方程组的准确解,因而得到了广泛的应用,但其仅适用于求解周期性结构的电磁场问题。
通过电磁场的求解可得到光栅的辐射特性。光栅结构与其辐射特性有着密切关系,因而可通过优化设计光栅几何形状获得具有某种辐射特性的特殊光栅,也可根据光栅辐射特性反演得到光栅的几何形状。
王强等[7]利用二次函数表示光栅的几何形状,采用RCWA法求解光栅内部电磁场问题得到光栅衍射效率,然后采用遗传算法(Genetic Algorithm,GA)改变二次函数中各系数项从而优化光栅面形,设计得到了衍射效率达到90%以上、偏振相关损耗小于0.1 dB的光栅面形。董健[8]以航天器热控制为应用背景,采用RCWA法和GA相结合优化设计了一维矩形光栅、双槽光栅、薄膜光栅以及可移动光栅的几何形状,得到了在10μm处具有发射峰的特殊辐射特性光栅。Chen等[9]采用RCWA法求解了二元光栅和塔形光栅内电磁场,采用差分进化(Differential Evolution,DE)算法和微差分进化(Micro-DE,μDE)算法优化设计了具有窄带峰值和宽带峰值的红外辐射器。结果表明当优化设计参数较少时DE算法计算效果优于μDE算法,对于多参数反演问题μDE算法要优于DE算法。
然而,在GA和DE算法中都存在着过早收敛、计算精度较低的缺点,而且交叉、变异以及差分进化等操作较复杂,使这些算法的应用受到一定限制。微粒群优化(Particle Swarm Optimization,PSO)算法是美国心理学家Kennedy和电气工程师Eberhart受鸟类觅食行为启发,于1995年提出的一种群体智能优化算法[10],它采用简单的速度-位移模型,需要调整的参数少,逻辑清晰且易于编程实现,因而得到广泛的应用。Zhao等[11]采用RCWA法求解正问题模型,采用LC等效电路模型获得光栅几何参数的初始值及搜索区间,然后采用PSO算法优化目标函数得到光栅几何形状。但是在基本PSO算法中,仍然存在过早收敛、容易陷入局部最优等缺点。
为了改进PSO算法的全局收敛性能,曾建潮等[12-13]提出了随机微粒群优化(Stochastic PSO,SPSO)算法。该算法将微粒速度进化公式中的权重因子设置为0,去除了当前速度项的影响,同时在搜索空间内随机产生一个微粒位置来改善算法的全局搜索能力,使微粒能更快地搜索到全局最优值,防止种群陷入局部最优。
本文以一维矩形光栅为研究对象,光栅和基底材料均设置为铝。采用RCWA法求解Maxwell方程,根据求得的光栅光谱反射率建立目标函数。采用SPSO算法优化目标函数,反演得到单槽及双槽矩形光栅的几何结构参数,包括光栅周期、凸脊宽度以及凹槽深度。同时分析了SPSO算法中种群大小和搜索区间对光栅结构反演的影响。
1 正问题模型 任意介质中电磁波的传播可由以下微分形式的Maxwell方程组表示[6]:
 | (1) |
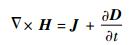 | (2) |
 | (3) |
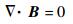 | (4) |
式中:E为电场强度,V/m;B为磁通量密度,Wb/m2;H为磁场强度,A/m;J为电流密度,A/m2;D为电通量密度,C/m2;Jm为磁流密度,V/m2;ρe为电荷密度,C/m2。对于线性、各向同性介质,其本构关系式可表示为[6]
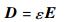 | (5) |
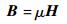 | (6) |
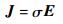 | (7) |
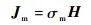 | (8) |
式中:ε为介电常数,F/m;μ为磁导系数,H/m;σ为电导率,S/m;σm为磁导率,Ω/m。
RCWA法求解电磁场问题主要可分为3步[14]:①求解Maxwell方程组得到反射区和透射区的电磁场解的形式;②对光栅区电磁场进行Fourier展开得到耦合波方程;③对反射区、光栅区和透射区边界面上施加边界条件,并与耦合波方程联立求得各阶衍射波。下面以横电波(TE波)为例介绍RCWA法的求解过程。
单位振幅的TE波以入射角θ角入射到沿x方向周期变化的矩形光栅上,示意图如图 1所示,d为光栅凹槽深度,Λ为光栅周期。光栅顶部位于光栅z=0处,光栅与基底交界面为z=d。求解过程中将整个空间划分为3个区域:反射区(z < 0)、光栅区(0 < z < d)和透射区(z>d)。
 |
| 图 1 TE波入射矩形光栅示意图 Fig. 1 Schematic of rectangular grating with a TE wave irradiation |
| 图选项 |
反射区和透射区的电场可分别表示为[14]
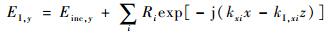 | (9) |
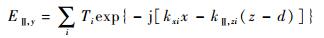 | (10) |
式中:Einc, y为入射TE波的电场强度;Ri和Ti分别表示第i阶反射波和透射波的归一化振幅;kxi、kⅠ, xi、kⅡ, zi等系数可根据Floquet条件确定。
由Maxwell方程可得反射区和透射区的磁场可表示为[14]
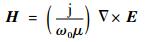 | (11) |
式中:ω0为角频率。
对于光栅区,电场切分量(y方向)和磁场切分量(x方向)可分别表示为空间谐波的Fourier级数形式[14]:
 | (12) |
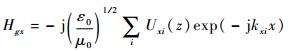 | (13) |
式中:ε0为真空中的介电常数;μ0为真空磁导系数; Syi和Uxi分别为第i阶空间谐波的磁场和电场切向分量。
同时,电场和磁场切分量满足如下Maxwell方程[14]:
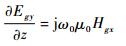 | (14) |
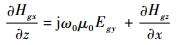 | (15) |
式中:Hgz为磁场在z方向的切分量。
联立式(12)~式(15)可得耦合波方程[14]:
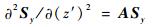 | (16) |
式中:Sy为由Syi组成的矩阵;z′=k0z,k0=2π/λ0,λ0为真空中的电磁波波长;A=Kx2-E,Kx为对角线元素为kxi/k0的对角矩阵,E由介电常数谐波项组成。
在z=0和z=d处,电磁场边界条件可分别表示为[14]
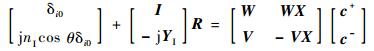 | (17) |
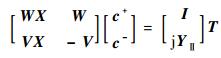 | (18) |
式中:δi0为克罗内克算符;nⅠ为反射区的折射率;I为单位矩阵;R和T分别为总反射率和总透射率;V=WQ,W为特征向量矩阵,Q为对角矩阵;c+、c-为位置系数矩阵;X、YⅠ和YⅡ分别为由exp(-k0qmd)、kⅠ, zi/k0和kⅡ, zi/k0组成的对角矩阵,qm为矩阵A中特征值的正平方根。
联立式(17)和式(18)即可求得各阶衍射波[14]:
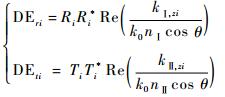 | (19) |
式中:DEri和DEti分别为区域Ⅰ中反射波和区域Ⅱ中透射波的各阶衍射效率。
当横磁波(TM波)入射时,Maxwell方程组的求解过程从磁场开始,求解思路与TE波入射时大致相同,这里不再作介绍,详细推导可参考文献[14]。
2 反问题模型 2.1 微粒群优化算法 PSO算法中,每只觅食的鸟用一个没有质量和体积的微粒代替,每个微粒代表空间内的一个潜在解,个体之间相互协作寻找搜索区域内的最优解。基本PSO算法采用简单的速度-位移模型,在D维搜索空间内,每个微粒的速度和位置更新公式表示为[10]
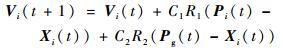 | (20) |
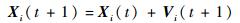 | (21) |
式中:Vi(t)和Vi(t+1)分别为第t代和t+1代微粒i的速度;Pi(t)和Pg(t)分别为在群体第t代微粒群的局部最优位置和全局最优位置;C1和C2为加速系数,为正常数;R1和R2为在区间[0, 1]内均匀分布的随机数。
为了进一步调节微粒的探测和开发能力,在标准PSO算法中引入了惯性权重调节当前速度的影响,微粒速度更新公式变为[15]
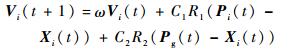 | (22) |
式中:ω为迭代权重因子。研究表明,当按式(23)线性减小时要比其取固定值时更有利于算法快速搜索到最优解:
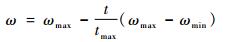 | (23) |
式中:ωmax和ωmin分别为惯性权重因子的最大值和最小值;t和tmax分别为当前迭代次数和最大迭代次数。
PSO算法计算流程图如图 2所示。
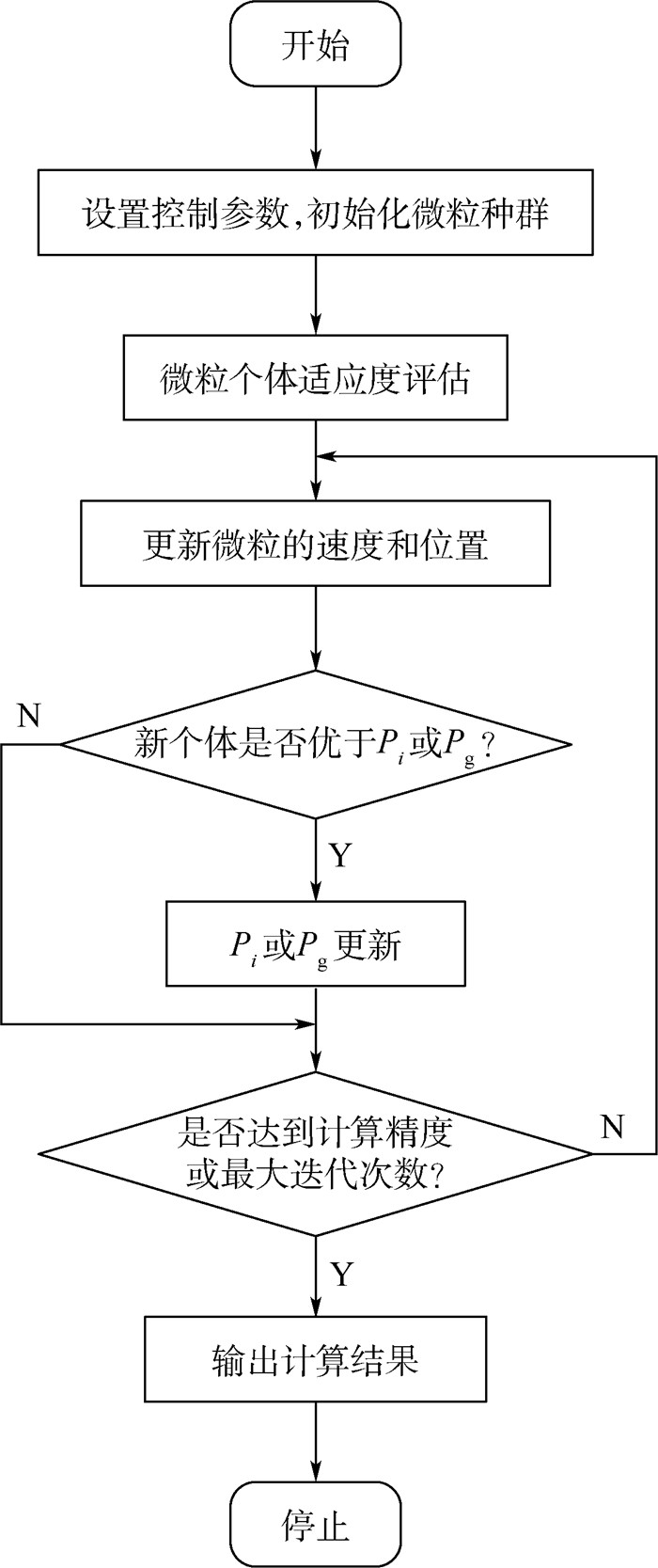 |
| 图 2 PSO算法计算流程图 Fig. 2 Calculation flowchart of PSO algorithm |
| 图选项 |
2.2 随机微粒群优化算法 在SPSO算法中,微粒速度进化过程中去除了当前速度的影响,即令ω=0,此时微粒速度进化公式变为[12-13]
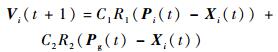 | (24) |
与基本PSO算法相比,微粒的局部搜索能力增强了,但种群的全局的搜索能力下降[12]。为了提高算法的全局搜索能力,在空间中根据下列过程随机产生一个新的微粒j:
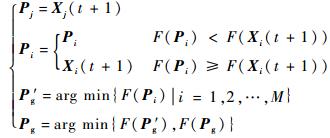 | (25) |
式中:F为目标函数。
在完成上述更新后,执行以下判断:
1) 如果Pg=Pj,表示随机产生的微粒即为当前全局最优位置,此时保存最优位置并在搜索空间内再重新产生一个微粒,其他微粒在更新Pg和Pj后继续演化。
2) 如果Pg≠Pj,且当代没有新的全局最优位置产生,那么所有微粒均按式(24)更新位置。
3) 如果Pg≠Pj,且当代有新的全局最优位置产生,即存在微粒k(k≠j)使得Xk(t+1)=Pg,此时微粒k在搜索空间内停止更新和再生,其他微粒在更新Pg和Pj后继续演化。
3 结果与讨论 3.1 单槽矩形光栅结构反演 一维周期性矩形光栅示意图如图 1所示,基底和光栅材料均为铝,凸脊宽度为l,槽宽为w,且满足Λ=w+l。光栅结构可表示为向量形式a=[Λ, l, d],铝的介电常数及其他物性参数可参见文献[16]。正问题模型采用捷克理工大学的Kwiecien编写的开源代码求解,衍射级数取m=41。为反演得到光栅结构参数,根据正问题求得的光栅光谱反射率建立如下目标函数:
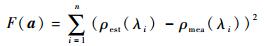 | (26) |
式中:ρest和ρmea分别为光栅光谱反射率反演值和测量值;n为波长[λ1, λ2]范围内目标波长的个数,λ1和λ2为根据辐射特性选定的波长范围。
为了衡量反演计算精度,相对误差定义为
 | (27) |
TM波以θ=30°入射到几何结构为aest=[1.0, 0.9, 0.6] μm的矩形光栅时,光谱反射率如图 3中实点所示。采用SPSO算法对此结构光栅进行反演计算,参数设置如表 1所示,M、Vmax、ε1分别为种群数、最大速度、收敛精度。
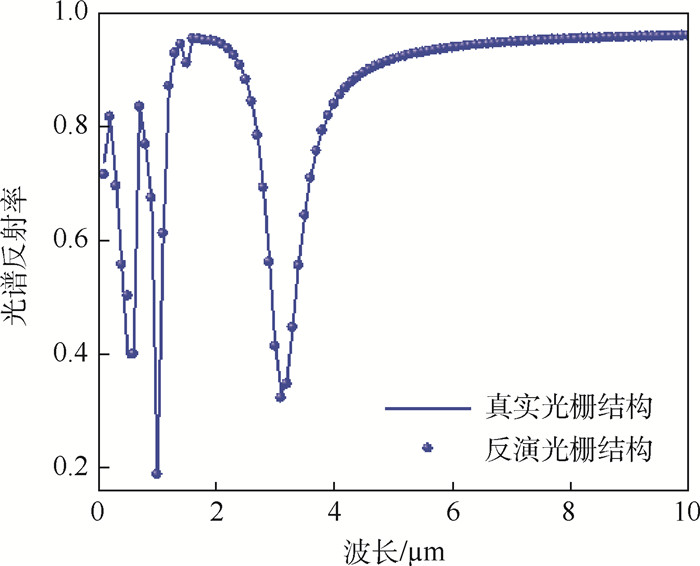 |
| 图 3 单槽光栅光谱反射率 Fig. 3 Spectral reflectance of single-slot grating |
| 图选项 |
表 1 SPSO算法参数设置 Table 1 Parameter setting of SPSO algorithm
| 参数 | 数值 |
| M | 50 |
| Vmax | 3.0 |
| C1 | 1.2 |
| C2 | 0.8 |
| tmax | 100 |
| ε1 | 10-6 |
| λ1/μm | 0.1 |
| λ2/μm | 5.0 |
| n | 100 |
表选项
反演过程中光栅周期、高度及槽宽变化曲线如图 4所示,反演得到光栅结构参数为aest=[Λ±σ, l±σ, d±σ]=[0.999 1, 0.900 3, 0.599 6] μm,对应光谱发射率如图 3实线所示。结果表明,SPSO算法可以很好地反演光栅的几何结构参数,光谱反射率平均相对误差为0.38%。
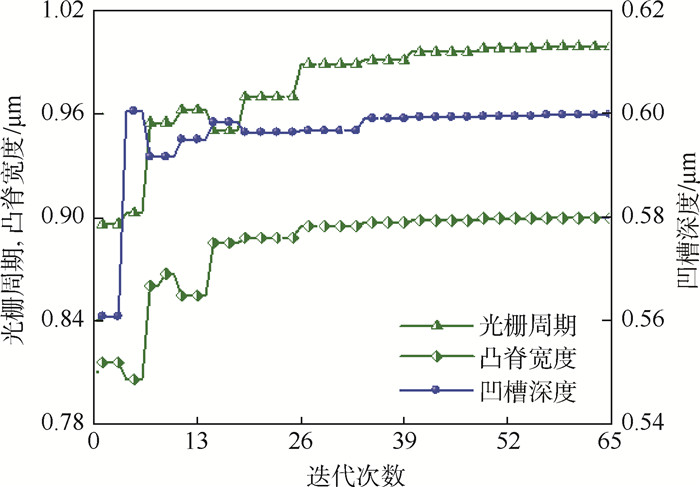 |
| 图 4 单槽光栅几何参数反演结果 Fig. 4 Inverse estimation results of single-slot grating geometry parameters |
| 图选项 |
分别采用基本PSO算法、标准PSO算法、SPSO算法及混合算法PSO-GA[17]对该光栅进行反演时,目标函数值变化曲线如图 5所示。可以看出,SPSO算法收敛速度要明显快于基本PSO、标准PSO及混合PSO-GA算法。
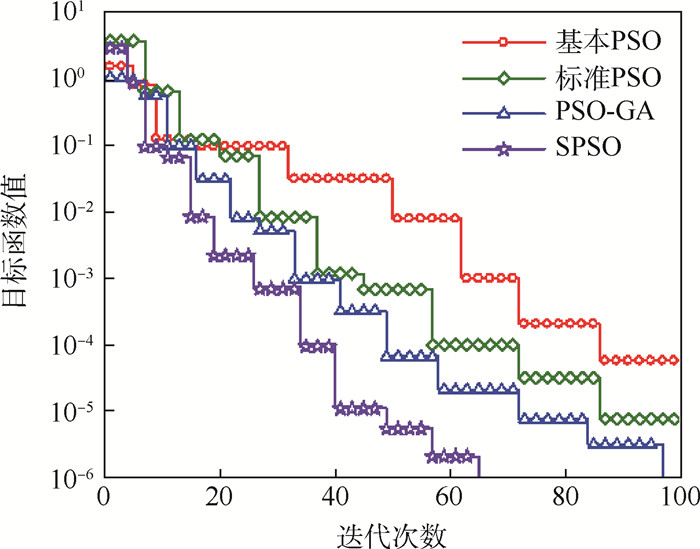 |
| 图 5 4种PSO算法目标函数值变化曲线 Fig. 5 Changing curves of objective function values of four PSO algorithms |
| 图选项 |
光栅光谱反射率与入射波入射角度有关,因此研究了TM波以不同角度入射时的反演结果。由于智能算法存在较大随机性,因而各算例都独立运行20次。光栅结构参数反演结果如表 2所示。可以看出,不同角度入射下都得到了良好的反演结果,最大相对误差小于3%。
表 2 不同入射角度下反演结果 Table 2 Inverse estimation results with different incident angles
| 入射角度/(°) | aest/μm | 平均相对误差/% | 最大相对误差/% |
| 0 | [1.000 6±1.26×10-3, 0.899 2±3.61×10-3, 0.600 4±2.51×10-3] | 0.380 5 | 2.852 6 |
| 30 | [0.999 3±3.09×10-3, 0.899 3±4.59×10-3, 0.599 2±2.99×10-3] | 0.368 9 | 2.863 1 |
| 60 | [0.999 4±2.90×10-3, 0.900 5±3.23×10-3, 0.599 3±3.02×10-3] | 0.376 6 | 2.799 9 |
表选项
此外,采用SPSO算法对不同光栅结构参数进行了反演研究。当TM波以30°角入射到不同光栅结构时,SPSO算法反演结果如表 3所示。结果表明,对于不同的光栅结构,SPSO算法都可以准确反演得到其结构参数。
表 3 不同结构参数下反演结果 Table 3 Inverse estimation results with different structure parameters
| aexa/μm | aest/μm | 平均相对误差/% | 最大相对误差/% |
| [1.0, 0.9, 0.6] | [0.999 3±3.09×10-3, 0.899 3±4.59×10-3, 0.599 2±2.99×10-3] | 0.368 9 | 2.863 1 |
| [3.0, 2.5, 1.5] | [2.999 1±3.11×10-3, 2.500 5±1.19×10-3, 1.499 4±2.95×10-3] | 0.359 6 | 2.904 0 |
| [5.0, 4.0, 2.0] | [5.000 6±3.33×10-3, 3.999 2±4.14×10-3, 2.000 6±3.20×10-3] | 0.331 5 | 2.882 3 |
表选项
3.2 SPSO算法参数影响分析 分别设置3种不同参数搜索区间,SPSO算法反演结果见表 4, 光栅结构参数aexa=[Λ, l, d]。从表中可以看出,随着搜索区间增大,所需迭代次数增加,计算误差也随之增大。这是由于SPSO算法中微粒搜索具有随机性,搜索区间增大使微粒搜索难度增加。
表 4 不同搜索区间下反演结果 Table 4 Inverse estimation results with different searching spaces
| 算例 | Λ /μm | l /μm | d/μm | 迭代次数 | 目标函数值 | 平均相对误差/% |
| 算例1 | [0.9, 1.1] | [0.8, 1.0] | [0.5, 0.7] | 59 | 3.25×10-7 | 0.020 9 |
| 算例2 | [0.8, 1.2] | [0.7, 1.1] | [0.4, 0.8] | 71 | 9.19×10-7 | 0.115 5 |
| 算例3 | [0.5, 1.5] | [0.4, 1.4] | [0.1, 1.1] | 100 | 8.11×10-6 | 0.206 4 |
表选项
SPSO算法种群大小直接影响每代计算时间和每次所能处理的候选解个数,因而对反演结果有很大影响。分别设置为种群数M=10、30和50,反演过程中目标函数值变化曲线如图 6所示。
 |
| 图 6 不同种群大小下目标函数值变化曲线 Fig. 6 Changing curves of objective function values under different population sizes |
| 图选项 |
从图 6中可以看出,随着种群数增加,目标函数下降速度加快,所需计算代数缩短。但是种群数量增加,每次迭代所需计算时间也随之线性增加。综合考虑计算时间和收敛速度,推荐取种群数M=30。
3.3 双槽矩形光栅结构反演 双槽光栅是将单槽光栅每2个凹槽中的其中1个的深度改变,使更多波长的电磁波在光栅表面产生磁极化,从而改变光栅的光谱辐射特性。Cheng等[18]研究了矩形硅光栅在太阳能电池中的应用并提出了多槽光栅模型,结果表明双槽光栅在可见光和近红外波段的吸收效果要优于其他类型。本文双槽矩形光栅的基底和光栅区材料均选取为铝,结构示意图如图 7所示。与单槽光栅不同,双槽光栅具有2个凹槽深度参数d1和d2,且光栅周期满足Λ=2(w+l)。此时光栅结构参数可用向量a=[Λ, l, d1, d2]表示。
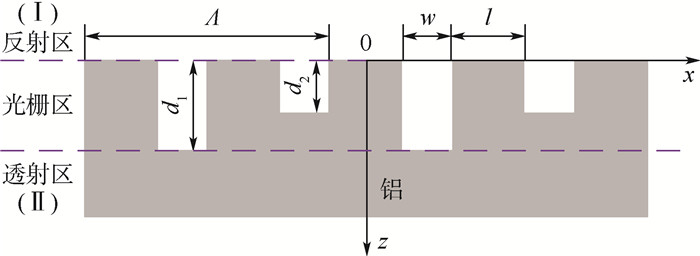 |
| 图 7 双槽矩形光栅示意图 Fig. 7 Schematic of rectangular double-slot grating |
| 图选项 |
双槽矩形光栅结构参数设置为aexa=[2.0, 0.9, 0.6, 0.3] μm,TM波以θ=0°。入射时的光谱反射率如图 8中圆点所示。采用SPSO算法对该光栅结构进行反演,各参数变化曲线如图 9所示。反演得到光栅结构参数为aest=[1.998 6, 0.896 3, 0.603 3, 0.300 2] μm,对应光谱反射率如图 8实线所示。结果表明,SPSO算法可以准确地反演得到双槽光栅的几何形状参数,平均相对误差为0.42%,体现了SPSO算法在光栅结构反演中的可行性和较强的鲁棒性。
 |
| 图 8 双槽光栅光谱反射率 Fig. 8 Spectral reflectance of double-slot grating |
| 图选项 |
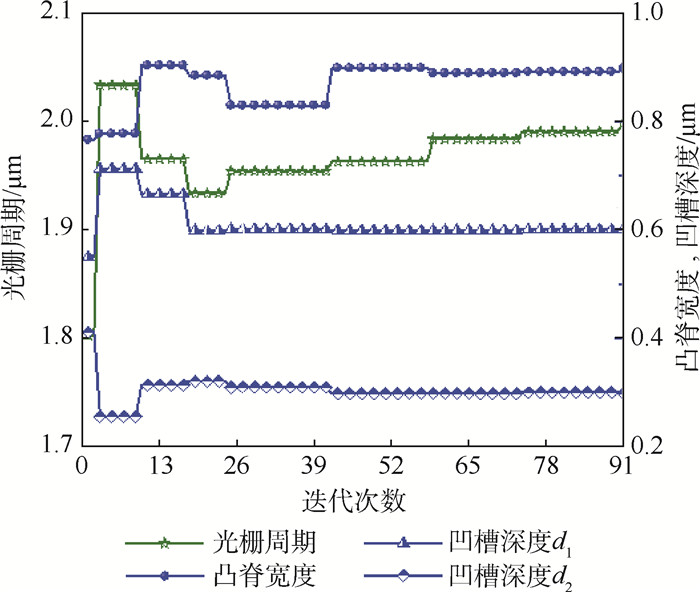 |
| 图 9 双槽光栅几何参数反演结果 Fig. 9 Inverse estimation results of double-slot grating geometry parameters |
| 图选项 |
4 结论 本文研究了一维矩形光栅几何结构参数反演问题,主要得出以下结论:
1) SPSO算法可以准确地反演得到光栅的几何形状参数,包括单槽和双槽矩形光栅,平均相对误差分别为0.38%和0.42%,计算精度较高。
2) SPSO算法在计算效率方面要明显优于基本PSO算法、标准PSO算法及PSO-GA算法。
3) 分析了SPSO算法中搜索区间及种群大小对光栅结构参数反演的影响。结果表明,随着搜索区间增大,所需迭代次数增加,相对误差也随之增大;综合考虑计算时间和收敛速度,推荐种群数取30。
参考文献
| [1] | 梁铨廷. 物理光学[M].北京: 电子工业出版社, 2009: 1-11. LIANG Q T. Physical optics[M].Beijing: Publishing House of Electronics Industry, 2009: 1-11.(in Chinese) |
| [2] | LEE B J, WANG L P, ZHANG Z M. Coherent thermal emission by excitation of magnetic polaritons between periodic strips and a metallic film[J].Optical Express, 2008, 16(15): 11328–11336.DOI:10.1364/OE.16.011328 |
| [3] | JIAO Y, LIU L H, LIU L J, et al. Radiative properties tailoring of grating by comb-drive microactuator[J].Journal of Quantitative Spectroscopy and Radiative Transfer, 2014, 143: 35–45.DOI:10.1016/j.jqsrt.2014.01.010 |
| [4] | CHEN Y B, ZHANG Z M. Design of tungsten complex gratings for thermophotovoltaic radiators[J].Optics Communications, 2007, 269(2): 411–417.DOI:10.1016/j.optcom.2006.08.040 |
| [5] | QIU J, LIU L H, HSU P F. FDTD analysis of infrared radiative properties of microscale structure aluminum surfaces[J].Journal of Quantitative Spectroscopy and Radiative Transfer, 2010, 111(12-13): 1912–1920.DOI:10.1016/j.jqsrt.2010.04.026 |
| [6] | ZHANG Z M. Nano/microscale heat transfer[M].New York: McGraw-Hill Professional, 2007: 1-36. |
| [7] | 王强, 沈国土, 杨宝成, 等. 遗传算法在光栅面形状优化设计中的应用[J].红外与激光工程, 2005, 34(4): 410–414. WANG Q, SHEN G T, YANG B C, et al. Application of genetic algorithm in the design optimization of grating profile[J].Infrared and Laser Engineering, 2005, 34(4): 410–414.(in Chinese) |
| [8] | 董健. 一维微结构光栅辐射特性的反设计方法[D]. 哈尔滨: 哈尔滨工业大学, 2013. DONG J.Inverse design method on radiative properties of one dimensional micro/nano scale grating[D].Harbin:Harbin Institute of Technology, 2013(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10213-1014001130.htm |
| [9] | CHEN J S, LIN P D, CHIU F C, et al. Grating profile optimization for narrow-band or broad-band infrared emitters with differential evolution algorithms[J].Optical Letters, 2012, 37(16): 3399–3401.DOI:10.1364/OL.37.003399 |
| [10] | KENNEDY J, EBERHART R C.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks.Piscataway, NJ:IEEE Press, 1995:1942-1948. |
| [11] | ZHAO J M, QIU J, LIU L H.Accurate geometry design of magnetic polariton with specified resonance wavelength:A combined LC circuit model and inverse technique[C]//ASME 20165th Micro/Nanoscale Heat and Mass Transfer International Conference.New York:ASME, 2016:V001T05A008. |
| [12] | 曾建潮, 崔志华. 一种保证全局收敛的PSO算法[J].计算机研究与发展, 2004, 41(8): 1333–1338. ZENG J C, CUI Z H. A guaranteed global convergence particle swarm optimizer[J].Journal of Computer Research and Development, 2004, 41(8): 1333–1338.(in Chinese) |
| [13] | CUI Z H, ZENG J C, CAI X J.A new stochastic particle swarm optimizer[C]//Proceedings of IEEE International Congress on Evolutionary Computation.Piscataway, NJ:IEEE Press, 2004:316-319.http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1330873 |
| [14] | MOHARAM M G, GRANN E B, POMMET D A. Formulation for stable and efficient implementation of the rigorous coupled-wave analysis of binary gratings[J].Journal of the Optical Society of America A, 1995, 12(5): 1068–1076.DOI:10.1364/JOSAA.12.001068 |
| [15] | SHI Y H, EBERHART R C.A modified particle swarm optimizer[C]//Proceedings of IEEE International Conference on Evolutionary Computation.Piscataway, NJ:IEEE Press, 1998:69-73. |
| [16] | WAKAKI M, KUDO K, SHIBUYA T. Physical properties and data of optical materials[M].Boca Raton: CRC Press, 2007: 1-10. |
| [17] | ROBINSON J, SINTON S, RAHMAT-SAMⅡ Y.Particle swarm, genetic algorithm, and their hybrids:Optimization of a profiled corrugated horn antenna[C]//IEEE Antennas and Propagation Society International Symposium.Piscataway, NJ:IEEE Press, 2002:314-317.http://ieeexplore.ieee.org/xpls/icp.jsp?arnumber=1016311 |
| [18] | CHENG Q, LI P P, LU J, et al. Silicon complex grating with different groove depths as an absorber for solar cells[J].Journal of Quantitative Spectroscopy & Radiative Transfer, 2014, 132: 70–79. |
