目前,数值方法研究热化学非平衡效应对高超声速气动热环境影响在国内外均得到广泛应用。Yumusak和Eyi[5]对高超声速飞行器气动外形优化设计时,研究不同飞行马赫数下热化学非平衡效应的影响,马赫数越大,热化学非平衡效应越明显,主要对驻点区域气动热特性影响大,而远离驻点区域因流场温度迅速减小而影响较弱。Bhutta和Lewis[6]构建新的热化学非平衡离散方法研究三维钝锥在高马赫数大迎角下的气动热环境,因背风比迎风高温流场区域要厚,O2和N2在背风区域离解较多,NO+浓度较大。随着来流流速增大,电子密度在背风区域也会大量增加。Zoby等[7]研究并分析热化学非平衡效应对不同锥角和钝头半径的细长钝锥体壁面热流载荷影响,指出钝头半径对壁面最大热流载荷的影响要比锥角小。Pezzella和Votta[8]数值研究返回舱在不同飞行高度环境下的壁面热流载荷特性,随着飞行高度增加,绕流气体稀薄,激波层内的气体压强和密度变低,气体分子发生热化学反应数量减少,壁面热流载荷受热化学非平衡效应的影响逐渐减弱。柳军等[9]采用三维热化学非平衡计算程序对Apollo飞船返回舱再入流场进行模拟,指出热化学非平衡效应可能是造成返回舱飞行试验与风洞试验数据不一致的重要原因。董维中等[10]开展了空气组分下不同化学反应模型和热力学模型对气动热环境数值计算影响研究,对比分析了球头在不同计算模型下的壁面热流分布特性。李康等[11]研究了热化学非平衡效应中热化学反应对HB2模型边界层温度、密度和组分浓度变化与壁面压强之间的关系,得出流场组分浓度变化对压强影响小,而因热化学反应中离解及复合过程所造成的温度改变对压强影响较大的结论。此外,周禹[12]和周印佳[13]等也对热化学非平衡效应进行了相关研究。
本文采用CFD-FASTRAN软件,数值计算研究空气来流下5组元(N2,O2,N,O,NO),17组化学反应的热化学非平衡效应对高超声速飞行器气动热环境影响。首先,通过与未考虑离解及热化学反应的完全气体模型流场激波距离、流场温度、壁面气动力和气动热载荷比较,研究分析热化学非平衡效应下的气动热环境特性。其次,将热化学非平衡与热化学平衡模型的气动热特性进行对比,分析不同热化学反应程度下的气动热环境之间的区别。通过对Gupta和Park热化学非平衡模型对比研究,为高超声速飞行器在热化学非平衡效应下的气动热环境可靠预测提供参考。
1 控制方程与数值方法 直角坐标系,高温热化学非平衡二维控制方程形式如下:
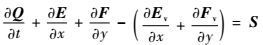 | (1) |
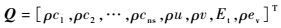 | (2) |
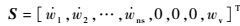 | (3) |
 | (4) |
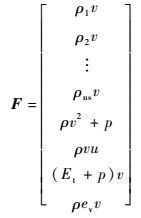 | (5) |
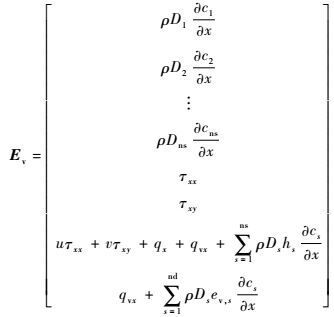 | (6) |
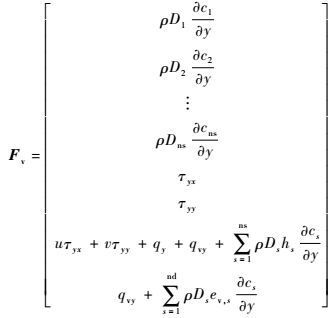 | (7) |
式中:Q为守恒向量;E、F、Ev和Fv分别为x、y方向上的无黏矢通量和黏性矢通量;S为热化学反应源项;ns为混合气体组元总数;nd为混合气体中分子组元总数;u、v为速度分量;τxx、τxy、τyy为切应力分量;Et为混合气体总能;ev为单位质量混合气体振动能(原子组元没有振动能);ev, s为混合气体中组元s单位质量振动能;ρ、p和wv分别为混合气体密度、压强和振动能源项;
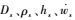
有限体积法对控制方程进行离散。无黏通量离散选用Roe的FDS(Flux Difference Splitting)上差分风格式,黏性通量采用二阶中心差分格式进行离散,限制器选综合性能良好的二阶min mod,时间方向推进采用隐式欧拉格式。
2 热化学非平衡 2.1 热化学非平衡模型 高超声速来流混合气体组元数为ns,组元所发生化学反应式数为nr,其通用化学反应式形式如下:
 | (8) |
式中:as, r和bs, r分别为组元s在第r反应式中为反应物和生成物时的化学反应计量系数;kf, r和kb, r分别为第r反应式的正向和逆向化学反应速率。对于混合气体中的组元Zs,其质量生成率
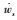
 | (9) |
 | (10) |
式中:Ms为组元s的摩尔质量。
化学反应速率可以由Arrhenius公式[14]求取:
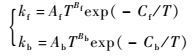 | (11) |
 | (12) |
式中: T为温度;A为频率因子;B为温度指数;C为组元反应活化温度;Kc为化学反应平衡常数;Af、Bf、Cf、Ab、Bb和Cb均为与各化学反应式相关的常数。
对于空气绕流下的高超声速热化学非平衡气动热环境特性,根据本文所选验证模型的来流条件,研究5组元(N2,O2,N,O,NO),17组热化学反应问题。根据化学反应速率公式中各常数取值不同,Gupta[15]和Park[16]模型是目前2种应用较广泛的高温空气化学反应模型,分别如表 1和表 2所示。热力学非平衡模型采用Park双温度模型[17],且不考虑壁面催化作用。
表 1 Gupta化学反应模型 Table 1 Gupta's chemical reaction model
| 化学反应式 | Af/(cm3·(mol·s)-1) | Bf | Cf/K |
| N2+M1?2N+M1 | 1.92×1017 | -0.5 | 113 100 |
| N2+N?2N+N | 4.15×1022 | -1.5 | 113 100 |
| O2+M2?2O+M2 | 3.61×1018 | -1 | 59 400 |
| NO+M2?N+O+M2 | 3.97×1020 | -1.5 | 75 600 |
| N2+O?NO+N | 6.75×1013 | 0 | 37 500 |
| NO+O?O2+N | 3.18×109 | 1 | 19 700 |
| ??注:M1=N2, O2, O, NO; M2=N2, O2, N, O, NO。 | |||
表选项
表 2 Park化学反应模型 Table 2 Park's chemical reaction model
| 化学反应式 | Af/(cm3·(mol·s)-1) | Bf | Cf/K |
| N2+M1?2N+M1 | 3.0×1022 | -1.6 | 113 200 |
| N2+M2?2N+M2 | 7.0×1021 | -1.6 | 113 200 |
| O2+M1?2O+M1 | 1.0×1022 | -1.5 | 59 360 |
| O2+M2?2O+M2 | 2.0×1021 | -1.5 | 59 360 |
| NO+M3?N+O+M3 | 1.1×1017 | 0 | 75 500 |
| NO+M4?N+O+M4 | 5.0×1015 | 0 | 75 500 |
| N2+O?NO+N | 5.7×1012 | 0.42 | 42 938 |
| NO+O?O2+N | 8.4×1012 | 0 | 19 400 |
| ??注:M1=N, O; M2=N2, O2, NO; M3=N, O, NO; M4=N2, O2。 | |||
表选项
2.2 气体输运参数 混合气体中组元s的黏性系数μs:
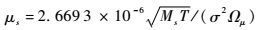 | (13) |
式中:σ为分子特征直径;Ωμ为黏性碰撞积分。
Eucken半经验公式[18]求解混合气体中组元s的热传导系数κs和振动热传导系数κv, s:
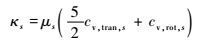 | (14) |
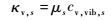 | (15) |
式中:
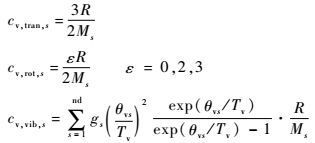 |
式中:cv, tran, s、cv, rot, s和cv, vib, s分别为混合气体中组元s的平动定容比热、旋转定容比热和振动定容比热;ε为分子旋转自由度,其中,单原子ε=0,双原子分子或线性多原子分子ε=2,非线性多原子分子ε=3;R为摩尔气体常数;gs、θvs和Tv分别为混合气体中分子组元的简并因子、振动特征温度和振动温度。
混合气体的黏性系数μ、热传导系数κ和振动热传导系数κv可以由Wilke半经验公式[19],通过混合气体中各组元的黏性和导热系数确定:
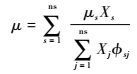 | (16) |
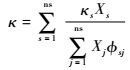 | (17) |
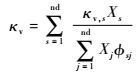 | (18) |
 | (19) |
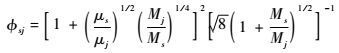 | (20) |
式中:Xs为组元s的摩尔分数;M为混合气体平均摩尔质量。
Fick定理[20]认为混合气体中各组元的扩散系数Ds相同,并通过以下公式求取:
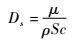 | (21) |
式中:Sc为施密特数,且对中性气体组元Sc=0.5。
3 数值计算与分析 3.1 完全气体与热化学非平衡气动热环境对比分析 选用文献[21]中的高超声速绕流实验圆柱,对其在完全气体模型与考虑热化学非平衡效应下的气动热环境进行数值计算对比分析。圆柱直径d=89 mm。自由来流参数:马赫数Ma∞=17.9,静温T∞=156 K,静压P∞=40.3 Pa,单位雷诺数Re=3.4×105/m;壁面条件为非催化等温壁面Tw=300 K。空气来流组元为N2和O2,质量分数分别为cN2=0.79,cO2=0.21。二维圆柱网格模型结点数分布为120×135(流向×法向)。
3.1.1 激波距离 图 1给出了高超声速绕流在完全气体模型和Gupta热化学非平衡气体模型下流场马赫数分布特性。完全气体模型下的激波距离相比热化学非平衡气体模型的要大。
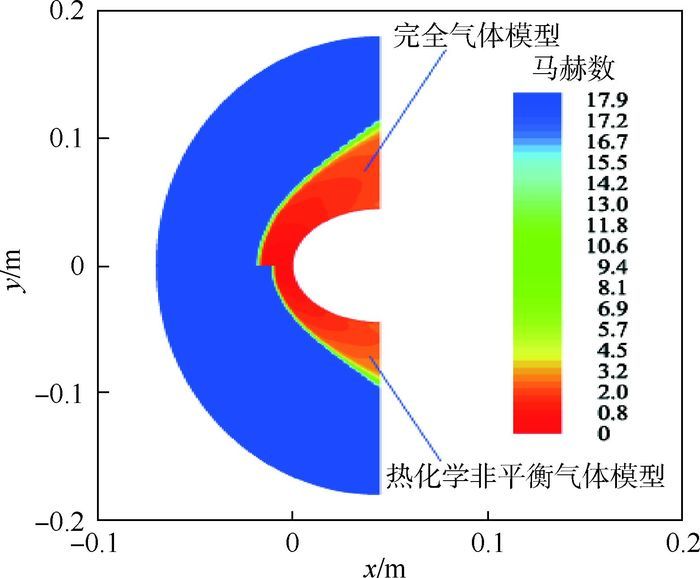 |
| 图 1 完全气体与热化学非平衡气体模型马赫数 Fig. 1 Mach numbers of perfect gas and thermo-chemical non-equilibrium gas models |
| 图选项 |
圆柱体的激波距离Δ可以通过如下公式来计算[22]:
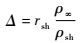 | (22) |
式中:rsh为激波曲率半径;ρ∞ 和ρsh分别为自由来流气体密度和激波后气体密度。考虑到激波曲率半径rsh与圆柱半径r相差较小,可以假设rsh=r,因此有如下关系:
 | (23) |
由式(23) 可知,激波距离Δ与激波后气体密度ρsh密切相关,而且两者成反比关系。
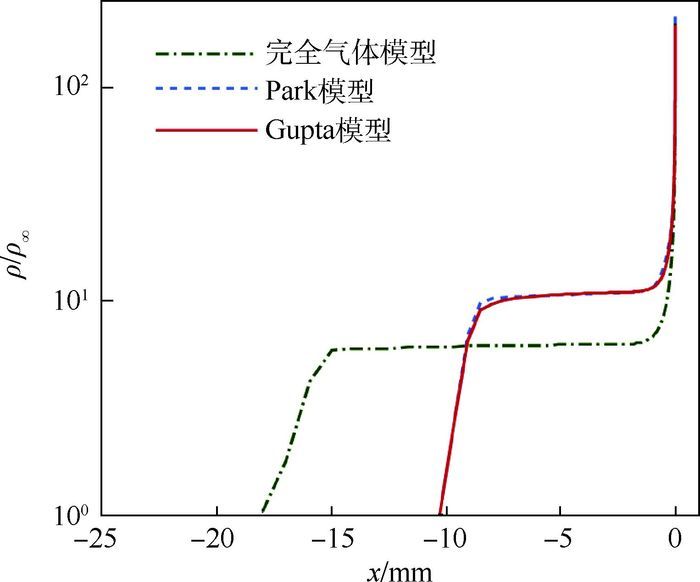
图 2给出了不同气体模型下,沿驻点线的气体密度ρ与自由来流气体密度ρ∞比值变化特性,可体现出气体受激波压缩程度。
 |
| 图 2 驻点线气体密度比 Fig. 2 Gas density ratios along stagnation point line |
| 图选项 |
图 2显示,考虑高超声速飞行热化学非平衡效应对气动热环境影响时,通过Park和Gupta2种热化学非平衡气体模型数值计算所获得的激波后气体密度均要比采用完全气体模型的气体密度明显增大,几乎大一倍,由式(23) 可知,热化学非平衡气体模型下的激波距离必然要比完全气体模型下的小很多。因此,热化学非平衡效应使得激波对气体压缩作用增强,激波距离减小。
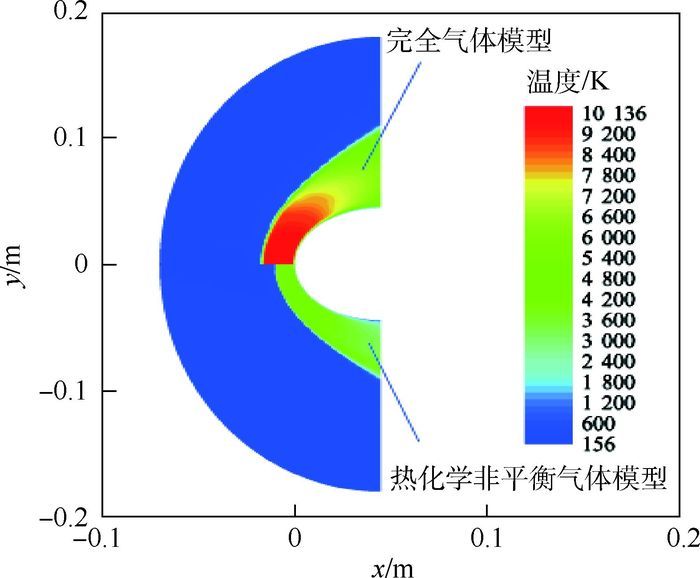
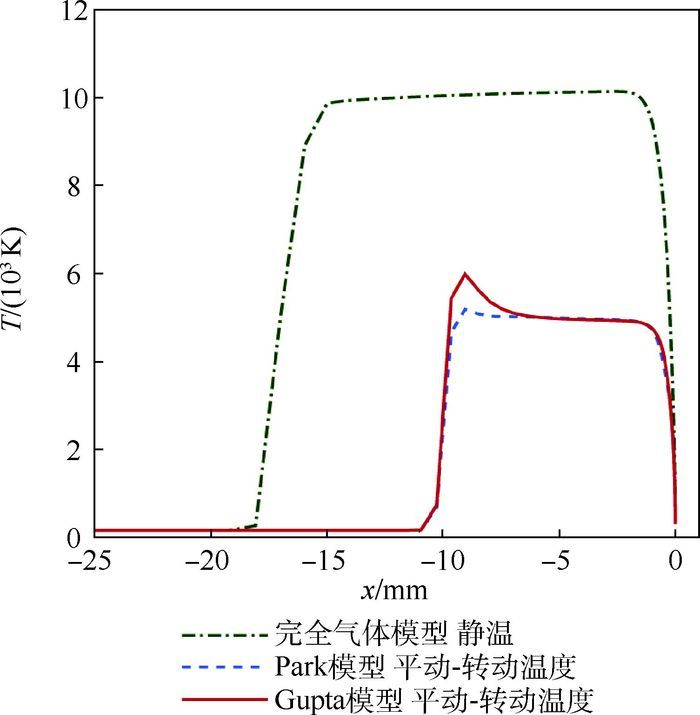
3.1.2 气动热环境特性 完全气体模型流场静温和Gupta热化学非平衡气体模型下的流场平动-转动温度分布特性如图 3所示。图 4给出了不同气体模型下,不同气体温度T沿驻点线分布特性。
 |
| 图 3 完全气体模型静温与热化学非平衡气体模型平动-转动温度 Fig. 3 Static temperatures of perfect gas model and translational-rotational temperatures of thermo-chemical non-equilibrium gas model |
| 图选项 |
 |
| 图 4 驻点线不同温度分布 Fig. 4 Different temperature distributions along stagnation point line |
| 图选项 |
高超声速飞行时,激波压缩作用使得激波后气体温度急剧增加。图 3显示,完全气体模型流场静温高温区域范围及最大温度均要比热化学非平衡气体模型下的流场平动-转动温度要大。图 4中,气动热环境数值计算采用完全气体模型所获得的流场最大静温为T =10 136 K,比Park和Gupta热化学非平衡气体模型中气体最大平动-转动温度分别大48.3%和40.7%。由于热化学非平衡效应的存在,气体分子在激波后的高温环境中出现离解,化学反应等现象,消耗了大量能量,从而使得激波后气体温度明显减小。
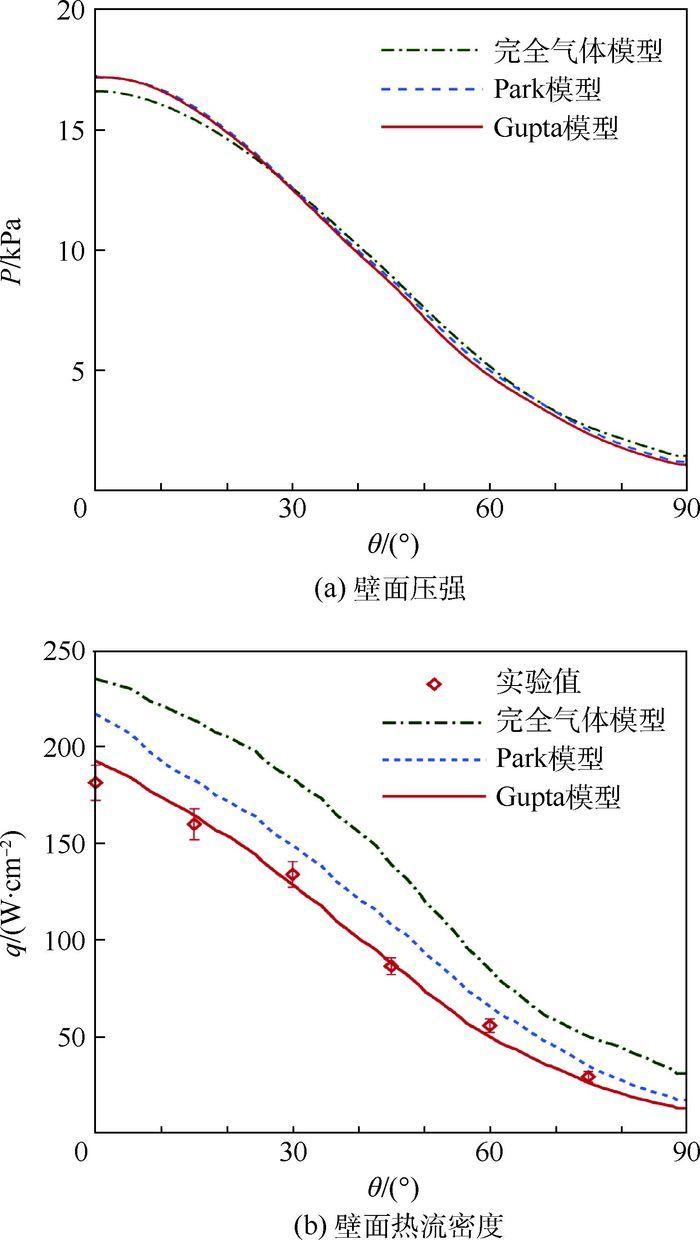
图 5中所示为圆柱壁面压强P及热流密度q沿图柱周角θ分布特性。图 5(a)显示,Park和Gupta 2种热化学非平衡气体模型所获得的壁面压强分布曲线几乎重合,驻点最大压强均比完全气体模型的略大,这是由于热化学非平衡效应使得激波更贴近壁面,从而引起驻点压强增大。
 |
| 图 5 完全气体模型与热化学非平衡气体模型壁面压强和热流密度 Fig. 5 Wall pressures and heat fluxes of perfect gas and thermo-chemical non-equilibrium gas models |
| 图选项 |
图 5(b)中,完全气体模型下的圆柱壁面热流密度整体上要比实验值偏大,而采用热化学非平衡气体模型的壁面热流密度值与实验结果符合的要相对好些,这是因为考虑热化学非平衡效应时,因激波后热化学反应吸收能量,气体温度减小,导致壁面热流密度降低。通过实验测量的驻点最大热流密度值约为181.5 W/cm2,采用完全气体模型,Park和Gupta 2种热化学非平衡气体模型数值计算所获得的最大热流密度与实验值的相对误差分别为30%、20%和6.4%。Gupta模型和Park模型数值计算的最大热流密度及壁面热流密度分布与实验值相比,Gupta模型均要符合得更好些。因此,考虑高温热化学非平衡效应时,数值计算所获得的壁面热载荷更能反应出高超声速飞行器实际的气动热环境特性。
3.2 热化学非平衡与平衡气动热环境对比分析 选用文献[23]中的钝圆锥体实验验证模型。模型前缘半径rn=38.1 mm,前半锥角β=70°,后半锥角β=-40°,基圆半径rb=76 mm, 肩部圆角半径rc=1.087 mm。自由来流参数:马赫数Ma∞=14.9,静温T∞=190 K,静压P∞=18.24 Pa,单位雷诺数Re=9.9×104/m,迎角α=0°;壁面条件为非催化等温壁面Tw=300 K。空气来流组元为N2和O2,它们的质量分数分别取为cN2=0.79,cO2=0.21。二维钝圆锥体半模网格结点数分布为120×140(流向×法向),如图 6所示。
 |
| 图 6 数值计算网格模型 Fig. 6 Grid model for numerical calculation |
| 图选项 |
图 7所示为分别采用热化学平衡气体模型和Gupta热化学非平衡气体模型所获得的二维钝圆锥体绕流流场平动-转动温度分布特性。热化学非平衡状态下,激波后的气体分子因在高温环境下出现的离解,化学反应等现象未能够得到充分有效的完成,相比热化学平衡状态下所消耗的能量减少,因而其激波后的气体最大温度要比热化学平衡状态下的要高一些。同时,热化学非平衡气体模型相比于热化学平衡气体模型,其激波后的气体分子离解量少,气体密度增量相对较小,使得热化学非平衡气体模型下的激波距离要大一些。
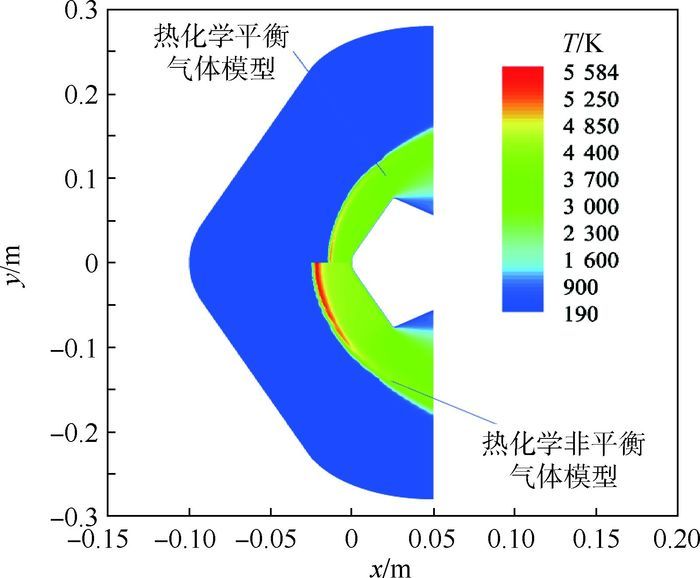 |
| 图 7 热化学平衡与非平衡气体模型流场平动-转动温度 Fig. 7 Flow field translational-rotational temperatures of thermo-chemical equilibrium and non-equilibrium gas models |
| 图选项 |
图 8(a)所示为采用热化学平衡气体模型、Park和Gupta热化学非平衡气体模型分别数值计算,获得的壁面压强分布特性。Park和Gupta模型获得的壁面压强分布曲线几乎重合,且驻点处最大压强均比采用热化学平衡气体模型计算值要略小些。因后半锥角β=-40°,气流绕过肩部圆角后膨胀,使得壁面压强在肩部圆角后迅速减小。
 |
| 图 8 热化学平衡与非平衡气体模型壁面压强和热流密度 Fig. 8 Wall pressures and heat fluxes of thermo-chemical equilibrium and non-equilibrium gas models |
| 图选项 |
图 8(b)中,热化学非平衡气体模型及平衡气体模型下的壁面热流密度与实验值变化趋势相同,肩部圆角处热流密度出现第二峰值。热化学平衡气体模型的壁面热流密度总体比实验值偏大,其驻点处最大热流密度计算值与实验值分别为88.2 W/cm2和77 W/cm2,相对误差为14.5%,选用热化学平衡气体模型不能对壁面热流密度进行可靠预测。Gupta和Park热化学非平衡气体模型驻点最大热流密度与实验值相对误差分别为3%和8.7%,Gupta模型壁面热流密度分布与实验符合得也要更好些。因此,气动热环境数值计算时,合理选取热化学反应模型,对高超声速飞行器气动热环境可靠预测非常重要。
Gupta和Park模型数值计算获得混合气体各组元的质量分数沿驻点线变化特性如图 9所示。由于氧气分子O2比氮气分子N2发生离解的温度要低很多,氧气分子在激波后高温环境下几乎全部离解为氧原子O,而氮气分子N2离解量很少,低温壁面附近氧气分子质量分数逐渐增加。由于Gupta模型激波距离略小,激波后流场温度比Park模型高,一氧化氮NO质量分数增量及驻点x=0 mm近壁面区域氧原子O质量分数均较大。
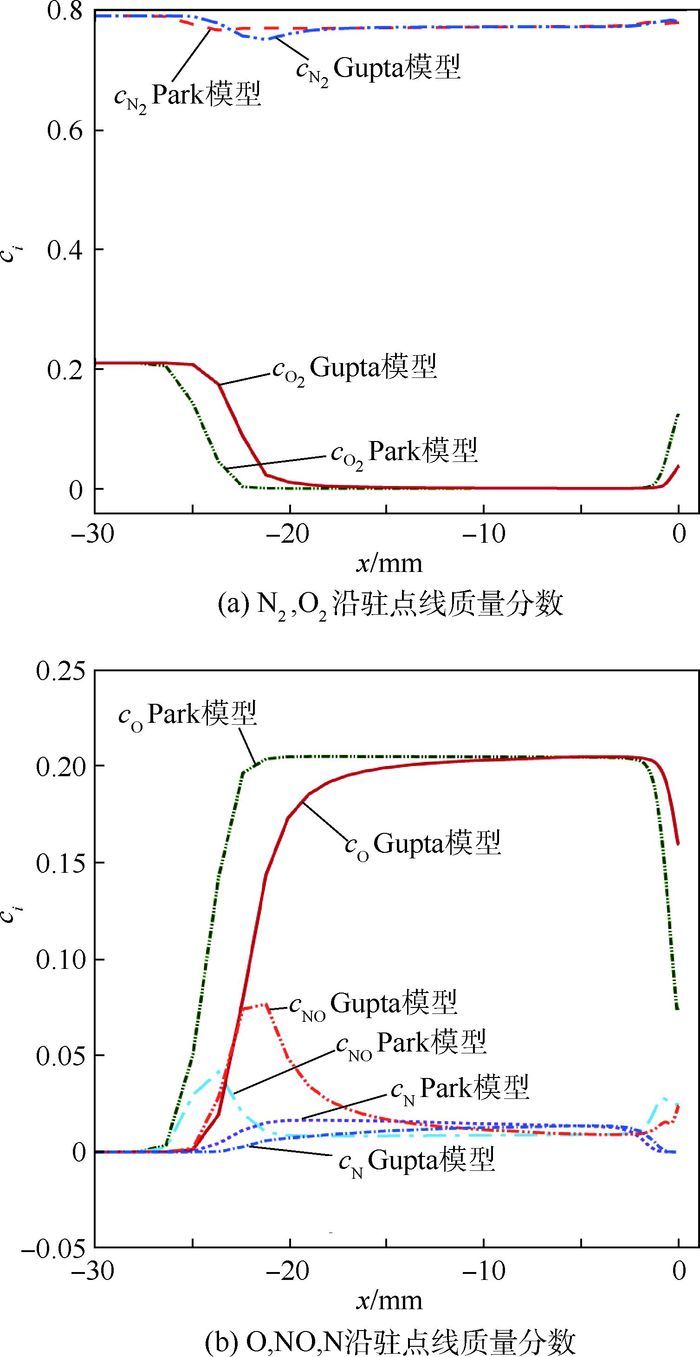 |
| 图 9 气体组元沿驻点线质量分数 Fig. 9 Gas species' mass fraction along stagnation point line |
| 图选项 |
3.3 热化学非平衡气体模型对比 对比Park和Gupta 2种热化学非平衡气体模型,选用文献[23]中的钝圆锥体实验模型进行气动热环境数值计算。实验模型前缘半径rn=38.1 mm,前半锥角β=70°,后半锥角β=-40°,基圆半径rb=69.5 mm, 肩部圆角半径rc=10.925 mm。自由来流参数:马赫数Ma∞=14.9,静温T∞=190 K,静压P∞=18.24 Pa,单位雷诺数Re=9.9×104/m,迎角α=10°;壁面条件为非催化等温壁面Tw=300 K。空气来流组元为N2和O2,它们的质量分数分别取为cN2=0.79,cO2=0.21。三维钝圆锥体半模网格结点数分布为75×90×70 (流向×周向×法向)。
图 10所示为分别采用Park和Gupta 2种热化学非平衡气体模型数值计算,获得的三维钝圆锥体壁面热流密度分布特性。沿来流方向,随着气动加热作用逐渐减弱,壁面热流密度不断减小,壁面热流密度值较大区域分布在前锥壁面,后锥壁面上的热流密度值较小。由于迎角α=10°影响,前锥壁面迎风区热流密度要比背风区上的热流密度值大。采用Park模型数值计算获得的壁面最大热流密度值比Gupta模型热流密度大。
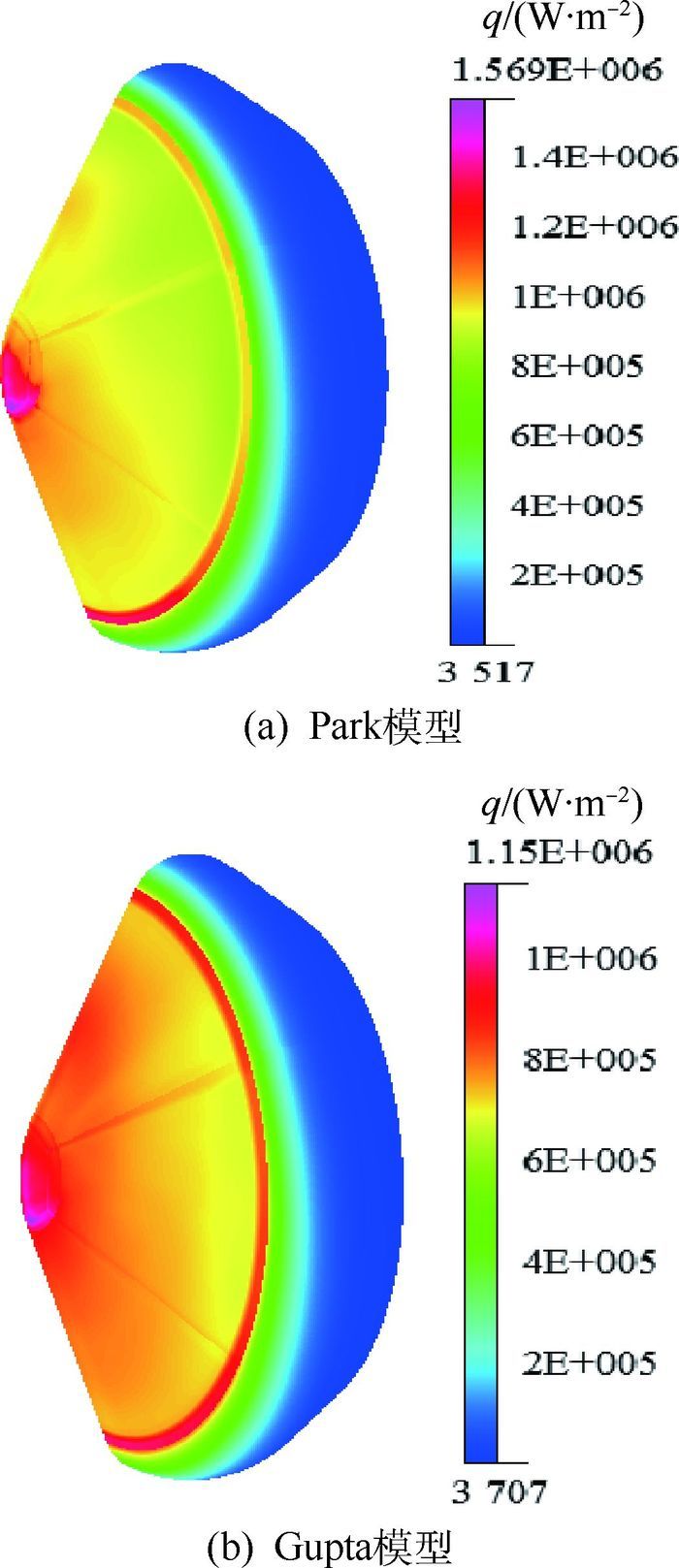 |
| 图 10 Park与Gupta模型壁面热流密度分布 Fig. 10 Wall heat flux distributions of Park's and Gupta's model |
| 图选项 |
图 11给出了分别采用Park和Gupta 2种热化学非平衡气体模型数值计算,所获得的壁面压强沿背风(φ=0°)与迎风(φ=180°)线上的分布特性。因气流绕过肩部圆角后膨胀,后锥壁面上的压强迅速减小。图 11(a)所示背风线与图 11(b)所示迎风线上的壁面压强分布曲线各自几乎重合。因此,Park与Gupta 2种热化学非平衡气体模型对气动力载荷数值计算区别不大。
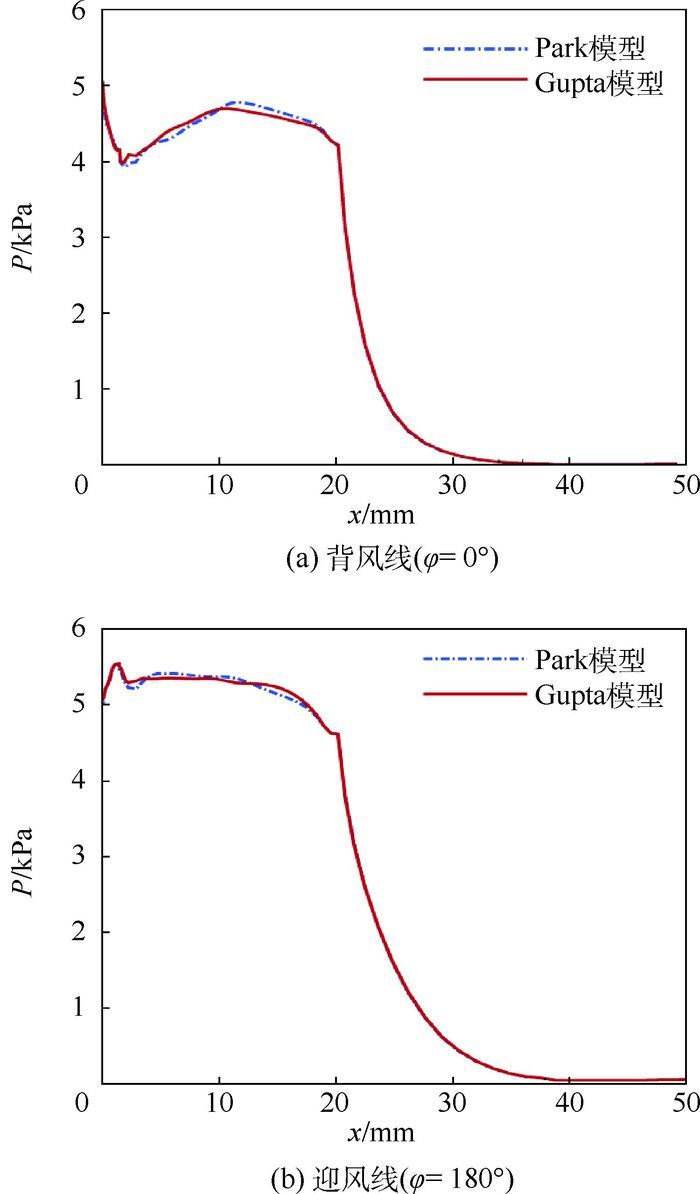 |
| 图 11 壁面压强沿背风与迎风线分布 Fig. 11 Distribution of wall pressures along leeward and windward lines |
| 图选项 |
图 12(a)中,分别采用Park和Gupta模型数值计算,前锥壁面背风线(φ=0°)热流密度计算值均比实验结果偏大,而后锥壁面上的热流密度计算值要小,主要因较大迎角下,实际绕流流动特性在后锥体区域较复杂造成。Gupta模型获得的背风线上最大热流密度计算值与实验值误差要比Park模型的误差小。图 12(b)所示为迎风线(φ=180°)壁面热流密度分布特性,驻点和肩部区域出现2个热流密度峰值。实验最大热流密度测量值为99 W/cm2,Gupta和Park热化学非平衡气体模型数值计算的最大热流密度值与实验值相对误差分别为16.2%和58.5%。迎风线上的壁面热流密度分布,Park模型整体偏大,Gupta模型与实验结果符合得要更好些。因此,壁面热流数值计算时,Park和Gupta 2种热化学非平衡气体模型差别较大,采用Gupta模型比Park模型能更好地对高超声速飞行器气动热载特性进行可靠预测。
 |
| 图 12 壁面热流密度沿背风与迎风线分布 Fig. 12 Distribution of wall heat fluxes along leeward and windward lines |
| 图选项 |
4 结论 数值计算研究了热化学非平衡效应对高超声速气动热环境的影响,结论如下:
1) 热化学非平衡效应使得完全气体假设失效。高温环境下出现离解,化学反应等热化学非平衡现象,消耗了大量能量,激波后的流场温度明显降低。考虑热化学非平衡效应时,激波后气体密度增量比完全气体模型大,激波离体距离变小。
2) 热化学非平衡状态因离解、化学反应等未能充分完成,消耗的能量相对较少,激波后气体温度比热化学平衡状态下的要大。热化学状态对壁面气动热载荷的影响比气动力载荷大。热化学平衡模型壁面热载荷计算值偏大,采用热化学非平衡模型能更好地体现实际气动热载荷特性。
3) Park和Gupta 2种热化学非平衡模型,对高超声速飞行器热化学非平衡效应下的激波离体距离及壁面气动力载荷数值计算差别很小。Gupta模型激波后流场温度比Park模型略大。Park模型壁面热载荷计算值偏大,Gupta模型与实际气动热载特性要符合得更好。因此,数值计算采用Gupta模型,可以对高超声速飞行器热化学非平衡效应下的气动热环境进行有效预测。
参考文献
| [1] | SCALABRIN L C, BOYD I D.Numerical simulation of weakly ionized hypersonic flow for reentry configurations:AIAA-2006-3773[R].Reston:AIAA, 2006. |
| [2] | PANDOLFI M, ARINA R, BOTTA N. Nonequilibrium hypersonic flows over corners[J].AIAA Journal, 1991, 29(2): 235–241.DOI:10.2514/3.10569 |
| [3] | FREDERICKSON K, LEONOV S, NISHIHARA M, et al. Energy conversion in high enthalpy flows and non-equilibrium plasmas[J].Progress in Aerospace Sciences, 2015, 72: 49–65.DOI:10.1016/j.paerosci.2014.09.004 |
| [4] | AIT-ALI-YAHIA D, HABASHI W G. Finite element adaptive method for hypersonic thermochemical nonequilibrium flows[J].AIAA Journal, 1997, 35(8): 1294–1302.DOI:10.2514/2.260 |
| [5] | YUMUSAK M, EYI S.Aerothermodynamic shape optimization of hypersonic blunt bodies:AIAA-2013-2693[R].Reston:AIAA, 2013. |
| [6] | BHUTTA B A, LEWIS C H. Three-dimensional hypersonic nonequilibrium flows at large angles of attack[J].Journal of Spacecraft and Rockets, 1989, 26(3): 158–166.DOI:10.2514/3.26048 |
| [7] | ZOBY E V, LEE K P, GUPTA R N, et al. Viscous shock-layer solutions with nonequilibrium chemistry for hypersonic flows past slender bodies[J].Journal of Spacecraft and Rockets, 1989, 26(4): 221–228.DOI:10.2514/3.26058 |
| [8] | PEZZELLA G, VOTTA R.Finite rate of chemistry effects on the high altitude aerodynamics of an Apollo-shaped reentry capsule:AIAA-2009-7306[R].Reston:AIAA, 2009. |
| [9] | 柳军, 刘伟, 曾明, 等. 高超声速三维化学非平衡流场的数值模拟[J].力学学报, 2003, 35(6): 730–734. LIU J, LIU W, ZENG M, et al. Numerical simulation of 3D hypersonic thermochemical nonequilibrium flow[J].Acta Mechanica Sinica, 2003, 35(6): 730–734.(in Chinese) |
| [10] | 董维中, 丁明松, 高铁锁, 等. 热化学非平衡模型和表面温度对气动热计算影响分析[J].空气动力学学报, 2013, 31(6): 692–698. DONG W Z, DING M S, GAO T S, et al. The influence of thermo-chemical non-equilibrium model and surface temperature on heat transfer rate[J].Acta Aerodynamica Sinica, 2013, 31(6): 692–698.(in Chinese) |
| [11] | 李康, 胡宗民, 姜宗林. 热化学非平衡流动中粘性干扰和化学反应对HB2气动力的影响[J].中国科学:物理学, 力学和天文学, 2015, 45(4): 044702. LI K, HU Z M, JIANG Z L. Effect of viscosity and chemical reactions on aerodynamic force in chemical nonequilibrium flow[J].Scientia Sinica:Physica, Mechanica & Astronomica, 2015, 45(4): 044702.(in Chinese) |
| [12] | 周禹, 阎超. 高超声速热化学非平衡空间格式的扩展与改进[J].北京航空航天大学学报, 2010, 36(2): 193–197. ZHOU Y, YAN C. Extension and improvement for schemes in hypersonic thermal and chemical non-equilibrium flows[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(2): 193–197.(in Chinese) |
| [13] | 周印佳, 孟松鹤, 解维华, 等. 高超声速飞行器热环境与结构传热的多场耦合数值研究[J].航空学报, 2016, 37(9): 2739–2748. ZHOU Y J, MENG S H, XIE W H, et al. Multi-field coupling numerical analysis of aerothermal environment and structural heat transfer of hypersonic vehicles[J].Acta Aeronautica et Astronautica Sinica, 2016, 37(9): 2739–2748.(in Chinese) |
| [14] | FORD D I, JOHNSON R E.Dependence of rate rate constants on vibrational temperatures:An arrhenius description:AIAA-1988-0461[R].Reston:AIAA, 1988. |
| [15] | GUPTA R N, YOS J M, THOMPSON R A, et al.A review of reaction rates and thermodynamic and transport properties for an 11-species air model for chemical and thermal nonequilibrium calculations to 30000K:NASA RP-1232[R].Washington, D.C.:NASA, 1990. |
| [16] | PARK C.On convergence of computation of chemical reacting flows:AIAA-1985-0247[R].Reston:AIAA, 1985. |
| [17] | PARK C.Problems of rate chemistry in the flight regimes of aeroassisted orbital transfer vehicles:AIAA-1984-1730[R].Reston:AIAA, 1984. |
| [18] | CANDLER G V, MACCORMACK R W.The computation of hypersonic ionized flows in chemical and thermal nonequilibrium:AIAA-1988-0511[R].Reston:AIAA, 1988. |
| [19] | WILKE C R. A viscosity equation for gas mixtures[J].Journal of Chemical Physics, 1950, 18(4): 517–519.DOI:10.1063/1.1747673 |
| [20] | YOON B, RASMUSSEN M L. Diffusion effects in hypersonic flows with a ternary mixture[J].KSME International Journal, 1999, 13(5): 432–442.DOI:10.1007/BF02939331 |
| [21] | MACLEAN M, MARINEAU E, PARKER R, et al. Effect of surface catalysis on measured heat transfer in expansion tunnel facility[J].Journal of Spacecraft and Rockets, 2013, 50(2): 470–474.DOI:10.2514/1.A32327 |
| [22] | HORNUNG H G, WEN C Y.Nonequilibrium dissociationg flow over spheres:AIAA-1995-0091[R].Reston:AIAA, 1995. |
| [23] | STEWART D A, CHEN Y K. Hypersonic convective heat transfer over 140-deg blunt cones in different gases[J].Journal of Spacecraft and Rockets, 1994, 31(5): 735–743.DOI:10.2514/3.26506 |
