近年来,利用雷达系统进行低空空域目标监测的研究发展迅速,并取得一定成果。文献[1-3]考虑了雷达低空目标测量中海面和复杂地形造成的多径干扰,通过建立相应的多径信号模型,分别利用最大似然估计和稀疏贝叶斯学习方法实现了对低空目标高度和到达角的估计。文献[4]给出了一种低空目标的机载预警雷达回波模型,通过几何关系建立4种多径信号传播路径,最终采用概率密度假设和蒙特卡罗方法仿真了低空目标的雷达回波信号。文献[5]以城市复杂环境下的雷达目标监测为目的,利用射线追踪法分析了城市多径效应对雷达目标到达角估计的影响。
然而,除了多径效应,杂波强度也是影响雷达低空目标测量效能的重要因素之一。尤其在城市环境下,建筑物带来的遮挡与起伏、大气折射等因素,将使电磁传播和地表电磁散射特性产生复杂变化[6]。因此,建立真实、灵活的地杂波强度分布模型是进行雷达系统性能预估、站址选择和杂波特性分析的基础。本文针对低空空域监测中城市复杂地形对雷达信号传播的影响,利用宽角抛物方程(Parabolic Equation, PE)模型,考虑城市高层建筑引起的雷达信号反射、绕射和多径效应,以及大气结构造成的折射效应,通过三维高斯型天线方向图获得立体空间内的传播因子;在此基础上,计算雷达杂波单元的后向散射系数和有效照射面积,最终实现地杂波强度分布模型的有效建立。
1 PE模型 PE模型是一种确定性传播模型,是由二维标量波动方程得到的一种近似,可应用于海洋[7-8]以及陆地环境[9]的电磁传播特性预测。PE模型认为电磁波的主能量在抛物线轴向锥形的区域前向传播[9]。考虑直角坐标系下的电磁传播过程,传统的麦克斯韦方程可化简为二维波动方程:
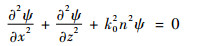 | (1) |
式中:x为传播区域水平方向;z为高度方向;k0=2π/λ为真空中的波数,λ为雷达信号波长;n为介质中的折射指数。定义传播方向上的波函数为u(x, z)=ψ(x, z)e-ik0x,则式(1)可表示为
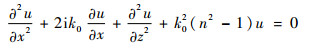 | (2) |
对式(2)进行因式分解可得
 | (3) |
式中:伪微分算子Q定义为
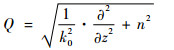 | (4) |
式(3)第1个式子表征了直角坐标系下的电磁波前向传播的PE模型。
常用的PE模型求解方法包括有限差分法和分步傅里叶法(Split-Step Fourier Method,SSFM)。后者在求解速度和稳定性上具有明显优势,且迭代步长几乎不受电磁波波长影响[10]。此外,由于城市低空空域监测易受高层建筑等影响,通常需要增加俯仰向范围以实现对指定空域的有效覆盖。
因此,本文的研究将采用Feit-Fleck近似法[11]得到的宽角PE模型,即
 | (5) |
在此基础上,采用SSFM算法得到理想导体边界条件下的PE模型的解为
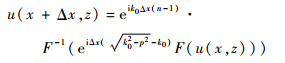 | (6) |
式中:p为空间频率。
SSFM算法的迭代求解过程可以描述为:根据距离向x处的场值u(x, z),结合大气折射项因子以及障碍物绕射项因子,以距离向采样间隔Δx为步进迭代单位,利用傅里叶正反变换得到距离向x+Δx处的场值u(x+Δx, z),依次进行迭代得到整个计算域的场值。其迭代过程如图 1所示。可以看出使用SSFM算法在PE模型的迭代求解过程中存在2个关键问题:初始场设置、边界条件。
 |
| 图 1 PE迭代求解过程 Fig. 1 Iterative procedure of PE solution |
| 图选项 |
由于远场天线方向图f(p)与孔径场分布u(0, z)之间构成一组傅里叶变换对[12],结合镜像原理可以得到水平和垂直极化情况下地表以上空间初始场对应的傅里叶变换fg//(p)和fg⊥(p)为:
 | (7) |
 | (8) |
式中:H为天线高度。
通过傅里叶逆变换就可以得到初始场分布。对于高斯型天线方向图有f(p)=e-p2ω2/4,式中ω=
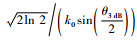
上边界采用Tukey窗函数以满足Sommerfeld辐射条件,即电磁波在到达上边界时,不能透射出计算域也不能在上边界发生反射[10]。Tukey窗函数如式(9)所示,其设置区域为

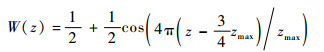 | (9) |
实际地表对入射到表面的能量有一定的吸收,下边界条件通常用阻抗边界条件[13]来描述,即
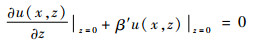 | (10) |
式中:阻抗系数β′为
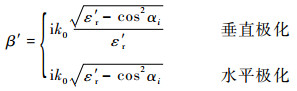 | (11) |
其中:εr′为复相对介电常数; αi为掠射角。
对于阻抗边界条件使用离散混合傅里叶变换算法能够有效提高PE模型的稳定性与计算效率[14]。
相比于其他电磁波传播特性预测模型,如射线追踪法和波导模理论,PE模型具有如下主要特点[10]:①包含了传播过程中的反射、折射、绕射等效应,并且不用考虑其发生位置及判定机制;②考虑了大气环境和复杂地形影响;③不仅能够预测点对点的传播关系,还能预测整个计算区域的电磁波传播特性,从而得到空间场分布。
2 雷达地杂波强度分布模型 雷达在城市环境下的低空空域监测性能很大程度上受到地杂波强度的影响。杂波图能够记录雷达站周围环境的杂波强度分布,在目标监测和跟踪等方面具有重要应用。雷达地杂波强度分布主要与雷达信号传播衰减特性以及地表的后向散射能力有关。在城市环境下,首先,通过将PE模型理论与地表建筑物特征相结合,建立城市环境下的电磁传播PE模型,预测雷达信号的传播衰减特性;其次,根据地表散射强度的相关原理,最终可实现对地杂波强度分布的有效计算。主要步骤如图 2所示。
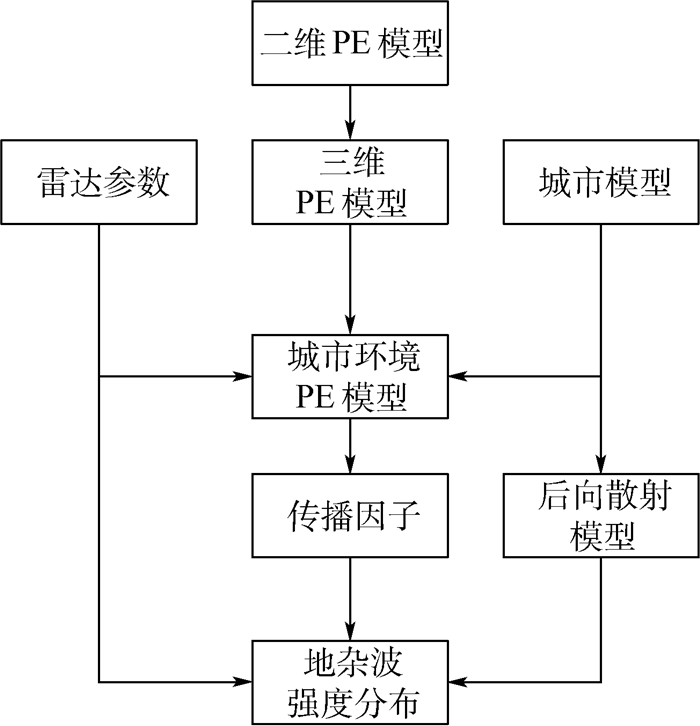 |
| 图 2 地杂波强度分布建模流程图 Fig. 2 Flowchart of land clutter power map modeling |
| 图选项 |
2.1 城市环境PE模型 人造建筑遮挡、建筑表面和地面反射、大气折射将是影响城市环境下雷达信号传播衰减特性的主要因素。因此,本文在使用PE模型对城市环境下的电磁波传播特性进行预测时,将结合城市建筑模型、阻抗边界条件和大气折射指数影响进行俯仰向上的传播因子计算,在此基础上,通过方位采样处理得到最终的三维PE模型。
2.1.1 城市建筑模型 建筑物遮挡是城市环境中雷达信号传播衰减的主要因素。常见的城市建筑模型包括阶梯形、矩形、帆形、橄榄形等,其二维剖面简化模型如图 3所示。此外,城市建筑在空间上多呈现为带状或集团状。
 |
| 图 3 简化建筑模型 Fig. 3 Simplified building models |
| 图选项 |
由于计算地杂波强度分布需要在雷达坐标系下进行,因此,需将包含城市建筑模型的地面网格变换到雷达坐标系下完成。具体处理步骤将在2.2节阐述。
2.1.2 边界平移法 边界平移法[15]能够在PE模型的应用中有效地考虑建筑物的高低起伏。边界平移法根据前后步进海拔差,在高度向上进行场值平移,实现过程简单,在大坡度条件下同样适用。
边界平移法在帆形建筑的实现过程如图 4所示。
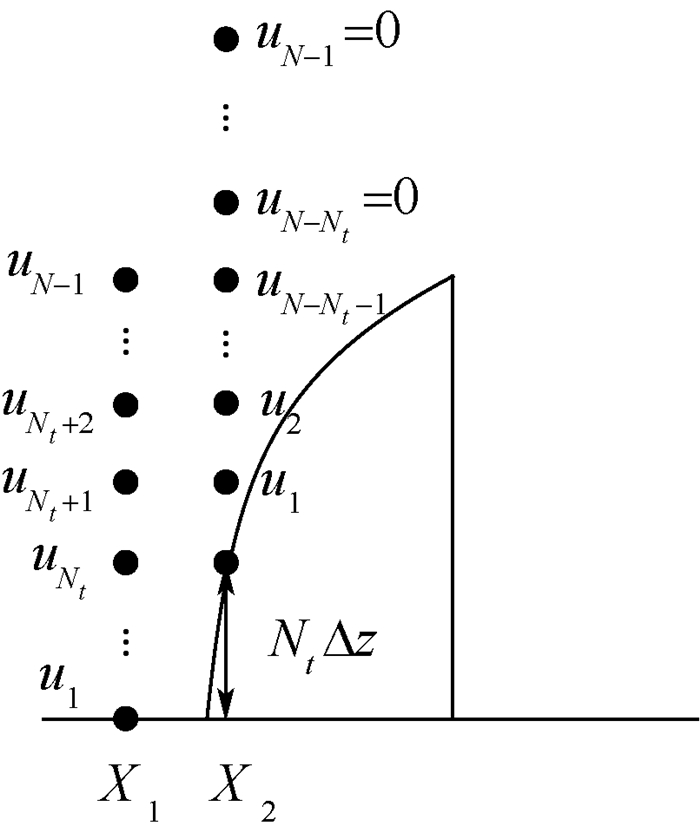 |
| 图 4 边界平移法 Fig. 4 Boundary shift method |
| 图选项 |
高度差确定的点数为Nt。当坡度为正时,由X1处的场迭代计算得到的X2处的场将向下移动Nt个单元,即X1处的uNt+1对应X2处的u1,依次类推。当坡度为负时,场值将向上移动Nt个单元。边界平移法不需要对地形做转换处理,不必改变大气折射指数项因子以及障碍物绕射项因子,实现过程最为简单。能够有效解决复杂的大气环境中由建筑物高低起伏所引起的不规则地形条件下的雷达信号传播问题。
2.1.3 大气结构影响 大气结构是影响雷达信号传播的重要因素之一,其对电磁传播特性的作用主要由大气折射指数n确定。随着高度改变,大气折射指数会改变雷达信号在介质中的传播速度,从而使得雷达信号在大气传播中产生折射,当雷达信号传播距离较远的时候,需要考虑地球曲率影响,可采用修正的大气折射率M将地球曲面近似处理为平面。
 | (12) |
式中:K为大气折射率;d/dz为高度向上的折射率梯度。修正的大气折射率在高度向上的梯度不同,雷达信号在大气中会产生不同的折射效应。
2.1.4 三维PE模型 传统的二维PE模型仅考虑了雷达信号在给定方位向上的传播特性。对于城市环境雷达信号传播,需要预测整个三维区域的雷达信号覆盖情况,因此需要利用二维PE模型解决三维的估计问题。
为了获取雷达信号在方位向上的传播特性,本文采用文献[16-17]方法将传统的二维PE模型扩展到三维空间。在三维PE模型中,雷达位置不变,根据天线指向和波束宽度,在有效方位角范围内,按照固定方位向间隔形成一系列的二维空间计算域切片,从而提取对应方位向上的地形,在每一个地形上分别利用二维PE模型进行求解。其中,三维PE模型中初始场的设置根据三维高斯天线方向图,分别在每一个角度间隔单元上获取方向图切片进行傅里叶逆变换得到对应二维空间的初始场分布。可见,在该三维PE模型方法中,相邻切片对应的二维计算区域之间并无电磁传播影响。
2.2 地杂波强度计算 根据雷达方程,地杂波强度与雷达系统参数、目标雷达散射截面积(Radar Cross Section, RCS)、传播损耗等因素有关,可表示为[18]
 | (13) |
式中:Pc为杂波功率;σ0为杂波单元平均反射系数;A0为雷达有效照射面积;F2为传播因子;Pt为雷达发射功率;G为雷达增益;L为系统损耗;R为目标径向距离。
考虑杂波单元大于地面网格单元的场景,本文将采用正向法[19]将地面直角坐标系转换到雷达坐标系,如图 5所示。
 |
| 图 5 直角坐标系到雷达极坐标系的正向转换 Fig. 5 Forward transformation from Cartesian grid to radar polar coordinate system |
| 图选项 |
使用正向法进行坐标系转换时,需要在雷达极坐标系下求出雷达杂波单元所包含的地面杂波块面积和后向散射系数等参数,再通过求和方式得到整个雷达杂波单元的地杂波强度。
2.2.1 后向散射模型 雷达散射截面积σRCS与杂波单元平均反射系数σ0、雷达有效照射面积A0的关系可以表示为:σRCS=σ0A0。不同媒质对雷达信号的后向散射能力通常不同。本文采用Constant-γ模型进行后向散射系数的计算,其表达式为σ0=γsin α,α为入射余角,γ为散射系数。
2.2.2 有效照射面积 在地基雷达低空空域监测条件下,擦地角通常较小,因此,天线波束照射范围一般大于雷达脉冲距离门对应范围[20],如图 6所示。β为建筑曲面坡度,φ为擦地角,η为建筑曲面法向量与雷达指向之间的夹角,Δθ为雷达天线波束的方位向宽度,B为发射信号带宽,c为光速。
 |
| 图 6 照射面积计算示意图 Fig. 6 Illustration of clutter irradiated area calculation |
| 图选项 |
根据图 6所示关系,照射面积计算公式为
 | (14) |
上述面积为雷达波束在水平面上的投影面积,在计算RCS时,应求取系统的有效照射面积。由于建筑物高低起伏影响,雷达有效照射面积需要根据建筑物参数和擦地角等,由投影面积A得到有效照射面积A0,即
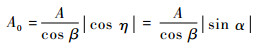 | (15) |
3 仿真结果与分析 设雷达高度为100 m,雷达发射频率为3 GHz,最大传播仰角为15°,采用高斯型天线方向图,波束宽度为2°,大气结构为标准大气环境。
在PE模型中,环境因素对电磁波传播的影响主要通过不同的电磁参数体现,包括复相对介电常数εr′以及电导率σ。在本节仿真中,假设建筑表面材料为良导体,其复相对介电常数εr′=80+i79.1[16],地表媒质假设为中等干燥地表类型。
对于二维PE模型,设建筑物与雷达水平距离为10 km,径向宽度为200 m,帆形建筑的曲线轮廓满足如下方程:
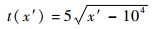 | (16) |
其中:x′表示曲线轮廓上各点与雷达之间的水平径向距离。为保证矩形建筑与帆形建筑高度相同,根据式(16),设置矩形建筑高度约为70.7 m。
图 7和图 8分别给出了在矩形和帆形建筑条件下基于二维PE模型的雷达信号传播特性预测结果。观察可知,在建筑物之前的区域,雷达信号传播主要受大气波导折射效应影响,传播因子随高度在0值附近振荡变化,对应于图 7(a)和图 8(a)中明暗相间的条状分布。在建筑物遮挡区内,传播因子大幅衰减,表明建筑物对于雷达信号传播具有显著的阻碍作用。但由于大气折射、信号绕射等现象的存在,建筑物并未完全阻断雷达信号传播,并且部分遮挡区域的雷达信号强度依然较强。此外,在约70 m以上的高度区域,遮挡逐渐减弱,大气波导折射效应再次成为影响雷达信号传播的主要因素,此时传播因子变化趋势与建筑物之前区域相同,即在0值附近振荡。建筑外形对传播因子的影响则主要表现为遮挡区域衰减强度的不同。比较图 7(b)和图 8(b)可知,矩形建筑比帆形建筑对电磁波传播的衰减更大,但在建筑高度以上的区域,衰减特性几乎相同。
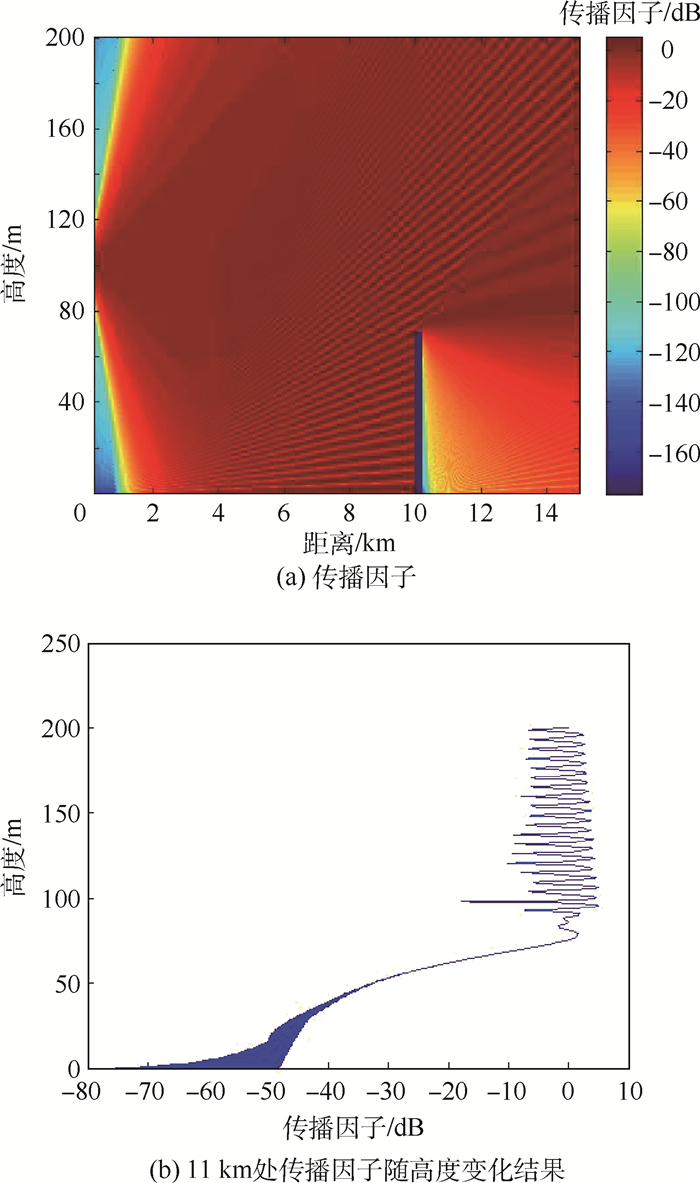 |
| 图 7 矩形建筑条件下的雷达信号传播特性 Fig. 7 Propagation characteristics of radar signals over a rectangular building |
| 图选项 |
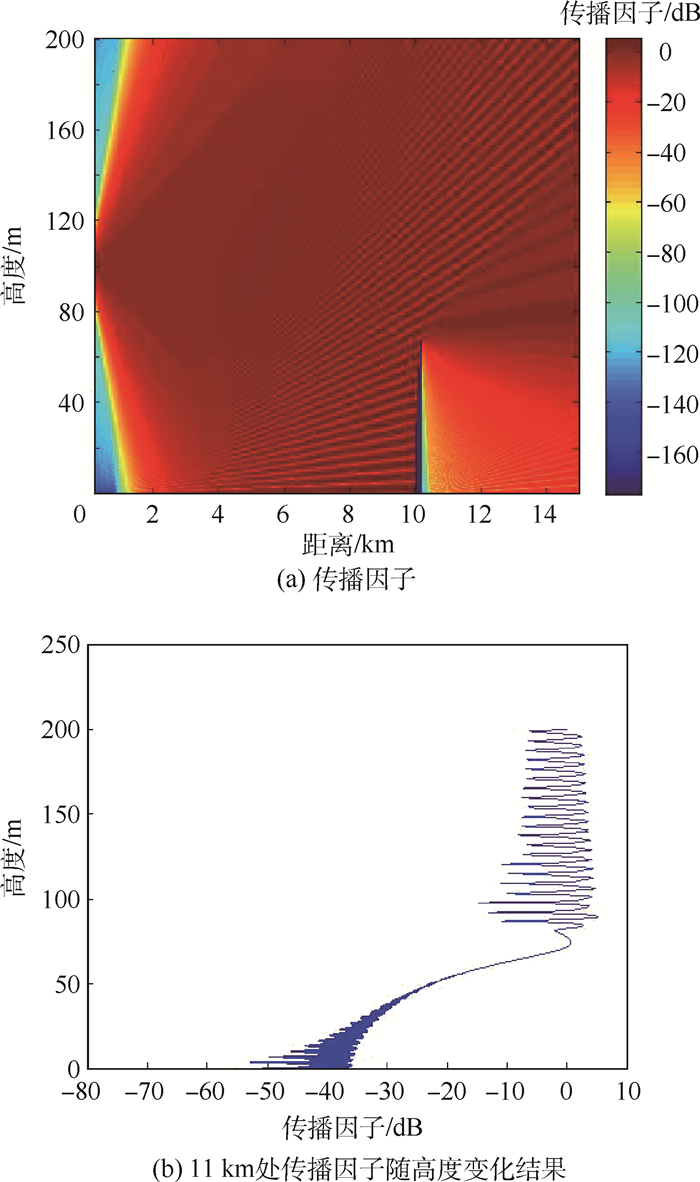 |
| 图 8 帆形建筑条件下的雷达信号传播特性 Fig. 8 Propagation characteristics of radar signals over a sail-shaped building |
| 图选项 |
对于三维PE模型,考虑雷达天线方位向变化范围为-30°~30°,以0°为中心,左右变化间隔均为2°,且在每一方位指向上的二维PE计算域切片间隔为0.5°;设2组建筑群中心分别处于±2°方位向上,其各包含9栋独立建筑,如图 9所示。各建筑的方位向宽度为60 m,径向宽度为200 m,距离雷达位置分别为9、10和11 km;帆形建筑剖面方程为
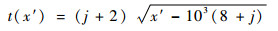 | (17) |
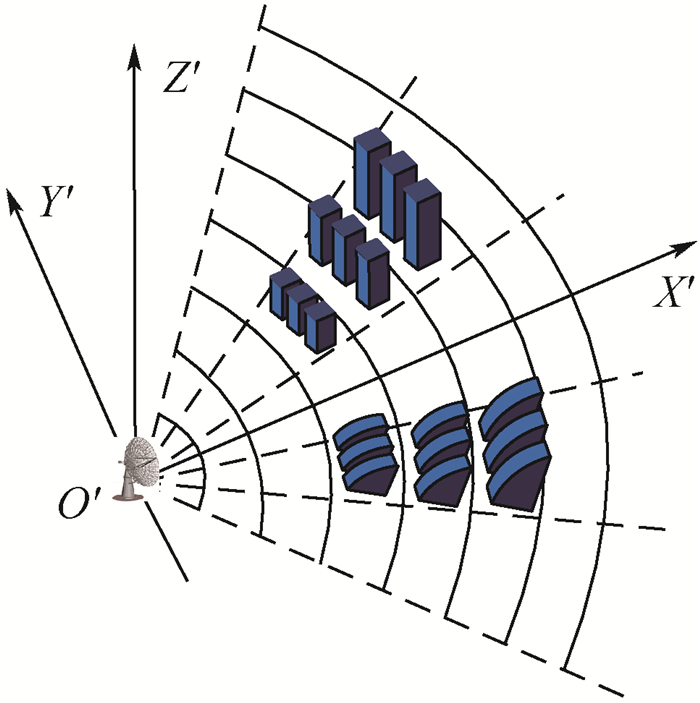 |
| 图 9 建筑群分布示意图 Fig. 9 Illustration of building distribution |
| 图选项 |
式中:j=1, 2, 3,分别对应第1~3排帆形建筑。同理于单建筑场景,根据式(17),选取对应的每排矩形建筑高度分别约为42.4、56.6和70.7 m。
图 10给出了不同形状建筑群条件下的雷达信号传播特性预测结果。该结果表明,经多个建筑物遮挡,雷达信号传播损耗更大。此外,帆形建筑对信号传播的绕射效应较矩形建筑更为明显,从而导致帆形建筑前表面部分以及遮挡区域的雷达信号传播因子大于矩形建筑。而在建筑物高度以上区域的传播衰减则主要受大气折射效应影响。
 |
| 图 10 城市建筑群环境下的雷达信号传播特性 Fig. 10 Propagation characteristics of radar signals over urban buildings |
| 图选项 |
设雷达发射功率为200 kW;根据文献[21],对于城市建筑,取Constant-γ模型中γ=-5 dB。图 11给出了雷达极坐标系下的地杂波强度分布结果。为了突出局部细节特征,这里采用1:2比例尺将分布结果方位向角度进行均匀放大。由于地表和大气结构的同质性,无人造建筑区域的地杂波强度在同等距离条件下相同。而当存在建筑物时,雷达天线与建筑的空间几何关系、传播因子大小差异等因素导致帆形建筑区域的杂波强度明显增大。此外,因为建筑物遮挡区域面积小于杂波单元面积,并且遮挡区域的地杂波强度非常小,所以其所在杂波单元中其他地表区域对地杂波的贡献更为显著。
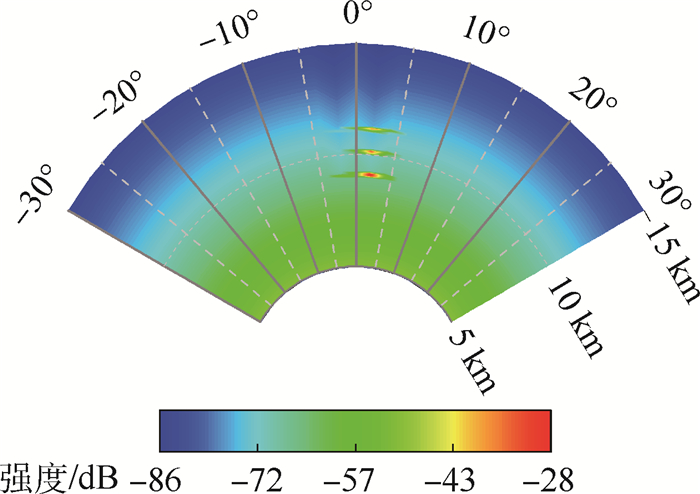 |
| 图 11 地杂波强度分布结果 Fig. 11 Result of land clutter power map |
| 图选项 |
4 结论 本文以地基雷达低空空域监测为背景,研究了基于PE的城市地杂波强度分布建模方法,其结果表明:
1) 由于反射、绕射和多径效应的存在,城市建筑遮挡虽然会对雷达信号传播产生明显的衰减作用,但不会完全阻断,并且建筑越高,衰减效果越明显。
2) 在同等条件下,矩形建筑遮挡比帆形建筑遮挡对雷达信号的衰减作用更大。
3) 在地基雷达低空空域监测条件下,传播因子是影响地杂波强度的重要因素之一。
参考文献
| [1] | 陈唯实, 宁焕生. 利用一次雷达实现低空空域的安全监视[J].北京航空航天大学学报, 2012, 38(2): 143–148. CHEN W S, NING H S. Security surveillance of low-altitude airspace with primary radar[J].Journal of Beijing University of Aeronautics and Astronautics, 2012, 38(2): 143–148.(in Chinese) |
| [2] | TAKAHASHI R, HIRATA K, MANIWA H. Altitude estimation of low elevation target over the sea for surface based phased array radar[C]//Proceedings of IEEE Radar Conference. Piscataway, NJ: IEEE Press, 2010: 123-128. |
| [3] | ZHENG Y S, CHEN B X. Altitude measurement of low-angle target in complex terrain for very high-frequency radar[J].IET Radar Sonar Navigation, 2015, 9(8): 967–973.DOI:10.1049/iet-rsn.2014.0544 |
| [4] | MAN M Y, LEI Z Y, XIE Y J, et al. Monte Carlo simulation of the echo signals from low-flying targets for airborne radar[J].International Journal of Antennas & Propagation, 2014: 416985. |
| [5] | GREENBERG E, NAOR M. Direction of arrival estimation in urban multipath environments[C]//Proceedings of European Conference on Antennas and Propagation. Piscataway, NJ: IEEE Press, 2016: 1-5. |
| [6] | ANDERSON K D. Radar detection of low-altitude targets in a maritime environment[J].IEEE Transactions on Antennas and Propagation, 1995, 43(6): 609–613.DOI:10.1109/8.387177 |
| [7] | SIRKOVA I. Brief review on PE method application to propagation channel modeling in sea environment[J].Central European Journal of Engineering, 2012, 2(1): 19–38. |
| [8] | ZHAGN P, BAI L, WU Z, et al. Applying the parabolic equation to tropospheric groundwave propagation:A review of recent achievements and significant milestones[J].IEEE Antennas & Propagation Magazine, 2016, 58(3): 31–44. |
| [9] | DONOHUE D J, KUTLER J R. Modeling radar propagation over terrain[J].Johns Hopkins APL Technical Digest, 1997, 18(2): 279–287. |
| [10] | 胡绘斌. 预测复杂环境下电波传播特性的算法研究[D]. 长沙: 国防科学技术大学, 2006: 4-8. HU H B. Study on the algorithms of predicting the radio propagation characteristics in complex environments[D]. Changsha: National University of Defense Technology, 2006: 4-8(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-90002-2007141048.htm |
| [11] | THOMSON D J, CHAPMAN N R. A wide-angle split-step algorithm for the parabolic equation[J].Journal of the Acoustical Society of America, 1983, 74(6): 1848–1854.DOI:10.1121/1.390272 |
| [12] | BARRIOS A E. A terrain parabolic equation model for propagation in the troposphere[J].IEEE Transactions on Antennas and Propagation, 1994, 42(1): 90–98.DOI:10.1109/8.272306 |
| [13] | LI L, LIN L K, WU Z S, et al. Study on the maximum calculation height and the maximum propagation angle of the troposcatter wide-angle parabolic equation method[J].IET Microwaves Antennas & Propagation, 2016, 10(6): 686–691. |
| [14] | KUTTLER J R, JANASWAMY R. Improved Fourier transform methods for solving the parabolic wave equation[J].Radio Science, 2002, 37(2): 1–11. |
| [15] | BARRIOS A E. Considerations in the development of the advanced propagation model (APM) for U. S. navy applications[C]//Proceedings of the International Radar Conference. Piscataway, NJ: IEEE Press, 2003: 77-82. |
| [16] | AWADSALLAH R S, GEHMAN J Z, KUTTLER J R, et al. Modeling radar propagation in three-dimensional environments[J].Johns Hopkins APL Technical Digest, 2004, 25(2): 101–111. |
| [17] | NORMAN E D. Assessment of the wind farm impact on the radar: 1002. 2654v1[R]. Limours: Thales Air Systems, 2010: 1-55. |
| [18] | LIN C C, REILLY J P. A site-specific model of radar terrain backscatter and shadowing[J].Johns Hopkins APL Technical Digest, 1997, 18(3): 432–447. |
| [19] | 米切尔. 雷达系统模拟[M].北京: 科学出版社, 1982: 124-127. MITCHELL R L. Radar signal simulation[M].Beijing: Science Press, 1982: 124-127.(in Chinese) |
| [20] | 许小剑, 黄培康. 雷达系统及其信息处理[M].北京: 电子工业出版社, 2010: 156-158. XU X J, HUANG P K. Radar system and signal processing[M].Beijing: Publishing House of Electronics Industry, 2010: 156-158.(in Chinese) |
| [21] | FENG S, CHEN J. Law-angle reflectivity modeling of land clutter[J].IEEE Geosciences and Remote Sensing Letters, 2006, 3(2): 254–258.DOI:10.1109/LGRS.2005.863847 |
