针对流体静压轴承在液体火箭发动机涡轮泵中低温低黏环境下的应用,国内外展开过一系列的理论和试验研究。国外最早在20世纪60年代,Reddecliff和Vohr[4]进行了液氢、液氧润滑静压轴承的静态特性试验,液氢润滑轴承转速最高达到40 000 r/min,液氧润滑轴承转速达到30 000 r/min,经过多次模拟涡轮泵启动—关机工作过程的试验之后,轴承状态依然完好。在20世纪90年代,San Andres等[5]通过数值计算和试验方法研究了采用黏度较低的水作为润滑介质时,流体静压轴承在高速条件下的承载力、流量、刚度和阻尼特性。之后Yang等[6]以航天飞机主发动机涡轮泵为应用背景,采用绝热和等温模型研究了液氧润滑静压轴承的性能,结果显示2种模型计算的轴承性能接近,但轴承温升会同时对润滑介质物性和轴承结构造成影响。作为重复使用发动机涡轮泵的关键储备技术之一,日本的Ohta等[7]设计了便于安装的剖分式流体静压轴承,并安装到LE-5发动机液氢涡轮泵进行了试验,得到了较好的试验结果。法国的Edeline等[8]以低成本可重复使用火箭发动机为应用背景,设计了采用流体静压轴承支撑的发动机液氢涡轮泵验证机,并成功进行了试验。2012年,日本的Oike等[9]用液氮作为润滑介质对内径为60 mm的动静压轴承的稳定性进行了试验研究,最高转速达75 000 r/min,其结果表明在转速低于60 000 r/min时轴承有足够的稳定裕度。国内以液体火箭发动机为应用背景的流体静压轴承研究主要有:戴学余等[10]计算分析了不同结构形式的动静压轴承在水、液氧等低黏度介质润滑下的性能,为在低温环境下工作的动静压轴承的设计和试验提供了参考。张国渊等[11-12]进行了流体动静压轴承水润滑试验研究,最高转速接近20 000 r/min,验证了水润滑动静压轴承在高速、高压下的工作能力,在后续研究中还通过数值方法分析了低温介质润滑下气液两相流对静压轴承性能的影响。
与用油作为润滑介质在常温下工作的流体静压轴承相比,氢氧发动机涡轮泵中的静压轴承用低温、低黏的推进剂液氢或液氧作为润滑介质,其工作条件与油润滑有很大不同,因而其性能特性和设计方法与前者也有较大差异。对传统的油润滑动静压轴承,国内外都已有较为完善的研究,但对低温、低黏介质润滑的动静压轴承,相比较而言,国内的相关研究特别是试验研究不够充分。
本文以液体火箭发动机涡轮泵为应用背景,对低温、低黏度介质润滑下的流体静压轴承性能展开研究。首先,设计一个4腔结构的流体静压径向轴承,通过数值方法求解流体润滑雷诺方程,对分别采用水和液氮作为润滑介质时轴承的静态性能特性进行计算分析,为开展水和液氮润滑的试验研究提供指导。然后,设计建造流体静压轴承试验系统,用水作为润滑介质进行试验。最后,将水润滑试验结果与数值计算结果进行对比分析,为进行进一步液氮低温润滑试验奠定基础。
1 数值计算 本文所研究流体静压轴承的结构形式及周向展开的润滑液膜流场示意图如图 1所示。图 1(a)轴颈在轴承中的运动用坐标系O1x1y1表示,ω为轴颈角速度,Δy1为主轴的浮起量,图 1(b)展开后的液膜流场用坐标系Oxz表示。轴承周向均布4个相同尺寸的节流孔,与轴承内表面的4个凹腔相联。外部系统供给一定压力的润滑介质,经节流孔流入凹腔,再流入轴与轴承之间的间隙形成润滑液膜,为主轴提供支撑。轴承的主要结构参数如表 1所示。
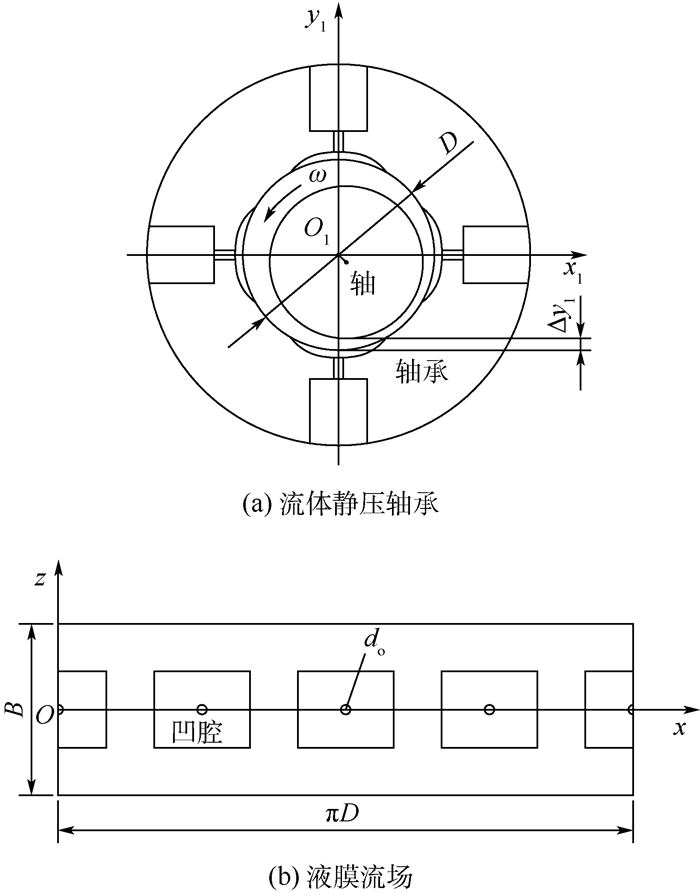 |
| 图 1 流体静压轴承及液膜流场示意图 Fig. 1 Schematic of hydrostatic journal bearing and fluid film field |
| 图选项 |
表 1 轴承的主要参数 Table 1 Main parameters of bearing
| 参数 | 数值 |
| 轴承内径D/mm | 20 |
| 轴承宽度B/mm | 14 |
| 平均半径间隙h0/μm | 35 |
| 节流孔直径do/mm | 0.64 |
| 凹腔数目n | 4 |
表选项
1.1 计算模型 根据流体润滑理论,流体静压轴承润滑液膜的稳态压力分布满足雷诺方程[13]
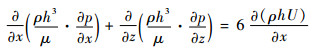 | (1) |
式中:ρ为润滑介质密度;p为润滑液膜压力;h为液膜厚度;μ为润滑介质动力黏度;U为轴颈表面的线速度。
对本文所研究的水和液氮润滑的流体静压轴承,在数值计算中引入以下假设:润滑介质的密度和黏度均为常数,轴承液膜中的流态为层流。
计算中引入以下无量纲参数:
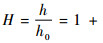

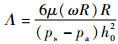
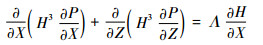 | (2) |
对流体静压润滑,式(2)的边界条件为:①轴承两侧出口边界:P=0;②轴承凹腔压力边界:PR=PRi;③对称边界条件:(dP/dZ)0=0;④周期边界条件:P(0, Z)=P(2π, Z)。其中:PR为凹腔压力;PRi为轴承第i个凹腔内的压力,需根据凹腔流入和流出的流量平衡条件确定。
1.2 计算方法 与流体动压润滑相比,静压润滑雷诺方程求解的难点在于凹腔内压力边界条件的处理,各凹腔内压力需根据流量平衡条件确定。对此,多数的流体静压数值求解采用的方法是在液膜压力分布迭代循环的外层引入流量平衡的迭代循环。这种方法的缺点在于每迭代修正一次凹腔压力后,都需要重新迭代求解液膜压力分布,计算量较大,且在偏心率较大时收敛性不好。针对气体静压润滑中同样的问题,文献[14]提出采用优化算法求解静压气体润滑雷诺方程,在一定程度上解决了偏心率较大时不收敛的问题。
本文在文献[15]的基础上,利用式(2)所示线性雷诺方程解的可加性,将各凹腔内压力边界条件分开处理,得到不同凹腔压力下的液膜压力分布,再根据凹腔的流量平衡方程,仅通过一次迭代求出各凹腔压力对整个液膜压力分布的影响因子,最后将计算结果叠加得到液膜压力分布。
根据线性方程解的可加性,将式(2)中的凹腔压力边界条件分开处理,则液膜无量纲压力分布可表示为
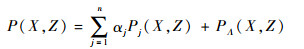 | (3) |
式中:αj为各凹腔压力影响因子; 压力分布Pj和PΛ分别根据以下控制方程计算。
压力分布Pj的控制方程为
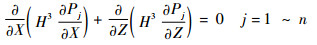 | (4) |
边界条件为式(2)的①、③、④及PRj=1,其他PR=0。
压力分布PΛ的控制方程为
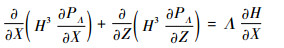 | (5) |
边界条件为式(2)的①、③、④及所有PR=0。
式(4)和式(5)中凹腔的压力边界PR是已知的,可直接对方程进行中心差分离散,迭代求出Pj (j=1~n)和PΛ,其求解过程可参考文献[13]。
在式(3)的无量纲压力分布P下,轴承的第i个凹腔流出的质量流量可表示为
 | (6) |
式中:Qij和QΛi分别为
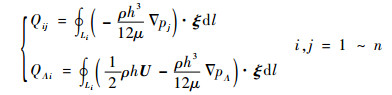 | (7) |
其中:Li为包围凹腔i的凹腔边缘;ξ为垂直于凹腔边缘的单位向量;U为轴颈表面速度矢量;pj和pΛ分别为Pj和PΛ的有量纲形式。
在式(3)的无量纲压力分布P下,综合式(3)~式(5)可知,轴承的第i个凹腔内的无量纲压力为αi,则经节流孔流入凹腔的质量流量可表示为
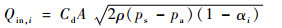 | (8) |
式中:A为节流孔面积;Cd为流量系数。
此处需特别指出的是,在前期数值计算分析中发现流量系数对轴承性能计算结果有较大影响,故本文针对节流孔的流量特性进行了试验研究,拟合出流量系数用于数值计算。后文将给出流量特性的试验结果。
在得出凹腔流入和流出流量关系式之后,根据凹腔的流量平衡条件Qout, i=Qin, i(i=1~n),可得关于凹腔压力影响因子αi的方程组。对本文所研究轴承,其流量平衡方程组为
 | (9) |
式中:Qij已知,Qin, i与影响因子αi有关,方程组非线性,可采用迭代方法求出αi (i=1~n)。
在以上求解的基础上,将压力分布Pj、PΛ和影响因子αi代入式(3),即可得轴承液膜的无量纲压力分布P(X, Z),积分可求出轴承的承载力W,轴承的质量流量Qm可根据式(6)或式(8)得出。以上求解过程对应的数值计算流程图如图 2所示。
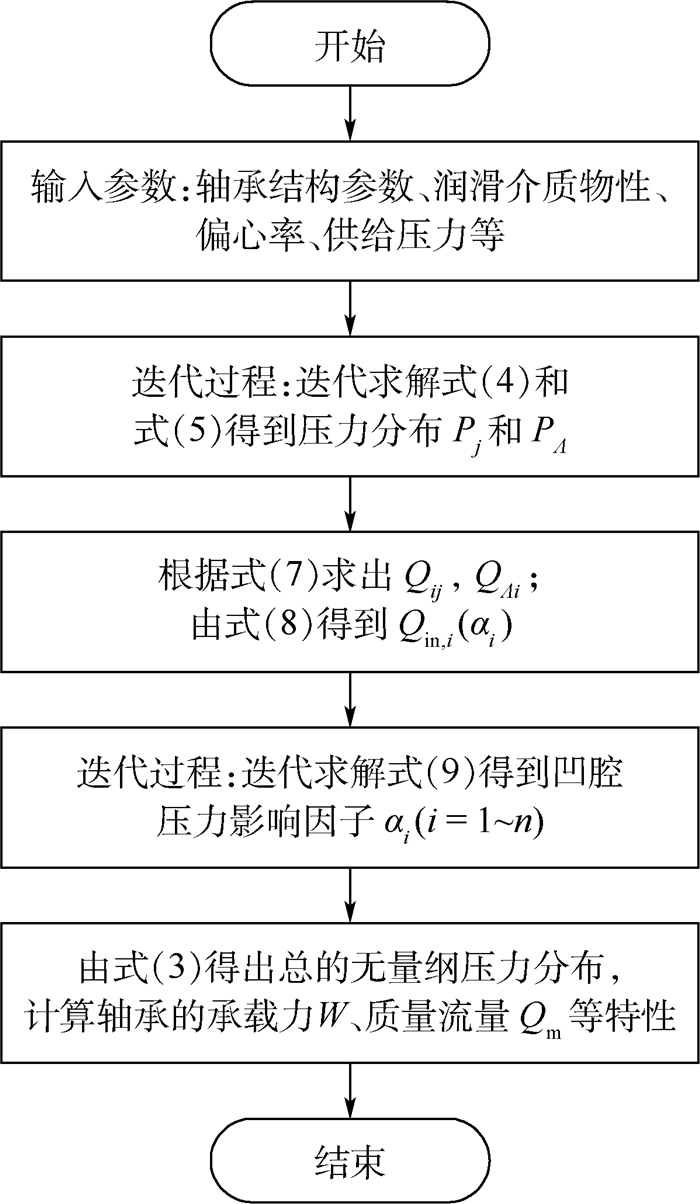 |
| 图 2 数值计算流程图 Fig. 2 Flowchart of numerical calculation |
| 图选项 |
综合以上数值求解过程,式(4)和式(5)均为给定凹腔压力下的液膜压力分布求解,仅需一次迭代过程,凹腔内的流量平衡通过迭代式(9)实现。与一般的在流量平衡迭代循环内嵌套液膜压力分布迭代循环的方法相比,本文所采用方法避免了迭代循环的嵌套,计算量较小。其局限性在于仅适用于求解线性雷诺方程,对非线性雷诺方程不适用。
1.3 计算结果与分析 在以液氢-液氧火箭发动机涡轮泵为应用背景的流体静压轴承研究中,通常采用成本低、危险性小的水和液氮作为模拟润滑介质进行基础试验研究。本节针对图 1所示轴承,采用1.2节中的数值计算方法,计算分析了分别采用水和液氮作为润滑介质时,轴承的静态承载力和流量特性随偏心率和供给压力的变化,为相应的试验研究提供参考。
在计算分析轴承特性与偏心率的关系时,考虑到涡轮泵工作压力较高,设定供给压力保持4.0 MPa不变;计算轴承特性随供给压力的变化情况时,考虑到偏心率过小时轴承的承载力很小,不能很好区分2种润滑介质的不同,而偏心率过大与轴承的实际工作状态有较大差异,故选取具有代表性的偏心率为0.5进行计算。
在数值计算中,所采用的水和液氮的相关物性参数如表 2所示[16]。
表 2 润滑介质物性参数[16] Table 2 Physical property parameters of lubricants [16]
| 润滑介质 | 温度/K | 密度/(kg·m-3) | 黏度/(10-6Pa·s) |
| 水 | 293 | 998.2 | 1 005 |
| 液氮 | 77 | 807.7 | 163 |
表选项
1.3.1 压力分布对比 为直观比较不同润滑介质下流体静压轴承液膜的压力分布情况,图 3给出了供给压力为4.0 MPa,偏心率为0.5的条件下,水和液氮润滑时轴承液膜的无量纲压力分布情况。
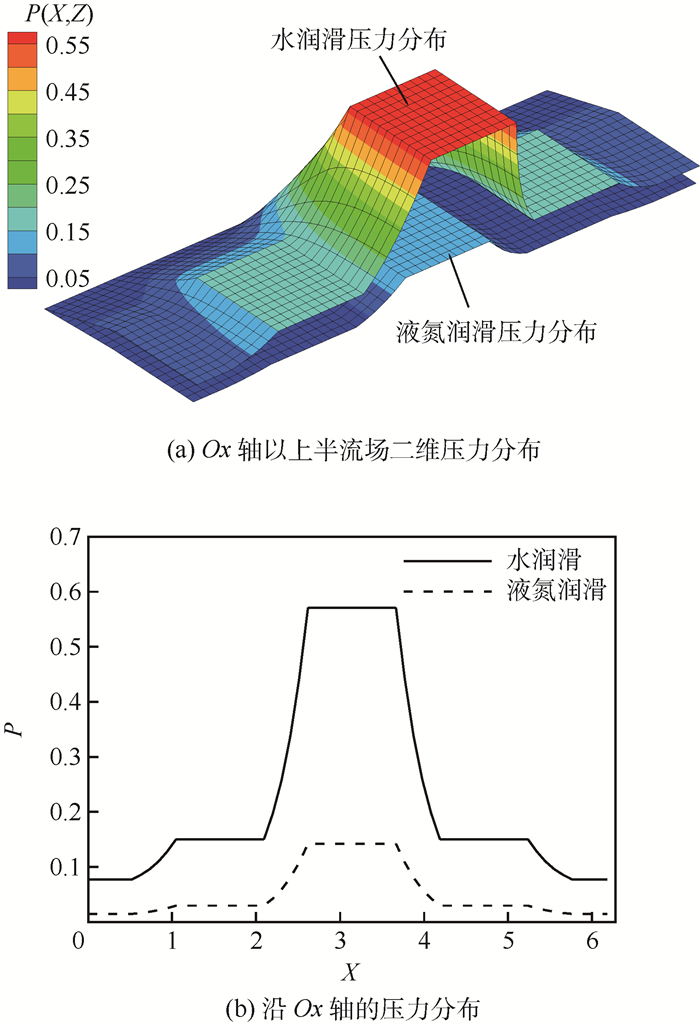 |
| 图 3 轴承液膜压力分布 Fig. 3 Pressure distribution of bearing fluid film |
| 图选项 |
从图 3中看出,在给定的供给压力和偏心率下,水润滑液膜压力明显高于液氮润滑时的压力,这主要是因为液氮的黏度小于水的黏度,液氮在轴承间隙的流动阻力远低于水的流阻。图 3(b)中轴承间隙最小位置(X=3.14)处的凹腔压力明显高于两侧压力,这说明静压轴承的静态承载力主要取决于间隙最小处凹腔的压力。
1.3.2 承载力特性 流体静压轴承的承载力是其主要特性之一,图 4(a)、(b)分别给出了承载力与偏心率和供给压力的关系。
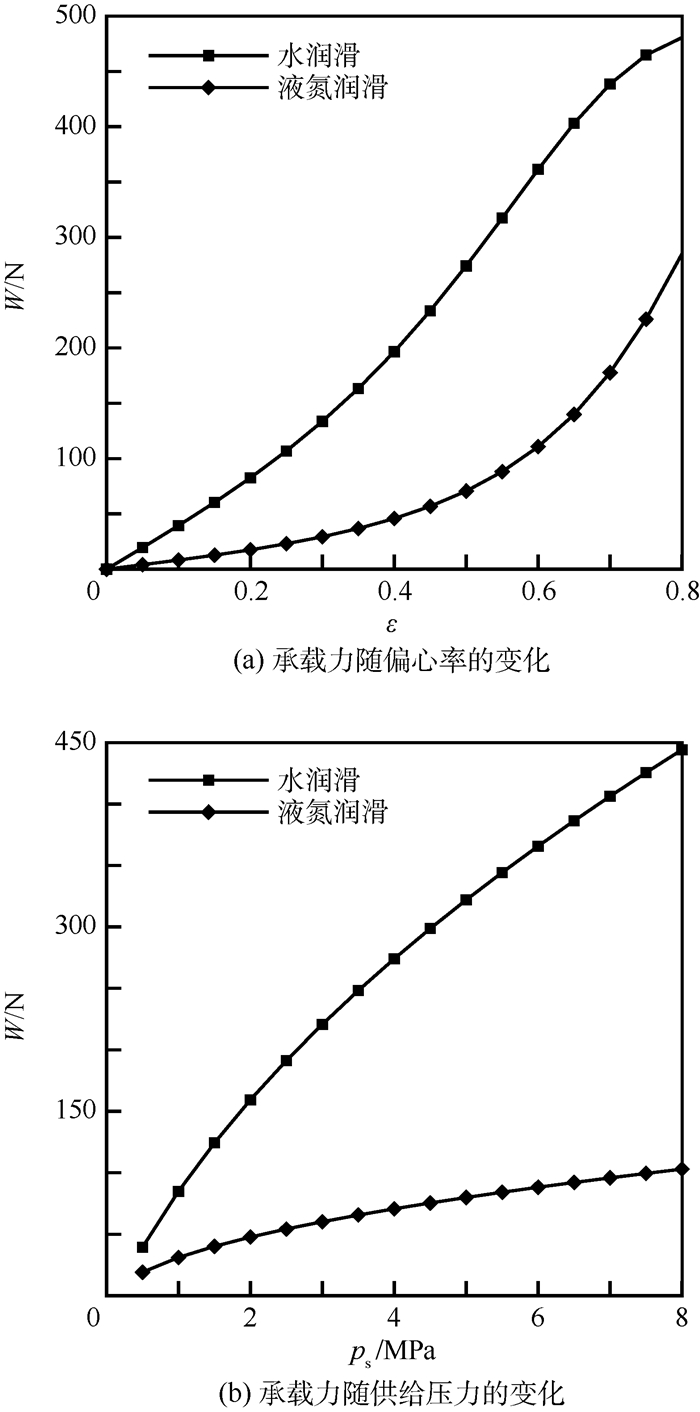 |
| 图 4 水和液氮润滑轴承的承载力特性 Fig. 4 Load capacity characteristics of bearing lubricated with water and liquid nitrogen |
| 图选项 |
从图 4可以看出,在给定供给压力和偏心率的条件下,水润滑轴承的承载力明显大于液氮润滑时的承载力,这在图 3中压力分布图上表现为水润滑液膜的压力高于液氮润滑液膜压力。
从图 4(a)可以看出,在所计算的偏心率范围内,随着偏心率的增大,轴承的承载力也逐渐增大。在偏心率小于0.5时,水润滑承载力变化曲线的斜率明显大于液氮润滑时的斜率。这说明在偏心率较小时,轴承在水润滑下的静刚度要大于在液氮润滑下的静刚度。这主要是因为本文中轴承节流孔的节流流阻与轴承间隙流阻之比不仅与偏心率有关,而且与润滑介质的密度和黏度有关,因此轴承刚度会随着供给压力、偏心率、密度和黏度的变化而改变,且变化规律不是单调的。
从图 4(b)看出,水和液氮润滑下轴承的承载力都随着供给压力的升高而增大。在相同的压力增量下,水润滑轴承承载力的增大量明显大于液氮润滑时的增大量。这说明水润滑静压轴承的承载力对供给压力的变化比液氮润滑时更加敏感。
1.3.3 流量特性 流体静压轴承的流量特性对试验中供应系统供给能力的设计具有指导意义,图 5中给出了轴承流量与偏心率和供给压力的关系。
 |
| 图 5 水和液氮润滑轴承的流量特性 Fig. 5 Flow characteristics of bearing lubricated with water and liquid nitrogen |
| 图选项 |
从图 5可看出,相同工况下水和液氮润滑的质量流量非常接近。从定性分析的角度来看,这主要是因为:液氮的黏度小于水的黏度,在流过轴承间隙时液氮的流阻较小,因此其体积流量应大于水的流量;但又因液氮的密度小于水的密度,因此两者的质量流量较为接近。
从图 5(a)看出,随着偏心率的增大,水和液氮润滑的质量流量总体呈减小趋势。在计算的偏心率变化范围内,水和液氮的质量流量的最大变化量在8%以内。因此,流体静压轴承试验系统的设计中,可以认为轴承的质量流量与偏心率无关。从图 5(b)看出,水和液氮润滑时轴承的流量均随供给压力的增加而增大。
综合图 5可知,在相同的供给压力和偏心率下,水和液氮润滑的质量流量十分接近,这对在水润滑试验的基础上进行液氮低温润滑试验具有指导意义。
2 轴承试验系统 2.1 流体静压轴承试验台 流体静压轴承试验系统示意图如图 6所示。其中轴承试验台为对称结构,主轴由2个完全相同的图 1所示的流体静压轴承支撑,采用气动涡轮驱动主轴旋转,在涡轮两侧安装有气体止推轴承,以控制主轴的轴向运动。
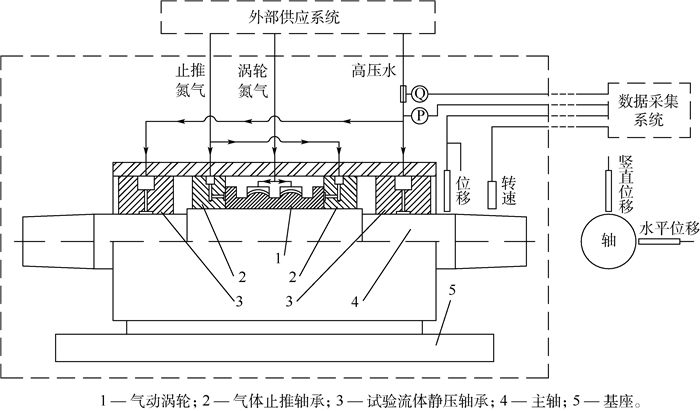 |
| 图 6 流体静压轴承试验系统示意图 Fig. 6 Schematic of hydrostatic journal bearing test system |
| 图选项 |
2.2 外部供应及测量系统 试验台的外部供应系统包括高压氮气供应系统和高压水供应系统。气体供应系统的高压氮气经过配气台调节后,用于涡轮、气体止推轴承和水的增压;高压水供应系统用于常温下流体静压轴承的水润滑试验,试验中为获得稳定且连续可调的供水压力,首先将水注入高压储罐,然后用高压氮气来给储罐中水增压后供给到流体静压轴承。测量系统主要采集测量主轴的径向位移、转速,轴承的供给压力、流量等数据。
3 试验结果与分析 3.1 节流孔流量特性试验 流体静压润滑的数值计算中,准确的节流孔流量模型是提高轴承性能计算准确性的基础。静压轴承设计中常用的固定节流孔流量模型通常有小孔节流器(薄壁孔)和毛细管节流器(毛细孔)流量模型,但本文在水润滑静压轴承数值计算与试验测量的流量对比中发现:若直接按照小孔节流器或毛细管节流器流量模型进行计算,数值计算与试验结果存在较大差异。针对本文中的节流孔,分析采用上述2种模型计算结果不准确主要有2方面原因:①节流孔尺寸既非典型的薄壁孔也不是典型的毛细孔;②本文所研究润滑介质的黏度较低,节流孔中流态与一般的油润滑有较大差异。因此,本文用水对实际加工轴承的节流孔进行了流量特性试验。
如图 1所示,本文所研究流体静压轴承有4个相同尺寸的节流孔(孔长为2.2 mm),流量特性试验时用质量流量计测量了不同压差Δp下4个节流孔的总流量如表 3所示。
表 3 流量特性试验结果 Table 3 Results of flow characteristics test
| 测点 | 第1次试验 | 第2次试验 | 第3次试验 | |||||
| Δp/ MPa | Qm/ (kg·s-1) | Δp/ MPa | Qm/ (kg·s-1) | Δp/ MPa | Qm/ (kg·s-1) | |||
| 1 | 0.99 | 0.049 7 | 0.91 | 0.049 0 | 0.95 | 0.050 9 | ||
| 2 | 1.81 | 0.069 3 | 1.74 | 0.068 2 | 1.80 | 0.069 5 | ||
| 3 | 2.76 | 0.085 4 | 2.76 | 0.085 2 | 2.72 | 0.084 9 | ||
| 4 | 3.67 | 0.097 8 | 3.71 | 0.098 4 | 3.74 | 0.098 5 | ||
| 5 | 4.59 | 0.108 5 | 4.61 | 0.109 3 | 4.59 | 0.109 1 | ||
表选项
本文中轴承节流孔(长径比3.4)属于非典型小孔,其尺寸不在《机械设计手册》[17]静压轴承设计中小孔节流和毛细管节流模型的适用范围。但根据液压系统中的相关理论,该尺寸的小孔可称之为短孔,其流量可按薄壁孔流量公式计算[18],流量系数需另取。故以下按照薄壁小孔的流量公式来拟合流量系数。从薄壁孔流量公式可知,流量与Δp0.5是线性关系,根据表 3中试验测量结果绘制出流量与Δp0.5的关系曲线如图 7所示。
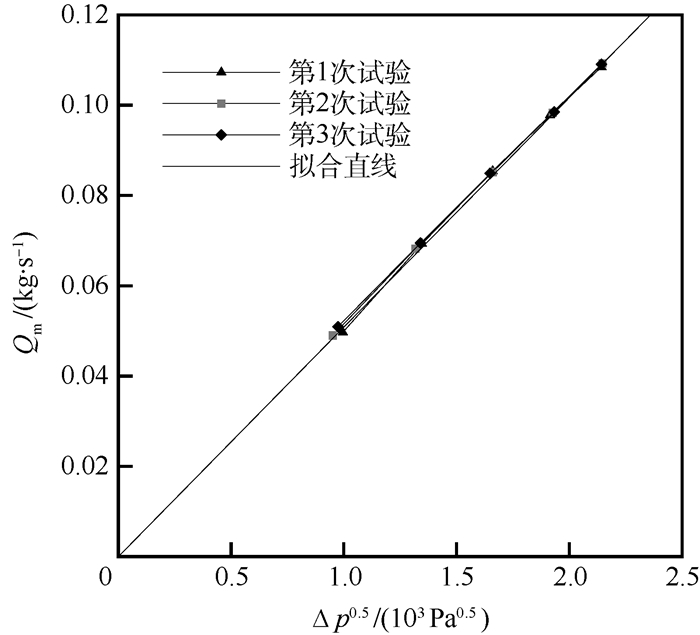 |
| 图 7 节流孔流量系数拟合 Fig. 7 Orifice flow coefficient fitting |
| 图选项 |
从图 7中可以看出,3次试验测量结果与拟合直线基本完全重合,说明测量流量与Δp0.5具有较好的线性关系,从而确定本文所研究轴承节流孔的流量公式符合
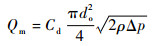 |
式中:do的单位为m;ρ的单位为kg/m3;Δp的单位为Pa。
根据试验结果拟合流量系数时,注意到试验中测量流量为轴承中4个节流孔的总流量。在实际加工中4个节流孔的直径不能保证完全相同,但实际测量发现,节流孔直径之间相差很小(在5%以内),因此可以认为4个节流孔的流量系数相同。在计算中取4个节流孔的实际直径的均方根值,认为各节流孔尺寸相同。表 1中节流孔直径即为实际直径的均方根值。
从图 7中的拟合直线可计算得到流量系数Cd=0.877,这一流量系数远超出了静压轴承设计中小孔节流器(薄壁孔)的流量系数0.6~0.7[17]的范围。本文中数值计算部分涉及节流特性的计算均是采用此次试验拟合的流量系数。
3.2 静态特性试验 静态特性试验中,首先在主轴的两端添加一定质量的载荷,然后给轴承供给一定压力的润滑介质,同时测量供给压力、流量和主轴位移的变化,研究分析轴承的静态特性。因图 6所示试验台具有对称结构,试验中2个静压轴承的工作状态基本相同,因此,在试验结果分析时可将载荷、流量等参数等效到单个轴承进行研究。以下分析中未特别说明时,载荷和流量都是针对单个轴承。
与数值计算中直接研究轴承特性随偏心率和供给压力的变化关系不同,在具体试验中,考虑到测量给定偏心率下轴承的承载力和流量的试验方法因操作的复杂性可能引起较大的试验偏差,本文通过研究给定载荷下,主轴的浮起量(或偏心率)随供给压力的变化,来分析流体静压轴承的承载力特性;同时测量轴承流量的变化,分析润滑介质流量与偏心率和供给压力之间的关系。
在主轴空载的情况下,转子作用在轴承上的载荷为0.4 kg。图 8给出了主轴空载和两端分别增加0.5 kg的载荷时,计算得到的偏心率随供给压力的变化曲线与试验结果的对比。图 9中给出了在不同载荷条件下,试验测得的轴承质量流量随供给压力的变化曲线与数值计算的偏心率为0时质量流量随供给压力变化曲线的对比。
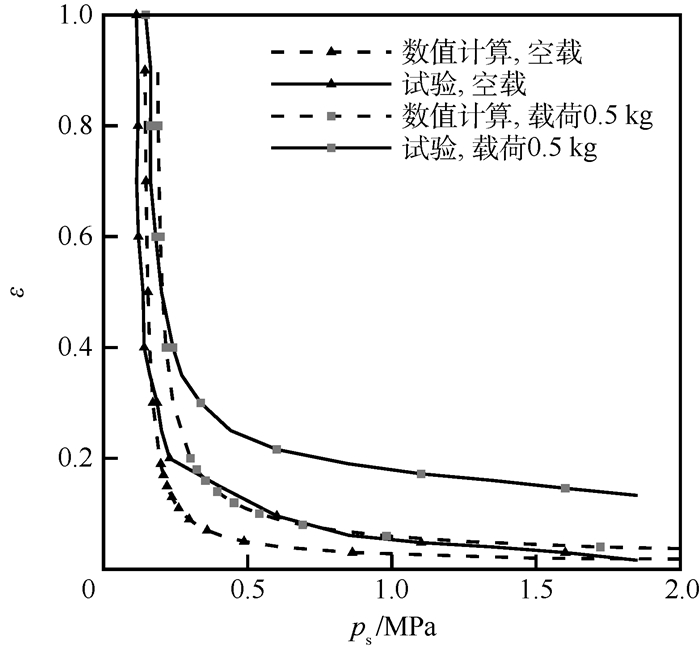 |
| 图 8 不同载荷下偏心率与供给压力的关系 Fig. 8 Eccentricity ratio versus supply pressure under different load conditions |
| 图选项 |
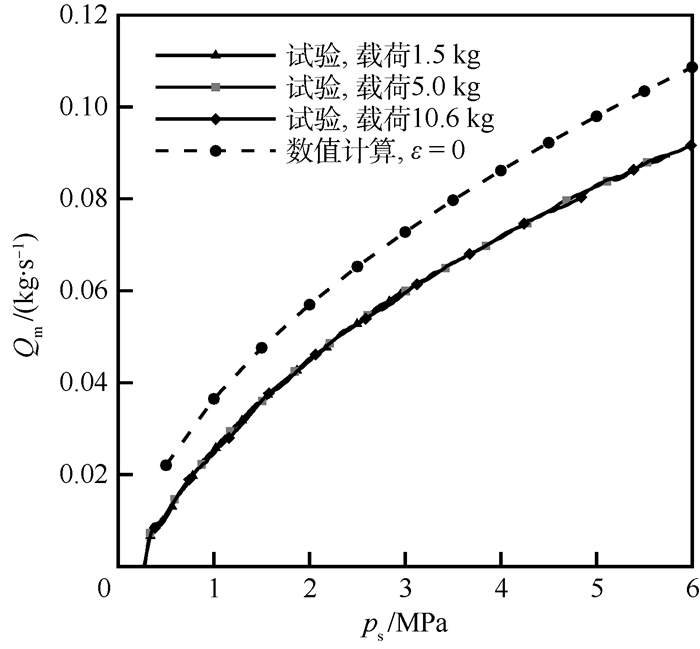 |
| 图 9 不同载荷下质量流量与供给压力的关系 Fig. 9 Mass flow rate versus supply pressure under different load conditions |
| 图选项 |
从图 8看出,在2种载荷条件下,数值计算与试验得到的偏心率随供给压力的变化趋势相同。在2种载荷下,主轴都是在供给压力提高到一定值后迅速浮起,之后继续提高供给压力,偏心率变化很小。
空载时,试验与数值计算的偏心率相差最大为0.07左右,即位移相差2.5 μm;在供给压力小于0.5 MPa时,偏心率对供给压力的变化十分敏感,在供给压力大于0.5 MPa时,主轴的偏心率小于0.2,且对供给压力的变化不敏感,说明主轴已完全浮起。载荷为0.5 kg时,数值计算与试验结果的变化趋势一致,但供给压力大于0.3 MPa时,两者有较大差异,试验测量的偏心率值比数值计算结果大0.1左右,即位移相差3.5 μm。这可能是加载之后主轴有一定弯曲变形,从而使得主轴浮起后测得的浮起量比实际值要小。
从图 9可以看出,试验测得的不同载荷条件下轴承流量随供给压力变化的曲线基本完全重合。根据分析可知,供给压力相同时,载荷不同则主轴的偏心率不同,这说明不同偏心率下供给压力相同则水润滑轴承流量相同,这与之前的理论分析一致,说明了水润滑轴承的流量与偏心率基本无关。从图 9中数值计算与试验结果的对比来看,相同供给压力下数值计算得到的流量与试验测量流量有一定差距,但总体变化趋势一致,计算得到的质量流量与试验结果的最大相差0.016 kg/s。
3.3 动态特性初步试验 在水润滑静态试验的基础上,进行了主轴空载条件下的动态转动试验。试验中,先将轴承供水压力提高到约1.6 MPa,使主轴完全浮起,再开启止推轴承供气,然后给涡轮供气,逐渐提高主轴的转速,测量主轴在水平和竖直方向的位移,研究主轴的位移变化情况。
在试验中实际测得的不同转速N下测点处的轴心轨迹如图 10所示,图中xs和ys分别为传感器测得的水平和竖直方向的轴心位移。图 10(a)、(b)中轴心轨迹凸出的尖角,可能是由轴的加工缺陷造成的;图 10(c)、(d)所示轨迹与图 10(a)、(b)相比有明显棱角,这主要是因数据采集过程中采样频率固定,随着转速的不断提高,在一个旋转周期内采集的点变少,因此得到的轨迹不够平滑。从图 10中可以看出:轴心轨迹接近椭圆形,并且随着转速的提高轴心轨迹也不断扩大,根据分析这主要是由转子所受不平衡力引起的;但涡动轨迹的中心,即主轴的平衡位置基本保持不变。
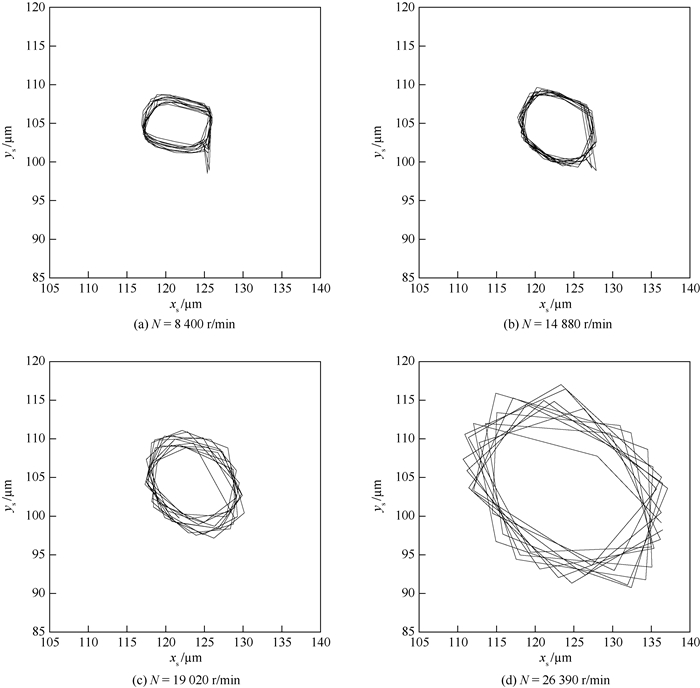 |
| 图 10 不同转速下的轴心轨迹 Fig. 10 Shaft center orbits at different rotational speeds |
| 图选项 |
为分析在转速变化过程中主轴平衡位置的变化情况,同时消除测点处轴的加工误差和噪声信号的影响,可对测得的位移信号进行处理,分析主轴平均浮起量的变化。图 11给出了整个0~30 000 r/min的动态试验中,主轴平均浮起量Δy1和转速的变化曲线。
 |
| 图 11 平均浮起量和转速随时间的变化 Fig. 11 Averaged floating displacement and rotational speed versus time |
| 图选项 |
从图 11可以看出,在30 s左右供水压力提高后主轴迅速浮起,浮起量在32 μm左右,接近平均半径间隙35 μm,说明主轴浮起状态良好。在90 s左右主轴转速从0开始逐渐增大,在230 s左右达到30 000 r/min,转速保持一段时间后开始逐渐减速到0,之后随着供给压力的降低主轴也落回原位。
为分析试验中供给压力对主轴平衡位置的影响,图 12中给出了主轴平均浮起量随供给压力的变化曲线。从图中可以看出,供给压力在0.2 MPa时,主轴基本完全浮起,但为保证试验中轴承的刚度以提高稳定性,最终将供给压力提高到约1.6 MPa。图中虚线圆内聚集点即为轴转动过程中的平衡位置点。
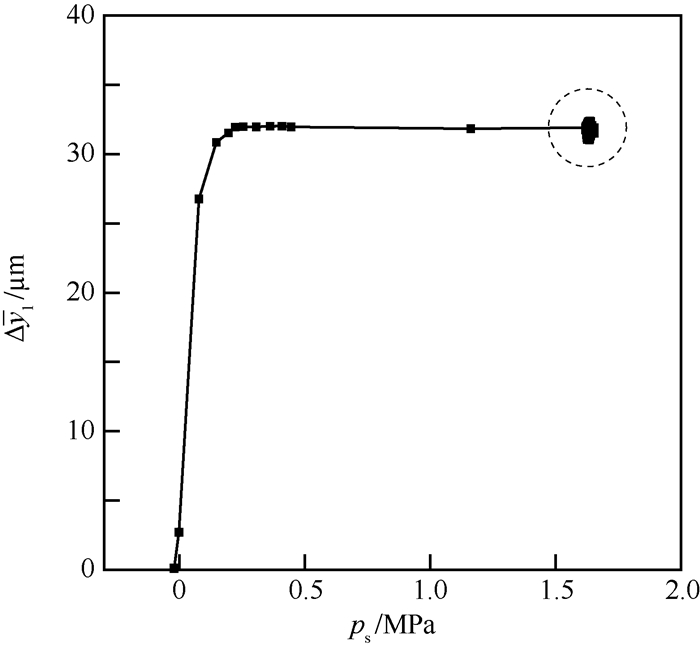 |
| 图 12 平均浮起量与供给压力的关系 Fig. 12 Averaged floating displacement versus supply pressure |
| 图选项 |
为分析试验中主轴平衡位置与转速之间的关系,图 13给出了转速从0逐渐提高到最大值的过程中,主轴平均浮起量随转速变化的曲线。图中转速为0时浮起量从0增大到约32 μm的部分为主轴随供给压力增加而逐渐浮起的过程,在分析平衡位置与转速关系时不予考虑。从图中可以看出转速从0增大到30 000 r/min时,主轴平均浮起量的变化量小于1.5 μm。这说明主轴完全浮起之后,在转速逐渐提高过程中,轴的平衡位置基本保持不变。
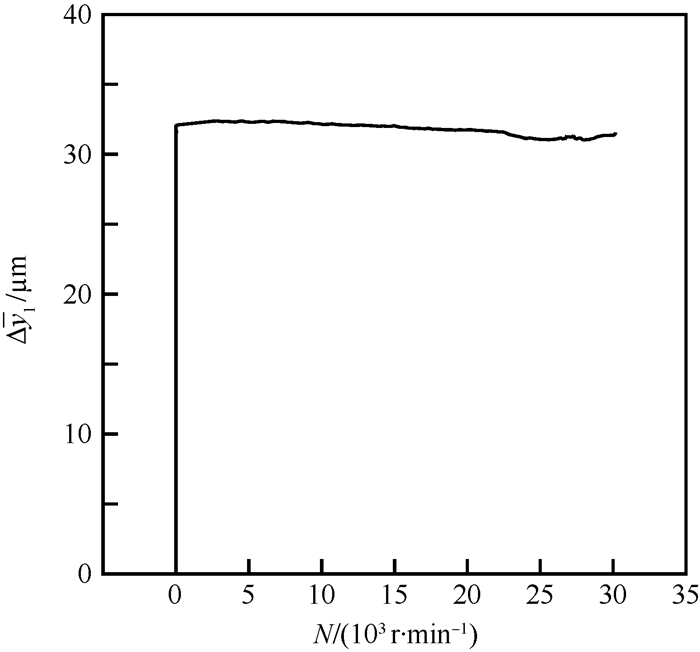 |
| 图 13 平均浮起量与转速的关系 Fig. 13 Averaged floating displacement versus rotational speed |
| 图选项 |
综合以上图 10~图 13可知,主轴在流体静压轴承中浮起后的平衡位置主要由供给压力决定;对本文中轴承,在0~30 000 r/min的转速范围内,随着转速的提高,轴的平衡位置基本保持不变,这说明没有明显的动压效应;但从图 10可看出,因转子不平衡质量的影响,随着转速的提高,轴心的涡动轨迹有扩大的趋势,在其他工况不变的情况下,进一步提高转速可能导致主轴与轴承的碰摩失稳。
4 结论 1) 根据水润滑轴承流量特性试验,短孔节流器的流量可按照薄壁孔的流量公式进行计算,但其流量系数远超出静压轴承设计中常用的小孔节流器(薄壁孔)流量系数的参考范围。
2) 就本文研究条件,在相同工况下,计算得到的水润滑时轴承的静态承载力大于液氮润滑时的承载力,但两者的质量流量较为接近。
3) 在本文计算条件下,偏心率小于0.5时,轴承在水润滑下的静刚度要大于在液氮润滑下的静刚度。
4) 计算和试验结果均显示,静压轴承的质量流量主要由供给压力决定,与偏心率基本无关。
5) 主轴在轴承中浮起后的平衡位置主要由供给压力决定,在转速为0~30 000 r/min的水润滑试验中,随着转速提高主轴的平衡位置基本不变,说明没有明显的动压效应。
参考文献
| [1] | VAN HOOSER K, BRADLEY D P.Space shuttle main engine-the relentless pursuit of improvement:AIAA-2011-7159[R].Reston:AIAA, 2011. |
| [2] | 王松岭, 张建斌. 浅谈发动机涡轮泵动静压轴承研究状况[J].机械制造与自动化, 2006, 35(3): 7–8. WANG S L, ZHANG J B. Discussion of the research status of hybrid bearing on LH2/LO2 engine turbopump of rocket[J].Machine Building & Automation, 2006, 35(3): 7–8.(in Chinese) |
| [3] | 苗旭升, 李斌, 黄智勇. 发动机涡轮泵流体动静压轴承应用分析[J].火箭推进, 2004, 30(6): 1–4. MIAO X S, LI B, HUANG Z Y. Application analysis of liquid hybrid bearing for engine turbopumps[J].Journal of Rocket Propulsion, 2004, 30(6): 1–4.(in Chinese) |
| [4] | REDDECLIFF J M, VOHR J H. Hydrostatic bearings for cryogenic rocket engine turbopumps[J].Journal of Lubrication Technology, 1969, 91(3): 557–575.DOI:10.1115/1.3554989 |
| [5] | SAN ANDRES L, CHILDS D, YANG Z. Turbulent-flow hydrostatic bearings:Analysis and experimental results[J].International Journal of Mechanical Sciences, 1995, 37(8): 815–829.DOI:10.1016/0020-7403(94)00104-R |
| [6] | YANG Z, SAN ANDRES L, CHILDS D W. Thermal effects in liquid oxygen hydrostatic journal bearings[J].Tribology Transactions, 1996, 39(3): 654–662.DOI:10.1080/10402009608983579 |
| [7] | OHTA T, KITAMURA A, OGATA H.LH2 turbopump test with hydrostatic bearing[C]//35th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit.Reston:AIAA, 1999:1-6. |
| [8] | EDELINE E, FAYOLLE P, FONTEYN P, et al.Development and testing of a fluid film bearing LH2 turbopump demonstrator[C]//40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit.Reston:AIAA, 2004:1-7. |
| [9] | OIKE M, KIKUCHI M, TAKADA S, et al. Robustness of cryogenic hybrid journal bearings[J].Tribology Online, 2012, 7(3): 171–178.DOI:10.2474/trol.7.171 |
| [10] | 戴学余, 苗旭升, 富彦丽, 等. 几种低粘度润滑介质下动静压轴承的性能分析[J].润滑与密封, 2004(3): 10–13. DAI X Y, MIAO X S, FU Y L, et al. Analysis of a hybrid bearing with several low-viscosity fluids[J].Lubrication Engineering, 2004(3): 10–13.(in Chinese) |
| [11] | 张国渊, 袁小阳, 苗旭升, 等. 水润滑高速动静压轴承试验研究[J].摩擦学学报, 2006, 26(3): 238–241. ZHANG G Y, YUAN X Y, MIAO X S, et al. Experiment for water-lubricated high-speed hydrostatic journal bearings[J].Tribology, 2006, 26(3): 238–241.(in Chinese) |
| [12] | 张国渊, 袁小阳. 基于混合均质模型的气液两相流润滑动静压轴承性能分析[J].低温工程, 2010(2): 8–13. ZHANG G Y, YUAN X Y. Performance analysis of hybrid journal bearings in two phase flow based on liquid-vapor mixture model[J].Cryogenics, 2010(2): 8–13.(in Chinese) |
| [13] | 张直明. 滑动轴承的流体动力润滑理论[M].北京: 高等教育出版社, 1986: 46-63. ZHANG Z M. Hydrodynamic lubrication theory of sliding bearings[M].Beijing: Higher Education Press, 1986: 46-63.(in Chinese) |
| [14] | 闫攀运, 梁国柱. POWELL优化算法在混合气体轴承数值计算中的应用[J].润滑与密封, 2013, 38(8): 96–100. YAN P Y, LIANG G Z. Application of POWELL optimization algorithm in numerical calculation of hybrid gas bearing[J].Lubrication Engineering, 2013, 38(8): 96–100.(in Chinese) |
| [15] | CASTELLI V, SHAPIRO W. Improved method for numerical solutions of the general incompressible fluid film lubrication problem[J].Journal of Lubrication Technology, 1967, 89(2): 211–218.DOI:10.1115/1.3616950 |
| [16] | 陈国邦, 包锐, 黄永华. 低温工程技术:数据卷[M].北京: 化学工业出版社, 2005: 41-42. CHEN G B, BAO R, HUANG Y H. Cryogenic engineering technology:Data volume[M].Beijing: Chemical Industry Press, 2005: 41-42.(in Chinese) |
| [17] | 闻邦椿. 机械设计手册[M].北京: 机械工业出版社, 2010: 13-82. WEN B C. Machine design handbook[M].Beijing: China Machine Press, 2010: 13-82.(in Chinese) |
| [18] | 詹永麒. 液压传动[M].上海: 上海交通大学出版社, 1999: 28. ZHAN Y Q. Hydraulic transmission[M].Shanghai: Shanghai Jiao Tong University Press, 1999: 28.(in Chinese) |
