在理想的情况下,力传感器模型通常是一个由顶端质量和基部质量组成的二阶弹簧-阻尼系统[4]。在工程中,普遍将力传感器的输出值当做其实际的负载。而在实际的动态测量中,当负载作用在力传感器的激励端时,其响应端将会因自重和换能元件的分布质量而产生一个微小的惯性质量[5]。该惯性质量通过力传感器模型产生一个额外的惯性力。同时,惯性质量引起的惯性力会随着运动加速度的增大而显著增大,严重干扰力传感器的测量精度。为了将该额外的惯性力从传感器模型中分离出来,必须对传感器模型中的惯性质量做出准确的估计。
目前,力传感器惯性质量的校准方法主要有2类。第1类为直接测量法。该方法通过建立力传感器灵敏度、敏感面有重力静态输出与敏感面无重力静态输出三者之间的模型,求解出惯性质量[6]。由于惯性质量较小,重力和干扰信号均会产生较大的估计误差。为了解决该问题,Fujii提出了一种动态估计方法,通过采集连续激振时的力传感器参考频点的输出电压和加速度,根据牛顿第二定律求出力传感器的惯性质量[7-8]。由于动态激振过程中存在着灵敏度漂移,利用未修正的静态灵敏度往往会导致较大的精度损失。
第2类为间接测量法。为了规避灵敏度的动态漂移对测量精度的影响,在Fujii[7-8]的基础上,Bruel & Kj?r公司提出了一种一次配重技术。该技术分别测量出力传感器在空载激振和配重激振状态的输出,利用比较法消去模型中动态漂移的灵敏度,求得力传感器的惯性质量[9-10]。遗憾的是,空载输出时的灵敏度往往会因噪声干扰而产生非线性畸变,造成较大的模型误差。近年来,发展起来的多次配重技术能消除加速度和灵敏度的干扰,已被广泛地用于惯性质量的求解[11-13]。虽然增加配重次数能降低灵敏度漂移的影响,但电压和加速度的测量噪声会导致模型的病态,增大误差累积。
为了改善力传感器模型的病态,本文提出一种改进Monte Carlo校准(MMCC)的惯性质量校准方法。利用伪随机数生成技术,分别对力传感器模型中的配重质量、加速度和电压值进行样本空间的全域模拟;根据区间判断准则,筛选出满足预设精度的有效样本;结合有效样本概率和测量值来校准力传感器的惯性质量。本文还研制了一种力传感器的动态校准装置,用于该方法有效性的验证。
1 力传感器的惯性质量模型 力传感器的惯性质量是由二阶模型的顶端质量与作用在其上的附加质量共同耦合产生的,如图 1所示。
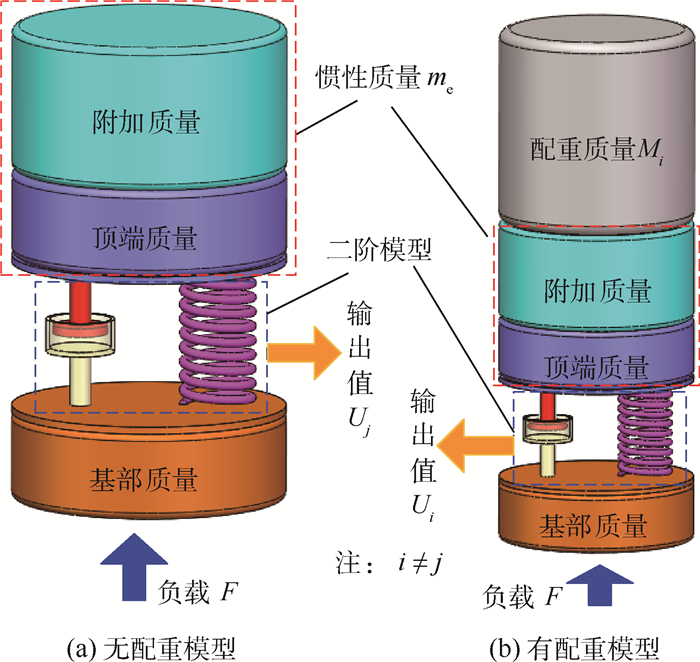 |
| 图 1 力传感器的二阶模型 Fig. 1 Quadratic model of a force transducer |
| 图选项 |
为了估计该惯性质量me,可以对力传感器模型进行重复配重,建立惯性质量与传感器传递函数之间的关系,即配重模型
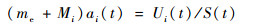 | (1) |
式中:Mi为第i次配重的质量;ai(t)为t时刻的加速度;Ui(t)为对应时刻力传感器的输出电压;S(t)为力传感器的静态灵敏度。
在动态测量过程中,力传感器的灵敏度会动态漂移至Sd(t)。式(1)可以进一步简化为
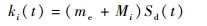 | (2) |
式中:传递系数ki(t)=Ui(t)/ai(t),电压Ui(t)和加速度ai(t)均为动态测量值。
由式(2)可知,通过2次配重建立的二元二次方程组,可求解惯性质量。但在实际测量中,配重质量和传递系数均会引起惯性质量的求解误差。这是因为若配重过大,可能会淹没惯性质量产生的电压输出;反之,若配重过小,则会引起较大的灵敏度漂移;再者,加速度ai(t)和电压Ui(t)的测量误差会直接通过传递系数ki累积到惯性质量上。因此,为了降低模型误差,需要保证每次配重质量Mi下传递系数的误差均最小,即
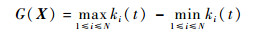 | (3) |
式中:X为估计量,且X =[me, Sd(t)];N为测量次数。
式(3)的求解精度与变量Ω={Mi, 1≤i≤N}和ki(t)的样本空间大小密切相关。也就是说,样本空间越大,目标函数越接近于0。为了实现目标函数G(X)在Ω空间内最小,设初始样本M={M1, M2, …, MN},对应的传递系数为k(t)={k1(t), k2(t), …, kN(t)}。
2 改进Monte Carlo校准方法 在测量过程中,配重质量Mi和传递系数ki(t)均为惯性质量me的随机变量。其中,Mi在区间(0, M)内服从均匀分布;作为加速度ai(t)和电压Ui(t)的测量值,传递系数ki(t)服从标准正态分布[14-16]。这2种分布的概率密度函数可分别表示为
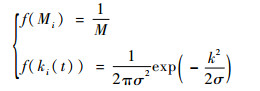 | (4) |
式中:σ为加速度和电压共同引起的测量不确定度。
对式(4)进行离散逆变换,分别抽样出配重质量Mi和传递系数ki(t)的样本,即
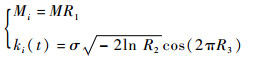 | (5) |
式中:R1、R2和R3为区间(0, 1)内的伪随机数。
根据式(5),可以将配重模型进一步变换为
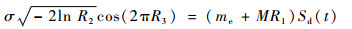 | (6) |
为了避免该模型中样本集的退化,在进行Monte Carlo估计之前,利用式(3)对式(6)随机生成的样本进行判断。使得满足G(X)最小化的样本集保留,并剔除不满足式(3)的样本,从而实现样本集的优化,MMCC方法的流程图如图 2所示。
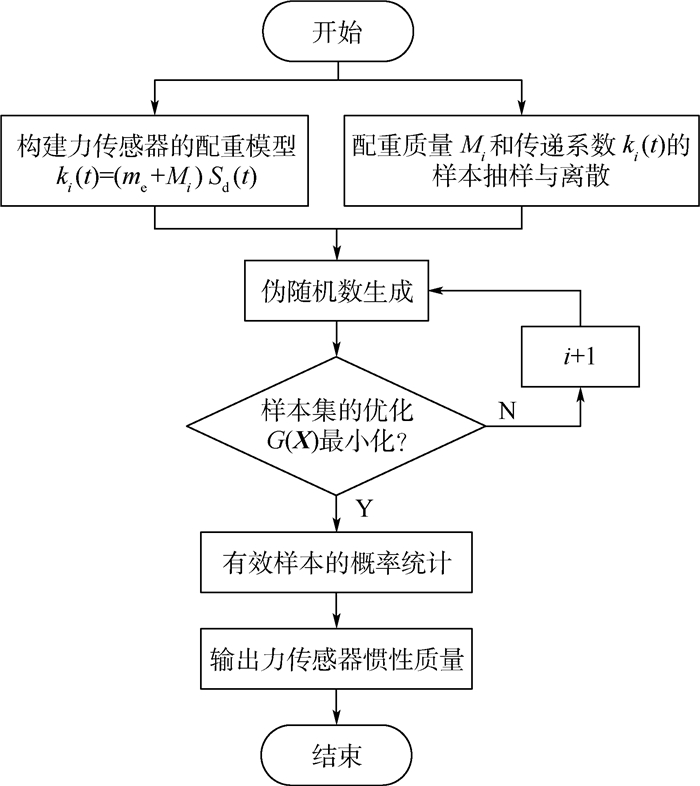 |
| 图 2 MMCC方法的流程图 Fig. 2 Flowchart of MMCC method |
| 图选项 |
分别设传感器的初始灵敏度为Sd(0)(t),初始惯性质量为me(0)。根据传感器的初始灵敏度,在随机变量{Mi, ki(t)}的N个样本中,分别对R1、R2和R3进行伪随机数生成,当模拟值经过区间(式(7))的条件成立时,有效样本N′加1,即N′(n+1)=N′(n)+1;否则,保持有效样本量不变。对变量经过N次伪随机生成之后,就可在配重区间(0, M)内形成一个梯形区域,如图 3所示。
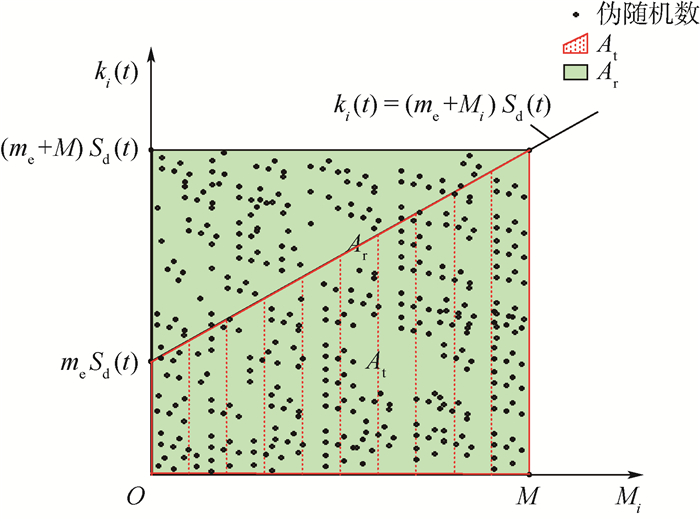 |
| 图 3 惯性质量的伪随机数模拟分布 Fig. 3 Simulated distribution of pseudo-random numbers for inertia mass |
| 图选项 |
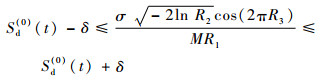 | (7) |
式中:δ为灵敏度的最大允许偏差。
由几何关系,落入梯形区域内的伪随机数的概率即为有效样本的概率
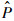
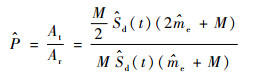 | (8) |
式中:
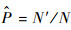
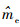
整理式(8)可得
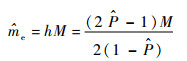 | (9) |
式中:质量系数
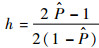
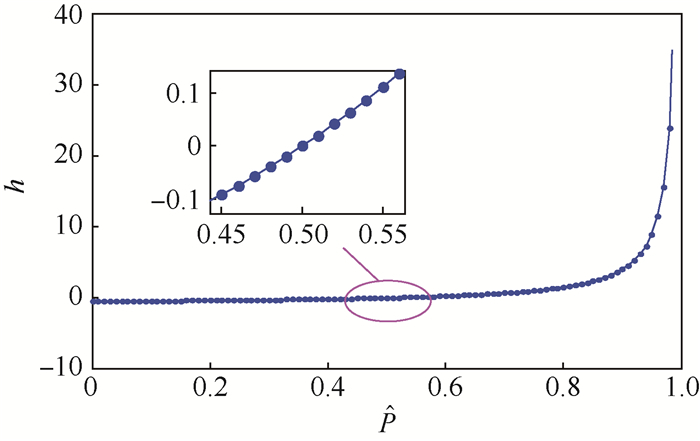 |
| 图 4 质量系数的增长趋势模拟 Fig. 4 Growth tendency simulation of mass coefficient |
| 图选项 |
当概率
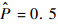
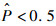
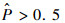
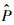
由式(9)可知,一旦知道配重范围(0, M)和N次模拟的概率
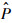
3 校准实验与数据分析 3.1 校准装置的设计 为了验证MMCC方法的准确性,研制了力传感器动态校准装置,通过测量不同配重时的力传感器输出,来实现其动态特性的校准。该装置主要由激振系统、测量系统和控制系统组成,如图 5所示。激振系统主要包括正弦激振台、隔振基座和测量支架;测量系统包括被校准力传感器、不同的配重和双频激光干涉仪;控制系统包括二维精密微动平台、数据采集单元和安装在PC机中的虚拟测控平台。
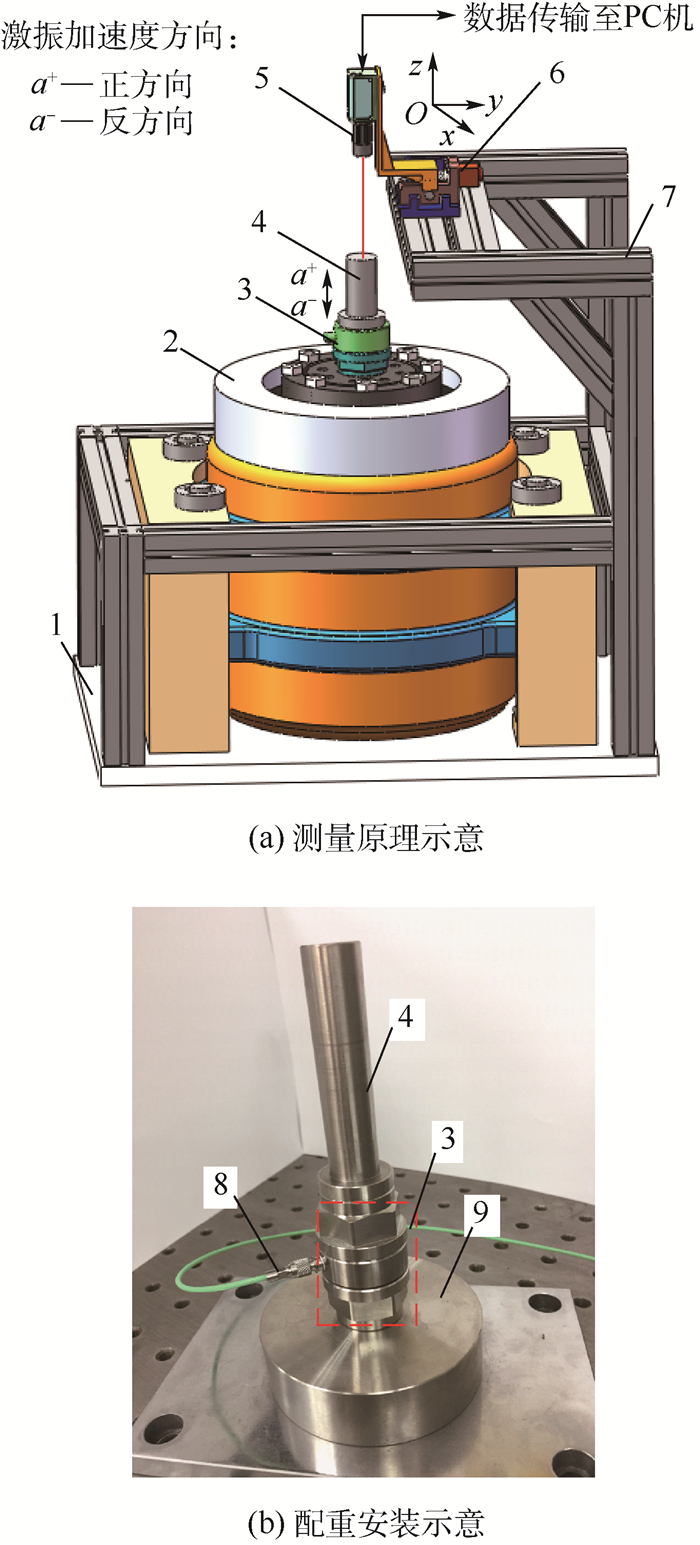 |
| 1—隔振基座;2—正弦激振台;3—被校准力传感器;4—配重;5—双频激光干涉仪;6—二维精密微动平台;7—测量支架;8—信号传输线;9—传感器基座。 图 5 力传感器动态校准装置 Fig. 5 Dynamic calibration device of a force transducer |
| 图选项 |
选用Kistler 9331B型力传感器作为被校准对象。测量过程主要包括3步。第1步,将被校准力传感器安装在正弦激振台上方的传感器基座上;通过二维精密微动平台调整双频激光干涉仪出射光线的方向,使激光轴近似对准被校准力传感器的中心。第2步,将不同质量的配重Mi安装在传感器的输出端;启动正弦激振台以频率f=450 Hz开始激振。第3步,利用双频激光干涉仪实时测量配重质量的激振加速度ai(t);同时,测控平台通过PCI-1711UL数据采集卡记录被校准力传感器的输出电压Ui(t),如表 1所示。
表 1 力传感器的激励与响应 Table 1 Excitations and responses of force transducer
| No. | 117.931 g配重 | 229.562 g配重 | 4 476.340 g配重 | 7 621.833 g配重 | |||||||
| ai(t)/(m·s-2) | Ui(t)/mV | ai(t)/(m·s-2) | Ui(t)/mV | ai(t)/(m·s-2) | Ui(t)/mV | ai(t)/(m·s-2) | Ui(t)/mV | ||||
| 1 | 151.92 | 623.69 | 158.78 | 650.83 | 165.65 | 679.46 | 178.68 | 732.70 | |||
| 2 | 152.61 | 623.46 | 159.47 | 654.34 | 166.33 | 682.31 | 179.37 | 736.02 | |||
| 3 | 153.29 | 629.81 | 160.16 | 656.49 | 167.02 | 685.99 | 180.05 | 739.03 | |||
| 4 | 153.98 | 633.01 | 160.84 | 659.73 | 167.70 | 688.37 | 180.74 | 739.89 | |||
| 5 | 154.67 | 634.48 | 161.53 | 662.12 | 168.39 | 691.56 | 181.43 | 745.46 | |||
| 6 | 155.35 | 636.03 | 162.21 | 665.26 | 169.08 | 694.24 | 182.11 | 747.95 | |||
| 7 | 156.04 | 636.83 | 162.90 | 668.72 | 169.76 | 696.18 | 182.79 | 750.59 | |||
| 8 | 156.73 | 642.98 | 163.59 | 669.61 | 170.45 | 699.95 | 183.48 | 753.29 | |||
| 9 | 157.41 | 645.64 | 164.27 | 670.38 | 171.13 | 702.01 | 184.17 | 755.78 | |||
| 10 | 158.09 | 648.50 | 164.96 | 673.33 | 165.65 | 679.46 | 184.86 | 758.45 | |||
表选项
3.2 数据分析与处理 将上述测量数据作为初值,解算力传感器的初始灵敏度;通过建立的力传感器MMCC方法,对[0, 7 621.833] g区间的实测配重进行N次模拟估计,得到不同配重质量的有效样本的概率,如图 6所示。能看出,在配重质量范围一定的情况下,概率估计值会随着抽样次数的增加而趋于稳定。说明随着样本空间的增大,估计值逐渐收敛。
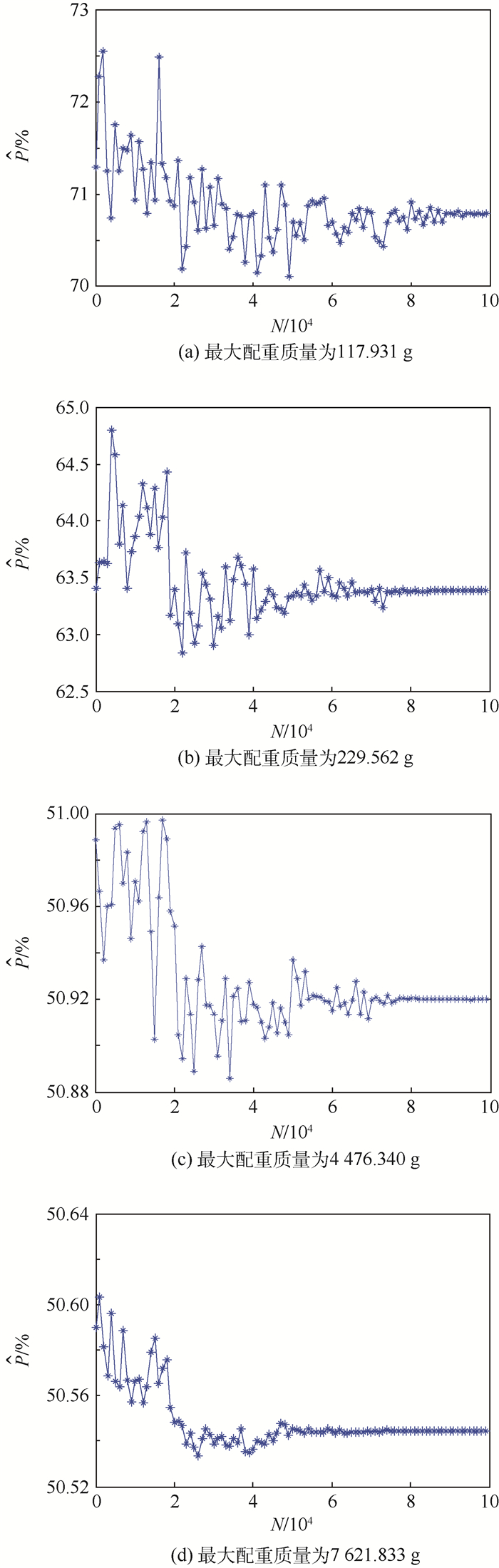 |
| 图 6 不同配重质量的有效样本概率 Fig. 6 Probability of valid samples for different additional mass |
| 图选项 |
另外,当抽样次数一定时,随着配重质量的模拟范围增大,概率估计值会逐渐降低并无限接近50%。说明较大的配重质量会抑制估计值的振荡幅值。在抽样次数较少时,较大的配重质量具有更快的收敛速度。当配重质量过大时,惯性质量将容易被模型误差淹没而无法实现估计。
根据概率估计值,利用式(9)可估计出力传感器的惯性质量,如图 7所示。可以看出,在不同的配重质量下,惯性质量的估计值不尽相同。但是,随着抽样次数的增加,惯性质量的估计值逐渐收敛。惯性质量的估计误差可用不同条件下估计值的估计误差Er(n)和Bessel标准差ε来表示,即
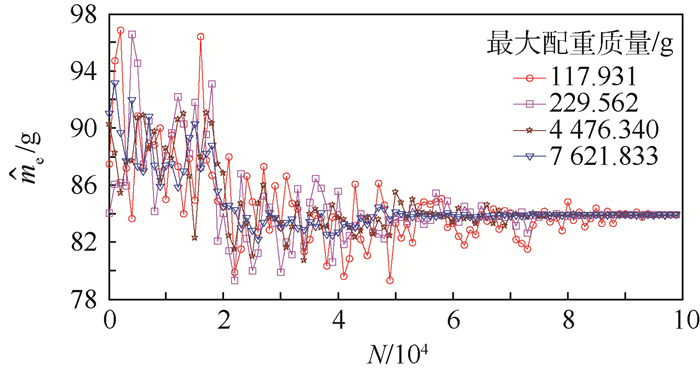 |
| 图 7 力传感器惯性质量的估计值 Fig. 7 Estimated inertia mass of a force transducer |
| 图选项 |
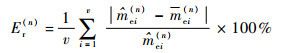 | (10) |
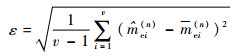 | (11) |
式中:v为配重次数,本实验取
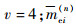
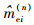
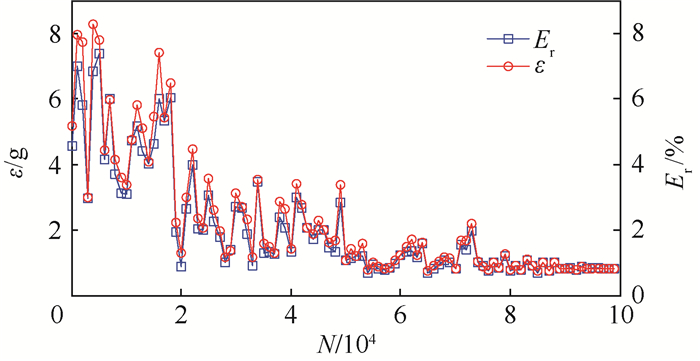 |
| 图 8 MMCC方法的估计误差和标准差 Fig. 8 Estimation error and standard deviation of MMCC method |
| 图选项 |
相应地,传统的二次配重法和多次配重法的计算结果如表 2所示。可以看出,二次配重法的估计误差为2.13%,标准差为2.24 g;多次配重法的估计误差降低到1.28%,标准差降低至1.34 g。但是,当抽样次数超过7.6×104次之后,MMCC方法的平均相对误差低于二次配重法和多次配重法。
表 2 传统配重法的估计误差 Table 2 Estimation error of traditional additional mass method
| 方法 | 估计值/g | 标准差/g | 估计误差/% |
| 二次配重法 | 85.70 | 2.24 | 2.13 |
| 多次配重法 | 84.98 | 1.34 | 1.28 |
表选项
将改进MMCC方法和传统方法的估计值均用于Kistler 9331B型力传感器的动态校准,其动态力校准的相对误差Err为
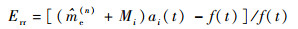 | (12) |
式中:
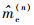
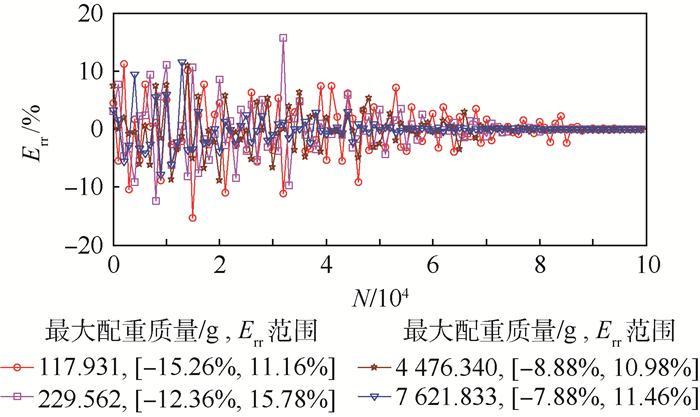 |
| 图 9 MMCC方法的动态力校准误差 Fig. 9 Dynamic force calibration error of MMCC method |
| 图选项 |
4 结论 1) 提出一种MMCC方法,用于力传感器动态特性的校准。该方法利用伪随机数生成技术,对力传感器模型中的配重质量、加速度和电压进行抽样模拟;根据区间判断准则求出有效样本,准确估计力传感器的惯性质量。
2) 利用MMCC方法,设计了一种力传感器动态校准的实验装置。结果表明,在相同的预设精度下,增大模拟配重质量能够降低算法的抽样空间,提高估计值的收敛速度。当抽样次数超过7.6×104次后,MMCC方法的误差低于二次配重法和多次配重法;经过N=105次抽样,Kistler 9331B型力传感器的惯性质量的估计值为83.91 g,估计误差为0.67%,标准差为0.74 g,估计值达到最优。
3) 将惯性质量估计值用于Kistler 9331B型力传感器的动态校准。结果表明动态力的校准误差随着样本量的增大而减小;配重质量的增大会提高校准误差的改善速度;当最大配重质量为7 621.833 g时,动态力的校准误差范围为[-7.88%, 11.46%]。然而,传统的二次配重法和多次配重法的动态力校准误差分别为27.53%和-21.83%。因此,本文方法的动态力校准误差更小。
参考文献
| [1] | VLAJIC N, CHIJIOKE A. Traceable dynamic calibration of force transducers by primary means[J].Metrologia, 2016, 53(4): S136–S148.DOI:10.1088/0026-1394/53/4/S136 |
| [2] | REZAYAT A, NASSIRI V, PAUW D, et al. Identification of dynamic forces using group-sparsity in frequency domain[J].Mechanical Systems and Signal Processing, 2016, 70(71): 756–768. |
| [3] | 姚建涛, 李立建, 许允斗, 等. 超静定六维力传感器静定测量模型及标定方法[J].仪器仪表学报, 2013, 34(9): 1927–1933. YAO J T, LI L J, XU Y D, et al. Statically determinate measurement model and calibration method of statically indeterminate six-axis force sensor[J].Chinese Journal of Scientific Instrument, 2013, 34(9): 1927–1933.(in Chinese) |
| [4] | SCHLEGEL C, KIECKENAP G, GL?CKNER B, et al. Traceable periodic force calibration[J].Metrologia, 2012, 49(3): 224–235.DOI:10.1088/0026-1394/49/3/224 |
| [5] | 高云凯, 冯海星, 方剑光, 等. 基于质量线法的驾驶室惯性参数识别试验研究[J].振动与冲击, 2013, 32(16): 193–197. GAO Y K, FENG H X, FANG J G, et al. Experimental study on identification of inertia parameters of truck cab based on mass line method[J].Journal of Vibration and Shock, 2013, 32(16): 193–197.DOI:10.3969/j.issn.1000-3835.2013.16.034(in Chinese) |
| [6] | KUMME R. Investigation of the comparison method for the dynamic calibration of force transducers[J].Measurement, 1998, 23(4): 239–245.DOI:10.1016/S0263-2241(98)00027-X |
| [7] | FUJⅡ Y. Proposal for a step response evaluation method for force transducers[J].Measurement Science and Technology, 2003, 14(10): 1741–1746.DOI:10.1088/0957-0233/14/10/301 |
| [8] | FUJⅡ Y. Toward dynamic force calibration[J].Measurement, 2009, 42(7): 1039–1044.DOI:10.1016/j.measurement.2009.03.006 |
| [9] | SHABANI R, TARIVERDILO S, SALARIEH H. Nonlinear identification of electro-magnetic force model[J].Journal of Zhejiang University:Science A, 2010, 11(3): 165–174.DOI:10.1631/jzus.A0900203 |
| [10] | QIAO B, ZHANG X, WANG C, et al. Sparse regularization for force identification using dictionaries[J].Journal of Sound and Vibration, 2016, 368(1): 71–86. |
| [11] | 汪凤泉, 许秀之. 动态力传感器校准的两次配重消去法[J].计量学报, 1990, 11(4): 304–310. WANG F Q, XU X Z. The elimination method by adding balance weight twice in calibration of dynamic force transducer[J].Acta Metrologica Sinica, 1990, 11(4): 304–310.(in Chinese) |
| [12] | 孙兴盛, 刘杰, 丁飞, 等. 基于矩阵摄动的随机结构动态载荷识别技术[J].机械工程学报, 2014, 50(13): 148–156. SUN X S, LIU J, DING F, et al. Identification method of dynamic loads for stochastic structures based on matrix perturbation theory[J].Journal of Mechanical Engineering, 2014, 50(13): 148–156.(in Chinese) |
| [13] | 杨子凯, 王建林, 于涛, 等. 基于预测误差法的加速度传感器动态模型参数辨识[J].仪器仪表学报, 2015, 36(6): 1244–1249. YANG Z K, WANG J L, YU T, et al. Dynamic model parameter identification of the acceleration sensor based on the prediction error method[J].Chinese Journal of Scientific Instrument, 2015, 36(6): 1244–1249.(in Chinese) |
| [14] | THOMAS B, SARA S, POSSOLO A. Force calibration using errors in variables regression and Monte Carlo uncertainty evaluation[J].Metrologia, 2016, 53(3): 965–971.DOI:10.1088/0026-1394/53/3/965 |
| [15] | 王中宇, 刘智敏, 夏新涛, 等. 测量误差与不确定度评定[M].北京: 科学出版社, 2008: 17-21. WANG Z Y, LIU Z M, XIA X T, et al. Measurement error and uncertainty evaluation[M].Beijing: Science Press, 2008: 17-21.(in Chinese) |
| [16] | JIANG W S, WANG Z Y, MOURELATOS Z P. Application of non-equidistant fractional order accumulation model on trajectory prediction of space manipulator[J].IEEE/ASME Transactions on Mechatronics, 2016, 21(3): 1420–1427.DOI:10.1109/TMECH.2016.2517183 |
