加速退化试验(ADT)由于不需观测到产品实际失效发生,只需要获取产品在高应力水平下的性能退化数据,通过向正常应力水平下的外推进行寿命评估,使得加速试验技术的应用和高可靠长寿命产品寿命评估得到了长足的发展和广泛应用。加速试验方案优化设计的研究可追溯到20世纪60年代。现有加速退化试验设计方法主要有基于解析的加速退化试验设计方法和基于仿真的加速退化试验设计方法。基于解析的加速退化试验设计方法发展较早,也更为成熟。Yu研究了在一定试验费用约束下,以产品p分位寿命的均方差最小为目标的加速退化试验方案优化设计问题[1]。在此基础上,Yu进一步考虑了产品的退化速率服从逆Weibull分布情况下的优化设计问题[2]。Weaver和Meeker采用大样本近似方法基于随机效应线性退化模型研究了单应力加速退化试验设计和评估问题[3]。Hu等研究了基于Wiener过程的步进加速退化试验方案设计,并证明了多水平步进加速退化试验在一定的准则和约束下会退化为一个恒定应力加速试验[4]。Wang等研究了退化模型为逆高斯过程的试验方案设计问题,得到了在费用约束下的最小p分位寿命渐进方差的优化设计方案,并验证该方法的稳健性[5]。Tsai和Ling等考虑了退化过程中的单调性,采用Gamma过程对产品的退化行为进行建模,同样以费用为约束,以平均故障前时间(MTTF)的最小渐进方差为目标进行优化设计,并进行了敏感性分析[6-7]。而Shi和Meeker则先后用非贝叶斯和贝叶斯方法研究了破坏性加速退化试验方案的优化设计问题[8-9]。
基于解析的加速退化试验设计方法虽然能够准确得到试验的最优设计方案,然而对于某些复杂的试验情形则难以得到解析解。随着计算机的计算能力不断提高,基于仿真的加速退化试验设计方法越来越被科学家和工程人员所接受和广泛运用。Li和Kececioglu以LED为对象,考虑应力水平设置因素,给出了基于仿真的加速退化试验设计方法[10]。Nasir和Pan利用仿真方法基于Hellinger距离和DIC准则考虑加速试验设计中的模型鉴别问题[11]。Wang等利用基于仿真的试验设计方法优化了多应力加载条件下的各应力水平的样本数,测量频率及试验终止时间[12]。上述加速退化试验设计方法的研究主要基于统计和优化方法,如果能够利用产品的故障行为模型(FBM),融合物理和其他试验信息,将能快速给出一种试验应力水平设计方法,并且根据文献调研目前还鲜有针对惯导产品的加速退化试验设计方法相关研究。
本文以典型惯导产品加速度计为例,在通过对产品特性和主机理分析基础上,确定表征产品寿命特征参数及试验应力。根据仿真计算、强化试验分析结果以及工程经验,确定各试验应力极限,从而确定试验应力的最高水平和最低水平。根据考虑分散性的故障行为模型,给定置信度下,高应力水平下的置信下限与低应力水平下的置信上限不交叉的原则,在最高应力水平和最低应力水平之间,确定中间应力水平,从而给出了基于故障行为模型的加速度计加速退化试验设计方法。
1 加速度计故障行为模型 石英挠性加速度计是一种机械摆式加速度计,由表头本体和伺服放大电路两部分组成,表头主要由软磁体、磁钢、摆片、力矩器线圈等构成,表头结构见图 1。
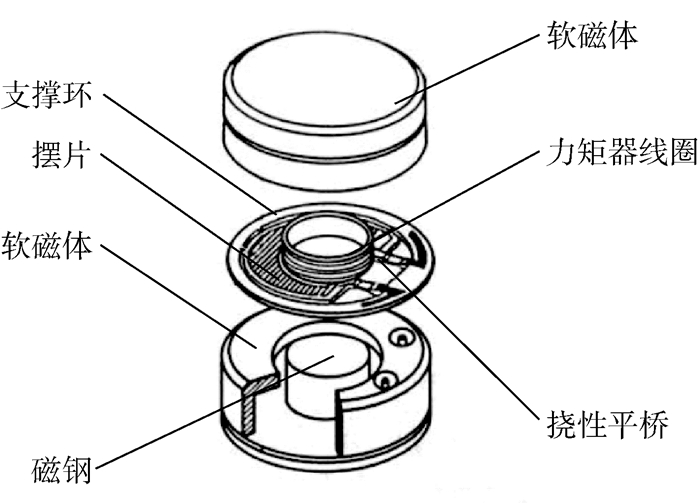 |
| 图 1 石英挠性加速度计表头结构 Fig. 1 Structure of quartz flexible accelerometer header |
| 图选项 |
故障行为即产品或单元在不同的环境条件和输入条件下,随时间表现出来的,可从外部探知的非正常状态。故障行为模型是描述多种机理作用下产品故障规律的模型,可以用状态变化模型或失效时间模型来表示[13]。
在贮存过程中,由于石英挠性加速度计内的石英摆片、环氧树脂胶等材料均耐潮,并且考虑实际贮存剖面为不通电的密封恒温环境(-5~40℃的室温条件),因此,仅考虑贮存过程中的温度因素对加速度计参数的影响,而不再考虑湿度、磁场和电应力等。标度因数是加速度计的重要参数。通过主机理分析可以得知标度因数变化主要由于温度作用下磁钢退磁[14]。加速度计标度因数主要呈现退化状态,由此描述标度因数随时间和应力变化规律的故障行为模型如下[15]:
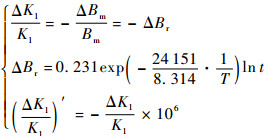 | (1) |
即
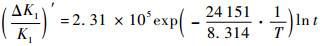 | (2) |
式中:ΔBm和Bm分别为最大磁感应强度变化量和最大磁感应强度;ΔBr为剩余磁感应强度变化量;K1为标度因数;ΔK1为t时刻标度因数与t=0时刻标度因数之差;t为时间,h;T为绝对温度,K。
考虑模型参数的分散性,根据式(2),建立标度因数加速退化的随机模型为
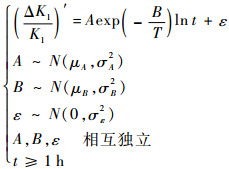 | (3) |
式中:μA=2.31×105;

2 基于故障行为模型的加速退化试验设计方法 基于故障行为模型的加速退化试验设计方法针对缺乏预试验数据的情况下粗略给出试验应力水平问题,利用故障行为模型可描述参数加速时变规律的特性,根据考虑分散性的故障行为模型,给定置信度下,以高应力水平下的置信下限与低应力水平下的置信上限不交叉为原则,设计给出试验剖面应力水平。
2.1 含置信度的故障行为模型包络 首先确定应力水平极限条件。根据加速度计强化试验分析结果以及工程经验,确定了温度极限,高温环境下加速度计加速退化机理不变的温度上限为90℃。
在确定工作极限条件后,根据考虑分散性的标度因数加速退化模型,即式(3),采用一阶泰勒展开可以近似得到t时刻
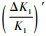
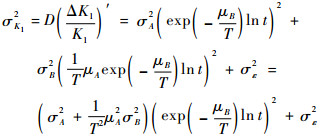 | (4) |
假设
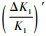
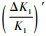
 | (5) |
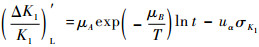 | (6) |

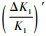
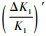
根据考虑分散性的故障行为模型式(5),图 2给出了25、60和90 ℃下10年内的标度因数退化置信曲线(γ=90%),可以看出3个应力水平下的置信曲线没有交叉。
 |
| 图 2 含置信度的标度因数退化曲线(γ=90%) Fig. 2 Degradation curves of scale factor with confidence coefficient (γ=90%) |
| 图选项 |
2.2 试验应力水平设计方法 本试验采用基于仿真的加速退化试验方法。在试验样本量、检测时间间隔以及最高应力水平给定的情况下,主要对低应力和中间应力2个水平进行优化。优化时考虑的约束为根据考虑分散性的故障行为模型,给定置信度下,高应力水平下退化量的置信下限与低应力水平下退化量的置信上限不交叉的原则,在最高应力水平和最低应力水平之间,确定中间应力水平。其具体过程如图 3所示。
 |
| 图 3 T2可选范围确认流程示意图 Fig. 3 Schematic diagram of optional range validation procedure for T2 |
| 图选项 |
步骤1??根据式(3)生成进行N次仿真,按退化量由小到大对N次仿真进行排序,得到
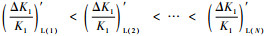
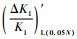
步骤2??由图 2可知,其置信下限曲线为一条光滑曲线,将其近似看成某一温度下的退化轨迹,由式(3)反推得到近似等效温度T′1。
步骤3??令T2=T′1-1,在T2温度下进行N次仿真,得到退化量在90%置信度下的双侧置信上限。
步骤4??若在任一时刻T′1的置信下限均大于T2的置信上限,则T2此时的值为T2可选温度范围的上限值;若不成立,则令T2=T2-1,重复步骤4,直至满足条件跳出循环为止。
同理可以获得T2可选温度的下限值和T3可选温度的上限值。为了保证一定的加速效果,T3可选温度的下限值已经确定为30℃。
2.3 确定试验最优方案 确定T2和T3的可选温度范围并进一步确定备选方案后,需要对备选方案进行优选,其流程如图 4所示,Ti为第i应力水平的温度。
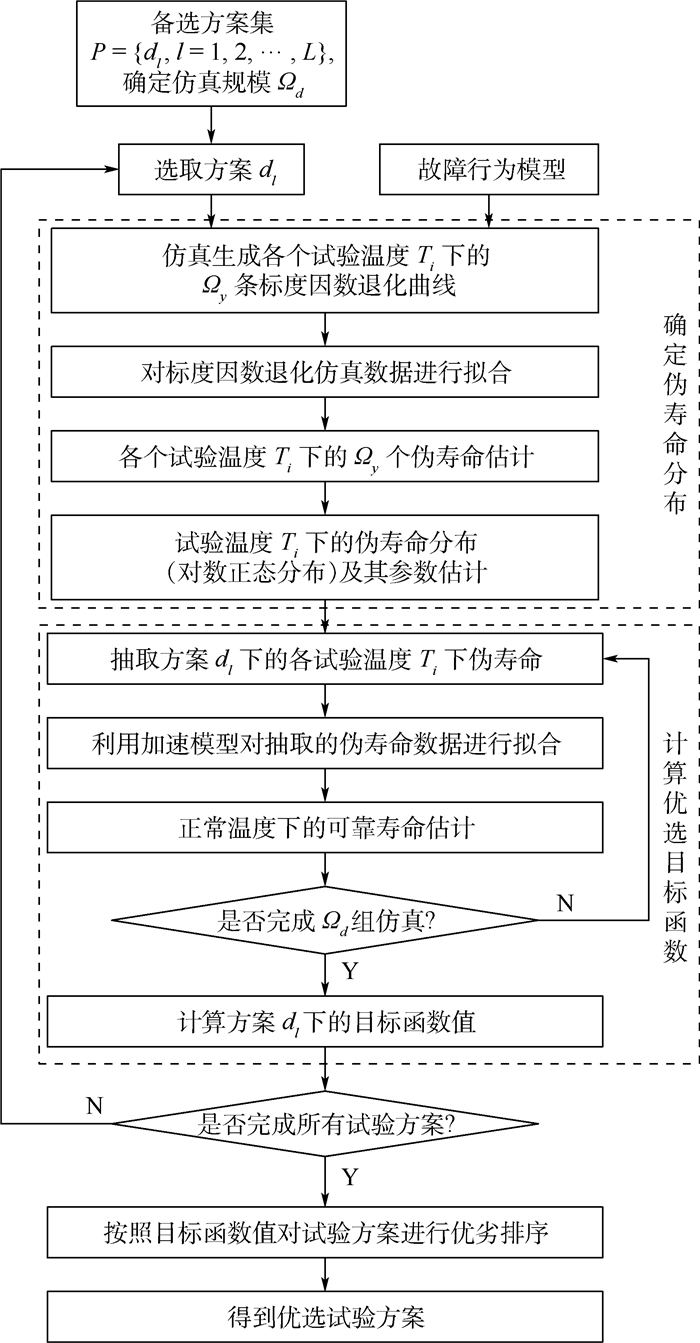 |
| 图 4 加速度计标度因数加速退化试验方案优选流程 Fig. 4 Optimization procedure of accelerometer scale factor accelerated degradation test scheme |
| 图选项 |
步骤1??在进行优化设计前,首先确定备选方案集、优化目标函数、故障行为模型(即加速退化模型)和仿真规模Ωd。
步骤2??根据故障行为模型和备选方案dl,仿真得到该方案中的各加速应力下Ωd条标度因数的退化曲线。
步骤3??利用加速度计标度因数的加速退化模型对仿真得到的退化曲线进行拟合,得到备选方案dl下各加速应力下的伪寿命分布及其参数估计。
步骤4??从步骤3中的各加速应力下的伪寿命分布中分别抽取一组伪寿命,构成备选方案dl下一组加速应力下伪寿命仿真数据。
步骤5??利用加速模型对步骤4中的伪寿命仿真数据进行拟合,并外推得到正常温度下可靠寿命估计。
步骤6??重复步骤4和步骤5直至完成Ωd次仿真。
步骤7??对备选方案dl下的Ωd个正常温度下的寿命估计值计算目标函数值。
步骤8??重复步骤2至步骤7直至完成所有仿真计算。
步骤9??对所有备选方案的目标函数值进行排序,确定其中的最优试验方案。
3 案例分析 根据图 3所阐述的方法和流程进行仿真,得到T2可选温度的上限值为75.85℃、下限值为43.85℃,T3可选温度的上限值为61.85℃。其中,T2为可选温度的上限值和T3为可选温度的上限值时,其退化轨迹如图 5所示。
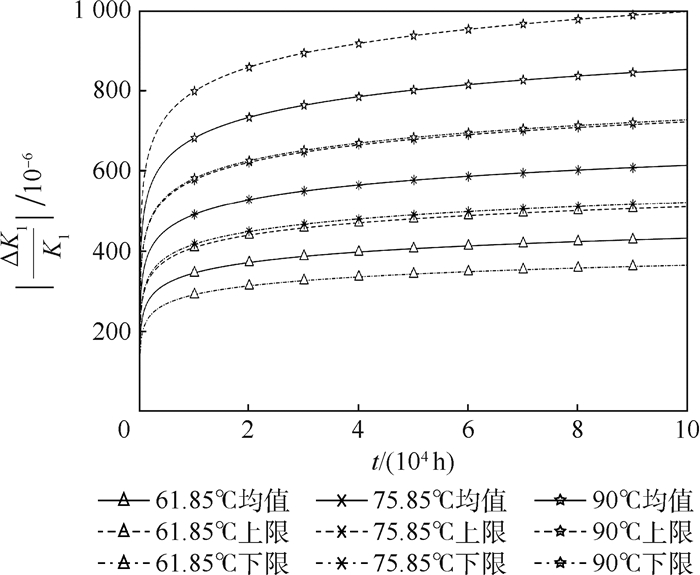 |
| 图 5 T2, T3温度可选范围上限时的标度因数退化曲线 Fig. 5 Degradation curves of scale factor under optional range upper limit of temperature T2, T3 |
| 图选项 |
根据上述仿真结果得到的温度选择范围,结合工程实践中所需考虑的温度梯度问题,确定备选方案的应力设置如表 1所示, 1个T2和T3构成一组备选方案。
表 1 备选方案T2, T3温度设置 Table 1 Optional plan of temperature setting of T2, T3
| ℃ | |
| T2 | T3 |
| 75 | 60, 55, 50, 45, 40, 35, 30 |
| 70 | 55, 50, 45, 40, 35, 30 |
| 65 | 50, 45, 40, 35, 30 |
| 60 | 45, 40, 35, 30 |
| 55 | 40, 35, 30 |
| 50 | 35, 30 |
| 45 | 30 |
表选项
以备选方案1“T2=75℃, T3=60℃”为例,分别生成3个应力水平下的20 000条退化轨迹,通过非线性拟合得到每条退化轨迹的参数估计值,再分别外推得到每个样本的伪寿命值。在得到的试验温度Ti下的Ωy个伪寿命估计的基础上,进行伪寿命分布的估计,确定伪寿命的分布类型和分布参数。根据图 6显示的概率分布可以看出,对数正态分布可以有效拟合伪寿命数据。
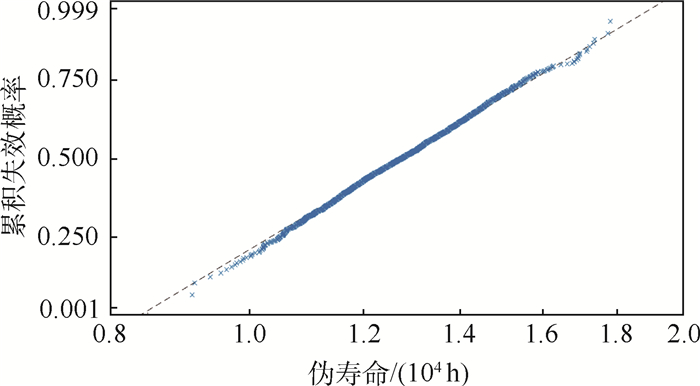 |
| 图 6 90℃伪寿命对数正态分布概率图 Fig. 6 Probability graph of lognormal distribution of pseudo life at 90℃ |
| 图选项 |
鉴于伪寿命可用对数正态分布近似描述,那么正常贮存温度下的对数寿命服从正态分布,此时的寿命点估计值同时是样本的中位数,能有效反应群体的平均寿命情况。因此选择正常贮存温度下寿命的对数方差作为优化目标函数比较合适。根据式(3),伪寿命加速模型为
 | (7) |
式中:

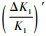
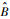

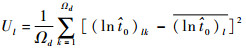 |
式中:

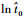
优化结果如图 7所示,从图 7中可以看出当T2=75℃, T3=55℃(图中黑点处)时,目标函数达到最小值0.064 2。
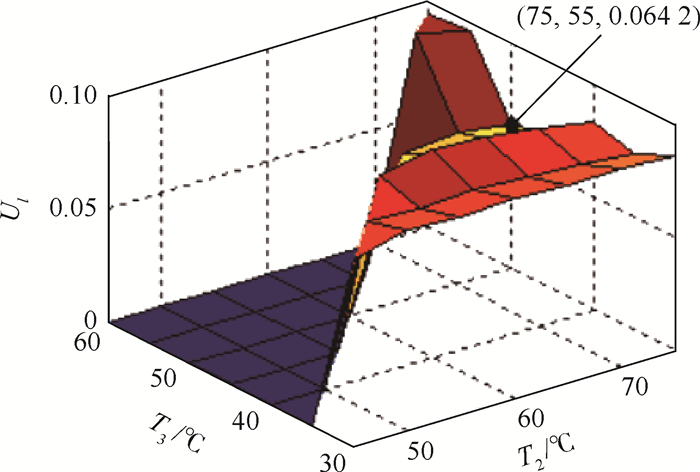 |
| 图 7 备选方案优化目标函数值 Fig. 7 Optimization objective function value of optional plan |
| 图选项 |
4 结论 1) 本文提出了一种基于故障行为模型的加速退化试验设计方法。以高应力水平下的置信下限与低应力水平下的置信上限不交叉为原则,采用基于仿真的加速退化试验方法,优化确定了试验方案,从而解决了缺乏预试验数据情况下试验设计问题。
2) 以典型惯导产品加速度计为对象,进行了方法可行性和有效性验证。通过主机理分析得到加速度计主要参数标度因数变化的主退化机理为温度作用下的磁钢退磁,并得到描述标度因数应力作用下时变规律的故障行为模型。在加速度计最高温度应力水平为90℃条件下,基于该模型设计加速度计加速退化试验的优选应力为T2=75℃, T3=55℃。该设计方法为提高基于加速退化试验的产品可靠寿命评估精度提供了前提保障。
参考文献
| [1] | YU H. Designing an accelerated degradation experiment by optimizing the estimation of the percentile[J].Quality and Reliability Engineering International, 2003, 19(3): 197–214.DOI:10.1002/(ISSN)1099-1638 |
| [2] | YU H. Designing an accelerated degradation experiment with a reciprocal Weibull degradation rate[J].Journal of Statistical Planning and Inference, 2006, 136(1): 282–297.DOI:10.1016/j.jspi.2004.06.030 |
| [3] | WEAVER B P, MEEKER W Q. Methods for planning repeated measures accelerated degradation tests[J].Applied Stochastic Models in Business and Industry, 2014, 30(6): 658–671.DOI:10.1002/asmb.2061 |
| [4] | HU C, LEE M, TANG J. Optimum step-stress accelerated degradation test for Wiener degradation process under constraints[J].European Journal of Operational Research, 2015, 241(2): 412–421.DOI:10.1016/j.ejor.2014.09.003 |
| [5] | WANG H, WANG G, DUAN F. Planning of step-stress accelerated degradation test based on the inverse Gaussian process[J].Reliability Engineering & System Safety, 2016, 154: 97–105. |
| [6] | TSAI T, SUNG W, LIO Y L, et al. Optimal two-variable accelerated degradation test plan for Gamma degradation processes[J].IEEE Transactions on Reliability, 2016, 65(1): 459–468.DOI:10.1109/TR.2015.2435774 |
| [7] | LING M H, TSUI K L, BALAKRISHNAN N. Accelerated degradation analysis for the quality of a system based on the Gamma process[J].IEEE Transactions on Reliability, 2015, 64(1): 463–472.DOI:10.1109/TR.2014.2337071 |
| [8] | SHI Y, MEEKER W Q. Bayesian methods for accelerated destructive degradation test planning[J].IEEE Transactions on Reliability, 2012, 61(1): 245–253.DOI:10.1109/TR.2011.2170115 |
| [9] | SHI Y, MEEKER W Q. Accelerated destructive degradation test planning[J].Technometrics, 2009, 51(1): 1–13.DOI:10.1198/TECH.2009.0001 |
| [10] | LI Q, KECECIOGLU D B. Design of an optimal plan for an accelerated degradation test:A case study[J].International Journal of Quality & Reliability Management, 2013, 23(4): 426–440. |
| [11] | NASIR E A, PAN R. Simulation-based Bayesian optimal ALT designs for model discrimination[J].Reliability Engineering & System Safety, 2015, 134(2): 1–9. |
| [12] | WANG Y, ZHANG C, ZHANG S, et al. Optimal design of constant stress accelerated degradation test plan with multiple stresses and multiple degradation measures[J].Journal of Risk and Reliability, 2015, 229(1): 83–93. |
| [13] | ZENG Z G, KANG R, WEN M, et al. Measuring reliability during product development considering aleatory and epistemic uncertainty[C]//Proceedings of the Annual Reliability and Maintainability Symposium. Piscataway, NJ: IEEE Press, 2015: 1-6. |
| [14] | XU D, CHEN Y X, KANG R. Quartz flexible accelerometer stability duration prediction on storage condition based on accelerated degradation test[J].Chemical Engineering Transactions, 2013, 33(1): 541–546. |
| [15] | 许丹, 廖寻, 陈云霞, 等. 加速度计贮存稳定期分析[J].北京航空航天大学学报, 2013, 39(2): 173–177. XU D, LIAO X, CHEN Y X, et al. Analysis of the storage stability of accelerometers[J].Journal of Beijing University of Aeronautics and Astronautics, 2013, 39(2): 173–177.(in Chinese) |
