浮空器高空飞行时,囊体内部氦气温度不断变化,白天太阳辐射囊体导致其内部温度增高,夜间囊体内部温度降低,对于长航时浮空器来说,昼夜温差导致囊体产生内外压差,且昼夜温差越大囊体内外压差越大,昼夜温差越小内外压差越小。因此,减小囊体昼夜温差至关重要。
文献[5]对比了囊体吸收率、发射率和吸收发射比等辐射参数对浮空器热性能的影响;文献[6]列出了飞艇热特性模型建立的难点问题,并提出了建模的一些建议;文献[7]分析了囊体蒙皮热特性和云层对浮空器热特性的影响;文献[8]建立了飞艇的传热数学模型,仿真分析了蒙皮的温度以及艇内气体的温度;文献[9]建立了浮空器的热动力模型,分析了浮空器在上升和下降过程中的热特性;文献[10]建立了浮空器热力学模型,并且通过地面试验验证了热力学模型的正确性;文献[11]通过地面试验分析了浮空器在不同太阳光辐射和空气对流情况下的热特性,证明了太阳辐射对浮空器热特性起到了关键性的作用;文献[12]建立了浮空器热力学模型,得出囊体内部不同部位的温度相差20 K;文献[13]运用传热学基本原理分析了浮空器热状况的形成机制与影响因素;文献[14]对浮空器上升过程中超冷和下降过程中的超热问题进行了研究;文献[15]采用了25 m和35 m长度的飞艇进行了热力学测试,并成功预测了飞艇的上升过程和飞行轨迹。
Kriging优化方法已经应用于各领域[16-17]。文献[18-19]将Kriging优化方法应用于气动优化设计;文献[20]将Kriging优化方法应用于结构优化设计,得到了金属加筋板的优化布局;文献[21]将Kriging优化方法应用于机械零件的形状优化,结合有限元分析,得到最优的零件形状。
本文将囊体分为48个部分,每个部分采用不同吸收率和发射率的涂层材料。建立浮空器囊体热力学模型,采用拉丁超立方体方法选取样本点,对样本点进行热力学分析得到响应值,采用Kriging模型进行模拟,并求出囊体最优的材料分布。
1 Kriging模型 Kriging模型利用样本点的响应可以得出最优解。若已知样本点X=[x1 x2 … xm]T,xi为n维行向量,其维数为设计变量的个数,对应的响应为Y=[y1 y2 … ym]T为q维行向量。第i维响应yi可以表示为
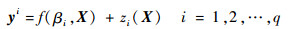 | (1) |
式中:f(βi, X)为回归模型, βi为回归系数;zi(X)为随机过程。
Kriging模型要求预测模型的方差最小,可以得出待测点的响应估计值为
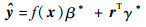 | (2) |
式中:β*、γ*为权重系数,样本点一定时,β*、γ*为固定值。计算出f(x)和r(x),即可求出待测点的响应值。
2 浮空器囊体热力学模型 2.1 大气模型 根据国际标准大气模型,不同高度H下的大气参数计算公式为
 |
式中:T为大气温度,K;P为大气压强,Pa;ρ为大气密度,kg/m3。
浮空器飞行在20 km高空,大气环境温度为216.5 K,大气压力为5 475 Pa,大气密度为0.089 kg/m3。
2.2 太阳辐射模型 太阳方位通过太阳高度角α、方位角θ表示,如图 1所示。太阳光线的方向计算公式为
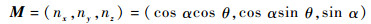 | (3) |
 |
| 图 1 太阳高度角与方位角 Fig. 1 Solar altitude angle and azimuth angle |
| 图选项 |
太阳高度角α计算公式为
 | (4) |
式中:φ为当地纬度;δ为太阳赤纬角;ω为时角,上午为负,中午为0,下午为正。
太阳赤纬角和时角计算公式为
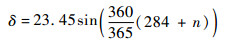 | (5) |
 | (6) |
式中:n为当天在一年中的顺序数,如元旦为n=1;ts为真太阳时。
太阳方位角θ的计算公式为
 | (7) |
太阳对地面的辐射强度QD计算公式为
 | (8) |
式中:S为大气上方的太阳辐射,根据世界气象组织测量数据,S=1 367 W/m2;B为大气消光系数。
大气散射辐射强度QAtm计算公式为
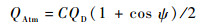 | (9) |
式中:C为常数;ψ为散射面与水平面之间的夹角。
地面反射辐射强度QRef计算公式为
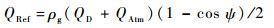 | (10) |
式中:ρg为地面的平均反射率,地面的反射率与地区纬度、地面情况等因素有关。北京地区草地地面反射率测量数据为0.174~0.219,混凝土地面反射率可达0.33~0.37,因此本文中计算时选取地面反射率ρg=0.2。
2.3 云遮系数 浮空器飞行过程中,空中云的数量直接影响飞艇表面受到的太阳辐射、大气散射和地面反射辐射。云遮系数CF定义为天空被云层全部遮挡的比例。云遮系数可以通过天空云量计算,本文中分析时假设云遮系数CF=0.9。
云遮系数对太阳辐射与地面反射辐射的影响如表 1所示。
表 1 云遮系数对太阳辐射的影响 Table 1 Influence of cloud cover coefficient on solar radiation
| 条件 | 太阳直接辐射强度 | 地面反射辐射强度 |
| H>Hc | QD, real =QD | QRef=[C2ρg+(1-CF)ρc]·(QD+ QAtm) |
| H<Hc | QD, real =CQD | QRef=Cρg(QD+ QAtm) |
| 注:Hc—云层高度;ρc—云层反射率。 | ||
表选项
浮空器飞行高度为20 km,云层在对流层高空,高度小于20 km,因此本文分析时取H>Hc。云层中水滴和冰晶的散射,使云层表面形成了比较强的反射面,不同类型的云层反射率均不同,云层的平均反射率为60%[22],本文选取ρc=0.6。
2.4 浮空器蒙皮辐射
2.4.1 浮空器蒙皮外表面辐射 浮空器蒙皮外表面辐射包括蒙皮外表面与地面和大气之间的长波辐射。
浮空器蒙皮外表面与地面的长波辐射强度计算公式为
 | (11) |
式中:ε为蒙皮发射率;Ta为蒙皮温度;Tg为地球表面温度,地球表面平均温度为288 K[22];σ为斯蒂芬-玻尔兹曼常数,σ=5.67×10-8 W/(m2·K4);?a为接受辐射的表面对地面的角系数; τa为红外透射率。
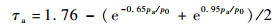 | (12) |
其中:pa为浮空器周围大气压力;p0为地球表面的大气压力。
浮空器蒙皮外表面与大气的长波辐射强度计算公式为
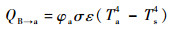 | (13) |
式中:φa为接受辐射的表面对天空的角系数;Ts为天空的有效温度,计算公式为
 | (14) |
其中:TAtm为大气的温度。
2.4.2 浮空器蒙皮内表面辐射 假设浮空器由N个灰表面组成的封闭腔体,内表面是漫射的。若每个表面的温度Ti已知,任意表面的辐射换热计算公式为
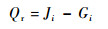 | (15) |
式中:
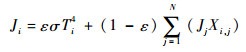 | (16) |
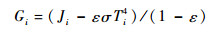 | (17) |
其中:Ji为离开表面i的辐射,包括自身热辐射和反射;Gi为投入到表面i的辐射;Xi, j为表面j对表面i的角系数。
2.5 浮空器蒙皮对流换热
2.5.1 浮空器蒙皮外表面强迫对流换热 浮空器蒙皮外表面对流换热计算公式为
 | (18) |
式中:Tf, i为蒙皮第i个单元的温度;Af, i为蒙皮第i个单元的面积;hC为对流换热系数,其计算公式为
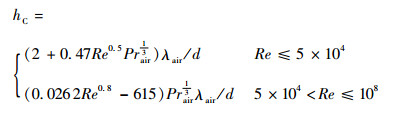 | (19) |
其中:λair为空气的热传导系数;Prair为空气的普朗特数;d为浮空器的直径;Re为空气的雷诺数。
2.5.2 浮空器蒙皮内表面自然对流换热 浮空器内表面与囊体内氦气产生自然对流换热,对流换热计算公式为
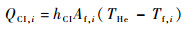 | (20) |
式中:THe为氦气的温度; hCI为内表面对流换热系数, 其计算公式为
 | (21) |
其中:λHe为氦气的热传导系数;PrHe为氦气的普朗特数。
2.5.3 氦气温度计算 内部氦气的平均温度计算公式为[23]
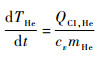 | (22) |
式中:cv为氦气的定容比热容;mHe为氦气的质量;QCI, He为氦气与蒙皮交换热量,其计算公式为
 | (23) |
将式(23)代入式(22),可得氦气温度与蒙皮温度的关系表达式为
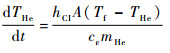 | (24) |
式中:Tf为蒙皮的平均温度;A为蒙皮的面积。
2.6 浮空器蒙皮热平衡模型 将浮空器囊体划分为N个微元,第i个囊体微元的热平衡方程为
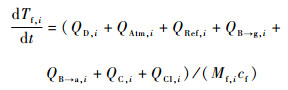 | (25) |
式中:Mf, i为第i个蒙皮微元的质量;cf为材料的比热容;QD, i为太阳直接辐射;QAtm, i为大气散射辐射;QRef, i为地面反射辐射;QB→g, i为蒙皮外表面与地面之间的长波辐射;QB→a, i为蒙皮外表面与大气之间的长波辐射。
3 优化方法 3.1 试验设计方法 囊体热力学优化设计变量为囊体蒙皮涂层材料的吸收率和发射率。优化目标为囊体内氦气昼夜温差最小。
优化(优化流程如图 2所示)分为2个部分:第1部分是囊体热力学计算,第2部分是Kriging模型优化。囊体热力学计算在CFD/FLUENT软件中完成,计算出蒙皮的温度分布和囊体内部气体的平均温度。Kriging模型优化在ISIGHT软件中完成,ISIGHT软件通过样本点的响应值建立Kriging模型,得出最优解。
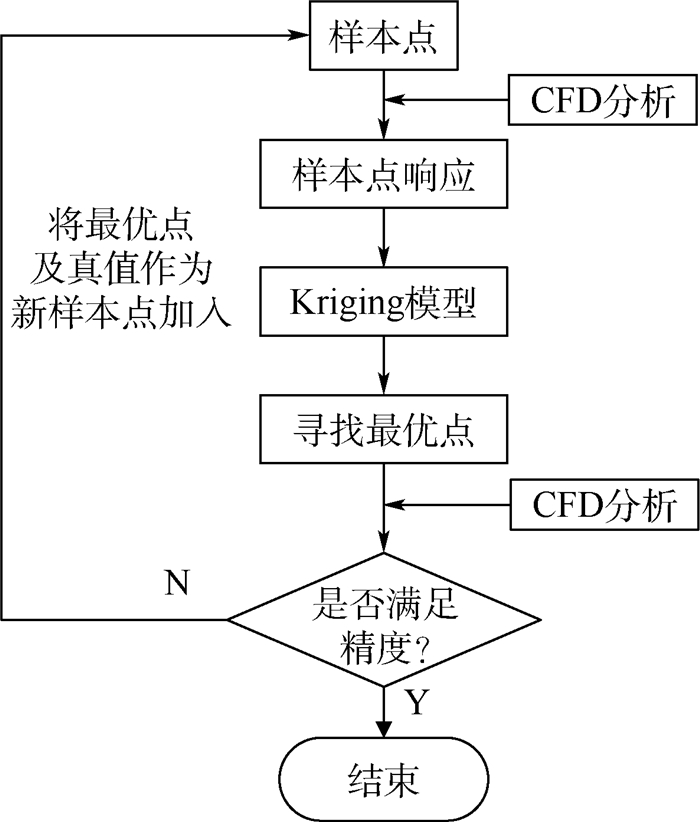 |
| 图 2 优化流程示意图 Fig. 2 Schematic of optimization process |
| 图选项 |
3.2 优化流程 囊体内部氦气温度与蒙皮温度计算如式(24)所示。可以看出,氦气温度最终与蒙皮温度相等。为了提高计算效率,本文以蒙皮昼夜温差最小为目标,优化完成后,计算氦气昼夜温差。
假设TD表示N个蒙皮微元白天的平均温度,TN表示N个蒙皮微元晚上的平均温度。白天TD的计算公式为
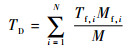 | (26) |
假设?T=TD-TN,优化目标?T为最小,即
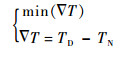 | (27) |
4 算例分析 4.1 算例描述 算例为正球形囊体,具体尺寸和飞行参数如表 2所示,浮升气体为氦气。
表 2 浮空器参数 Table 2 Parameters of aerostat
| 参数 | 数值 |
| 直径/m | 30 |
| 面积/m2 | 2 826 |
| 体积/m3 | 14 130 |
| 飞行高度/km | 20 |
| 飞行时间 | 6月21日(夏至日) |
| 飞行纬度/(°N) | 40 |
表选项
常用蒙皮材料吸收率η、发射率ε的参数值如表 3所示。
表 3 常用材料的热辐射特性参数 Table 3 Thermal radiation characteristic parameters of common materials
| 材料 | η | ε |
| 白色PVF | 0.25~0.40 | 0.75~0.90 |
| 白色PU | 0.35 | 0.8~0.9 |
| 镀银Teflon | 0.10~0.25 | 0.5~0.8 |
表选项
根据浮空器热平衡模型,分析不同吸收率、发射率特性蒙皮材料对氦气平衡温度的影响。分析对象特征如下:取蒙皮材料发射率ε=η+0.5(0.1≤η≤0.4)。
将囊体划分为48个部分,如图 3所示。
 |
| 图 3 囊体划分图 Fig. 3 Envelop division map |
| 图选项 |
4.2 算例仿真 首先检验CFD/FLUENT囊体热特性分析的有效性,根据文献[5],蒙皮材料吸收率为0.1,发射率为0.6时囊体的昼夜温差最小,囊体的温度分布如图 4所示。
 |
| 图 4 囊体温度分布 Fig. 4 Temperature distribution of envelop |
| 图选项 |
分析可得囊体内部氦气昼夜温差为31 K,与文献[5]相近。证明热力学模型的准确性。
采用拉丁超立方体方法选取样本点500个,取样本点1,其48个面的参数如表 4所示,其囊体温度分布如图 5所示,昼夜温差为54 K。
表 4 样本点1的吸收率 Table 4 Absorption rate of sample point 1
| 编号 | 吸收率 |
| 1 | 0.34 |
| 2 | 0.23 |
| 3 | 0.12 |
| 4 | 0.36 |
| 5 | 0.23 |
| 6 | 0.13 |
| 7 | 0.43 |
| 8 | 0.32 |
| 9 | 0.24 |
| 10 | 0.14 |
| 11 | 0.10 |
| 12 | 0.49 |
| 13 | 0.35 |
| 14 | 0.18 |
| 15 | 0.25 |
| 16 | 0.26 |
| 17 | 0.18 |
| 18 | 0.47 |
| 19 | 0.42 |
| 20 | 0.48 |
| 21 | 0.17 |
| 22 | 0.37 |
| 23 | 0.29 |
| 24 | 0.45 |
| 25 | 0.39 |
| 26 | 0.33 |
| 27 | 0.25 |
| 28 | 0.28 |
| 29 | 0.46 |
| 30 | 0.19 |
| 31 | 0.38 |
| 32 | 0.28 |
| 33 | 0.41 |
| 34 | 0.42 |
| 35 | 0.12 |
| 36 | 0.16 |
| 37 | 0.28 |
| 38 | 0.11 |
| 39 | 0.31 |
| 40 | 0.28 |
| 41 | 0.18 |
| 42 | 0.37 |
| 43 | 0.27 |
| 44 | 0.12 |
| 45 | 0.41 |
| 46 | 0.23 |
| 47 | 0.26 |
| 48 | 0.18 |
表选项
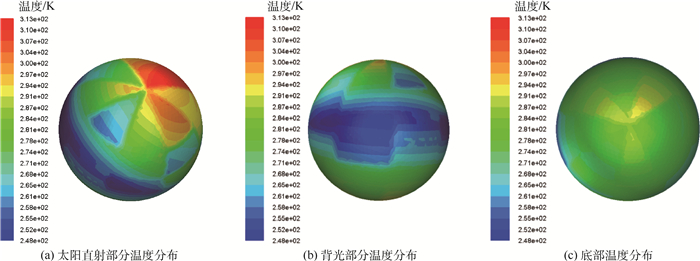 |
| 图 5 样本点1温度分布 Fig. 5 Temperature distribution of sample point 1 |
| 图选项 |
经过优化后,囊体白天蒙皮温度分布如图 6所示,夜间囊体温度与样本点1相差不大,昼夜温差为28.6 K。优化前,囊体内部氦气的昼夜温差为31 K, 因此经过优化,囊体内部氦气昼夜温差减少7.7%。
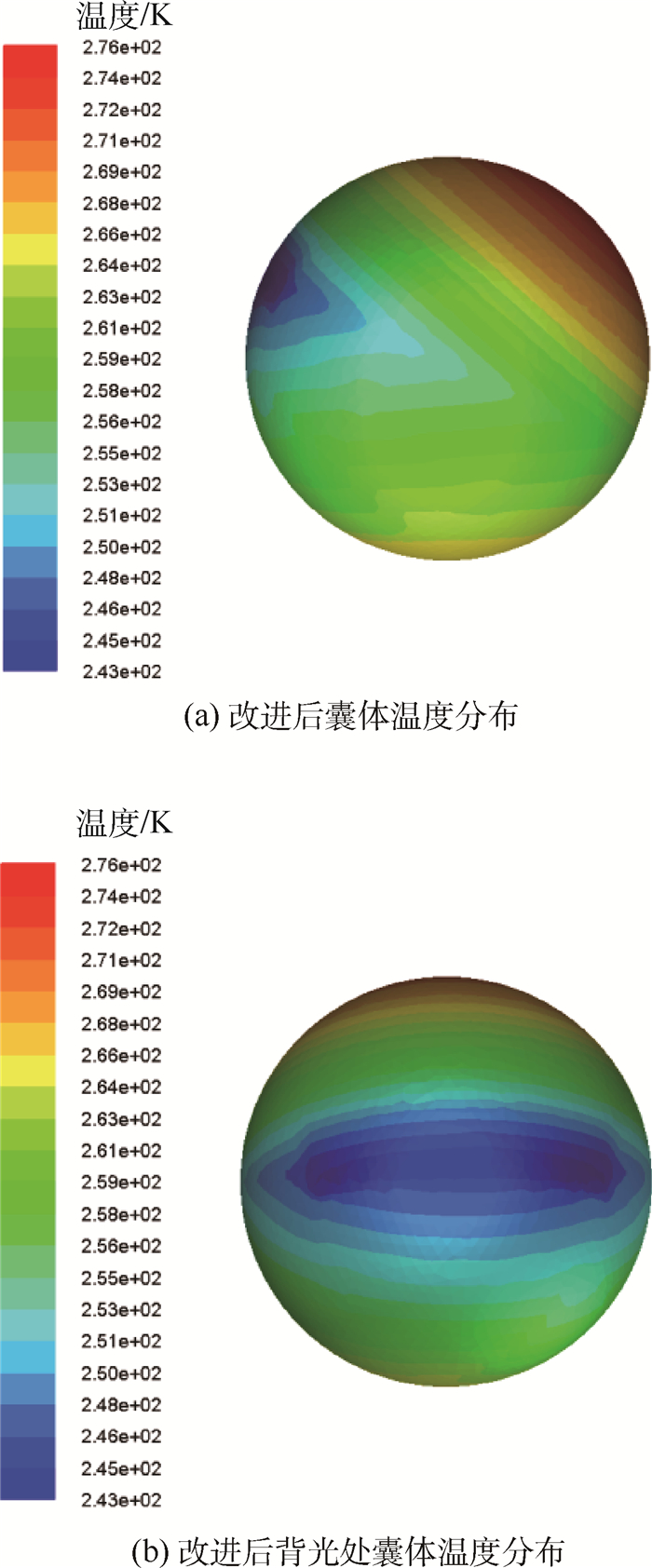 |
| 图 6 改进后囊体白天温度分布 Fig. 6 Temperature distribution of envelop during day after improvement |
| 图选项 |
5 结论 1) 优化后氦气昼夜温差减小至28.6 K,比采用同一种蒙皮材料加工的囊体昼夜温差减少7.7%。
2) 优化结果为囊体背光部位采用发射率为0.9的材料, 其他部位采用吸收率为0.1的材料。
囊体迎光面和背光面采用不同热特性材料时可降低氦气昼夜温差。囊体背光面与浮空器飞行地点的纬度、太阳赤纬角、时角和囊体姿态有关,在进行囊体实际设计中,可以根据浮空器飞行地点和飞行时间判断背光面的位置。浮空器飞行时可以调节囊体姿态,使得囊体背光面始终背对太阳光。因此,本文提出的优化与设计方法对工程应用有一定的指导意义。
参考文献
| [1] | NISHIMURA J. Scientific ballooning in Japan-An view of recent activites[J].Advances in Space Research, 2006, 37(11): 2005–2014.DOI:10.1016/j.asr.2005.03.053 |
| [2] | COLOZZA A, DOLCE J L. High-altitude, long-endurance airships for coastal surveillance: NASA/TM-2005-213427[R]. Washington, D. C. : NASA Glenn Research Center, 2005. |
| [3] | ANDROULAKAKIS S P, JUDY R A. Status and plans of high altitude airships program[C]//Aerodynamic Decelerator Systems Technology Conferences. Reston: AIAA, 2013. |
| [4] | LEE Y G, KIM D M, YEOM C H. Development of Korean high altitude platform systems[J].International Journal of Wireless Information Networks, 2006, 13(1): 31–42.DOI:10.1007/s10776-005-0018-6 |
| [5] | 刘东旭, 杨永强, 吕明云, 等. 蒙皮热辐射特性对平流层浮空器氦气温度影响[J].北京航空航天大学学报, 2010, 36(7): 836–840. LIU D X, YANG Y Q, Lü M Y, et al. Effect of envelop thermal radiative properties on the stratospheric super-pressure LAT vehicle helium temperature[J].Journal of Beijing University of Aeronautics and Astronautics, 2010, 36(7): 836–840.(in Chinese) |
| [6] | WU J T, FANG X D, WANG Z G, et al. Thermal modeling of stratospheric airships[J].Aerospace Sciences, 2015, 75: 26–37.DOI:10.1016/j.paerosci.2015.04.001 |
| [7] | DAI Q M, FANG X D, LI X J, et al. Performance simulation of high altitude scientific balloons[J].Advances in Space Research, 2012, 49(6): 1045–1052.DOI:10.1016/j.asr.2011.12.026 |
| [8] | 方贤德, 王伟志, 李小建. 平流层飞艇热仿真初步探讨[J].航天返回与遥感, 2007, 28(2): 5–9. FANG X D, WANG W Z, LI X J. A study of thermal simulation of stratospheric airships[J].Spacecraft Recovery and Remote Sensing, 2007, 28(2): 5–9.(in Chinese) |
| [9] | LIU Q, WU Z, ZHU M, et al. A comprehensive numerical model investigating the thermal-dynamic performance of scientific ba-lloon[J].Advances in Space Research, 2014, 53(2): 325–338.DOI:10.1016/j.asr.2013.11.011 |
| [10] | LIU Q, LI Z J, YANG Y C, et al. Thermal simulation and expe-riments for a stratospheric balloon gondola[C]//AIAA Modeling and Simulation Technologies Conference. Reston: AIAA, 2015, 6: 325-338. |
| [11] | LI D F, XIA X L, SUN C. Experimental investigation of transient thermal behavior of an airship under different solar radiation and airflow conditions[J].Advances in Space Research, 2014, 53(5): 862–869.DOI:10.1016/j.asr.2013.12.032 |
| [12] | XIA X L, LI D F, SUN C, et al. Transient thermal behavior of stratospheric balloons at float conditions[J].Advances in Space Research, 2010, 46(9): 1184–1190.DOI:10.1016/j.asr.2010.06.016 |
| [13] | 夏新林, 李德福, 杨小川. 平流层浮空器的热特性与研究现状[J].航空学报, 2009, 30(4): 577–583. XIA X L, LI D F, YANG X C. Thermal characteristics of stratos-pheric aerostats and their research[J].Acta Aeronautica et Astronautica Sinica, 2009, 30(4): 577–583.(in Chinese) |
| [14] | YAO W, LU X C, WANG C, et al. A heat transient model for the thermal behavior prediction of stratospheric airships[J].Applied Thermal Engineering, 2014, 70(1): 380–387.DOI:10.1016/j.applthermaleng.2014.05.050 |
| [15] | KENYA H, KUNIHISA E, MASAAKI S, et al. Experimental study of thermal modeling for stratospheric platform airships[C]//AIAA's 3rd Aviation Technology, Integration, and Operations(ATIO) Conference. Reston: AIAA, 2003, 5: 74-89. |
| [16] | SIMPSON T W, MAUERY T M, KOPTEE J J, et al. Kriging models for global approximation in simulation based multidisciplinary design optimization[J].AIAA Journal, 2001, 39(12): 2233–2241.DOI:10.2514/2.1234 |
| [17] | TOAL D J J, BRESSLOFF N W, KEAN A J. Kriging hyperparameter tuning strategies[J].AIAA Journal, 2008, 46(5): 1240–1252.DOI:10.2514/1.34822 |
| [18] | LIU J, HAN Z H, SONG W P. Efficient kriging-based optimization design of transonic airfoils: Some key issues: AIAA-2012-0967[R]. Reston: AIAA, 2012. |
| [19] | HAN Z H, LIU J, SONG W P, et al. Surrogate-based aerodynamic shap optimization with application to wind turbine airfoils: AIAA-2013-1108[R]. Reston: AIAA, 2013. |
| [20] | 张柱国, 姚卫星, 刘克龙. 基于进化Kriging模型的金属加筋板结构布局优化方法[J].南京航空航天大学学报, 2008, 40(4): 497–500. ZHANG Z G, YAO W X, LIU K L. Configuration optimization method for metallic stiffened panel structure based on updated Kriging model[J].Journal of Nanjing University of Aeronautics and Astronautics, 2008, 40(4): 497–500.(in Chinese) |
| [21] | 肖立峰, 张广泉, 张以都. 基于进化Kriging代理模型的结构形状优化方法[J].机械设计, 2009, 26(7): 57–60. XIAO L F, ZHANG G Q, ZHANG Y D. Optimization method of structural shape based on Kriging surrogate model[J].Journal of Machine Design, 2009, 26(7): 57–60.(in Chinese) |
| [22] | 周秀骥, 陶善昌, 姚克亚. 高等大气物理学(上册)[M].北京: 气象出版社, 1991: 85-95. ZHOU X J, TAO S C, YAO K Y. Advanced atmospheric physics(Ⅰ)[M].Beijing: China Meteorological Press, 1991: 85-95.(in Chinese) |
| [23] | FARLEY R E. BalloonAscent: 3-D simulation tool for the ascent and float of high-altitude balloons[C]//AIAA's 5th Aviation, Technology, Integration, and Operations (ATIO) Conference. Reston: AIAA, 2005. |
