为了进一步提高传统飞行器的性能并实现飞行器的智能化，基于智能材料的自适应机翼结构已逐渐成为研究热点，尤其是在高速发展的无人飞行器(UAV)设计领域。其中，“Morphing”(变体)^[1-3]的概念在机翼的设计中得到了广泛关注。人们希望能够通过对机翼的变形控制实现对飞行的控制或对飞行器结构参数的调整。相关的研究主要包括可变弧形翼(翼面展向弯曲)^[4-5]、上反角可调机翼^[6]和可扭曲机翼^[7-9]几种形式。最早提出的变形设计方案是通过改变机翼扭转角的分布来提高飞行性能和控制能力。但在早期的刚性机翼结构设计中却因结构重量和刚度而难以实现。随着飞行器的小型化、无人化，并得益于材料科学与技术的发展，越来越多的飞行器开始采用柔性构件^[10]。柔性机翼的出现也使得可扭转机翼的设计重新受到研究者们的关注。特别是在柔性结构中采用主动材料结构一体化设计的方式，其有着传统驱动方式无可比拟的优势。利用智能材料的特性人为驱动机翼扭曲变形可为机翼减轻阵风和机动载荷、提高升力和取代传统控制面。因此对自适应机翼扭曲变形的研究尤为重要。
压电纤维材料(Macro Fiber Composite，MFC)^[11]克服了传统压电材料易损、难结合的缺点，具有高输出、高带宽及能量密度高的优点，因此在飞行器自适应结构中具有更好的应用前景^[12-13]。在采用压电材料对结构进行形状控制的一些基本研究中，文献[14]研究了指定扭曲变形下压电片厚度、布置位置和驱动电压的优化。文献[15]通过拓扑优化基板结构实现了压电驱动扭曲变形效率的提升。文献[16]采用非矩形压电片对压电复合板进行扭曲变形控制。文献[17]针对形状控制的应用优化了压电片的几何形状。已有的研究多是基于传统压电片进行形状控制的分析，而采用MFC来进行形状控制也多是基于45°的对称铺设的方案^[18]。这些研究忽略了压电纤维方向对形状控制的影响，同时也缺少压电纤维材料与不同驱动方案结合所带来不同效果的相关研究。
板结构作为机翼结构最基本构成形式，如何设计才能使得复合板在压电纤维材料的驱动下获得更高的扭曲变形效率，对于采用这种主动复合材料的自适应机翼的性能提升有着重要的参考意义。本文基于Ritz法假设双向梁函数组合级数的位移场，建立了压电纤维材料驱动下复合板变形的求解方法。在此基础上针对压电纤维材料的方向性以及正负输出的差异性(MFC的电压驱动范围是-500~1 500 V，导致正负输出能力不对称)对压电纤维材料驱动下复合板扭曲变形效率进行了详细分析，为MFC铺设角度的选择、获得单层和双层压电纤维复合板的最佳扭曲变形提供了理论依据。
1 MFC复合板分析模型 在自适应结构中为了获得较大的形变量多采用薄板结构。本文的分析亦基于薄板理论，采用的坐标系如图 1所示，其中x轴为板长方向，y轴为板宽方向，z轴垂直于板面；①和②分别对应具有单层MFC和双层MFC的复合板结构。采用单层MFC时材料主轴方向与x轴夹角为θ，双层MFC时，上下两层材料主轴方向与x轴夹角分别为θ_up和θ_down。t为复合板厚度，t₁和t₂分别为单层和双层MFC复合板厚度，t_a为MFC厚度，t_b为基板厚度，L和W分别为板的长度和宽度。以下分析不受外力作用的MFC复合板在电压驱动下的变形。

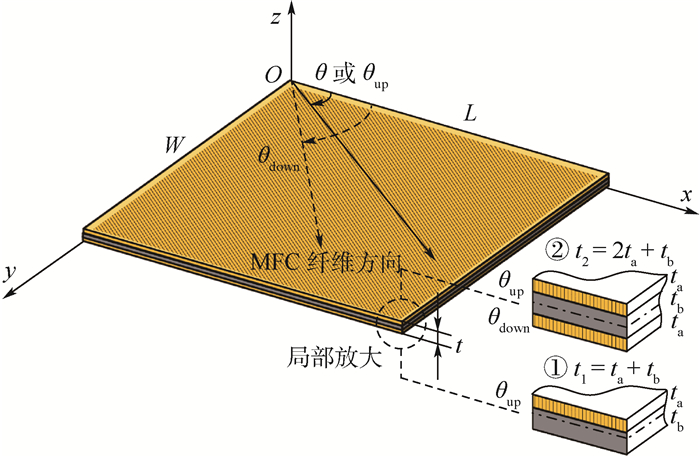图 1 MFC复合板的几何结构及坐标系 Fig. 1 Geometry and coordinate system of MFC composite plate

图选项

设u，v，w为板内任意一点(x, y, z)沿3个坐标方向的位移分量；u⁰和v⁰分别为板的中面沿x和y方向的位移分量。根据薄板理论，在薄板整体坐标系中有如下关系式：

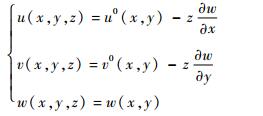(1)

由式(1)的位移关系可得MFC复合板应变向量的表达式为

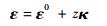(2)

式中：ε⁰为中面应变向量。κ为中面曲率变化向量。这2个变量的表达式为(式中右上方标“0”的变量对应中面的变量):

(3)

在没有外力作用的情况下，主动材料结构的变形可通过改变外界电压(电流、磁场或温度场)引起，称对应的应变Λ为主动应变。在复合材料结构中主动材料的变形受到被动材料的限制，因此MFC复合板的应变ε由2部分组成：

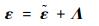(4)

式中：由基板对MFC的反作用力引起，也称为被动应变。复合板第k层中应变ε与应力σ的关系为

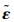
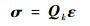(5)

设第k层应变为主动应变Λ_k，则与该应变对应的等效加载应力为

(6)

式中：Q_k为复合板坐标系下第k层材料的刚度矩阵。当该层材料主轴坐标系与复合板坐标系的夹角为θ_up时，Q_k与材料主轴坐标系下的刚度矩阵Q_k有如下关系：

(7)

式中：T为各层纤维方向与主轴夹角所对应的转换矩阵。复合板坐标系下主动纤维材料的输出应变Λ_k与其在材料主轴坐标系下的应变Λ_k的关系为

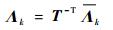(8)

根据复合板应力、应变的关系可以推导出复合板内力与位移的关系。
对应板中的弹性变形，复合板厚度上单位长度的内力N和内力矩M为

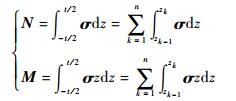(9)

式中：z_k为各层界面在复合板坐标系下所对应的纵坐标。将式(2)和式(5)代入式(9)并化简得到

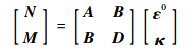(10)

式中：矩阵A、B和D构成了主动复合板的刚度矩阵。同理，由式(6)可得对应主动应变的等效驱动力N_Λ和等效驱动力矩M_Λ为

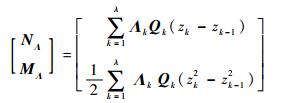(11)

式中：λ为MFC复合板层数，单层时λ=2，双层时λ=3。
基于上述复合板内力与变形的关系即可获得主动复合板的能量表达式，进而可利用最小势能原理对复合板的形变进行求解。
复合板的应变势能U为

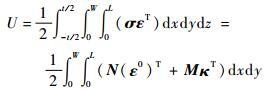(12)

主动材料驱动应变的等效力和等效力矩做功W_Λ为

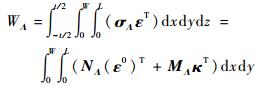(13)

通过式(12)和式(13)相减得到主动复合板的总势能E_t为

(14)

根据最小势能原理，在所有满足变形协调和边界位移条件的结构位移中，对应系统实际位移的势能最小。以下应用Ritz法，将复合板的位移表示成具有待定系数的、一系列满足位移边界条件的双向梁函数(Ritz基)的组合，然后通过对复合板的总势能求极值来确定位移表达式中的待定系数。假设主动复合板的位移场为

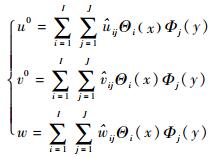(15)

式中：Θ_i(x)为复合板在x方向的Ritz基函数；Θ_j(y)为复合板在y方向的Ritz基函数。根据Ritz法原理，Θ_i(x)和Θ_j(y)仅需满足位移边界条件，因此取满足位移边界条件的梁振型函数作为Ritz基函数。I和J分别为在x和y方向所采用的梁函数阶数，和为待定系数。对应不同边界条件的各阶次梁函数在有关振动基础理论方面的著作中均可查到^[19-20]。
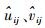
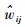
根据最小势能原理，位移场的待定系数和需满足如下关系：

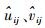
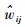
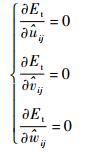(16)

将基于位移场表达式(15)的主动复合板的应变场和应力场代入式(9)~式(14)，即可推导出主动复合板总势能的表达式，再将该表达式代入式(16)便可得到位移场待定系数的求解方程组:

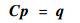(17)

式中：p为位移场待定系数向量；q为与主动材料输出相关的常数向量；C为3IJ×3IJ 阶系数矩阵，可以划分为9个子块矩阵

(18)

C中的每个子块均为I×J 阶矩阵。经推导各子块矩阵中元素表达式为

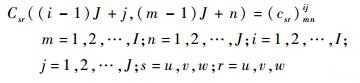(19)

(20)

p和q均为3×I×J维列向量，分别由3个子向量构成

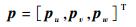(21)

(22)

其中的子向量中元素为

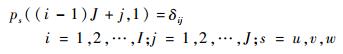(23)

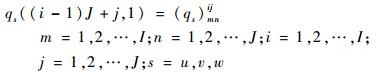(24)

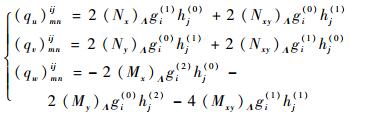(25)

式(20)中：A_ij、B_ij、D_ij(i=1, 2, 6; j=1, 2, 6)分别为式(10)中矩阵A、B、D中的元素；g_i、g_ij和h_i、h_ij为与所选取梁函数相关的积分值，其中g_i、g_ij为与x方向梁函数相关的积分值，表达式为

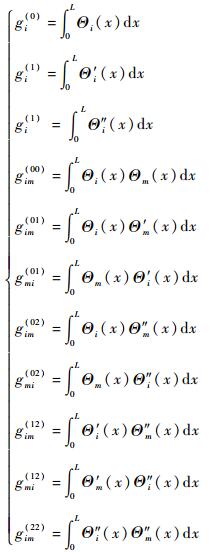(26)

将式(26)中的i，m，Θ_i(x)和L分别替换为j，n，∏_j(y)和W，可以得到与y方向梁函数有关的积分值。
将各积分值及式(18)~式(26)逐次代入到式(17)，式(21)作为一个以p为未知元的向量方程，其系数矩阵C和常数矩阵q得到完备，由

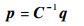(27)

便可求得假设位移场中梁函数组合级数的待定系数，从而获得MFC复合板驱动变形的位移结果。
2 实验验证 为验证本文所建立的分析模型、所采用的基本假设以及计算方法在求解MFC主动应变驱动下复合板位移场时的有效性，对由2片M-8528-F1 MFC构成的MFC复合板试件进行了相关实验测试。MFC、基板的材料参数和试件的几何参数分别在表 1、表 2中给出, 其中E、υ和G分别为材料的弹性模量、泊松比和剪切模量，1、2表示材料的主轴方向。
表 1 MFC和基板的材料参数 Table 1 Material parameters of MFC and substrate

材料	E/GPa			υ		G/GPa	t/mm	Λ/10-6
	E1	E2		υ12	υ21
M-8528-F1	30.336	15.857		0.31	0.16	5.515	0.3	[1 350, 0, 0]T
基底	44			0.27		3.1	0.3	—

表选项






表 2 试件的几何参数 Table 2 Geometric parameters of specimen

试件	布置形式	x方向边界条件	y方向边界条件	W/mm	L/mm	θup/(°)	θdown/(°)
1#	bimorph	C-F	F-F	35	95	45	-45

表选项






测试时复合板的固定方式为固定1个边，其余3边为自由状态(见图 2)。2片MFC均采用最高正电压驱动(1 500 V/1 500 V)，对应的驱动应变参见表 1。采用激光位移传感器对MFC复合板上沿x方向的5条等距线(L₀, L₁, …, L₄)进行了挠度测试，从而获得复合板不同位置处相应位置的位移。

图 2 MFC复合板扭曲实验测试 Fig. 2 Experimental test of twist actuation of MFC composite plate

图选项

测试之前先对测试状态下复合板的形变按本文第1节给出的方法进行理论预测。在计算中x方向选取固支-自由边界条件对应的梁函数Θ(x)，y方向选取自由-自由边界条件对应的梁函数，上下层MFC纤维的角度分别为45°和-45°；在函数阶次选取方面，采用满足边界条件的梁函数作为李兹基函数来模拟板的静力弯曲变形时，一般取前3阶即可以得到较好的结果。而复合板在电压驱动下不仅产生弯曲变形还同时产生扭曲变形。理论上Ritz法随函数阶数的增加会提高精度但取值的无限增加会急剧的加大计算量；综合考虑计算量和精度，在x和y方向均取前10阶梁函数进行计算，所得MFC复合板试件的位移场如图 3所示。

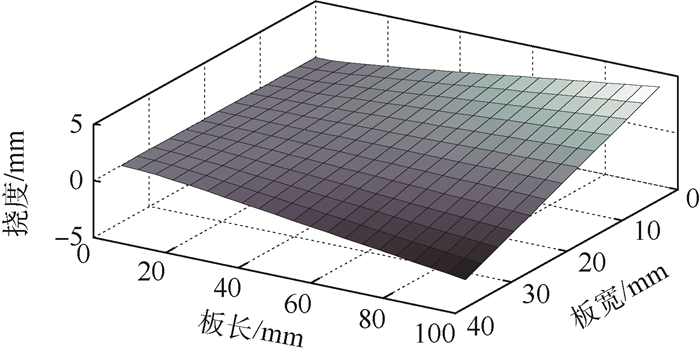图 3 MFC复合板试件在MFC驱动下的位移场预测 Fig. 3 Predicted displacement field of specimen (MFC composite plate) under actuation of MFC

图选项

实验所测得的挠度同计算得到的位移进行了对比，对比结果在图 4中给出。图中离散点为测试结果，连续的线段为理论计算结果。

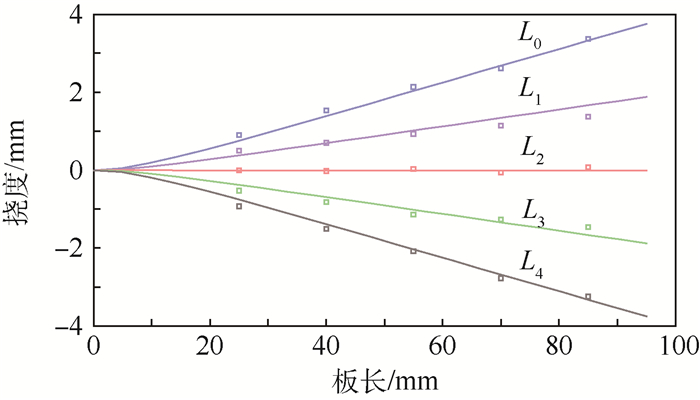图 4 MFC复合板多点挠度测试与计算结果的对比 Fig. 4 Comparison of deflection measurement on multi-points and calculation results of MFC composite plate

图选项

图 4中的实验结果与计算结果吻合得较好，验证了第1节所建立的模型、基本假设及计算方法在求解MFC驱动下复合板位移场的有效性。通过该模型可以对MFC复合板的相关参数特性进行准确分析。
3 受MFC驱动的复合板的扭曲变形效率 理论与实测结果表明，主动纤维驱动下复合板产生了弯扭耦合变形。如何布置MFC纤维的方向并选择合理的驱动方式才能获得更大的扭曲变形效率是本文分析的主要目的。本文针对MFC在自适应翼面中应用的2种典型模式(见图 5)进行研究，其力学模型可以分别简化为边界条件为1边固支3边自由(CFFF，对应图 5(a)中的应用模式)和2边固支2边自由(CFCF，对应图 5(b)中的应用模式)的复合板。

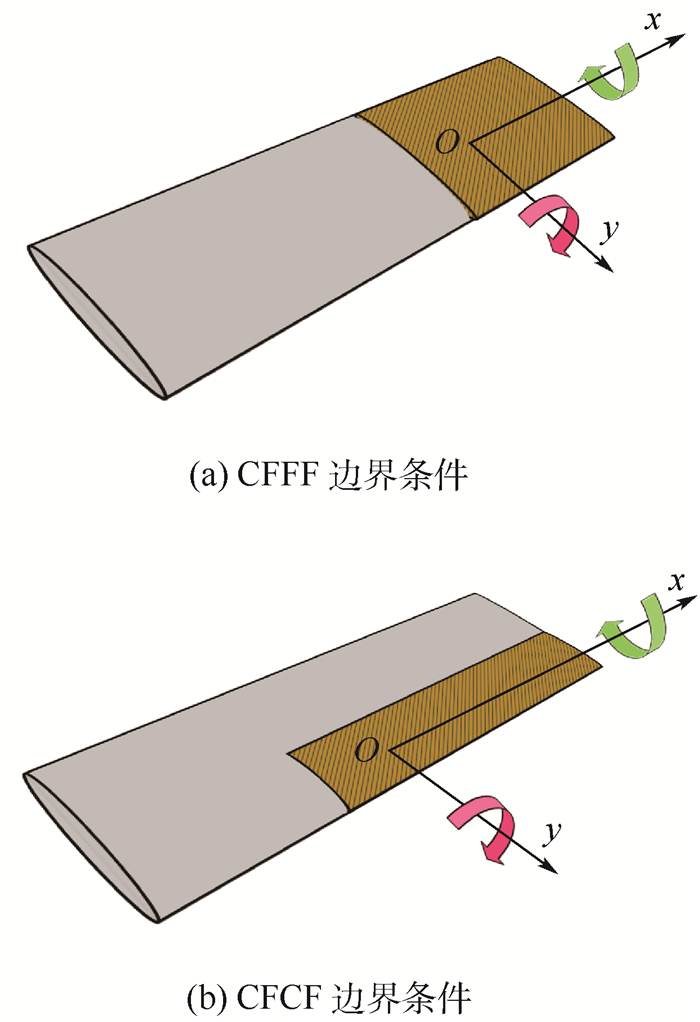图 5 主动材料在一体化自适应翼面中的典型应用模式 Fig. 5 Typical application modes of active material in integrated adaptive wing surface

图选项

为了衡量MFC复合板的扭曲变形程度，定义与固支边平行的任意截面相对固支边的等效扭转角为：变形后该截面中线两端点连线与固支边所形成的夹角β，如图 6所示。

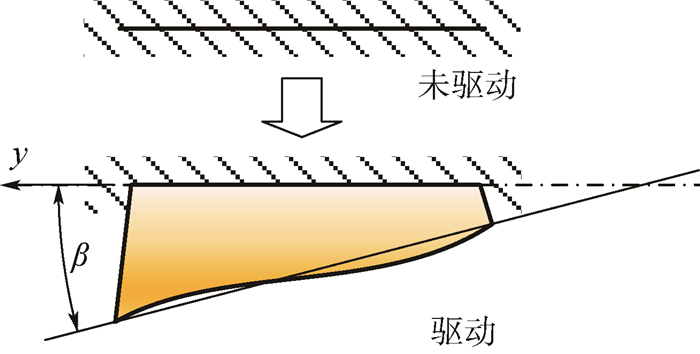图 6 MFC复合板等效扭转角β Fig. 6 Equivalent torsional angle β of MFC composite plate

图选项

根据几何关系有如下表达式：

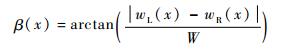(28)

式中：w_L(x)和w_R(x)分别为垂直于固定边的两侧边的挠度；若其中一个边也被固定，以y= 0的一侧边被固定为例，则有w_L(x)=0。显然与固定边相对的自由端截面(x=L时)的等效扭转角为最大扭转角。
为了衡量MFC复合板的弯曲变形程度，定义与固支边平行的任意截面相对固定截面的等效弯转角α的正切为：该截面中线挠度的均值与该截面至固定端的距离之比(如图 7所示)：

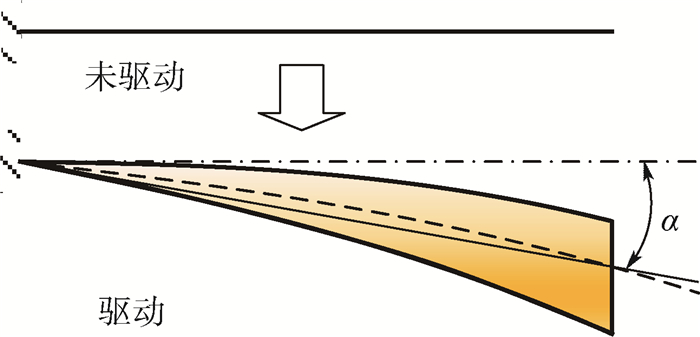图 7 MFC复合板等效弯转角α Fig. 7 Equivalent bending angle α of MFC composite plate

图选项

(29)

式中：W_i(x)为垂直固定边的第i个截面中线的挠度；n为所计算或所测试的垂直固定边的截面挠度个数。显然与固定边相对的自由端截面(x=L)的等效弯转角为最大弯转角。
即使受到同样的电压驱动，对应不同的结构形式、电压驱动方式或不同的MFC纤维方向，复合板所获得的扭曲程度也不同，扭曲变形越大说明扭曲变形效率越高。为了评估MFC复合板在不同条件下的驱动效果，定义压电纤维复合板驱动扭曲变形效率为

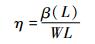(30)

式中：β(L)为与固定截面平行的截面中最大的等效扭转角，即自由端截面(x=L)的等效扭转角。该效率的物理意义是单位面积的压电纤维材料复合板所能实现的扭曲变形程度。
由式(30)可知，当复合板的几何尺寸一定时，复合板自由端截面(x=L)的等效扭转角β(L)(式(28))即可被用来衡量复合板的扭曲变形效率。
以下在对MFC复合板驱动扭曲变形效率的计算分析中，MFC和基板采用表 1中所给出的相关参数。
3.1 单层MFC驱动下复合板扭曲变形效率分析 由于正电压下MFC的驱动能力高于负电压，单层MFC复合板一般采用正电压驱动模式。在单层MFC驱动下，压电纤维布置的方向对MFC复合板扭曲变形效率的影响是分析的重点。根据复合板扭曲变形效率的定义，对于给定的复合板，在最高正电压(1 500 V)驱动下自由端截面等效扭转角随MFC铺设角度的变化就反映了扭曲变形效率随MFC铺设角度的变化。

3.1.1 CFFF约束下单层MFC驱动下复合板的扭曲变形效率 在复合板的结构参数中，复合板的长宽比例与纤维的布置方向关系密切。图 8给出了具有不同长宽比的单层MFC驱动复合板扭曲变形随压电纤维铺设角度的变化；利用结构的对称性，θ_up的取值范围为0°~90°。

图 8 单层MFC驱动下压电纤维方向对复合板的自由边截面等效扭转角的影响(CFFF) Fig. 8 Effect of piezoelectric fiber direction on equivalent torsional angle at free edge section of composite plate actuated by single layer of MFC (CFFF)

图选项

由图 8可以看出，随着压电纤维铺设角θ_np的增加，MFC驱动下复合板的自由边截面等效扭转角均为先递增后减小的规律。而随着复合板长宽比(L/W)的减小，自由边截面等效扭转角极值所对应的铺设角度值(图中点划线与每条曲线的交点对应的θ_up角度)逐渐递增。所得到的结果表明对于具有CFFF边界条件的单层MFC复合板，为了获得更高的扭曲变形效率，其压电纤维的铺设角度一般不为45°或复合板对角线所对应的角度，而是具备随长宽比减小而增加的规律。

3.1.2 CFCF约束下单层MFC驱动下复合板的扭曲变形效率 边界条件为CFCF的单层MFC驱动复合板的扭曲变形效率如图 9所示。

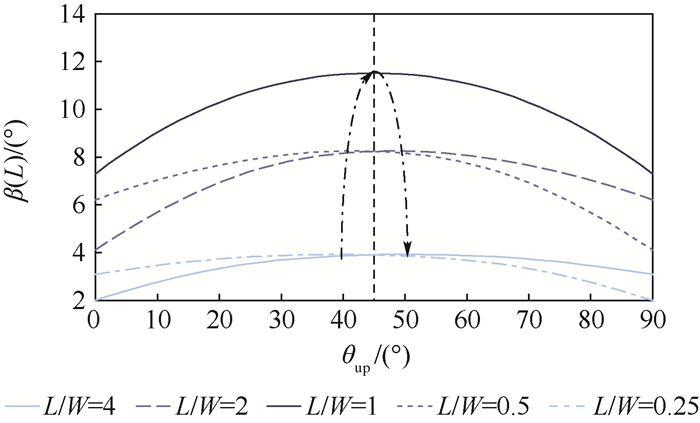图 9 单层MFC驱动下压电纤维方向对复合板的自由边截面等效扭转角的影响(CFCF) Fig. 9 Effect of piezoelectric fiber direction on equivalent torsional angle at free edge section of composite plate actuated by single layer of MFC (CFCF)

图选项

对应不同的长宽比，扭曲变形效率随压电纤维铺设角的增大也具有先增加后减小的规律。与CFFF边界条件不同的是其压电纤维的优选铺设角度(图中点划线与每条曲线的交点对应的θ_np角度)随复合板长宽比的增加而增加。由于边界条件的对称性，在复合板长宽比为1时，压电纤维的铺设角应选为45°。
3.2 双层MFC驱动下复合板扭曲变形效率分析 相对单层MFC复合板，双层MFC复合板(MFC分设于基板的上下层，参见图 1)存在更为多样性的驱动模式，驱动电压模式可分为2种，2层MFC均采用正电压(+/+)驱动和一正一负(+/-)的电压驱动模式。压电材料的特性使得MFC的驱动电压在正负范围内不对称，一般的电压驱动范围为(-500~1 500 V)。本节分别讨论正电压取1 500 V、负电压取-500 V情况下(此时对应MFC的最大驱动能力)，正电压(+/+)对称驱动和一正一负(+/-)非对称驱动方式下压电纤维的铺设方向对扭曲变形效率的影响。设θ_up和θ_down分别为上下压电纤维铺设角度，取值范围均为-90°~90°。

3.2.1 CFFF约束下双层MFC驱动下复合板扭曲变形效率 通常MFC复合板的面外变形包含了扭曲变形和弯曲变形，变形能一定时弯曲变形程度越小则能量越集中于扭曲变形。因而本节除了对MFC复合板驱动等效扭转角的分析外还分析了等效弯转角，以了解MFC复合板驱动扭曲变形效率与驱动的弯曲变形程度之间的联系，从而进一步获得有关如何进行压电纤维铺设的更普适的规律。
图 10和图 11分别给出了双层MFC (+/+)电压驱动模式和(+/-)电压驱动模式下复合板的自由边截面等效扭转角(图 10(a)、11(a))和等效弯转角(图 10(b)、11(b))随上下层压电纤维方向(θ_up和θ_down)的变化规律。如前述，在驱动电压保持不变的条件下(+/+)驱动模式的驱动电压为(1 500 V/1 500 V)，(+/-)驱动模式的驱动电压为(1 500 V/-500 V)，复合板的自由边截面等效扭转角的变化就代表了扭曲变形效率的变化。

图 10 双层MFC复合板在(+/+)电压驱动模式下自由边截面等效扭转角、弯转角随压电纤维方向的变化(L/W=1, CFFF) Fig. 10 Evolution of equivalent torsional and bending angles at free edge section of composite plate with piezoelectric fiber direction (two layers of MFC, (+/+) actuation mode, L/W=1, CFFF)

图选项

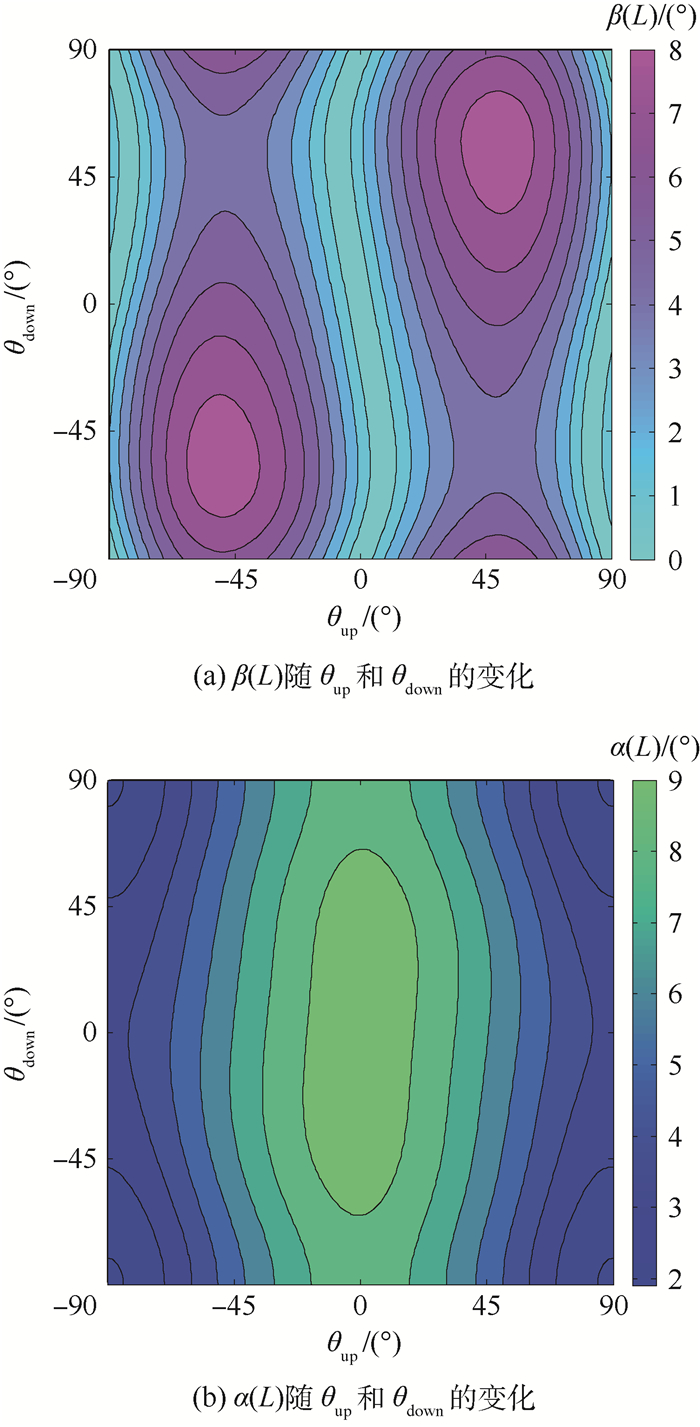图 11 双层MFC复合板在(+/-)电压驱动模式下自由边截面等效扭转角、弯转角随压电纤维方向的变化(L/W=1, CFFF) Fig. 11 Evolution of equivalent torsional and bending angles at free edge section of composite plate with piezoelectric fiber direction (two layers of MFC, (+/-) actuation mode, L/W=1, CFFF)

图选项

图 10和图 11的结果是在复合板长宽比为1的条件下得出的。对比不同长宽比的计算结果表明，图 10和图 11所展现出的规律不受复合板长宽比的影响，不同长宽比改变的是等效扭转角和等效弯转角的极值。因此在以下的分析中，2种驱动模式所获得的自由边截面等效扭转角及对应的纤维铺设角不再以云图的结果展示，仅以表 3形式列出。
表 3 CFFF约束的MFC复合板在2种驱动模式下的自由边截面等效扭转角极值 Table 3 Maximum equivalent torsional angles of free edge section of MFC composite plate under two actuation modes with constraint condition of CFFF

L/W	驱动模式	βmax/(°)	θup/(°)	θdown/(°)
2	+/+	15.75	-46.8	46.8
	+/-	9.50	46.8	54
1	+/+	13.90	-47.7	47.7
	+/-	8.59	50.4	55.8
0.25	+/+	5.82	-50.4	50.4
	+/-	3.93	55.8	57.6

表选项






从表 3中可以看出：①对于具有同一长宽比的复合板，(+/+)电压驱动模式所能获得的自由边截面等效扭转角大于(+/-)电压驱动模式下的自由边截面等效扭转角，因此在CFFF的边界条件下，(+/+)电压驱动方式是更佳的驱动方案。②对于(+/+)的电压驱动方式，上下两层的压电纤维铺设角度满足关系式θ_up=θ_down时扭曲变形效率最高。从图 10(a)可看出，当θ_up=θ_down时复合板自由边截面的等效扭转角最大；图 10(b)表明在满足对称轴条件θ_up=θ_down时复合板的等效弯转角为零，由此解释了此时扭曲变形效率最大的原因。如第1节实验中采用的反对称铺设的MFC复合板在MFC驱动下，复合板在y=W/2的轴线上不存在平面外的位移(矩形板的中间对称线即图 2中的L₂没有产生挠度)。这一特性具有较大的工程意义, 它使得设计和制备都相对简单。在设计时，最佳的上下两层压电纤维的铺设角度便可简化到在满足关系θ_up=θ_down的方案中寻找。
当满足关系θ_up=-θ_down时，扭曲变形效率随铺设角的变化如图 12所示。

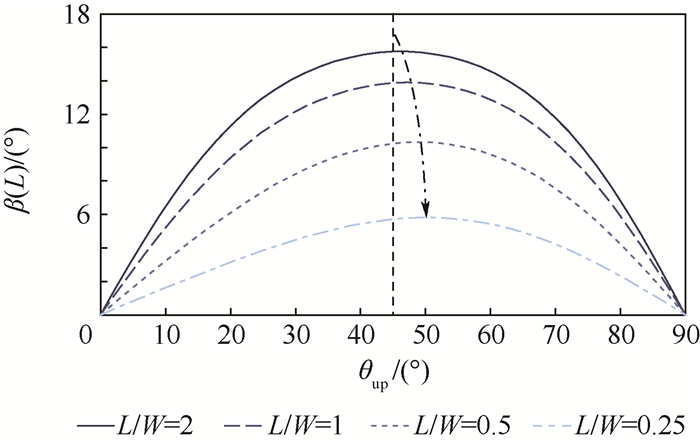图 12 双层MFC复合板(+/+)电压驱动模式下压电纤维铺设角度(θup=-θdown)对复合板扭曲变形效率的影响(CFFF) Fig. 12 Effect of piezoelectric fiber laying angle (θup=-θdown) on efficiency of twist deformation of bimorph MFC composite plate under (+/+) actuation mode (CFFF)

图选项

图 12所得到的关系与单层MFC驱动下的规律相似，即对应最高扭曲变形效率的铺设角度(图中点划线与每条曲线的交点对应的角度)随着复合板长宽比的减小而增加。然而相对单层MFC复合板，该效率对板的长宽比的敏感性要小得多，长宽比从0.25到2增加了7倍，反映扭曲变形效率的自由边截面等效扭转角仅变化了3°左右。此外图 12还表明，在最高扭曲变形效率所对应的铺设角度附近，复合板扭曲变形效率对铺设角度的变化不敏感。因此从MFC复合板制备工艺的角度来看，采用θ_up=-θ_down的铺设工艺时，长宽比的影响可以忽略。

3.2.2 CFCF约束下双层MFC驱动下复合板扭曲变形效率 CFCF约束的双层复合板在2种电压驱动模式下的自由边截面等效扭转角和等效弯转角随上下层压电纤维方向的变化规律如图 13、图 14所示。同CFFF边界条件，该规律也不受复合板长宽比的影响，不同长宽比改变的是自由边截面等效扭转角和等效弯转角的极值。2种电压驱动模式下的自由边截面等效扭转角在表 4中列出。

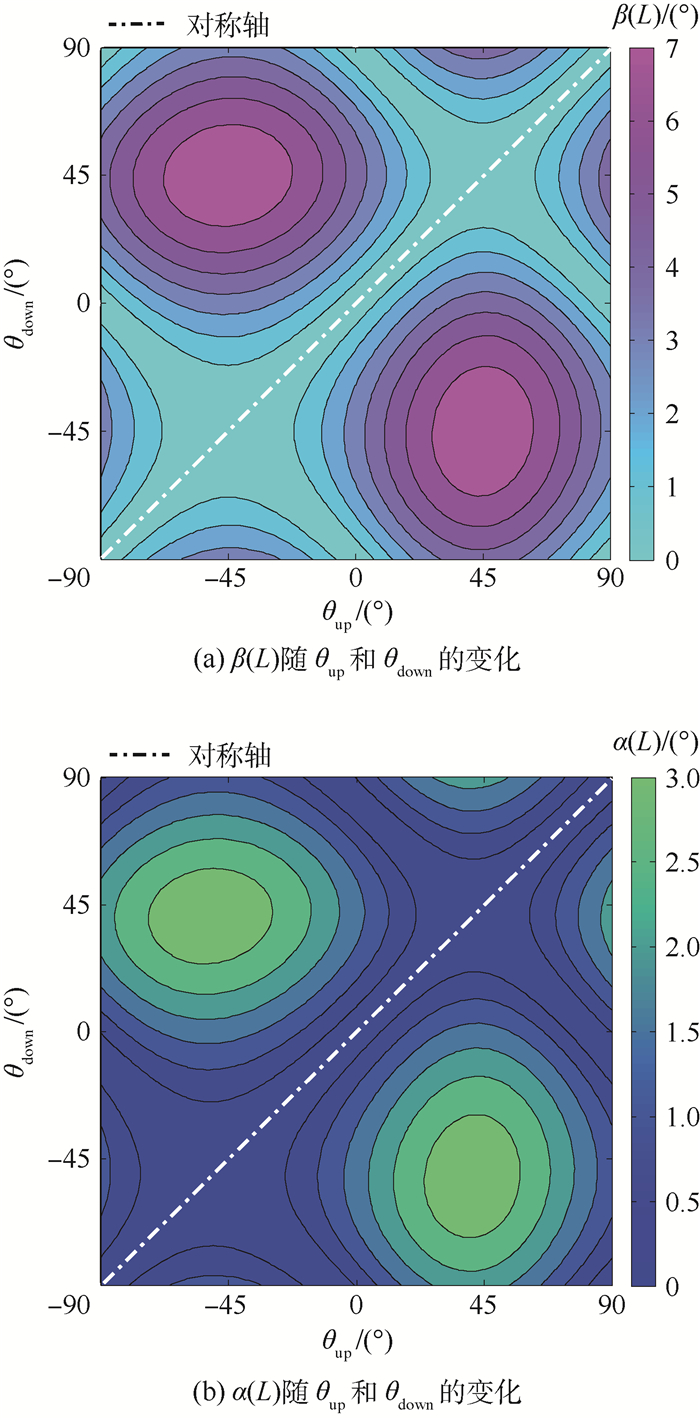图 13 双层MFC复合板在(+/+)电压驱动模式下自由边截面等效扭转角、等效弯转角随压电纤维方向的变化(L/W=1, CFCF) Fig. 13 Evolution of equivalent torsional and bending angles at free edge section of composite plate with piezoelectric fiber direction (two layers of MFC, (+/+) actuation-mode, L/W=1, CFCF)

图选项

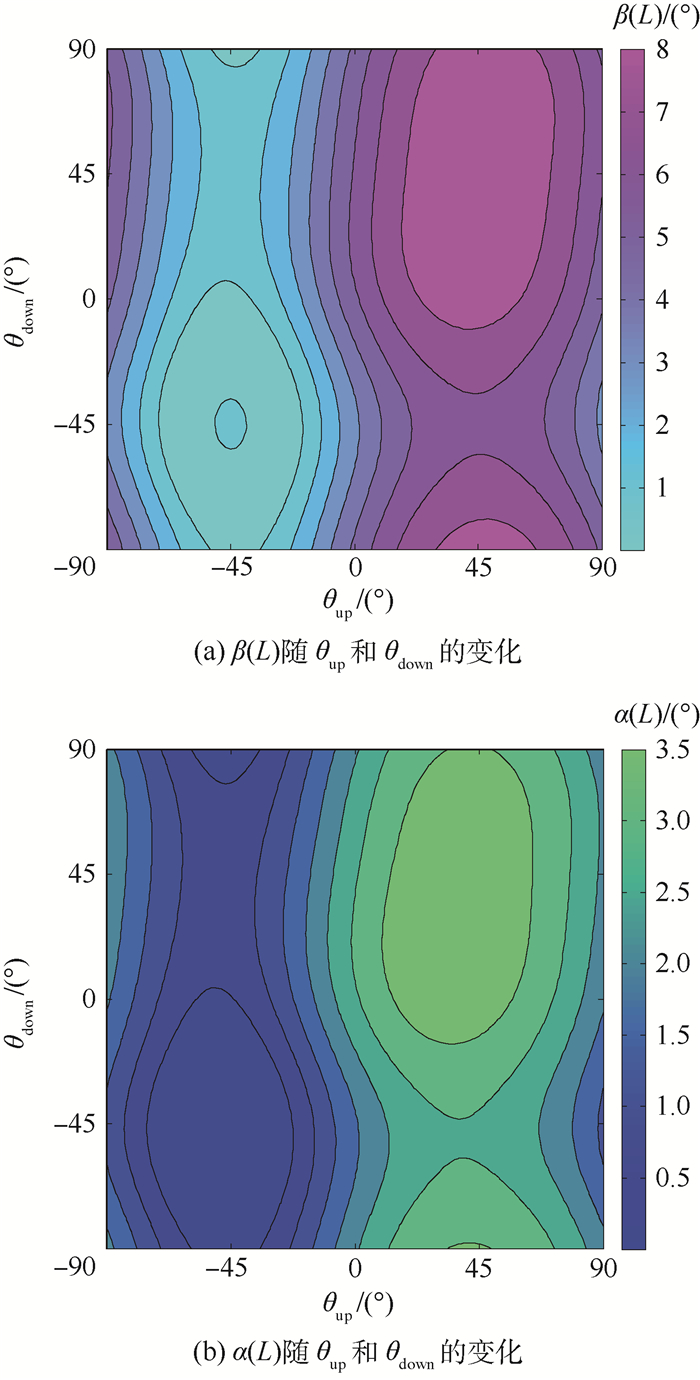图 14 双层MFC复合板在(+/-)电压驱动模式下自由边截面.等效扭转角、等效弯曲角随压电纤维方向的变化(L/W=1, CFCF) Fig. 14 Evolution of equivalent torsional and bending angles at free edge section of composite plate with piezoelectric fiber direction (two layers of MFC, (+/-) actuation-mode, L/W=1, CFCF)

图选项

表 4 CFCF约束的MFC复合板在2种驱动模式下的自由边截面等效扭转角极值 Table 4 Maximum equivalent torsional angles of free edge section of MFC composite plate under two actuation modes with constraint condition of CFCF

L/W	驱动模式	βmax/(°)	θup/(°)	θdown/(°)
4	+/+	3.05	-34.2	50.4
	+/-	3.98	41.4	-34.2
1	+/+	7.84	-45	45
	+/-	8.93	45	45
0.25	+/+	3.05	-55.8	39.6
	+/-	3.98	48.6	55.8

表选项






与CFFF边界条件的复合板相反，相同长宽比的复合板在(+/+)电压驱动下所能获得的自由边截面等效扭转角总是低于(+/-)驱动模式产生的自由边截面等效扭转角，因此在CFCF的边界条件下，(+/-)的电压驱动方式是更优的驱动方案。不过二者的差别不像CFFF约束的复合板那样显著，而且除了方板(L/W=1)外，2种电压驱动模式下最高扭曲变形效率的MFC铺设方案都不再满足关系式θ_up=-θ_down的特点。
由图 14(a)中的等高关系可看到在(+/-)电压驱动模式下，最大扭曲变形效率对MFC纤维的铺设角度不是特别敏感。这说明在一些简单的应用中采用θ_up=θ_down=45°的传统铺设方案也可以得到不错的驱动效率。
4 结论 在自适应翼面等结构的设计中，尽可能提高MFC驱动下复合板结构的扭曲变形效率至关重要。为了对MFC驱动复合板变形特性进行分析，本文推导了MFC的主动应变与复合板的内力与变形之间的关系，建立了复合板受主动应变驱动时的位移求解方程，所得分析结果经由实验验证。为了评价具有弯扭耦合变形特点的MFC复合板对扭曲变形的驱动效果，本文定义了MFC复合板在主动应变驱动下的等效扭转角和等效弯转角，并提出了主动复合板驱动扭曲变形效率的概念。在此基础上，研究了2种约束条件的压电纤维复合板结构受电压驱动的扭曲变形效率，得到以下结论：
1) 单层MFC复合板受电压驱动时，其最大扭曲变形效率对应的MFC铺设角度与复合板长宽比相关；板边界的约束为CFFF形式时，长宽比越小，MFC铺设角度越大。板边界的约束为CFCF形式时则相反，且长宽比为1时对应最大扭曲变形效率的铺设角度为45°。
2) 双层MFC复合板受电压驱动的模式可以分为(+/+)对称驱动和(+/-)非对称驱动2类。板边界的约束为CFFF形式时，(+/+)电压驱动模式的扭曲变形效率较高。在这种电压驱动模式下，为实现高扭曲变形效率，上下2层MFC的铺设角应满足关系θ_up=θ_down。
3) 在CFCF边界条件下，双层MFC复合板的驱动电压应选择上下层(+/-)驱动模式。在该种驱动模式下对应高扭曲变形效率的铺设角度可选范围较大(即在这种情况下扭曲变形效率对纤维方向的改变不敏感)，可取θ_up=θ_down=45°的传统铺设方案。

参考文献

[1]	BARBARINO S, BILGEN O, AJAJ R M, et al. A review of morphing aircraft[J].Journal of Intelligent Material Systems & Structures, 2011, 22(9): 823–877.
[2]	SOFLA A Y N, MEGUID S A, TAN K T, et al. Shape morphing of aircraft wing:Status and challenges[J].Materials & Design, 2010, 31(3): 1284–1292.
[3]	冷劲松, 孙健, 刘彦菊. 智能材料和结构在变体飞行器上的应用现状与前景展望[J].航空学报, 2014, 35(1): 29–45. LENG J S, SUN J, LIU Y J. Application status and future prospect of smart materials and structures in morphing aircraft[J].Acta Aeronautica et Astronautica Sinica, 2014, 35(1): 29–45.(in Chinese)
[4]	MANZO J, GARCIA E, WICKENHEISER A, et al. Design of a shape-memory alloy actuated macro-scale morphing aircraft mechanism[J].Proceedings of SPIE-the International Society for Optical Engineering, 2005, 5764: 232–240.
[5]	MANZO J, GARCIA E. Demonstration of an in situ morphing hyperelliptical cambered span wing mechanism[J].Smart Materials & Structures, 2010, 19(19): 328–335.
[6]	SHELTON A, TOMAR A, PRASAD J, et al. Active multiple winglets for improved unmanned-aerial-vehicle performance[J].Journal of Aircraft, 2015, 43(43): 110–116.
[7]	BARTLEY-CHO J D, WANG D P, MARTIN C A, et al. Development of high-rate, adaptive trailing edge control surface for the smart wing phase 2 wind tunnel model[J].Journal of Intelligent Material Systems & Structures, 2004, 15(4): 279–291.
[8]	BARRETT R M. Design, fabrication, and testing of a new twist-active wing design[J].Proceedings of SPIE-the International Society for Optical Engineering, 1998: 3329.
[9]	柴双双, 张卫平, 柯希俊, 等. 仿昆扑翼微飞行器中压电驱动器的性能参数分析[J].上海交通大学学报, 2015, 49(5): 663–668. CHAI S S, ZHANG W P, KE X J, et al. Piezoelectric actuators for insect-like flapping-wing micro aerial vehicle[J].Journal of Shanghai Jiaotong University, 2015, 49(5): 663–668.(in Chinese)
[10]	程春晓, 李道春, 向锦武, 等. 柔性后缘可变形机翼气动特性分析[J].北京航空航天大学学报, 2016, 42(2): 360–367. CHENG C X, LI D C, XIANG J W, et al. Analysis on aerodynamic characteristics of morphing wing with flexible trailing edge[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(2): 360–367.(in Chinese)
[11]	LIN X J, ZHOU K C, ZHANG X Y. Development, modeling and application of piezoelectric fiber composites[J].Transactions of Nonferrous Metals Society of China, 2013, 23(1): 98–107.DOI:10.1016/S1003-6326(13)62435-8
[12]	COBB R, BROWNING J, CANFIELD R, et al. F-16 ventral fin buffet alleviation using piezoelectric actuators[C]//AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Reston: AIAA, 2009.
[13]	OHANIAN O, HICKLING C, STILTNER B, et al. Piezoelectric morphing versus servo-actuated MAV control surfaces[C]//AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Resson: AIAA, 2012: 23-26.
[14]	LIU S, TONG L, LIN Z. Simultaneous optimization of control parameters and configurations of PZT actuators for morphing structural shapes[J].Finite Elements in Analysis & Design, 2008, 44(6-7): 417–424.
[15]	LUO Q, TONG L. Design and testing for shape control of piezoelectric structures using topology optimization[J].Engineering Structures, 2015, 97: 90–104.DOI:10.1016/j.engstruct.2015.04.006
[16]	QUAN N, TONG L. Shape control of smart composite plate with non-rectangular piezoelectric actuators[J].Composite Structures, 2004, 66(1-4): 207–214.DOI:10.1016/j.compstruct.2004.04.039
[17]	MUKHERJEE A, JOSHI S. Piezoelectric sensor and actuator spatial design for shape control of piezolaminated plates[J].AIAA Journal, 2015, 40(6): 1204–1210.
[18]	BüTER A, BREITBACH E. Adaptive blade twist-calculations and experimental results[J].Aerospace Science & Technology, 1999, 4(5): 309–319.
[19]	曹志远. 板壳振动理论[M].北京: 中国铁道出版社, 1989: 32-51. CAO Z Y. Vibration theory of plates and shells[M].Beijing: China Railway Publishing House, 1989: 32-51.(in Chinese)
[20]	毛柳伟, 王安稳, 胡明勇. 粘-弹层合悬臂板瞬态响应的近似解析解[J].固体力学学报, 2010, 31(4): 379–384. MAO L W, WANG A W, HU M Y. Approximate analytical solution for transient response of a visco-elastic laminated cantilever plate[J].Chinese Journal of Solid Mechanics, 2010, 31(4): 379–384.(in Chinese)