对大挠性结构进行振动抑制能够改善飞行器姿态和轨道控制效果,抑制方法可以分为被动振动抑制和主动振动抑制。被动振动抑制方法[1]通过改变结构、增加阻尼材料、增大模态阻尼,将振动能量转化为其他形式的能量,达到振动抑制的目的,此方法简单可靠,但灵活性低,抑制效果不明显。主动振动抑制方法可分为2种:一种是前馈控制方法,包括分力合成方法[2]和输入成型方法[3];另一种是闭环反馈控制方法,其采用智能材料[4],通过实时测量振动,再用执行器对挠性体施加作用力或力矩,达到振动抑制的目的,多采用分布粘贴的执行器布局形式,执行器作动器一般是压电陶瓷或记忆合金等。主动振动抑制方法灵活性高,可以改变结构刚度和结构模态,有能力应对不断变化的外部环境(如负载变化或形状变化)和内部环境(如损坏或故障)。采用压电陶瓷片实现主动振动抑制时,通常采用同位控制[5],即压电执行器和压电传感器对位分别贴于薄板结构两侧,控制方法有速率反馈控制、谐振控制[6]、正向位置反馈(Positive Position Feedback,PPF)[7]和改进型正向位置反馈(Modified Positive Position Feedback,MPPF)[8]等。
Moheimani和Andrew[9]在薄板智能结构传递函数中引入了馈通项作为对截断模态的补偿,设计了相应的PPF控制器,对稳定性进行了重新推导。并通过悬臂梁试验验证了PPF控制器的有效性。PPF控制器同时具有阻尼和刚度补偿性能,当提高控制阻尼时,控制器角频率会发生偏移,从而降低刚度补偿的效果。Mahmoodi等[10]根据PPF的缺点,提出了MPPF,引入了刚度和阻尼2个补偿器,解决了传统PPF控制器参数选择困难的问题,并采用悬臂梁进行了试验验证。
目前针对挠性飞行器的动力学建模,大多仅考虑挠性结构与中心刚体的转动耦合特性。Gennaro[11]建立了简化的挠性飞行器姿态动力学模型,考虑了挠性结构与中心刚体的转动耦合特性。胡庆雷和马广富[12]根据Gennaro[11]提出的简化挠性飞行器姿态动力学模型,设计了变结构姿态控制器,并采用压电智能元件作为执行器设计了PPF振动抑制控制器,采用最优二次型的原理对多模态抑制的PPF控制器参数进行了优化。袁国平等[13]采用H∞振动抑制控制器和自适应鲁棒姿态控制器相结合的方法,提高了姿态控制的精度。
针对机动飞行器,当挠性附件的挠性较大时,对挠性结构的振动抑制不仅需要考虑挠性附件与中心刚体的转动耦合特性,还应当考虑平移耦合特性。Sabatini等[14-15]对具有对称帆板布局的飞行器动力学进行了研究,将平移耦合模态和转动耦合模态描述为对称模态和反对称模态;且提出了几种前馈振动抑制控制方法提高姿态控制效果,并且在一个气浮式模拟器上进行了试验验证。
本文在同时考虑转动耦合模态和平移耦合模态的基础上,采用压电元件对大挠性结构进行主动振动抑制。首先建立了包含转动耦合和平移耦合模态的动力学模型,推导了耦合模态参数;然后基于MPPF控制律,设计了对转动耦合模态和平移耦合模态同时进行抑制的主动振动控制器,并采用M范数方法进行了参数优化,采用压电智能材料构建了主动振动控制系统。
1 机动飞行器耦合动力学模型与耦合模态参数 针对处于无约束状态的机动飞行器建立完整的耦合动力学模型。将带有双侧对称帆板的飞行器简化为中心刚体加挠性梁的模型,为了研究方便,仅考虑面内的运动,坐标系定义如图 1所示,图中OXYZ为惯性坐标系; 飞行器轨道机动位移为z; 姿态机动角度为θ; 帆板动挠度为w(y, t),其中y为帆板上某点与帆板安装点的距离。
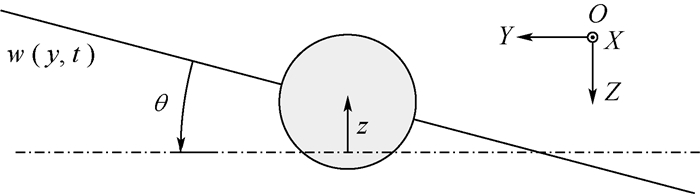 |
| 图 1 带有双侧对称帆板的飞行器模型 Fig. 1 Spacecraft model with two-side symmetric solar planes |
| 图选项 |
1.1 耦合动力学模型 带挠性附件的飞行器为多柔体结构,多采用混合坐标法描述其动力学特性。通常,混合坐标法中的耦合系数通过悬臂状态下帆板的有限元模型计算得到,当飞行器在空间中处于自由-自由的状态时,挠性结构的振动模态和频率与悬臂状态不相同。为了建立自由-自由状态下的动力学模型,将带有双侧对称帆板的飞行器简化为一个无约束梁模型,对应悬臂状态下帆板的第1阶模态,飞行器整体的耦合模态振型[14-15]如图 2所示。
 |
| 图 2 飞行器整体的耦合模态振型[14-15] Fig. 2 Global coupling model shape of spacecraft[14-15] |
| 图选项 |
当飞行器做平移运动时,平移耦合模态振型被激发;当飞行器做转动运动时,转动耦合模态振型被激发。对于同时进行姿态和轨道机动的机动飞行器,其挠性结构的振动同时存在这2个模态。推而广之,针对挠性帆板在悬臂状态下的某一阶弯曲模态,总是对应着自由-自由状态下飞行器整体的两阶弯曲模态:平移耦合模态和转动耦合模态。仅考虑前N阶模态,带有双侧对称帆板的机动飞行器耦合动力学描述为
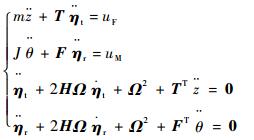 | (1) |
式中:m和J分别为中心刚体的质量和转动惯量;T∈R1×N和F∈R1×N分别为在质心坐标系下描述的挠性帆板平移耦合系数和转动耦合系数;ηt∈RN和ηr∈RN分别为平移耦合模态坐标和转动耦合模态坐标;H=diag(ξk),Ω=diag(ωk),ξk和ωk分别为挠性帆板在悬臂状态下测量得到的第k阶模态阻尼和模态频率;uF和uM分别为驱动力和力矩。
1.2 耦合模态参数 令式(1)中uF=0,uM=0,消去
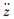
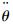
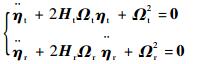 | (2) |
式中:
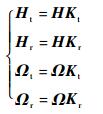 |
其中:Kt=diag(κtk),κtk=(1-2Fk2/m)-1/2; Kr=diag(κrk),κrk=(1-2Tk2/J)-1/2; Fk和Tk分别为F和T的第k个元素。
一般来说帆板的质量较轻,但惯量较大,针对其中第k阶模态,各个频率存在以下关系:κtk < κrk?ωk < ωtk < ωrk,ωtk和ωrk分别为Ωt和Ωr对角线上第k个元素,表示平移耦合模态频率和转动耦合模态频率。目前飞行器的质量惯量分布仍是中心刚体占优,ωk、ωtk和ωrk比较接近。
2 控制系统设计 飞行器在机动时,其挠性帆板的振动包含平移耦合模态和转动耦合模态。为了防止因振动而导致轨道控制和姿态控制的精度降低,甚至发散,采用压电元件对挠性帆板进行振动抑制。设计振动抑制控制器时,要考虑2种模态的存在,针对这2种模态进行振动抑制。将压电传感器和压电执行器对位粘贴在挠性帆板表面,设在帆板长度方向上布有p对传感器执行器,Si为第i号传感器,Ai为第i号执行器,帆板安装坐标系OXpYpZp如图 3所示,压电片长度方向坐标为(yi1, yi2),宽度方向中轴坐标为x0,帆板的长度为l。
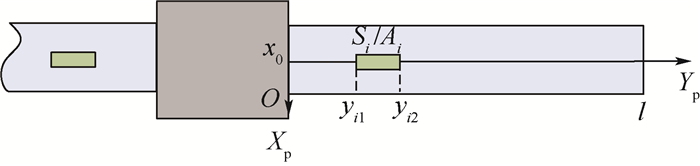 |
| 图 3 压电元件基本配置 Fig. 3 Basic configuration of piezoelectric elements |
| 图选项 |
2.1 压电传感器建模 压电片式传感器利用压电效应,当传感器发生应变时,传感器上下表面的电极会产生电荷,通过线性电荷放大器,得到电压模拟量,从而测量得到传感器处的平均应变。压电片式传感器具有一个主方向,其电荷量的变化与主方向上的应变成正比,压电片式传感器的主方向为Yp方向,即帆板的长度方向。
当飞行器做姿态和轨道机动时,压电片式传感器测量得到的应变是整体机动产生的应变和挠性振动产生的应变的叠加,如图 4所示。
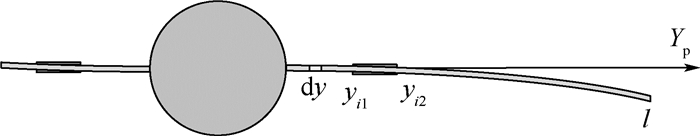 |
| 图 4 挠性结构弯曲引起压电片应变 Fig. 4 Strain of piezoelectric elements caused by bending of flexible structure |
| 图选项 |
设帆板上某一点挠度为w(y, t),根据欧拉-伯努利梁假设,可得
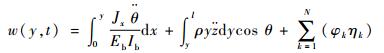 | (3) |
式中:

式(3)等号右边第1项为整体转动运动导致的挠度变化,第2项为整体平移运动导致的挠度变化,第3项为挠性帆板振动带来的挠度变化。前2项是整体机动带来的测量偏置量。
压电片式传感器所产生的电荷量Qi与应变关系[9]为
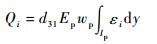 | (4) |
式中:d31为压电常数; Ep为压电材料弹性模量;wp为压电片宽度;εi为第i片压电陶瓷片长度方向上的应变; lp为压电片长度。
利用欧拉-伯努利梁假设,可得应变与挠度关系:
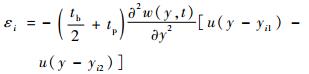 | (5) |
式中:u(y)为阶跃函数;tb和tp分别为帆板和压电片的厚度。
将式(3)、式(5)代入式(4)得
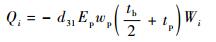 | (6) |
式中:
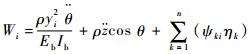
设电荷放大器增益为gs,则电荷放大器输出电压为
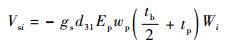 | (7) |
定义:
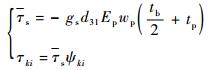 |
如果不考虑整体机动带来的偏置量,则输出电压与模态坐标之间的关系为
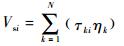 | (8) |
2.2 压电执行器建模 压电执行器的原理是逆压电效应,在压电片式执行器2个表面电极上施加电压,会在其主方向上产生应变,从而对帆板产生弯矩的作用,第i个执行器电压Vai(t)与弯矩Mi的关系如下:
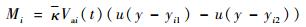 | (9) |
式中:κ为与帆板、压电陶瓷尺寸和弹性模量有关的常数;Vai(t)为第i个执行器上施加的电压。模态坐标与压电执行器电压的关系可以描述为
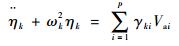 | (10) |
式中:γki=ψkiκ/ρ。
2.3 控制器设计 针对第k阶模态,并只考虑对位安装一个压电传感器和一个压电执行器,即i=1,令τk=τk1,γk=γk1,MPPF控制律的基本结构为
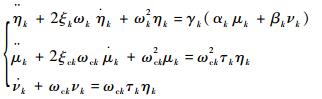 | (11) |
式中:第1行为第k阶模态的动力学方程;第2行为刚度补偿器;第3行为阻尼补偿器;ξck为控制器阻尼;ωck为控制器频率,一般选择ξck?ξk,ωck=ωk;αk和βk分别为刚度增益和阻尼增益;μk和νk为控制器中间变量。
考虑前Nc阶平移耦合模态和前Nc阶转动耦合模态,MPPF控制系统可描述为
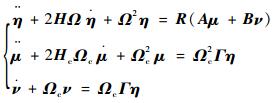 | (12) |
式中:
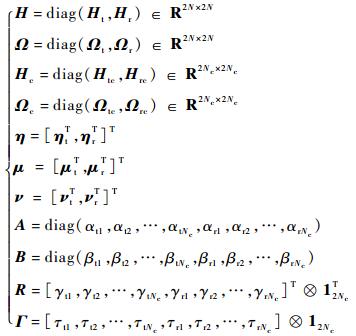 |
其中:12Nc为全1列矢量;?为克罗内克积; 变量的下标中,t和r分别表示平移耦合模态和转动耦合模态,Htc=diag(ξtck),ξtck为第k阶平移耦合模态对应的控制器阻尼;μt=[μt1, μt2, …, μtNc]T,νt=[νt1, νt2, …, νtNc]T,μtk和νtk为第k阶平移耦合模态对应的控制变量,同样的方式可以定义第k阶平移耦合模态对应的参数αtk、βtk、γtk和τtk,以及其他对应第k阶转动耦合模态的参数。
利用文献[8]中的定理2,可得式(12)描述的系统的稳定性条件,即矩阵A和B满足
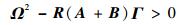 | (13) |
结构振动在模态频率处有最大的振幅,如果将模态频率处传递函数的增益降低到最小,并满足系统的稳定性条件式(13),就能达到最优的振动抑制效果。为了获得最优的控制器参数矩阵,令D=HΩ,并考虑在执行器上施加激励干扰d,系统的状态空间描述如下:
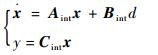 | (14) |
式中:
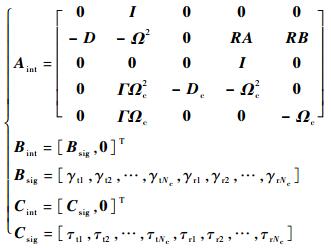 |
则闭环传递函数为
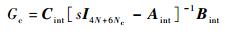 | (15) |
设置评价函数[16]为M范数
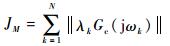 | (16) |
式中:λk为根据每个振动模态的重要性设计的权重。
3 仿真分析 为了验证所设计控制器的有效性,设置中心刚体加双侧挠性板构型的结构,如图 5所示,图中惯性坐标系定义与图 1相同,单块挠性板质量为2.5 kg,长度为1 700 mm,宽度为200 mm,相对于中心刚体旋转轴的惯量为5 kg·m2,中心刚体为圆柱形,直径800 mm,高300 mm,质量为260 kg,绕X轴的惯量为60 kg·m2,压电元件的粘贴位置如图所示,设置一对传感器/执行器(S1/A1)对位于板根部,压电元件的长度为40 mm,宽度20 mm,厚度0.2 mm,压电常数d31=-190 pC/N。
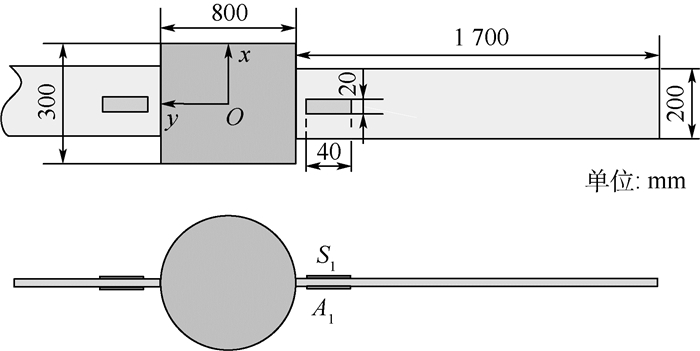 |
| 图 5 仿真配置 Fig. 5 Simulation configuration |
| 图选项 |
3.1 参数优化 挠性板的振动主要是前两阶振动,取截断模态阶数N=2,且Nc=2,采用有限元的方法得悬臂状态下挠性板的模态频率(单位为rad/s)为
Ω=2πdiag(0.761, 9.025)
结构阻尼设置为
H=diag(0.002, 0.002)
计算挠性板悬臂状态下前两阶弯曲模态的耦合系数
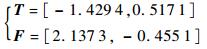 |
其中:T的单位为
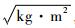

根据2.2节,可得耦合模态频率
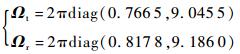 |
频率大小满足Ω < Ωt < Ωr。
采用以上参数,构成式(14),闭环系统具有2个输入,u=[uF, uM],驱动力激发平移耦合模态,驱动力矩激发转动耦合模态,分别采用M范数根据系统频率响应特性对控制参数A和B进行优化,得
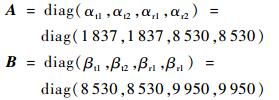 |
加入优化参数后,振动抑制控制与不加振动抑制控制的系统的频率响应曲线如图 6所示。
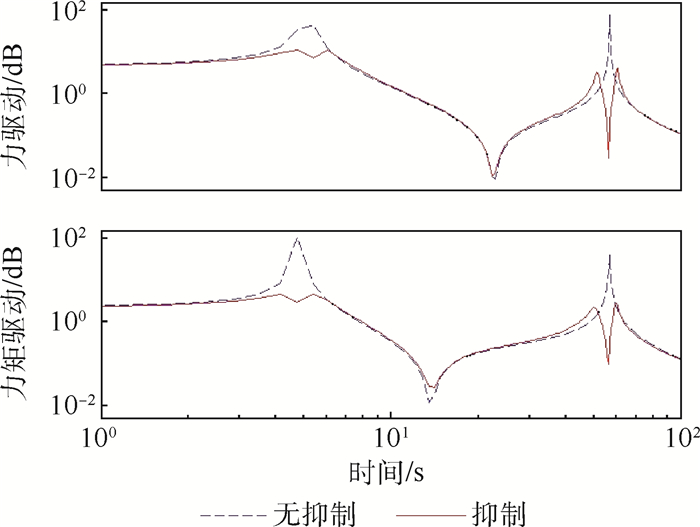 |
| 图 6 系统幅频响应曲线 Fig. 6 System amplitude frequency response curves |
| 图选项 |
由图中可以看出,经过参数优化后,2种输入下的幅频响应曲线在共振频率点的增益与不进行抑制相比均大大降低。
3.2 仿真算例及结果分析
3.2.1 仿真算例1 采用MATLAB/Simulink构建仿真模型,飞行器采用路径规划的方法生成指令路径,采用PID控制器进行位姿闭环控制,推力器的开关指令由PWM调制器生成,控制周期和调制周期均为100 ms,考虑位姿传感器测量误差和系统时延等的干扰,初始位置为(0, -3 266, 1 878) mm,欧拉角描述的初始姿态为(-5.02 6°, 0°, 0°),目标位置为(0, -3 266, 2 878) mm,目标角度为(0°, 0°, 0°),以完成一次典型的跟踪指向任务,在机动过程中挠性板的振动被激发。
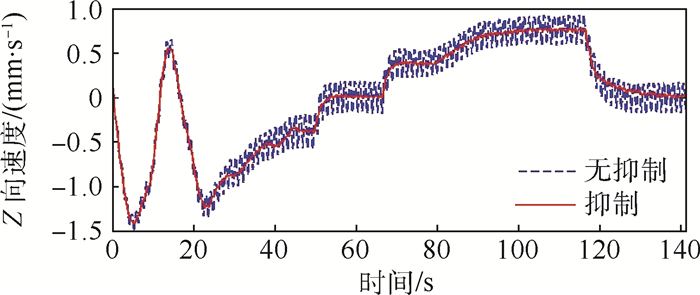
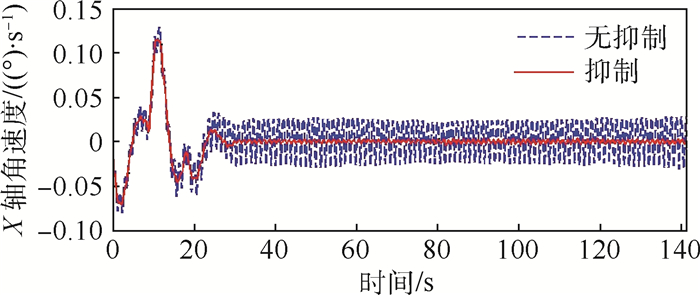
以Z方向速度跟踪误差、绕X轴角速度跟踪误差和挠性帆板与中心刚体相互作用的力矩为最终评价指标,如图 7~图 12所示,图中无抑制表示不加振动抑制控制,抑制表示进行振动抑制控制。
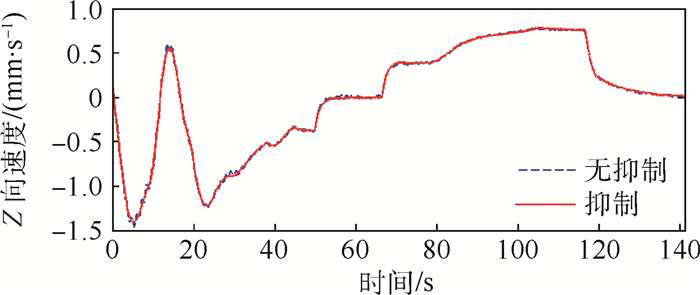 |
| 图 7 Z向速度(算例1) Fig. 7 Z-direction velocity (Example 1) |
| 图选项 |
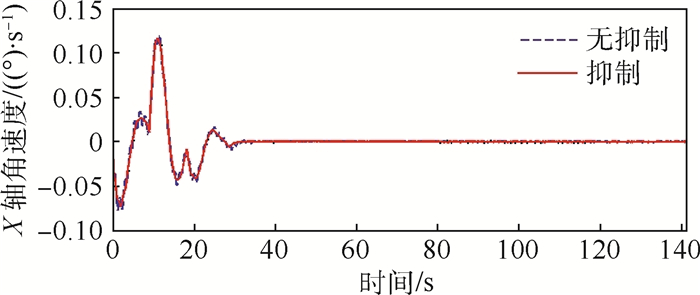 |
| 图 8 X轴角速度(算例1) Fig. 8 X-axis angular velocity (Example 1) |
| 图选项 |
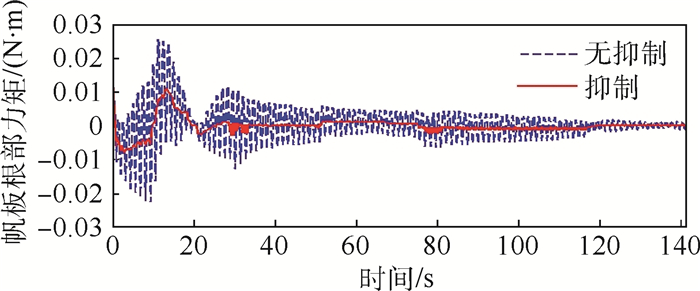 |
| 图 9 帆板根部力矩(算例1) Fig. 9 Solar plane root moment (Example 1) |
| 图选项 |
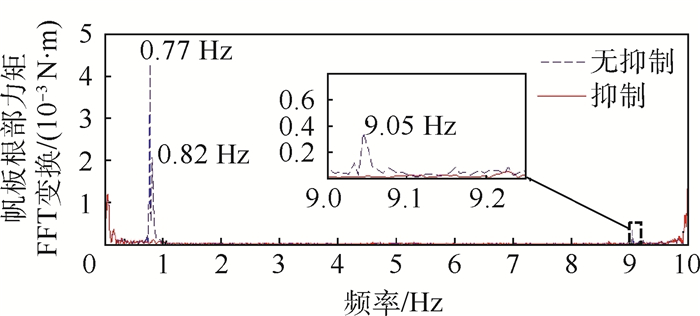 |
| 图 10 帆板根部力矩的FFT变换(算例1) Fig. 10 FFT transform of solar plane root moment (Example 1) |
| 图选项 |
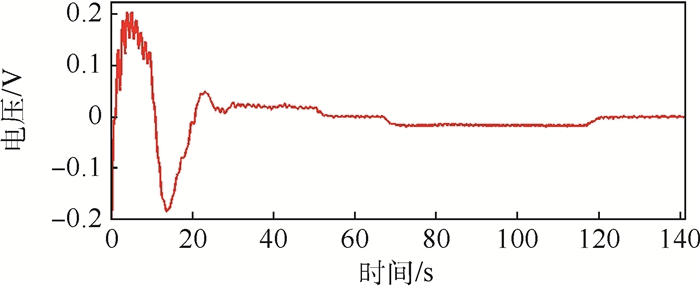 |
| 图 11 传感器采集电压(算例1) Fig. 11 Sensor voltage (Example 1) |
| 图选项 |
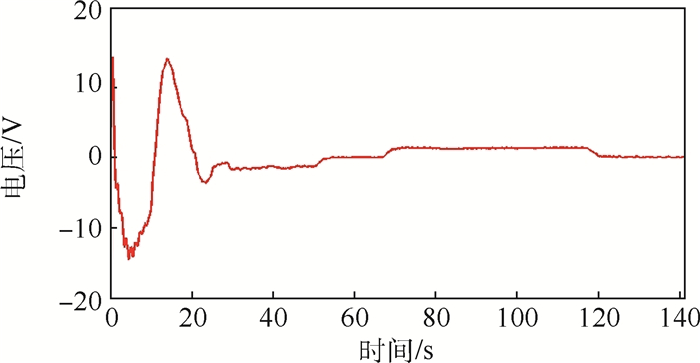 |
| 图 12 执行器输入电压(算例1) Fig. 12 Actuator input voltage(Example 1) |
| 图选项 |
从根部力矩的FFT变换上可以看出在0.761 Hz频率附近存在平移耦合模态频率0.77 Hz和转动耦合模态频率0.82 Hz,振幅较大,在9.025 Hz附近存在平移耦合模态频率9.05 Hz,该平移耦合模态被轻微激发,但加入振动抑制后,被抑制下来,几乎没有振幅,转动耦合模态没有被激发,帆板的振动主要是第1阶面外弯曲模态振动,对应着机动飞行器整体的第1阶平移耦合模态振动和第1阶转动耦合模态振动。从X轴角速度曲线上可以看出,在不进行振动抑制时,挠性帆板的振动会使角速度出现小的波动,这将影响机动过程中的跟踪指向精度。帆板的质量相比中心刚体的质量来说很小,因此帆板的振动对Z向位置和速度的影响不大。从挠性帆板根部力矩曲线上可以看出,当整体做位姿机动时,帆板根部力矩有一定的偏置量,不进行振动抑制时挠性振动被激发,而且衰减的很慢,即使飞行器整体稳定下来,具有一定的残余振动,采用MPPF控制器可以很好的将挠性帆板的振动抑制下来。从根部力矩的FFT变换曲线上可以看出,采用MPPF控制器进行抑制后的平移运动耦合模态和转动耦合模态频率位置的能量要远小于不进行抑制时对应频率位置的振动能量,进一步说明了所设计的控制器的有效性。
3.2.2 仿真算例2 设计较为极端的条件进行考核控制器的性能,令机动飞行器受到一个幅值为0.015 N·m、频率为0.82 Hz的绕X轴的简谐振荡的外界干扰力矩,仿真结果如图 13~图 18所示。
 |
| 图 13 Z向速度(算例2) Fig. 13 Z-direction velocity (Example 2) |
| 图选项 |
 |
| 图 14 X轴角速度(算例2) Fig. 14 X-axis angular velocity (Example 2) |
| 图选项 |
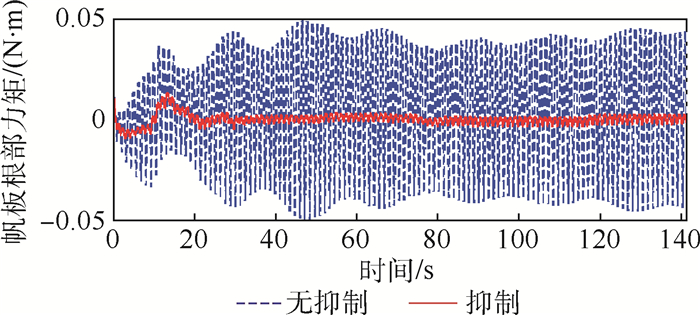 |
| 图 15 帆板根部力矩(算例2) Fig. 15 Solar plane root moment (Example 2) |
| 图选项 |
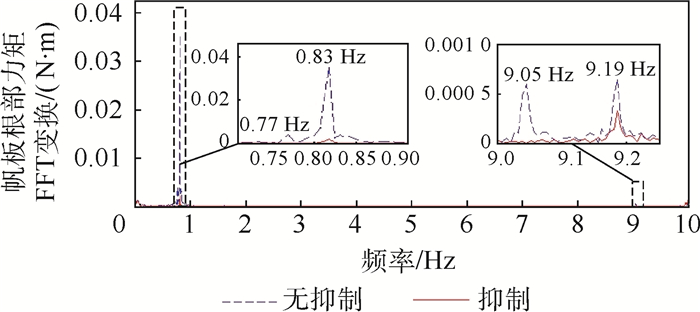 |
| 图 16 帆板根部力矩的FFT变换(算例2) Fig. 16 FFT transform of solar plane root moment (Example 2) |
| 图选项 |
 |
| 图 17 传感器采集电压(算例2) Fig. 17 Sensor voltage (Example 2) |
| 图选项 |
 |
| 图 18 执行器输入电压(算例2) Fig. 18 Actuator input voltage (Example 2) |
| 图选项 |
可以看出,当加入干扰力矩后,如果不进行振动抑制,帆板的振动出现发散现象,Z向速度和X轴角速度的跟踪误差也由于耦合作用而出现振荡发散的现象,Z向位置与X轴角度出现了偏差。加入MPPF振动抑制后,帆板根部力矩振荡被很好地抑制下来,第1阶平移耦合模态和转动耦合模态的振动幅值衰减了90%,没有出现发散的情况,第2阶平移耦合模态和转动耦合模态的振动幅值均有较大的衰减,同时Z向位置和X轴角度的跟踪精度较高,没有出现耦合振荡发散的情况。
4 结论 本文针对集成压电元件的机动飞行器挠性结构振动抑制控制方法进行了研究。
1) 首先建立了自由自由状态下的机动飞行器耦合动力学模型,基于经典欧拉伯努利梁理论,给出了压电执行器模型和压电传感器模型。
2) 根据耦合动力学模型的特点,设计了整合的MPPF控制律,并提出了相应的振动抑制控制器设计方法。
3) 使用MATLAB/Simulink对设计的控制系统进行了仿真,结果表明所设计的控制器能够很好的实现机动飞行器自由自由状态下机动飞行器挠性结构的振动抑制,根部的力矩振动较快收敛,提高了机动飞行器的跟踪精度。
本文所提出的MPPF控制系统同时考虑了机动飞行器挠性结构与中心刚体之间的平移耦合模态和转动耦合模态,能够较好的实现挠性结构的主动振动抑制控制,对提高机动飞行器的跟踪精度具有积极作用。
参考文献
| [1] | 杜华军, 黄文虎, 邹振祝. 航天支架结构的被动振动控制[J].应用力学学报, 2002, 19(3): 10–13. DU H J, HUANG W H, ZOU Z Z. Passive vibration control(PVC) of aerospace supporter[J].Chinese Journal of Applied Mechanics, 2002, 19(3): 10–13.(in Chinese) |
| [2] | 陕晋军, 刘暾. 应用分力合成方法改善柔性系统性能的研究[J].系统仿真学报, 2002, 14(11): 1536–1540. SHAN J J, LIU T. Study on performance improvement of flexible systems using component synthesis method[J].Journal of System Simulation, 2002, 14(11): 1536–1540.DOI:10.3969/j.issn.1004-731X.2002.11.036(in Chinese) |
| [3] | 陕晋军, 刘暾. 挠性结构的输入成型与分力合成主动振动抑制方法研究[J].中国机械工程, 2002, 13(5): 379–383. SHAN J J, LIU T. Study on input shaping and component synthesis method of flexible structure[J].Chinese Journal of Mechanical Engineering, 2002, 13(5): 379–383.(in Chinese) |
| [4] | 胡庆雷, 马广富. 挠性航天器姿态机动控制的主动振动抑制[J].振动工程学报, 2005, 18(3): 375–380. HU Q L, MA G F. Active vibration control of flexible spacecraft during attitude maneuver[J].Journal of Vibration Engineering, 2005, 18(3): 375–380.(in Chinese) |
| [5] | 陈勇, 陶宝祺, 刘果, 等. 柔性结构振动控制的初步分析与试验研究[J].机械强度, 1998, 20(3): 207–211. CHEN Y, TAO B Q, LIU G, et al. Analysis and experimental study on the vibration control of flexible structures[J].Journal of Mechanical Strength, 1998, 20(3): 207–211.(in Chinese) |
| [6] | BALAS M J. Active control of flexible systems[J].Journal of Optimization Theory and Applications, 1978, 25(3): 415–436.DOI:10.1007/BF00932903 |
| [7] | FANSON J L, CAUGHEY T K. Positive position feedback control for large space structures[J].AIAA Journal, 1990, 28(4): 717–724.DOI:10.2514/3.10451 |
| [8] | MAMODI S N, AHMADIAN M. Active vibration control with modified positive position feedback[J].Journal of Dynamic Systems, Measurement and Control, 2009, 131(4): 442–447. |
| [9] | MOHEIMANI S O R, ANDREW J F. Piezoelectric transducers for vibration control and damping[M].Berlin: Springer, 2006: 9-66. |
| [10] | MAHMOODI S N, AHMADIAN M, INMAN D J. Adaptive modified positive position feedback for active vibration control of structures[J].Journal of Intelligent Systems and Structures, 2010, 21(6): 571–578.DOI:10.1177/1045389X10361631 |
| [11] | GENNARO D. Output stebilizama of flerible spacecraft with active vibration suppresson[J].IEEE Transactrons on Aerospace and Flearanic System, 2003, 39(3): 747–759.DOI:10.1109/TAES.2003.1238733 |
| [12] | 胡庆雷, 马广富. 改进型正位置反馈/变结构卫星姿态主动控制[J].振动工程学报, 2007, 20(4): 324–329. HU Q L, MA G F. Maneuvering and vibration damping of flexible spacecraft using adaptive variable structure control and suboptimal positive position feedback[J].Journal of Vibration Engineering, 2007, 20(4): 324–329.(in Chinese) |
| [13] | 袁国平, 史小平, 李隆. 飞行器姿态机动的自适应鲁棒控制及主动振动抑制[J].振动与冲击, 2013, 32(12): 110–115. YUAN G P, SHI X P, LI L. Adaptive robust attitude maneuver control of a flexible spacecraft with active vibration suppression[J].Journal of Vibration and Shock, 2013, 32(12): 110–115.DOI:10.3969/j.issn.1000-3835.2013.12.021(in Chinese) |
| [14] | GASBARRI P, SABATINI M, LEONANGELI N, et al. Flexibility issues in discrete on-off actuated spacecraft:Numerical and experimental tests[J].Acta Astronautica, 2014, 101: 81–97.DOI:10.1016/j.actaastro.2014.04.012 |
| [15] | SABATINI M, GASBARRI P, PALMERINI G B. Delay compensation for controlling flexible space multibodies:Dynamic modeling and experiments[J].Control Engineering Practice, 2015, 45: 147–162.DOI:10.1016/j.conengprac.2015.09.013 |
| [16] | OMIDI E, MCCARTY R, MAHMOODI S N. Implementation of modified positive velocity feedback controller for active vibration control in smart structures[C]//Conference on Active and Passive Smart Structures and Integrated Systems. Bellingham: SPIE, 2014, 9057: 90571N.http://spie.org/x648.xml?product_id=2044478 |
