目前国内外对移动机器人的空间姿态模型进行了大量的研究。徐坤等针对六轮腿式机器人,提出了建立单腿正运动学和逆运动学模型的方法[4]。周开波等通过对六轮摇臂式探测车的分析,利用位姿变换矩阵推导出了空间姿态参数与轮心相对位置之间的运动学关系[5]。崔莹和高峰针对四轮摇臂悬架可变直径轮月球探测车,以闭链坐标变换和瞬时重合坐标法为基本工具,推导出了运动学模型逆解的理论解法[6]。然而,移动机器人空间位姿与路面环境间的运动学关系往往是非线性的,传统的求解方法较为复杂,难以满足控制系统实时性的需求。遗传算法采用选择、交叉和变异算子进行搜索,具有较强的全局求解能力。使用结合非线性规划的遗传算法对约束条件下的移动机器人运动学模型求解,将会在很大程度上降低求解过程的复杂程度[7]。
本文的研究对象是具有平衡摇臂机构的移动机器人,针对其在越过障碍时的主动姿态控制算法进行研究,并设计基于非线性规划遗传算法的姿态控制算法,关键点包括:①移动机器人空间姿态与障碍路面间的数学关系的推导;②遗传算法适应度函数的设计。
本文首先利用空间机构学位姿变换方程,推导出移动机器人空间姿态参数与轮心相对位置之间的数学关系。其次,在考虑到移动机器人越障过程中工作平台的俯仰角、侧倾角以及质心的波动等因素下,设计了基于机器人运动学模型的遗传算法适应度函数,利用非线性规划遗传算法求解得到目标姿态控制参数。
1 平衡摇臂式移动机器人机构原理 平衡摇臂式移动机器人的移动装置采用了连杆平衡机构与摇臂支腿机构,包括支腿、摇臂、拉杆、平衡杆和机器人主体5部分,是一类新型的移动平台。工作平台固定于平衡摇臂式移动机器人主体上,如图 1所示。摇臂、拉杆与平衡杆构成平衡摇臂机构,起到均化两侧摇臂的俯仰扰动输入的作用;该机构的另一个重要作用是调整移动机器人重力在各轮上的分配[8]。摇臂支腿机构通过旋转副与移动机器人主体连接,实现越障过程中四轮同时着地。采用该类移动装置的移动机器人具有较强的仿地形能力。
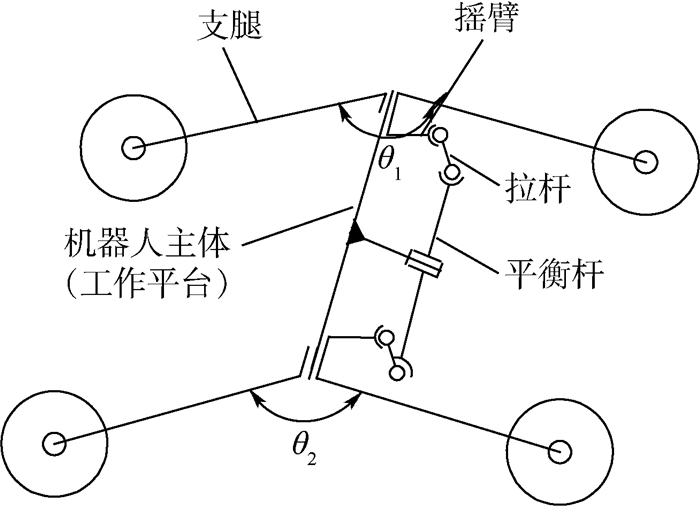 |
| 图 1 平衡摇臂式移动机器人简化模型 Fig. 1 Simplified model of balancing-arm mobile robot |
| 图选项 |
平衡摇臂式移动机器人主动姿态控制是通过调节两侧支腿间的夹角θ1与θ2实现的。同时调节θ1与θ2的大小,能够实现调整整机的离地间隙,提高通过性能;分别调节θ1与θ2为不同值,能够实现两侧离地间隙不同,提高越障平稳性。
2 平衡摇臂式移动机器人空间姿态建模 平衡摇臂式移动机器人具有自适应路面和主动姿态调整的特点,在越障过程中,其空间姿态是关于障碍路面的变化过程。移动机器人的主动姿态控制以障碍路面作为输入量,空间姿态作为控制量与目标量。针对该类移动机器人,定义表征其空间状态的参数,并推导出空间姿态与障碍路面之间的关系,为设计主动姿态控制算法提供理论依据。
2.1 空间姿态参数定义与坐标系建立 平衡摇臂式移动机器人在越过障碍时具有变化的空间姿态。定义四轮等高且两侧支腿间夹角为初始值时的状态为初始状态,并建立如图 2所示坐标系。图中,O0X0Y0Z0为空间绝对坐标系;O1X1Y1Z1原点与移动机器人传动轴中心位置重合,X1轴水平指向移动机器人前进方向,相对于工作平台固结;O2X2Y2Z2与O3X3Y3Z3分别与旋转副J1、J7旋转中心重合。其中,O2X2Y2Z2与右侧摇臂相固结,绕运动副J1转动;O3X3Y3Z3与左侧摇臂相固结,绕运动副J7转动。w1~w4分别表示4个轮心在O0X0Y0Z0中的坐标值。
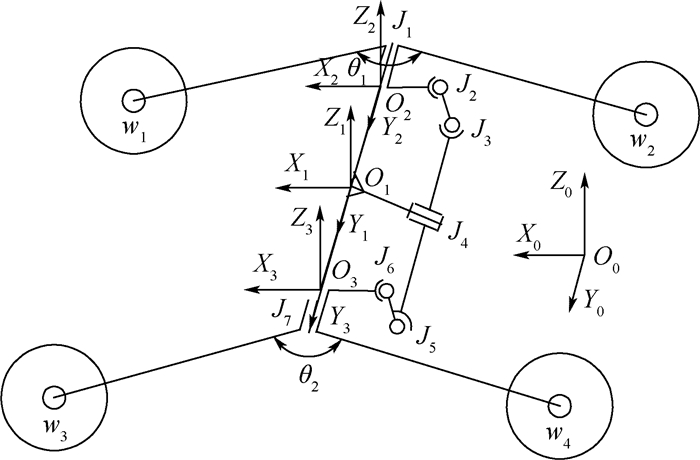 |
| 图 2 平衡摇臂式移动机器人空间坐标系 Fig. 2 Space coordinate system of balancing-arm mobile robot |
| 图选项 |
移动机器人在越过障碍的过程中,空间姿态不同于初始状态,将O1X1Y1Z1原点平移到空间绝对坐标原点,如图 3所示。定义γ1、γ2分别为工作平台的俯仰角和侧倾角并取其为表征移动机器人工作平台空间姿态的参数,可确定铰链点J1、J4和J7在O0X0Y0Z0中的坐标值;平衡杆与X1轴间夹角记为α,两侧支腿摇臂机构围绕X1轴的转动角度记为φ1、φ2,如图 4所示。取α为已知姿态参数,根据平衡摇臂机构的运动关系,可确定铰链点J2、J3、J5和J6在O0X0Y0Z0中的坐标值以及φ1、φ2的角度值;根据右侧支腿夹角θ1,左侧支腿夹角θ2可最终确定轮心w1~w4的空间位置。故,定义表征平衡摇臂式机器人空间姿态的参数为γ1、γ2、θ1、θ2和α。
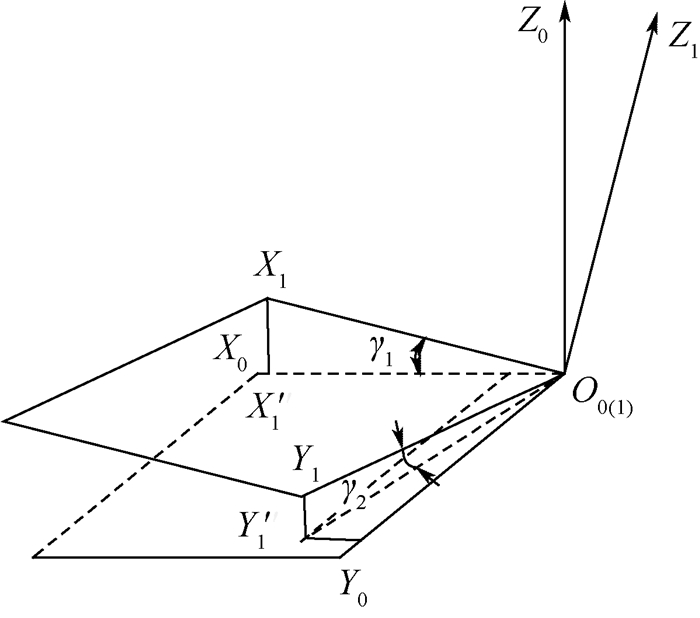 |
| 图 3 机器人主体坐标系与空间绝对坐标系的位置关系 Fig. 3 Position relationship between robot body coordinate system and space absolute coordinate system |
| 图选项 |
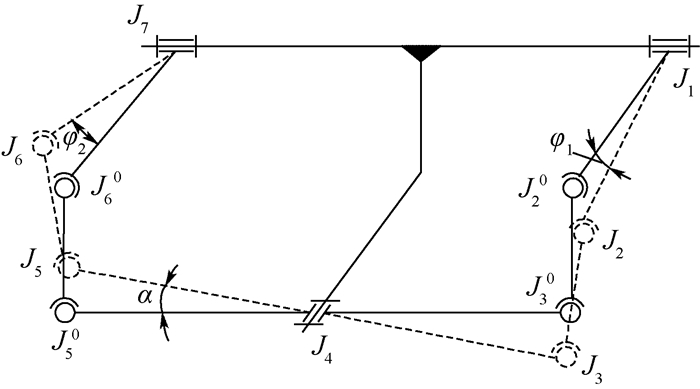 |
| 图 4 平衡摇臂机构简图 Fig. 4 Schematic diagram of mechanism with balancing-arm |
| 图选项 |
2.2 平衡摇臂机构运动关系 平衡摇臂机构由摇臂、拉杆以及平衡杆组成,进行合理的简化,得到如图 4所示的机构模型。该机构可看作2个对称的RSSR空间连杆机构(R为旋转副,S为球面副)。
平衡杆绕旋转副J4旋转角度α,铰链点J3在O1X1Y1Z1中的坐标将由初始点J30变为
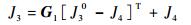 | (1) |
式中:G1为J3点空间坐标变换矩阵,
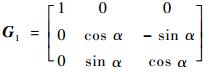 | (2) |
右侧摇臂绕Y1轴转动角度φ1,J2点的坐标将由初始点J20变为
 | (3) |
式中:G2为J2点空间坐标变换矩阵,
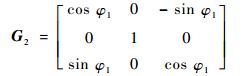 | (4) |
考虑到拉杆的长度为恒定值,记为l,则有
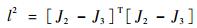 | (5) |
将式(1)、式(3)代入式(5)可建立右侧摇臂相对于移动机器人主体的转角φ1与α之间的关系:
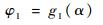 | (6) |
同理,可建立左侧摇臂绕移动机器人主体的转角φ2与α的关系:
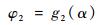 | (7) |
2.3 空间姿态参数与轮心相对位置之间的关系 为推导出空间姿态参数与障碍路面之间的关系,定义4个轮心的空间绝对坐标为
 | (8) |
首先,建立O1X1Y1Z1与O0X0Y0Z0之间的坐标变换矩阵,包括平移变换矩阵和旋转变换矩阵。将O1X1Y1Z1进行平移,使原点O1与空间绝对坐标系原点O0重合。可得到平移变换矩阵:
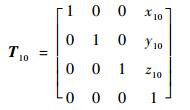 | (9) |
式中:x10、y10、z10为O1与O0在绝对坐标系下的坐标差。
将两坐标系各轴所在单位向量作为三维空间的2组基向量,分别记为[αx,αy,αz]与[βx,βy,βz][5]。其中[αx,αy,αz]=I,I为单位矩阵。
根据图 3所示的关系,有以下方程:
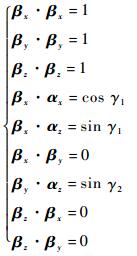 |
且有
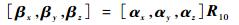 |
故可得旋转坐标变换矩阵:
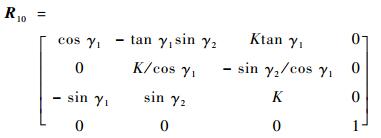 | (10) |
式中:
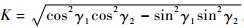
同理,可推导出O2X2Y2Z2和O3X3Y3Z3相对于坐标系O1X1Y1Z1的旋转及平移坐标变换矩阵:
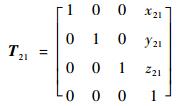 | (12) |
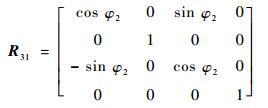 | (13) |
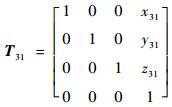 | (14) |
式中:x21、y21和z21为O2与O1在O1X1Y1Z1中的坐标差;x31、y31和z31为O3与O1在O1X1Y1Z1中的坐标差;φ1、φ2可通过式(6)、式(7)由α得到。
根据空间机构学位姿变换方程可得到4个轮心的绝对坐标与空间姿态参数之间的关系方程
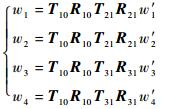 | (15) |
式中:w′1、w′2为右侧2个轮心在O2X2Y2Z2中的坐标值,是关于θ1的函数;w′3、w′4为左侧2个轮心在O3X3Y3Z3中的坐标值,是关于θ2的函数。故定义平衡摇臂式机器人空间姿态与障碍路面之间的正运动学模型:
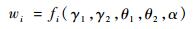 | (16) |
逆运动学模型:
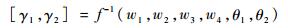 | (17) |
3 姿态控制算法设计 3.1 控制系统模型 移动机器人在越障过程中的主动姿态控制需要综合考虑俯仰角、侧倾角、质心波动等因素,其本质是一个多目标优化控制的过程。遗传算法采用选择、交叉和变异进行搜索,通过设计合理的适应度函数有效地解决此类多目标优化控制的问题。
设计遗传控制算法,对θ1与θ2进行调节,如图 5所示。机器人在越过障碍时,通过安装在其上的传感器获取空间姿态参数,根据式(16)得到各轮心间的相对位置。设计基于非线性规划遗传算法的控制算法,以轮心相对位置为输入量,目标姿态参数作为输出量,实现机器人越障过程空间姿态的实时控制。
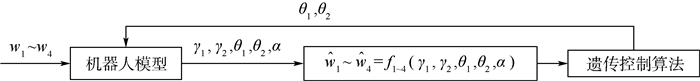 |
| 图 5 姿态控制算法框图 Fig. 5 Block diagram of attitude control algorithm |
| 图选项 |
3.2 非线性规划遗传算法控制器设计 在多目标优化求解问题中,遗传算法具有较强的全局搜索能力,但局部搜索能力不足;而非线性规划具有较强局部搜索能力[9-10]。为提高算法的速度与效率,将非线性规划与遗传算法相结合,利用遗传算法进行全局搜索,非线性规划算法进行局部搜索,以得到全局最优解。
设计非线性规划遗传算法如图 6所示, 图中M为整数。在合理的范围内随机产生控制参数θ1、θ2,并将每一个体代入式(17)中,得到机器人相应的俯仰角、侧倾角。以移动机器人稳定性为约束设计适应度函数,得到不同个体的适应度值。从随机产生的初始解的位置开始进行搜索,按照遗传算法进化法则进行选择、交叉、变异操作产生新的解。当进化一定的代数时,采用非线性寻优的方法,以加快进化[11-13]。
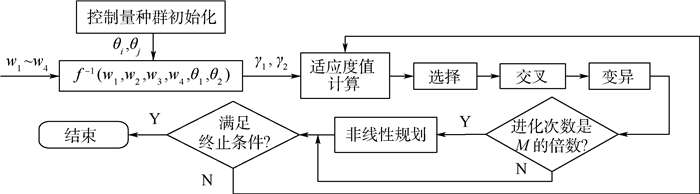 |
| 图 6 非线性规划遗传算法框图 Fig. 6 Block diagram of nonlinear programming genetic algorithm |
| 图选项 |
1) 遗传算法种群边界
合理的设置及更新遗传算法的种群边界能够提高控制算法的计算效率。种群边界更新规则如下所示:
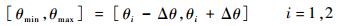 | (18) |
式中:θi为当前支腿夹角;
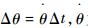
2) 适应度函数设计
适应度函数是进行自然选择的依据[14]。移动机器人工作平台的平稳性影响因素包括俯仰角、侧倾角、质心波动等。从移动机器人的稳定性出发,还需要保证控制参数变化量Δθ1与Δθ2尽可能得小。因此,设计遗传算法适应度函数如下:
 | (19) |
式中:Δh为质心高度变化幅值。该适应度函数可分为3部分:第1部分表征工作平台俯仰和侧倾的角度;第2部分表征支腿夹角的调节量;第3部分表征机器人越障过程中质心高度的变化。其中a为支腿夹角变化量对机器人平稳性的影响因子,b为质心波动对移动机器人工作平台平稳性的影响因子。
3) 选择操作
根据不同个体的适应度函数值按照一定的概率选择优良的个体组成新的种群,以繁殖得到下一代个体。选用轮盘赌法对个体进行选择,即基于适应度的选择策略,第i个个体被选中的概率为
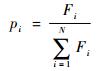 | (20) |
式中:Fi为个体适应度函数值;N为种群个体数目。
4) 交叉操作
从种群中随机选择2个个体,通过2个染色体的交换组合,将父代的优秀特征遗传给子代,从而产生优秀的个体[14]。第k个染色体ak和第m个染色体am在j位置进行交叉操作方法为
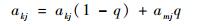 | (21) |
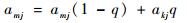 | (22) |
式中:q为[0, 1]区间的随机数。
5) 变异操作
从种群中随机选取一个个体,并选择一点进行变异以产生优秀的个体。变异操作的主要目的是维持种群多样性。第i个个体的第j个基因aij进行变异的操作方法为
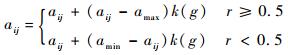 | (23) |
式中:[amin, amax]为基因aij边界;k(g)=r2(1-g/Dmax)2,r2为一个随机数,g为当前迭代次数,Dmax为最大进化次数;r为[0, 1]区间上的随机数。
6) 非线性寻优
当遗传算法进化一定的代数后,以所得到的结果为初始值,利用非线性规划的方式进行局部寻优,并将局部寻优得到的最优值作为新个体染色体继续进化。
4 仿真验证与分析 为验证所设计的基于非线性规划遗传算法的姿态控制器的性能,在ADAMS软件建立移动机器人模型和障碍路面模型,并联合MATLAB/Simulink对机器人进行了运动学仿真[15-16]。仿真所用的平衡摇臂式移动机器人结构尺寸参数如图 7所示。非线性规划遗传算法参数设计如下:最大进化次数n设为30,种群大小为50,影响因子a为0.005,影响因子b的值为0.1,进化次数为10的整数倍时进行非线性规划寻优。以上参数的设置是在多次进行仿真实验的基础上确定的。
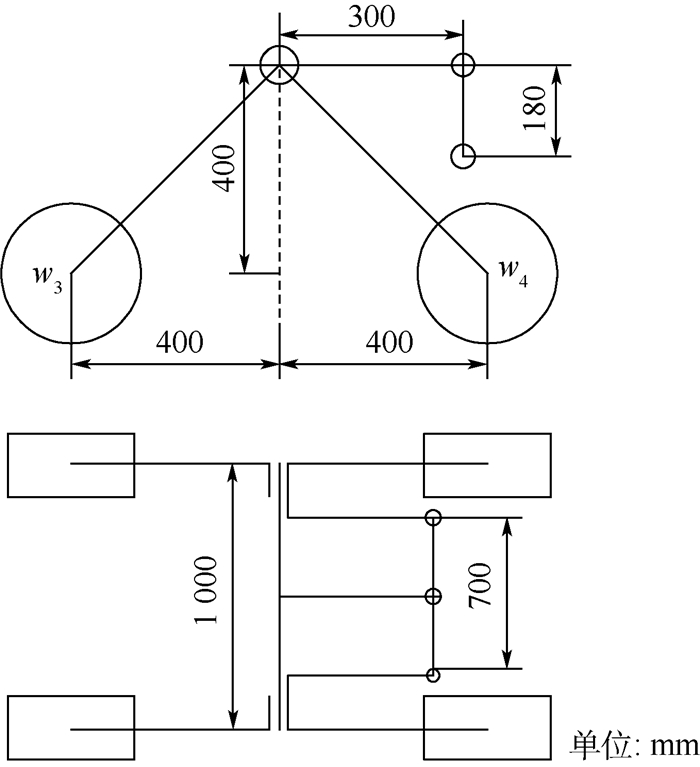 |
| 图 7 平衡摇臂式移动机器人结构尺寸参数 Fig. 7 Structural dimension parameters of balancing-arm mobile robot |
| 图选项 |
对移动机器人匀速通过一段障碍路面时进行仿真,并假设移动机器人越障过程为准静态过程。路面设计如式(24)~式(26)所示。该路面下,4个轮心的高度与行驶距离间的关系如下:
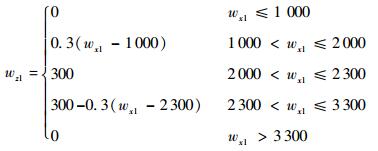 | (24) |
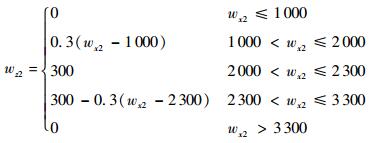 | (25) |
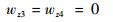 | (26) |
式中:wx1=400+v0t,wx2=-400+v0t,v0为机器人移动速度。该段路面下,移动机器人共经历8种状态,如图 8所示。
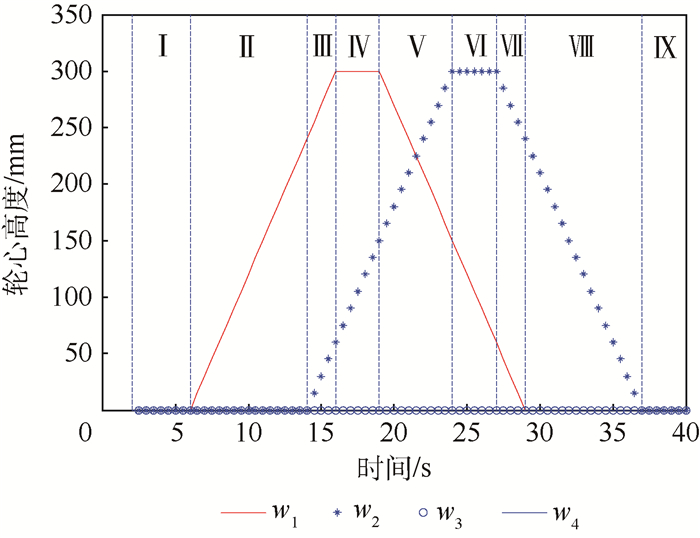 |
| 图 8 轮心相对位置随时间变化 Fig. 8 Variation of wheel centret relative position with time |
| 图选项 |
在ADAMS软件中搭建移动机器人和路面模型,并联合MATLAB/Simulink对控制算法进行仿真。图 9所示为移动机器人越障过程中姿态调整的机构演示图,调节两侧支腿间的夹角,以保持移动机器人的平稳性。为了验证所设计的基于非线性规划遗传算法的控制算法对机器人越障性能的提升,进行了3个仿真实验。仿真实验1中,移动机器人越障过程中支腿间夹角始终保持初始值;仿真实验2采用本文所设计的基于非线性规划遗传算法的控制法对两侧支腿间夹角进行主动控制;仿真实验3采用单一的遗传控制算法对两侧支腿间夹角进行主动控制,以验证非线性规划对姿态控制效果的影响。其中,仿真实验3与仿真实验2中的遗传算法设置相同参数。
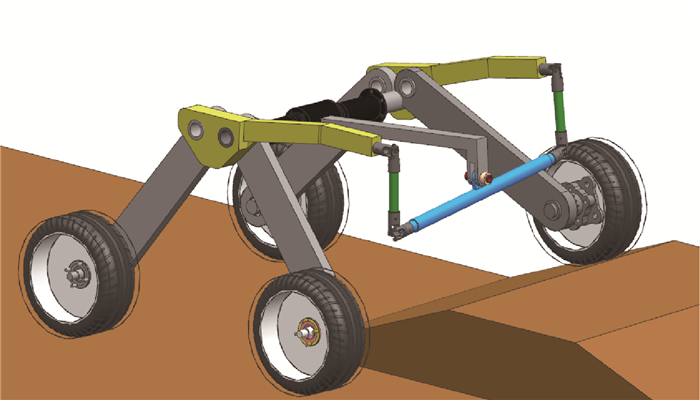 |
| 图 9 姿态调整机构演示图 Fig. 9 Mechanism demonstration for attitude adjusting |
| 图选项 |
3组仿真实验中移动机器人的侧倾角和质心高度变化分别如图 10、图 11所示。移动机器人匀速通过障碍路面时,在所设计的控制算法下,与不施加主动姿态控制相比较,最大侧倾角由10.8°降低到了1.8°,质心高度变化幅度由96.4 mm降低到了34.9 mm;而与单一的遗传算法相比较,所设计的姿态控制算法能够在较少的进化迭代次数下达到较优的控制效果。主动姿态控制算法的设计过程中,适应度函数由移动机器人侧倾角、质心波动范围以及支腿间夹角调节量决定。因此,该控制算法在移动机器人越障过程中降低侧倾角和质心波动范围方面表现出较优的控制性能。
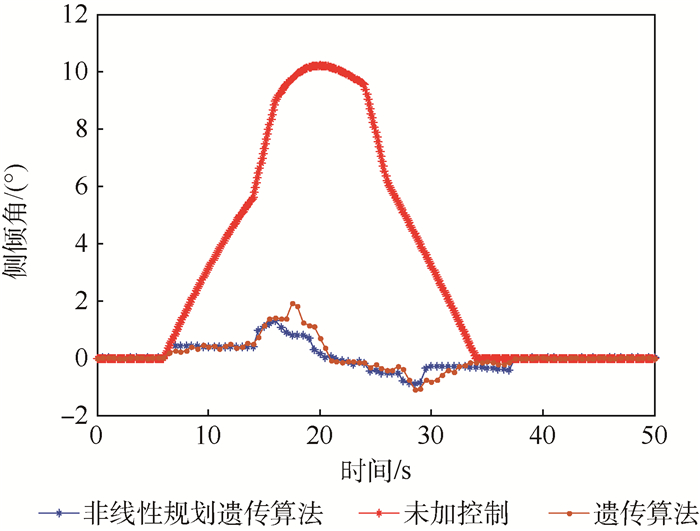 |
| 图 10 侧倾角随时间变化关系 Fig. 10 Variation of roll angle with time |
| 图选项 |
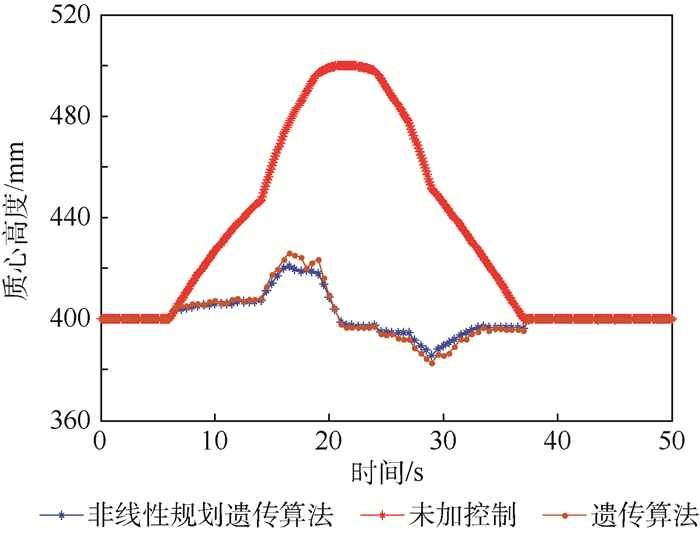 |
| 图 11 质心高度随时间变化关系 Fig. 11 Variation of height of mass center with time |
| 图选项 |
5 结论 本文针对具有平衡摇臂机构的移动机器人越障时的姿态控制问题,设计了一种基于非线性规划遗传算法的主动姿态控制算法,以实现移动机器人平稳性的通过障碍路面。在ADAMS中搭建移动机器人和障碍路面模型,并联合MATLAB/Simulink进行了运动学仿真。仿真结果表明:
1) 在所设计的姿态控制算法下,与不施加主动姿态控制相比较,移动机器人越障过程中最大侧倾角由10.8°降低到了1.8°,质心高度变化幅度由96.4 mm降低到了34.9 mm。移动机器人越障过程中工作平台的稳定性得到了提升。
2) 遗传算法与非线性规划相结合,能够有效提高控制算法的计算效率和控制效果。
参考文献
| [1] | 马金猛, 李小凡, 姚辰, 等. 地面移动机器人越障动力学建模与分析[J].机器人, 2008, 30(3): 273–278. MA J M, LI X F, YAO C, et al. Dynamic modeling and analysis for obstacle negotiation of ground mobile robot[J].Robot, 2008, 30(3): 273–278.(in Chinese) |
| [2] | 叶锦华. 不确定非完整轮式移动机器人的运动控制研究[D]. 广州: 华南理工大学, 2013: 6-13. YE J H. Research on motion control of uncertain nonholonomic wheeled mobile robot[D]. Guangzhou: South China University of Technology, 2013: 6-13(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10561-1014153433.htm |
| [3] | 王佐伟, 梁斌, 吴宏鑫. 六轮月球探测车运动学建模与分析[J].宇航学报, 2003, 24(5): 1–10. WANG Z W, LIANG B, WU H X. Kinematical modeling and analysis of six-wheel lunar rover[J].Journal of Astronautics, 2003, 24(5): 1–10.(in Chinese) |
| [4] | 徐坤, 郑羿, 丁希仑, 等. 六轮腿式机器人结构设计与运动模式分析[J].北京航空航天大学学报, 2016, 42(1): 59–71. XU K, ZHENG Y, DING X L, et al. Structure designe and motion mode analysis of a six wheel-legged robot[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(1): 59–71.(in Chinese) |
| [5] | 周开波, 王旭永, 罗小桃, 等. 摇臂式六轮探测车空间姿态建模与求解[J].上海交通大学学报, 2013, 47(7): 1093–1098. ZHOU K B, WANG X Y, LUO X T, et al. Spatital attitude model of six-wheeled rocker rover and its mathematical solution[J].Journal of Shanghai Jiaotong University, 2013, 47(7): 1093–1098.(in Chinese) |
| [6] | 崔莹, 高峰. 可变直径轮月球探测车运动学建模与分析[J].北京航空航天大学学报, 2008, 34(3): 348–352. CUI Y, GAO F. Kinematic modeling and analysis of variable diameter wheeled lunar rover[J].Journal of Beijing University of Aeronautics and Astronautics, 2008, 34(3): 348–352.(in Chinese) |
| [7] | PANSINI V, MONNET A, SALLERON J, et al. Development of a genetic algorithm for multi-objective assembly line balancing using multiple assignment approach[J].The International Journal of Advanced Manufacturing Technology, 2015, 77(5): 1419–1432. |
| [8] | 陶建国, 邓宗全, 高海波, 等. 月球车连杆式差速平衡机构的运动学分析[J].哈尔滨工业大学学报, 2009, 41(9): 21–26. TAO J G, DENG Z Q, GAO H B, et al. Kinematics analysis of differential bar linkage on lunar rover[J].Journal of Harbin Institute of Technology, 2009, 41(9): 21–26.(in Chinese) |
| [9] | MICHALEWICZ Z, JANIKOW C Z, KRAWCZYK J B. A modified genetic algorithm for optimal control problems[J].Computers & Mathematics with Applications, 1992, 23(12): 83–94. |
| [10] | 朱会霞, 王福林, 张勇, 等. 改进遗传算法优化非线性规划问题[J].数学的实践与认识, 2013, 43(7): 117–125. ZHU H X, WANG F L, ZHANG Y, et al. Improved genetic algorithm to optimize the nonlinear programming problem[J].Mathematics in Practice and Theory, 2013, 43(7): 117–125.(in Chinese) |
| [11] | KWOK D P, SHENG F. Genetic algorithm and simulated annealing for optimal robot arm PID control[C]//IEEE Conference on Evolutionary Computation. Piscataway, NJ: IEEE Press, 1994, 2: 707-713.http://ieeexplore.ieee.org/xpls/abs_all.jsp?arnumber=349971 |
| [12] | FU Y Y, KO C N, LEE T L, et al. A nonlinear programming method for time-optimal control of an omni-directional mobile robot[J].Journal of Vibration & Control, 2008, 14(14): 1729–1747. |
| [13] | CHEN J L, CHANG W D. Feedback linearization control of a two-link robot using a multi-crossover genetic algorithm[J].Expert Systems with Applications, 2009, 36(2): 4154–4159.DOI:10.1016/j.eswa.2008.01.048 |
| [14] | 史峰, 王辉, 郁磊, 等. MATLAB智能算法[M].北京: 北京航空航天大学出版社, 2011: 17-24. SHI F, WANG H, YU L, et al. MATLAB intelligent algorithm[M].Beijing: Beihang University Press, 2011: 17-24.(in Chinese) |
| [15] | 李金良, 包继华, 于岩, 等. 基于遗传算法的腿轮式机器人运动姿态优化[J].机床与液压, 2010, 38(21): 23–25. LI J L, BAO J H, YU Y, et al. Kinetic optimization for a leg-wheeled robot based on genetic algorithm[J].Machine Tool & Hydraulics, 2010, 38(21): 23–25.(in Chinese) |
| [16] | ZHOU L F, HONG B R. A knowledge based genetic algorithm for path planning of a mobile robot[J].Acta Electronica Sinica, 2006, 34(5): 911–914. |
