一般用线圈来产生匀强磁场,其中最常用的是螺线管线圈和亥姆霍兹线圈[7-10]。无限长螺线管线圈可以产生理想的匀强磁场,但实际应用中线圈尺寸总是有限的,导致其产生的磁场均匀度变差;亥姆霍兹线圈结构简单、尺寸小,但产生的磁场均匀区较小,只能应用于对磁场均匀区要求不大的场合。为了在一定范围内产生高均匀度的磁场,****们展开了关于线圈的大量研究。提出由半径不同的线圈组成的多个线圈组[11-13],其产生的磁场均匀度都优于亥姆霍兹线圈,但其结构较复杂,不便加工。Wang等提出半径相同的3圆形线圈组[14],外侧线圈与内侧线圈安匝比为1.881 6,安匝比近似取整为111/59/111,产生的磁场均匀度优于亥姆霍兹线圈。文献[15]提出半径相同的4圆形线圈组,外侧线圈与内侧线圈安匝比为2.260 4,安匝比近似取整为9/4/4/9,产生的磁场均匀度优于3圆形线圈组。Baranova等提出半径相同的8圆形线圈组[16],安匝比近似取整为34/17/12/10/10/12/17/34,产生的磁场均匀度优于上述线圈。
本文基于线圈轴向磁场的泰勒展开式,提出任意线圈数下圆柱形线圈组各参数的计算方法,并给出9线圈组以内的线圈参数及其变化趋势。在要求各个线圈由整数匝线圈组成且各匝线圈电流相同的情况下,还提出一种线圈安匝比取整的方法。并对实际线圈组制作工艺产生的误差进行了仿真分析。
1 线圈参数的计算方法 在由N个半径均为R、中心轴线与柱坐标系z轴重合且关于z=0平面对称分布的圆形线圈组成的圆柱形线圈组中,有2种未知参数,即各个线圈安匝数和各个线圈在z轴的坐标。基于线圈轴向磁场的泰勒展开式可以计算这2种参数,结果一般为小数。小数坐标容易实现,小数安匝数可通过给线圈组中各个线圈通不同的电流来实现,若要求各个线圈由整数匝线圈组成且各匝线圈电流相等,则用第3节的方法进行安匝比取整。
圆柱形线圈组中,序号为i的线圈在z=di平面,安匝数为mi,其在空间任一点产生磁场的径向分量Br,i(r,z)和轴向分量Bz,i(r,z)分别为[14]
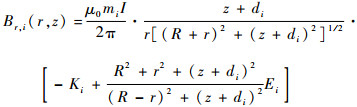 | (1) |
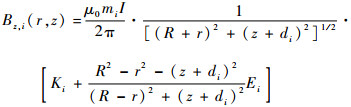 | (2) |
式中:μ0为真空磁导率;I为线圈所通电流;Ki和Ei分别为第一类和第二类完全椭圆积分。由于线圈分布的对称性,磁场在任一点的切向分量Bθ,i(r,z)=0,轴线上(r=0)磁场的径向分量Br,i(z)=0,轴线上总磁场等于轴向磁场。N个线圈在空间任一点产生的总磁场径向和轴向分量由每个线圈线性叠加得到:
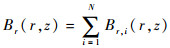 | (3) |
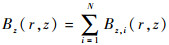 | (4) |
当线圈个数N为奇数时(N=5时如图 1(a)所示),中心线圈位于z=0平面(坐标d0=0),安匝数为m0;其余(N-1)/2对线圈关于z=0平面对称分布,每对线圈与z轴的坐标是±di(i=1, 2, …, (N-1)/2)且具有相同的安匝数mi=nim0,其中ni为安匝比。则轴线上总磁场等于轴向磁场:
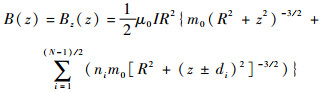 | (5) |
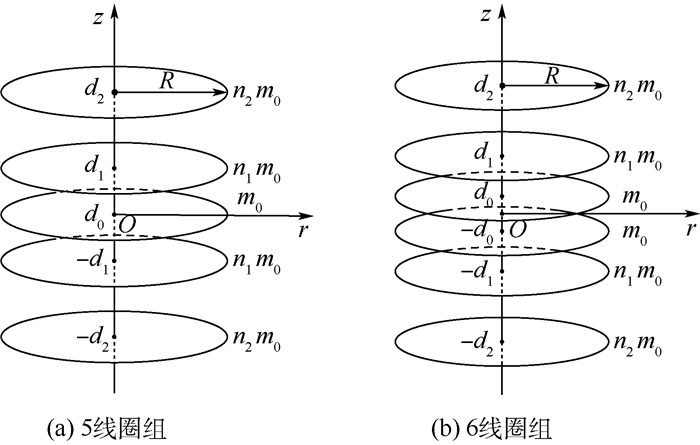 |
| 图 1 5线圈组和6线圈组结构示意图 Fig. 1 Configuration of five-coil and six-coil systems |
| 图选项 |
当线圈个数N为偶数时(N=6时如图 1(b)所示),N/2对线圈关于z=0平面对称分布且每对线圈的坐标是±di(i=0, 1, …, N/2-1),一对中心线圈(i=0)安匝数为m0,其余每对线圈的安匝数为nim0。则轴线上总磁场为
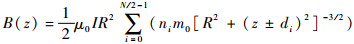 | (6) |
B(z)在z=0处的泰勒展开式可以写成
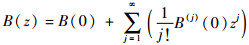 | (7) |
式中:B(j)(0)(j=1, 2, …)为B(z)的第j阶导数在z=0处的值。由于线圈分布的对称性,B(z)在z=0处的奇数阶导数均为0,式(7)可以简化为
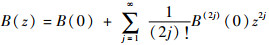 | (8) |
要产生理想匀强磁场,即要求B(z)=B(0)。由式(8)可知,即要求各阶导数(B(2)(0), B(4)(0), B(6)(0), …)为0。实际设计中要求低阶项为0,且为0的项数越多,均匀度越高。
为计算方便,设R=1,m0=1。当N为奇数时,求B(z)在z=0处的各阶导数,可以得到:
 | (9) |
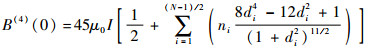 | (10) |
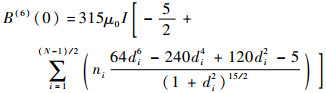 | (11) |
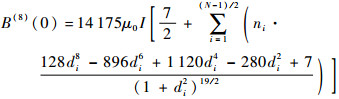 | (12) |
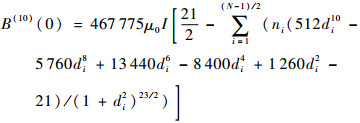 | (13) |
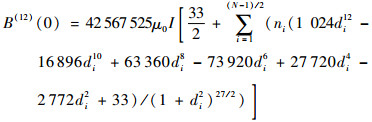 | (14) |
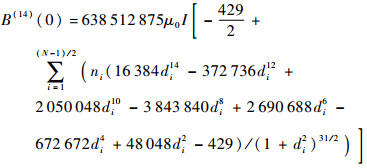 | (15) |
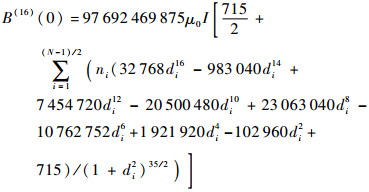 | (16) |
当N为偶数时,去掉式(9)~式(16)中括号内的常数项并将i的取值范围改为0~N/2-1即可得到B(z)在z=0处的各阶导数。
当线圈个数N为奇数时,共N-1个未知量,包括(N-1)/2个未知坐标di和(N-1)/2个未知安匝比ni。当线圈组数N为偶数时,也是N-1个未知量,包括N/2个未知坐标di和N/2-1个未知安匝比ni。因此,无论奇数还是偶数个线圈,都有N-1个未知量,要确定这些未知数,需要解含有N-1个方程的方程组。为此,令式(8)中前N-1个偶数阶导数为0,即
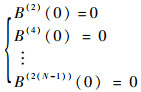 | (17) |
由此,可计算任意个线圈形成的圆柱形线圈组产生匀强磁场时的线圈参数,即线圈的轴向坐标di和线圈的安匝比ni。
2 理论参数与磁场均匀度分析 利用第1节给出的线圈参数计算方法,得到了N=2~9的圆柱形线圈组的理论参数,如表 1所示。由表 1可以得到线圈组轴向尺寸(即di的最大值与最小值之差)和线圈组最大安匝比(即ni最大值)随线圈个数N的变化曲线,如图 2所示。可见,随着N从2增大到9,线圈组轴向尺寸从R增大到2.894 6R,且增大趋势逐渐变缓;线圈组最大安匝比从1增大到5.302 8,且基本呈线性增大。
表 1 圆柱形线圈组的理论参数 Table 1 Theoretical parameters of cylindrical coil systems
| 线圈个数N | 各线圈到中心的距离(坐标)di | 各线圈与中心线圈的安匝比ni |
| 2 | ±0.5R | 1 |
| 3 | 0,±0.760 1R | 1/1.881 6 |
| 4 | ±0.243 2R,±0.940 8R | 1/2.260 4 |
| 5 | 0,±0.409 2R,±1.080 1R | 1/1.223 2/3.000 7 |
| 6 | ±0.162 6R,±0.537 0R,±1.193 9R | 1/1.347 7/3.455 2 |
| 7 | 0,±0.286 2R,±0.641 6R,±1.290 2R | 1/1.105 8/1.575 0/4.146 8 |
| 8 | ±0.122 4R,±0.386 7R,±0.730 3R,±1.373 6R | 1/1.173 3/1.730 5/4.636 0 |
| 9 | 0,±0.221 1R,±0.471 8R,±0.807 7R,±1.447 3R | 1/1.062 3/1.2952/1.955 8/5.3028 |
表选项
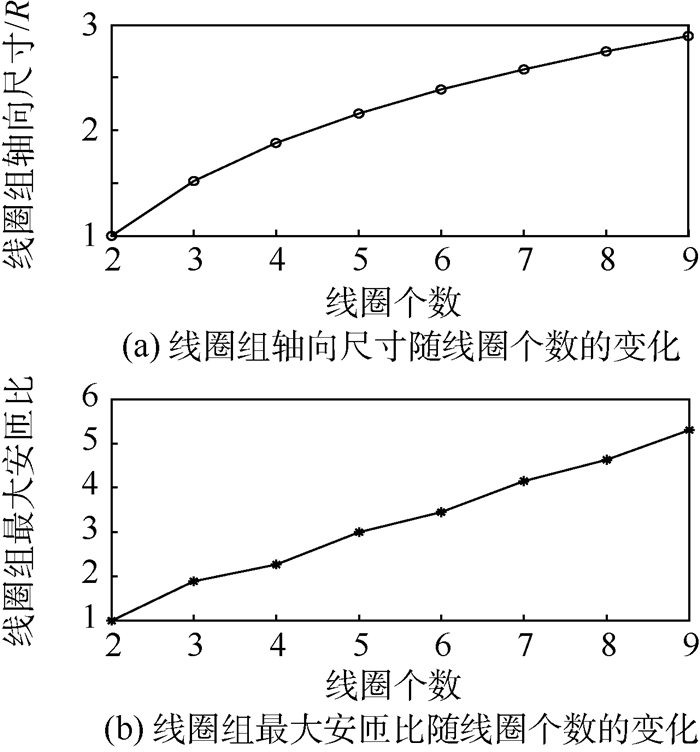 |
| 图 2 线圈组轴向尺寸和最大安匝比随线圈个数的变化 Fig. 2 Variation of coil systems' axial size and maximum ampere-turn ratio with coil number |
| 图选项 |
为分析各线圈组产生磁场的均匀度,定义无量纲磁场均匀度ε为空间任一点轴向磁场分量Bz相对中心磁场(r=0,z=0)的相对变化率的绝对值,即
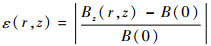 | (18) |
磁场均匀度ε越小,表示磁场变化越小,磁场越均匀。
根据表 1中的线圈参数,由式(4)和式(18)计算出各线圈组在rz平面产生的磁场均匀度分布及其等高线,如图 3所示。其中画出了ε分别为0.01%、0.1%、1%和10% 4条等高线。表 2列出了各线圈在rz平面内ε≤0.01%和ε≤0.1%区域的面积以及r和z的取值范围。磁场均匀区面积随线圈个数N的变化曲线如图 4所示。从表 2和图 4可以看出,随着线圈个数的增加,均匀区面积几乎线性增大。亥姆霍兹线圈ε≤0.01%和ε≤0.1%区域的面积分别为0.065R2和0.206R2;9线圈组ε≤0.01%和ε≤0.1%区域的面积分别为1.979R2和2.595R2,分别约为亥姆霍兹线圈的30倍和13倍。
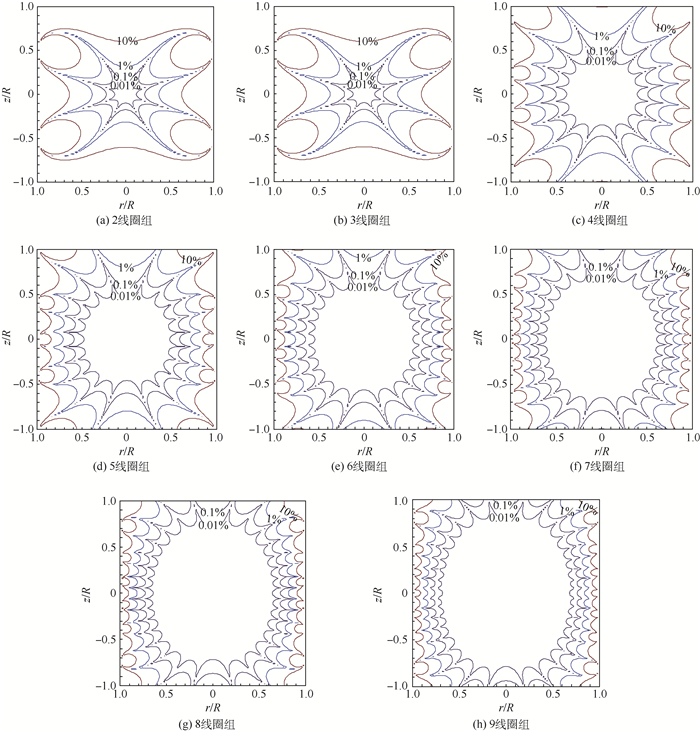 |
| 图 3 各线圈组产生磁场的均匀度等高线 Fig. 3 Contours of magnetic field uniformity for each coil system |
| 图选项 |
表 2 各线圈组ε≤0.01%和ε≤0.1%区域比较 Table 2 Comparison of each coil system between regions of ε≤0.01% and ε≤0.1%
| 线圈个数N | ε≤0.01%区域 | ε≤0.1%区域 | |||||
| |z|/R最大值 | r/R最大值 | 面积/R2 | |z|/R最大值 | r/R最大值 | 面积/R2 | ||
| 2 | 0.097 | 0.123 | 0.065 | 0.173 | 0.217 | 0.206 | |
| 3 | 0.226 | 0.267 | 0.271 | 0.336 | 0.384 | 0.584 | |
| 4 | 0.350 | 0.387 | 0.561 | 0.478 | 0.504 | 1.001 | |
| 5 | 0.458 | 0.479 | 0.873 | 0.597 | 0.588 | 1.396 | |
| 6 | 0.563 | 0.544 | 1.179 | 0.701 | 0.648 | 1.754 | |
| 7 | 0.649 | 0.608 | 1.467 | 0.791 | 0.696 | 2.074 | |
| 8 | 0.717 | 0.645 | 1.733 | 0.868 | 0.731 | 2.354 | |
| 9 | 0.789 | 0.679 | 1.979 | 0.940 | 0. 759 | 2.595 | |
表选项
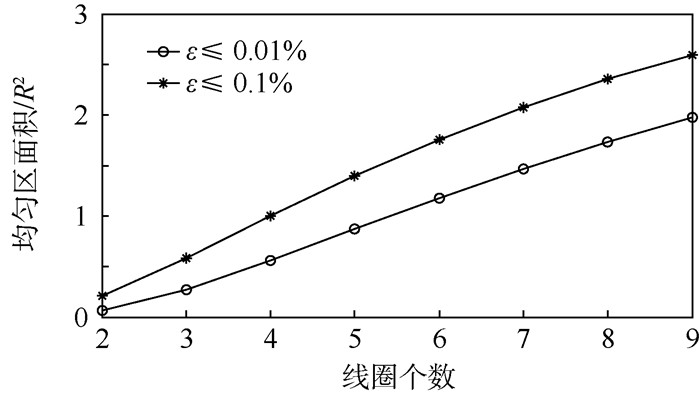 |
| 图 4 均匀区面积与线圈个数关系 Fig. 4 Variation of uniform region area with coil number |
| 图选项 |
3 线圈安匝比取整方法 在实际搭建圆柱形线圈组时,常要求各个线圈由整数匝线圈组成且各匝线圈电流相等。本节提出线圈安匝比取整的编程计算方法,用一系列整数之比近似小数安匝比,并且在保证均匀区基本不变的情况下线圈安匝数尽可能少。
假设线圈安匝比近似取整为m0/m1/…/mmax-1/mmax,其中m0为中心线圈安匝数,mmax为最外侧线圈安匝数。当线圈个数N为奇数时,max=(N-1)/2;当N为偶数时,max=N/2-1。程序开始时,m0从1开始逐步增大,mi∈[
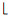

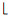

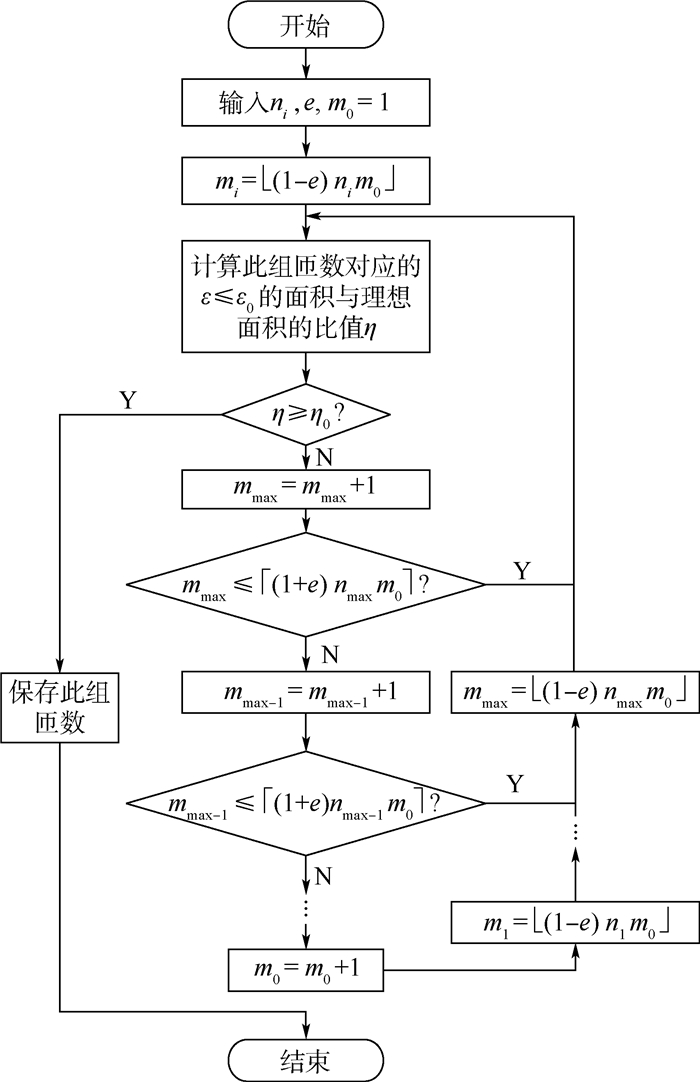 |
| 图 5 线圈安匝比取整程序流程图 Fig. 5 Program flowchart of coil ampere-turn ratio rounding |
| 图选项 |
表 3 各线圈组在η分别达到85%、95%和99%时的最小整数安匝比及实际面积 Table 3 Minimum integer ampere-turn ratio and actual area for each coil system when η is greater than or equal to 85%, 95% and 99%
| 线圈个数N | η ≥85% | η ≥95% | η ≥99% | |||||
| 最小整数安匝比 | 实际面积/R2 | 最小整数安匝比 | 实际面积/R2 | 最小整数安匝比 | 实际面积/R2 | |||
| 2 | 1/1 | 0.065 | 1/1 | 0.065 | 1/1 | 0.065 | ||
| 3 | 15/8/15 | 0.262 | 15/8/15 | 0.262 | 32/17/32 | 0.271 | ||
| 4 | 34/15/15/34 | 0.501 | 43/19/19/43 | 0.534 | 52/23/23/52 | 0.561 | ||
| 5 | 27/11/9/11/27 | 0.873 | 27/11/9/11/27 | 0.873 | 27/11/9/11/27 | 0.873 | ||
| 6 | 38/15/11/11/15/38 | 1.007 | 121/47/35/35/47/121 | 1.147 | 159/62/46/46/62/159 | 1.171 | ||
| 7 | 124/47/33/30/33/47/124 | 1.363 | 187/71/50/45/50/71/187 | 1.403 | 195/74/52/47/52/74/195 | 1.467 | ||
| 8 | 186/69/47/40/40/47/69/186 | 1.487 | 190/71/48/41/41/48/71/190 | 1.648 | 241/90/61/52/52/61/90/241 | 1.727 | ||
| 9 | 164/61/40/33/31/33/40/61/164 | 1.912 | 164/61/40/33/31/33/40/61/164 | 1.912 | 389/143/95/78/73/78/95/143/389 | 1.960 | ||
表选项
文献[14]中给出了3线圈系统的另一种近似安匝比111/59/111,经过计算得到ε≤0.01%区域的面积为0.271R2,达到了理想面积的100%。表 3中给出的3线圈组安匝比32/17/32,ε≤0.01%区域的面积也为0.271R2,二者得到的磁场基本相同,但32/17/32安匝数远少于111/59/111,方便构建。文献[15]中给出了4线圈系统的另一种近似安匝比9/4/4/9,经过计算得到ε≤0.01%区域的面积为0.298R2,只达到理想面积的53.12%,也小于表 3给出的4线圈组的均匀区面积,但远优于2线圈(亥姆霍兹线圈)的面积0.065R2。文献[16]中给出了8线圈系统的另一种近似安匝比34/17/12/10/10/12/17/34,经过计算得到ε≤0.01%区域的面积为0.305R2,只达到理想面积的17.6%,远小于表 3给出的8线圈组几种近似安匝比的结果。
4 线圈组制作工艺产生的误差分析 在实际圆柱形线圈组中,组成线圈的导线直径和导线间距等工艺参数会引起匀强磁场误差。导线密绕时,可认为组成每个线圈的各匝导线之间的间距为0,此时主要误差源是导线直径,导线直径在上文的分析中均假设为0,实际中导线直径为?。仿真计算时假设线圈由间距为?的细导线(即直径为0)组成。以5线圈组为例,线圈半径为R,线圈整数匝数取27/11/9/11/27,实际制作中线圈分布图如图 6所示,组成每个线圈的各匝导线密绕对称分布,每个线圈的中心匝导线分别位于该线圈的理论位置di处,其余各匝导线的位置分别为中心匝导线加上导线直径的相应整数倍。计算?/R在0~0.01时ε≤0.01%区域的面积,结果如图 7所示。可以看出,当?/R≤0.004时,均匀区面积都比较接近理想值。实际应用中,以小型化原子陀螺仪为例,按照原子陀螺仪结构尺寸和工作原理,半径R=15 mm的线圈组在中心区域需产生10 μT的磁场。由此计算出单匝线圈需要通入5.5 mA电流,对应铜导线直径?≥0.029 6 mm。可选择直径?=0.056 mm的铜导线,此时?/R=0.003 7≤0.004,因此可得到近似理想情况的匀强磁场。
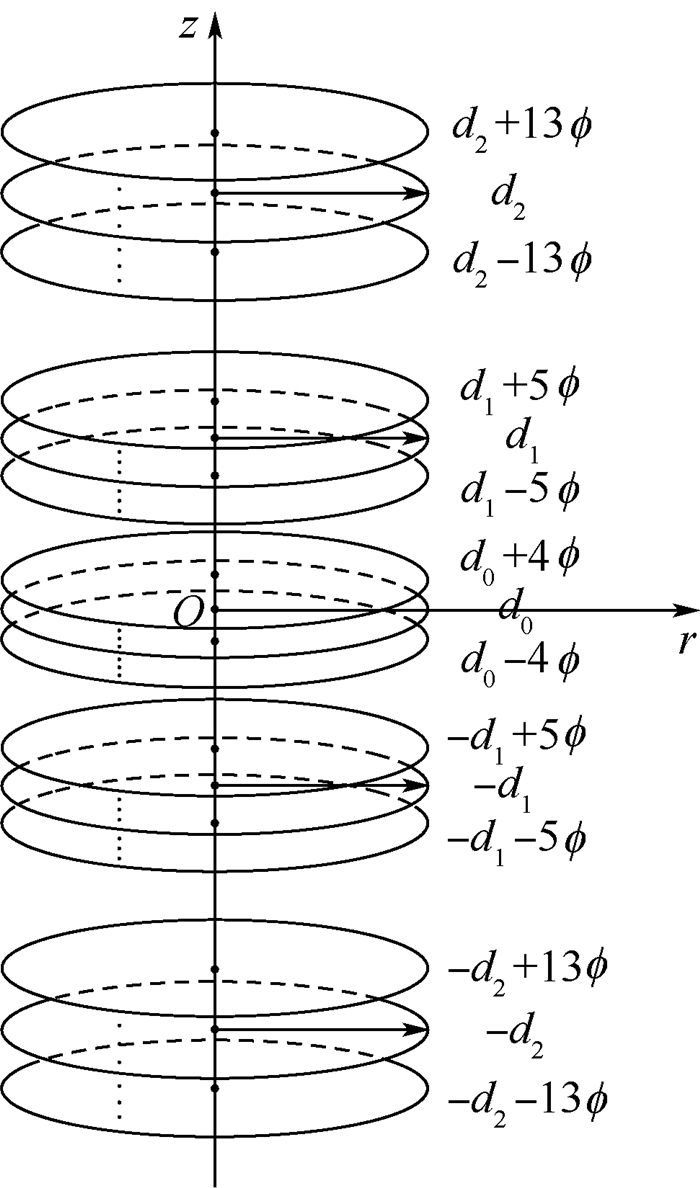 |
| 图 6 实际制作5线圈组线圈分布图 Fig. 6 Coil distribution diagram of practical five-coil system |
| 图选项 |
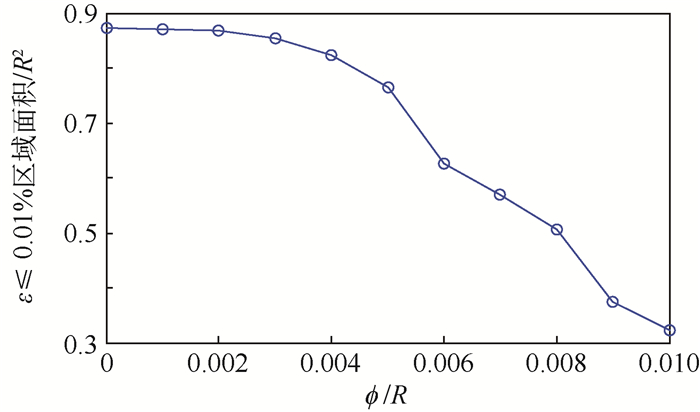 |
| 图 7 5线圈组ε≤0.01%区域面积与?/R关系 Fig. 7 Variation of five-coil system's region area(ε≤0.01%) with ?/R |
| 图选项 |
5 结论 本文利用轴向磁场的泰勒展开式,提出了由半径相同的圆形线圈组成的、产生匀强磁场的圆柱形线圈组在任意线圈数下各参数的计算方法,并给出了9线圈以内的线圈参数,分析了这些线圈产生磁场的均匀度和线圈参数变化趋势。针对实际线圈组制作中产生的误差进行了仿真分析。结果表明:
1) 随着线圈个数从2增大到9,磁场均匀度越来越高,均匀度小于等于0.01%和0.1%的区域面积都基本呈线性增大,9线圈组两区域的面积分别约为亥姆霍兹线圈的30倍和13倍。
2) 随着线圈个数从2增大到9,线圈组最大安匝比基本呈线性增大,线圈组轴向尺寸增大且增大趋势逐渐变缓。
3) 在要求各线圈电流相同的情况下,提出了一种线圈安匝比取整的方法,给出了2~9线圈组的安匝比取整结果。计算表明,相同线圈数下,设计的线圈组产生磁场的均匀度优于已有文献,或者在相同均匀度下设计的线圈安匝数比已有文献少。
4) 实际中用导线直接缠绕法制作线圈时,主要误差源是导线直径,对于5线圈组,当导线直径和线圈半径之比小于等于0.004时,均匀区面积接近理想值。
本文设计的圆柱形线圈组不仅可应用于原子陀螺仪和原子磁强计等量子传感器,而且可应用于精密测量和航空航天等领域其他需要产生高均匀度磁场的系统。实际应用中,可根据自身对磁场均匀度和线圈安匝比的要求,按照本文提出的方法计算满足自身要求的线圈安匝数。
参考文献
| [1] | MEYER D, LARSEN M. Nuclear magnetic resonance gyro for inertial navigation[J].Gyroscopy and Navigation, 2014, 5(2): 75–82.DOI:10.1134/S2075108714020060 |
| [2] | FANG J C, WAN S A. Atomic spin gyroscope based on 129Xe-Cs comagnetometer[J].Science Bulletin, 2013, 58(13): 1512–1515.DOI:10.1007/s11434-013-5759-5 |
| [3] | DANG H B, MALOOF A C, ROMALIS M V. Ultrahigh sensitivity magnetic field and magnetization measurements with an atomic magnetometer[J].Applied Physics Letters, 2010, 97(15): 151110.DOI:10.1063/1.3491215 |
| [4] | HILSCHENZ I, ITO Y, NATSUKAWA H, et al. Remote detected low-field MRI using an optically pumped atomic magnetometer combined with a liquid cooled pre-polarization coil[J].Journal of Magnetic Resonance, 2017, 274: 89–94.DOI:10.1016/j.jmr.2016.11.006 |
| [5] | GUSAROV A, LEVRON D, PAPERNO E, et al. Three-dimensional magnetic field measurements in a single SERF atomic-magnetometer cell[J].IEEE Transactions on Magnetics, 2009, 45(10): 4478–4481.DOI:10.1109/TMAG.2009.2021404 |
| [6] | EKLUND E J. Microgyroscope based on spin-polarized nuclei[D]. Irvine: University of California, 2008: 87-88. |
| [7] | HANSON R J, PIPKIN F M. Magnetically shielded solenoid with field of high homogeneity[J].Review of Scientific Instruments, 1965, 36(2): 179–188.DOI:10.1063/1.1719514 |
| [8] | SCHILL R A, HOFF K. Characterizing and calibrating a large Helmholtz coil at low ac magnetic field levels with peak magnitudes below the earth's magnetic field[J].Review of Scientific Instruments, 2001, 72(6): 2769–2776.DOI:10.1063/1.1368853 |
| [9] | WANG L, LI G X, XU C L, et al. Effect of characteristic parameters on the magnetic properties of solenoid valve for high-pressure common rail diesel engine[J].Energy Conversion & Management, 2016, 127: 656–666. |
| [10] | SONG X C. Comparison of magnetic field distribution and homogeneity between Helmholtz coil and Maxwell coil[J].Journal of Magnetic Materials & Devices, 2016, 47(5): 16–19. |
| [11] | GARRETT M W. Axially symmetric systems for generating and measuring magnetic fields.Part Ⅰ[J].Journal of Applied Physics, 1951, 22(9): 1091–1107.DOI:10.1063/1.1700115 |
| [12] | EVERETT J E, OSEMEIKHIAN J E. Spherical coils for uniform magnetic fields[J].Journal of Scientific Instruments, 1966, 43(43): 470–474. |
| [13] | GOTTARDI G, MESIRCA P, AGOSTINI C, et al. A four coil exposure system (tetracoil) producing a highly uniform magnetic field[J].Bioelectromagnetics, 2003, 24(2): 125–133.DOI:10.1002/(ISSN)1521-186X |
| [14] | WANG J, SHE S, ZHANG S. An improved Helmholtz coil and analysis of its magnetic field homogeneity[J].Review of Scientific Instruments, 2002, 73(5): 2175–2179.DOI:10.1063/1.1471352 |
| [15] | KIRSCHVINK J L. Uniform magnetic fields and double-wrapped coil systems:Improved techniques for the design of bioelectro-magnetic experiments[J].Bioelectromagnetics, 1991, 13(5): 401–411. |
| [16] | BARANOVA V E, BARANOV P F, MURAVYOV S V, et al. The production of a uniform magnetic field using a system of axial coils for calibrating magnetometers[J].Measurement Techniques, 2015, 58(5): 550–555.DOI:10.1007/s11018-015-0752-9 |
