通常情况下,多个设计目标之间是相互冲突的,解决MRDO问题需要在各目标之间进行权衡和折中,使各目标尽可能达到最优[3]。当前,MRDO的传统方法是按照重要程度赋予各目标权重,转化为单目标可靠性优化设计(Single-objective Reliability Design Optimization,SRDO)问题之后,再结合一次二阶矩(First Order Second Moment,FOSM)法等可靠性分析方法进行求解。Kogiso等利用加权法对汽车车身进行了基于可靠性的多目标优化设计[4];张瑞军等基于灰色理论确定各目标的权重,再采用加权法将机械产品的可靠性稳健优化设计问题转换为单目标优化设计问题[5];王若冰等将分层序列法应用于某型航空飞行器气动、质量与性能的三目标可靠性优化设计[6];于淼等采用物理规划法构造各目标的偏好函数,在此基础上通过非线性加权将MRDO问题转化为SRDO问题,并应用于湿式多盘制动器的设计[7]。上述研究中,各目标的权重系数或偏好函数的选取体现了设计者的主观意识,人为经验性较大,优化结果客观性较低。针对这一问题,后续研究产生了新的MRDO方法,例如,基于多目标粒子群优化(Multi-Objective Particle Swarm Optimization,MOPSO)算法或多目标遗传算法(Multi-objective Genetic Algorithm,MOGA)进行寻优,并利用FOSM等方法判断寻优点是否满足可靠性约束的要求。在岩土工程设计领域,Juang和Wang利用MOGA开展了扩展基础的多目标可靠性优化设计[8];张干清等则采用MOPSO算法对盾构机行星减速器进行了多目标可靠性优化设计[9]。但是,MOPSO等算法在处理MRDO问题时,需要求解大量Pareto非劣解,计算量巨大,收敛速度缓慢,这一问题随着设计目标与随机设计变量的增多会更加突出[10]。鉴于多目标优化设计与博弈之间的相似性,近年来,国内外不断有研究将博弈论应用于求解工程中的多目标优化设计问题。Song等将竞争博弈模型应用于汽车悬架参数的多目标优化设计[11];Desideri利用竞争博弈模型对某型机翼开展了外形与空气动力学的优化设计[12];Xiao等利用竞争博弈模型对小水线面双体船进行了多目标优化设计[13]。基于博弈的方法无需人为设置目标权重,相较于MOPSO等算法显著降低了计算量(无需求解Pareto非劣解集),在求解多目标优化设计问题时有着独特优势。当前,该方法多针对确定性的多目标优化设计问题,将其应用于MRDO鲜有研究成果发表。
为解决权重法所带来的优化结果客观性不足的问题,本文提出基于竞争博弈求解MRDO问题的方法。首先,将各设计目标视为不同的博弈方;其次,通过随机设计变量集映射(Random Design Variables Set Mapping,RDVSM)技术,将随机设计变量集分解为各博弈方所拥有的策略集;最后,各博弈方以自身收益最佳为目标,结合可靠性分析的性能测量方法(Performance Measurement Approach,PMA)在各自策略集中进行SRDO,由所有优化结果形成一轮博弈的策略组合,经过多轮博弈获得均衡解(即MRDO问题的优化解)。通过2个案例验证方法的有效性。
1 基础理论 1.1 可靠性分析的性能测量方法 考虑设计变量X={x1, x2, …, xn}的随机不确定性,MRDO问题的数学表达式可以描述为
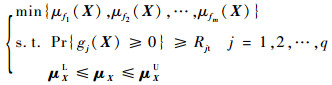 | (1) |
式中:m为目标函数的个数;q为可靠性约束个数;μfi(·)为第i个目标函数fi(·)的期望;gj(·)为第j个功能函数;Rjt为gj(·)对应的可靠度目标值;μXL和μXU分别为随机变量X均值μX的下限和上限。
式(1)中可靠性约束的分析评估本身是一个优化迭代过程。因此,MRDO问题最直接的求解方法可以表示为一个双层优化模型,外层为优化循环,里层为可靠性分析循环。高效、稳健的可靠性分析方法是求解MRDO问题的重要环节。针对这一要求,采用PMA进行可靠性分析[14]。该方法表述为功能函数的功能测量应不小于0,否则可靠性约束不满足。功能测量是指在规定的可靠度目标值下的最小功能函数值,其求解可以表示为一个优化问题:
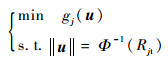 | (2) |
式中:u为标准正态分布随机变量;||u||为变量u的模;Φ-1(·)为标准正态分布逆函数。式(2)的最优解uRjtIMPP称为逆最大可能点(Inverse Most Probable Point,IMPP),由此可以得到gj(·)的功能度量gj(uRjtIMPP)。求解IMPP的迭代步骤如下:
步骤1??选择0点作为初始迭代点,求解gj(·)的梯度?gj(0)。
步骤2??求解第1次迭代计算之后得到的点u(1)=-(?gj(0)/||?gj(0)||)βjt,βjt为对应于Rjt的可靠度指标目标值。
步骤3??当k≥1时,求解第k+1个迭代点u(k+1)=-(?gj(u(k))/||?gj(u(k))||)βjt。
步骤4??当不等式|||u(k+1)||-||u(k)|||≤δ成立时(δ为收敛判据),可得到IMPP的值uRjtIMPP=u(k+1)。
1.2 博弈理论 博弈论是一种应用于存在利益冲突场合的数学工具,为分析各博弈方彼此间决策会相互影响的问题提供了有效的解决方案[13]。用G代表一个博弈,如果G有m个博弈方p1,p2,…,pm,每个博弈方可选择的全部策略的集合称为策略集,分别用S1,S2,…,Sm表示,每个博弈方做出策略决策之后的收益分别用u1,u2,…,um表示,则博弈G可以表示为
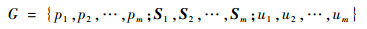 | (3) |
博弈分为竞争博弈与合作博弈2类[11]。竞争博弈是指各博弈方以竞争的方式追求自身收益最佳为目标;合作博弈是指各博弈方以合作的方式追求整体收益最佳。对于MRDO问题,各目标之间相互冲突与竞争,某个目标的改善可能引起其他目标的恶化,与竞争博弈高度类似。将MRDO模型中的设计目标对应于博弈方;随机设计变量集X对应于所有博弈方所拥有的策略集,并进一步将X分解为各博弈方所拥有的策略集S1,S2,…,Sm;目标函数的响应对应于博弈方的收益值;可靠性约束条件用于限制博弈方的策略取值。MRDO问题可以用博弈模型来描述,其中,S1={xi, xi+1, …, xj},S2={xk, xk+1, …, xl},…,Sm={xv, xv+1, …, xw},满足S1∪S2∪…∪Sm=X且Sc∩Sd=?(c, d=1, 2, …, m且c≠d);收益函数与目标函数之间的映射关系为ui(Si)=μfi(Si), i=1, 2, …, m。
2 MRDO的竞争博弈方法 基于竞争博弈求解MRDO问题,包含2项关键技术:各博弈方策略集的分解技术,竞争博弈的求解算法。
2.1 基于RDVSM的博弈方策略集分解 通过RDVSM,随机设计变量集X可以分解为各博弈方所拥有的策略集。RDVSM由影响因子集合构建、基于模糊聚类的策略集分解等2个部分组成。
1) 影响因子集合构建
构建影响因子集合用于形成分类样本,然后通过模糊聚类方法对样本进行分类处理以便获得各博弈方的策略集。影响因子集合的构建步骤如下:
步骤1??结合PMA,对式(1)中的m个目标函数分别进行SRDO,得到的目标函数最优值分别为μf1(X1*), μf2(X2*), …, μfm(Xm*),其中:Xi*=[xi1*, xi2*, …, xij*, …, xin*],i=1, 2,…, m; j=1, 2,…, n。
步骤2??将与随机设计变量xj相关的变量Xij=[xi1*, xi2*, …, xi(j-1)*, xj, xi(j+1)*, …, xin*]代入目标函数μfi(·)中,并对xj的均值μxj求偏导数得到灵敏度函数hi(xj)=?μfi/?μxj。
步骤3??设λj为一常数,其由关于xj的所有灵敏度函数所决定,其数学表达式为
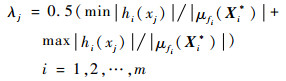 | (4) |
步骤4??求解不等式|hi(xj)|/|μfi(Xi*)|≥λj,得到μxj占其可行域[μxjL, μxjU]的比例ηji,ηji为xj对目标函数μfi(·)的影响因子。xj对所有目标函数的影响因子集为ηj={ηj1, ηj2, …, ηjm}。
步骤5??随机设计变量集X对所有目标函数的影响因子集为η={η1, η2, …, ηn}。
2) 基于模糊聚类的策略集分解
对影响因子集η进行聚类,将关联性和相似性较强的样本划分为同一类。由于xj与ηj之间的一一对应关系,η的聚类结果就代表了X的聚类结果。将待分类的对象严格地划分到某个类中,存在不合理之处,为此采用模糊方法处理η的聚类。
① 构建模糊相似矩阵R。
在模糊聚类之前,首先需要建立η上的模糊相似关系,可以表示为一个模糊相似矩阵R=(γij)n×n,其中γij为任意2个影响因子ηi与ηj之间的相似度,且0≤γij≤1,数学表达式为[15]
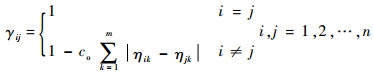 | (5) |
式中:co为常数。
② 构建模糊等价矩阵
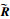
模糊相似矩阵R不满足传递性,无法直接对其进行聚类。采用平方法求解R的模糊等价矩阵
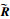
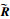
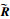
③ 模糊聚类。
记置信水平为θ,且θ∈[0, 1]。选取适当的θ值,按照如下方式对
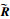
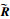
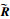
2.2 竞争博弈的求解算法 在一个竞争博弈模型G中,各博弈方的策略组合s*={s1*, s2*, …, si*, …, sm*}称为一个博弈均衡:如果对任意博弈方i来说,策略si*是在给定其余博弈方的策略组合
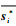
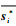
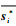
步骤1??通过RDVSM,得到隶属于各博弈方的策略集S1, S2, …, Sm。
步骤2??在所有博弈方的策略集中形成一个初始策略组合s(0)={s1(0), s2(0), …, si(0), …, sm(0)}。
步骤3??假设
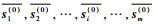
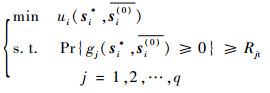 | (6) |
步骤4??将新的策略组合表示为s(1)={s1*, s2*, …, si*, …, sm*},计算相邻2个策略组合s(0)与s(1)之间的距离是否满足不等式||s(1)-s(0)||≤ξ,其中常数ξ为博弈收敛判据,若满足,则竞争博弈过程结束;否则以s(1)为基础转至步骤3继续执行,直至所有博弈方的最优策略不再随迭代过程而发生变化,得到博弈均衡解。
3 案例分析 3.1 压力容器MRDO案例 1) 压力容器MRDO数学模型
图 1为某型压力容器的示意图[16]。案例包含:3个正态分布的随机设计变量,概率分布参数如表 1所示;4个可靠性约束条件;2个设计目标,分别使得质量w(·)的期望最小,容积v(·)的期望最大。
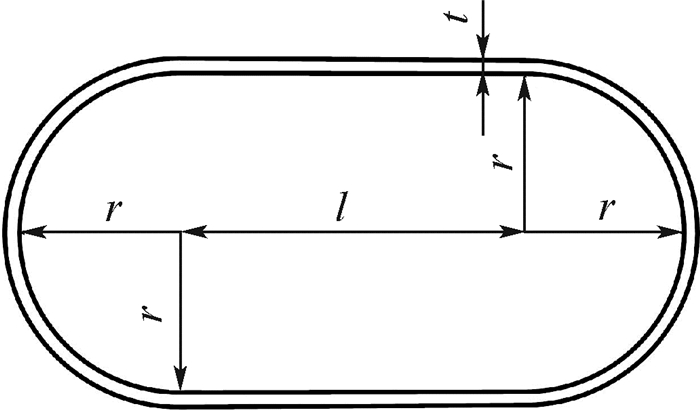 |
| 图 1 压力容器示意图[16] Fig. 1 Schematic diagram of pressure vessel[16] |
| 图选项 |
表 1 压力容器随机变量的概率分布 Table 1 Probability distribution of random variables of pressure vessel
| 变量 | 均值 | 变异系数 | 均值范围 |
| r/mm | 595.8611 | 0.05 | [2.54, 914.4] |
| l/mm | 999.7745 | 0.05 | [2.54, 3556] |
| t/mm | 62.4510 | 0.05 | [12.7, 152.4] |
表选项
压力容器的MRDO数学模型如式(7)所示,w(·)和v(·)的表达式如式(8)所示:
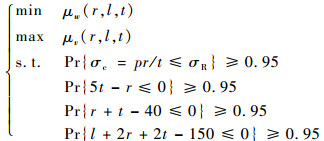 | (7) |
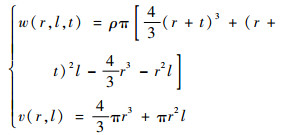 | (8) |
式中:σc为圆周应力;σR=241.3 MPa为材料的许用抗拉强度;ρ=7 833.4 kg/m3为密度;p=26.8 MPa为压强。
2) 基于RDVSM的策略集分解
首先,计算3个设计变量r、l和t对2个目标函数μw(·)和μv(·)的影响因子集分别为:η1={0.505 2, 0}、η2={1, 0}、η3={0.387 1, 0}。然后,对集合η={η1, η2, η3}进行模糊聚类可得:策略集S1={r, t}隶属于博弈方μw(·),S2={l}隶属于博弈方μv(·)。
3) 竞争博弈求解
在所有的博弈方策略集中形成初始策略组合s(0)={s1(0), s2(0)},其中,s1(0)={595.861 1, 62.451 0}、s2(0)={999.774 5}。依据竞争博弈算法的步骤,得到的博弈均衡解为s1*={702.334 6, 106.996 2}、s2*={1 725.805 5},相应的目标函数值分别为μw*=12 889.816 6,μv*=4.123 5,实际的可靠度指标为Ra=[0.999 9, 0.999 9, 0.999 9, 0.999 9],满足约束要求。
4) 优化结果对比分析
通过多学科优化设计软件iSIGHT中的带精英策略的快速非支配排序遗传算法(Non-dominated Sorting Genetic Algorithm Ⅱ,NSGA-Ⅱ),结合PMA对压力容器进行MRDO,NSGA-Ⅱ的参数设置为,种群规模12,交叉概率0.9,变异概率0.01,最大进化代数100,得到部分Pareto非劣解及相应的目标函数值如表 2所示,其中μtN、μlN和μrN为优化后的设计变量均值,μwN和μvN为优化后的目标函数值。利用加权法将多目标问题转换为单目标问题,结合PMA与序列二次规划(Sequential Quadratic Programming,SQP)算法进行SRDO,SQP算法的参数设置为:最大迭代次数40,终止精度10-6,步长0.001,得到的优化结果如表 3所示,其中ω1和ω2分别为2个目标函数的权重系数,μtW、μlW和μrW为优化后的设计变量均值,μwW和μvW为优化后的目标函数值。
表 2 基于NSGA-Ⅱ的压力容器部分优化结果 Table 2 Part optimization results of pressure vessel based on NSGA-Ⅱ
| 变量 | 非劣解1 | 非劣解2 | 非劣解3 |
| μtN/mm | 107.554 0 | 108.746 8 | 106.403 1 |
| μlN/mm | 1 059.278 0 | 1 509.354 4 | 1 601.394 3 |
| μrN/mm | 795.133 5 | 815.710 1 | 827.923 2 |
| μwN/kg | 12 393.860 9 | 15 135.898 9 | 15 523.401 2 |
| μvN/m3 | 4.207 6 | 5.425 9 | 5.822 7 |
表选项
根据表 2,基于竞争博弈的目标函数值μw*=12 889.816 6和μv*=4.123 5分别接近于非劣解1所对应的2个目标函数值μw=12393.8609N和μvN=4.207 6,表明利用竞争博弈求解MRDO问题的可行性、结果的有效性。竞争博弈方法的本质是多方决策,通过各博弈方的多轮博弈实现收益均衡、满足设计要求,期间不存在人为干预,博弈结果具有较高的客观性。
根据表 3可得:①对比权重组合3~权重组合5,目标函数值μwW和μvW均随着权重的变化而产生显著的变化,随着权重的增大,容器质量μwW呈现减小趋势,容积μvW呈现减小趋势,体现出设计者的主观偏好;②对比权重组合1~权重组合3,权重的显著差异并未造成明显不同的优化结果,相反这3组权重组合所对应的目标函数值十分接近,并没有反映出设计者的主观偏好。产生上述结果的原因在于:权重法本质上属于单方决策,人为将多目标问题转化为单目标问题,掩盖了各目标间的冲突,使得优化结果缺乏客观性,甚至无法保证可信度。
表 3 基于加权法的压力容器优化结果 Table 3 Optimization results of pressure vessel based on weighted method
| 变量 | 权重组合1(ω1=0.01,ω2= 0.99) | 权重组合2(ω1=0.1,ω2= 0.9) | 权重组合3(ω1= ω2= 0.5) | 权重组合4(ω1=0.9,ω2=0.1) | 权重组合5(ω1=0.99,ω2= 0.01) |
| μtW/mm | 105.092 8 | 105.099 4 | 105.096 6 | 83.953 1 | 12.7 |
| μlW/mm | 1 719.527 4 | 1 713.351 9 | 1 721.302 9 | 2 093.012 8 | 962.011 8 |
| μrW/mm | 840.228 2 | 841.113 6 | 837.490 1 | 672.022 5 | 71.356 5 |
| μwW/kg | 16 187.338 1 | 16 184.143 9 | 16 121.364 6 | 10 387.539 0 | 54.265 2 |
| μvW/m3 | 6.295 3 | 6.297 5 | 6.250 2 | 4.238 7 | 0.016 9 |
表选项
3.2 减速器MRDO案例 1) 减速器MRDO数学模型
图 2为某小型航空发动机齿轮减速器传动原理的示意图[17]。案例包含1个确定性设计变量(齿轮1齿数),6个正态分布随机设计变量,概率分布参数见表 4;6个可靠性约束条件,其中c1为轮齿弯曲应力约束,c2为轮齿接触应力约束,c3和c4分别为轴1和轴2的横向变形约束,c5和c6分别为轴1和轴2的应力约束;5个由经验规定的确定性几何约束c7~c11;3个设计目标分别使得减速器体积f1(·)、齿轮轴1及齿轮轴2的应力f2(·)和f3(·)的期望最小。f1(·)、f2(·)与f3(·)的表达式如式(9)所示,减速器的MRDO数学模型如式(10)所示:
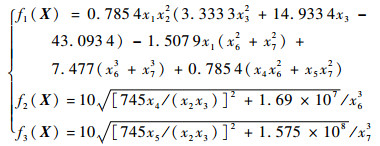 | (9) |
 | (10) |
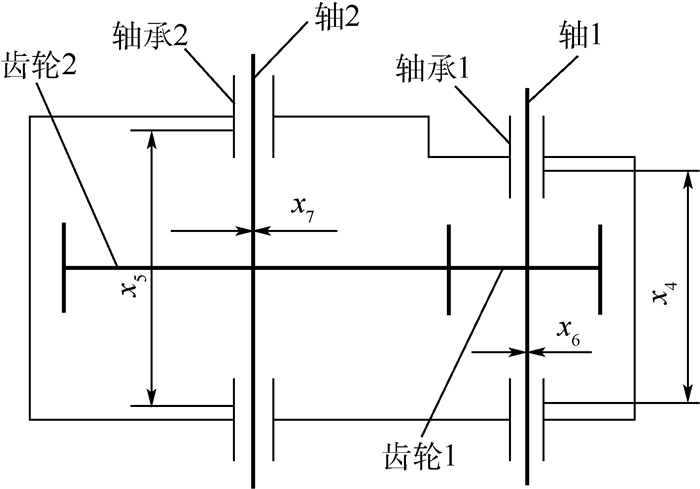 |
| 图 2 减速器传动原理示意图[17] Fig. 2 Schematic diagram of drive principle of reducer[17] |
| 图选项 |
表 4 减速器随机变量的概率分布 Table 4 Probability distribution of random variables of reducer
| cm | |||
| 变量 | 均值 | 标准差 | 均值范围 |
| 齿面宽度x1 | 3.58 | 0.05 | [2.6, 3.6] |
| 齿轮模数x2 | 0.72 | 0.01 | [0.7, 0.8] |
| 轴1轴承间距x4 | 7.48 | 0.05 | [7.3, 8.3] |
| 轴2轴承间距x5 | 7.83 | 0.05 | [7.3, 8.3] |
| 轴1直径x6 | 3.37 | 0.05 | [2.9, 3.9] |
| 轴2直径x7 | 5.26 | 0.05 | [5.0, 5.5] |
| 注:齿轮1齿数x3(取整数)均值范围为[17, 28]。 | |||
表选项
2) 减速器的博弈均衡解
根据竞争博弈求解算法的步骤,在对齿轮1的齿数x3进行圆整处理之后,得到的博弈均衡解为s1*={3.6, 0.7, 17, 8.176 0, 8.3},s2*={3.489 2},s3*={5.430 7};相应的目标函数值分别为μf1*=3 186.060 6,μf2*=97.526 6,μf3*=78.422 9;Ra=[0.999 4, 0.999 9, 0.999 9, 1.0, 0.997 0, 0.998 0]满足可靠度要求。
3) 优化结果对比分析
结合NSGA-Ⅱ和PMA对减速器进行MRDO,NSGA-Ⅱ的参数设置为:种群规模12,交叉概率0.92,变异概率0.01,最大进化代数120。所得Pareto非劣解集的一部分如表 5所示,其中μx1N~μx7N为优化后的设计变量均值,μf1N、μf2N和μf3N为优化后的目标函数值。利用加权法并结合SQP算法与PMA进行减速器的SRDO,SQP算法的参数设置为,最大迭代次数60,终止精度10-6,步长0.001,得到的优化结果如表 6所示,其中ω1~ω3分别为3个目标函数的权重系数,μx1W~μx7W为优化后的设计变量均值,μf1W、μf2W和μf3W为优化后的目标函数值。
表 5 基于NSGA-Ⅱ的减速器部分优化结果 Table 5 Part optimization results of reducer based on NSGA-Ⅱ
| 变量 | 非劣解1 | 非劣解2 | 非劣解3 |
| μx1N/cm | 3.579 8 | 3.588 4 | 3.582 3 |
| μx2N/cm | 0.701 7 | 0.700 9 | 0.701 1 |
| μx3N | 17 | 17 | 17 |
| μx4N/cm | 8.042 3 | 8.043 8 | 8.039 6 |
| μx5N/cm | 7.927 6 | 7.962 3 | 8.046 0 |
| μx6N/cm | 3.537 9 | 3.456 1 | 3.509 1 |
| μx7N/cm | 5.379 2 | 5.390 5 | 5.395 9 |
| μf1N/cm3 | 3 194.976 0 | 3 195.355 4 | 3 210.576 2 |
| μf2N/MPa | 93.504 2 | 100.295 7 | 95.823 8 |
| μf3N/MPa | 80.688 1 | 80.183 7 | 79.944 4 |
表选项
根据表 5的最后3行数据,基于竞争博弈的目标函数值μf1*=3 186.060 6、μf2*=97.526 6和μf3*=78.422 9接近于3个非劣解对应的目标函数值,表明博弈均衡解的有效性和正确性。
根据表 6可得:①分别对比权重组合1与权重组合2(ω1存在显著差异)、权重组合4与权重组合5(ω2和ω3均存在显著差异),权重的差异没有引起目标函数值μf1W、μf2W和μf3W明显的改变,未能体现出设计者的主观偏好;②分别对比权重组合4与权重组合1、权重组合4与权重组合2、权重组合5与权重组合1、权重组合5与权重组合2,目标函数值随着权重的变化而产生了明显的改变,但是权重的选取依赖于主观经验,设计结果个性化明显,客观性不足。
表 6 基于加权法的减速器优化结果 Table 6 Optimization results of reducer based on weighted method
| 变量 | 权重组合1(ω1=0.02, ω2=ω3=0.49) | 权重组合2(ω1=0.2, ω2=ω3=0.4) | 权重组合3(ω1=ω2=ω3=1/3) | 权重组合4(ω1=0.8, ω2=ω3=0.1) | 权重组合5(ω1=0.98, ω2=ω3=0.01) |
| μx1W/cm | 3.50 | 3.50 | 3.50 | 3.50 | 3.50 |
| μx2W/cm | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 |
| μx3W | 17 | 17 | 17 | 17 | 17 |
| μx4W/cm | 7.986 8 | 7.750 1 | 7.750 6 | 7.475 1 | 7.476 4 |
| μx5W/cm | 7.950 1 | 7.952 0 | 8.112 9 | 7.995 9 | 7.995 3 |
| μx6W/cm | 3.9 | 3.9 | 3.9 | 3.434 2 | 3.434 0 |
| μx7W/cm | 5.5 | 5.5 | 5.369 0 | 5.369 2 | 5.369 2 |
| μf1W/cm3 | 3 313.345 3 | 3 310.516 3 | 3 226.071 3 | 3 077.533 3 | 3 077.463 2 |
| μf2W/MPa | 69.813 3 | 69.783 6 | 69.783 7 | 102.155 3 | 102.177 7 |
| μf3W/MPa | 75.490 7 | 75.493 9 | 81.153 4 | 81.143 2 | 81.143 2 |
表选项
4 结论 1) 基于竞争博弈提出了一种解决MRDO问题的方法。通过RDVSM将随机设计变量集转换成策略集,所有博弈方均以自身收益为目标在各自策略集中进行SRDO,由优化结果构成一轮博弈的策略组合,然后经过多轮博弈获得均衡解。2个案例设计结果表明了方法的可行性,所求博弈均衡解具有较高的客观性。
2) 在利用PMA对MRDO模型中的可靠性约束进行分析评估时,只考虑了单一的随机不确定性,工程实际当中有多种类型不确定性共存,应考虑在此基础上对基于竞争博弈的MRDO求解方法做进一步的研究和改进。
参考文献
| [1] | 许孟辉, 邱志平. 结构模糊非概率混合可靠性分析方法[J].北京航空航天大学学报, 2014, 40(2): 222–228. XU M H, QIU Z P. Reliability analysis of structures with fuzzy and non-probabilistic hybrid variables[J].Journal of Beijing University of Aeronautics and Astronautics, 2014, 40(2): 222–228.(in Chinese) |
| [2] | 孟广伟, 冯昕宇, 李锋, 等. 基于降维算法和Edgeworth级数的结构可靠性分析[J].北京航空航天大学学报, 2016, 42(3): 421–425. MENG G W, FENG X Y, LI F, et al. Structural reliability analysis based on dimensionality reduction and Edgeworth series[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(3): 421–425.(in Chinese) |
| [3] | GARG H, RANI M, SHARMA S P, et al. Intuitionistic fuzzy optimization technique for solving multi-objective reliability optimization problems in interval environment[J].Expert Systems with Applications, 2014, 41(7): 3157–3167.DOI:10.1016/j.eswa.2013.11.014 |
| [4] | KOGISO N, KODAMA R, TOYODA M. Reliability-based multi-objective optimization using the satisficing trade-off method[J].Mechanical Engineering Journal, 2014, 1(6): 1–12. |
| [5] | 张瑞军, 邱继伟, 贾庆轩. 灰色系统理论的多目标可靠性稳健设计[J].北京邮电大学学报, 2014, 37(3): 23–26. ZHANG R J, QIU J W, JIA Q X. Multi-objective robust design for reliability based on grey system theory[J].Journal of Beijing University of Posts and Telecommunications, 2014, 37(3): 23–26.(in Chinese) |
| [6] | 王若冰, 谷良贤, 龚春林. 随机-区间混合不确定性分层序列化多学科可靠性分析方法[J].西北工业大学学报, 2016, 34(1): 139–146. WANG R B, GU L X, GONG C L. A stratified sequencing multi-disciplinary reliability analysis method under random and interval uncertainty[J].Journal of Northwestern Polytechnical University, 2016, 34(1): 139–146.(in Chinese) |
| [7] | 于淼, 石博强, 姜勇. 基于物理规划的湿式多盘制动器不确定性优化设计[J].农业机械学报, 2011, 42(4): 22–26. YU M, SHI B Q, JIANG Y. Application of physical programming in uncertainty optimization design of multi-disc wet brake[J].Transactions of the Chinese Society of Agricultural Machinery, 2011, 42(4): 22–26.(in Chinese) |
| [8] | JUANG C H, WANG L. Reliability-based robust geotechnical design of spread foundations using multi-objective genetic algorithm[J].Computers and Geotechnics, 2013, 48(4): 96–106. |
| [9] | 张干清, 龚宪生, 王欢欢, 等. 基于可靠灰色粒子群算法的盾构机行星减速器轮系的多目标优化设计[J].机械工程学报, 2010, 46(23): 135–145. ZHANG G Q, GONG X S, WANG H H, et al. Multi-objective optimization design on gear train of planetary reducer in shield tunneling machine based on reliably grey particle swarm optimization[J].Journal of Mechanical Engineering, 2010, 46(23): 135–145.(in Chinese) |
| [10] | 龙腾, 李学亮, 黄波, 等. 基于自适应代理模型的翼型气动隐身多目标优化[J].机械工程学报, 2016, 52(22): 101–111. LONG T, LI X L, HUANG B, et al. Aerodynamic and stealthy performance optimization of airfoil based on adaptive surrogate model[J].Journal of Mechanical Engineering, 2016, 52(22): 101–111.(in Chinese) |
| [11] | SONG C Z, ZHAO Y Q, WANG L. Tri-objective co-evolutionary algorithm and application of suspension parameter design based on lizard behavior bionics[J].Journal of Mechanical Science and Technology, 2014, 28(12): 4857–4867.DOI:10.1007/s12206-014-1106-2 |
| [12] | DESIDERI J A. Cooperation and competition in multidisciplinary optimization application to the aero-structural aircraft wing shape optimization[J].Computational Optimization and Applications, 2012, 52(1): 29–68.DOI:10.1007/s10589-011-9395-1 |
| [13] | XIAO M, SHAO X Y, GAO L, et al. A new methodology for multi-objective multidisciplinary design optimization problems based on game theory[J].Expert Systems with Applications, 2015, 42(3): 1602–1612.DOI:10.1016/j.eswa.2014.09.047 |
| [14] | YAO W, CHEN X Q, OUYANG Q, et al. A reliability-based multidisciplinary design optimization procedure based on combined probability and evidence theory[J].Structural and Multidisciplinary Optimization, 2013, 48(2): 339–354.DOI:10.1007/s00158-013-0901-1 |
| [15] | 曲福恒, 崔广才, 李岩芳, 等. 模糊聚类算法及应用[M].北京: 国防工业出版社, 2011: 57-66. QU F H, CUI G C, LI Y F, et al. Fuzzy clustering algorithm and its application[M].Beijing: National Defense Industry Press, 2011: 57-66.(in Chinese) |
| [16] | RAO J R J, BADHRINATH K, PAKALA R, et al. A study of optimal design under conflict using models of multi-player games[J].Engineering Optimization, 1997, 28(1-2): 63–94.DOI:10.1080/03052159708941127 |
| [17] | GOLINSKI J. Optimal synthesis problems solved by means of nonlinear programming and random methods[J].Journal of Mechanisms, 1970, 5(3): 287–309.DOI:10.1016/0022-2569(70)90064-9 |
