高阶谱分析具有时移不变性、相位保持性、尺度不变性以及抑制高斯噪声性等特点,能够有效保留信号的振幅与相位信息[4-5]。国内外许多****在利用高阶谱,尤其双谱进行特征提取方面也有广泛研究,主要是通过在获取信号双谱的基础上进行特征的多次提取。文献[6]提取信号双谱后计算双谱围线积分,利用围线积分提取均值、波形熵和双谱熵作为量化特征进行个体识别;文献[7]通过计算信号双谱后利用奇异值分解提取到双谱奇异谱熵,对不同雷达脉内调制进行识别;文献[8]在利用信号双谱的基础上将Bhattacharyya分离度准则作为特征的二次提取,在6种雷达信号中的平均识别率可达95%。然而上述文献都是直接利用双谱的高维数据进行二次特征提取,在计算量上较为复杂。
信号分形维数特征度量了信号的复杂度和不规则度,在信号检测、目标识别和故障诊断等领域中备受关注[9-10]。分形维数可分为单分形和多重分形,其中单分形仅仅从事物的平均或整体角度进行度量,很难描述不同调制的信号波动特征;而多重分形能够从信号的全局和局部出发研究信号的内部特征,并且对于信号处理的计算量较小[11-12]。
本文使用目前应用较为广泛的FMCW、Frank、BPSK和FSK/PSK 4种LPI雷达信号作为研究对象。首先通过计算信号的双谱对角切片(Bispectra Diagonal Slice, BDS),降低数据维度,减少二次计算的复杂度;然后在对角切片的基础上,利用多重分形中的广义维数(Generalized Dimension, GD)刻画不同信号切片特征;最后通过最小二乘支持向量机(LSSVM)进行分类识别。仿真实验表明,本文方法提取的信号特征在不同信噪比条件下具有较高的识别准确率。
1 双谱对角切片提取 双谱是高阶谱中最简单的形式,是信号三阶累积量谱的简称,通过对信号三阶累积量进行2次傅里叶变换得到。相比于功率谱等二阶统计量,双谱包含了二阶统计量没有的相位信息,并且相对于阶数更高的其他高阶谱,双谱运算可以较好地避免维度过高产生的“维数灾难”[13],因此双谱在信号特征表示和识别中得到广泛运用。
对于零均值信号,其高阶累计量Ckx(τ1, τ2, …, τk-1)是绝对可积的,即
 | (1) |
式中:τ为随机变量。
则k阶谱定义为k阶累计量的k-1维离散傅里叶变换,即
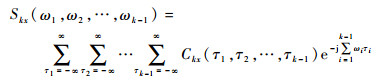 | (2) |
式中:ω为频率。
当k=3时,即可得三阶累积量谱,即双谱
 | (3) |
式中:C3x(τ1, τ2)为信号的三阶相关函数,表达式为
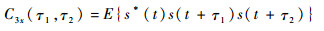 | (4) |
式中:t为时间。
假设接收到的LPI信号为x(t)=s(t)+n(t),s(t)为原始的LPI信号,n(t)为高斯白噪声,且s(t)与n(t)相互独立。含高斯白噪声的信号的三阶累积量与高斯白噪声无关[14],估计出的双谱中只包含发射信号信息本身、非高斯噪声的特征以及相关常量。因此对于接收到的LPI信号,其双谱可以有效抑制高斯白噪声的影响,并能主要体现信号本身固有的信息,进而得到不同LPI信号特有的信号特征。
双谱估计常用的方法有直接法和间接法,为适用于实时性处理[15],本文对LPI雷达信号FMCW、Frank、BPSK和FSK/PSK采用直接法估计信号双谱。图 1为4种LPI雷达信号的双谱三维图,从图中可知4种信号的双谱图相对有一定的差异,可以选择信号双谱特征作为雷达信号识别依据。
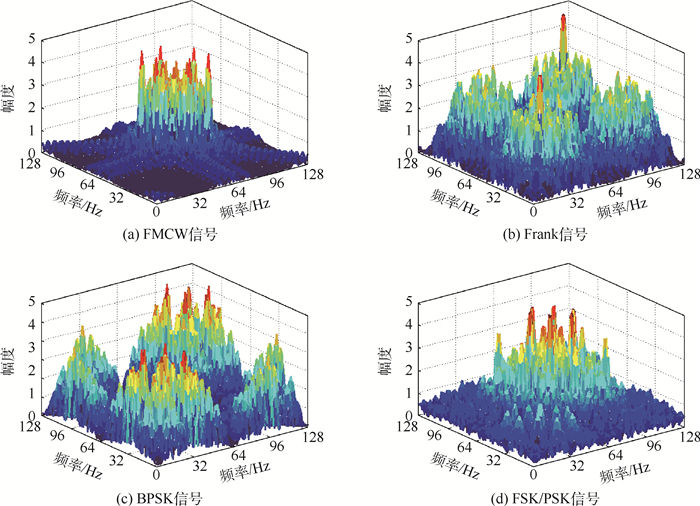 |
| 图 1 4种LPI雷达信号的双谱示例 Fig. 1 Bispectra example of LPI four kinds of LPI radar signals |
| 图选项 |
双谱是信号三阶自相关的二维傅里叶变换,呈现为三维谱。从实时性处理角度来说,若直接应用三维双谱的数据进行相关二次计算,将大大增加计算的工作量以及复杂度。从特征提取出发,最重要目的是找到使信号间区分度较大的特征,因此在实际中只需要提取到能够区分不同信号的信息即可。针对双谱的大信息量,本文采用双谱对角切片的形式对信号双谱进行局部信息提取,图 2为某一常规雷达信号的双谱二维投影图,由于三阶自相关函数在(τ1, τ2)平面有6种对称关系,因此只要知道信号在平面内12个区域中任意一个的值,即可根据对称性质得到全平面的值。
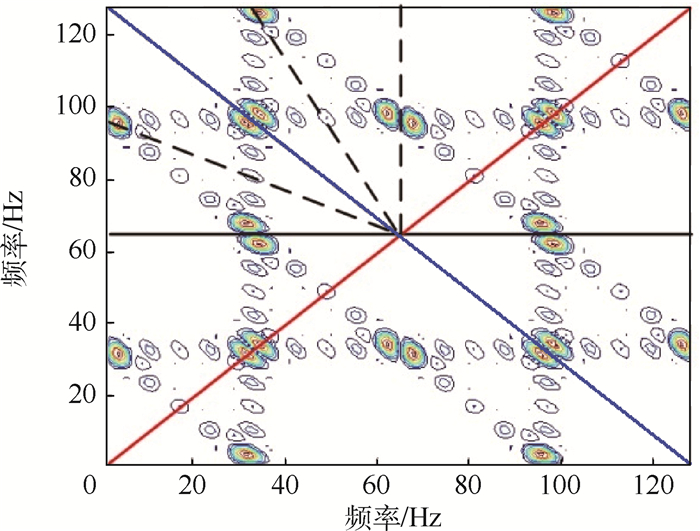 |
| 图 2 双谱的对称特性示意图 Fig. 2 Schematic of symmetry characteristic of bispectra |
| 图选项 |
考虑到双谱的对称特性,且在对角线上能够最大化地保留双谱切片信息,可选取双谱矩阵的双谱对角切片作为信号的特征,这样将128×128的矩阵转换成1×128的向量,即将矩阵运算转换成对一维序列数值的运算,二次计算的工作量大大降低。而在对角切片中有主对角线(蓝色实线)与次对角线(红色实线)之分(见图 2),文献[16]已经证明在都是一维序列中,次对角线的双谱切片相比于主对角包含更加丰富的信息,因此最终选择次对角的双谱切片作为二次计算的输入值。
为保证对比量纲的一致性,对LPI信号的双谱对角切片进行归一化处理,采用最大最小化方法对数据进行归一化,如式(5)所示:
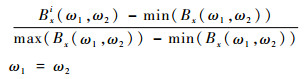 | (5) |
图 3为图 1中4种LPI信号双谱图的归一化对角切片。由图 3可以看出,4种LPI雷达信号的对角切片均关于中心对称,切面形状区分相对明显,因此可以作为信号识别依据。然而对于切片自身而言,维度依旧较大,需要进一步采取方法对切片降维,同时提取切片中能反映信号特有的细微特征。
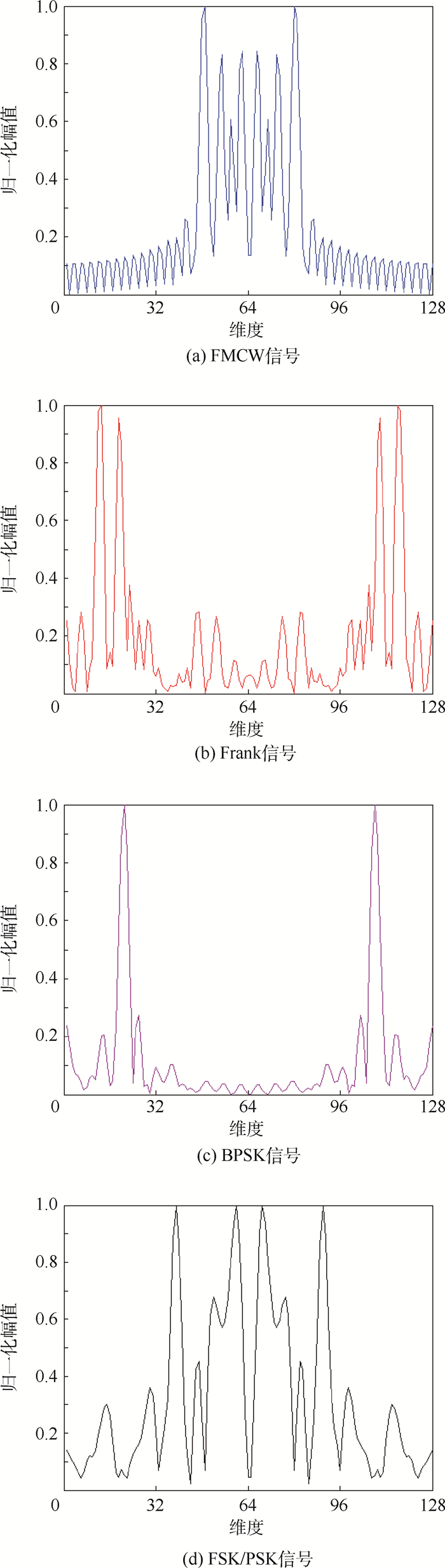 |
| 图 3 4种LPI雷达信号双谱归一化对角切片示例 Fig. 3 Example of bispectra normalized diagonal slice of four kinds of LPI radar signals |
| 图选项 |
2 基于广义维数的切片特征提取 2.1 多重分形 多重分形把分形结构中的整体视为由一些不同区域分形维数的局部结构组成,是由多个具有不同标度指数的奇异测度组成的集合。设X为一研究序列,将X用尺度L分成N个小单元Xi(i=1, 2, …, N),设第i个小单元的线度为γi,Pi为Xi上的测度,有
 | (6) |
测度与线度之间存在幂指数的关系,即
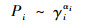 | (7) |
式中:αi称为Holder指数,也称奇异性指数或标度指数,用来衡量区域奇异性的强弱,且α的取值范围是有限的,即α∈[αmin, αmax]。具有相同的α值的小单元可构成一个子集,称为分形子集,而一个多重分形则看成由不同维数的分形子集构成。
令具有相同分形子集的盒子数为Nα(L),有
 | (8) |
式中:f(α)表示具有相同α的分形子集的维数。若研究单重分形,则f(α)为一个定值;若研究多重分形,则f(α)称为多重分形谱,是一条单峰曲线。
设M(L, q)为统计矩,表示每个单元的测度Pi(L)值的大小:
 | (9) |
式中:q为统计矩的阶,称为权重因子,可以取任意实数。给定一个q值,若满足式(10),将Dq=D(q)称为广义维数。
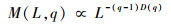 | (10) |
则
 | (11) |
当q=0时,D0就是通常意义的容量维;当q=1时,则可转化为信息维;当q=2时,则与相关维等价。因此广义维数Dq包含了分形所涉及的全部维数,本文采用Dq-q曲线反映不同信号之间的差异。
2.2 一维序列广义维数的计算 经过双谱对角切片处理后的LPI信号实际是一个一维序列信号的形式,因此对LPI信号的多重分形就是对一个序列进行分形分析。具体计算步骤如下:
1) 令{xk, k=1, 2, …, N}为LPI信号双谱对角切片序列,将该序列投入到d维的欧氏空间中,得到向量集Un(m),记为
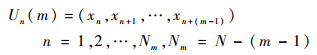 | (12) |
2) 在Nm个点中选取一个参考点Ui,计算Ui与其余Nm-1个点的欧氏距离为
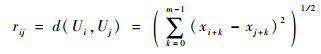 | (13) |
3) 重复步骤2)直至计算完成所有的Ui,定义q阶关联积分为
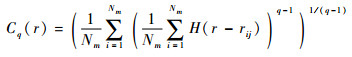 | (14) |
式中:H(·)为阶跃函数。
4) 广义维数Dq通过q阶关联积分计算得到:
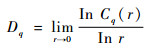 | (15) |
通过多重分形计算信号多重分形谱,如图 4所示,可以看出4种信号的多重分形谱曲线都是上凸的,表明了LPI信号具有多重分形的性质。
 |
| 图 4 LPI雷达信号多重分形谱曲线 Fig. 4 Multi-fractal spectrum curves of LPI radar signal |
| 图选项 |
经过上述一维序列广义维数的计算过程,可得到FMCW、Frank、BPSK和FSK/PSK 4种LIP雷达信号双谱对角切片的广义维数Dq与阶数q的曲线关系,如图 5所示,其中q在本文中取值范围为[-8, 10]。从图中可以看出,在不同的q值下,各信号广义维数曲线的差异较为明显,能够为识别提供依据。
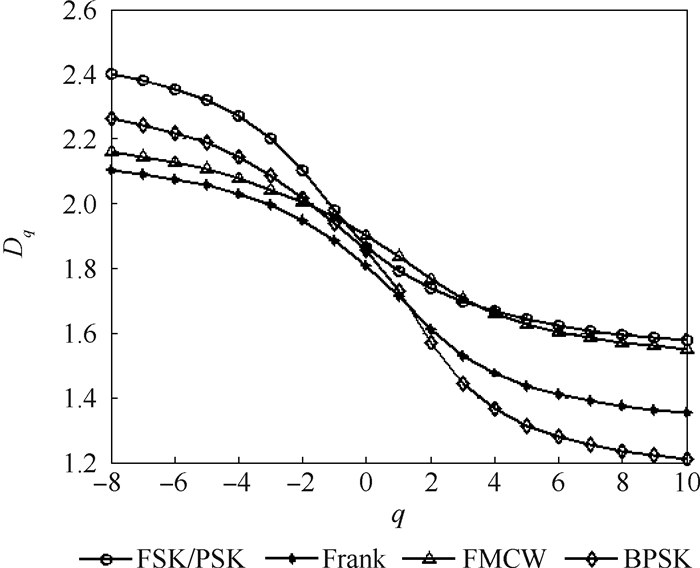 |
| 图 5 LPI雷达信号双谱对角切片的广义维数 Fig. 5 GD of LPI radar signal bispectra diagonal slice |
| 图选项 |
3 基于距离测度的特征值选择 从图 5可以看出,q值不同,信号广义维数的差异程度不同,而差异程度的大小决定着分类器设计的复杂程度以及最终分类识别的有效程度[17]。因此为提高识别的准确率,关键在于需要选择最具有分类特性,即广义维数差异最大所对应的特征q值。本文中对q值的特征评价基于距离测度公式。
假设共有m个q值,每个q值都包含n类信号,希望在每个q值中的n类信号自身具有较强的聚集性而每个q值间具有较大的离散性,因此利用距离测度将聚集性指标与离散性指标表达如下:
1) 聚集性指标
 | (16) |
式中:Cji表示第i个q值下第j类信号的聚集性指标;xl为信号内第l个样本点值;M为信号内样本个数;E(xj)为第j类信号的期望值。
2) 离散性指标
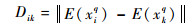 | (17) |
式中:Dik表示第i个q值与第k类个q值期望值间的离散指标;E(xiq)表示第i个q值包含所有数据点的期望。
依据聚集性与离散性指标,可以得到每一个q值的特征评价指标Si:
 | (18) |
当某一q值中信号自身聚集性指标越小,且各q值间的离散性指标越大时,则特征评价指标值越大。
4 仿真分析 4.1 实验设置 实验测试在PC上进行,实验环境为:CPU主频为3.30 GHz,内存为4 GB,Win7、32位操作系统。通过Low Probability of Intercept Toolbox产生实验所使用的LPI雷达信号,包括FMCW信号、Frank信号、BPSK信号和FSK/PSK信号,每种信号的参数设置如下:①FMCW信号:载频为1 kHz,采样频率为1 kHz,调制带宽为300 Hz,周期为100 ms,采用三角波波形。②Frank信号。载频为1 kHz,采样频率为1 kHz,步进频率8个。③BPSK信号。载频为1 kHz,采样频率为3 kHz,编码周期为100 ms,采用7位巴克码。④FSK/PSK信号。采用基于Costas序列跳频,跳频序列为[3 2 6 4 5 1] kHz,采样频率为5 kHz,采用5位巴克码。
由于接收机收到的真实雷达信号不可能是纯净信号,而往往是噪声污染过的。因此,对每种信号在信噪比为0~20 dB(以5 dB为间隔步进)仿真环境下,各随机产生100组作为训练样本,产生200组作为测试样本,共500组训练样本和1 000组测试样本。
4.2 数据预处理 由于实验环境中给出的信噪比变化范围跨度大,噪声对信号双谱对角切片的提取以及广义维数的计算都会造成一定的影响,图 6给出了4种LPI信号在去噪前不同信噪比下的广义维数对比。从图中可以看出,不同信噪比下的广义维数曲线呈发散状态,相对于均值有较大的差异,在不同信噪比条件下有较大的变化,若不经过去噪处理,提取的维数特征受噪声的影响较大,数值很不稳定,这将影响识别效果。
 |
| 图 6 4种LPI雷达信号去噪前广义维数曲线 Fig. 6 GD curves of four LPI radar signals before denoising |
| 图选项 |
因此,本文对含噪LPI信号在接收时经过小波包变换去噪预处理,得到图 7。经过去噪处理后,可以发现不同信噪比下,各广义维数曲线相对去噪前更为集中,对特征提取的效果更为稳定,从而增加了识别算法对噪声的容限。
 |
| 图 7 4种LPI雷达信号去噪后广义维数曲线 Fig. 7 GD curves of four LPI radar signals after denoising |
| 图选项 |
4.3 信号特征提取 文献[11]提取了多重分形谱奇异指数的最大值、最小值、谱宽度和谱值的跨度等13种分形特征参数,可以有效地从不同方面得到区分信号的特征,但是这要求计算量较多,且寻找特征的过程较繁琐,本文就得到的广义维数曲线进行特征提取。
结合第3节中给出的基于距离测度对q值计算特征评价指标S,图 8为在不同信噪比下,通过距离测度计算得到不同q值的特征评价指标。
 |
| 图 8 特征q值的评价指标曲线 Fig. 8 Evaluation index curves of feature q |
| 图选项 |
从图 8中可以看出,不同信噪比下评价指标的变化趋势基本一致,且随着信噪比的减小,评价指标值也逐渐减小,原因在于同类数据点之间聚集性减弱,并且不同q值的数据点相互间距离减小。因此提取到前3个较大的评价指标所对应的q值,如图中出的红色实线所示,将q=-1,1,10对应的广义维数作为三维特征向量。以信噪比10 dB和0 dB为例,得到不同信号在特征空间的分布,如图 9和图 10所示。
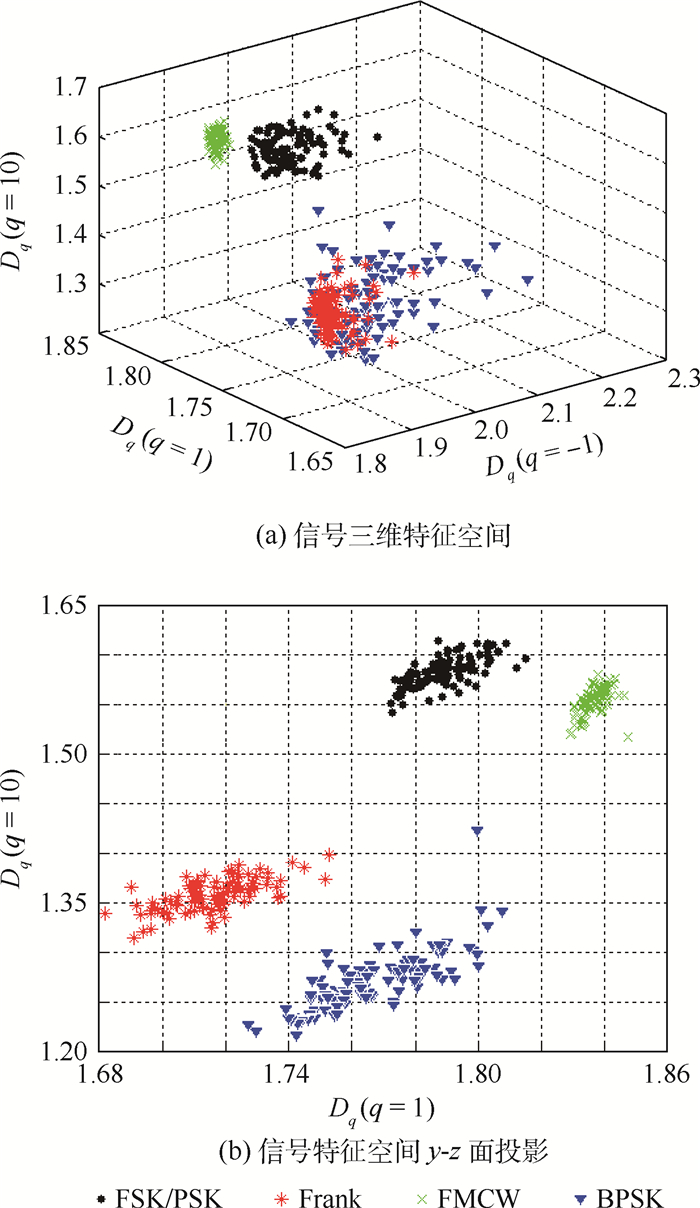 |
| 图 9 LPI雷达信号特征空间分布(信噪比为10 dB) Fig. 9 Space distribution of LPI radar signal feature (SNR 10 dB) |
| 图选项 |
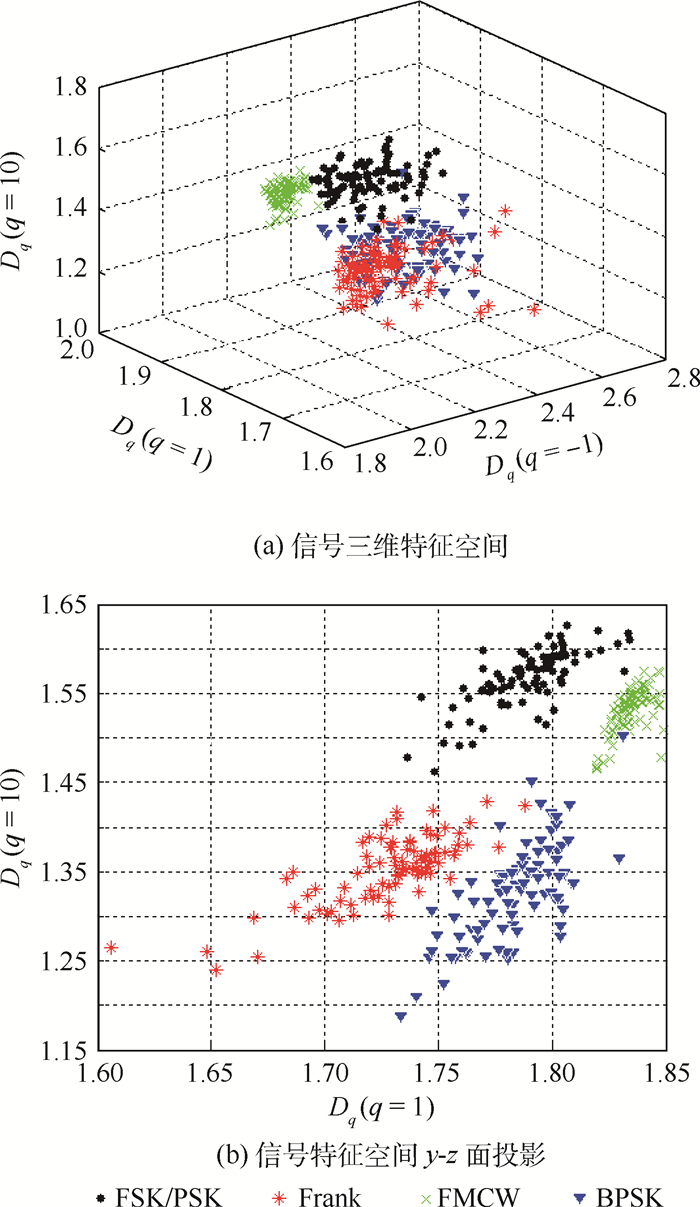 |
| 图 10 LPI雷达信号特征空间分布(信噪比为0 dB) Fig. 10 Space distribution of LPI radar signal feature (SNR 0 dB) |
| 图选项 |
从图 9和图 10可以看出,LPI信号在10 dB噪声条件下所提取的特征空间中,不同信号间的分离度较大,且每种信号之间自身的聚集性较好,分布的差距较为明显;随着信噪比的减小,信号的分离度性能降低,但可以看出在0 dB噪声条件下,但每种信号自身依然具有一定的聚集性,且FMCW信号的聚集性最好。因此可作为识别方法的输入特征。
4.4 信号识别准确率对比 不同调制方式信号的特征非线性分布比较明显,因此在分类器的选择上,使用线性分类器进行识别的效果可能较差,因此本文采用LSSVM对信号进行分类识别。
LSSVM采用最小二乘线性系统作为损失函数,相比于传统支持向量机采用的二次规划方法,在降低运算复杂性的同时保持较高的识别准确率,能够较为有效地解决参数间存在模糊关系的非线性分类问题。本文对LSSVM采用网格搜索与K-fold交叉验证实现对惩罚因子C和核函数宽度γ参数寻优。
图 11(a)为在不同信噪比下,各类LPI信号的识别准确率。从图可以看出,在信噪比为10 dB时,所有信号的识别准确率已经达到100%,且对于FMCW信号在特征空间的聚集度较高,数据点离散程度小,因此相对于其他3种信号能较快达到完全识别。信噪比在0 dB时,所有信号的识别准确率均在85%以上。
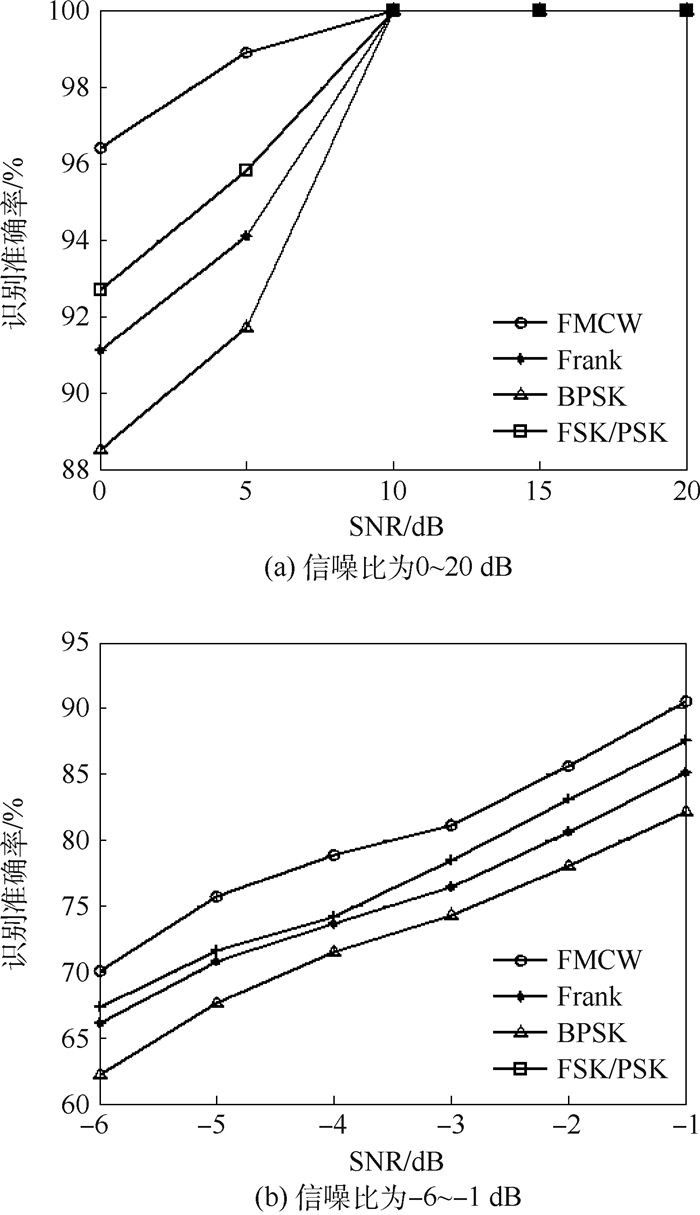 |
| 图 11 LPI雷达信号在不同信噪比下的识别准确率对比 Fig. 11 Comparison of recognition accuracy rate of LPI radar signals under different SNRs |
| 图选项 |
为了验证方法在更低信噪比下对信号的识别能力,重新产生-6~-1 dB高斯白噪声环境下的LPI信号,步进为1 dB,训练和测试样本数量不变,如图 11(b)所示。结果表明。在低信噪比下,FMCW仍然保持比其他3种高的识别准确率,且在-6 dB下,仍有70%的识别准确率。随着信噪比下降,BPSK信号识别准确率下降最快,在-6 dB时下降到65%以下,原因是在特征空间中数据点聚集性下降并与其他信号数据点混合较为严重。
为验证方法的有效性,将本文方法与GD-LSSVM、BDS-LSSVM、BDS-PCA-LSSVM以及文献[6-7]采用的算法进行对比。其中GD-LSSVM表示将原始信号直接经过广义分形变换后,提取区分度较大的3个q值对应的广义维数特征输入到LSSVM中;BDS-LSSVM表示将原始信号经过双谱变换,提取对角切片后输入到LSSVM中;BDS-PCA-LSSVM表示将双谱对角切片经过主成分分析后,提取前3个主要成分输入到LSSVM中。
表 1为在信噪比为0、5、10、15、20 dB时,不同方法识别准确率对比,从表 1可以看出,仅仅提取信号的广义维数进行识别的效果最差,原因在于信号间时域特征较为相似,直接提取到的各类信号广义维数曲线相似程度大,其数据在特征空间中混叠度较大,从而导致识别准确率低;对于信号提取的双谱对角切片,由于各类信号对角切片形状有所差异,其识别准确率大于GD-LSSVM,然而对角切片的维度还是较大,由于BDS-PCA-LSSVM算法通过主成分分析降低了切片维度,且提取到信号的主要特征,使信号间的区分度增大,相比于BDS-LSSVM有效地提高了识别准确率;文献[6]在双谱基础上提取的奇异谱熵,即使在去噪的情况下,依然对噪声较为敏感,特征空间信号的重叠度相对较大,因此识别效果与其他算法相比较差;文献[7]与BDS-LSSVM类似,围线积分与对角切片相比使用了双谱更多的信息,但是两者都提取到了不同信号最具有区别性的特征,所以在识别准确率上文献[7]与BDS-LSSVM相近,然而计算双谱围线积分的时间大于提取对角切片的时间;本文方法结合了对角切片与多重分形维数的特点,在提取到已经具有一定区分度的对角切片的基础上,使用多重分形中的广义维数更进一步描述切片内部特征,提取的特征在特征空间中区分度大,从而能有效地进行分类识别,获得更高的识别准确率。
表 1 不同方法识别准确率对比 Table 1 Accuracy rate of recognition among different methods
| % | ||||||
| 方法 | 识别准确率 | 平均识别准确率 | ||||
| 0 dB | 5 dB | 10 dB | 15 dB | 20 dB | ||
| GD-LSSVM | 78.2 | 84.1 | 88.6 | 93.2 | 98.8 | 88.6 |
| BDS-LSSVM | 82.3 | 88.9 | 93.2 | 96.4 | 100 | 92.1 |
| BDS-PCA-LSSVM | 84.8 | 90.6 | 94.5 | 98.1 | 100 | 93.5 |
| 文献[6] | 80.6 | 85.6 | 91.7 | 96.5 | 99.1 | 90.7 |
| 文献[7] | 84.1 | 89.4 | 94.3 | 96.8 | 100 | 92.9 |
| 本文 | 92.2 | 95.3 | 100 | 100 | 100 | 97.5 |
表选项
5 结论 本文提出将双谱对角切片与广义维数相结合的信号识别方法,能够利用双谱对角切片数据量小但具有信号特征的特点,通过广义维数降低数据维度,将信号切片内部特征通过广义维数曲线描述出来,依据特征评价指标提取其中区分度大的特征q值作为特征向量,使用最小二乘支持向量机进行分类识别。仿真结果验证了方法提取到的特征的优良性能,能够在较低信噪比下取得较高的识别准确率。
参考文献
| [1] | 王文哲, 吴华, 王经商, 等. 基于CEEMDAN的雷达信号脉内细微特征提取法[J].北京航空航天大学学报, 2016, 42(11): 2532–2539. WANG W Z, WU H, WANG J S, et al. Subtle intrapulse feature extraction based on CEEMDAN for radar signal[J].Journal of Beijing University of Aeronautics and Astronautics, 2016, 42(11): 2532–2539.(in Chinese) |
| [2] | LIU Y J, XIAO P, WU H C, et al. LPI radar signal detection based on radial integration of Choi-Williams time-frequency image[J].Journal of Systems Engineering and Electronics, 2015, 26(5): 973–981.DOI:10.1109/JSEE.2015.00106 |
| [3] | 王星, 周一鹏, 周东青, 等. 基于深度置信网络和双谱对角切片的低截获概率雷达信号识别[J].电子与信息学报, 2016, 38(11): 2972–2976. WANG X, ZHOU Y P, ZHOU D Q, et al. Research on low probability of intercept radar signal recognition using deep belief network and bispectra diagonal slice[J].Journal of Electronic & Information Technology, 2016, 38(11): 2972–2976.(in Chinese) |
| [4] | 陈涛, 姚文杨, 瞿孝霏, 等. 雷达辐射源信号双谱估计的物理意义及其辐射源个体识别[J].中南大学学报(自然科学版), 2013, 44(1): 179–187. CHEN T, YAO W Y, ZHAI X F, et al. Bispectrum physical meaning and emitter individual recognition of radar emitter signal[J].Journal of Central South University (Science and Technology), 2013, 44(1): 179–187.(in Chinese) |
| [5] | YOU M L, JIANG T. New method for target identification in a foliage environment using selected bispectra and particle swarm optimistion-based support vector machine[J].IET Signal Processing, 2014, 8(1): 76–84.DOI:10.1049/iet-spr.2012.0389 |
| [6] | 陈韬伟, 金炜东, 李杰. 基于围线积分双谱的雷达辐射源信号个体特征提取[J].计算机工程与应用, 2013, 49(8): 209–212. CHEN T W, JIN W D, LI J. Individual feature extraction from radar emitter signals based on surrounding-line integral bispectrum[J].Computer Engineering and Applications, 2013, 49(8): 209–212.(in Chinese) |
| [7] | 张彦龙, 张登福, 王世强, 等. 一种雷达辐射源双谱二次特征提取方法[J].现代雷达, 2013, 35(3): 28–33. ZHANG Y L, ZHANG D F, WANG S Q, et al. A new scheme for bispectrum cascade feature extraction of intra-pulse modulated radar signals[J].Modern Radar, 2013, 35(3): 28–33.(in Chinese) |
| [8] | 王世强, 张登福, 毕笃彦, 等. 双谱二次特征在雷达信号识别中的应用[J].西安电子科技大学学报(自然科学版), 2012, 39(2): 127–132. WANG S Q, ZHANG D F, BI D Y, et al. Research on recognizing the radar signal using the bispectrum cascade feature[J].Journal of Xidian University (Natural Science), 2012, 39(2): 127–132.(in Chinese) |
| [9] | 丁凯, 方向, 张卫平, 等. 基于声信号多重分形和支持向量机的目标识别研究[J].兵工学报, 2012, 33(12): 1521–1526. DING K, FANG X, ZHANG W P, et al. Target identification of acoustic signals based on multifractal analysis and support vector machine[J].Acta Armamentarii, 2012, 33(12): 1521–1526.(in Chinese) |
| [10] | HARTMANN A, MUKLI P, NAGY Z, et al. Real-time fractal signal processing in the time domain[J].Physica A:Statistical Mechanics and Its Applications, 2013, 392(1): 89–102.DOI:10.1016/j.physa.2012.08.002 |
| [11] | 陈红, 蔡晓霞, 徐云, 等. 基于多重分形特征的通信调制方式识别研究[J].电子与信息学报, 2016, 33(4): 863–869. CHEN H, CAI X X, XU Y, et al. Communication modulation recognition based on multi-fractal dimension characteristics[J].Journal of Electronic & Information Technology, 2016, 33(4): 863–869.(in Chinese) |
| [12] | CHAKRABORTY B, HARIS K, LATHA G, et al. Multifractal approach for seafloor characterization[J].IEEE Geoscience and Remote Sensing Letters, 2014, 11(1): 54–58.DOI:10.1109/LGRS.2013.2245856 |
| [13] | 黄家圣. 调频信号指纹特征研究[D]. 北京: 北京邮电大学, 2011: 12-13. HUANG J S. Study on fingerprint features of frequency hopping spread spectrum signals[D]. Beijing: Beijing University of Posts and Telecommunications, 2011: 12-13(in Chinese).http://cdmd.cnki.com.cn/Article/CDMD-10013-1011120377.htm |
| [14] | 何永亮, 陈西豪, 许华, 等. 利用信号围线积分双谱分形特征实现电台识别[J].电讯技术, 2014, 54(10): 1354–1359. HE Y L, CHEN X H, XU H, et al. Individual transmitter identification based on fractal feature of surrounding-line integral bispectrum[J].Telecommunication Engineering, 2014, 54(10): 1354–1359.DOI:10.3969/j.issn.1001-893x.2014.10.008(in Chinese) |
| [15] | 梁华东, 韩江洪. 采用双谱多类小波包特征的雷达信号聚类分选[J].光子学报, 2014, 43(3): 152–159. LIANG H D, HAN J H. Clustering and sorting radar signal based on multi-wavelet packets characteristics of bispectrum[J].Acta Photonica Sinica, 2014, 43(3): 152–159.(in Chinese) |
| [16] | 肖乐群, 张玉灵, 赵拥军. 基于对角积分双谱的雷达辐射源信号识别[J].信息工程大学学报, 2012, 13(1): 95–99. XIA L Q, ZHANG Y L, ZHAO Y J. Radar emitter signal recognition based on diagonally integral bispectrum[J].Journal of Information Engineering University, 2012, 13(1): 95–99.(in Chinese) |
| [17] | 邓延丽, 金炜东, 李家会, 等. 基于聚集离散性与可分性的雷达信号特征评价[J].计算机应用, 2013, 33(7): 1946–1949. DENG Y L, JIN W D, LI J H, et al. Feature evaluation of radar signal based on aggregation, discreteness and divisibility[J].Journal of Computer Application, 2013, 33(7): 1946–1949.(in Chinese) |
