碰撞概率是目前国内外广泛使用的判断2个空间目标发生碰撞的可能性大小的重要判据。当前,国内外对碰撞概率方法的理论研究已经相对成熟。文献[1]采用Monte Carlo方法得到了碰撞概率的计算结果;Foster和Estes[2]、Patera[3]和Alfano[4]提出了不同的碰撞概率数值积分模型;Chan[5-6]提出了一种将积分式进行近似的解析方法。
Monte Carlo方法以及Foster和Estes[2]提出的数值方法可以得到精度较高的碰撞概率结果但是计算速度较慢。Chan[5-6]解析方法计算速度快,但精度劣于数值方法。解析方法中比较经典的为Chan方法,根据文献[7]中对该方法的精度分析,在概率密度函数(Probability Density Function,PDF)接近圆分布时,能够较好地近似碰撞概率的真实值。但在PDF分布椭圆的长短轴之比较大时,误差较大,并且由于该方法对积分域进行了近似,导致近似积分模型与原积分模型产生了无法准确衡量的偏差。
针对上述方法中的不足,本文在参考文献[8]的基础上,基于拉普拉斯变换的相关理论,推导了碰撞概率的幂级数表达式;研究了幂级数表达式的截断误差计算方法;讨论了在不同精度需求下幂级数项数的取值;通过对2009年美俄卫星碰撞事件的仿真计算,将基于拉普拉斯变换方法的碰撞概率计算结果与Chan方法、Monte Carlo方法的计算结果进行对比,验证了基于拉普拉斯变换方法在计算精度上的优势。
1 碰撞概率计算的基本方法 1.1 碰撞概率计算假设 碰撞概率的计算不仅涉及到接近时刻(Time of Closet Approach,TCA)和接近距离(Miss Distance,MD),还涉及到轨道的误差协方差信息。由于2个空间目标在碰撞时所受的力比较复杂,误差数据会根据目标运动状态的改变发生变化,因此,为了简化碰撞概率的计算过程,得到较准确的碰撞概率值,本文做出以下假设[9-11]:
1) 由于2个目标的相遇时间非常短,可将相遇期间内2个目标的相对运动视为速度恒定的线性运动。
2) 在碰撞时,目标的相对速度非常大,并且碰撞时间很短,因此,可以忽略2个目标速度的不确定性。
3) 2个目标的位置误差互不关联。
4) 在2个目标间的相对运动过程中,相遇时间非常短,因此认为误差椭球在相遇期间内保持不变。
5) 2个空间目标均等效为半径已知的球体。
6) 由于2个目标的误差都是随机的,可以认为2个目标的位置误差都服从三维高斯分布。
当2个目标间的距离小于其等效半径之和时,被判定为发生碰撞。
1.2 相遇坐标系与位置误差的投影
1.2.1 相遇坐标系 令在TCA处,与2个目标的相对速度矢量垂直并且经过相对距离矢量的平面为相遇平面。在相遇平面内建立对应的相遇坐标系,即可消去速度方向的误差并且进行碰撞概率计算。相遇坐标系以主目标O1为坐标原点,xe轴指向从目标O2在相遇平面内的投影点,ze轴指向2个目标间相对速度的方向,ye轴在相遇平面内垂直于xe轴, 相遇坐标系如图 1所示。
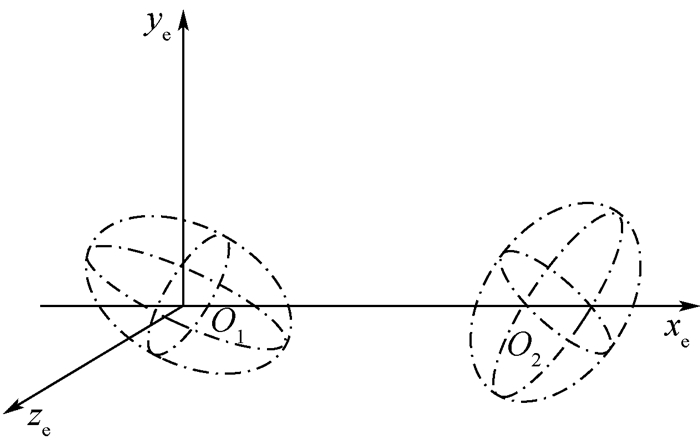 |
| 图 1 相遇坐标系示意图 Fig. 1 Schematic diagram of encounter coordinate system |
| 图选项 |
3个轴的单位矢量可表示为
 | (1) |
式中:ρTCA和vrel分别为TCA处目标间的相对距离矢量和相对速度矢量。
1.2.2 位置误差的投影 通过误差分析方法即可得到2个空间目标的误差协方差矩阵。将2个目标的误差椭球、相对运动状态矢量分别投影到相遇平面内,由于2个目标的随机位置矢量相互独立且满足三维高斯分布,2个目标在相遇平面内的位置矢量满足三维高斯分布,相对位置矢量也是满足高斯分布的随机矢量。因此,在接近时刻处,令2个空间目标在相遇平面内的位置矢量分别为re1和re2,则相遇平面内的目标间相对位置矢量rerel的均值为
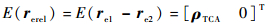 | (2) |
目标间相对位置矢量的误差方差矩阵为
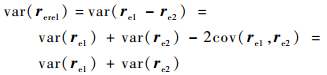 | (3) |
通过式(2)和式(3),即可将2个目标的位置误差椭球投影到相遇平面内并形成联合误差椭圆域。若将2个目标看作是半径分别为R1和R2的均匀球体,则可以根据2个目标的半径大小形成联合球体,将联合球体投影到相遇平面内形成联合圆域,圆域的有效半径为R=R1+R2。图 2为相遇坐标系内的联合圆域和联合误差椭圆域示意图。
 |
| 图 2 联合圆域和联合误差椭圆域示意图 Fig. 2 Schematic diagram of combined disk and combined error ellipse |
| 图选项 |
1.3 碰撞概率计算的简化 在定义了相遇坐标系后,碰撞概率的计算就被简化为一个对PDF的二重积分过程,PDF表示为
 | (4) |
式中:μx和μy分别为联合误差椭圆沿x和y方向的期望值;σx和σy分别为联合误差椭圆沿x和y方向的标准差。
碰撞概率Pc的计算式为
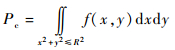 | (5) |
2 基于拉普拉斯变换的碰撞概率计算模型 2.1 计算流程 基于拉普拉斯变换的碰撞概率计算主要有3个步骤:
1) 将由式(5)表示的二维PDF积分公式重写为g(λ),其中λ=R2,函数g(λ)的拉普拉斯变换Lg在闭合域内进行。将Lg进行泰勒展开,然后使用拉普拉斯逆变换将原始的积分函数写成幂级数的形式。
2) 计算得到幂级数的相关系数。
3) 得到碰撞概率计算结果。
从数值计算的角度考虑,直接计算g(λ)值是比较困难的。即使g(λ)的级数展开式是收敛的,但是由于每一项的大小接近、符号相反,会造成在一定精度下,级数的每一项加起来的和为0,结果为无效数字。在该情况下,对于较大数值的λ而言,级数展开是没有意义的[12]。因此,在运算前应设置一个函数ψ,使用ψ·g替换g,以避免幂级数包含无用项,并且防止经过展开后的幂级数项在相加后出现高消去现象。
2.2 拉普拉斯变换与幂级数表达式
2.2.1 拉普拉斯变换 在进行拉普拉斯变换之前将碰撞概率改写为Pc=g(R2)的形式,函数g:

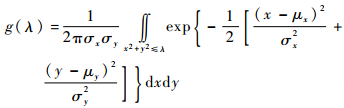 | (6) |
文献[13]阐述了选择ψ的方法,从拉普拉斯变换的角度考虑,本文使用的函数ψ的形式为ψ=epλ,其中p为待定因子。
2.1节因为把原二重积分公式重写为了函数g(λ),所以若要求解原积分公式的拉普拉斯变换,首先需求得函数g(λ)的拉普拉斯变换。由拉普拉斯变换定理可得函数g(λ)的拉普拉斯变换为
 | (7) |
式中:s为复数变量。
根据富比尼定理[14]:
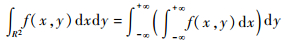 | (8) |
以及当f(x, y)=a(x)b(y)时有
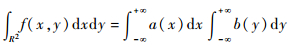 | (9) |
可得Lg(s)的最终表达式为
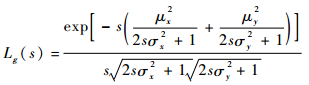 | (10) |
定义函数
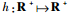
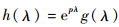 | (11) |
式中:p∈R+。则h的拉普拉斯变换Lh可表示为
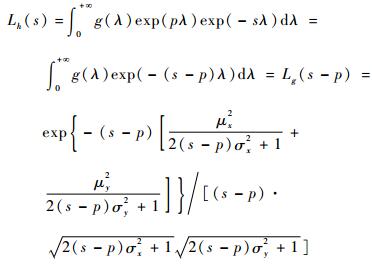 | (12) |
式中:|s|>p,将式(12)转化为
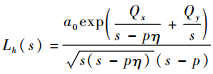 | (13) |
式中:η、Qx、Qy、a0各项被定义为
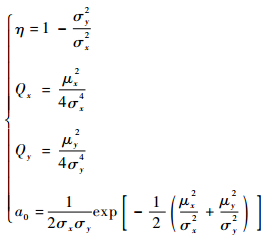 | (14) |
为了得到积分公式的幂级数表达式,可将Lh(s)进行泰勒展开,然后对该泰勒展开式的每一项进行拉普拉斯逆变换,再通过一系列计算得到积分公式的幂级数表达式。
2.2.2 幂级数表达式 令Lh(s-1)的值定义为
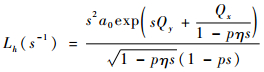 | (15) |
定义Hh(s)=s-2Lh(s-1),则Hh(s)的导数为
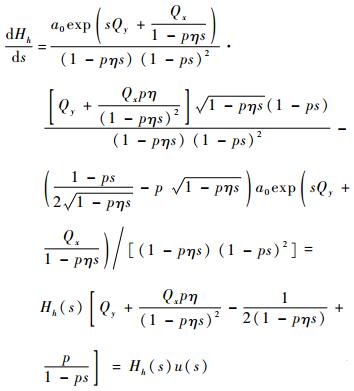 | (16) |
由Hh(0)=a0以及式(16)可知,Hh(s)在复平面内是复可微的,根据幂级数的定义[14],Hh(s)可展开为幂级数的形式。幂级数的求解复杂,因此使用了Maple数学工具(世界上最为通用的数学工具之一,如MATLAB、Mathematica等,可在www.maplesoft.com下载)对其进行系数的求值。根据Hh(s)=s-2Lh(s-1),可知Lh(s)的幂级数形式为
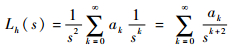 | (17) |
式中:ak为系数。将式(17)中的每一项进行拉普拉斯逆变换,即可得到积分公式的幂级数形式。根据有理函数拉普拉斯变换与逆变换列表中的
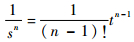 | (18) |
式中:n=0, 1, …。碰撞概率积分公式的幂级数形式可表示为
 | (19) |
式中:
 | (20) |
根据文献[13]中级数展开的定义以及文献[8],函数ψ中的因子p可表示为
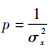 | (21) |
3 截断误差与幂级数项数的确定 3.1 截断误差 假设取幂级数的前n项和作为碰撞概率的值,那么就会存在截断误差。令幂级数前n项的和表示为P′c,则截断误差Sn为
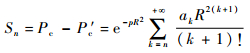 | (22) |
从式(22)可看出,截断误差在n以及R确定的情况下只与ak有关。假设有2个变量ak以及
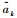
 | (23) |
通过计算可以得到以下关系:
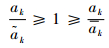 | (24) |
根据式(20)和式(24)可得ak、
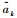
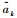
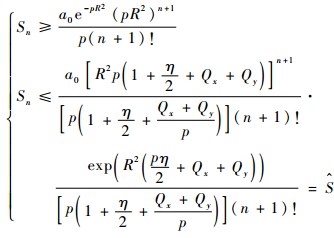 | (25) |
3.2 幂级数项数的确定 国际上通用的规避机动概率黄色门限值为10-5、红色门限值为10-4[15]。在计算中,可以将碰撞概率的门限值设为Dd,为了保证碰撞概率的计算精度至少保持在
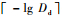

将截断误差
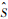
 | (26) |
由于斯特林公式(Stirling’s Approximation)对n!的定义为
 | (27) |
则
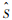
 | (28) |
令
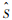
 | (29) |
则可得到如下关系式:
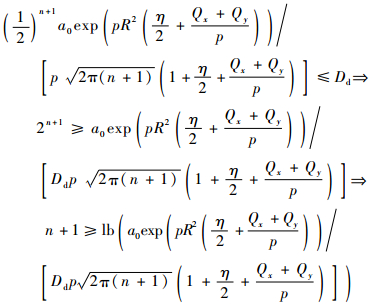 | (30) |
令n+1=n1,由于n1≥1,则式(30)中的最后一个不等式可写为
 | (31) |
式中:A=η/2+(Qx+Qy)/p。通过计算,幂级数项数n的表达式为
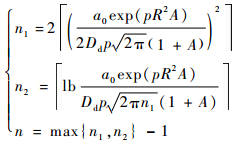 | (32) |
若将Dd的值取为10-20~100,则n的计算结果如图 3所示。
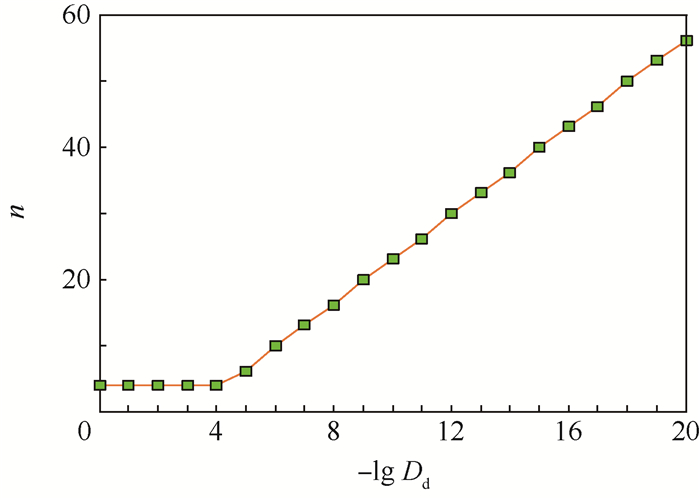 |
| 图 3 幂级数项数随概率门限值的变化 Fig. 3 Variation of number of terms of power series with probability threshold |
| 图选项 |
若将2个目标的联合有效半径R的值取设为5、10、15、50、100、200、500和1000 m,则n在不同联合有效半径以及不同概率门限值下的计算结果如图 4所示。
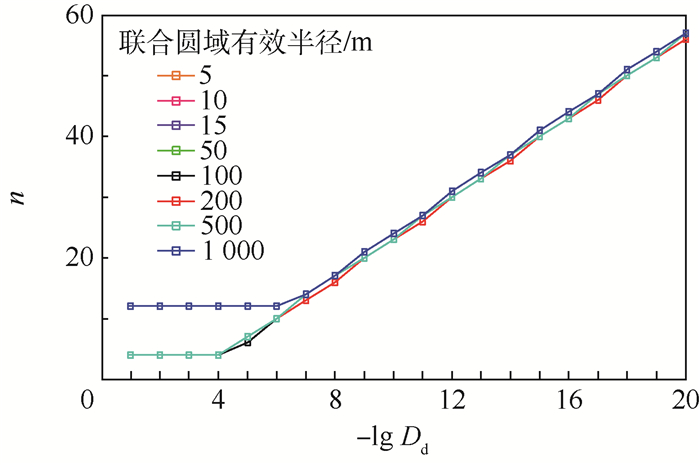 |
| 图 4 幂级数项数随概率门限值以及联合圆域有效半径的变化 Fig. 4 Variation of number of terms of power series with probability threshold and radius of combined disk |
| 图选项 |
从图 3和图 4结果可以看出,使用基于拉普拉斯变换的碰撞概率方法可以根据所需门限值(也作为计算精度的需求)的不同,得到不同的幂级数项数。从图 4可知,当R在1 000 m以内、计算精度需求为
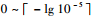
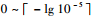
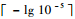
4 碰撞实例仿真验证 本文以2009年2月10日,美俄卫星发生的碰撞实例作为仿真算例。其中,美国卫星为铱星公司的Iridium-33(ID:24946),俄罗斯失效卫星为Cosmos-2251(ID:22675)。通过接近分析得到,TCA[5]为2009年2月10日16:55:59.8 094 031,MD[5]为0.578 479 931 6 km。美俄卫星在TCA的运动状态如表 1和表 2所示。
表 1 主、从目标的位置参数 Table 1 Position parameters of primary and secondary object
| km/s | |||
| 目标 | x | y | z |
| 主目标 | -1 457.353 760 | 1 589.546 912 | 6 814.195 621 |
| 从目标 | -1 457.572 590 | 1 589.024 470 | 6 814.313 123 |
表选项
表 2 主、从目标的速度参数 Table 2 Velocity parameters of primary and secondary objectkm/s
| km/s | |||
| 目标 | vx | vy | vz |
| 主目标 | -7.001 700 | -2.439 510 | -0.926 295 |
| 从目标 | 3.578 697 | -6.172 823 | 2.200 328 |
表选项
4.1 不同误差椭球分布下的碰撞概率变化 令2个空间目标的半径都为5 m,假设2个目标的位置误差椭球大小相等,误差椭球沿星基坐标系RSW的坐标轴R、S、W方向的比值σR:σS:σW不同时,Chan方法与基于拉普拉斯变换方法计算出的概率随σS变化的情况如图 5所示。
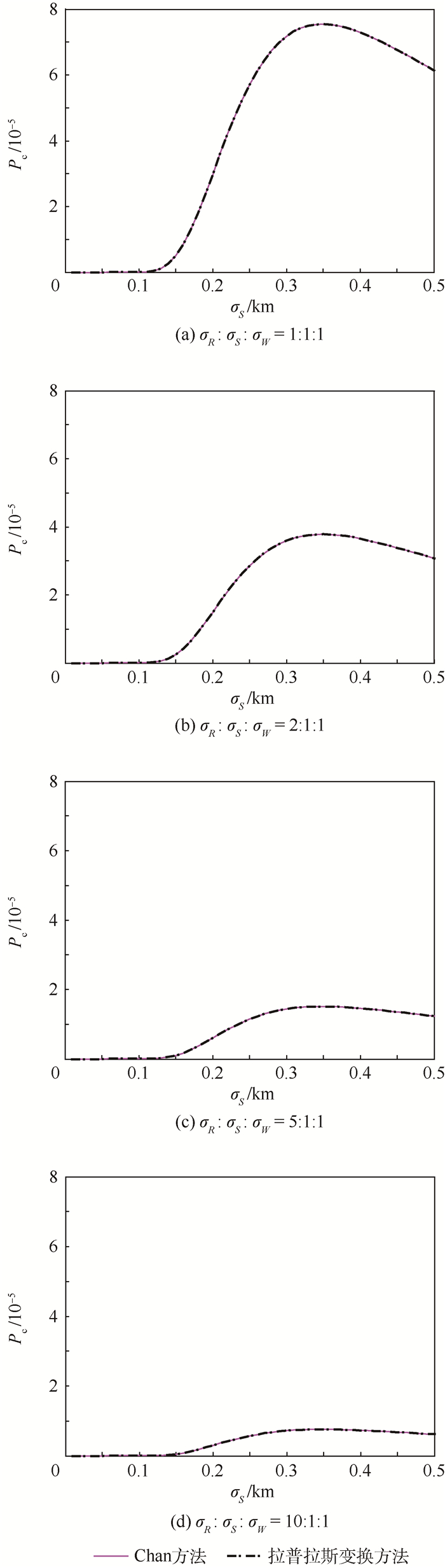 |
| 图 5 不同球形分布下碰撞概率的变化趋势 Fig. 5 Change trend of collision probability under different spherical distribution |
| 图选项 |
从图 5可以看出,误差值对碰撞概率的计算结果影响较大。使用基于拉普拉斯变换方法的计算结果曲线与Chan方法的计算结果曲线基本重合,初步证明了基于拉普拉斯变换的碰撞概率计算方法是正确的并且符合初步的碰撞预警的精度需求。
4.2 不同方法的碰撞概率计算结果比较 通过误差分析,美俄卫星R、S、W方向的位置误差标准差如表 3所示。
表 3 主、从目标在RSW坐标系下的位置误差标准差 Table 3 Standard deviation of position error of primary and secondary object in RSW coordinate system
| 目标 | σR/km | σS/km | σW/km |
| 主目标 | 0.231 207 | 0.206 188 5 | 0.071 975 |
| 从目标 | 0.036 323 4 | 0.410 206 9 | 0.034 114 |
表选项
令2个目标的半径都为5 m,通过计算可得,在TCA处,2个目标在相遇平面内的3σ联合误差椭圆和碰撞圆域,如图 6所示。
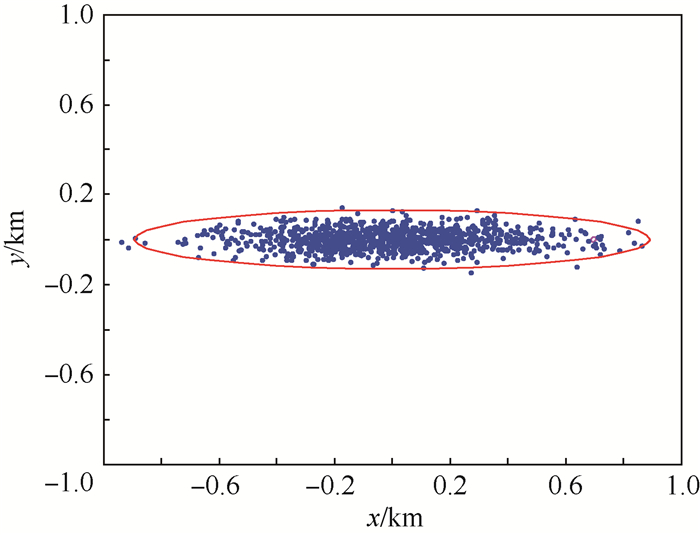 |
| 图 6 3σ联合误差椭圆和碰撞圆域 Fig. 6 3σ combined error ellipse and collision disk |
| 图选项 |
对于Chan方法,取无穷级数的前10项以近似PDF积分式的值Pk,计算过程中,碰撞概率无穷级数形式的前10项结果如表 4所示。
表 4 Chan方法下Pk的计算结果 Table 4 Calculation results of Pk by Chan method
| k | Pk/10-4 |
| 1 | 1.817 439 461 411 834 |
| 2 | 1.828 466 082 330 511 |
| 3 | 1.828 488 389 607 843 |
| 4 | 1.828 488 412 175 072 |
| 5 | 1.828 488 412 188 786 |
| 6 | 1.828 488 412 188 801 |
| 7 | 1.828 488 412 188 806 |
| 8 | 1.828 488 412 188 808 |
| 9 | 1.828 488 412 188 809 |
| 10 | 1.828 488 412 188 809 |
表选项
当使用基于拉普拉斯变换的方法对2个目标进行碰撞概率计算时,将幂级数的项数取值为k=1, 2, …, 10,则得到的碰撞概率值Pk和截断误差Sk如表 5所示。
表 5 基于拉普拉斯变换方法下Pk和Sk的计算结果 Table 5 Calculation results of Pk and Sk based on Laplace transformation method
| k | Pk/10-4 | Sk |
| 1 | 1.772 573 705 611 427 | 8.291 431 627 403 867×10-7 |
| 2 | 1.815 996 175 328 694 | 2.031 139 453 405 921×10-8 |
| 3 | 1.817 048 378 909 693 | 3.317 101 046 456 115×10-10 |
| 4 | 1.817 052 720 190 974 | 4.062 926 108 033 688×10-12 |
| 5 | 1.817 053 331 566 511 | 3.981 155 431 361 421×10-14 |
| 6 | 1.817 053 372 236 674 | 3.250 858 729 893 972×10-16 |
| 7 | 1.817 053 375 065 217 | 2.275 308 404 578 399×10-18 |
| 8 | 1.817 053 375 264 924 | 1.393 447 138 227 291×10-20 |
| 9 | 1.817 053 375 279 203 | 7.585 569 687 077 649×10-23 |
| 10 | 1.817 053 375 280 234 | 3.716 451 044 970 535×10-25 |
表选项
当无穷级数和幂级数项数分别取10时,Monte Carlo方法、Chan方法以及使用基于拉普拉斯变换方法的碰撞概率计算结果如表 6所示。
表 6 Monte Carlo方法、Chan方法、基于拉普拉斯变换方法的碰撞概率计算结果 Table 6 Collision probability calculation results of Monte Carlo, Chan and based on Laplace transformation methods
| 方法 | 碰撞概率 |
| Monte Carlo | 0.000 181 848 841 218 880 |
| Chan | 0.000 182 848 841 218 880 9 |
| 拉普拉斯变换 | 0.000 181 705 337 528 023 4 |
表选项
从表 6可以看出,基于拉普拉斯变换方法与Chan方法、Monte Carlo方法所计算得到的Pc都大于红色门限值,说明在该接近点发生碰撞的可能性非常大,进一步证明了基于拉普拉斯变换的碰撞概率计算方法是正确有效的。表 7列出了Chan方法、基于拉普拉斯变换方法所计算的碰撞概率与Monte Carlo方法所计算的碰撞概率的相对误差。
表 7 Chan方法、基于拉普拉斯变换方法与Monte Carlo方法的碰撞概率相对误差 Table 7 Relative error of collision probability between Monte Carlo method and Chan, based on Laplace transformation method
| 方法 | 相对误差/% |
| Chan | 0.549 9 |
| 拉普拉斯变换 | 0.078 9 |
表选项
基于拉普拉斯变换方法的碰撞概率与Chan方法、Monte Carlo方法的相对误差分别为0.625 4%、0.078 9%,而Chan方法与Monte Carlo方法的相对误差为0.549 9%。结果表明,基于拉普拉斯变换的碰撞概率计算精度不仅能够满足风险评估的要求,而且在项数取10时比Chan方法的计算精度高。
同时,随着幂级数项数n的取值增大,基于拉普拉斯变换方法计算的碰撞概率的截断误差随之减小。当n的取值小于5时,每一个项数所对应的碰撞概率结果相差较大,而在n大于5时,其结果基本没有变化。因此,对于实例1,幂级数项数n取5,即可满足初步的碰撞预警要求。需要注意的是,由于2种方法的模型不同,当Chan方法和拉普拉斯变换方法的级数同时取首项时,Chan方法的计算结果精度要比拉普拉斯方法高,但却不满足碰撞风险评估的要求,所以为了尽可能的提高计算精度,项数n的取值应选择较大的值。
4.3 计算精度需求对幂级数项数的影响分析 为了分析计算精度需求对幂级数项数n及碰撞概率的影响,现将
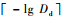
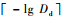
表 8 精确位数-lg Dd不同时所需的幂级数项数、碰撞概率和截断误差 Table 8 Number of terms of power series, collision probability and truncation error with different exact digits -lg Dd
| -lg Dd | n | Pc | Sn |
| 4 | 3 | 0.000 181 704 837 890 969 3 | 9.122 027 877 754 318×10-10 |
| 5 | 6 | 0.000 181 705 337 223 667 4 | 5.108 492 289 833 384×10-16 |
| 6 | 9 | 0.000 181 705 337 527 920 3 | 8.344 126 655 785 414×10-23 |
表选项
从表 8可以看出,随着计算精度要求不断提高,幂级数项数n的值不断增大,截断误差不断减小,碰撞概率值也更加精确。可以预见,只需将幂级数项数设置为较大的值,碰撞概率的计算结果将会足够精确,但是为了提高计算速度,可根据黄色门限值大小来确定精度需求,从而计算幂级数项数的值。
4.4 基于拉普拉斯变换方法与Chan方法的计算时间比较 Monte Carlo方法是数值方法之一,由于数值方法没有简化,所以精度高,但是计算速度慢。因此本节只对解析方法中的Chan方法和拉普拉斯变换方法的计算时间进行实验比较,以验证拉普拉斯变换方法在计算速度上的优势。
依旧以美俄卫星碰撞实例为算例,以表 1~表 3中的运动状态与误差数据作为2个目标的参数数据,在实验环境相同的条件下,当幂级数项数n取不同的值时,Chan方法和拉普拉斯变换方法所花费的计算时间比较结果如图 7所示。
 |
| 图 7 Chan方法和拉普拉斯变换方法的计算时间结果 Fig. 7 Results of computation time of Chan and Laplace transformation methods |
| 图选项 |
通过计算,充分证明了基于拉普拉斯的变换方法与Chan方法相比,在速度上有所提高。基于拉普拉斯变换的方法是对原积分模型直接进行拉普拉斯变换和泰勒展开,从而获得幂级数表达式的碰撞概率计算方法,虽然没有对积分域进行近似,但却是一种解析方法,因此兼具了精度和速度方面的优势。
5 结论 基于拉普拉斯变换的碰撞概率计算方法是一种解析方法,该方法避免了对二维积分近似过程中的误差,因此,兼具计算精度和速度上的优势。
1) 基于拉普拉斯变换的碰撞概率计算方法将概率密度函数的积分公式转换到复平面内进行计算,再通过拉普拉斯逆变换并使用Maple数学工具将原积分公式表示为幂级数形式,这使得原本在实数域中计算较复杂的问题变得简单和易理解。
2) 通过对幂级数项数的确定,可以在保证计算精度的条件下,提高碰撞概率的计算速度。
3) 针对美俄卫星碰撞实例,将基于拉普拉斯变换方法的碰撞概率计算结果与Chan方法和高精度的基于Monte Carlo数值方法的概率计算结果进行比较。结果表明,基于拉普拉斯变换的碰撞概率计算方法与Chan方法相比,能够避免积分域的近似,在计算精度上有所提高,能够满足碰撞预警的精度要求。
参考文献
| [1] | ALFANO S. Satellite conjunction Monte Carlo analysis[J].Advances in the Astronautical Sciences, 2009, 134: 2007–2024. |
| [2] | FOSTER J L, ESTES H S. A parametric analysis of orbital debris collision probability and maneuver rate for space vehicles: NASA/JSC-25898[R]. Houston: NASA Johnson Space Flight Center, 1992. |
| [3] | PATERA R P. General method for calculating satellite collision probability[J].Journal of Guidance, Control, and Dynamics, 2001, 24(4): 716–722.DOI:10.2514/2.4771 |
| [4] | ALFANO S. Satellite collision probability enhancements[J].Journal of Guidance, Control, and Dynamics, 2006, 29(3): 588–592.DOI:10.2514/1.15523 |
| [5] | CHAN F K. Collision probability analysis for earth orbiting satellites[J].Advances in the Astronautically Sciences, 1997(96): 1033–1048. |
| [6] | CHAN F K. Spacecraft collision probability[M].El Segundo, CA: Aerospace Press, 2008. |
| [7] | 陈磊, 韩蕾, 白显宗, 等. 空间目标轨道力学与误差分析[M].长沙: 国防科技大学出版社, 2010: 178-180. CHEN L, HAN L, BAI X Z, et al. Orbit target orbit mechanics and error analysis[M].Changsha: National University of Defense Technology Press, 2010: 178-180.(in Chinese) |
| [8] | SERRA R, ARZELIER D, JOLDES M, et al. Fast and accurate computation of orbital collision probability for short-term encounters[J].Journal of Guidance, Control, and Dynamics, 2016, 39(5): 1–13. |
| [9] | ALFRIEND K T., AKELLAM R, FRISBEE J, et al. Probability of collision error analysis[J].Space Debris, 1999, 1(1): 21–35.DOI:10.1023/A:1010056509803 |
| [10] | AKELLA M R, ALFRIEND K T. Probability of collision between space objects[J].Journal of Guidance, Control, and Dynamics, 2000, 23(5): 769–772.DOI:10.2514/2.4611 |
| [11] | ALFANO S. A numerical implementation of spherical object collision probability[J].Journal of the Astronautical Sciences, 2005, 53(1): 103–109. |
| [12] | CHEVILLARD S, MEZZAROBBA M. Multiple-precision evaluation of the Airy Ai function with reduced cancellation[C]//21st IEEE Symposium on Computer Arithmetic (ARITH). Piscataway, NJ: IEEE Press, 2013: 175-182. |
| [13] | GAWRONSKI W, MVLLER J, REINHARD M. Reduced cancellation in the evaluation of entire functions and applications to the error function[J].SIAM Journal on Numerical Analysis, 2007, 45(6): 2564–2576.DOI:10.1137/060669589 |
| [14] | HACKBUSCH W, SCHWARZ H R. Teubner-taschenbuch der mathematik[M].Berlin: Springer, 2013: 595. |
| [15] | 李甲龙, 熊建宁, 许晓丽, 等. 碰撞风险评估标准适用性分析[J].天文学报, 2014, 55(5): 404–414. LI J L, XIONG J N, XU X L, et al. A research on adaptability of collision criteria[J].Acta Astronomica Sinica, 2014, 55(5): 404–414.(in Chinese) |
